LMI Pole Regions for a Robust Discrete-Time Pole Placement Controller Design
Abstract
1. Introduction
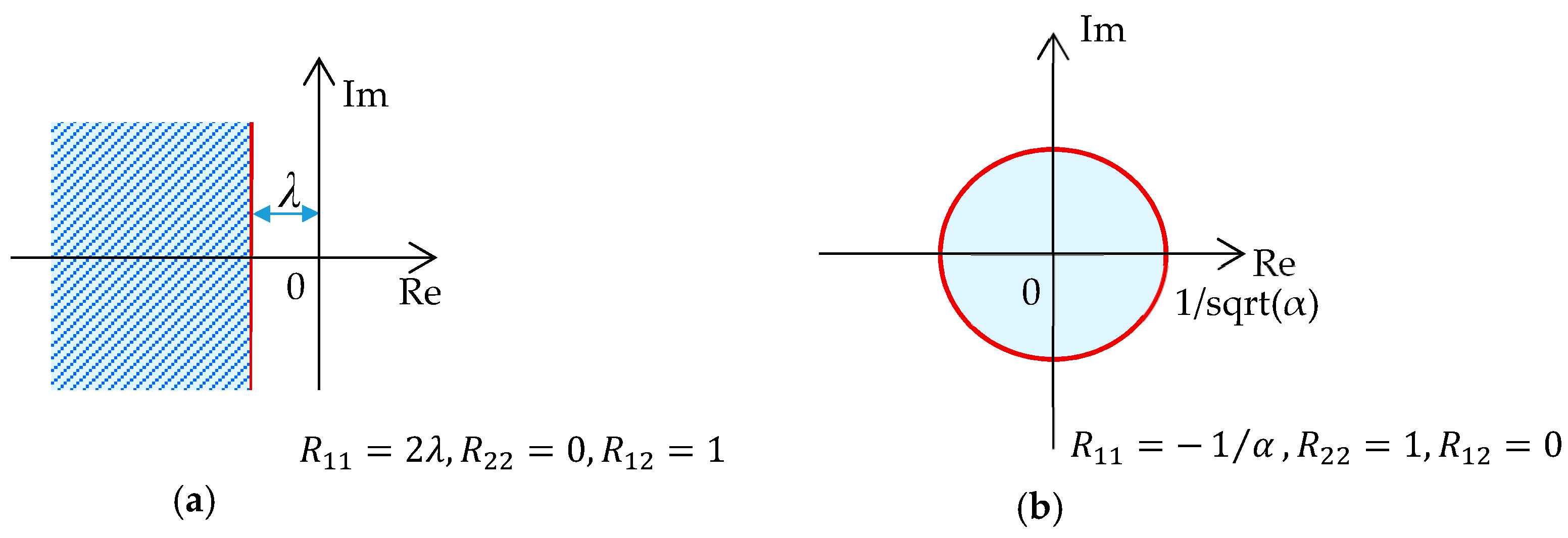
2. Preliminaries and Discrete-Time Pole Region Problem Formulation
2.1. DR Regions for a Robust Pole Placement
- regions are symmetric with respect to the real axis of complex plane;
- Matrix is —stable if and only if all its eigenvalues lie in the corresponding region;
- Intersection of regions is again region (due to convexity).
2.2. Robust Pole Placement for the Defined DR Region via State Feedback
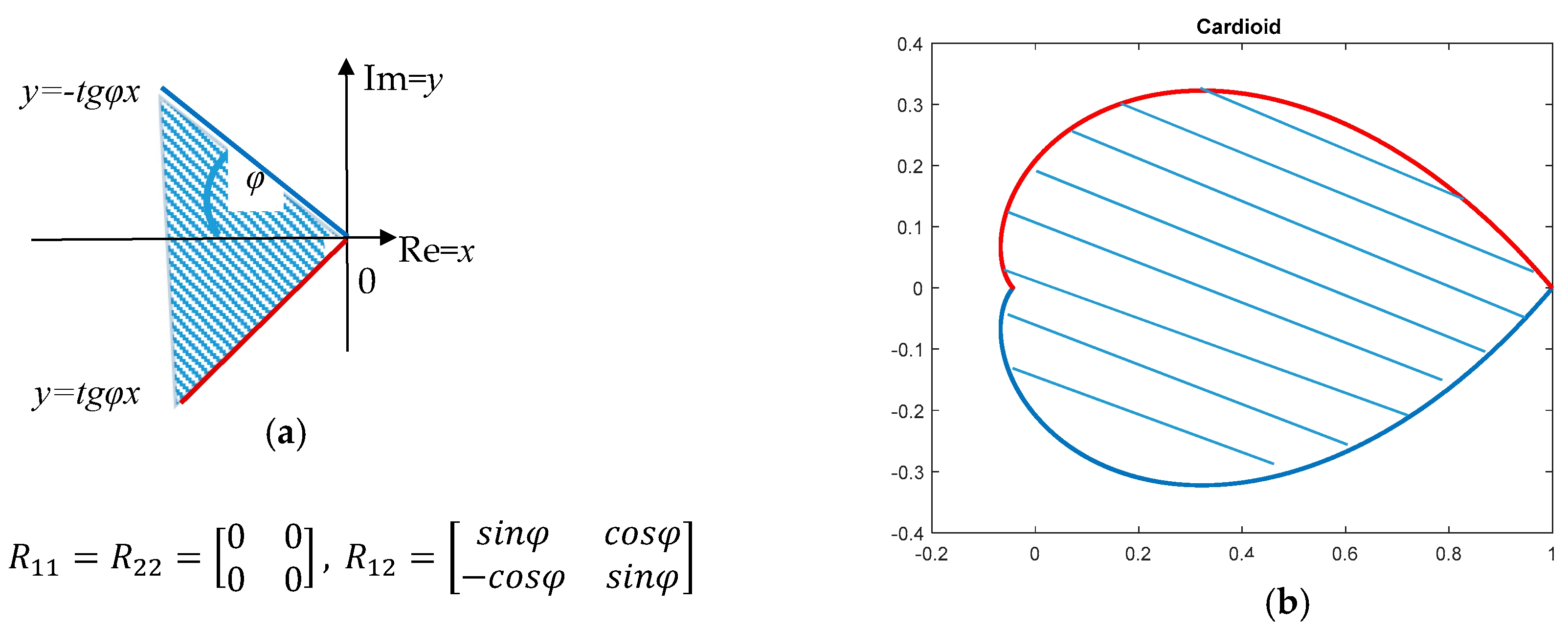
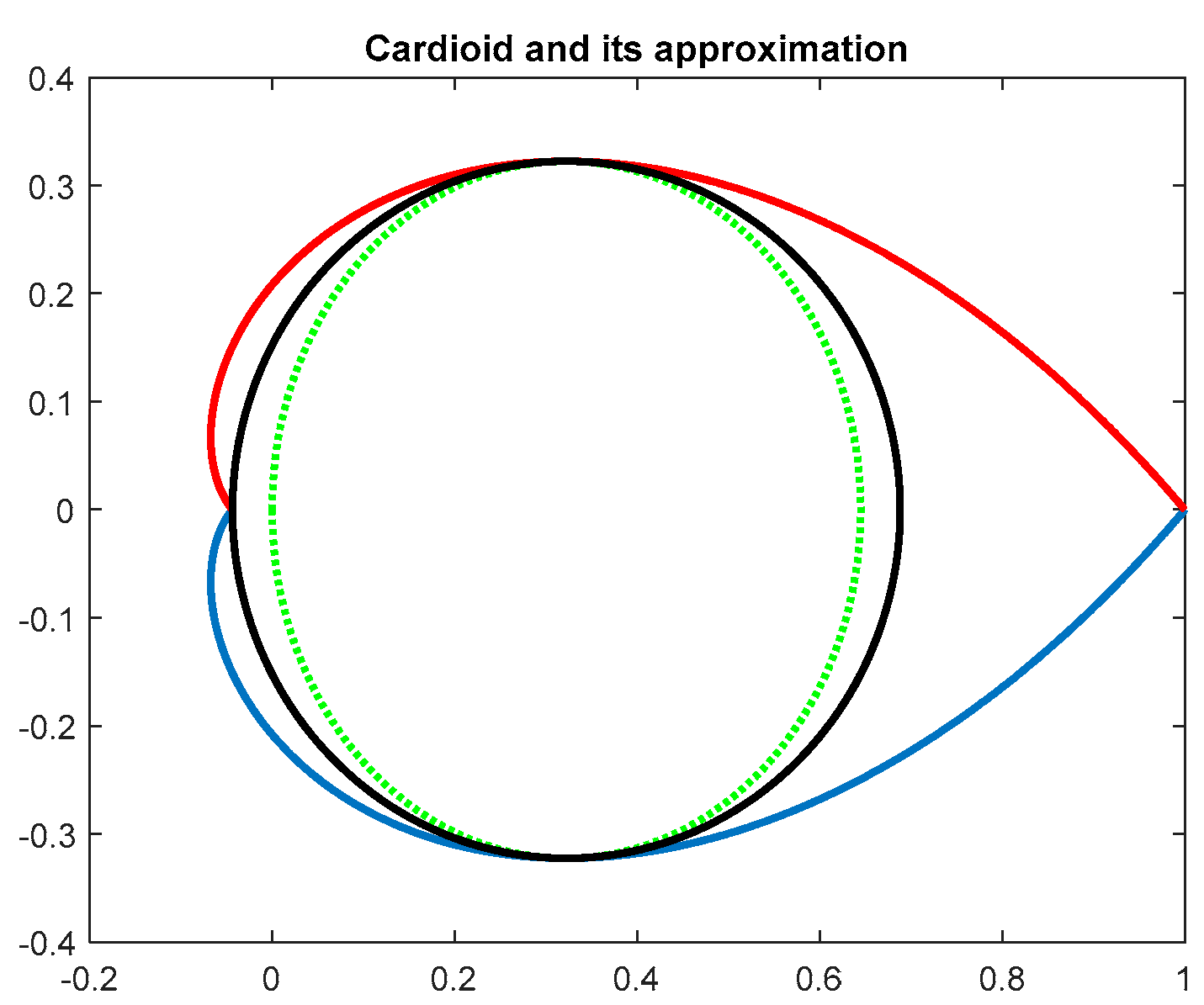
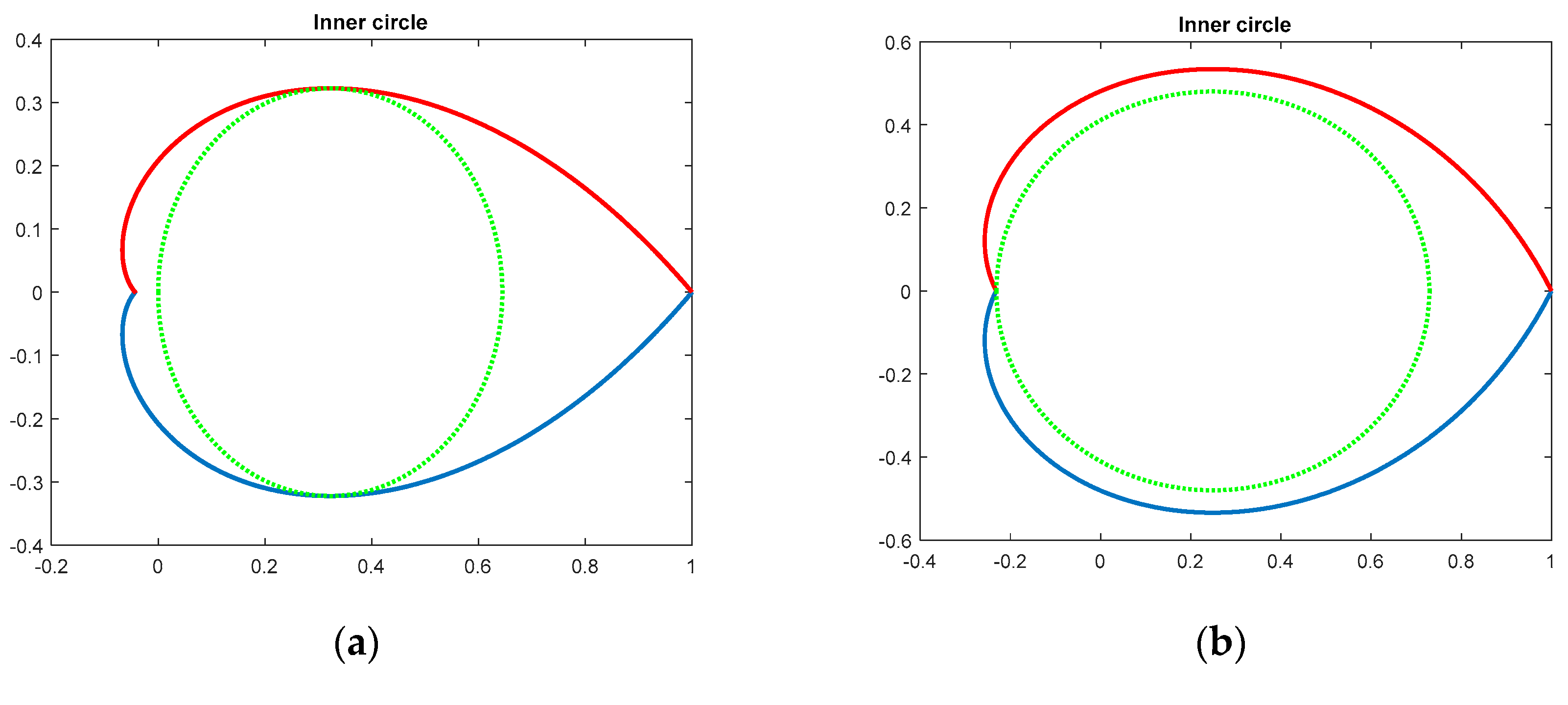
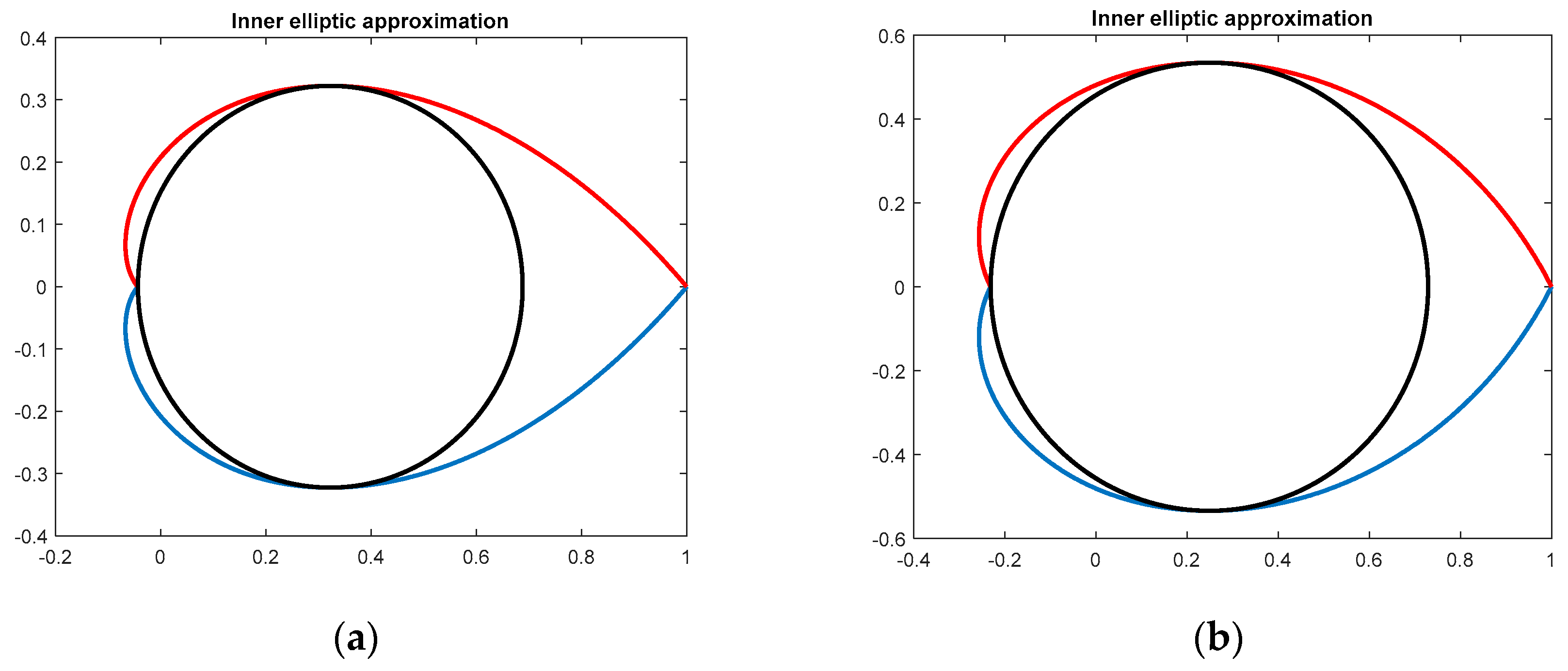
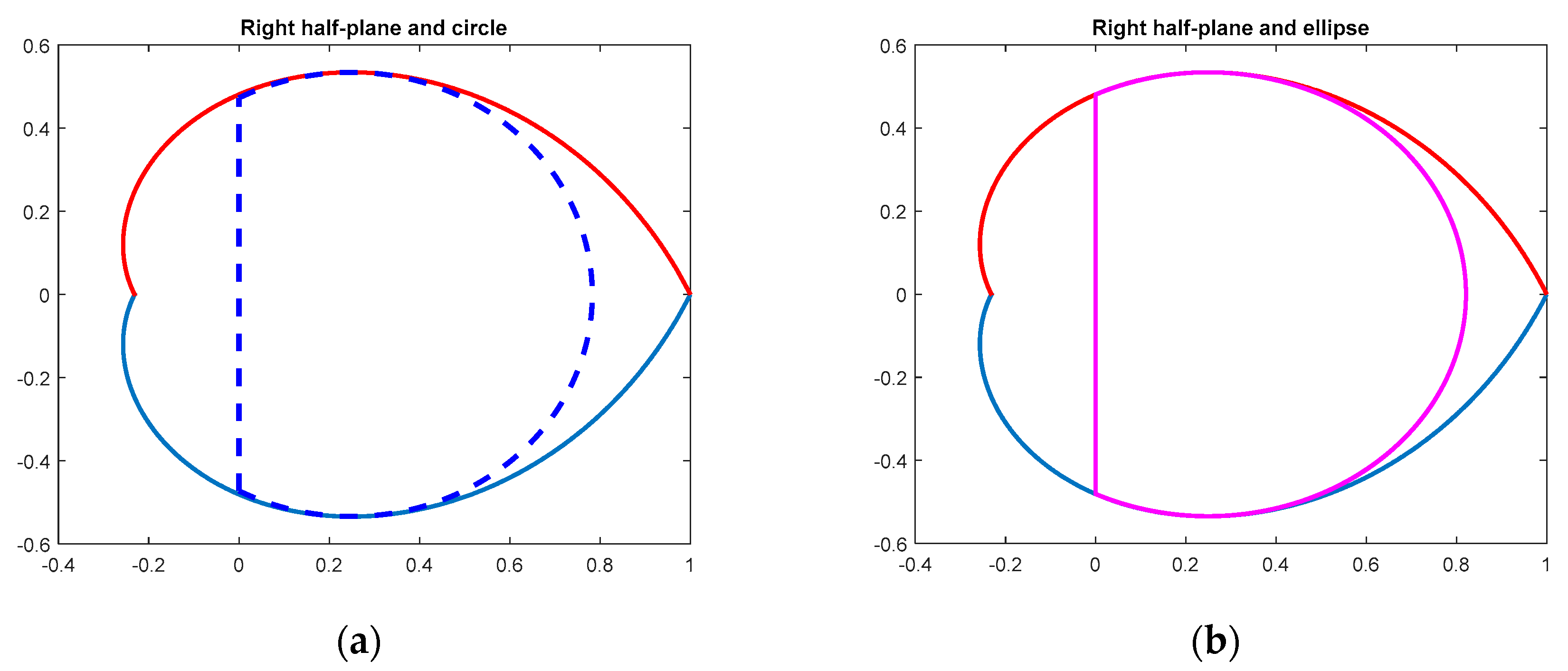
3. Inner Convex Approximations to a Discrete-Time Pole Region for the Prescribed Damping
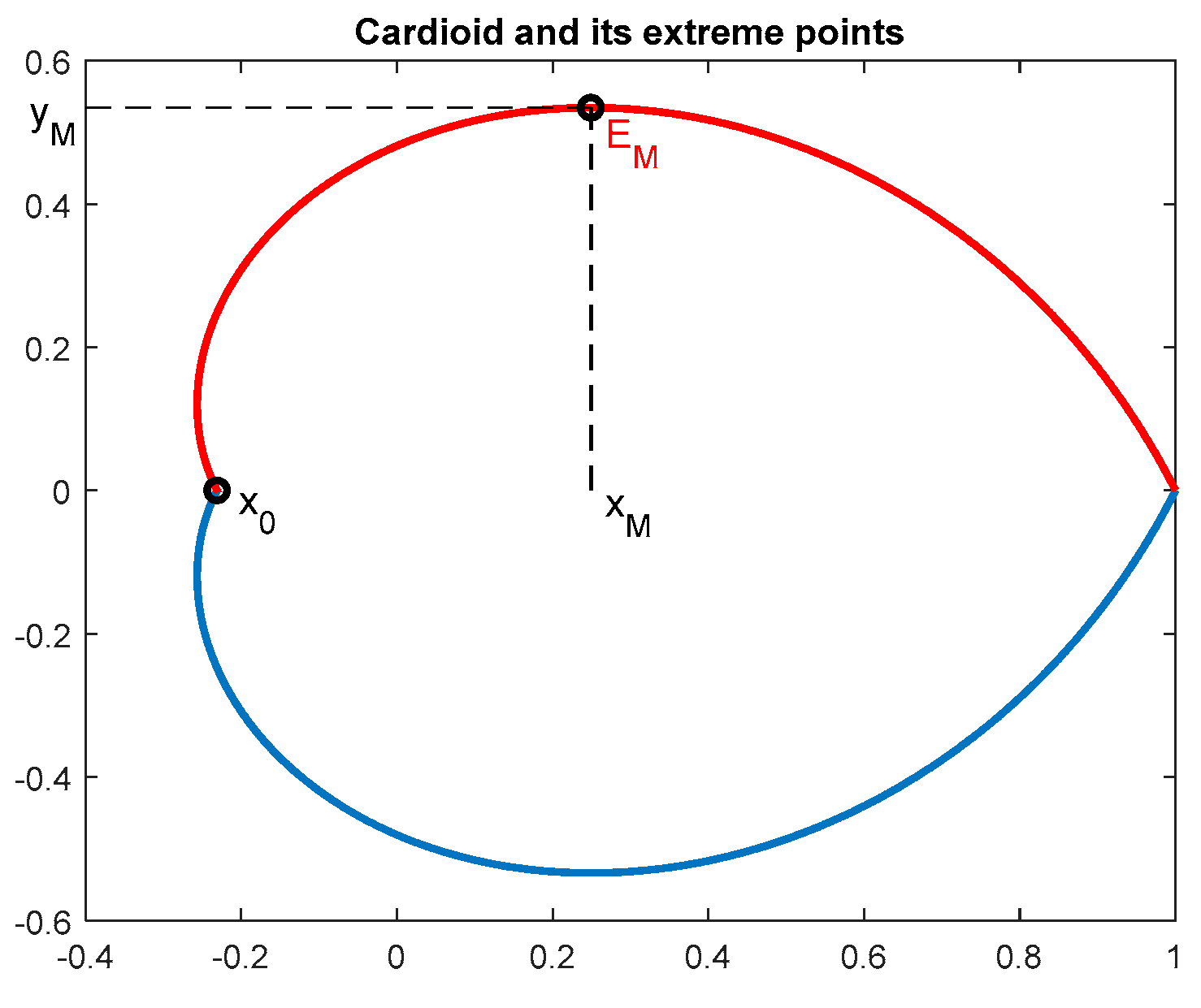
3.1. Logarithmic Spirals Corresponding to the Prescribed Damping and Their Extreme Points
3.2. Inner Convex Approximations to the Nonconvex Domain Corresponding to the Prescribed Damping
- ak = xM − x0;
- bk = yM;
- r = min(ak, bk);
- R11 = xM^2 − r^2;
- R12 = −xM;
- R22 = 1;
- ak = xM − x0;
- bk = yM;
- R11 = [−1 − xM/ak;− xM/ak − 1];
- R12 = [0 (1/ak − 1/bk)/2; (1/ak + 1/bk)/2 0];
- R22 = zeros(2, 2);
- R11 = [0 0; 0 (xM^2 − r^2)];
- R12 = [−1 0; 0 − xM];
- R22 = [0 0; 0 1];
- y3 = exp (−pi/(2*tan(fi*pi/180)));
- ak = xM*yM/sqrt (yM^2 − y3^2);
- bk = yM;
- R11 = [0 0 0; 0 − 1 − xM/ak; 0 −xM/ak −1];
- R12 = [−1 0 0; 0 0 (1/ak − 1/bk)/2; 0 (1/ak + 1/bk)/2 0];
- R22 = zeros (3, 3);
- xse = (1 + x0)/2;
- ak = (1 − x0)/2;
- bk = ye*ak/sqrt (ak^2− (xe − xse)^2);
- R11e = [−1 – xse/ak; − xse/ak − 1];
- R12e = [0 (1/ak − 1/bk)/2; (1/ak + 1/bk)/2 0];
- R22e = zeros (2, 2).
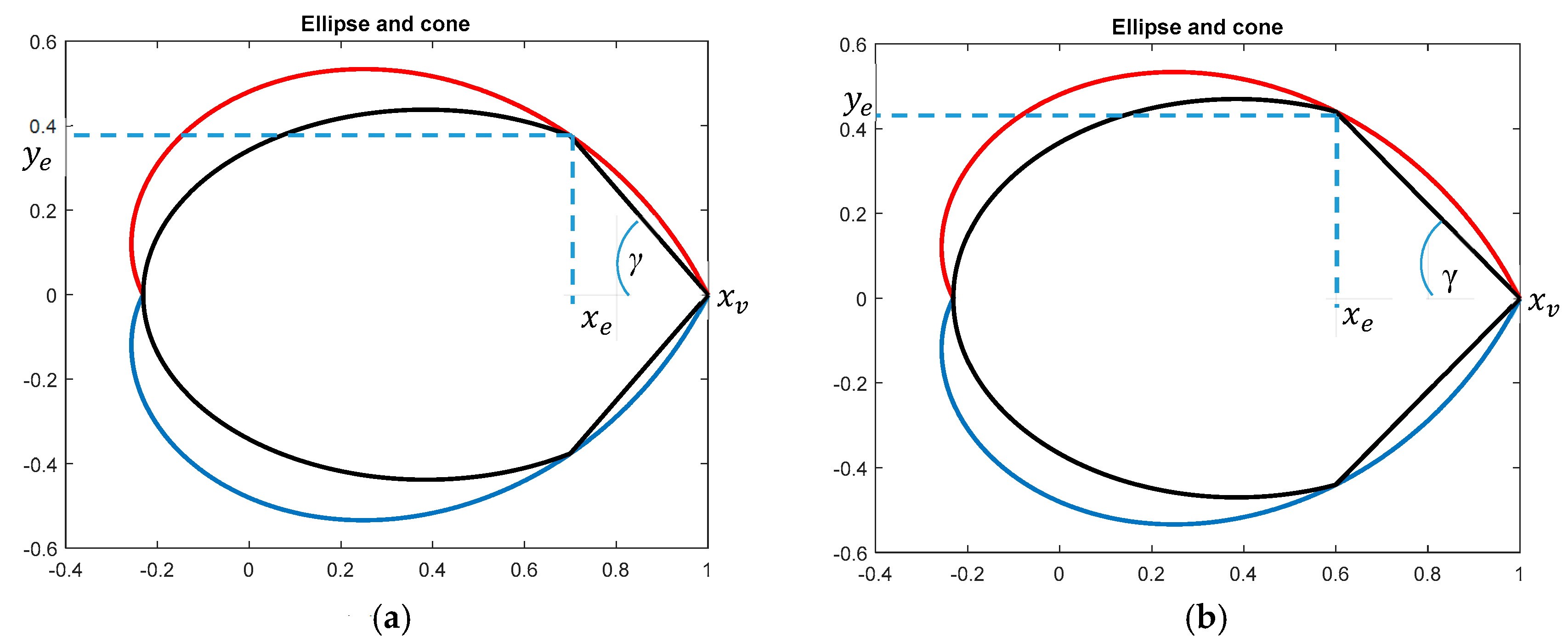
- ga = atan(ye/(1 − xe));
- R11v = [−xv*sin(ga)*2 0; 0 − xv*sin(ga)*2];
- R12v = [sin(ga) cos(ga); − cos(ga) sin(ga)];
- R22v = [0 0; 0 0].
- Z = zeros (2, 2);R11 = [R11e Z; Z R11v];
- R12 = [R12e Z; Z R12v];
- R22 = [R22e Z; Z R22v].
4. Discrete-Time Robust Pole Placement Control for Magnetic Levitation (ML) Laboratory Plant
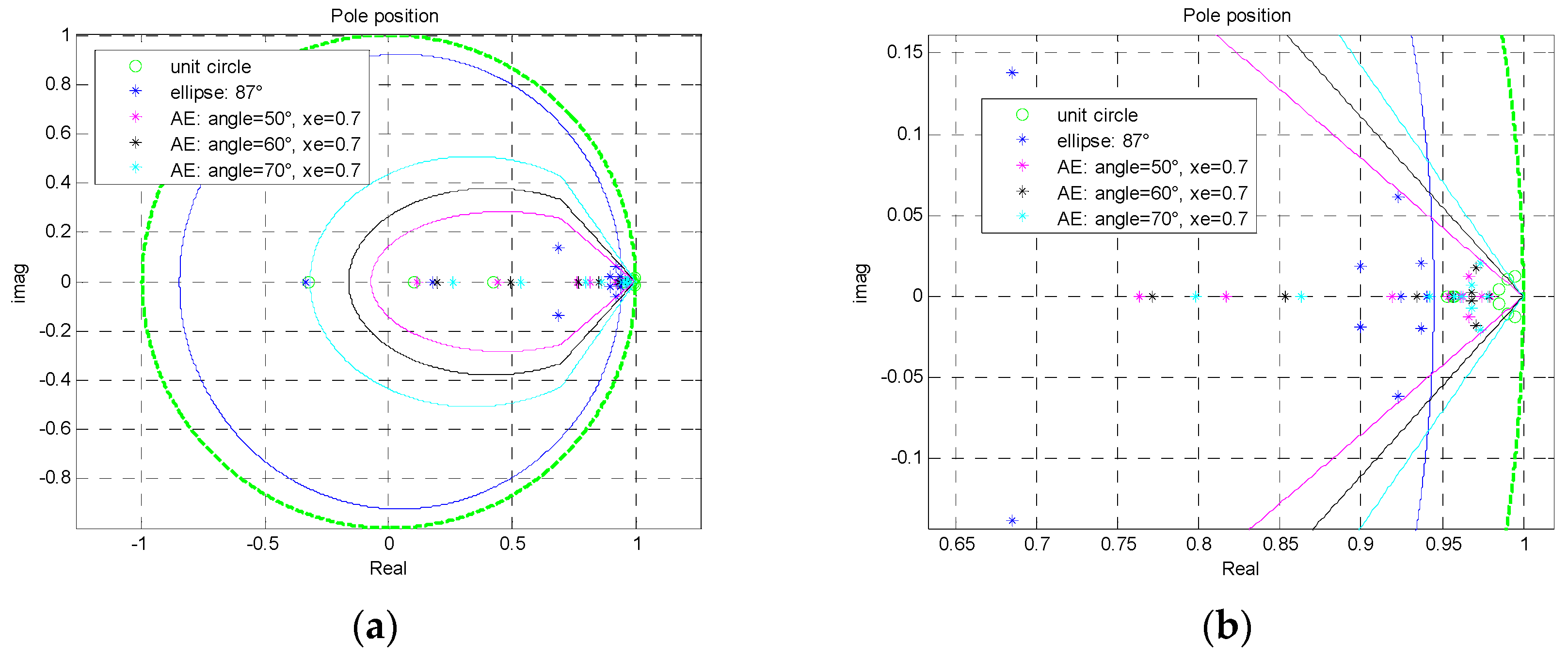
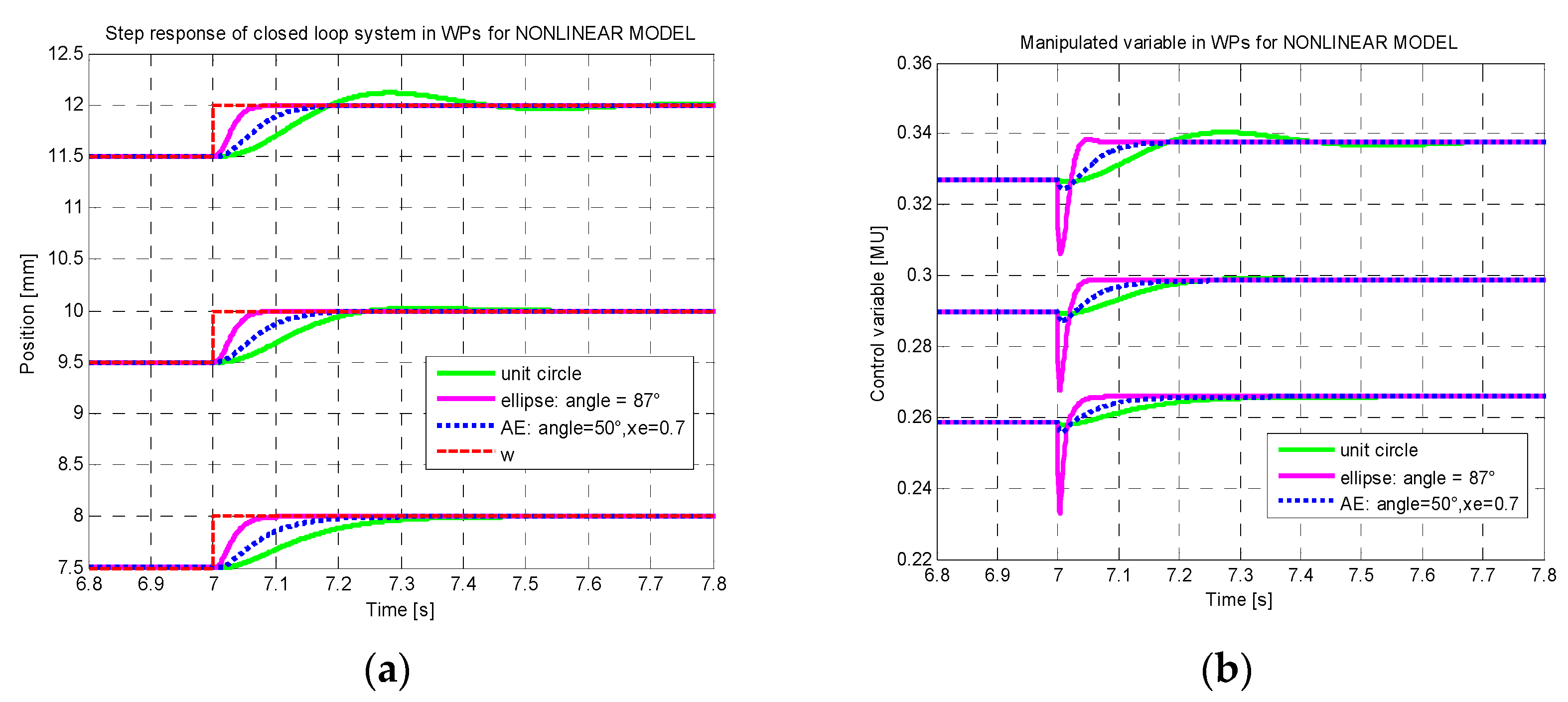
- Stabilization only: required pole region is unit circle;
- Elliptic inner approximation for 87° damping angle;
- New proposed ellipse-cone approximation for 50°, 60°, and 70° damping angles. For numerical reasons, in this case we considered and stability degree .
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Skelton, R.E.; Iwasaki, T.; Grigoriadis, K. A Unified Algebraic Approach to Linear Control Design; Taylor and Francis: London, UK, 1998. [Google Scholar]
- Ebihara, Y.; Peaucelle, D.; Arzelier, D. S-Variable Approach to LMI-Based Robust Control; Springer: London, UK, 2015. [Google Scholar]
- Liu, K.-Z.; Yao, Y. Robust Control: Theory and Applications; John Wiley & Sons (Asia): Singapore, 2016. [Google Scholar]
- Mansouria, B.; Manamannia, N.; Guelton, K.; Djemai, M. Robust pole placement controller design in LMI region for uncertain and disturbed switched systems. Nonlinear Anal. Hybrid Syst. 2008, 2, 1136–1143. [Google Scholar] [CrossRef]
- Dos Santos, J.F.S.; Pellanda, P.C.; Simões, A.M. Robust pole placement under structural constraints. Syst. Control Lett. 2018, 116, 8–14. [Google Scholar] [CrossRef]
- Peaucelle, D.; Arzelier, D.; Bachelier, O.; Bernussou, J. A new robust D-stability condition for real convex polytopic uncertainty. Syst. Control Lett. 2000, 40, 21–30. [Google Scholar] [CrossRef]
- Botto, M.A.; Babuška, R.; da Costa, J. Discrete-time robust pole-placement design through global optimization. In Proceedings of the 15th IFAC World Congress, Barcelona, Spain, 21–26 July 2002. [Google Scholar]
- Chilali, M.; Gahinet, P.; Apkarian, P. Robust pole placement in LMI regions. IEEE Trans. Autom. Control 1999, 44, 2257–2270. [Google Scholar] [CrossRef]
- Boroujeni, E.A.; Daryabor, A.; Momeni, H.R. Designing robust pole placement control for Roll Motions of Ships via LMIs. In Proceedings of the IEEE International Conference on Control, Automation and Systems, Seoul, Korea, 14–17 October 2008. [Google Scholar]
- Aunsiri, T.; Numanoy, N.; Hemsuwan, W.; Srisertpol, J. Servo System Using Pole-Placement with State Observer for Magnetic Levitation System. Lect. Notes Electr. Eng. 2014, 309, 921–926. [Google Scholar]
- Rao, P.S.; Sen, I. Robust pole placement stabilizer design using linear matrix inequalities. IEEE Trans. Power Syst. 2000, 15, 313–319. [Google Scholar] [CrossRef]
- Turner, R.; Walton, S.; Duke, R. Robust High-Performance Inverter Control Using Discrete Direct-Design Pole Placement. IEEE Trans. Ind. Electron. 2011, 58, 348–357. [Google Scholar] [CrossRef]
- Lassere, J.B. An Introduction to Polynomial and Semi-Algebraic Optimization; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar]
- Rosinová, D.; Holič, I. LMI Approximation of Pole-region for Discrete-time Linear Dynamic Systems. In Proceedings of the 15th International Carpathian Control Conference, Velké Karlovice, Czech Republic, 28–30 May 2014; pp. 497–502. [Google Scholar]
- Rosinová, D.; Hypiusová, M. Robust Pole Placement DR—regions for Discrete-time Systems. In Proceedings of the 22nd International Conference on Process Control, Štrbské Pleso, Slovakia, 11–14 June 2019. [Google Scholar]
- Isermann, R. Digital Control Systems; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Morari, M.; Zafiriou, E. Robust Process Control; Prentice Hall: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Lofberg, J. YALMIP: A toolbox for modelling and optimization in Matlab. In Proceedings of the CACSD Conference, Taipei, Taiwan, 2–4 September 2004. [Google Scholar]
- Magnetic Levitation System 2EM—User’s Manual; Inteco Ltd.: Krakow, Poland, 2008.
- Balko, P.; Rosinová, D. Modeling of magnetic levitation system. In Proceedings of the 21st International Conference on Process Control, Štrbské Pleso, Slovakia, 6–9 June 2017. [Google Scholar]
- Francis, B.A.; Wonham, W.M. The internal model principle of control theory. Automatica 1976, 12, 457–465. [Google Scholar] [CrossRef]
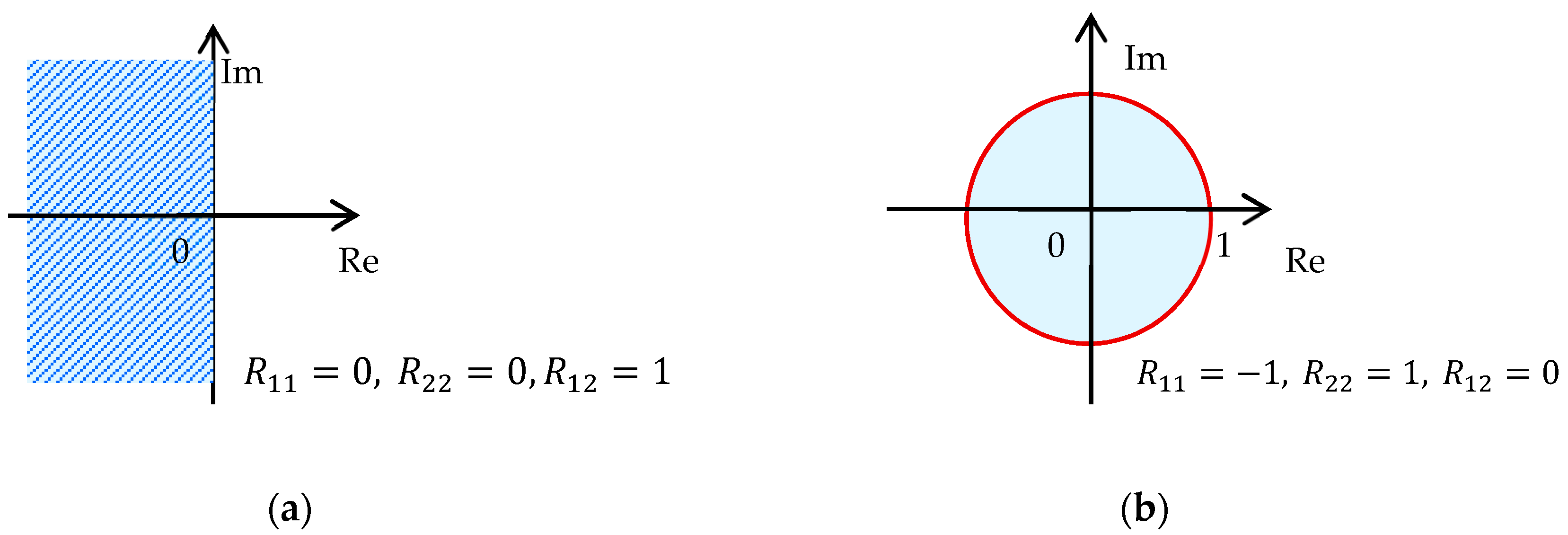
| D_R Region | P | I |
|---|---|---|
| Unit circle | [106.7, 2.47, −0.617] | 0.3527 |
| Ellipse (87°) | [952.4, 9.75, −0.653] | 26.88 |
| Ellipse-cone (70°) | [134.2, 2.55, −0.275] | 1.222 |
| Ellipse-cone (60°) | [154.7, 2.93, −0.317] | 1.420 |
| Ellipse-cone (50°) | [190.7, 3.56, −0.368] | 1.831 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rosinová, D.; Hypiusová, M. LMI Pole Regions for a Robust Discrete-Time Pole Placement Controller Design. Algorithms 2019, 12, 167. https://doi.org/10.3390/a12080167
Rosinová D, Hypiusová M. LMI Pole Regions for a Robust Discrete-Time Pole Placement Controller Design. Algorithms. 2019; 12(8):167. https://doi.org/10.3390/a12080167
Chicago/Turabian StyleRosinová, Danica, and Mária Hypiusová. 2019. "LMI Pole Regions for a Robust Discrete-Time Pole Placement Controller Design" Algorithms 12, no. 8: 167. https://doi.org/10.3390/a12080167
APA StyleRosinová, D., & Hypiusová, M. (2019). LMI Pole Regions for a Robust Discrete-Time Pole Placement Controller Design. Algorithms, 12(8), 167. https://doi.org/10.3390/a12080167




