A Collocation Method for the Numerical Solution of Nonlinear Fractional Dynamical Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Nonlinear Fractional Dynamical Systems
2.2. The Cardinal B-Splines
2.3. B-Spline Bases on the Semi-Infinite Interval
2.4. The Fractional Derivative of the Cardinal B-Splines
2.5. The Collocation Method
3. Results
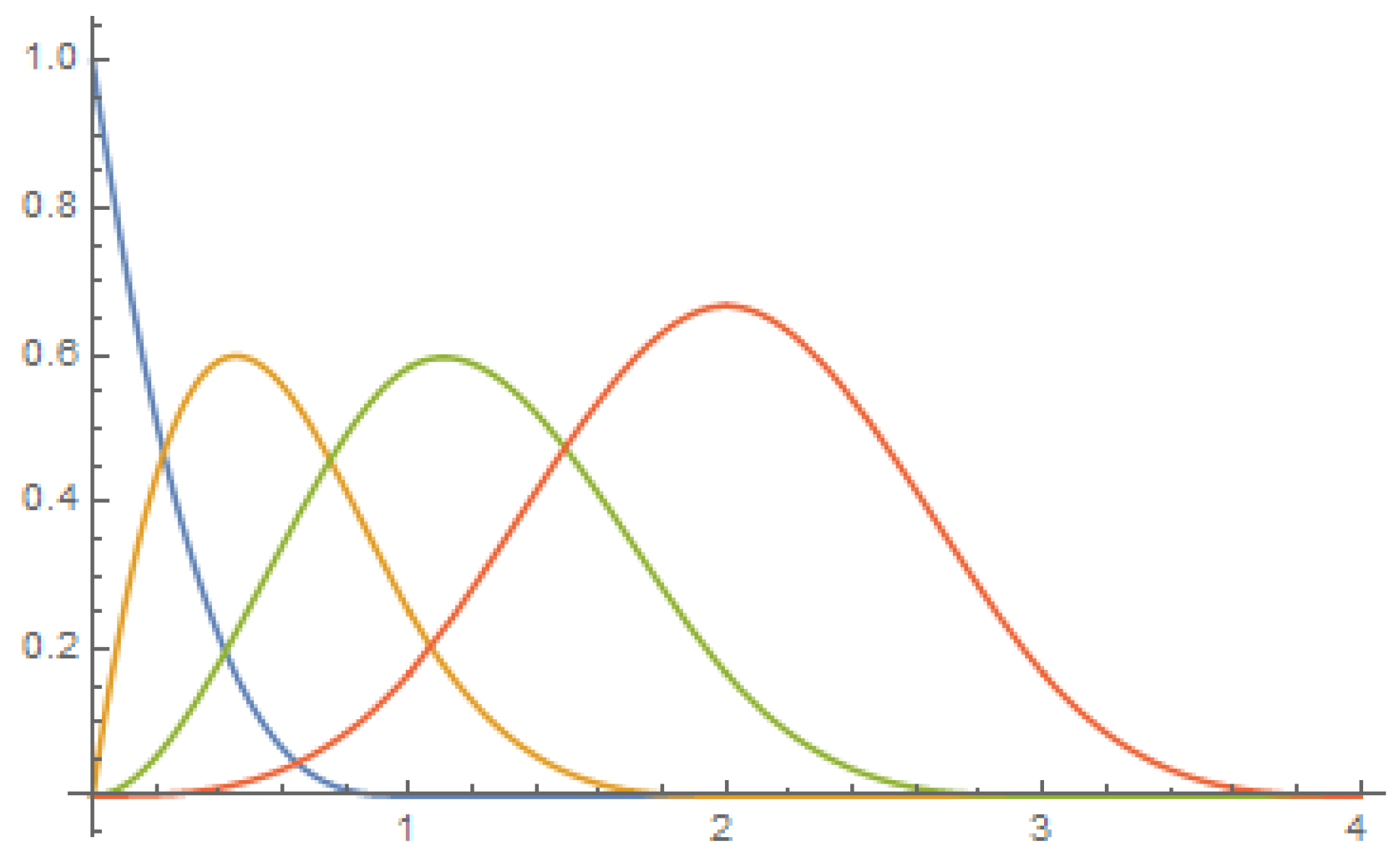
3.1. The Linear B-Spline Basis
3.2. The Cubic B-Spline Basis
3.3. Numerical Solution of Linear Dynamical Systems
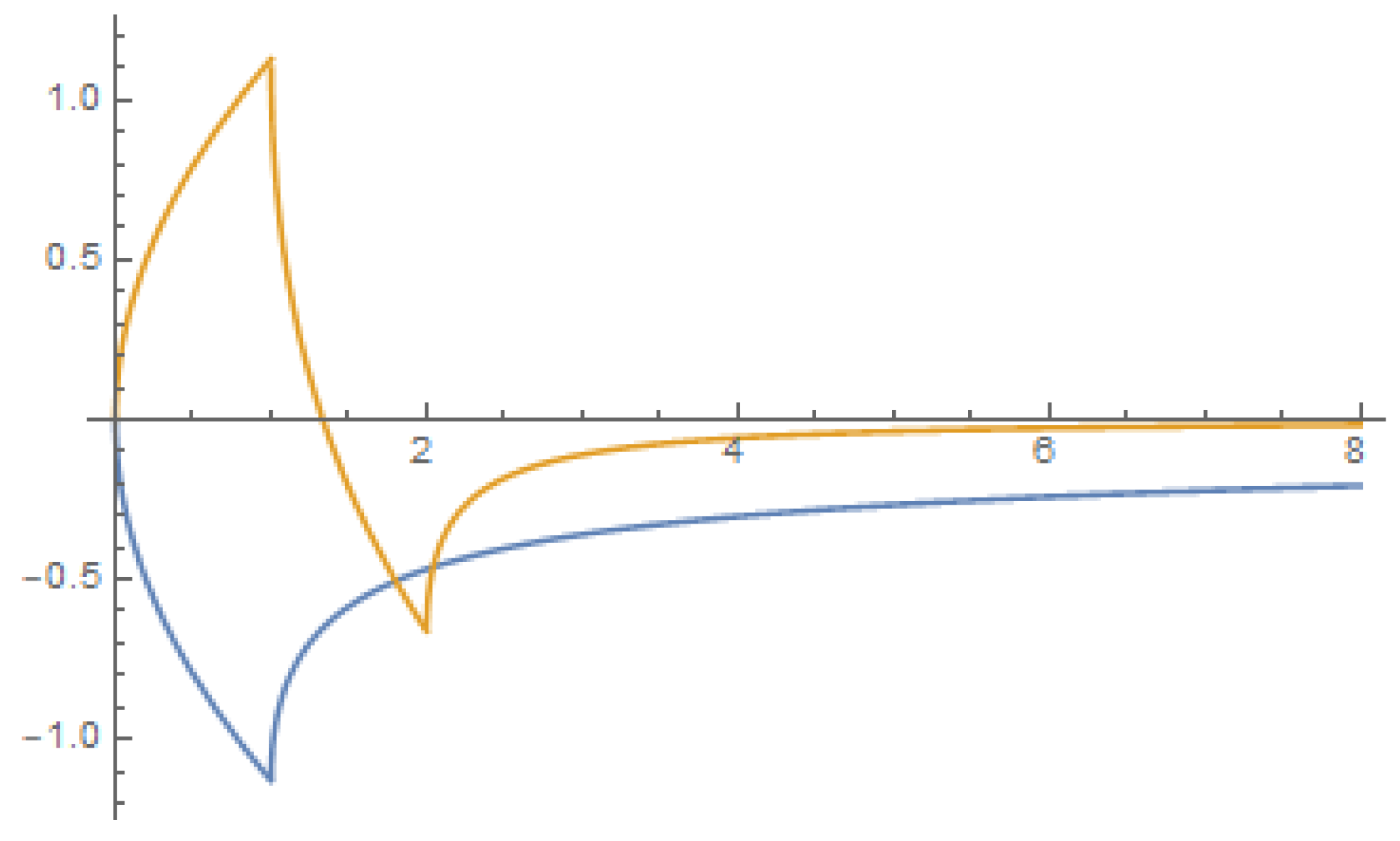
3.4. Numerical Solution of Nonlinear Dynamical Systems
4. Discussion
5. Conclusions
Supplementary Materials
Funding
Conflicts of Interest
References
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; World Scientific: Singapore, 2010. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics. Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Nonlinear Physical Science; Springer: Berlin, Germany, 2010. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific: Singapore, 2016. [Google Scholar]
- Li, C.; Zeng, F. Numerical Methods for Fractional Calculus; A Chapman & Hall Book/CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Li, C.; Chen, A. Numerical methods for fractional partial differential equations. Int. J. Comput. Math. 2018, 95, 1048–1099. [Google Scholar] [CrossRef]
- Pezza, L.; Pitolli, F. A multiscale collocation method for fractional differential problems. Math. Comput. Simul. 2018, 147, 210–219. [Google Scholar] [CrossRef]
- Pezza, L.; Pitolli, F. A fractional spline collocation-Galerkin method for the time-fractional diffusion equation. Commun. Appl. Ind. Math. 2018, 9, 104–120. [Google Scholar] [CrossRef]
- Pitolli, F. A fractional B-spline collocation method for the numerical solution of fractional predator-prey models. Fractal Fract. 2018, 2, 13. [Google Scholar] [CrossRef]
- Pellegrino, E.; Pezza, L.; Pitolli, F. A collocation method in spline spaces for the solution of linear fractional dynamical systems. arXiv 2019, arXiv:1907.10927. [Google Scholar]
- Wolfram Research, Inc. Mathematica, Version 12.0.0.0; Wolfram Research: Champaign, IL, USA, 2019. [Google Scholar]
- Diethelm, K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type; Springer: Berlin, Germany, 2010. [Google Scholar]
- Sabatier, J.; Agrawal, O.; Tenreiro Machado, J.A. Advances in Fractional Calculus; Springer: Berlin, Germany, 2007. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon & Breach Science Publishers: London, UK, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Pedas, A.; Tamme, E.; Vikerpuur, M. Smoothing transformation and spline collocation for nonlinear fractional initial and boundary value problems. J. Comput. Appl. Math. 2017, 317, 1–16. [Google Scholar] [CrossRef]
- Vainikko, G. Multidimensional Weakly Singular Integral Equations; Lecture Notes in Mathematics; Springer: Berlin, Germany, 1993. [Google Scholar]
- Schumaker, L.L. Spline Functions: Basic Theory; Cambridge University Press: Vambridge, UK, 2007. [Google Scholar]
- Pitolli, F. Optimal B-spline bases for the numerical solution of fractional differential problems. Axioms 2018, 7, 46. [Google Scholar] [CrossRef]
- Unser, M.; Blu, T. Fractional splines and wavelets. SIAM Rev. 2000, 42, 43–67. [Google Scholar] [CrossRef]
- Ascher, U. Discrete least squares approximations for ordinary differential equations. SIAM J. Num. Anal. 1978, 15, 478–496. [Google Scholar] [CrossRef]
- Li, C.; Ma, Y. Fractional dynamical system and its linearization theorem. Nonlinear Dyn. 2013, 71, 621–633. [Google Scholar] [CrossRef]
- Calvetti, D.; Pitolli, F.; Somersalo, E.; Vantaggi, B. Bayes meets Krylov: Statistically inspired preconditioners for CGLS. SIAM Rev. 2018, 60, 429–461. [Google Scholar] [CrossRef]
- Mallat, S. A Wavelet tour of Signal Processing. The Sparse Way; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]





© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pitolli, F. A Collocation Method for the Numerical Solution of Nonlinear Fractional Dynamical Systems. Algorithms 2019, 12, 156. https://doi.org/10.3390/a12080156
Pitolli F. A Collocation Method for the Numerical Solution of Nonlinear Fractional Dynamical Systems. Algorithms. 2019; 12(8):156. https://doi.org/10.3390/a12080156
Chicago/Turabian StylePitolli, Francesca. 2019. "A Collocation Method for the Numerical Solution of Nonlinear Fractional Dynamical Systems" Algorithms 12, no. 8: 156. https://doi.org/10.3390/a12080156
APA StylePitolli, F. (2019). A Collocation Method for the Numerical Solution of Nonlinear Fractional Dynamical Systems. Algorithms, 12(8), 156. https://doi.org/10.3390/a12080156




