A Collocation Method for the Numerical Solution of Nonlinear Fractional Dynamical Systems

Abstract

Fractional differential problems are widely used in applied sciences. For this reason, there is a great interest in the construction of efficient numerical methods to approximate their solution. The aim of this paper is to describe in detail a collocation method suitable to approximate the solution of dynamical systems with time derivative of fractional order. We will highlight all the steps necessary to implement the corresponding algorithm and we will use it to solve some test problems. Two Mathematica Notebooks that can be used to solve these test problems are provided.

1. Introduction

Presently, fractional differential problems are well established models to describe a great variety of real-world phenomena [1,2,3,4]. Since their analytical solution can be obtained in just a few cases, numerical methods are required for its approximation. A key point to construct efficient numerical methods is the ability to reproduce the nonlocal behavior of the fractional derivative. This is a challenging goal especially in cases of nonlinear problems.

In the literature several methods, such as finite difference methods, spectral methods, finite element methods, collocation methods, were proposed to solve fractional differential problems [5,6,7]. In this context, collocation methods are revealed particularly attractive since their global nature is suitable to catch the non-locality of the fractional derivative.

The aim of this paper is to describe in detail how to apply the fractional collocation method introduced in [8] for the numerical solution of nonlinear dynamical systems with time derivative of fractional order. The method was already used to numerically solve some linear and nonlinear problems with fractional time derivative [9,10,11]. Here, we will describe how to use the method to solve differential problems of a more general form and discuss its implementation issues. To allow the reader to easily follow the description of the algorithm, we limit ourselves to the case when the approximate solution belongs to the spline space. In particular, we will show some numerical tests when using both linear and cubic splines and provide two Mathematica Notebooks [12] that can be used to solve such test problems.

The paper is organized as follows. In Section 2 the fractional differential problem we are interested in and the collocation method we use are briefly recalled. In particular, the spline space we use to construct the approximate solution is described in Section 2.2 and Section 2.3; the analytical expression of both the basis functions and their fractional derivative is given in Section 2.3 and Section 2.4; the algorithm of the collocation method is described in Section 2.5. The results of the numerical tests are shown in Section 3 and briefly discussed in Section 4. Finally, in Section 5 some conclusions are given.

2. Materials and Methods

In this section, after describing the differential problem we are interested in, we recall the main features of the numerical method we use to approximate its solution.

2.1. Nonlinear Fractional Dynamical Systems

Let $Y\left(t\right):\mathbb{R}\to {\mathbb{R}}^m$ and $F:{\mathbb{R}}^{m+1}\to {\mathbb{R}}^m$ be real-valued vector functions, and $Y_0\in {\mathbb{R}}^m$ be a real vector. A nonlinear dynamical system with derivative of fractional, i.e., noninteger, order in time can be written as

$$\left\{\begin{array}{c}{}_C{D}_t^{\beta }Y\left(t\right)=F(t,Y\left(t\right)),t>0,0<\beta <1,\hfill \\ Y\left(0\right)=Y_0.\hfill \end{array}\right.$$

(1)

where ${}_C{D}_t^{\beta }Y\left(t\right)$ denotes the Caputo fractional derivative with respect to the time t. For a sufficiently smooth vector function $Y\left(t\right)={[y_1\left(t\right),y_2\left(t\right),\dots ,y_m\left(t\right)]}^T$, its Caputo derivative is defined as

$$D_t^{\beta }Y\left(t\right):={\left[D_t^{\beta }{y}_1\left(t\right),D_t^{\beta }{y}_2\left(t\right),\dots ,D_t^{\beta }{y}_m\left(t\right)\right]}^T,$$

(2)

where

$$D_t^{\beta }y\left(t\right):=\frac{1}{\Gamma (k-\beta )}{\int }_0^x\frac{y^{\left(k\right)}\left(\tau \right)}{{(x-\tau )}^{\beta +1-k}}d\tau ,k-1<\beta <k,k\in \mathbb{N},t>0,$$

(3)

and $\Gamma$ denotes the Euler’s gamma function. For details on fractional calculus and fractional derivatives see, for instance, [13,14,15,16].

The existence, unicity and smoothness of the solution to (1) can be analyzed by transforming the problem into an integral equation [17,18].

2.2. The Cardinal B-Splines

The cardinal B-splines are piecewise polynomials with breakpoints on integer knots. Given the sequence of simple integer knots $\mathcal{I}=\{0,1,\dots ,n+1\}$, the Cardinal B-spline of integer degree $n\ge 0$ can be defined by applying the divided difference operator to the truncated power function $t_{+}^n:=max{(t,0)}^n$ on the knots $\mathcal{I}$:

$$\begin{array}{ccc}{B}_n\left(t\right)\hfill & :=& (n+1)[0,1,\dots ,n+1]{(x-t)}_{+}^n=\hfill \\ & =& {\displaystyle (n+1)\frac{\left|M\left(\begin{array}{c}1,x,x^2,\cdots ,x^n,{(x-t)}_{+}^n\\ 0,1,2,\cdots ,n,n+1\end{array}\right)\right|}{\left|M\left(\begin{array}{c}1,x,x^2,\cdots ,x^n,x^{n+1}\\ 0,1,2,\cdots ,n,n+1\end{array}\right)\right|}=\frac{1}{n!}{\Delta }^{n+1}{t}_{+}^n,}\hfill \end{array}$$

(4)

where

$$M\left(\begin{array}{cccc}{f}_1\left(x\right),& f_2\left(x\right),& \cdots ,& f_n\left(x\right)\\ x_1,& x_2,& \cdots ,& x_n\end{array}\right)=\left[\begin{array}{cccc}{f}_1\left(x_1\right)& f_n\left(x_1\right)& \cdots & f_n\left(x_1\right)\\ f_1\left(x_2\right)& f_n\left(x_2\right)& \cdots & f_n\left(x_2\right)\\ \cdots & \cdots & \cdots & \cdots \\ f_1\left(x_n\right)& f_n\left(x_n\right)& \dots & f_n\left(x_n\right)\end{array}\right]$$

is the collocation matrix of the function system $\{f_1\left(x\right),f_2\left(x\right),\dots ,f_n\left(x\right)\}$ on the nodes $\{x_1,x_2,\dots ,x_n\}$ and

$${\Delta }^{n}f\left(t\right)=\sum _{k=0}^n{(-1)}^k\left(\genfrac{}{}{0pt}{}{n}{k}\right)f(t-k)$$

is the backward finite difference operator.

We recall that $B_n\left(t\right)$ is compactly supported on $[0,n+1]$, is positive in $(0,n+1)$ and belongs to $C^{n-1}\left(\mathbb{R}\right)$. For details and further properties on polynomial B-splines, see, for instance, [19].

2.3. B-Spline Bases on the Semi-Infinite Interval

The system of the integer translates ${\mathcal{B}}_n=\left\{B_n(t-k),k\in \mathbb{Z}\right\}$ forms a function basis for the space of piecewise polynomials of degree n on the real line and enjoys many useful properties that make it especially suitable in approximation problems. In particular, ${\mathcal{B}}_n$ is a partition of unity, reproduces polynomials up to degree n, satisfies the Strang-Fix theory and has approximation order $n+1$ (cf. [19]).

To construct a function basis in the semi-infinite interval $[0,\infty )$ we restrict ${\mathcal{B}}_n$ to this interval. The interior functions, i.e., the functions $B_n(t-k)$ with $k\ge 0$, which have support $[k,k+n+1]$ all contained in $[0,\infty )$, remain unchanged. The left-edge boundary functions, i.e., the functions $B_n(t-k)$ with $-n\le k\le -1$, whose support is not all contained in $[0,\infty )$, are modified introducing a knot of multiplicity $n+1$ at the left-edge of the interval. Thus, the B-spline basis on the semi-infinite interval $[0,\infty )$ is

$${\mathcal{N}}_n=\{N_{kn}\left(t\right),0\le k\le n-1\}\cup \{B_n(t-k),k\ge 0\},t\in [0,\infty ),$$

where $N_{kn}\left(t\right)$, $0\le k\le n-1$, are the left-edge boundary functions. In [20] their analytical expressions is given in terms of suitable collocation matrices:

$$N_{kn}\left(t\right)=(k+1)\frac{|T_{nk}|}{|P_{kn}|},0\le k\le n-1,$$

(5)

where $T_{kn}$ is the $(k+1)$ order collocation matrix

$$T_{kn}=M\left(\begin{array}{ccccc}{x}^{n-k+1},& x^{n-k+2},& \cdots & x^n,& {(x-t)}_{+}^n\\ 1,& 2,& \cdots & k,& k+1\end{array}\right),$$

and $P_{kn}$ is the ($k+1$) order collocation matrix

$$P_{kn}=M\left(\begin{array}{ccccc}{x}^{n-k+1},& x^{n-k+2},& \cdots & x^n,& x^{n+1}\\ 1,& 2,& \cdots & k,& k+1\end{array}\right).$$

The B-spline bases can be generalized to any sequence of equidistant knots on the interval $[0,\infty )$ by mapping $t\to t/h$, where $h>0$ is the refinement step:

$${\mathcal{N}}_{nh}=\{N_{knh}\left(t\right),k\ge 0\},t\in [0,\infty ),$$

where $N_{knh}\left(t\right)=N_{kn}\left(\frac{t}{h}\right)$, $0\le k\le n-1$, are the left-edge functions and $N_{knh}\left(t\right)=B_n\left(\frac{t}{h}-(k-n)\right)$, $k\ge n$, are the interior functions. We observe that at the left-edge of the interval the basis functions satisfy the initial conditions

$$N_{knh}\left(0\right)={\delta }_{k0},$$

(6)

where ${\delta }_{kj}$ denotes the Kronecker delta. Consequently, just the first basis function $N_{0nh}$ does not vanish in the origin with $N_{0nh}\left(0\right)=1$.

2.4. The Fractional Derivative of the Cardinal B-Splines

The Caputo fractional derivative of the interior functions can be easily evaluated by the differentiation rule (cf. [8,21])

$${}_C{D}_t^{\beta }{B}_n\left(t\right)=\frac{{\Delta }^{n+1}{t}_{+}^{n-\beta }}{\Gamma (n-\beta +1)},t\ge 0,0<\beta <n-1.$$

(7)

The Caputo fractional derivative of the left-edge boundary functions can be obtained by applying the fractional differentiation operator to their analytical expression [20]:

$${}_C{D}_t^{\beta }{N}_{kn}\left(t\right)=\frac{(k+1)}{|P_{kn}|}\sum _{r=1}^{k+1}{(-1)}^{r+k+1}{}_C{D}_t^{\beta }{(r-t)}_{+}^n\left|T_{kn}^r\right|,0\le k\le n-1,$$

(8)

where

$$T_{kn}^r=\left(\begin{array}{cccc}1& 1& \dots & 1\\ 2^{n-k+1}& 2^{n-k+2}& \dots & 2^n\\ \dots & \dots & \dots & \dots \\ {(r-1)}^{n-k+1}& {(r-1)}^{n-k+2}& \dots & {(r-1)}^n\\ {(r+1)}^{n-k+1}& {(r+1)}^{n-k+2}& \dots & {(r+1)}^n\\ \dots & \dots & \dots & \dots \\ {(k+1)}^{n-k+1}& {(k+1)}^{n-k+2}& \dots & {(k+1)}^n\end{array}\right).$$

Equation (8) shows that ${}_C{D}_t^{\beta }{N}_{kn}$ is a linear combination of the fractional derivative of the translates of the truncated power function whose expression is given by

$$\begin{array}{cc}\hfill {}_C{D}_t^{\beta }{(r-t)}_{+}^n& {\displaystyle =\frac{1}{\Gamma (k+1-\beta )}\frac{{(-1)}^{k}n!}{(n-k)!}\frac{r^{n-k}}{t^{\beta -k}}\sum _{\ell =0}^{n-k}{(-1)}^{\ell }\left(\genfrac{}{}{0pt}{}{n-k}{\ell }\right)\frac{{\left(1\right)}_{\ell }}{{(k+1-\beta )}_{\ell }}{\left(\frac{t}{r}\right)}^{\ell }}\\ & {\displaystyle +\frac{{(-1)}^{n+k}n!}{\Gamma (n+1-\beta )}{(t-r)}_{+}^{n-\beta },k-1<\beta <k,}\end{array}$$

(9)

where ${\left(p\right)}_{\ell }$ denotes the rising Pochhammer symbol [20].

2.5. The Collocation Method

We approximate the solution to the dynamical system (1) by a linear combination of the functions belonging to the basis ${\mathcal{N}}_{nh}$:

$$Y_{nh}\left(t\right)=\sum _{k\ge 0}{\Lambda }_k{N}_{knh}\left(t\right),t\ge 0,$$

(10)

where ${\Lambda }_k\in {\mathbb{R}}^m$, $k\ge 0$, are unknown vectors that can be determined requiring that $Y_{nh}\left(t\right)$ satisfies the differential problem (1) on a set of collocation points.

Let $I=[0,T]$ be the discretization interval and let $\mathcal{T}=\{0<t_1<\cdots <t_{n_p-1}<t_{n_p}=T\}$ be a set of $n_p$ collocation points. The restriction of $Y_{nh}\left(t\right)$ to the interval I is

$$Y_{nh}\left(t\right)=\sum _{k=0}^{n_k}{\Lambda }_k{N}_{knh}\left(t\right),t\in I,$$

(11)

where $n_k=T/h+n-1$. Thus, the discretized version of (1) reads

$$\left\{\begin{array}{c}{}_C{D}_t^{\beta }{Y}_{nh}\left(t_p\right)=F(t_p,Y_{nh}\left(t_p\right)),1\le p\le n_p,\hfill \\ Y_{nh}\left(0\right)=Y_0.\hfill \end{array}\right.$$

(12)

First of all, we observe that due to (6) and the partition of unity property, the initial condition is easily satisfied by setting

$$Y_{nh}\left(t\right)=Y_0+\sum _{k=1}^{n_k}{\Lambda }_k{N}_{knh}\left(t\right).$$

(13)

Now, using (13) in the first Equation of (12), we get

$$\sum _{k=1}^{n_k}{\Lambda }_k{}_C{D}_t^{\beta }{N}_{knh}\left(t_p\right)=F\left(t_p,Y_0+\sum _{k=1}^{n_k}{\Lambda }_k{N}_{knh}\left(t_p\right)\right),1\le p\le n_p.$$

(14)

This is a nonlinear system with $m\times n_p$ equations and $m\times n_k$ unknowns. The existence of a unique solution to (14) depends on the existence of a unique solution to (1) [17,18,22].

The convergence and the stability of the method can be proved following the same line of reasoning in [8,11] (cf. also [22]). For sufficiently smooth $Y\left(t\right)$ the method is stable and the convergence is guaranteed with convergence order at least $\beta$, i.e., $\parallel Y\left(t\right)-Y_{nh}{\left(t\right)\parallel }_{\infty }\le \kappa h^{-\beta }$, where ${\parallel Y\left(t\right)\parallel }_{\infty }={max}_{1\le i\le m}({max}_{t\in [0,T]}|y_i\left(t\right)\left|\right)$ and $\kappa$ is a constant independent of h. Moreover, polynomial reproduction implies that the spline approximation $Y_{nh}\left(t\right)$ is exact whenever the solution $Y\left(t\right)$ is a polynomial of degree at most n.

The solution to the nonlinear system (14) can be approximated by the Gauss-Newton method. Let

$$\mathsf{L}={[{\Lambda }_1,{\Lambda }_2,\dots ,{\Lambda }_{n_k}]}^T\in {\mathbb{R}}^{m{n}_k}$$

be the unknown vector and let

$${\mathsf{M}}_0=\left[N_{knh}\left(t_p\right),1\le p\le n_p,1\le k\le n_k\right]\in {\mathbb{R}}^{n_p\times n_k},$$

$${\mathsf{M}}_{\beta }=\left[{{}_{C}D}_t^{\beta }{N}_{knh}\left(t_p\right),1\le p\le n_p,1\le k\le n_k\right]\in {\mathbb{R}}^{n_p\times n_k}$$

be the collocation matrices of the basis functions and of their fractional derivative, respectively. Let $G:{\mathbb{R}}^{m{n}_k}\to {\mathbb{R}}^{m{n}_p}$ be the vector-valued function whose entries are the equations of the nonlinear system (14). Then, the nonlinear system can be written as

$$G\left(\mathsf{L}\right)=\left({\mathsf{I}}_m\otimes {\mathsf{M}}_{\beta }\right)\mathsf{L}-\mathsf{Q}\left(\mathsf{L}\right)=0,$$

(15)

where ${\mathsf{I}}_m$ is the identity matrix of order m and the vector $\mathsf{Q}\left(\mathsf{L}\right)=F(\mathcal{T},Y_{nh}\left(\mathcal{T}\right))\in {\mathbb{R}}^{m{n}_p}$ stands for the know term F evaluated in all the collocation points. Here, the symbol ⊗ denotes the Kronecker product on two matrices. The Gauss-Newton method starts by an initial guess ${\mathsf{L}}^{\left(0\right)}$ and approximates the solution to the nonlinear system by the iterative procedure

$${\mathsf{L}}^{(\ell +1)}={\mathsf{L}}^{(\ell )}-{\mathsf{V}}^{(\ell )},\ell \ge 0,$$

(16)

where the vector ${\mathsf{V}}^{(\ell )}$ is the solution to the linear system

$${\mathcal{J}}_G\left({\mathsf{L}}^{(\ell )}\right){\mathsf{V}}^{(\ell )}=G\left({\mathsf{L}}^{(\ell )}\right),$$

(17)

and ${\mathcal{J}}_G\left(\mathsf{L}\right)$ is the Jacobian matrix of $G\left(\mathsf{L}\right)$. For a general nonlinear fractional differential problem of type (1) the Jacobian matrix can be written as

$${\mathcal{J}}_G\left(\mathsf{L}\right)={\mathsf{I}}_m\otimes M_{\beta }-{\mathcal{J}}_F(\mathcal{T},Y_{nh}\left(\mathcal{T}\right))\circ ({\mathsf{I}}_m\otimes M_0).$$

(18)

where ${\mathcal{J}}_F(\mathcal{T},Y_{nh}\left(\mathcal{T}\right))$ denotes the Jacobian matrix of the known term F evaluated in the collocation points. Here, the symbol ∘ denotes the entrywise product of arrays. To have a unique solution to the linear system (17), the number of the collocation points and the number of basis functions must be chosen so that $n_p\ge n_k$. In case of equality the linear system is squared otherwise we get an overdetermined linear system that can be solved by the least squares method (cf. [11]).

In practical computation, the iterative procedure is stopped when $\parallel {\mathsf{V}}^{(\ell )}\parallel /\parallel {\mathsf{L}}^{(\ell +1)}\parallel \le \tau$, where $\tau$ is a given tolerance. It is known that the local convergence of the Gauss-Newton method is not guaranteed, and particular attention should be paid in implementing the method.

The flow chart showing all the steps needed to implement the method is displayed in Figure 1.

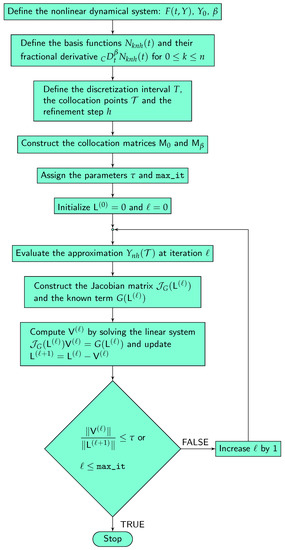
Figure 1. The flow chart of the collocation method described in Section 2.

3. Results

In this section, we give some algorithmic details on the collocation method described in the previous section when using linear or cubic splines to approximate its solution. Two Mathematica Notebooks (Supplementary Materials) [12] describing all the necessary steps to implement the algorithm for solving some numerical tests are provided as Supplementary Materials.

3.1. The Linear B-Spline Basis

Given a finite interval $[0,T]$, the linear B-spline basis

$${\mathcal{N}}_{1h}=\{N_{k1h}\left(t\right),0\le k\le n_k\},t\in [0,T],$$

has just one left-edge boundary function, i.e., $N_{01h}\left(t\right)$, and $n_k$ interior functions, i.e., $N_{k1h}\left(t\right)$, $1\le k\le n_k$, where $n_k=T/h$. Obviously, T and h must be chosen in order $n_k\in \mathbb{N}$. The explicit expression of the basis functions is well known and is given by

$$\begin{array}{cc}\hfill N_{01}\left(t\right)& =\left\{\begin{array}{cc}{\displaystyle (1-t),}\hfill & 0\le t\le 1,\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \\ \hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill N_{k1}\left(t\right)& =B_1(t-k+1),1\le k\le n_k,\hfill \end{array}$$

(20)

where

$$B_1\left(t\right)=\left\{\begin{array}{cc}t,\hfill & 0\le t\le 1,\hfill \\ 2-t,\hfill & 1\le t\le 2,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(21)

The Caputo derivative of fractional order $0<\beta <1$ of the basis functions has the following expression

$$\begin{array}{cc}\hfill {}_C{D}_t^{\beta }{N}_{01}\left(t\right)& =\frac{1}{\Gamma (2-\beta )}\left(t^{1-\beta }+{(t-1)}_{+}^{1-\beta }\right),\hfill \\ \hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {}_C{D}_t^{\beta }{N}_{k1}\left(t\right)& {=}_C{D}_t^{\beta }{B}_1(t-k+1),1\le k\le n_k,\hfill \end{array}$$

(23)

where

$${}_C{D}_t^{\beta }{B}_1\left(t\right)=\frac{1}{\Gamma (2-\beta )}{\Delta }^2{t}_{+}^{1-\beta }$$

(24)

is the Caputo derivative of the linear B-spline.

The edge function $N_{01}$ and the linear cardinal B-spline $B_1$ are shown in Figure 2 while their fractional derivative of order $\beta =0.5$ is shown in Figure 3.

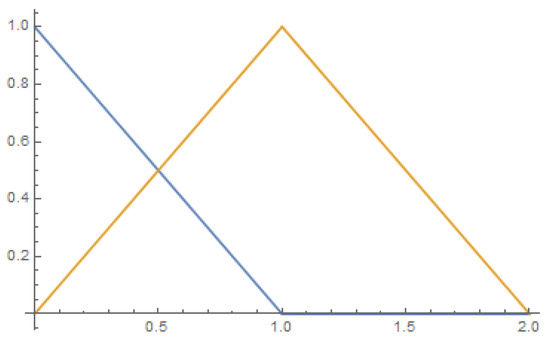
Figure 2. The left-edge function $N_{01}$ (blue) and the linear cardinal B-spline $B_1$ (orange).

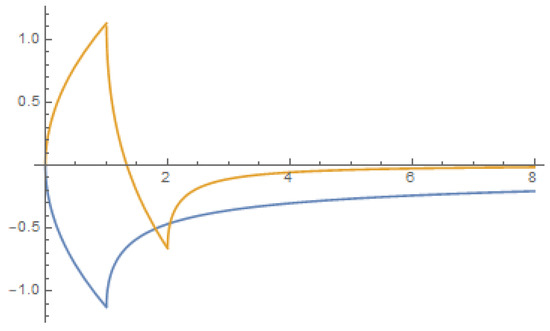
Figure 3. The fractional derivatives ${}_C{D}_t{N}_{01}$ (blue) and ${}_C{D}_t{B}_1$ (orange).

3.2. The Cubic B-Spline Basis

Given a finite interval $[0,T]$, the cubic B-spline basis

$${\mathcal{N}}_{3h}=\{N_{k3h}\left(t\right),0\le k\le n_k\},t\in [0,T],$$

consists of 3 left-edge boundary functions, i.e., $N_{k3h}\left(t\right)$, $0\le k\le 2$, and $n_k-2$ interior functions, i.e., $N_{k3h}\left(t\right)$, $3\le k\le n_k$, where $n_k=T/h+2\in \mathbb{N}$. Their explicit expression can be evaluated by Equations (4) and (5). For the convenience of the reader we give the resulting expression taken from [20]:

$$\begin{array}{cc}\hfill N_{03}\left(t\right)& =\left\{\begin{array}{cc}{\displaystyle {(1-t)}^3,}\hfill & 0\le t\le 1,\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \\ \hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill N_{13}\left(t\right)& =\left\{\begin{array}{cc}{\displaystyle \frac{1}{4}{(2-t)}^3-2{(1-t)}^3,}\hfill & 0\le t\le 1,\hfill \\ {\displaystyle \frac{1}{4}{(2-t)}^3,}\hfill & 1<t\le 2,\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.\hfill \\ \hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill N_{23}\left(t\right)& =\left\{\begin{array}{cc}{\displaystyle \frac{1}{6}{(3-t)}^3-\frac{3}{4}{(2-t)}^3+\frac{3}{2}{(1-t)}^3,}\hfill & 0\le t\le 1,\hfill \\ {\displaystyle \frac{1}{6}{(3-t)}^3-\frac{3}{4}{(2-t)}^3,}\hfill & 1<t\le 2,\hfill \\ {\displaystyle \frac{1}{6}{(3-t)}^3,}\hfill & 2<t\le 3,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \\ \hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill N_{k3}\left(t\right)& =B_3(t-k+3),3\le k\le n_k,\hfill \end{array}$$

(28)

where

$$B_3\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{6}{t}^3,}\hfill & 0\le t\le 1,\hfill \\ {\displaystyle \frac{1}{6}\left(-3t^3+12t^2-12t+4\right),}\hfill & 1\le t\le 2,\hfill \\ {\displaystyle \frac{1}{6}\left(-3{(4-t)}^3+12{(4-t)}^2-12(4-t)+4\right),}\hfill & 2\le t\le 3,\hfill \\ {\displaystyle \frac{1}{6}{(4-t)}^3,}\hfill & 3\le t\le 4,\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(29)

The Caputo derivative of fractional order $0<\beta <1$ of the basis functions has analytical expression

$$\begin{array}{cc}\hfill {}_C{D}_t^{\beta }{N}_{03}\left(t\right)& =\frac{3}{\Gamma (4-\beta )}\left(-\left(2t^2-2(3-\beta )t+{(2-\beta )}_2\right)t^{1-\beta }+2{(t-1)}_{+}^{3-\beta }\right),\hfill \\ \hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill {}_C{D}_t^{\beta }{N}_{13}(t)& =\frac{3}{\Gamma (4-\beta )}\left(\left((\frac{7}{2}{t}^2-3(3-\beta )t+{(2-\beta )}_2\right)t^{1-\beta }-4{(t-1)}_{+}^{3-\beta }+\frac{1}{2}{(t-2)}_{+}^{3-\beta }\right),\hfill \\ \hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill {}_C{D}_t^{\beta }{N}_{23}(t)& =\frac{3}{\Gamma (4-\beta )}\left(\left(-\frac{11}{6}{t}^2+(3-\beta )t\right)t^{1-\beta }+3{(t-1)}_{+}^{3-\beta }-\frac{3}{2}{(t-2)}_{+}^{3-\beta }+\frac{1}{3}{(t-3)}_{+}^{3-\beta }\right),\hfill \\ \hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill {}_C{D}_t^{\beta }{N}_{k3}(t)& {=}_C{D}_t^{\beta }{B}_3(t-k+3),3\le k\le n_k,\hfill \end{array}$$

(33)

where

$${}_C{D}_t^{\beta }{(r-t)}_{+}^3=-\frac{3}{\Gamma (4-\beta )}\left((2t^2-2(3-\beta )rt+{(2-\beta )}_2{r}^2)t^{1-\beta }-2{(t-r)}_{+}^{3-\beta }\right)$$

(34)

and

$${}_C{D}_t^{\beta }{B}_3\left(t\right)=\frac{1}{\Gamma (4-\beta )}{\Delta }^4{t}_{+}^{3-\beta }$$

(35)

are the Caputo derivatives of the truncated power function of degree 3 and of the cubic B-spline, respectively.

The edge functions $N_{03}$, $N_{13}$, $N_{23}$ and the cubic cardinal B-spline $B_3$ are shown in Figure 4 while their fractional derivative of order $\beta =0.5$ is shown in Figure 5.

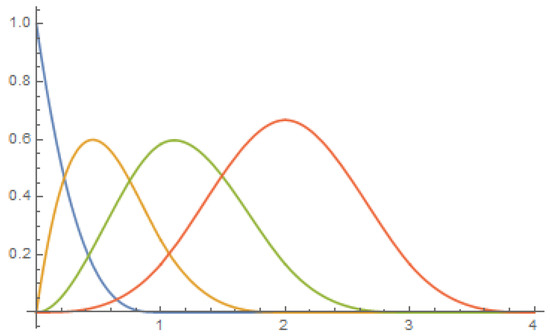
Figure 4. The left-edge functions $N_{03}$ (blue), $N_{13}$ (orange), $N_{23}$ (green), and the cubic cardinal B-spline $B_3$ (red).

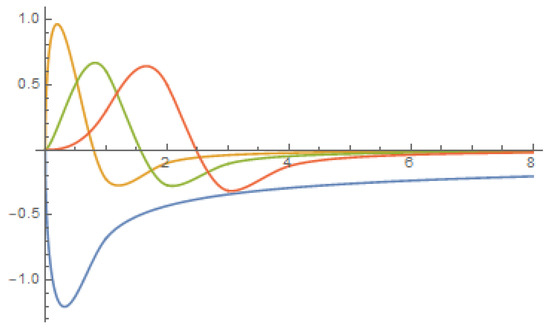
Figure 5. The fractional derivatives ${}_C{D}_t{N}_{03}$ (blue), ${}_C{D}_t{N}_{13}$ (orange), ${}_C{D}_t{N}_{23}$ (green), ${}_C{D}_t{B}_3$ (red).

3.3. Numerical Solution of Linear Dynamical Systems

The collocation method described in Section 2.5 can be also used to solve linear problems of type

$$\left\{\begin{array}{cc}{}_C{D}_t^{\beta }Y\left(t\right)=AY\left(t\right),\hfill & t>0,0<\beta <1,\hfill \\ Y\left(0\right)=Y_0,\hfill \end{array}\right.$$

(36)

where $A\in {\mathbb{R}}^{m\times m}$ is a real matrix. In this case, the Jacobian matrix is independent of ℓ and reduces to

$${\mathcal{J}}_G={\mathsf{I}}_m\otimes M_{\beta }-A\circ ({\mathsf{I}}_m\otimes M_0),$$

so that the numerical solution is computed by solving a linear system (cf. [11]). As a test problem we consider the linear dynamical system

$$\left\{\begin{array}{c}{}_C{D}^{\frac{1}{2}}{y}_1\left(t\right)=y_1\left(t\right)+y_2\left(t\right)+y_3\left(t\right),\hfill \\ {}_C{D}^{\frac{1}{2}}{y}_2\left(t\right)=-y_1\left(t\right)+y_2\left(t\right)-y_3\left(t\right),t>0,\hfill \\ {}_C{D}^{\frac{1}{2}}{y}_3\left(t\right)=-\frac{\sqrt{\pi }}{2}{y}_3\left(t\right),\hfill \\ y_1\left(0\right)=0.05,y_2\left(0\right)=0.05,y_3\left(0\right)=0.05.\hfill \end{array}\right.$$

(37)

taken from [23]. We solved the problem on the discretization interval $[0,8]$ using a set of equidistant collocation nodes with time step $\Delta t=\frac{1}{32}$ for a total of 254 collocation points. We used as function basis the cubic B-spline basis and the linear B-splines basis with $h=\frac{1}{16}$ so that the basis has 131 functions and 129 functions, respectively. Thus, the final linear system to be solved has 765 equations and 390 unknowns in the first case and 765 equations and 384 unknowns in the second case. The numerical solutions obtained by the algorithm implemented in the Mathematica Notebooks (Supplementary Materials) are displayed in Figure 6.

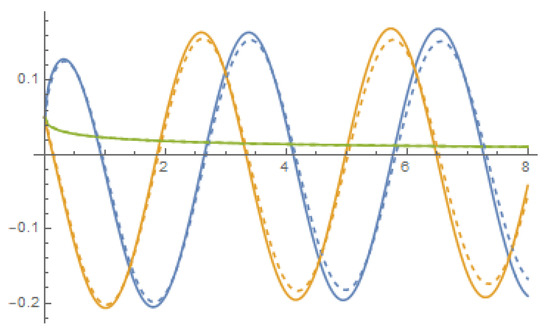
Figure 6. The numerical solution $Y_{nh}\left(t\right)$ for $n=3$ (solid lines) and $n=1$ (dashed line) of the linear dynamical system (37). In both cases $h=\frac{1}{16}$. The first, second and third entries of the vector $Y_{nh}\left(t\right)$ are displayed in blue, yellow and green, respectively.

3.4. Numerical Solution of Nonlinear Dynamical Systems

We solved the nonlinear dynamical system (cf. [23])

$$\left\{\begin{array}{c}{}_C{D}^{\frac{1}{2}}{y}_1\left(t\right)=y_1\left(t\right)+y_2\left(t\right)+100\sqrt{\pi }{y}_1^2\left(t\right)+y_3\left(t\right),\hfill \\ {}_C{D}^{\frac{1}{2}}{y}_2\left(t\right)=-y_1\left(t\right)+y_2\left(t\right)+100\sqrt{\pi }{y}_1^2\left(t\right)-y_3\left(t\right),t>0,\hfill \\ {}_C{D}^{\frac{1}{2}}{y}_3\left(t\right)=y_3^2\left(t\right)-{\displaystyle \frac{\sqrt{\pi }}{200}}{y}_3\left(t\right),\hfill \\ y_1\left(0\right)=0.05,y_2\left(0\right)=0.05,y_3\left(0\right)=0.05.\hfill \end{array}\right.$$

(38)

using the same collocation points and the same function basis as in the linear case.

The numerical solutions obtained by the algorithm implemented in the Mathematica Notebooks (Supplementary Materials) are displayed Figure 7.

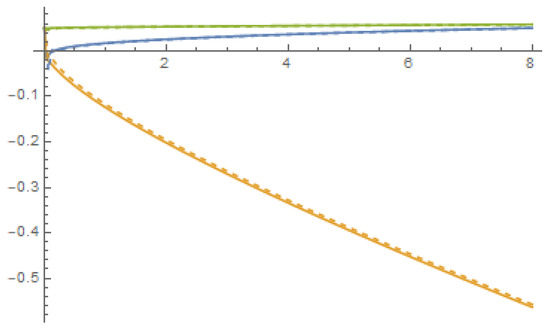
Figure 7. The numerical solution $Y_{nh}\left(t\right)$ for $n=3$ (solid lines) and $n=1$ (dashed line) of the nonlinear dynamical system (38). In both cases $h=\frac{1}{16}$. The first, second and third entries of the vector $Y_{nh}\left(t\right)$ are displayed in blue, yellow and green, respectively.

4. Discussion

The examples above show that the collocation method described in Section 2 is easy to implement and give accurate results both in the linear and cubic case. We notice that the Mathematica Notebooks (Supplementary Materials) we provided are just intended for explaining in detail the algorithm shown in Figure 1. To solve high dimensional problems the algorithm should be implemented in a more efficient way. For instance, the slight instabilities appearing near the initial point in Figure 7 can be avoided by solving the overdetermined linear system (17) by Krylov methods [24]. Moreover, the Jacobian matrix ${\mathcal{J}}_G$ can be compressed by usual techniques [25]. Taking these remarks into account, the method can be used not only to solve several kinds of initial problems but also to solve boundary value problems.

5. Conclusions

We presented a collocation method suitable to solve nonlinear differential problems with time fractional derivative. The strength of the method is its ability to approximate exactly the fractional derivative of the approximating function by using the explicit formulas (7) and (8). Moreover, the method is easy to implement since required just the construction of the nonlinear system (14). With respect to the collocation method considered in [17], where the number of equations is equal to the number of unknowns, in our examples the number of equations is almost twice the number of unknowns. To apply the method in case of high dimensional problems, the number of equations should be reduced. This can be done, for instance, using non-equidistant collocation points as done in [17]. In particular, using Gaussian nodes instead of equidistant nodes not only could reduce the dimension of the nonlinear system but could also improve the accuracy of the method. Finally, a detailed analysis of the stability and the convergence of the method should be conducted. This will be the subject of a forthcoming paper.