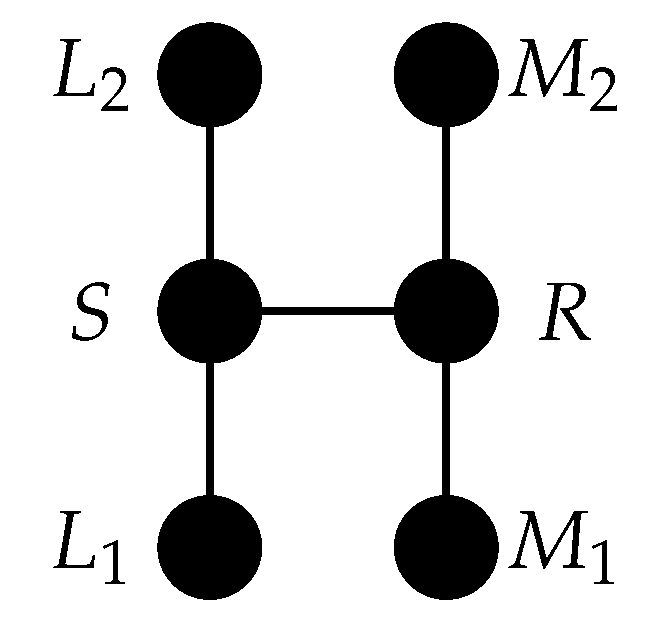1. Introduction
Let G be a graph and let v be a vertex of G. The open neighbourhood of a vertex v, denoted , is the set of vertices adjacent to v, and the closed neighbourhood of a vertex v, denoted , is . For a subset of vertices S, we say and . A subset of vertices D is a dominating set of G if , that is, every vertex not in D is adjacent to a vertex in D. The domination number of a graph G, denoted , is the minimum cardinality of a dominating set of G. A dominating set of minimum cardinality is said to be a γ-set.
For a dominating set D of G and a vertex , the set of D-private neighbours of x, denoted , is , that is, the set of vertices in the closed neighbourhood of x and not in the closed neighbourhood of any other vertex in D. If , then x is a D-self private neighbour in D and if and , then y is an D-external private neighbour of x in D. If D is a -set, then every vertex in D has a private neighbour.
The
γ-graph of a graph
G, introduced by Fricke et al. [
4], is a graph denoted
, has its vertex set as the
-sets of
G, and two
-sets
and
are adjacent in
if there is a vertex
and a vertex
such that
and
. Starting with
, we think of making a
swap, that is, changing vertex
u for
v, to form
. For convenience throughout the paper, we equate each node in
with its corresponding
-set of
G. A slightly different model, in which
need not be an edge in
G, was introduced independently by Subramanian and Sridharan [
8]; we do not consider this model here. Fricke et al. [
4] studied properties of
-graphs, and raised the following open questions:
Is for every tree T of order n?
Is for every tree T of order n?
Is for every tree T?
Which graphs are -graphs of trees?
Which graphs are -graphs? Can you construct a graph H that is not a -graph of any graph G?
For which graphs G is ?
Under what conditions is a disconnected graph?
The first three questions were solved by Edwards, MacGillivray, and Nasserasr [
3] and the fifth question was answered by Connelly, Hutson, and Hedetneimi [
2]; the other three questions remain open. The question of which graphs are
-graphs of trees was restated in a recent survey by Mynhardt and Nasserasr [
5] as a primary direction of study in this area.
Some
-graphs of trees were determined by Fricke et al. [
4], as well as a couple of general properties. A
stepgrid is the induced subgraph of the
grid graph
defined as follows:
, where
Proposition 1. .
For , .
.
.
.
Theorem 1. [4] Let T be a tree, and let be a vertex that does not appear in any γ-set of T. Let be the disjoint subtrees created by deleting x from T, and let be the vertex in subtree adjacent to the vertex x. Let be the set of minimum dominating sets of subtree and let be the γ-graph of subtree using only those γ-sets of that do not contain . Then Theorem 2. [4] The γ-graph of every tree T is a connected graph. Theorem 3. [4] For any tree T, is -free, for any odd . [That is, is bipartite.] The main objective of this paper is the investigation of open question 4. In
Section 2, we develop a method for constructing the
-graph of a tree. In
Section 3, we characterize those trees which are
-graphs of trees. Finally, in
Section 4, we state some further results for graphs which are
-graphs of trees.
The following observations are used, frequently without reference, throughout the paper.
Observation 1. If and with are two distinct γ-sets of a tree, then .
Observation 2. If is such that , then for each , we have that D is adjacent to .
Observation 3. If , and with are three distinct -sets of a tree, then .
Note that Observations 1 and 3 do not hold for general graphs.
2. Computing -Graphs of Trees
While Fricke et al. [
4] developed a method to determine the
-graphs of trees that contain a vertex not appearing in any
-set (Theorem 1), there are trees for which every vertex appears in some
-set. We present a general algorithm to determine the
-graph of a tree. We first state the following results of Edwards, MacGillivray, and Nasserasr [
3] which will aid in verifying the algorithm. If
D is a
-set of a rooted tree
, then the
depth of
D, denoted
(referred to as the height of
D in [
3]), is
. Define
D to be a
higher-set than
F if
and
D to be a
highest γ-set if
for all
-sets
F of
T. That is the minimum depth is equal to the greatest height.
Lemma 1. [3] A γ-set D is a highest γ-set of a tree T rooted at a vertex c if and only if every has a child . Theorem 4. [3] Let T be a tree rooted at a vertex c. Then T has a unique highest γ-set. The algorithm DOMSET, developed by Cockayne, Goodman, and Hedetniemi [
1] finds a minimum dominating set of a tree in linear time. We demonstrate that with a slight modification to the algorithm not affecting the run time, i.e., we exclude the root from being an eligible end vertex, the algorithm finds the highest minimum dominating set of a rooted tree.
Theorem 5. Let T be a tree rooted at a vertex c. The output, S, of HIGHEST (see Algorithm 1) is the highest γ-set of T.
| Algorithm 1 Let T be a tree rooted at a vertex c. We construct the highest -set S of as follows: |
- 1:
procedureHIGHEST() - 2:
Set ; ; label each vertex of T as bound. - 3:
while G has an endvertex adjacent to a vertex u do - 4:
if v is free then - 5:
. - 6:
else if v is bound then - 7:
Relabel u as required; - 8:
. - 9:
else if v is required then - 10:
; - 11:
If u is bound then relabel u as free; - 12:
. - 13:
end if - 14:
end while - 15:
if c is not free then - 16:
. - 17:
end if - 18:
end procedure
|
Proof. Let D be the -set output by HIGHEST. By Lemma 1, D is a highest -set of T if and only if every has a child . Suppose there exists an such that x has no child in . Let y be a child of x. Either or some child of y was in S. In the first case, y was relabelled required when it was processed by HIGHEST and in the latter case y was labelled required or free, when it was processed by HIGHEST. In either case y was not labelled bound. But then, as y was arbitrary, x could not have been labelled as required before being processed by HIGHEST, and so , contradicting our assumption. Hence, together with Theorem 4, S is the highest -set of T. □
We now present the following algorithm for determining the
-graph of a tree. For each vertex
v in
T, let
be its index in a breadth-first traversal of
T. We note that any such algorithm must be exponential as the number of gamma sets of a tree is potentially exponential. Recently, Rote [
6] provided a family of trees, referred to as the
star of snowflakes, with
vertices and at least
minimum dominating sets, i.e., trees whose number of
-sets is on the order of
, establishing a lower bound on the maximum number of minimum dominating sets.
The remainder of this section is devoted to verifying the correctness of GAMMATREE(). The index of a -set D, denoted here , is defined on line 16 of Algorithm 2. We first prove the following lemma regarding the value of the index of a -set.
| Algorithm 2 Let T be a tree rooted at a vertex c and let S be the highest -set of T. For each vertex v in T, let be its index in a breadth-first traversal of T. We construct the -graph of T, , as follows: |
- 1:
procedureGAMMATREE() - 2:
; . - 3:
; ; . - 4:
for all do - 5:
for all do - 6:
if then - 7:
. - 8:
else if then - 9:
. - 10:
else - 11:
. - 12:
end if - 13:
for all do - 14:
. - 15:
; . - 16:
; ; . - 17:
. - 18:
for all do - 19:
for all do - 20:
if then - 21:
. - 22:
. - 23:
. - 24:
end if - 25:
end for - 26:
end for - 27:
end for - 28:
end for - 29:
end for - 30:
end procedure
|
Lemma 2. Let T be a tree rooted at a vertex c and let S be the highest γ-set of T. For every γ-set found by GAMMATREE(), Proof. Suppose is the first -set of T found by GAMMATREE() such that is not the largest index of the vertices of not appearing in S. By definition of , there exists a -set D and vertices such that , and .
Suppose first that y is a vertex in such that . By choice of , we have that and since , . Hence, , which is a contradiction. Therefore, for all and if so we assume .
Hence any vertex in with an index at least must also be in S. In particular, x, and every descendant of x in must also be in S. By Lemma 1, x, and every descendant of x in S has a child S-private neighbour which is also a child -private neighbour. Let w be a child S-private neighbour of x which is also a child -private neighbour of x. Clearly . As D is dominating and , it must be the case that . Hence , which is a contradiction as . The result follows. □
Theorem 6. Let T be a tree rooted at a vertex c and let S be the highest γ-set of T. Every γ-set of T is obtained by GAMMATREE().
Proof. Assume there is a -set of T which is not obtained by GAMMATREE(. For a -set of T, we define , where . Let be the -set not obtained by GAMMATREE() for which is lexicographically smallest. Let x be so that . Then every descendant of x in has a higher index and hence is also in S. It follows from Lemma 1, each descendant of x in has a child -private neighbour. If x also has a child -private neighbour, then every higher -set of T must contain x, contradicting that . Hence, no child of x is a -private neighbour. Therefore, if v is the parent of x, then the set is a -set of T. Since is lexicographically smaller than , D is found by GAMMATREE(). Clearly each vertex in has a smaller index than x, so . Further, as D and are both -sets of T, , so for , . Hence, is found by GAMMATREE(), which is a contradiction proving the theorem. □
Finally, we will show GAMMATREE() obtains every edge of . We first demonstrate that the -sets are obtained by GAMMATREE in order of depth.
Lemma 3. The algorithm GAMMATREE can be implemented so that the γ-sets of T are obtained in order of depth.
Proof. Let D be a -set obtained by GAMMATREE(. As GAMMATREE( runs, store the dominating sets of T (these are the elements of V) in a queue, so that first one discovered by GAMMATREE( is the first one processed by GAMMATREE(. It suffices to prove that every -set found from D (i.e., at line 14) is such that . We observe that for adjacent vertices v and x. If , then every has a child , so x is a child of v and as desired. Now suppose . If , then by Lemma 2, and every descendant of v which is in D is also in S. It follows that v has a child , so x must be a child of v, and as desired. Otherwise, and . Then it is clear that x is a child of v, and the result again follows. □
Theorem 7. Let T be a tree rooted at a vertex c and let S be the highest γ-set of T. The algorithm GAMMATREE can be implemented so that each edge in is obtained by GAMMATREE().
Proof. Implement algorithm GAMMATREE
as required in Lemma 3 and suppose not all edges of
are obtained. Let
be the first
-set found by GAMMATREE(
) such that there exists a
-set
, found before
, where
,
, but edge
is not obtained by GAMMATREE(
). By Lemma 3,
. As
and
are both
-sets of
T, we have
. Suppose
. Then by Lemma 3,
was found while processing a set
, where
w is the parent of
x in
T. Clearly, neither
nor
is
S. Hence, there exists a
-set
such that
. Moreover, since
w is the parent of
x, we have
so
is found before
and
by Lemma 3. Hence,
and
were both obtained by GAMMATREE(
). In particular,
and
. Thus, we obtain the edge
when processing
, which is the contradiction proving the theorem. □
The correctness of the algorithm immediately follows.
Corollary 1. Let T be a tree rooted at a vertex c and let S be the highest γ-set of T. The algorithm GAMMATREE() can be implemented to produce .
Proof. By Theorem 6, we obtain every vertex of , and by Theorem 7, we obtain every edge of . The result follows. □
3. -Trees of Trees
In this section, we characterize the trees which are -graphs of trees. We first consider properties of the -sets corresponding to the leaves of a -graph. (Recall we equate each node in with its corresponding -set of G.)
Lemma 4. Let T be a tree with at least three vertices and let be the γ-graph of T. If D is a leaf in , then exactly one vertex has fewer than two D-external private neighbours. Furthermore either v has exactly one D-external private neighbours or v is both a leaf in T and a D-self private neighbour.
Proof. Note that if every vertex of dominating set D in a tree has at least two D-external private neighbours, D has no neighbours in . If a vertex x in T has exactly one external private neighbour y in D, then is a -set of T adjacent to D. If a vertex z in T has no external private neighbours in D, then z must be a self private neighbour in D and for every , is a -set of T adjacent to D. As D is adjacent to exactly one -set, the result follows. □
Next, we prove a fundamental result on the number of private neighbours of a vertex in adjacent -sets of a tree.
Lemma 5. Let D and F be γ-sets of a tree T which are adjacent in and let . Then and .
Proof. Suppose for adjacent vertices y and z in T. Let . Suppose the result is false and assume without loss of generality that . If x is a D-self private neighbour, but not an F-self private neighbour, then and z is adjacent to a D-external private neighbour of x, say w. Then of is a 3-cycle in T, which contradicts that T is a tree. Otherwise, x has at least two D-external private neighbours that are adjacent to z, so is a 4-cycle in T, which contradicts that T is a tree. The result follows. □
We now consider the -sets of leaves adjacent to the same stem.
Lemma 6. Let T be a tree and let be the γ-graph of T. If S is a stem in with degree at least three and are the leaves of S, then there exists vertices and so that and for .
Proof. If , the statement is trivial, so assume . As S is adjacent to in , for each i there exists vertices and so that and . Let . Suppose . By Lemma 4, is the only vertex in with fewer than two -external private neighbours. In particular, if , then has at least two -external private neighbours. It now follows from Lemma 5, that each has an S-external private neighbour.
If , then is not a -set of T as and are leaves of . Hence there exists a vertex which is not dominated by . It must be the case that both and are neighbours of . If , then each such must be identical or T is not a tree, but then is dominating, a contradiction. Hence we assume , say . Note that for , . As each has an S-external private neighbour, is an S-private neighbour of . Hence for , may only swap with . Furthermore as is the only vertex in with fewer than two -external private neighbours, and have only one common neighbour, , and since T has no cycles, it follows that and are the only vertices in S with fewer than two S-external private neighbours. Thus, S, , and are the only -sets of T, contradicting that S has degree at least three. Hence, , which completes the proof. □
Our next step is to show the graph
H, pictured in
Figure 1, is not a
-graph of a tree.
Lemma 7. No tree has H as its γ-graph.
Proof. Let
H be labeled as in
Figure 1 and suppose
H is the
-graph of a tree
T. By Lemma 6, there exists vertices
and
so that
and
where
and
. Further there exists
so that
with
. By Observation 3,
x has no
S-external private neighbours and
w has no
R-external private neighbours.
Suppose first . Then and by Lemma 5, x has at most one R-external private neighbour. Hence, there exists a vertex such that is a -set of T. As and R has only three neighbours, it follows that and therefore . By Observation 2, and and therefore . Without loss of generality . Then . Thus, and are neighbours in H, which is a contradiction.
Hence it must be that . By symmetry, . It follows that and . In particular, . But as w has no R-external private neighbours, it is a self private neighbour in R, and hence must be an external private neighbour of x in S. But x has no S-external private neighbours, which is a contradiction. The result follows. □
We now show that if a graph is a -graph of a tree, then deleting leaves produces graphs that must also be -graphs of trees. In particular, if a tree is a -graph of a tree, then all subtrees are also -graphs of trees.
Lemma 8. If G is a γ-graph of a tree T, D is a leaf of G and has fewer than two D-external private neighbours, then D is the unique γ-set of T containing x.
Proof. Consider a component of . Then is clearly a dominating set of . If is not also a -set of , then D is not minimal. Hence is a -set of and since each vertex of has at least two D-external private neighbours, has no neighbours in . It follows from Theorem 2 that is the only -set of . As T is a tree, the vertices in are adjacent to at most one vertex in . Recall each vertex of has at least two D-external private neighbours. Let E be a -set of T containing x. Then must contain at least vertices. Since was arbitrary, and , the set E has at most one vertex in , namely x. For any component, of , is the unique -set of . Therefore D is the unique -set of T containing x. □
Theorem 8. If G is a γ-graph of a tree T and L is a leaf of G, then is a γ-graph of some tree .
Proof. By Lemma 4, exactly one vertex x in L has fewer than two L-external private neighbours. Moreover, either x has exactly one L-external private neighbour or x is a leaf in T and an L-self private neighbour. By Lemma 8, L is the unique -set of T containing x.
If x is a leaf of T and is an L-self private neighbour, then is formed by adding a leaf to the stem of x. Suppose on the other hand, x has exactly one external private neighbour y. If x is a self private neighbour, then is formed by rooting T at y, deleting the descendants of x, and adding a leaf to y. Otherwise, is formed by rooting T at y, and deleting x and its descendants. □
Corollary 2. If G is a tree and a γ-graph of a tree T, then every subtree of G is a γ-graph of some tree.
Corollary 3. If G is a tree and a γ-graph of a tree T, then is not a subtree of G.
Proof. The result immediately follows from Lemma 7 and Corollary 2. □
From the previous corollary, we know that if a tree is a -graph of a tree, then the vertices of degree at least three are not adjacent. We now wish to show all trees without adjacent vertices of degree at least three are the -graph of a tree. The proof is constructive. We establish first some building blocks.
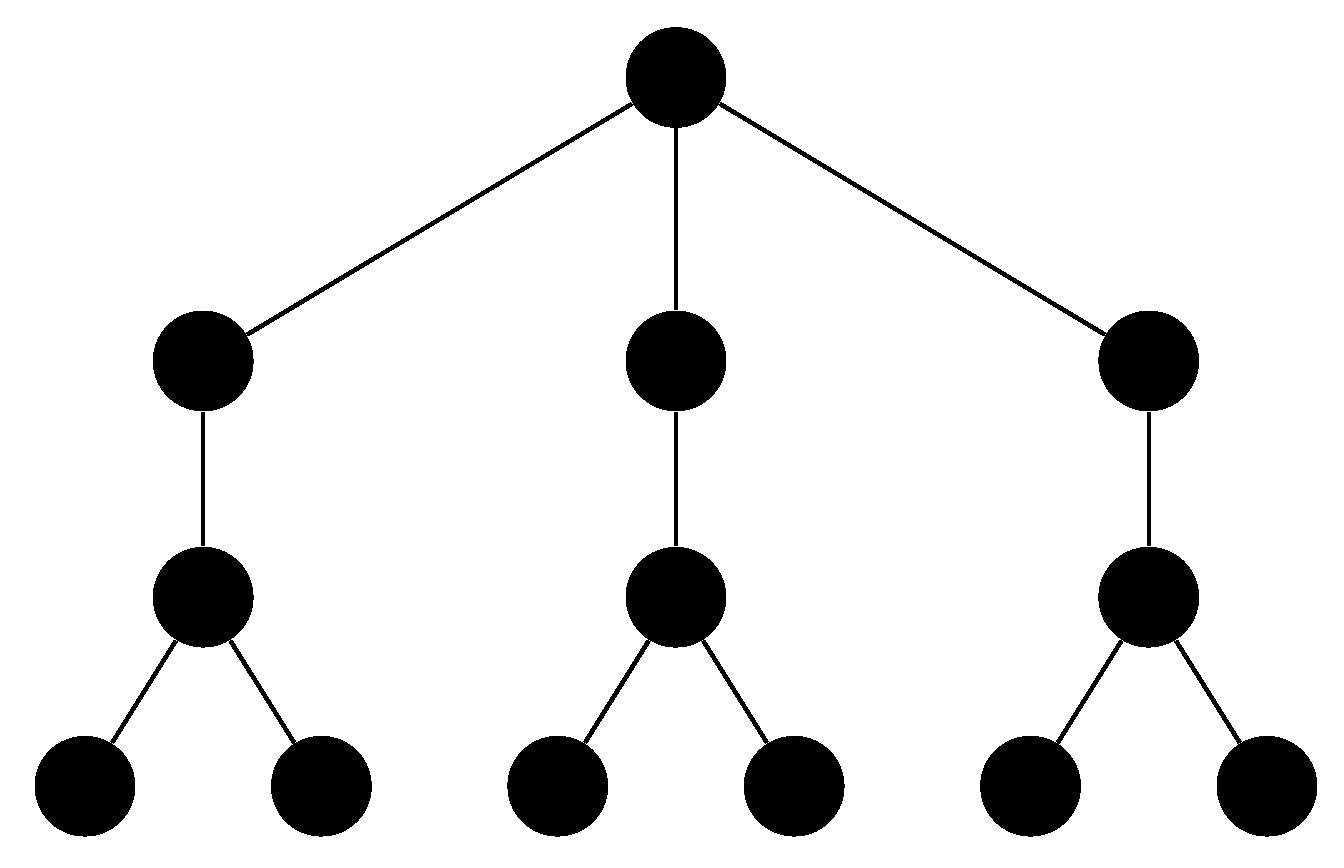
Theorem 9. Let be the graph obtained by taking n copies of and joining a leaf of each copy to a common vertex (see Figure 2 for an example). Then , and in every γ-set which is a leaf of , every vertex has an external private neighbour. Proof. Since every stem of is adjacent to two leaves, every -set of must contain every stem. Only the common centre vertex is left to be dominated, so we can form a -set by adding this vertex or any of its neighbours. Further, the only edges are between the -set containing the common centre vertex and each of the other -sets. Finally, in each of these other -sets, every stem has at least two external private neighbours, its leaves, and the additional vertex has the common centre vertex as its private neighbour. The result follows. □
We now provide a tool for combining these building blocks.
Lemma 9. Suppose for , is a γ-graph of tree , is a leaf of and every vertex in the dominating set has at least one -external private neighbour. By Lemma 4, in each there is exactly one vertex with fewer than two -external private neighbours. Then G, the graph formed by identifying and is the γ-graph of a tree , the tree formed by linking and by creating a new vertex v adjacent to and .
Furthermore let be a dominating set of and be the corresponding dominating set of T. If every vertex of Y has a Y-external private neighbour, then every vertex in has a -external private neighbour.
Proof. By Lemma 4, exactly one vertex in has fewer than two external private neighbours. It follows that has exactly one external private neighbour. Form T from and by adding a new vertex v with . We now show that .
It is clear that . Suppose some -set D of T contains v. Then without loss of generality, . Let be a -set of . Then no neighbour of is in . Hence is a -set of and has no external private neighbours. Then, by Lemma 8, is the unique -set of containing , so . But this contradicts the presupposition that every vertex in has an -external private neighbour. Hence no -set of T contains v, and every -set of T is the union of a -set of and a -set of .
Every -set of T must contain or for v to be dominated. Let . It is clear that X is the unique -set containing both and . Since every other vertex in X has least two external private neighbours, and and have exactly one external private neighbour, X is adjacent to two -sets. Let D be a dominating set of T other than X. If and by Lemma 8, and every vertex in has at least two D-external private neighbours. Therefore the subgraph of the -sets of T containing in is and similarly the subgraph of the -sets of T containing in is . Hence, the -graph of T is G as required. The final statement follows directly from the above construction. □
We can now prove the main result.
Theorem 10. If G is a tree, then G is a γ-graph of some tree if and only if H is not a subtree of G.
Proof. Necessity follows by Corollary 3; it remains to show sufficiency. The result trivially holds for as ; so suppose G has at least two vertices. We proceed by induction on k, the number of degree two vertices of G. If , then , and by Theorem 9, is the -graph of , and in every -set which is a leaf of , every vertex has an external private neighbour.
Assume and that every tree F not containing H as a subtree with fewer than k degree two vertices is the -graph of some tree and in every -set which is a leaf of F, every vertex has an F-external private neighbour. Let x be a degree two (cut-)vertex in G, and let and be the two components of . As and each have fewer than k degree two vertices, then by the induction hypothesis, each is the -graph of a tree (say and respectively) and in every -set which is a leaf of and repsectively, every vertex has an external private neighbour. By Lemma 9, there are vertices and so that the -graph of is G and by construction, in every -set which is a leaf of G, every vertex has an external private neighbour. The result follows. □
4. Properties of -Graphs of Trees
In this section, we investigate general properties of -graphs of trees. We begin with a result classifying the edges in -graphs of trees, highlighting the importance of cut edges and 4-cycles in these graphs.
Lemma 10. Let T be a tree and let be the γ-graph of T. Every edge of is a cut-edge or is contained in a 4-cycle.
Proof. Let e be an edge which is not a cut-edge of . Then e is contained in a cycle. But cycles in Algorithm 2 are only created at line 21, which always creates a 4-cycle. The result follows. □
We now show that a cut-edge, not incident with a leaf allows you to decompose a -graph of a tree into two smaller graphs, both of which are also -graphs of trees.
Lemma 11. Let G be a γ-graph of a tree T with a cut-edge e, and let and be the components of . Then and are each γ-graphs of trees.
Proof. Let with and and assume . Let be the set of vertices that can be swapped from B. Form by adding a leaf to each . Since e is a cut-edge, cannot be swapped in A, and hence each has exactly one external private neighbour in B. But B is also a -set of , and each has two external private neighbours. Moreover, each -set in is also a -set of , so it follows that is the -graph of . By symmetry, is also the -graph of a tree. □
Setting
(see
Figure 1) and
e the edge joining the two stems of
H, shows the converse of Lemma 11 does not necessarily hold. That is both
and
are each
-graphs of trees, but
is not a
-graph of any tree. Lemma 11 does provide a tool for showing a graph with a cut-edge not incident to a leaf is not the
-graph of any tree
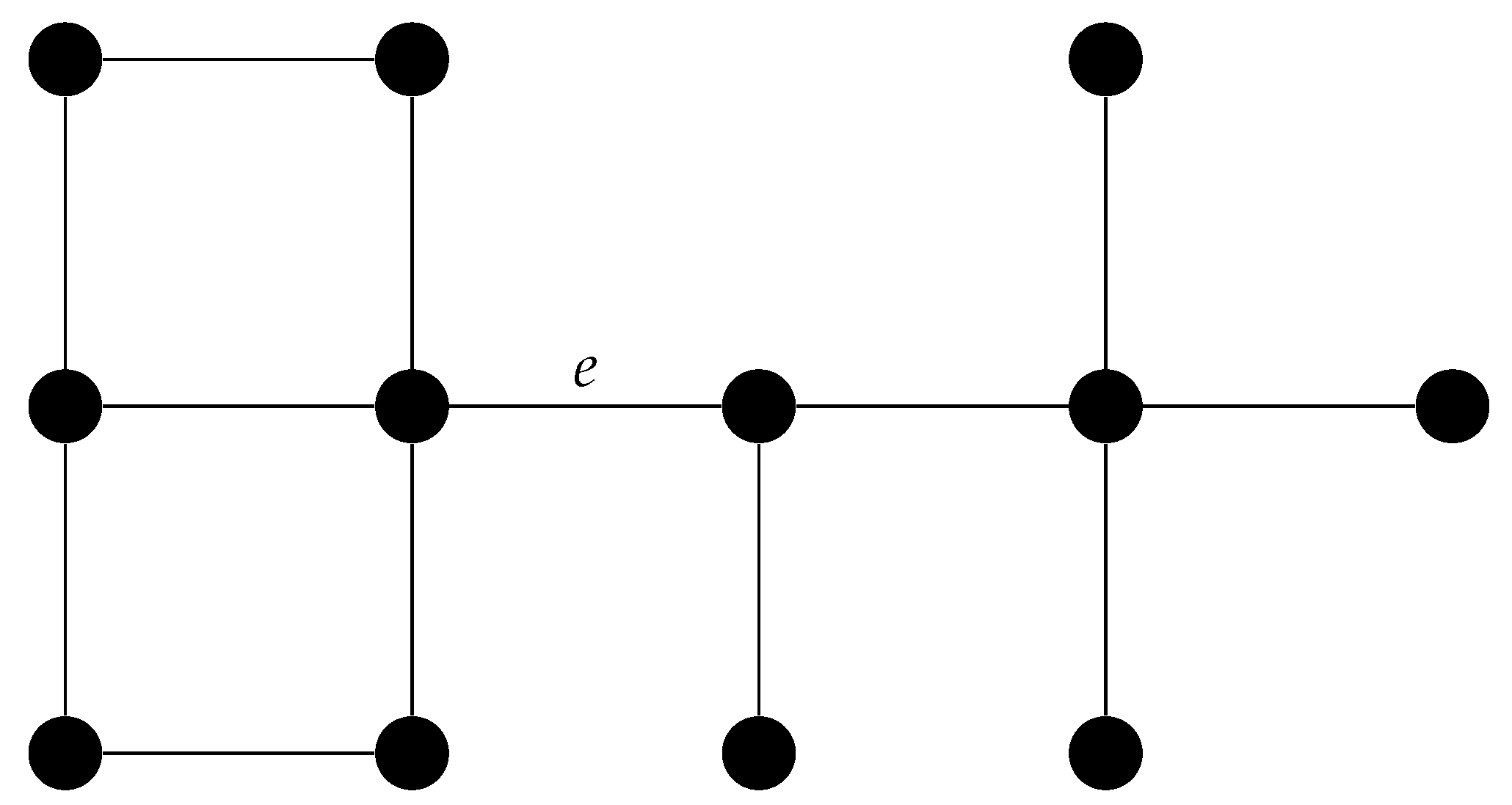
T. For example, consider the graph
Z shown in
Figure 3. Let
and
be the components of
Z obtained by deleting the edge
e, where
is a tree. Then
is a tree with adjacent vertices of degree at least 3 and thus by Theorem 10,
is not the
-graph of any tree
T. It now follows from Lemma 11 that
Z is not the
-graph of any tree
T.
The remainder of the paper will focus on
-graphs of trees where every edge is in a 4-cycle or incident with a leaf. We first present the following useful result due to Edwards, MacGillivray, and Nasserasr [
3], which will be applied throughout.
Lemma 12. [3] For a γ-set D of a tree T and a vertex , there is at most one vertex such that is also a γ-set of T. We now demonstrate a key property of the -sets which when equated to their vertices form a 4-cycle of ) that we will make extensive use of in our next set of results.
Proposition 2. If G is a γ-graph of a tree T and is a 4-cycle of G, then for some distinct and distinct with and , , and .
Proof. For some and with and we have and . It follows from Lemma 12 that . If , then as , for some vertex , with , and with . But then is a 4-cycle in T, which contradicts that T is a tree. Hence either or . Suppose without loss of generality . In the case that , then and therefore . This implies s is adjacent to q in T and r is adjacent to p in T (with ). But then is a 4-cycle in T, contradicting that T is a tree. Hence, . If , then there exists a vertex so that and hence both s and q are adjacent to u in T. It follows that is a cycle in T, showing that p and r are distinct. Thus , as required. □
4.1. Cartesian Product and -Graphs of Trees
Every edge in the Cartesian product of two connected graphs of order at least two is in a 4-cycle. Theorem 1 highlights one aspect of the connection between
-graphs and the Cartesian product. When movement of the dominating set in one part of a graph has no effect on movement of the dominating set in another part of the graph, the Cartesian product frequently arises. In this section we exploit this connection and establish that the Cartesian product can both decompose
-graphs of trees into smaller
-graphs of trees and be used to combine
-graphs of trees to discover other
-graphs of trees. We first consider
Cartesian product graphs, the set of graphs which can be obtained from the Cartesian product of graphs of order at least two. Sabidussi [
7] and Vizing [
9] independently demonstrated a prime factorization of graphs, analogous to the Fundamental Theorem of Arithmetic.
Theorem 11. [7,9] All finite connected graphs have a unique prime factorization with respect to Cartesian multiplication. We show that if G is a `composite’ graph, then each of its prime factors are -graphs of trees if and only if G is also the -graph of a tree. Hence, to characterize -graphs of trees, we need only consider `prime’ graphs under Cartesian multiplication. The proof in one direction is technical and so we first provide an example to demonstrate the proof. We require a definition. Let T be a tree and consider an edge of , where and are -sets of T. Define , the unique vertices x and y so that .
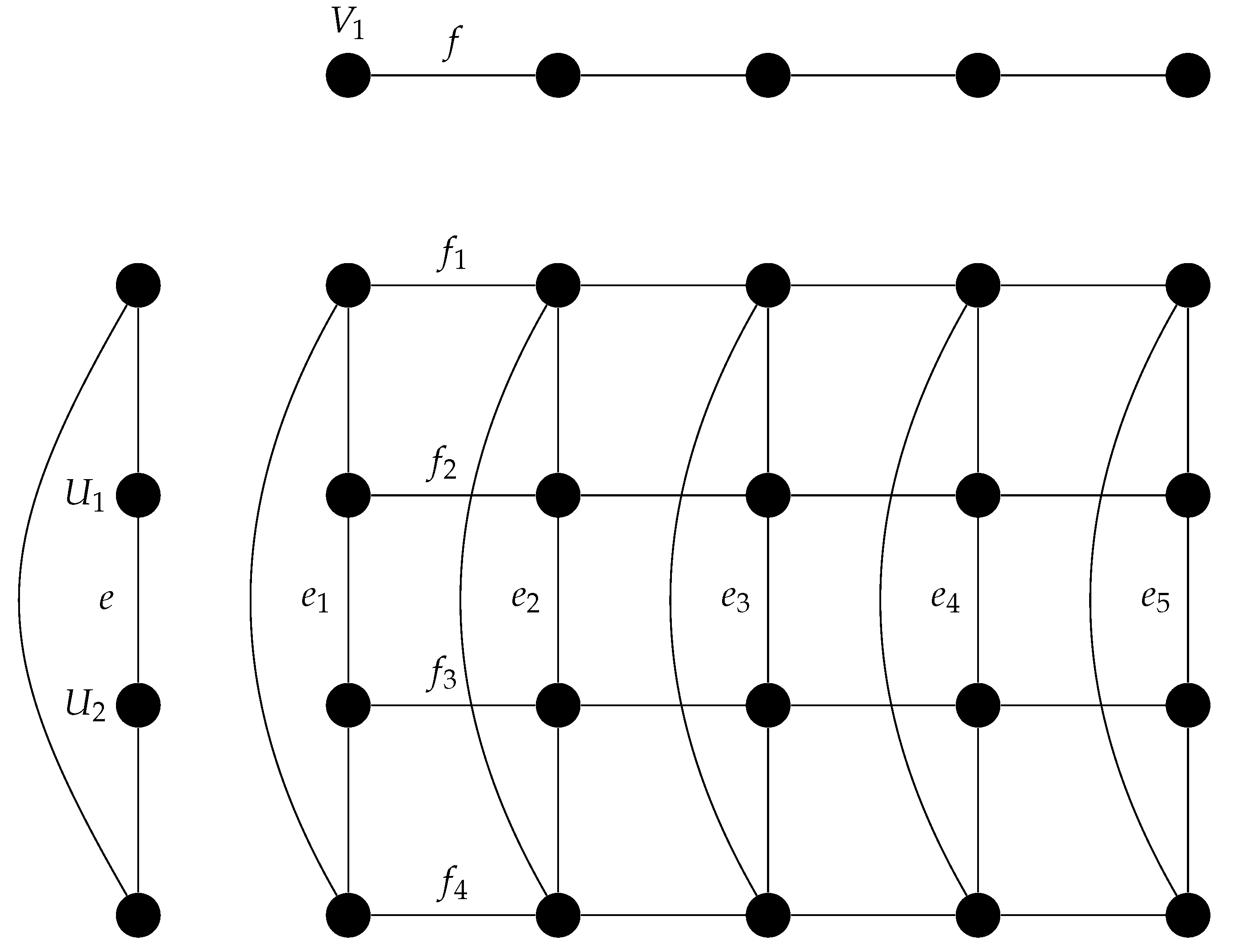
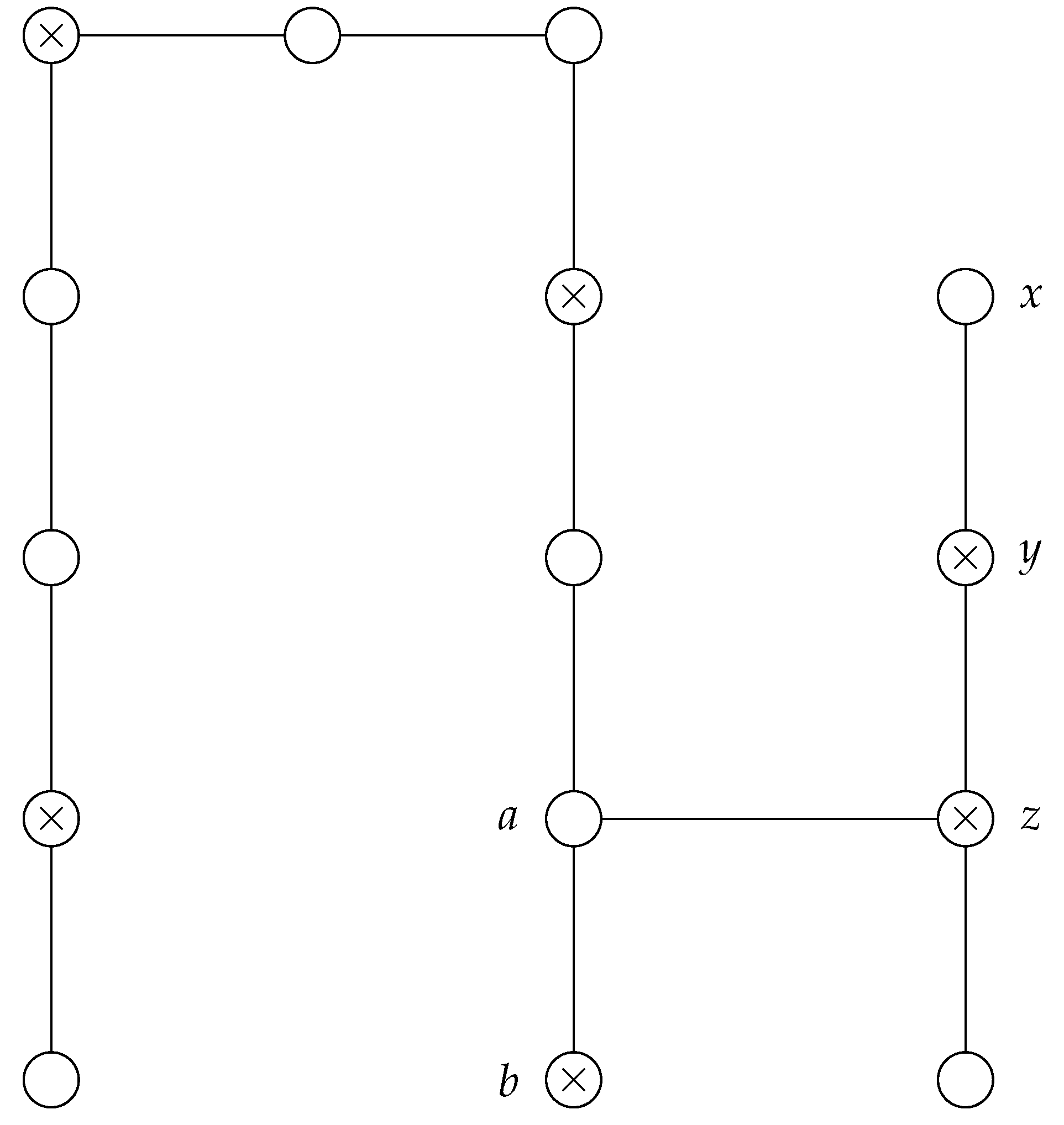
Consider
, shown in
Figure 4, is the
-graph of the tree
T shown in
Figure 5 and the edge
in
. The edges in
associated with
e are labelled
,
,
,
and
. Recall the two vertices incident with
, namely
and
in
are equated with
-sets of
T and since
is an edge in the
, there exists vertices
so that
. Hence
. By Proposition 2, it is also the case that
and if
is incident with
, then
and
. Repeated applications of Proposition 2 shows that each of
. Furthermore, Proposition 2 implies any edge
incident with
,
,
,
, or
has the property that
and
. Similarly there are vertices
so that
and that
and
for any edge
incident with
,
,
, or
. It follows that
. More generally let
be the set of edges of
associated with edges of
and let
be the set of edges of
associated with edges of
. Then it follows that
Now consider the set
of
T which is indicated in
Figure 5, by the vertices in
D being marked with an × symbols. Add two leaves to each vertex in
to form a tree
. Those vertices in the dominating set associated with edges of
must be in every
-set of
. It follows that
is isomorphic to
.
For convenience in the following proof if we will say v is swapped by e and that e swaps v.
Theorem 12. Let G be a Cartesian product graph with , . Then G is the γ-graph of a tree T if and only if each is the γ-graph of a tree .
Proof. Suppose , , is the -graph of a tree T. Let be an edge of and let and be any two edges associated with e in G on vertices and of respectively. That is and . As G is connected by Theorem 2, there is a path between and in G, and considering only the edges associated with edges in gives a path P between and in . Consider the subgraph of G. It follows from Proposition 2 that every edge associated with e in swaps the same pair of vertices. As and were arbitrary edges associated with e, then every edge associated with e in G swaps the same pair of vertices. By symmetry, this is true of every edge in or . Let be a vertex of G and for , let be the set of edges of G associated with the edges of . If a vertex is swapped by an edge in , it is not swapped by an edge in by Proposition 2. Hence, form by adding two leaves to any vertex in that is swapped by an edge in . Then it follows that . By symmetry, is also the -graph of a tree.
Conversely, suppose each is the -graph of a tree . Let T be the graph formed by adding an edge between any stem of and any stem of . It is easily verified that . □
4.2. Incident 4-Cycles in -Graphs of Trees
In this subsection we give some structure to how four cycles interact locally in -graphs of a trees. We first demonstrate that cannot be a subgraph of a -graph of a tree. As a consequence, we observe that two 4-cycles have at most two common vertices, and moreover, if two 4-cycles have two common vertices, then the two common vertices are adjacent.
Theorem 13. Let T be a tree and let be the γ-graph of T. Then does not contain as a subgraph.
Proof. For and let and be vertices of that induce . That is for each possible i and j. Then for each there exist vertices and with and . By Lemma 12, it must be the case that , and are all distinct. It follows from Theorem 3 that and are at distance two in . Therefore and so for some i, . Assume with out loss of generality . As it must be the case that . Then for some vertex with , , and it follows that and therefore . As each is distinct, we can assume without loss of generality that . Then . But , so , which shows it must be the case that . Clearly and are both adjacent to in T. Furthermore is adjacent to in G and so it must be the case that is adjacent to c in T. By definition, so either forms a cycle in T or . Both cases lead to a contradiction. □
We have shown that two 4-cycles in cannot overlap in more than two vertices. On the other hand, we can also say something about the structure required in when two 4-cycles have only one common vertex. We first establish the following.
Proposition 3. Let G be a γ-graph of a tree T and let be a 4-cycle of G. By Proposition 2 there are distinct and distinct with and , so that , and . If U and V are each adjacent to W but not part of a 4-cycle with a pair of vertices of C and and , then .
Proof. Suppose the opposite. It follows from Lemma 12 that c, d, f and h are all distinct. As neither U nor V is part of a 4-cycle with any two vertices of C, is not a -set of T. Hence, if , a and e have common neighbour i which is not adjacent to any vertex in . As b, , i is not adjacent to b or g in T. Similarly it can be seen , , and are not -sets of T. Hence, if , b and e have common neighbour j not adjacent to a or g, if , then a and g have common neighbour k not adjacent to b or e, and if , b and g have common neighbour l not adjacent to a or e. It can be seen that (if they exist) are all distinct.
Suppose . Then as a and b are distinct, . Hence, b and e have common neighbour j not adjacent to , a contradiction. Hence . Similarly we can show , and . But then is a cycle in T, contradicting that T is a tree. The result follows. □
Proposition 4. Let G be a γ-graph of a tree T and let and be 4-cycles of G. Then there must be a 4-cycle , with and .
Proof. Suppose not. Then neither S nor V is part of a 4-cycle with a pair vertices of . Hence, by Proposition 2 there are distinct vertices and , with and so that and . By Proposition 3, , a contradiction. The result follows. □
Define two 4-cycles of G to be adjacent if they share an edge and two adjacent cycles to be neighbours. Then Proposition 4 can be reworded to say that incident 4-cycles in a -graph of a tree must be adjacent to each other or have a common neighbour. We conclude our treatment of vertices of 4-cycles by demonstrating that adjacent vertices of a 4-cycle cannot both have vertex neighbours that are not part of neighbouring 4-cycles.
Proposition 5. Let G be the γ-graph of a tree and let C be an induced of G. Then in any two adjacent vertices of C at most one has a neighbour which is not part of a 4-cycle with a pair of vertices of C.
Proof. Suppose G is the -graph of a tree T. Let and suppose that W and X have neighbours U and V respectively, which are not part of a 4-cycle with any two vertices of C. Recall a vertex of the -graph is a -set. By Proposition 2, there are distinct vertices and so that , , , and . There are vertices , , and so that , , and . We note from Lemma 12 that d, f and c are all distinct and that d, h and a are all distinct. As neither U nor V is part of a 4-cycle with any two vertices of C we get:
if , then as is not a -set of T, a and e have a common neighbour .
if , then as is not a -set of T, b and e have a common neighbour .
if , then as is not a -set of T, b and g have a common neighbour .
if , then as is not a -set of T, c and g have a common neighbour .
Note that in the case they exist, and . If and , then is a cycle in T, contradicting that T is a tree. Hence, by symmetry, we may assume either or .
Assume first that . Then as a and b are distinct, . Therefore, from above and b have a common neighbour j. Since is a -set of T, it must be that (if , then is a 3-cycle in T). If and , then as , is a cycle in T, which contradicts that T is a tree. If , as and , From above c and have a common neighbour, but c and b are adjacent, contradicting that T is a tree. If , then the path in G corresponds to a swap of f and a, followed by a swap of a and c, followed by a swap of c and h. This corresponds to swaps of the four distinct vertices which induce a path in T and hence f and h are distance 3 apart in T. By Observation 1, , but no vertex is in the closed neighbourhood of both f and h, a contradiction.
Otherwise, assume . Then as a and b are distinct, . Therefore from above, a and have a common neighbour, and since Y is a -set, it must be d. If and , then either is a cycle in T or contains a cycle in T, which contradicts that T is a tree. If , then . So from above c and have a common neighbour l. As , so is a cycle in T, contradicting that T is a tree. If , then . From above b and have a common neighbour k. As , so is a cycle in T, contradicting that T is a tree. The result follows. □
While the evidence presented in this section is not conclusive, it highlights that locally, 4-cycles interact similarly to how 4-cycles interact in Cartesian Product graphs.
4.3. The Structure of Stems in 4-Cycles
Finally, we explore some properties of stems in a 4-cycle in the -graph of a tree. In particular we focus on the structure of the dominating set associated with the stem and the corresponding structure of the -graph. We first obtain the following Lemma.
Lemma 13. Let G be a γ-graph of a tree T, S be a stem of G, be the leaves of S, and . If every vertex in S has an S-external private neighbour, then .
Proof. By Lemma 6, there exists vertices and so that and for . By Lemma 4, every vertex except in has at least two -external private neighbours, so by Lemma 5, every vertex other than x in S has at least one S-external private neighbour. It follows that x has an S-external private neighbour and therefore by Observation 3, . □
Proposition 6. Let G be a γ-graph of a tree T, S be a stem of G, be the leaves of S, and . If , then is a Cartesian product graph if and only if every vertex in S has an S-external private neighbour.
Proof. By Lemma 6, there exists vertices and so that and for . By Lemma 4, every vertex except in has at least two -external private neighbours, so by Lemma 5, every vertex other than x in S has at least one S-external private neighbour. Let be the set of vertices that can be swapped from S. If , then z has two -external private neighbours, but has at exactly one S-external private neighbour. Therefore, each has a distinct common neighbour with x which is not adjacent to any vertex of . Furthermore, rooting T at x, each is in a distinct branch. By Observation 1, each is associated with exactly one edge incident with S in . Hence as , if x has no S-external private neighbour, then .
Suppose is a Cartesian product graph but some vertex in S has no S-external private neighbour. Then x has no S-external private neighbour and it follows that . For , let be distinct elements of Z and let be common neighbour of x and which is not adjacent to any vertex of . For a given i, is a -set of T in adjacent to S. Let . If is associated with an edge in and is associated with an edge in , note that is a 4-cycle which is a subgraph of . This contradicts that the vertices a and b in the statement of Proposition 2 are unique. Hence we may assume each is in . By Theorem 2, and are connected. Then there exists an edge e incident with S associated with an edge in . Then for each i, is 4-cycle which is a subgraph of . By Proposition 2, e swaps of some , . Hence if , there exists a vertex so that and is -set of T in . It follows from Observation 1 and that has an S-external private neighbour that . Consider the 4-cycle . By Proposition 2, is a -set of T with no neighbour of , a contradiction. Hence vertex in S has an S-external private neighbour.
Conversely, suppose every vertex in S has an S-external private neighbour. By Lemma 13, and it follows that, is the S-external private neighbour of x. Rooting T at x, every descendant of in has at least two -external private neighbours. Hence every descendant of in S has at least two S-external private neighbours. By Lemma 8, the only dominating set of T containing is and hence for every -set of T every descendant of in S has at least two D-external private neighbours and cannot be swapped. It follows that x is in every -set which corresponds to a vertex in . Then , and each has a distinct common neighbour with x. Each is in a distinct branch of T, and swaps occur in each such branch independently. Hence, is a Cartesian product graph. □
Note that in the proof of the converse of the previous proposition the line, , . For the result we require that . Hence when a stem in the -graph has fewer non-leaf neighbours, we obtain the result in one direction.
Proposition 7. Let G be a γ-graph of a tree T, S be a stem of G, be the leaves of S, and . If , and every vertex in S has an S-external private neighbour, then is a Cartesian product graph.
We immediately obtain the following result demonstrating where leaves cannot be attached to Cartesian product graphs. Recall the vertices of the graph are ordered n-tuples. In particular, each vertex can be written in the form , where for .
Corollary 4. Let G be a γ-graph of a tree T, S be a stem of G, be the leaves of S, and . If , , where each is `prime’, and , then each is a leaf in .
Proof. By Lemma 6, there exists vertices and so that and for . By Proposition 6, x has an S-external private neighbour and it follows from Lemma 13, that and is the only S-external private neighbour of x. Rooting T at x, and noting every descendant of in has at least two -external private neighbours, it follows that x is in every -set which corresponds to a vertex in .
Recalling that T is rooted at x let Z be the set of vertices that can be swapped from S in ; each has a distinct common neighbour with x and each is in a distinct branch of T. Swaps occur in each such branch independently. Therefore, if , where each is `prime’, then without loss of generality each swap occurs in a different . Hence is a leaf in as only one swap associated with an edge in can occur. □
Let denote the maximum number of edges incident with v with no pair of edges part of the same 4-cycle. We conclude by providing two additional tools to determine if graphs with stems are -graphs.
Lemma 14. Let G be a γ-graph of a tree T, S be a stem of G, be the leaves of S, and . If , then is a Cartesian product graph.
Proof. Suppose is not a Cartesian product graph. If (Lemma 6), then it follows from Proposition 6, that x has no S-external private neighbour. By Proposition 2 at x can be swapped from S in at most times, so . Let be the set of vertices that can be swapped from S. Then . It can be shown, as in previous proofs, each has a distinct common neighbour with x in , so and hence , which is a contradiction. Hence, is a Cartesian product graph. □
Proposition 8. Let G be the γ-graph of a tree T, S be a stem of G, be the leaves of S, and . If , S is in the 4-cycle , and every vertex adjacent to Q is in a 4-cycle with P or R, then is a Cartesian product graph.
Proof. Suppose is not a Cartesian product. Let (Lemma 6), then it follows from Proposition 6, that x has no S-external private neighbour. It follows from Lemma 14, that and hence . Rooting T at x each descendant of in S has at least two -external private neighbours, each descendant of in S is in every -set of T. Delete each from T and let be the component containing x. Then .
As , it follows from Proposition 2 only one swap in can use x, so . If z is the other swap possible from S, then x and z have a common neighbour w, and . Hence we may assume without loss of generality that the neighbours of S are and . By Proposition 2, . Let be the component of containing w and be the component of containing z. Let be the disjoint union of and .
Suppose A is a -set but not a -set of . If , then , which contradicts that A is a -set of . Hence, and . As v is dominated by A, but v is not in A, there exists a neighbour of v, . As , it follows that is a -set of . Hence, is a -set of with and and therefore O is adjacent to Q. However, by Proposition 2, O does not form a 4-cycle with P, as is not a -set of , and O does not form a 4-cycle with R, as is not a minimal dominating set (). Hence, every -set of is a -set of . Further, since x or w is in every -set in , no swap in uses the edge . Therefore, , which is a contradiction. □