Abstract
Multi-User (MU) Multiple-Input-Multiple-Output (MIMO) systems have been extensively investigated over the last few years from both theoretical and practical perspectives. The low complexity Linear Precoding (LP) schemes for MU-MIMO are already deployed in Long-Term Evolution (LTE) networks; however, they do not work well for users with strongly-correlated channels. Alternatives to those schemes, like Non-Linear Precoding (NLP), and hybrid precoding schemes were proposed in the standardization phase for the Third-Generation Partnership Project (3GPP) 5G New Radio (NR). NLP schemes have better performance, but their complexity is prohibitively high. Hybrid schemes, which combine LP schemes to serve users with separable channels and NLP schemes for users with strongly-correlated channels, can help reduce the computational burden, while limiting the performance degradation. Finding the optimum set of users that can be co-scheduled through LP schemes could require an exhaustive search and, thus, may not be affordable for practical systems. The purpose of this paper is to present a new semi-orthogonal user selection algorithm based on the statistical K-means clustering and to assess its performance in MU-MIMO systems employing hybrid precoding schemes.
1. Introduction
Multi-User (MU) Multiple-Input-Multiple-Output (MIMO) increases network capacity by multiplexing spatially-separated users in the same frequency and time resources. It requires transmission precoding, as a random geographic location of the receivers does not enable joint decoding. Thus, it is challenging to send independent data streams simultaneously to a set of properly-selected users to attain the spatial multiplexing gains offered by MU-MIMO. A recent evolution of MU-MIMO is known as massive MIMO or large-scale MIMO [1] and is characterized by Base Stations (BSs) with hundreds of antennas sending different data streams to tens of users. Massive MIMO has been identified as the air interface technology capable of addressing the massive capacity requirement of 5G networks.
Linear Precoding (LP) schemes for MU-MIMO eliminate the inter-user interference by projecting the intended user’s signal into the null space of the other users [2]. When their channels are strongly correlated, i.e., for closely-separated users, the projection operation makes it almost impossible to separate the received signals and results in high capacity loss [3]. Existing MU-MIMO schedulers estimate the spatial separation between users and try to serve the ones with near-orthogonal channels. The optimum set of users can be found through an exhaustive search. The combinatorial nature of these problems makes them computationally infeasible due to an expected large number of users and antennas in massive MIMO systems. Various sub-optimal user grouping strategies, like null space projection or spatial clustering classification, have already been evaluated in the literature, including [2] and the references therein.
To reduce the channel estimation overhead in massive MIMO Frequency Division Duplex (FDD) systems, a user grouping algorithm based on K-means clustering was proposed in [4,5]. The performance of a two-stage precoding algorithm with various distance metrics for user grouping was tested; however, all require complex matrix computations. The Block Diagonalization (BD) linear precoder [6,7] is used to cancel the inter-group interference. The results are not accurate enough, as the number of clusters is assumed to be known prior, and there are no insights of the spatial separation between the co-scheduled groups. In addition, the subspaces of groups (created using the average covariance matrix of the users in a group) are slightly different from the channel eigenspace of users. As such, the inter-group interference is not entirely canceled. Lastly, the employed intra-group precoder is based on linear regularized zero forcing [8]. While linear precoding mechanisms have a relatively low implementation complexity, they may not exhibit a good performance for highly-correlated channels, which is the case of users inside the same group [3,9]. Non-Linear Precoding (NLP) schemes, such as Tomlinson–Harashima Precoding (THP) [10], proposed in the standardization phase for 5G NR (New Radio) [11,12], or hybrid precoding [13], could behave better in such scenarios.
A user grouping algorithm based on an optimized K-means clustering is presented in the paper. This further reduces the complexity of the method proposed in [4,5] and ensures that, at a given time, at least one user in one group is scheduled. In contrast to the related work, the number of co-scheduled clusters is dynamically chosen, such that users of different clusters are separated enough in space to be served through an LP scheme. As users inside the same group have highly correlated channels, they will be scheduled in the same time-frequency resource through a second-stage non-linear precoder.
To assess the particularities of the proposed algorithm, the paper is organized into the following sections. Section 2 describes the basic principles of precoding, by identifying three types of precoding schemes. Section 3 defines a model for the spatial correlation in MU-MIMO channels and a metric for evaluating the separation between channels. The proposed user grouping solution is analyzed in detail in Section 4. Section 5 presents the simulation’s parameters used to test the performance of the proposed algorithm. The clustering of users and throughput performance of the MU-MIMO system are then evaluated in Section 6 for various user distributions and required angle separations. Finally, Section 7 presents the conclusion and research directions for future works.
2. Precoding Schemes
In this section, the precoding schemes are grouped into three categories, i.e., linear, non-linear, and hybrid.
2.1. Linear Precoding
Linear precoding schemes, as used in Long-Term Evolution (LTE), suppress the inter-user interference through channel inversion. Techniques like Zero Forcing (ZF) and Regularized Zero Forcing (RZF) for single-antenna User Equipment (UEs) or Block Diagonalization (BD) for multiple-antenna UE have reduced complexity [7].
The channel matrix with complex coefficients corresponding to transmit antennas and K single-antenna users is described by .
The precoder identified by the matrix and represented in Figure 1 can be defined by the following equations:
where is the set of complex symbols intended for every K user, is the received array of symbols by the K users, and is the vector of Additive White Gaussian Noise (AWGN) of variance . It follows a circularly-symmetric complex Gaussian distribution with zero mean and correlation matrix .
where is the total transmit power, is the expectation of a random variable x, is the L-norm of a vector , superscript H denotes the transpose complex conjugate, and is a normalization factor, such that the total transmit power does not change after precoding:
where is the trace of a square matrix .
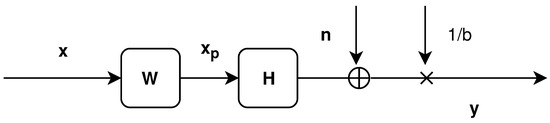
Figure 1.
Linear precoding scheme [3].
The previously-mentioned schemes are used for users with a single antenna. The signal transmitted for other users is treated as interference, and the precoder attempts to cancel it.
When users are equipped with multiple antennas, similar methods can be used. In this case, the signal intended for the same user, but for different antennas, is also treated as interference. As there is much more interference to cancel, noise is amplified at the receiver side.
In these scenarios, the BD precoder performs better. It works by decomposing the MU-MIMO downlink channel into multiple parallel independent single-user MIMO downlink channels. The precoding matrix is determined such that the intended signal is projected in the null space of all other users’ channel matrices. The remaining interference after the inter-user precoding can be canceled with any decoding or precoding techniques.
The received signal by K users equipped with antennas is:
where is the effective channel corresponding to the signal sent to user k and received by user u. This interferes with user k when . The effective channel matrix needs to be diagonalized in order to cancel the inter-user interference.
To prevent any power increase after precoding, the BD precoder matrix has to be unitary.
Assuming a matrix containing the channel gains of all users except u,
when , the Singular-Value Decomposition (SVD) of is:
where and contain singular vectors corresponding to the non-zero and zero singular values, respectively.
As lies in the null space of , the signal transmitted in the direction of is only received by user u. Its corresponding precoder is .
2.2. Non-Linear Precoding Schemes
Linear precoding has relatively low complexity; however, it has been shown that the sum rate of channel inversion is limited when increasing the number of users. Furthermore, linear precoding does not perform well in scenarios with high UE density and correlated channels.
Non-linear precoding schemes are valid alternatives, which instead of spatially separating the users, they eliminate the interference through non-linear operations. The non-linear concept was introduced in Dirty Paper Coding (DPC) [14]. It can achieve the maximum sum rate of the system when the full Channel State Information (CSI) is available at the transmitter side. The DPC’s pre-subtraction of the non-causally known interference has a high complexity, and as a result, sub-optimum non-linear precoding schemes such as Tomlinson–Harashima Precoding (THP) and Vector Perturbation (VP) were proposed as alternatives with lower complexity [10].
2.2.1. THP Precoding
The concept of THP is derived from the Decision Feedback Equalizer (DFE) technique. There, the interference resulting from the previously-estimated received symbols was reconstructed and subtracted from the actual received symbol. THP is represented in Figure 2. The power growth resulting from the successive cancellation step is limited by using the modulo function.
where:
and the feedback matrix is a unitary lower diagonal matrix, obtained through a QR decomposition of H, such that:
and .
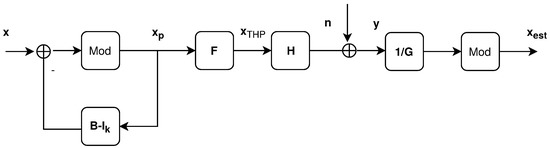
Figure 2.
THP block scheme [3].
At the receiver, the user’s k signal is firstly divided by , then passed through the modulo operation to be then sent to the Quadrature Amplitude Modulation (QAM) demodulator.
2.2.2. Vector Perturbation Precoding
Vector perturbation works similarly to THP, as the transmitted symbols are “perturbed” and moved from the original to a new constellation of points. On the receiver side, a diagonal matrix is used to scale the received signal, which is then reconstructed through a modulo operation.
2.3. Hybrid Precoding
Hybrid precoding, a mix of linear and non-linear precoding schemes, was proposed in [11,12,13] to enhance the robustness of non-linear precoding against channel imperfections and to reduce the complexity required for large-scale antenna systems.
Considering K users divided into G groups, the precoding mechanism is implemented in two stages. The first stage consists of a linear precoder used to eliminate the inter-group interference and assumes that the users from different groups have sufficiently uncorrelated channels. This stage can be realized through BD using long-term CSI measurements. Based on the degree of correlation between the users of the same group, linear or non-linear precoding schemes can be employed inside every group, in the second stage.
Figure 3 depicts a hybrid precoding scheme that uses BD and THP:
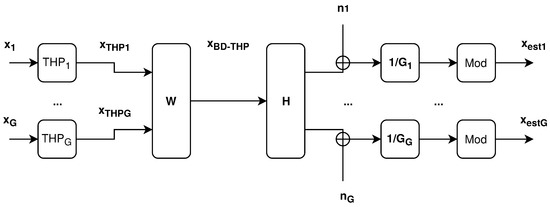
Figure 3.
Hybrid precoder block scheme [3].
2.4. Complexity Evaluation
The complexity can be evaluated by counting the number of Floating Point Operations (FLOPs) required for multiplications and additions of complex values. A multiplication and an addition requires six and two FLOPs, respectively. The computational complexity of the SVD decompositions required by the BD-THP precoder is neglected, being computed less when relying on statistical CSI. The complexity of the QR decomposition of channel matrix is . Generating the matrix for the RZF precoder uses FLOPs due to the Hermitian property of the Gram matrix. More details on how to evaluate the complexity calculations can be found in [13].
The complexity of various precoding schemes is represented in Table 1 [3,13], for users in each group.

Table 1.
Precoder’s complexity [3,13].
In Figure 4, the equations above are plotted for transmit antennas and single-antenna users grouped into groups. Although the BD-THP scheme is a good tradeoff between the THP and the RZF schemes in terms of the sum rate (as will be seen in the following sections), its complexity is below both of the previous schemes. The computation complexity required to generate T precoded data vectors can change the ranking of schemes (for low values of T); however, the BD-THP precoder will always show the lowest complexity among them.
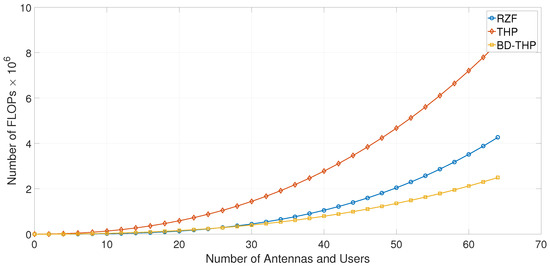
Figure 4.
Precoders complexity versus the number of antennas and users, for .
3. Spatial Compatibility and Channel Modeling
A set of users is spatially compatible if their channels, , can be separated in space through precoding. The purpose of this section is to define a metric that can evaluate how spatially compatible two users are. Assuming a spatial correlation model at the transmission, it can be shown that the separation between the channels of two users will depend only on their spatial correlation matrices and, in turn, on the angle between them relative to the antenna system.
3.1. Channels Separation Metric
The spatial channel correlation is important for multiple-antenna users (Single User (SU)-MIMO communications); however, in the context of single-antenna users, it is the set of spatial correlation matrices of users that determine the network performances.
A metric used to quantify how separated the channels of two users are was described in [15,16]. Assuming that and are the channels of two users, the channel separation metric is defined as:
where and is the variance of a random variable x.
The metric indicates how efficiently the transmitter can serve user i without affecting user k, and vice versa. Strongly-correlated channels exhibit higher values, whereas for Rayleigh uncorrelated fading, the variance is and decreases when the number of antennas increases. In general, the variance depends on the spatial channel correlation and equals zero when the users have orthogonal correlation matrices, .
In MU-MIMO systems, a set of users is called -orthogonal, if for every . The users can be grouped into disjoint sets according to a desired threshold , such that semi-orthogonal sets could be scheduled over independent resources.
3.2. Correlation Model
The authors in [17] mentioned that the channel separation metric should also be a function of the spatial correlation between and and considered the inner correlation of each multi-antenna user. However, the precoding performance was primarily affected by the correlation between transmit antennas, whereas receive antenna correlation had an insignificant impact on the precoding design [18]. In a MIMO context, a spatially-correlated random channel vector can be created using Karhunen–Loeve expansion [15]:
where and . The eigenvalue decomposition of is , where is a diagonal matrix containing positive non-zero eigenvalues of and contains the associated eigenvectors. The last part means that the distributions of of are identical.
It can be shown that the spatially-correlated Rayleigh channel corresponding to user k is a complex normal random vector, with zero mean and spatial correlation matrix , [15,19].
The normalized trace captures the average channel gain from one of the antennas at the base station to the UE and includes the macroscopic large-scale fading. The Rayleigh distribution of is motivated by the presence of small-scale fading due to multipath propagation. When the channel gains between different antennas are uncorrelated, the channel model can be referred to as uncorrelated Rayleigh fading. can be modeled as:
where D is the distance between the transmitter and receiver, is the path loss exponent, which determines how fast the signal attenuates with distances, and determines the median channel gain at a reference distance . In theoretical studies, those two parameters can be computed with one of the many established propagation models. The only non-deterministic terms is and represents the shadow fading that creates log-normal random variations around the mean value, . The shadow fading can be viewed as a model of blockage from large obstacles. The variance determines how large the variations are.
Realistic performance assessment of MIMO systems requires the use of a channel model that reflects the main characteristics of large antenna arrays such as the array geometry, the correlation between the channel responses of different antennas and the physical location and orientation of BSs and UEs. In [15], a correlation-based model was proposed, where the channel responses were all Gaussian distributed with zero mean and entirely defined through the correlation matrices. Having an intuitive structure, the correlation model allowed the subspaces of the correlation matrices to be parametrized by the azimuth angles of the UEs. This makes it easy to determine if two UEs are spatially separable by comparing their respective angles.
Since all the multipath components are assumed to arrive with the same delay, the model is a frequency flat-fading channel model. This limitation is less significant, as we focus only on communication over a coherence block, where the channel is assumed to be constant. For these reasons, in the context of user clustering for MU-MIMO, the model was employed in several publications like [13,19].
To model the small-scale fading, each path from the antenna to the user is assumed to represent a superposition of multipaths ( is a large number). It is assumed that the macro base station is elevated and that the scatterers only surround the user, and each multipath is a plane wave, leaving from the uniform linear spaced array at an angle . The equivalent channel of each user becomes:
where the channel vector of the nth path towards the antenna array is:
where denotes the transpose of an array , is a complex number that models the gain and phase of multipath n, and d is the array antenna spacing (measured in wavelengths).
It is assumed that the angles are random variables with the Probability Density Function (PDF) and are zero mean random variables with variance . The variance is the multipath component average gain, and the total gain of the multipaths is .
Using the multidimensional central limit theorem, when , where the convergence is in its distribution and has a spatial correlation matrix . This is the reason why the channel model is a correlated Rayleigh fading model.
The element of matrix is defined as:
As depends on the difference and not on each individual value, is a Toeplitz matrix.
It is assumed that the multipath components are originating from a scattering cluster around the user [due to the lack of scatterers around the Base Station (BS)], located at an angle . is a deterministic nominal angle, and is a random variable with a standard deviation from the nominal angle given by .
Depending on how is modeled, several correlation models can be found in the literature. The standard deviation is measured in radians and is called the Angular Standard Deviation (ASD). A usual value for urban environments is (), but smaller values are expected in rural areas or hills.
When follows a Gaussian distribution , an approximate closed-form expression that reduces the complexity of simulations can be used for , if is small:
Accounting for the spatial channel correlation model above, Equation (12) becomes:
Figure 5 plots the metric defined in Section 3.1 for a uniform linear antenna array of size , with the elements placed at half of wavelength and the angle of the reference user, set at . Over a certain interval, e.g., , the channel separation metric has a monotone variation with the angle between two co-scheduled users.
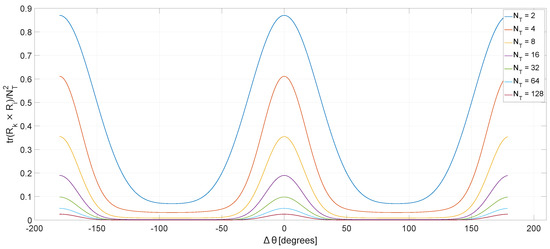
Figure 5.
Channel separation as a function of the angle between user k and i, for following a Gaussian distribution.
Assuming a precoder requires a 0.1 channel separation ( = 0.1), Figure 5 shows that this is achieved for any inter-user angle, when the number of transmit antennas () is greater than or equal to 32. For 16 antennas, the angle required between two co-scheduled users is and increases up to for the two transmit antennas case.
4. User Grouping
One of the objectives of MU-MIMO technology is to send independent data streams to different users. This implies that only a subset of the transmitted data symbols is useful for each co-scheduled user. In the MU-MIMO context, the user grouping is the task of forming a subset of users, according to a spatial compatibility metric. It can be shown that there is a correspondence between the precoding performance and the user grouping technique [9]. The scheduling of spatially-compatible users is crucial to suppress inter-user interference, whereas refining the power allocation and precoding weights requires less computational effort.
Most of the scheduling algorithms in the literature focus on constructing sets of users with orthogonal or semi-orthogonal MIMO channels [20]; however, the optimal solution for the user grouping involves an extensive search of all possible combinations. The complexity of the approach grows exponentially with the number of users and is not feasible for a moderate number of users.
Scheduling algorithms based on spatial clustering can improve the overall MU-MIMO performance by adjusting the parameter defined in Section 3.1, according to the number of users and the Signal-to-Noise Ratio (SNR). However, the optimum value is a deployment parameter and depends on the number of transmit antennas, the number of users, the precoder type, and is usually calculated through simulations.
Based on the above observations, in this section we propose a user grouping algorithm, whose aim is to cluster users that have similar directions in Euclidean space. Therefore, their channels exhibit a spatial correlation higher than and, consequently, cannot be co-scheduled in MU-MIMO through linear precoding schemes, as they may significantly interfere with each other.
To optimize the performance of the spatial clustering, K-means clustering algorithm [21] with a distance metric based on angles between users, is proposed. The algorithm groups the users into N clusters, such that each user belongs to the cluster whose center is the closest (forms the smallest angle from the serving sector perspective), as described in Algorithm 1.
| Algorithm 1 K-means clustering. |
|
Although this approach guarantees that users of the same cluster cannot be co-scheduled through linear precoders, it does not provide any information on the channel separation between users of different clusters. To decide whether users from different clusters can be co-scheduled, one can use the angles between the centers of clusters, instead of the angles for the entire set of users. The set of co-scheduled clusters should not include any cluster that has an angle smaller than , and its size should be less than or equal to the number of transmit antennas. The method of finding the optimum sets of co-scheduled clusters is another optimization problem and is not the purpose of this article.
To further reduce the computational burden, once the sets are created, the algorithm will schedule in the same time-frequency resource a subset of users in each cluster of the set through a non-linear precoding scheme. The user selection within each cluster is random; however, this could result in co-scheduling users with bad channel conditions, which would degrade the overall system performance. Employing more complex selection methods like semi-orthogonal or greedy user selection, as detailed in [4,20,22], would have severely increased the convergence time and the complexity of the algorithm, but was not in the scope of this article. In the context of a hybrid precoding scheme, in order to perform intra-cluster user selection, we would require knowing the effective channel matrix (including the inter-cluster linear precoding). This is conditioned on the users selected in other clusters. As such, the number of combinations is much higher and requires a search over the entire set of users, not only over those of the same cluster.
Note that after spatial clustering, the number of users in each cluster is not the same. Users that have fewer neighbors within their clusters could get higher throughput as they will be co-scheduled more often. For that, this approach is an overlapping user scheduling algorithm [22].
To evaluate the complexity of the spatial clustering algorithm compared to the state-of-the-art solutions, the number of FLOPs is represented for various distance metrics and clustering algorithms, in Figure 6. It can be noted that the complexity of the algorithms depends on the number of users K, the number of antennas , the number of clusters N, and the chosen distance metric. For a fixed number of clusters, and antennas, the proposed algorithm has better performance than the two-stage precoder with chordal distance (two-stage chordal), which is [23], compared to [5]. In addition, as the proposed metric remains in the Euclidean space, the K-means implementation based on Lloyd’s algorithm is optimized and has an complexity [24]. Fixing the number of iterations needed until convergence at , the optimized K-means also outperforms the ZF precoding with User Selection (ZF-US), which has an complexity [22]. The number of iterations will further decrease when the users already have a cluster structure, which is the case of a typical user distribution, as shown in Section 6.
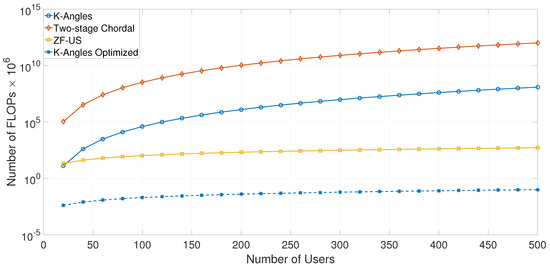
Figure 6.
User clustering complexity for various distance metrics and grouping algorithms. US, User Selection.
5. System Model
We consider the downlink of a single-cell MU-MIMO system, where a base station with a uniform linear array of antennas simultaneously transmits data to K single-antenna users. is the vector of precoded symbols using various precoding schemes p. The received signal vector of the users, , becomes:
where is the channel matrix, with being the channel vector for the user. The channel vector of each user is generated from a Rayleigh distribution, and the gains from different antennas are spatially correlated using the model introduced in Section 3.2, such that . is the spatial correlation matrix and is the vector of AWGN samples of the K users of variance .
In Figure 7, the system model is illustrated in the context of hybrid precoding. The user grouping algorithm proposed in Section 4 requires the AoA of each user to group the users into clusters. Once the users are clustered, a set of selected users is precoded in each cluster by a THP block. The set of selected clusters is then fed to the BD block to compute the inter-group precoding weights. Both BD and THP precoders require full CSI for the calculation of precoding weights.
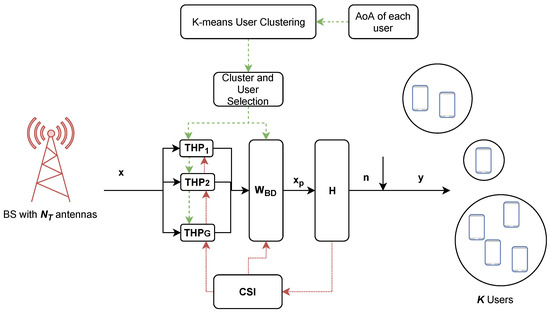
Figure 7.
Hybrid precoding with user clustering.
With a correlation-based propagation model assumption, the proposed clustering algorithm does not require full CSI. It only relies on the Angle of Arrival (AoA) to group users together based on their channel correlation. This is already included in modern communication standards like 5G NR, as they are required in beam management procedures, for instance. In our modeling, the angle of each user is assumed to be known at the base station and is computed directly based on its 3D coordinates.
The channel is assumed to be constant during a coherence block and perfectly known at the base station. It is assumed to change independently from one block to another, as a stationary ergodic random process. This assumption does not constrain the applicability of the problem. In the modern wireless communication systems, the Orthogonal Frequency Division Multiplex (OFDM) technology (or similar) is applied, along with a dense grid of pilot reference signals. Temporal variations are also handled through pilot signals and channel estimation. In addition, the channel model is spatially consistent; that is, the channel statistics for a given location are always the same and do not depend on the simulation runs.
The scenarios with users having very high mobility could limit the applicability of the clustering algorithm; however, in the evaluated results, we assumed the users had limited mobility. This is also in line with the distribution used for performance evaluation, where the traffic is focused mostly indoors.
Users with a full-buffer traffic model are distributed within each cell across a 2-km radius. The 3D traffic spatial distribution used was created in the radio planning and optimization software Planet [25], based on geolocated call traces and social media events, in the urban area of Ottawa.
The sum data rate is evaluated with respect to the energy per information bit, , divided by the one-sided noise power spectral density, , , where is the average total transmit power and M is the order of the QAM modulated data symbol.
6. Simulations
This section evaluates the performance in terms of the average sum rate and computational complexity of the presented precoding schemes. Spatio-temporally-correlated channels and perfect channel estimation were assumed. Monte Carlo simulations were performed in a single-cell MU-MIMO system with and single-antenna users. A 16 QAM modulation was used throughout the simulations. We assumed the channel changed non-coherently from one block to another.
Figure 8 evaluates the sum rate performance of the RZF and THP precoding schemes as a function of and the inter-user angular separation, when the users were equally spaced with an angle . The performance of both schemes decreased as the users became closer to each other; however, THP always outperformed RZF since it employs a more sophisticated successive interference cancellation technique. For example, to reach the 50 b/s/Hz, RZF requires 17 dB more when than when . In the same scenario, THP requires just 8 dB more . Although these results reflect the performance under equal angle separation, this is the lower bound in a worst case scenario, and similar trends are expected when certain users are separated at different angles.
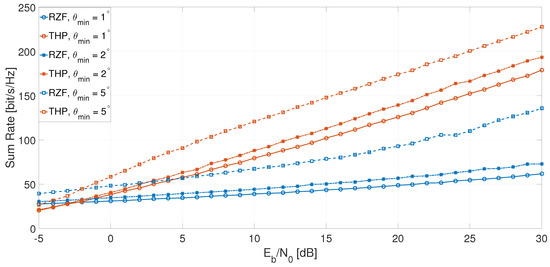
Figure 8.
Sum rate vs. and .
To plot the sum rate performance of a hybrid BD-THP precoding scheme in Figure 9, it was assumed that the users could be grouped into four groups located at . The users within each group were uniformly spread around and were equally spaced with an angle of . As the minimum angle between any two groups was and between any two users of the same group was , we could apply a linear precoding scheme between groups and non-precoding within the groups. The performance of hybrid BD-THP precoding was better than the RZF precoding, except for low values of , as BD did not account for the noise enhancement.
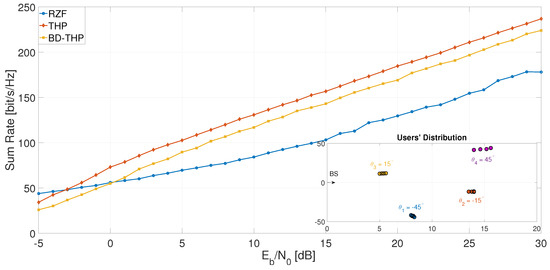
Figure 9.
Sum rate vs. for and .
In the following, the user groping algorithm and the performance of precoders are evaluated, accounting for a realistic user spatial distribution.
In Figure 10 and Figure 11, Sector B2 serves users spread using two different traffic distributions, in a 120 azimuth. The first distribution captured the working day traffic from the morning and the evening hours (busy hours) and the second, in between (working hours). Due the mobility of users, the busy hour traffic was spread more than during the working hours, when it was concentrated in hotspots (around office buildings). To limit the performance degradation of linear precoding schemes, the required angular separation between clusters was set to 30. This resulted in users being grouped into four clusters for the working hour user distribution and in three clusters during busy hours.
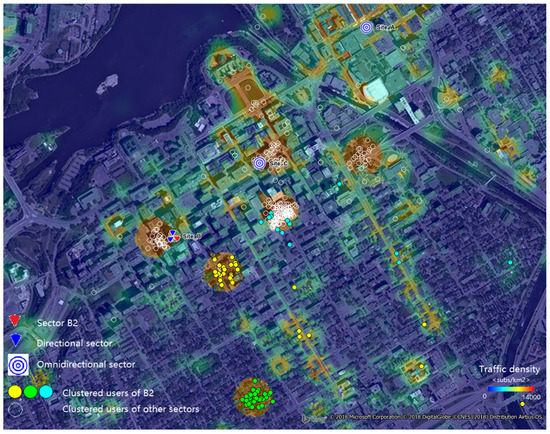
Figure 10.
Working hour user distribution and clustering for Sector B2 and .
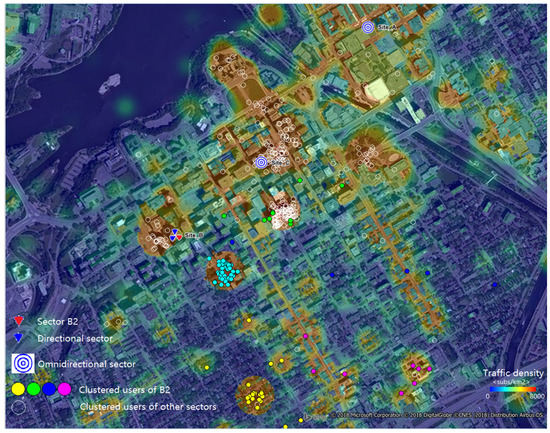
Figure 11.
Busy hour user distribution and clustering for Sector B2 and .
In practice, the AoA is not always perfectly estimated. For that, in Figure 12 and Figure 13, we evaluated the impact of the AoA estimation error on the clustering algorithm’s performance. The AoA estimation error was modeled as a normal random variable, with zero mean and a variable standard deviation. Because the angles between users were computed by the K-means clustering algorithm, the error was added to the actual coordinates of the users.
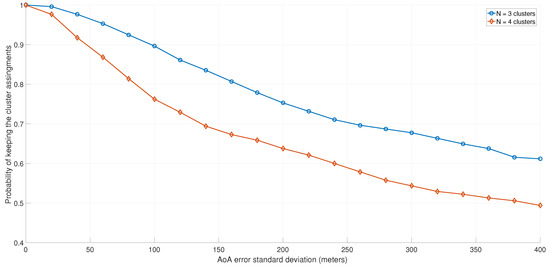
Figure 12.
Probability of users keeping the same clusters, as a function of the AoA error.
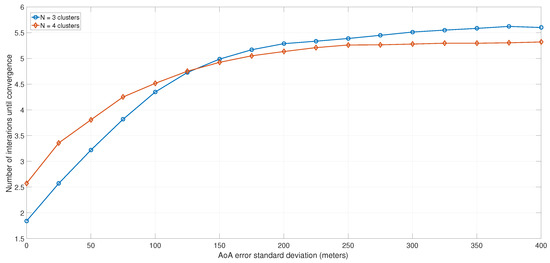
Figure 13.
Number of iterations until convergence, as a function of the AoA error.
In Figure 12, the probability of grouping users into the same clusters (as in the ideal case of perfect AoA estimation) was investigated for different values of the standard deviation error and number of clusters. As expected, as the AoA error increased, the probability of assigning users in the same clusters decreased. The impact was even higher when the number of clusters increased.
Figure 13 plots the average number of iterations until convergence as a function of the AoA standard deviation of error and the number of clusters. It can be noted that the convergence was less dependent on the error and slightly increased for higher AoA error values.
To plot the sum rate performance of a hybrid BD-THP precoding scheme, in Figure 14, we used the busy hour user distribution above and applied the BD linear precoding between the three clusters. Inside each cluster, 6, 6, and 4 users were randomly selected and precoded through a non-linear THP precoding scheme, as a total of 16 users could be co-scheduled through MU-MIMO. Compared to the state-of-the-art precoding schemes like THP and RZF, the hybrid precoding followed the trend of the THP precoding, although the performance was slightly reduced due to the inferior performance of the linear precoding. It can be shown that even in Rayleigh uncorrelated channels, the linear precoding performance is below the non-linear precoding performance.
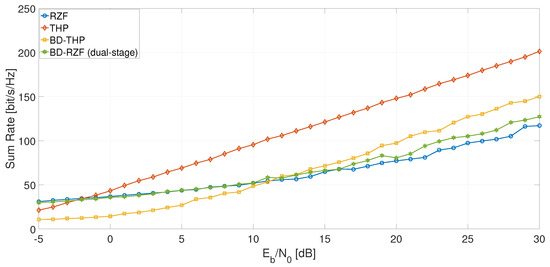
Figure 14.
Sum rate vs. for busy hour user distribution and random user selection.
In BD-RZF, K-means clustering with a chordal distance metric was used to group the users into a two-stage precoding scheme. BD-RZF scheme had lower performance than BD-THP because, for , there were not enough degrees of freedom to separate the users in the spatial domain when applying linear precoding techniques. The performance was even worse than of the RZF precoder, due to reducing the effective channel matrix and using statistical CSI to reduce the complexity. This observation is also in line with the findings in [13].
7. Conclusions
In this paper, a user grouping algorithm based on a modified K-means spatial clustering was proposed. The technique tried to address the complexity of scheduling spatially-compatible users, as required by different precoding schemes.
It was shown that the user’s channels inter-correlation depended on the transmit correlation matrix, for a base station with a uniform linear array of antennas and single antenna users, and that the user’s channels inter-correlation depended ultimately on the angles between the users.
The proposed grouping algorithm identified clusters of users where the average angle between users was minimized. Given that in real life, the locations of users follow a distribution with a clustered structure, the proposed approach could be a very efficient way of identifying users with separable channels. In this case, we showed that it had a linear complexity with the number of users.
The performance of various precoding schemes like linear RZF, BD, non-linear THP, and the hybrid, BD-THP, was evaluated, and it was shown that linear precoding schemes, like RZF, were more affected by users with correlated channels than the non-linear ones. For that reason, hybrid precoding is a good tradeoff between complexity and performance.
Finally, the performance of the hybrid BD-THP precoding scheme was evaluated on a realistic user distribution using the proposed clustering algorithm.
Although we showed that the AoA errors had a limited impact on the clustering results, more work is required to evaluate the overall precoding algorithm performance correctly under non-ideal channel estimation and AoA errors.
Author Contributions
Conceptualization, R.-F.T.; methodology, A.-A.E.; formal analysis, C.P.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chien, T.V.; Bjornson, E. Massive MIMO Communications, 5G Mobile Communications; Springer: Basel, Switzerland, 2017; pp. 77–116. [Google Scholar]
- Castaneda, E.; Silva, A.; Gameiro, A.; Kountouris, M. An Overview on Resource Allocation Techniques for MU-MIMO Systems. IEEE Commun. Surv. Tutor. 2016, 19, 239–284. [Google Scholar] [CrossRef]
- Trifan, R.F.; Paleologu, C. Non-Linear Precoding Performance in Spatio-Temporally Correlated MU-MIMO Channels. In Proceedings of the 2018 International Conference on Communications (COMM), Bucharest, Romania, 14–16 June 2018. [Google Scholar]
- Adhikary, A.; Caire, G. Joint Spatial Division and Multiplexing: Opportunistic Beamforming and User Grouping. IEEE J. Sel. Top. Signal Process. 2014, 8, 879–890. [Google Scholar]
- Xu, Y.; Yue, G.; Mao, S. User Grouping for Massive MIMO in FDD Systems: New Design Methods and Analysis. IEEE Access 2014, 2, 947–959. [Google Scholar] [CrossRef]
- Majumdar, I. Implementation of Block Diagonalization Type Precoding Algorithms for IEEE 802.11ac Systems. In Proceedings of the 2015 Fifth International Conference on Advances in Computing and Communications (ICACC), Kochi, India, 2–4 September 2015. [Google Scholar]
- Cho, Y.S.; Kim, J.; Yang, W.Y.; Kang, C.G. MIMO-OFDM Wireless Communications with Matlab; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Spencer, Q.H.; Swindlehurst, A.L.; Haardt, M. Zero-forcing methods for downlink spatial multiplexing in MU-MIMO channels. IEEE Trans. Signal Process. 2004, 52, 461–471. [Google Scholar] [CrossRef]
- Trifan, R.F.; Enescu, A.A. MU-MIMO Precoding Performance Conditioned by Inter-user Angular Separation. In Proceedings of the 2018 International Symposium on Electronics and Telecommunications (ISETC), Timisoara, Romania, 8–9 November 2018. [Google Scholar]
- Fischer, R.F.H.; Windpassinger, C.A. Improved MIMO Precoding for Decentralized Receivers Resembling Concepts from Lattice Reduction. In Proceedings of the GLOBECOM ’03, IEEE Global Telecommunications Conference (IEEE Cat. No.03CH37489), San Francisco, CA, USA, 1–5 December 2003. [Google Scholar]
- Hasegawa, F. MU-MIMO performance evaluation of nonlinear precoding schemes. In Proceedings of the 3GPP TSG RAN WG1 Meeting 88b, Spokane, WA, USA, 3–7 April 2017. [Google Scholar]
- Classon, B. Non-linear Precoding for Downlink MU-MIMO. In Proceedings of the 3GPP TSG RAN WG1 Meeting 88, Athens, Greece, 13–17 February 2017. [Google Scholar]
- Zarei, S.; Gerstacker, W.; Schober, R. Low Complexity Hybrid Linear/Tomlinson–Harashima Precoding for Downlink Large-Scale MU-MIMO Systems. In Proceedings of the 2016 IEEE Globecom Workshops (GC Wkshps), Washington, DC, USA, 4–8 December 2016. [Google Scholar]
- Costa, M. Writing on Dirty Paper. IEEE Trans. Inf. Theory 1983, 29, 439–441. [Google Scholar] [CrossRef]
- Bjornson, E.; Hoydis, J.; Sanguinetti, L. Massive MIMO Networks: Spectral, Energy, and Hardware Efficiency. Found. Trends Signal Process. 2017, 11, 154–655. [Google Scholar] [CrossRef]
- Herdin, M.; Czink, N.; Ozcelik, H.; Bonek, E. Correlation Matrix Distance, a Meaningful Measure for Evaluation of Non-Stationary MIMO Channels. In Proceedings of the 2005 IEEE 61st Vehicular Technology Conference, Stockholm, Sweden, 30 May–1 June 2005. [Google Scholar]
- Wang, B.H.; Hui, H.T.; Yu, Y.T. Maximum volume criterion for user selection of MU-MIMO downlink with multiantenna users and block diagonalization beamforming. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Toronto, ON, Canada, 11–17 July 2010; pp. 1–4. [Google Scholar]
- Godana, B.; Ekman, T. Parametrization Based Limited Feedback Design for Correlated MIMO Channels Using New Statistical Models. IEEE Trans. Wirel. Commun. 2013, 12, 5172–5184. [Google Scholar] [CrossRef]
- Adhikary, A.; Nam, J.; Ahn, J.Y.; Caire, G. Joint Spatial Division and Multiplexing The Large-Scale Array Regime. IEEE Trans. Inf. Theory 2013, 59, 6441–6463. [Google Scholar] [CrossRef]
- Yoo, T.; Goldsmith, A. On the Optimality of Multiantenna Broadcast Scheduling Using Zero-Forcing Beamforming. IEEE J. Sel. Areas Commun. 2006, 24, 528–541. [Google Scholar]
- Lloyd, S.P. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Tian, R.; Liang, Y.; Tan, X.; Li, T. Overlapping User Grouping in IoT Oriented Massive MIMO Systems. IEEE Access 2017, 5, 14177–14186. [Google Scholar] [CrossRef]
- Inaba, M.; Katoh, N.; Imai, H. Applications of weighted Voronoi diagrams and randomization to variance-based k-clustering. In Proceedings of the 10th ACM Symposium on Computational Geometry, Stony Brook, NY, USA, 6–8 June 1994. [Google Scholar]
- Hamerly, G. Making k-means Even Faster. In Proceedings of the SIAM International Conference on Data Mining, Columbus, OH, USA, 29 April–1 May 2010. [Google Scholar]
- Planet. Available online: https://www.infovista.com/products/planet-network-planning-solutions (accessed on 18 May 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).