A New Regularized Reconstruction Algorithm Based on Compressed Sensing for the Sparse Underdetermined Problem and Applications of One-Dimensional and Two-Dimensional Signal Recovery
Abstract
1. Introduction
2. Preliminaries
3. ReSL0 Algorithm
| Algorithm 1. The pseudo-code of the ReSL0 algorithm. |
| Initialization: |
| (1) Set and . |
| (2) Set and where . |
| While |
| (1) Let . |
| (2) Initialization: . |
| -for |
| (a) . |
| (b) . |
| (3) Set . |
| The estimated value is . |
4. CReSL0 Algorithm
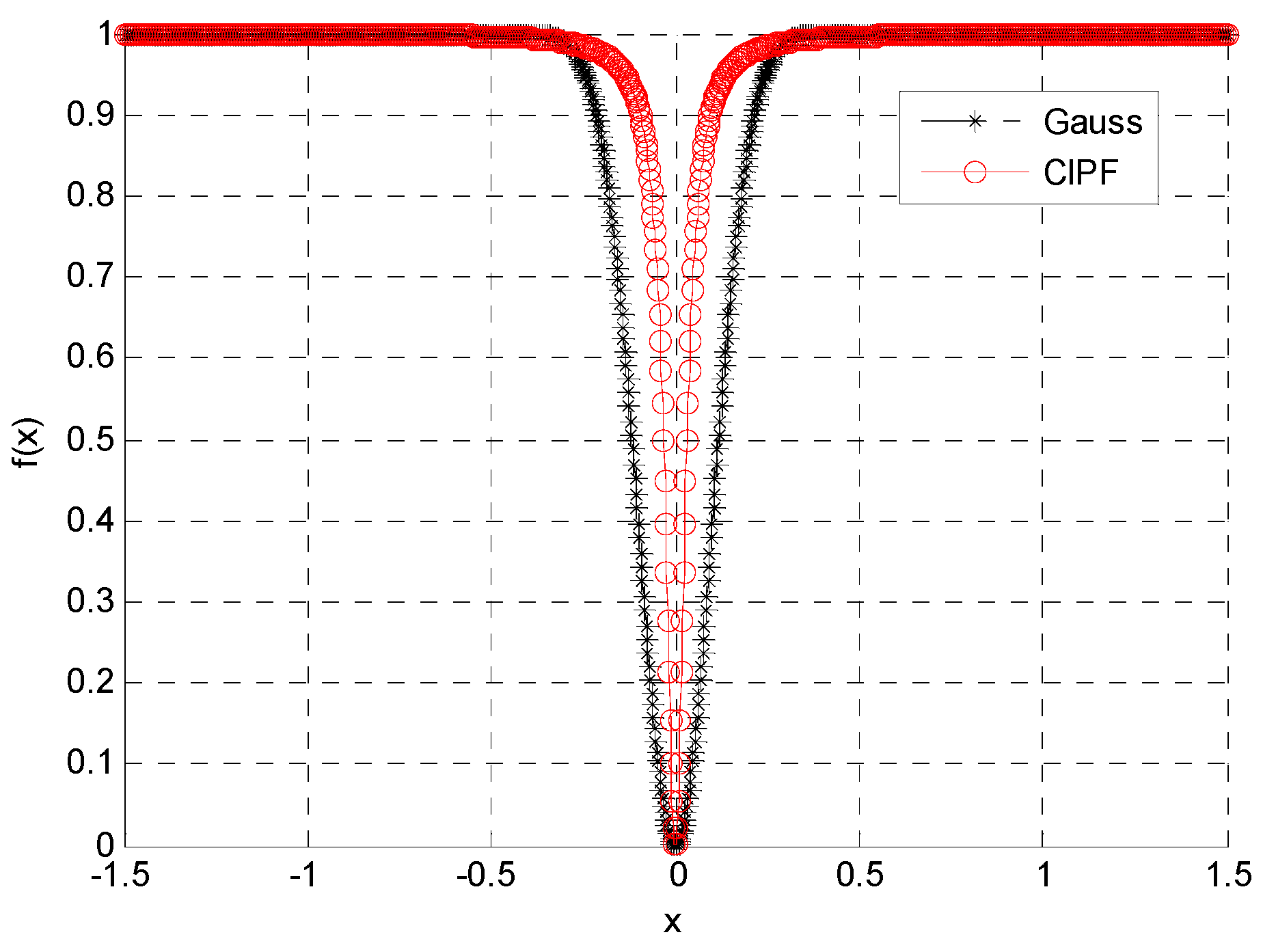
4.1. Selection of Approximation Function
4.2. Selection of Optimization Method
| Algorithm 2. The pseudocode of CReSL0 algorithm. |
| Initialization: |
| (1) Set and . |
| (2) Set . |
| While |
| (1) Let . |
| (2) Initialization: . |
| -for |
| If (a) . |
| (b) . |
| Else (c) . |
| (d) . |
| (3) Set . |
| The estimated value is . |
4.3. Selection of Parameters
5. Simulation and Results
5.1. Reconstruction of One-Dimensional Gauss Signal
5.2. Reconstruction of Two-Dimensional Image Signal
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Candés, E. Compressive sampling. In Proceedings of the international congress of mathematicians, Madrid, Spain, 22–30 August 2006; pp. 1433–1452. [Google Scholar]
- Baraniuk, R. Compressive sensing. IEEE Signal Process. Mag. 2007, 24, 118–121. [Google Scholar] [CrossRef]
- Candès, E.; Romberg, J.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 2006, 59, 1207–1223. [Google Scholar] [CrossRef]
- Wang, H.; Guo, Q.; Zhang, G.X.; Li, G.X.; Xiang, W. Thresholded smoothed ℓ° norm for accelerated Sparse recovery. IEEE Commun, Lett. 2015, 19, 953–956. [Google Scholar] [CrossRef]
- Bu, H.X.; Tao, R.; Bai, X.; Zhao, J. Regularized smoothed ℓ° norm algorithm and its application to CS-based radar imaging. Signal Process. 2016, 122, 115–122. [Google Scholar] [CrossRef]
- Goyal, P.; Singh, B. Subspace pursuit for sparse signal reconstruction in wireless sensor networks. Procedia. Comput. Sci. 2018, 125, 228–233. [Google Scholar] [CrossRef]
- Wei-Hong, F.U.; Ai-Li, L.I.; Li-Fen, M.A.; Huang, K.; Yan, X. Underdetermined blind separation based on potential function with estimated parameter’s decreasing sequence. Syst. Eng. Electron. 2014, 36, 619–623. [Google Scholar]
- Mallat, S.; Zhang, Z. Matching pursuit in time–frequency dictionary. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef]
- Pati, Y.C.; Rezaiifar, R.; Krishnaprasad, P.S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993; pp. 40–44. [Google Scholar]
- Dai, W.; Milenkovic, O. Subspace pursuit for compressive sensing signal reconstruction. IEEE Trans. Inf. Theory 2009, 5, 2230–2249. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J.A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Commun. ACM 2010, 12, 93–100. [Google Scholar] [CrossRef]
- Do, T.T.; Lu, G.; Nguyen, N.; Tran, T.D. Sparsity adaptive matching pursuit algorithm for practical compressed sensing. In Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008; pp. 581–587. [Google Scholar]
- Wang, J.; Li, P. Recovery of Sparse Signals Using Multiple Orthogonal Least Squares. IEEE Trans. Signal Process. 2017, 65, 2049–2061. [Google Scholar] [CrossRef]
- Ekanadham, C.; Tranchina, D.; Simoncelli, E.P. Recovery of Sparse Translation-Invariant Signals with Continuous Basis Pursuit. IEEE Trans. Signal Process. 2011, 10, 4735–4744. [Google Scholar] [CrossRef]
- Pant, J.K.; Lu, W.S.; Antoniou, A. New Improved Algorithms for Compressive Sensing Based on lp Norm. IEEE Trans. Circuits Syst. II Express Briefs 2014, 61, 198–202. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient Projection for Sparse Reconstruction: Application to Compressed Sensing and Other Inverse Problems. IEEE J. Sel. Top. Signal Process 2008, 1, 586–597. [Google Scholar] [CrossRef]
- Kim, D.; Fessler, J.A. Another look at the fast iterative shrinkage/thresholding algorithm (FISTA). Siam J. Optim 2018, 28, 223–250. [Google Scholar] [CrossRef]
- Mohimani, G.H.; Babaie-Zadeh, M.; Jutten, C. Fast sparse representation based on smoothed ℓ0 norm, in: Independent Component Analysis and Signal Separation. In Proceedings of the International Conference on Latent Variable Analysis and Signal Separation, London, UK, 9–12 September 2007; pp. 389–396. [Google Scholar]
- Wang, L.; Yin, X.; Yue, H.; Xiang, J. A regularized weighted smoothed L0 norm minimization method for underdetermined blind source separation. Sensors 2018, 18, 4260. [Google Scholar] [CrossRef] [PubMed]
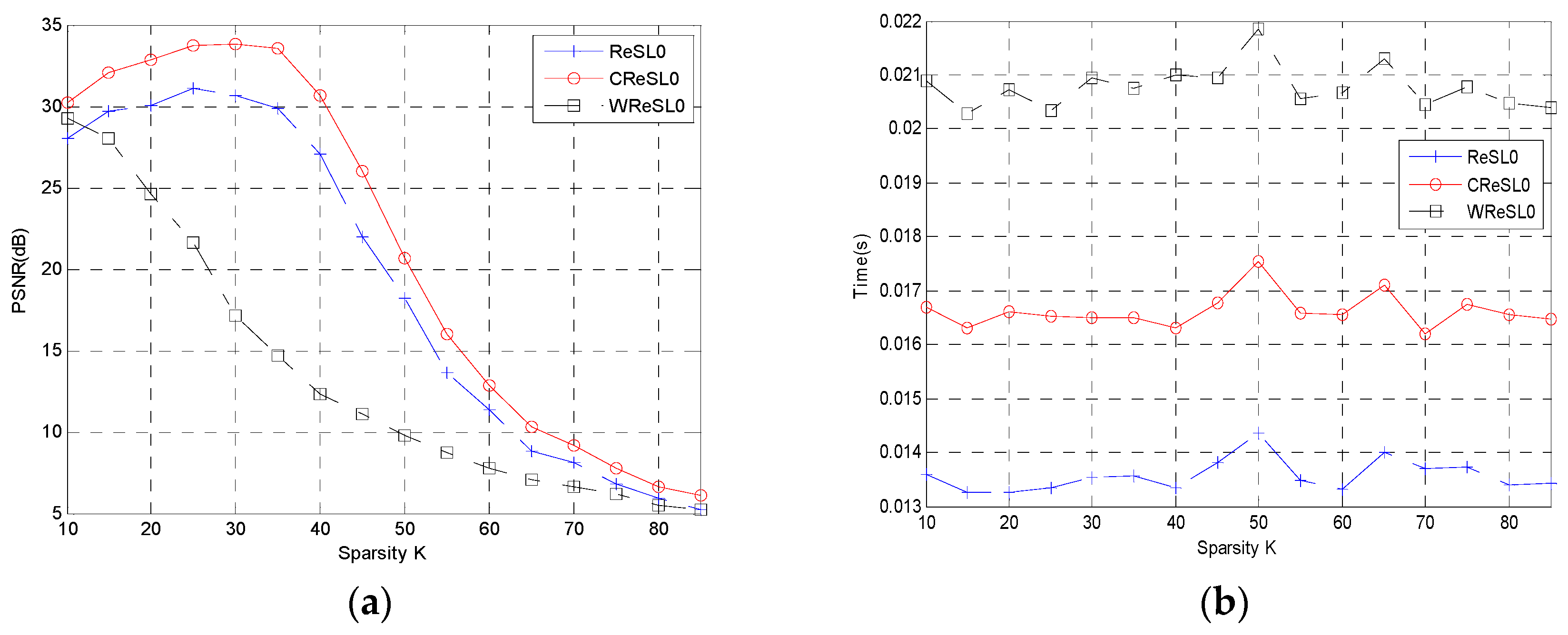



| Figure 4 | PSNR (dB) | Time (s) | PSNR/Time | ||||||
|---|---|---|---|---|---|---|---|---|---|
| CReSL0 | ReSL0 | WReSL0 | CReSL0 | ReSL0 | WReSL0 | CReSL0 | ReSL0 | WReSL0 | |
| a | 35.64 | 34.36 | 34.94 | 6.56 | 5.65 | 7.16 | 5.43 | 6.08 | 4.88 |
| b | 37.01 | 35.37 | 36.01 | 6.58 | 5.58 | 7.18 | 5.62 | 6.34 | 5.02 |
| c | 36.82 | 35.78 | 36.31 | 6.39 | 5.60 | 7.37 | 5.76 | 6.39 | 4.93 |
| d | 33.39 | 31.88 | 32.49 | 6.48 | 5.77 | 7.25 | 5.15 | 5.53 | 4.48 |
| e | 33.03 | 32.01 | 32.68 | 6.54 | 5.74 | 7.18 | 5.05 | 5.58 | 4.55 |
| CR | PSNR (dB) | Time (s) | PSNR/Time | ||||||
|---|---|---|---|---|---|---|---|---|---|
| CReSL0 | ReSL0 | WReSL0 | CReSL0 | ReSL0 | WReSL0 | CReSL0 | ReSL0 | WReSL0 | |
| 0.4 | 27.55 | 26.85 | 27.23 | 3.23 | 2.71 | 4.45 | 8.53 | 9.91 | 6.12 |
| 0.6 | 32.04 | 30.82 | 31.42 | 4.75 | 4.11 | 5.85 | 6.75 | 7.50 | 5.37 |
| 0.8 | 37.68 | 36.30 | 36.94 | 7.50 | 6.54 | 8.18 | 5.02 | 5.55 | 4.52 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Wang, L.; Yu, H.; Xin, F. A New Regularized Reconstruction Algorithm Based on Compressed Sensing for the Sparse Underdetermined Problem and Applications of One-Dimensional and Two-Dimensional Signal Recovery. Algorithms 2019, 12, 126. https://doi.org/10.3390/a12070126
Wang B, Wang L, Yu H, Xin F. A New Regularized Reconstruction Algorithm Based on Compressed Sensing for the Sparse Underdetermined Problem and Applications of One-Dimensional and Two-Dimensional Signal Recovery. Algorithms. 2019; 12(7):126. https://doi.org/10.3390/a12070126
Chicago/Turabian StyleWang, Bin, Li Wang, Hao Yu, and Fengming Xin. 2019. "A New Regularized Reconstruction Algorithm Based on Compressed Sensing for the Sparse Underdetermined Problem and Applications of One-Dimensional and Two-Dimensional Signal Recovery" Algorithms 12, no. 7: 126. https://doi.org/10.3390/a12070126
APA StyleWang, B., Wang, L., Yu, H., & Xin, F. (2019). A New Regularized Reconstruction Algorithm Based on Compressed Sensing for the Sparse Underdetermined Problem and Applications of One-Dimensional and Two-Dimensional Signal Recovery. Algorithms, 12(7), 126. https://doi.org/10.3390/a12070126




