A Cyclical Non-Linear Inertia-Weighted Teaching–Learning-Based Optimization Algorithm
Abstract
1. Introduction
2. Teaching–Learning-Based Optimization
2.1. Teacher Phase
2.2. Learner Phase
3. Cyclical Non-Linear Inertia-Weighted Teaching–Learning-Based Optimization (NIWTLBO) Algorithm
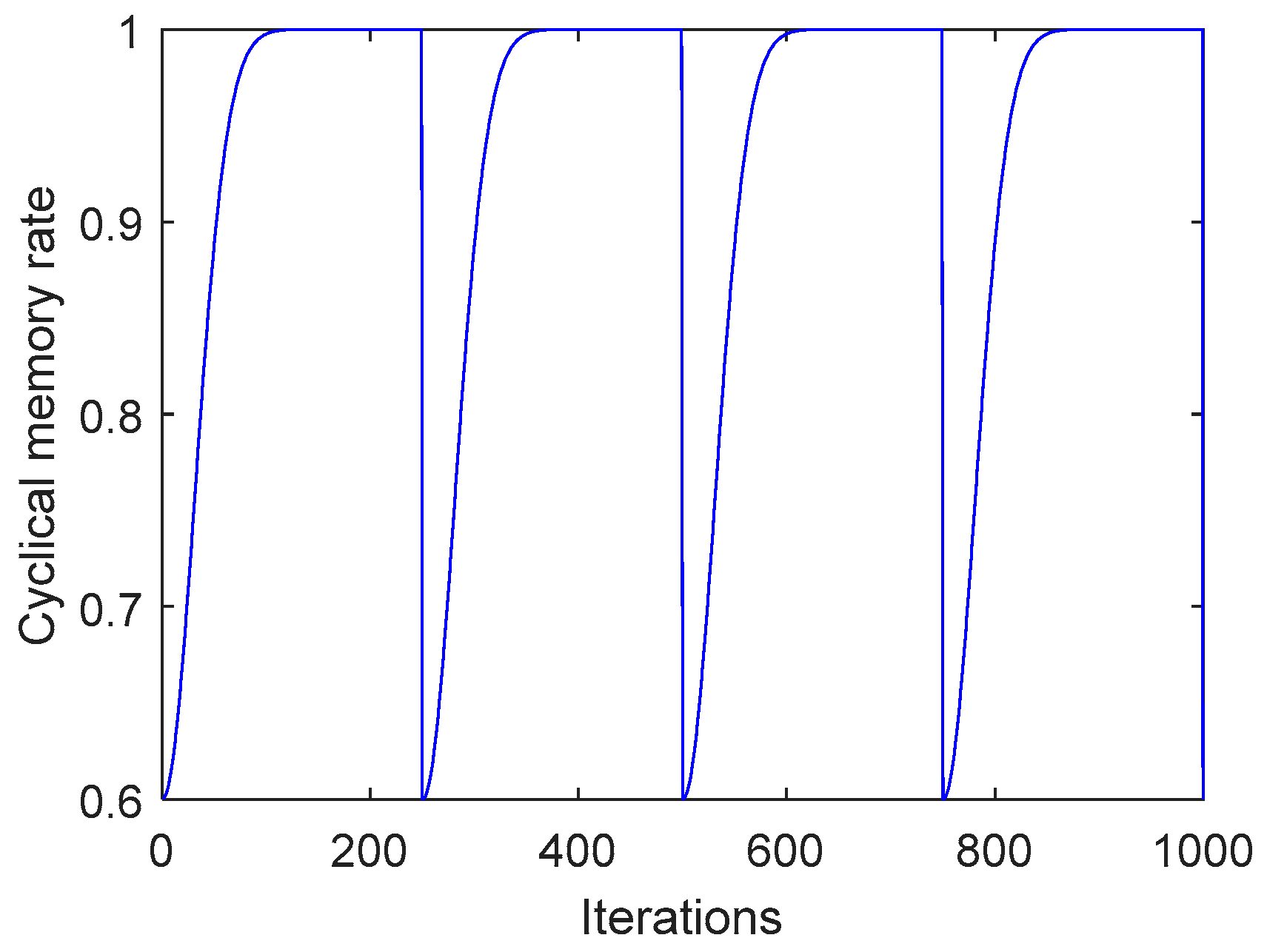
3.1. Algorithm Description
3.2. Behavior Parameter Analysis
3.3. Framework of CNIWTLBO
| Algorithm 1 The Framework of CNIWTLBO |
|
4. Benchmark Tests
4.1. CNIWTLBO vs. Particle Swarm Optimization (PSO), Artificial Bee Colony (ABC), Differential Evolution (DE) and Teaching–Learning-Based Optimization (TLBO)
4.2. CNIWTLBO vs. the Variants of PSO
4.3. CNIWTLBO vs. the Variants of ABC, DE
4.4. CNIWTLBO vs. the Variants of TLBO in Different Dimensions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Thakur, M. A new genetic algorithm for global optimization of multimodal continuous functions. J. Comput. Sci. 2014, 5, 298–311. [Google Scholar] [CrossRef]
- Hussein, H.A.; Demiroglu, I.; Johnston, R.L. Application of a parallel genetic algorithm to the global optimization of medium-sized Au–Pd sub-nanometre clusters. Eur. Phys. J. B 2018, 91, 34. [Google Scholar] [CrossRef]
- Chandra Mohan, B.; Baskaran, R. A survey: Ant colony optimization based recent research and implementation on several engineering domain. Expert Syst. Appl. 2012, 39, 4618–4627. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, R.L. Ant colony optimization with different crossover schemes for global optimization. Clust. Comput. 2017, 20, 1247–1257. [Google Scholar] [CrossRef]
- Ali, M.M.; Kaelo, P. Improved particle swarm algorithms for global optimization. Appl. Math. Comput. 2008, 196, 578–593. [Google Scholar] [CrossRef]
- Liu, P.; Jing, L. Multi-leader PSO (MLPSO): A new PSO variant for solving global optimization problems. Appl. Soft Comput. 2017, 61, 256–263. [Google Scholar] [CrossRef]
- Kang, F.; Li, J.; Ma, Z. Rosenbrock artificial bee colony algorithm for accurate global optimization of numerical functions. Inf. Sci. 2011, 181, 3508–3531. [Google Scholar] [CrossRef]
- Karaboga, D.; Gorkemli, B.; Ozturk, C.; Karaboga, N. A comprehensive survey: Artificial bee colony (ABC) algorithm and applications. Artif. Intell. Rev. 2014, 42, 21–57. [Google Scholar] [CrossRef]
- You, X.; Ma, Y.; Liu, Z.; Xie, M. An ABC Algorithm with Recombination. Int. J. Comput. Commun. Control 2018, 13, 590–601. [Google Scholar] [CrossRef]
- Mohamed, A.K.; Mohamed, A.W.; Elfeky, E.Z.; Saleh, M. Solving constrained non-linear integer and mixed-integer global optimization problems using enhanced directed differential evolution algorithm. In Machine Learning Paradigms: Theory and Application; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Mohamed, A.W. Solving large-scale global optimization problems using enhanced adaptive differential evolution algorithm. Complex Intell. Syst. 2017, 3, 205–231. [Google Scholar] [CrossRef]
- Nouioua, M.; Li, Z. Using differential evolution strategies in chemical reaction optimization for global numerical optimization. Appl. Intell. 2017, 47, 935–961. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput.-Aided Des. 2011, 43, 303–315. [Google Scholar] [CrossRef]
- Rao, R.V.; Savsani, V.J.; Vakharia, D.P. Teaching–learning-based optimization: An optimization method for continuous non-linear large scale problems. Inf. Sci. 2012, 183, 1–15. [Google Scholar] [CrossRef]
- Rao, R.V.; Patel, V. An elitist teaching-learning-based optimization algorithm for solving complex constrained optimization problems. Int. J. Ind. Eng. Comput. 2012, 3, 535–560. [Google Scholar] [CrossRef]
- Venkata Rao, R.; Kalyankar, V.D. Parameter optimization of modern machining processes using teaching–learning-based optimization algorithm. Eng. Appl. Artif. Intell. 2013, 26, 524–531. [Google Scholar] [CrossRef]
- Rao, R.V.; Patel, V. Multi-objective optimization of heat exchangers using a modified teaching-learning-based optimization algorithm. Appl. Math. Model. 2013, 37, 1147–1162. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A.R.; Niknam, T. A modified teaching–learning based optimization for multi-objective optimal power flow problem. Energy Convers. Manag. 2014, 77, 597–607. [Google Scholar] [CrossRef]
- Sultana, S.; Roy, P.K. Multi-objective quasi-oppositional teaching learning based optimization for optimal location of distributed generator in radial distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 534–545. [Google Scholar] [CrossRef]
- Ghasemi, M.; Ghavidel, S.; Gitizadeh, M.; Akbari, E. An improved teaching–learning-based optimization algorithm using Lévy mutation strategy for non-smooth optimal power flow. Int. J. Electr. Power Energy Syst. 2015, 65, 375–384. [Google Scholar] [CrossRef]
- Yang, Z.; Li, K.; Guo, Y.; Ma, H.; Zheng, M. Compact real-valued teaching-learning based optimization with the applications to neural network training. Knowl.-Based Syst. 2018, 159, 51–62. [Google Scholar] [CrossRef]
- Wang, B.C.; Li, H.X.; Feng, Y. An Improved teaching-learning-based optimization for constrained evolutionary optimization. Inf. Sci. 2018, 456, 131–144. [Google Scholar] [CrossRef]
- Kumar Shukla, A.; Singh, P.; Vardhan, M. Neighbour teaching learning based optimization for global optimization problems. J. Intell. Fuzzy Syst. 2018, 34, 1583–1594. [Google Scholar] [CrossRef]
- Chen, X.; Xu, B.; Mei, C.; Ding, Y.; Li, K. Teaching–learning–based artificial bee colony for solar photovoltaic parameter estimation. Appl. Energy 2018, 212, 1578–1588. [Google Scholar] [CrossRef]
- Satapathy, S.C. Weighted Teaching-learning-based optimization for global function optimization. Appl. Math. 2013, 4, 429–439. [Google Scholar] [CrossRef]
- Chen, D.; Zou, F.; Li, Z.; Wang, J.; Li, S. An improved teaching-learning-based optimization algorithm for solving global optimization problem. Inf. Sci. 2015, 297, 171–190. [Google Scholar] [CrossRef]
- Satapathy, S.C. Improved teaching learning based optimization for global function optimization. Decis. Sci. Lett. 2013, 2, 23–34. [Google Scholar] [CrossRef]
- Rao, R.V.; Patel, V. An improved teaching-learning-based optimization algorithm for solving unconstrained optimization problems. Sci. Iran. 2013, 20, 710–720. [Google Scholar] [CrossRef]
- Wu, Z.-S.; Fu, W.-P.; Xue, R. Nonlinear Inertia weighted teaching-learning-based optimization for solving global optimization problem. Comput. Intell. Neurosci. 2015, 2015, 292576. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Yuhui, S. Tracking and optimizing dynamic systems with particle swarms. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001; pp. 94–100. [Google Scholar]
- Shi, Y.; Eberhart, R.C. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, IEEE World Congress on Computational Intelligence, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Clerc, M.; Kennedy, J. The particle swarm—Explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evolut. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Frans, V.D.B.; Engelbrecht, A.P. A Cooperative approach to particle swarm optimization. IEEE Trans. Evolut. Comput. 2004, 8, 225–239. [Google Scholar]
- Liang, J.J.; Suganthan, P.N.; Qin, A.K.; Baska, S. Comprehensive Learning particle swarm optimizer for global optimization of multimodal functions. IEEE Trans. Evolut. Comput. 2006, 10, 281–295. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D. A modified artificial bee colony algorithm for real-parameter optimization. Inf. Sci. 2012, 192, 120–142. [Google Scholar] [CrossRef]
- Zhu, G.P.; Kwong, S. Gbest-guided artificial bee colony algorithm for numerical function. Appl. Soft Comput. 2010, 10, 445–456. [Google Scholar] [CrossRef]
- Gao, W.; Liu, S. Improved artificial bee colony algorithm for global optimization. Inf. Proc. Lett. 2011, 111, 871–882. [Google Scholar] [CrossRef]
| No. | Function | Formulation | C | D | Range | MinFunVal |
|---|---|---|---|---|---|---|
| f1 | Sphere | U | 30 | [−100, 100] | 0 | |
| f2 | SumSquares | U | 30 | [−100, 100] | 0 | |
| f3 | Tablet | U | 30 | [−100, 100] | 0 | |
| f4 | Schwefel 1.2 | U | 30 | [−100, 100] | 0 | |
| f5 | Schwefel 2.22 | U | 30 | [−10, 10] | 0 | |
| f6 | Schwefel 2.21 | U | 30 | [−100, 100] | 0 | |
| f7 | Zakharov | U | 30 | [−5, 10] | 0 | |
| f8 | Rosenbrock | U | 30 | [−4, 4] | 0 | |
| f9 | Schaffer | M | 2 | [−10, 10] | −1 | |
| f10 | Dropwave | M | 2 | [−2, 2] | −1 | |
| f11 | Bohachevsky1 | M | 2 | [−100, 100] | 0 | |
| f12 | Bohachevsky2 | M | 2 | [−100, 100] | 0 | |
| f13 | Six Hump Camel Back | M | 2 | [−5, 5] | −1.03163 | |
| f14 | Goldstein-Price | M | 2 | [−2, 2] | 3 | |
| f15 | Ackley | M | 30 | [−32, 32] | 0 | |
| f16 | Schwefel 2.26 | M | 30 | [−500, 500] | −837.9658 | |
| f17 | Multimod | M | 30 | [−10, 10] | 0 | |
| f18 | Rastrigin | M | 30 | [−5.12, 5.12] | 0 | |
| f19 | Griewank | M | 30 | [−600, 600] | 0 | |
| f20 | NCRastrigin | M | 30 | [−5.12, 5.12] | 0 | |
| f21 | Weierstrass | M | 30 | [−0.5, 0.5] | 0 |
| Algorithm | Parameter Settings |
|---|---|
| PSO | Population size NP = 40, Cognitive attraction C1 = 2, Social attraction C2 = 2, Inertia weight w = 0.9 |
| ABC | NP = 40 |
| DE | NP = 40, mutation rate F = 0.5, crossover rate R = 0.4 |
| TLBO | NP = 40 |
| CNIWTLBO | NP = 40, wcmin = 0.6, T = 250 |
| No. | PSO (Mean ± SD) | ABC (Mean ± SD) | DE (Mean ± SD) | TLBO (Mean ± SD) | CNIWTLBO (Mean ± SD) |
|---|---|---|---|---|---|
| f1 | 8.68E-12 ± 6.15E-12 | 9.53E-16 ± 5.13E-16 | 7.28E-27 ± 2.35E-26 | 3.42E-287 ± 0.00 | 0.00E+00 ± 0.00E+00 |
| f2 | 2.14E-10 ± 1.26E-10 | 7.38E-16 ± 1.32E-16 | 8.52E-26 ± 2.66E-26 | 8.74E-286 ± 0.00 | 0.00E+00 ± 0.00E+00 |
| f3 | 3.26E-08 ± 1.52E-08 | 8.62E-16 ± 1.29E-16 | 3.02E-26 ± 1.38E-26 | 6.28E-285 ± 0.00 | 0.00E+00 ± 0.00E+00 |
| f4 | 2.25E+05 ± 1.16E+05 | 7.52E+03 ± 1.46E+03 | 2.32E+04 ± 2.34E+03 | 2.48E-84 ± 1.29E-84 | 0.00E+00 ± 0.00E+00 |
| f5 | 5.02E-03 ± 3.26E-03 | 2.36E-14 ± 1.22E-14 | 4.57E-16 ± 1.16E-16 | 1.65E-143 ± 1.32E-143 | 4.62e-323 ± 0.00E+00 |
| f6 | 1.23E+00 ± 5.24E-01 | 3.67E+01 ± 1.05E+01 | 1.19E-02 ± 2.15E-03 | 7.68E-120 ± 3.82E-120 | 2.64E-315 ± 0.00E+00 |
| f7 | 1.58E+02 ± 4.72E+01 | 2.45E+02 ± 2.16E+01 | 5.63E+01 ± 6.74E+00 | 6.04E-51 ± 4.62E-51 | 1.82E-319 ± 0.00E+00 |
| f8 | 3.05E+01 ± 2.26E+01 | 1.12E+01 ± 2.43E+00 | 2.51E+01 ± 3.47E+00 | 1.32E+01 ± 4.36E+00 | 1.78E+01 ± 5.13E+00 |
| f9 | −1.00E+00 ± 0.00E+00 | −1.00E+00 ± 0.00E+00 | −1.00E+00 ± 0.00E+00 | −1.00E+00 ± 0.00E+00 | −1.00E+00 ± 0.00E+00 |
| f10 | −1.00E+00 ± 0.00E+00 | −1.00E+00 ± 0.00E+00 | −1.00E+00 ± 0.00E+00 | −1.00E+00 ± 0.00E+00 | −1.00E+00 ± 0.00E+00 |
| f11 | 0.00E+00 ± 0.00E+00 | 0.00E+00 ± 0.00E+00 | 0.00E+00 ± 0.00E+00 | 0.00E+00 ± 0.00E+00 | 0.00E+00 ± 0.00E+00 |
| f12 | 0.00E+00 ± 0.00E+00 | 0.00E+00 ± 0.00E+00 | 0.00E+00 ± 0.00E+00 | 0.00E+00 ± 0.00E+00 | 0.00E+00 ± 0.00E+00 |
| f13 | −1.03163 ± 0.00 | −1.03163 ± 0.00 | −1.03163 ± 0.00 | −1.03163 ± 0.00 | −1.03163 ± 0.00 |
| f14 | 3.00 ± 8.23E-15 | 3.00 ± 5.02E-15 | 3.00 ± 1.53E-15 | 3.00 ± 6.18E-16 | 3.00 ± 5.82E-16 |
| f15 | 1.48E+00 ± 3.85E-01 | 3.14E-13 ± 3.06E-14 | 2.56E-14 ± 6.07E-15 | 4.45E-15 ± 2.85E-16 | 8.88E-16 ± 0.00 |
| f16 | −8.79E+03 ± 4.27E+02 | −1.24E+04 ± 1.81E+02 | −1.15E+04 ± 1.58E+03 | −9.18E+03 ± 7.65E+02 | −7.33E+03 ± 1.66E+02 |
| f17 | 7.55E-67 ± 1.63E-66 | 6.83E-19 ± 1.62E-19 | 5.03-311 ± 0.00 | 0.00E+00 ± 0.00E+00 | 0.00E+00 ± 0.00E+00 |
| f18 | 1.12E+02 ± 2.24E+01 | 1.32E-13 ± 2.48E-13 | 9.02E+01 ± 8.57E+00 | 7.21E+00 ± 5.78E+00 | 0.00E+00 ± 0.00E+00 |
| f19 | 6.69E-03 ± 5.46E-04 | 7.15E-03 ± 6.86E-04 | 0.00E+00 ± 0.00E+00 | 0.00E+00 ± 0.00E+00 | 0.00E+00 ± 0.00E+00 |
| f20 | 1.78E+02 ± 3.22E+01 | 2.01E-14 ± 1.67E-14 | 6.82E+01 ± 8.75E+00 | 1.48E+01 ± 2.76E+00 | 0.00E+00 ± 0.00E+00 |
| f21 | 6.13E+01 ± 2.12E+01 | 1.36E-02 ± 8.06E-03 | 1.38E+01 ± 5.84E-01 | 0.00E+00 ± 0.00E+00 | 0.00E+00 ± 0.00E+00 |
| No. | PSO (Mean ± SD) | ABC (Mean ± SD) | DE (Mean ± SD) | TLBO (Mean ± SD) | CNIWTLBO (Mean ± SD) |
|---|---|---|---|---|---|
| f1 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 60,720 ± 2.15E+02 |
| f2 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 58,920 ± 2.08E+02 |
| f3 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 61,160 ± 2.26E+02 |
| f4 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 72,280 ± 1.38E+02 |
| f5 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 |
| f6 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 |
| f7 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 |
| f8 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 |
| f9 | 12,315 ± 3.26E+02 | 43,502 ± 3.12E+02 | 8594 ± 2.13E+02 | 9596 ± 2.04E+02 | 2840 ± 2.86E+02 |
| f10 | 11,406 ± 3.18E+01 | 13,749 ± 1.13E+02 | 5412 ± 1.46E+02 | 3002 ± 2.32E+02 | 1215 ± 3.18E+01 |
| f11 | 9356 ± 2.18E+02 | 3178 ± 7.85E+01 | 3916 ± 8.39E+01 | 2258 ± 3.64E+01 | 1232 ± 2.13E+01 |
| f12 | 9503 ± 1.25E+02 | 4685 ± 9.14E+01 | 4221 ± 1.14E+02 | 2556 ± 2.23E+01 | 1284 ± 2.38E+01 |
| f13 | 1915 ± 1.29E+02 | 1357 ± 1.26E+02 | 1735 ± 1.19E+02 | 718 ± 6.02E+01 | 1130 ± 8.16E+01 |
| f14 | 2102 ± 1.32E+02 | 1838 ± 1.51E+02 | 1702 ± 2.13E+02 | 1232 ± 6.67E+01 | 2810 ± 2.05E+02 |
| f15 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 |
| f16 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 |
| f17 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 28,215 ± 1.12E+02 | 8040 ± 8.44E+01 |
| f18 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 8120 ± 5.12E+01 |
| f19 | 80,000 ± 0.00 | 80,000 ± 0.00 | 52,326 ± 6.21E+02 | 12,003 ± 8.73E+02 | 8160 ± 3.86E+01 |
| f20 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 8080 ± 1.22E+02 |
| f21 | 80,000 ± 0.00 | 80,000 ± 0.00 | 80,000 ± 0.00 | 12,625 ± 1.13E+02 | 9040 ± 2.48E+02 |
| No. | Function | PSO-w | PSO-cf | CPSO-H | CLPSO | TLBO | CNIWTLBO | |
|---|---|---|---|---|---|---|---|---|
| f1 | Sphere | Mean | 7.96E-51 | 9.84E-105 | 4.98E-45 | 5.15E-29 | 0.00E+00 | 0.00E+00 |
| SD | 3.56E-50 | 4.21E-104 | 1.00E-44 | 2.16E-28 | 0.00E+00 | 0.00E+00 | ||
| f8 | Rosenbrock | Mean | 3.08E+00 | 6.98E-01 | 1.53E+00 | 2.46E+00 | 4.21E+00 | 6.68E+00 |
| SD | 7.69E-01 | 1.46E+00 | 1.70E+00 | 1.70E+00 | 6.83E-01 | 6.32E-01 | ||
| f15 | Ackley | Mean | 1.58E-14 | 9.18E-01 | 1.49E-14 | 4.32E-10 | 3.55E-15 | 8.44E-16 |
| SD | 1.60E-14 | 1.01E+00 | 6.97E-15 | 2.55E-14 | 8.32E-31 | 5.24E-17 | ||
| f16 | Schwefel2.26 | Mean | 3.20E+02 | 9.87E+02 | 2.13E+02 | 0.00E+00 | −4.01E+03 | −4.07E+03 |
| SD | 1.85E+02 | 2.76E+02 | 1.41E+02 | 0.00E+00 | 1.85E+02 | 1.14E+02 | ||
| f18 | Rastrigin | Mean | 5.82E+00 | 1.25E+01 | 2.12E+00 | 0.00E+00 | 6.77E-08 | 0.00E+00 |
| SD | 2.96E+00 | 5.17E+00 | 1.33E+00 | 0.00E+00 | 3.68E-07 | 0.00E+00 | ||
| f19 | Griewank | Mean | 9.69E-02 | 1.19E-01 | 4.07E-02 | 4.56E-03 | 0.00E+00 | 0.00E+00 |
| SD | 5.01E-02 | 7.11E-02 | 2.80E-02 | 4.81E-03 | 0.00E+00 | 0.00E+00 | ||
| f20 | NCRastrigin | Mean | 4.05E+00 | 1.20E+01 | 2.00E-01 | 0.00E+00 | 2.65E-08 | 0.00E+00 |
| SD | 2.58E+00 | 4.99E+00 | 4.10E-01 | 0.00E+00 | 1.23E-07 | 0.00E+00 | ||
| f21 | Weierstrass | Mean | 2.28E-03 | 6.69E-01 | 1.07E-15 | 0.00E+00 | 2.42E-05 | 0.00E+00 |
| SD | 7.04E-03 | 7.17E-01 | 1.67E-15 | 0.00E+00 | 1.38E-20 | 0.00E+00 |
| No. | Function | GABC | IABC | SaDE | JADE | TLBO | CNIWTLBO | |
|---|---|---|---|---|---|---|---|---|
| f1 | Sphere | Mean | 3.6E-63 | 5.34E-178 | 4.5E-20 | 1.8E-60 | 0.00E+00 | 0.00E+00 |
| FEs:1.5 × 105 | SD | 5.7E-63 | 0 | 1.9E-14 | 8.4E-60 | 0.00E+00 | 0.00E+00 | |
| f4 | Schwefel 1.2 | Mean | 4.3E+02 | 1.78E-65 | 9.0E-37 | 5.7E-61 | 0.00E+00 | 0.00E+00 |
| FEs:5.0 × 105 | SD | 8.0E+02 | 2.21E-65 | 5.4E-36 | 2.7E-60 | 0.00E+00 | 0.00E+00 | |
| f5 | Schwefel 2.22 | Mean | 4.8E-45 | 8.82E-127 | 1.9E-14 | 1.8E-25 | 0.00E+00 | 0.00E+00 |
| FEs:2.0 × 105 | SD | 1.4E-45 | 3.49E-126 | 1.1E-14 | 8.8E-25 | 0.00E+00 | 0.00E+00 | |
| f6 | Schwefel 2.21 | Mean | 3.6E-06 | 4.98E-38 | 7.4E-11 | 8.2E-24 | 0.00E+00 | 0.00E+00 |
| FEs:5.0 × 105 | SD | 7.6E-07 | 8.59E-38 | 1.82E-10 | 4.0E-23 | 0.00E+00 | 0.00E+00 | |
| f15 | Ackley | Mean | 1.8E-09 | 3.87E-14 | 2.7E-03 | 8.2E-10 | 4.44E-15 | 8.46E-16 |
| FEs:5.0 × 104 | SD | 7.7E-10 | 8.52E-15 | 5.1E-04 | 6.9E-10 | 2.58E-30 | 2.15E-31 | |
| f18 | Rastrigin | Mean | 1.5E-10 | 0.00E+00 | 1.2E-03 | 1.0E-04 | 1.88E+01 | 0.00E+00 |
| FEs:1.0 × 105 | SD | 2.7E-10 | 0.00E+00 | 6.5E-04 | 6.0E-05 | 4.65E+00 | 0.00E+00 | |
| f19 | Griewank | Mean | 6.0E-13 | 0.00E+00 | 7.8E-04 | 9.9E-08 | 0.00E+00 | 0.00E+00 |
| FEs:5.0 × 105 | SD | 7.7E-13 | 0.00E+00 | 1.2E-03 | 6.0E-07 | 0.00E+00 | 0.00E+00 |
| No. | Function | D | TLBO | WTLBO | ITLBO | I-TLBO (NT = 4) | NIWTLBO | CNIWTLBO |
|---|---|---|---|---|---|---|---|---|
| f1 | Sphere | 20 | 1.43E-315 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| 50 | 1.35E-274 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | ||
| 100 | 4.13E-251 | 2.85E-316 | 5.38E-312 | 0.00E+00 | 0.00E+00 | 0.00E+00 | ||
| f5 | Schwefel2.22 | 20 | 2.67E-158 | 3.72E-231 | 5.36E-182 | 7.48E-287 | 2.50E-322 | 2.47E-323 |
| 50 | 9.28E-138 | 5.16E-208 | 2.87E-168 | 3.62E-281 | 4.43E-318 | 1.04E-322 | ||
| 100 | 2.82E-130 | 2.58E-189 | 1.94E-152 | 4.26E-268 | 7.46E-310 | 3.41E-316 | ||
| f8 | Rosenbrock | 20 | 1.62E+01 | 1.83E+01 | 2.14E+01 | 1.11E+01 | 1.08E+01 | 1.12E+01 |
| 50 | 4.75E+01 | 5.02E+01 | 5.13E+01 | 4.39E+01 | 4.52E+01 | 4.43E+01 | ||
| 100 | 9.26E+01 | 9.78E+01 | 1.02E+02 | 9.52E+01 | 9.63E+01 | 9.41E+01 | ||
| f15 | Ackley | 20 | 4.44E-15 | 3.18E-15 | 3.55E-15 | 9.12E-16 | 8.88E-16 | 8.88E-16 |
| 50 | 4.44E-15 | 6.42E-14 | 5.28E-14 | 2.45E-15 | 4.44E-15 | 8.88E-16 | ||
| 100 | 7.99E-15 | 6.35E-15 | 6.87E-15 | 2.44E-15 | 4.44E-15 | 8.88E-16 | ||
| f16 | Schwefel2.26 | 20 | −6.49E+03 | −6.63E+03 | −7.52E+03 | −6.21E+03 | −5.74E+03 | −4.67E+03 |
| 50 | −2.05E+04 | −1.86E+04 | −2.23E+04 | −2.06E+04 | −1.32E+04 | −1.21E+04 | ||
| 100 | −2.35E+04 | −2.41E+04 | −2.47E+04 | −2.36E+04 | −2.39E+04 | −2.16 E+04 | ||
| f18 | Rastrigin | 20 | 1.98E+00 | 2.26E-251 | 4.12E-203 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| 50 | 2.38E+01 | 5.58E-235 | 1.84E-188 | 0.00E+00 | 0.00E+00 | 0.00E+00 | ||
| 100 | 4.83E+01 | 1.86E-186 | 3.12E-142 | 4.58E-322 | 0.00E+00 | 0.00E+00 | ||
| f19 | Griewank | 20 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 | 0.00E+00 |
| 50 | 0.00E+00 | 0.00E+00 | 4.64E-312 | 0.00E+00 | 0.00E+00 | 0.00E+00 | ||
| 100 | 0.00E+00 | 5.42E-324 | 2.83E-288 | 1.87E-323 | 0.00E+00 | 0.00E+00 | ||
| f20 | NCRastrigin | 20 | 1.30E+01 | 3.58E-250 | 2.67E-239 | 3.24E-318 | 0.00E+00 | 0.00E+00 |
| 50 | 3.12E+01 | 1.86E-238 | 3.18E-225 | 2.55E-301 | 0.00E+00 | 0.00E+00 | ||
| 100 | 5.03E+01 | 2.64E-216 | 1.83E-209 | 3.62E-287 | 1.35E-328 | 0.00E+00 | ||
| f21 | Weierstrass | 20 | 1.02E+00 | 2.72E-308 | 3.65E-285 | 6.12E-312 | 0.00E+00 | 0.00E+00 |
| 50 | 1.53E+01 | 2.37E-282 | 1.83E-256 | 4.63E-288 | 3.62E-323 | 0.00E+00 | ||
| 100 | 5.02E+01 | 4.68E-198 | 2.66E-186 | 2.14E-216 | 2.73E-312 | 0.00E+00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Xue, R. A Cyclical Non-Linear Inertia-Weighted Teaching–Learning-Based Optimization Algorithm. Algorithms 2019, 12, 94. https://doi.org/10.3390/a12050094
Wu Z, Xue R. A Cyclical Non-Linear Inertia-Weighted Teaching–Learning-Based Optimization Algorithm. Algorithms. 2019; 12(5):94. https://doi.org/10.3390/a12050094
Chicago/Turabian StyleWu, Zongsheng, and Ru Xue. 2019. "A Cyclical Non-Linear Inertia-Weighted Teaching–Learning-Based Optimization Algorithm" Algorithms 12, no. 5: 94. https://doi.org/10.3390/a12050094
APA StyleWu, Z., & Xue, R. (2019). A Cyclical Non-Linear Inertia-Weighted Teaching–Learning-Based Optimization Algorithm. Algorithms, 12(5), 94. https://doi.org/10.3390/a12050094




