Abstract
This paper assumes that multiple device-to-device (D2D) users can reuse the same uplink channel and base station (BS) supplies power to D2D transmitters by means of wireless energy transmission; the optimization problem aims at maximizing the total capacity of D2D users, and proposes a power control and channel allocation algorithm for the energy harvesting D2D communications underlaying the cellular network. This algorithm firstly uses a heuristic dynamic clustering method to cluster D2D users and those in the same cluster can share the same channel. Then, D2D users in the same cluster are modeled as a non-cooperative game, the expressions of D2D users’ transmission power and energy harvesting time are derived by using the Karush–Kuhn–Tucker (KKT) condition, and the optimal transmission power and energy harvesting time are allocated to D2D users by the joint iteration optimization method. Finally, we use the Kuhn–Munkres (KM) algorithm to achieve the optimal matching between D2D clusters and cellular channel to maximize the total capacity of D2D users. Simulation results show that the proposed algorithm can effectively improve the system performance.
1. Introduction
Device-to-device (D2D) communication is one of the key technologies in the next generation mobile communication network [1]. It can reduce the power consumption of users’ equipment and end-to-end transmission delay by allowing two users in close proximity to communicate directly without traversing the base station (BS) or other core networks. D2D communication allows more users to connect to the network by reusing spectrum of the cellular network, which can improve the spectrum utilization rate and system capacity [2].
However, there is inter-layer interference between D2D users and cellular users when D2D users reuse the channel of cellular users. In addition, there will be intra-layer interference between D2D users if one cellular user’s channel is reused by multiple D2D users. Therefore, interference management is an important issue in the heterogeneous network where cellular users and D2D users coexist. In [3], the authors consider the scenario of multiple D2D users reusing the same channel, model the D2D users’ power allocation problem as a Nash bargaining solution and Nash competition game respectively, and obtain the optimal transmission power to maximize the utility of D2D users. In [4], the authors aim at maximizing the energy efficiency of D2D users, derive the expression of optimal power by using the property of fractional programming, and complete the channel allocation by using the Hungarian algorithm. A Stackelberg game is used in [5] to maximize the utility function of cellular users and D2D users by optimizing the D2D users’ transmission power and the BS’s interference price. In [6], a sub-carrier allocation algorithm is proposed and a geometric water-filling method is used to allocate the optimal transmission power to D2D users. The above papers implicitly assume that the energy of the D2D transmitter is infinite, which does not always conform with reality because the energy of the D2D device is finite or a device needs to be charged.
One solution to solve the energy supply of equipment is to adopt-energy harvesting technology in a D2D communication network, where D2D equipment can harvest energy from the surrounding environment. In [7], the authors assume that energy arrives at the beginning of a time slot and is stored for later use, and use a Pareto-optimal boundary to allocate power for D2D users under the constraint of the harvested energy on transmission power. In [8], the harvested energy of D2D transmitters is considered to be independent of each other with uniform distribution, and the authors use a Lagrange multiplier method and binary search method to obtain the optimal transmission power. In [9], the arrival of energy is also modeled as a Poisson process, and the energy harvesting time slot allocation, power and resource block allocation are jointly optimized to maximize the average energy efficiency of D2D users. However, due to the uncertainty of the environment, it is difficult to predict the energy that will arrive.
Some scholars have studied the resource allocation when D2D users harvest energy by wireless power transfer, the energy that broadcast by power station is controllable. In [10], D2D links harvest energy from the wireless power transmitter located at the BS, D2D users communicate when the energy is above a lower threshold, and an iterative joint resource block and power resource allocation algorithm is proposed to maximize the sum throughput of D2D users. However, the authors in [10] assume that the channel of a cellular user is only reused by one D2D user; when multiple D2D users reuse a same channel to transmit information, the spectrum utilization can be improved through appropriate interference management. In [11], D2D transmitters adopt time-switching mode for energy harvesting and data transmission, the expression for coverage probability of D2D link and cellular uplink are derived, and the optimal energy harvesting time is optimized by maximizing the average coverage probability of the D2D link. In [12], energy harvesting enabled D2D users to act as relays operating in a half-duplex mode to enhance the data transmissions of other D2D users, and D2D relays were unable to harvest energy and transmit data simultaneously; the energy harvesting time and transmission power of relays are optimized to maximize the D2D users’ throughput. In [13], D2D users harvest energy from a power station and transmit information signals simultaneously, and the sum throughput is maximized via joint time scheduling and power control. Literature [11,12,13] assumes that the energy harvesting time of different D2D user is same, but in fact the energy harvesting time of multiple D2D transmitters is different because the distance between D2D transmitter and BS, the distance between D2D user pair are different.
In this paper, we consider that D2D transmitter can harvest energy by wireless power transfer, while the energy harvesting time of the different D2D users is different, multiple D2D users can reuse the same channel. The contributions of this paper are summarized as follows:
- (1)
- The optimization problem of joint power control and channel allocation is constructed by considering the constraints of harvesting energy on transmission power, QoS (Quality of Service) of cellular users and channel multiplexing, so as to maximize the total capacity of D2D users. The original mixed integer nonlinear problem is transformed into a convex optimization problem by variable substitution and fractional programming.
- (2)
- The optimal joint power control and channel allocation algorithm is proposed. The optimal transmission power and energy harvesting time of D2D users are determined by the joint iterative method. The KM algorithm is used to complete the optimal matching between D2D users and cellular users’ channel.
- (3)
- The simulation results of the proposed algorithm are provided to verify the effectiveness of the proposed resource allocation algorithm. The system performance of the proposed algorithm in terms of D2D users’ total capacity is compared with the algorithm in [13] and equal time allocation (ETA) methods. The simulation results show that the proposed algorithm can effectively improve the system performance.
The rest of this paper is organized as follows. We describe the system model of D2D communication based on energy harvesting in Section 2. Then, in Section 3, the proposed optimal joint power control and channel allocation algorithm is investigated. Simulation results are provided and analyzed in Section 4 to show the performance of the proposed algorithm. Finally, conclusions are drawn in Section 5.
2. System Model
As shown in Figure 1, we consider a single cell scenario, where a BS locates in the center of the cell and cellular users coexist with D2D pairs, we use and to indicate the sets of cellular users and D2D users, each pair of D2D user includes one D2D transmitter and one D2D receiver. Each cellular user occupies one uplink orthogonal channel to communicate with the BS; D2D users reuse the channels assigned to the cellular users, and each channel can be occupied by more than one D2D users but one D2D user just can reuse one channel of cellular user. Therefore, interference exists in cellular user and D2D users, D2D users also impose interference to each other that sharing the same channel.
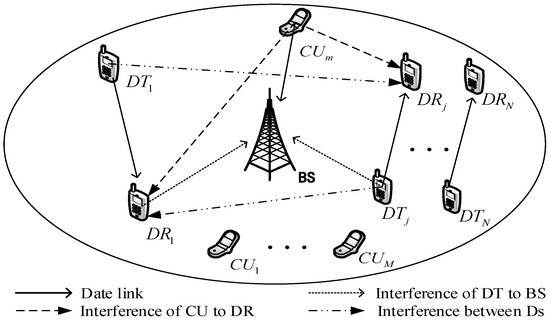
Figure 1.
System model of device-to-device (D2D) communication underlaying cellular network.
Assuming that BS supplies power to D2D transmitters by means of wireless energy transmission, the D2D user completes the energy harvesting and information transmission during the time period . In the time period of , the D2D transmitter harvests energy broadcast by the BS, and in the later time period, the D2D transmitter employs the harvested energy to communicate with D2D receiver. The harvested energy at the D2D transmitter is given by:
where is the transmit power of BS, is the channel gain between BS and D2D transmitter , denotes the energy harvesting efficiency of the D2D transmitter, which can be expressed as [14]:
where is matching efficiency, and it is related to the impedance of the rectifier antenna and the input impedance of the direct current (dc) converter. is the efficiency associated with parasitic losses. is the efficiency of conversion that is mainly related to the non-linear rectifier diode. is the efficiency of dc power transfer from the non-linear device to the dc load.
Suppose the number of D2D users share the channel of cellular user is , thus, the signal to inference plus noise ratio (SINR) of cellular user and D2D receiver can be expressed as:
The capacity of D2D user can be written as
where and are the transmission power of the cellular user and the D2D transmitter , is the channel gain between the cellular user and the BS, is the channel gain between the D2D transmitter and the BS, is the channel gain between the D2D pair , is the channel gain between the cellular user and D the 2D receiver sharing the same channel, is the channel gain between the D2D transmitter and the D2D receiver reusing the same channel, represents the spectral density of additive white Gaussian noise (AWGN) for the BS and the D2D receivers.
3. Optimal Joint Power Control and Channel Allocation Algorithm
3.1. Optimization Formulation
In this section, we analyze the optimal transmission power and energy harvesting time of D2D users, the optimal channel matching between cellular users and D2D users, taking the minimum QoS demands of cellular users and the limited transmission power into consideration, the optimization problem (P1) is established as
Subject to:
where is the channel reuse indicator of the D2D user, means the D2D user reuses the channel of cellular user , otherwise, it does not reuse. rthc represents the minimum SINR threshold of the cellular users, and represent the maximum transmit power of cellular users and D2D users, respectively. Equation (6) is the objective function of maximizing the total capacity of D2D users. Equation (7) guarantees the QoS requirement of cellular users. Equation (8) is the energy harvesting time constraint. Equation (9) is the energy causality constraint and means that the consumed energy for transmitting signals cannot exceed its harvested energy. Equation (10) indicates the limit transmission power of the cellular user and the D2D users. Equation (11) represents that one D2D user can reuse at most one channel.
The optimization problem P1 is a mixed-integer nonlinear programming problem, which is NP-hard and cannot be solved by standard convex optimization methods [15]. Therefore, we cluster D2D users according to interference weight graph in the first step, and those in the same cluster can share the same channel. Then, a joint iteration optimization method is used to determine the optimal transmission power and energy harvesting time. Last, we allocate channel for D2D users with the KM algorithm to maximize the total capacity of D2D users.
3.2. Optimal Joint Power Control and Channel Allocation Algorithm
The heuristic dynamic clustering method of [16] is used to divide the D2D users into clusters with the goal of minimizing the co-channel interference of D2D users in each cluster, and represents the set of D2D clusters. Thus, D2D clusters reuse channels of cellular users, each D2D cluster reuses one channel, and each cellular user’s channel is reused by one D2D cluster. In optimization problem P1, the channel allocation problem of D2D users can be transformed into the channel allocation problem of D2D clusters, and is used to denote the channel reuse indicator of D2D cluster, when D2D cluster reuses the channel of cellular user , , otherwise, .
Because different D2D clusters reuse channels of different cellular users, inter-layer interference only exists among D2D users in the same cluster. Therefore, the maximum capacity of a single D2D cluster can be solved first, and then the maximum total capacity of D2D users can be obtained by summing the maximum capacity of all D2D clusters. Assuming that D2D cluster reuses the channel of cellular user , that is , and the number of D2D users in D2D cluster is . The capacity of D2D cluster when it reuses the channel of cellular user can be calculated by:
Analyzing Equation (12) we can find that the capacity of D2D cluster is monotone decreasing with regard to , the capacity of D2D cluster can be optimal when the minimum value of is taken on the premise of satisfying the cellular user’s QoS. The lower bound of can be obtained from Equation (7) as:
The transmission power of D2D user is related to the energy harvested by D2D transmitter at the energy harvesting time. We define a new variable as:
Then the capacity expression of the D2D user is transformed into: , the numerator and denominator are all functions of energy harvesting time. Suppose the maximum capacity of D2D cluster is and denoted as:
According to [17], the maximum capacity of D2D cluster can be obtained if and only if,
Substituting Equations (13) and (14) into Equation (16), the optimization problem (P2) can be written as:
Subject to:
where , , , .
The Lagrange function of (17) with respect to Equation (19) is formulated as
where is the Lagrange multiplier. The D2D users that share the same channel are modeled as non-cooperative game, thus, for D2D user , the interference of other D2D users can be treated as noise in the solving process. We can get the following formulas through seeking the second partial derivative of Equation (21) with and
where . The formula Equations (22) and (23) are always less than zero, so is a convex function of and , according to the convex optimization theory, the solution of is the optimal solution of optimization problem P2.
The KKT condition of optimization problem P2 can be expressed as:
When , Equation (26) has no solution because of ; when , we can obtain the optimal value of and according to the equation set consists of Equations (24)–(26):
where .
When D2D users reuse the same channel, the transmission power of D2D user varies while other D2D users’ transmission power change, meanwhile, the transmission power of D2D user also affects the transmission power of other D2D users. Therefore, the transmission power of D2D users is dynamically adjusted by using the joint iterative optimization method until the optimal values are obtained.
After obtaining the optimal transmission power and energy harvesting time of D2D users in the cluster when each D2D cluster reuses the channels of cellular users respectively, the KM algorithm is used to achieve the optimal matching between D2D clusters and cellular users’ channels [18]. The optimization problem to maximize the total capacity of D2D users by allocating the cellular users’ channels for D2D clusters can be transformed into the optimal matching problem of a weighted bipartite graph, and the KM algorithm can transform the problem of the maximum weight matching into the problem of completeness matching by giving a label to each vertex. As shown in Figure 2, D2D clusters set and cellular users set respectively represents two mutually disjointed vertex sets in the bipartite graph, are two mutually disjointed vertex sets in the dichotomy graph respectively. When the D2D cluster reuses the channel of cellular user it will create a connecting line between the vertex and the vertex , and the weight value on the connecting line is , which indicates the capacity of the D2D cluster when it reuses the channel of cellular user .
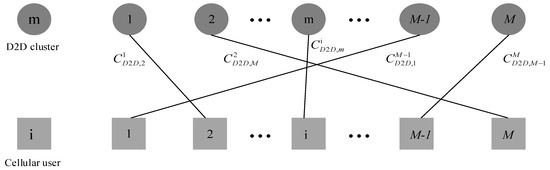
Figure 2.
Weighted bipartite graph for optimal matching problem of D2D clusters and cellular users’ channels.
According to the above analysis, the optimal joint power control and channel allocation algorithm is shown in Algorithm 1.
Complexity Analysis: The proposed optimal joint power control and channel allocation algorithm consists of three steps. In first step, clustering D2D users into clusters in iterations, the complexity is . In second step, allocating power to the users, the complexity is in the worst case, where is the iteration number. In third iteration, matching channels between D2D clusters and cellular users by KM algorithm, the complexity is . The overall computational complexity of the proposed algorithm is .
| Algorithm 1. Optimal joint power control and channel allocation algorithm |
| Input: the set of cellular users , the set of D2D users , the tolerance . Output: the optimal transmission power of cellular user and D2D user and , the optimal energy harvesting time , the channel reuse indicator of D2D user . 1) Initialization: , , . 2) Divide D2D users into M clusters according to interference weight graph [16]. 3) For 4) For 5) While do 6) For 7) Calculate and with Equations (29) and (30); 8) End for 9) Calculate with Equation (15); 10) End while 11) Calculate , and with Equations (12)–(14); 12) End for 13) End for 14) Use the KM algorithm to achieve the optimal matching between D2D clusters and cellular users’ channels. |
4. Simulation Results and Discussion
In this section, the simulation results of the proposed optimal joint power control and channel allocation algorithm in MATLAB R2015b are given, and the influence of the distance between D2D pair , the number of D2D users , and the number of cellular users on the total capacity of D2D users is analyzed. In this paper, we denote that channel gain consists of large-scale fading based on path loss and small-scale fading based on Rayleigh fading and is expressed as [15], where and respectively represents path loss constant and path loss exponent, is the distance between transmitter and receiver, and represents Rayleigh fading that follows the mean value of exponential distribution as 1. After analyzing and , the simulation diagram in [19] illustrates the relationship between converter efficiency and input power, according to the simulation diagram, we use an expression for energy harvesting efficiency in the simulation is . Other simulation parameters and their specific values are given in Table 1.

Table 1.
Simulation parameters.
Figure 3 shows the impact of different distance between D2D pair on the total capacity of D2D users, and the proposed algorithm in this paper is compared with the algorithm in [13] and the equal time allocation (ETA) method. The ETA method uses half the time to harvest energy and the other half to transmit information. Without loss of generality, we consider a standardized unit time period [20], that is . In the simulation, it is assumed that there are 10 D2D users and 5 cellular users in the cell. The channel gain of the D2D link decreases as the distance between the D2D pair increases, which leads to the decrease of D2D users’ total capacity; therefore, the total capacity of D2D users decreases with the increasing distance between D2D pair. Meanwhile, the proposed algorithm is superior to the algorithm in [13] and the ETA method, and the reason is that the proposed algorithm takes both the co-channel interference of D2D users and the limitation of the harvested energy into account with the aim of maximizing the total capacity of the D2D user to get each D2D user’s optimal transmission power, then determines energy harvesting time of each D2D transmitters. The [13] assumes that the energy harvesting time of multiple D2D transmitters on a same channel is same, however, the optimal transmission power and energy harvesting time of different D2D transmitters are different. When the ETA method is adopted, the transmission power of D2D users only depends on the harvested energy by the D2D transmitter and energy harvesting time is not optimized. Therefore, the algorithm in this paper can obtain bigger capacity than the algorithm in [13] and ETA method.
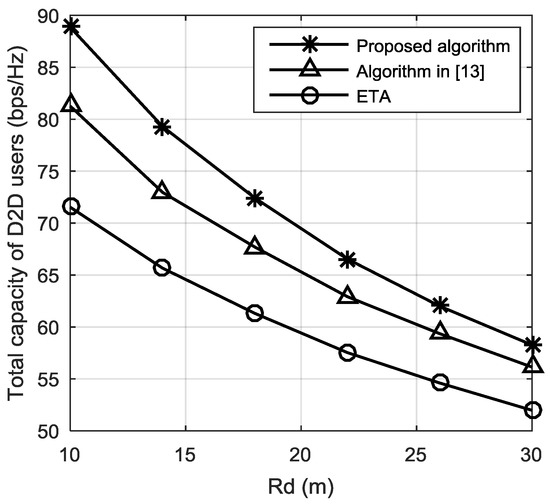
Figure 3.
Total capacity of D2D users with different distances between the D2D pair.
Figure 4 shows the total capacity of D2D users with the increasing number of D2D users. In the simulation, we assume that the distance between D2D pair is 10 m, and there are 5 cellular users in the cell. As can be seen from Figure 4, with the increasing number of D2D users, the total capacity of D2D users increases. This is because as the number of D2D users increases, more D2D users can reuse the channels of cellular users for communication, which increases the total capacity of D2D users. The complexity of the proposed power control algorithm is in the worst case, and the complexity of the power control algorithm in [13] is in the worst case, where and are iteration numbers, the ETA method does not optimize transmission power and energy harvesting time, and its complexity is . The complexity of the proposed power control algorithm is lower than [13] and improves the total capacity of D2D users, while the complexity of the proposed power control algorithm is higher than ETA method, but the total capacity of D2D users increases by 19%. Therefore, the system performance of the proposed power control algorithm is better than the algorithm in [13] and the ETA method.
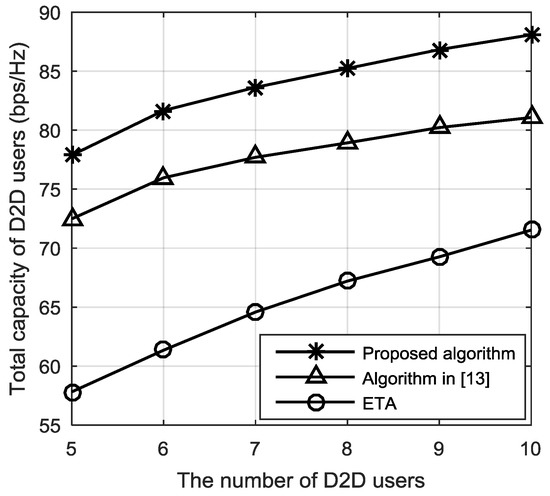
Figure 4.
Total capacity of D2D users with different number of D2D users.
Figure 5 illustrates the relationship between the total capacity of D2D users and the number of cellular users. In the simulation, it is assumed that there are 10 D2D users in the cell, and the distance between the D2D pair is 10 m. It can be discovered that as the number of cellular users increases, the total capacity of D2D users increases. This is because the number of cellular users increases meaning that the number of reusable channels increases, which leads to the number of D2D users in some clusters decreasing so that the mutual interference between D2D users in a same cluster decreases, and the total capacity of the D2D user is increased.
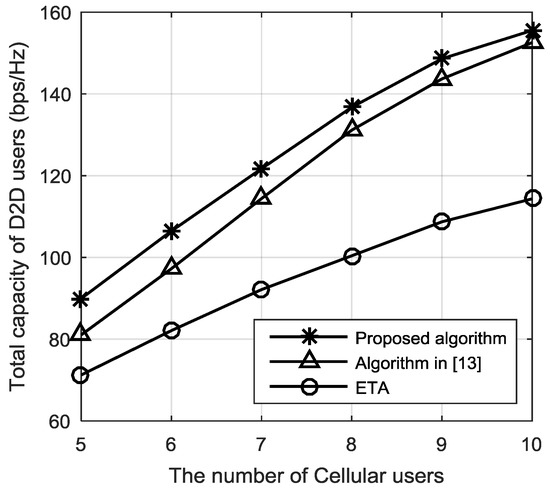
Figure 5.
Total capacity of D2D users with different number of cellular users.
5. Conclusions
In this paper, we investigate the problem of assigning optimal transmission power, energy harvesting time and channels to D2D users under the scenario where multiple D2D users reuse the same channel and energy harvesting technology is adopted by the D2D transmitter. An optimal joint power control and channel allocation algorithm is proposed to maximize the total capacity of D2D users while ensuring the QoS of cellular users and considering the power limitation of D2D users. The proposed algorithm firstly divides D2D users into several clusters by constructing the interference weight graph based on the channel gain between D2D users, and then D2D users in the same cluster are modeled as a non-cooperative game; the optimal transmission power and energy harvesting time are obtained through joint iteration optimization method for each D2D cluster reuse of each channel; and finally, according to the maximum cluster capacity of each cluster when it reuses every channel, the KM algorithm is used to allocate channels for D2D clusters to maximize the total capacity of D2D users. Simulation results show that the proposed algorithm outperforms the algorithm in [13] and the equal time allocation method in terms of total capacity of D2D users. In the next step, ways of harvesting energy from the environment will be considered, such as solar energy and wind energy, and other methods can be learned to study resource allocation in hybrid networks with D2D communication, such as random geometry and Q learning methods.
6. Patents
Name of patent: Power Control and Channel Allocation Algorithm for D2D Communication System Based on Energy Harvest. Number: 201811477473.5.
Author Contributions
Conceptualization, N.S. and Q.Z.; Data curation, N.S. and Q.Z.; Formal analysis, N.S. and Q.Z.; Funding acquisition, Q.Z.; Methodology, N.S. and Q.Z.; Project administration, Q.Z.; Software, N.S. and Q.Z.; Supervision, Q.Z.; Validation, Q.Z.; Visualization, N.S. and Q.Z.; Writing—original draft, N.S.; Writing—review and editing, Q.Z.
Funding
This work was funded by National Natural Science Foundation of China (No. 61571234 and 61631020).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ahmed, M.; Li, Y.; Waqas, M.; Sheraz, M.; Jin, D.; Han, Z. A survey on socially aware device-to-device communications. IEEE Commun. Surv. Tutor. 2018, 20, 2169–2197. [Google Scholar] [CrossRef]
- Jameel, F.; Hamid, Z.; Jabeen, F.; Zeadally, S.; Javed, M.A. A survey of device-to-device communications: Research issues and challenges. IEEE Commun. Surv. Tutor. 2018, 20, 2133–2168. [Google Scholar] [CrossRef]
- Baniasadi, M.; Maham, B.; Kebriaei, H. Power control for D2D underlay cellular communication: Game theory approach. In Proceedings of the 2016 8th International Symposium on Telecommunications, Tehran, Iran, 27–28 September 2016; pp. 314–319. [Google Scholar]
- Jiang, Y.X.; Liu, Q.; Zheng, F.C.; Gao, X.; You, X. Energy-efficient joint resource allocation and power control for D2D communications. IEEE Trans. Veh. Technol. 2016, 65, 6119–6127. [Google Scholar] [CrossRef]
- Zhang, G.D.; Hu, J.M.; Heng, W.; Li, X.; Wang, G. Distributed power control for D2D communications underlaying cellular network using Stackelberg Game. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference, San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Ferdouse, L.; Ejaz, W.; Raahemifar, K.; Anpalagan, A.; Markandaier, M. Interference and throughput aware resource allocation for multi-class D2D in 5G networks. IET Commun. 2017, 11, 1241–1250. [Google Scholar] [CrossRef]
- Saleem, U.; Jangsher, S.; Qureshi, H.K.; Hassan, S.A. Joint subcarrier and power allocation in the energy-harvesting-aided D2D communication. IEEE Trans. Ind. Inf. 2018, 14, 2608–2617. [Google Scholar] [CrossRef]
- Gupta, S.; Zhang, R.; Hanzo, L. Energy harvesting aided device-to-device communication underlaying the cellular downlink. IEEE Access 2017, 5, 7405–7413. [Google Scholar] [CrossRef]
- Kuang, Z.F.; Liu, G.; Li, G.Q.; Deng, X.H. Energy efficient resource allocation algorithm in energy harvesting-based D2D heterogeneous networks. IEEE Internet Things J. 2018, 6, 557–567. [Google Scholar] [CrossRef]
- Yu, S.; Ejaz, W.; Guan, L.; Anpalagan, A. Resource allocation for energy harvesting assisted D2D communications underlaying OFDMA cellular networks. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference, Toronto, ON, Canada, 24–27 September 2017; pp. 1–7. [Google Scholar]
- Wang, L.Y.; Liao, X.W.; Li, Y. Transmission strategy for D2D terminal with ambient RF energy harvesting. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference, Toronto, ON, Canada, 24–27 September 2017; pp. 1–5. [Google Scholar]
- Gong, S.M.; Shen, Y.Y.; Huang, X.X.; Wu, X.X.S.; So, A.M.C. Robust relay beamforming in device-to-device networks with energy harvesting constraints. In Proceedings of the 2016 IEEE Global Communications Conference, Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar]
- Wang, H.C.; Wang, J.L.; Ding, G.R.; Han, Z. D2D communications underlaying wireless powered communication networks. IEEE Trans. Veh. Technol. 2018, 67, 7872–7876. [Google Scholar] [CrossRef]
- Hemour, S.; Zhao, Y.P.; Lorenz, C.H.P.; Dimitri, H.; Gui, Y.S.; Hu, C.M.; Wu, K. Towards low-power high-efficiency RF and microwave energy harvesting. IEEE Trans. Microw. Theory. Technol. 2014, 62, 965–976. [Google Scholar] [CrossRef]
- Yu, B.Z.; Zhu, Q. A QoS-based channel allocation and power control algorithm for device-to-device communication underlaying cellular networks. J. Commun. 2016, 11, 624–631. [Google Scholar]
- Wei, L.; Wei, Z.; Wen, X.; Tao, S. Dynamic clustering based sub-band allocation in dense femtocell environments. In Proceedings of the 2012 IEEE 75th Vehicular Technology Conference, Yokohama, Japan, 6–9 May 2012; pp. 1–5. [Google Scholar]
- Dinkelbach, W. On nonlinear fractional programming. Manag. Sci. 1967, 13, 492–498. [Google Scholar] [CrossRef]
- Feng, D.Q.; Lu, L.; Yi, Y.W.; Li, G.Y.; Feng, G.; Li, S.Q. Device-to-device communications underlaying cellular networks. IEEE Trans. Commun. 2013, 61, 3541–3551. [Google Scholar] [CrossRef]
- Zoya, P.; Erez, A.F.; Daniel, C.; Regan, Z. Low-power far-field wireless powering for wireless senors. In Proceedings of the 2013 IEEE Radio and Wireless Symposium, Austin, TX, USA, 20–23 January 2013; pp. 31–33. [Google Scholar]
- Zheng, C.; Huan, X.N.; Tuan, A.L.; Karamanoglu, M.; Ever, E.; Yazici, A. Secure wireless powered and cooperative jamming D2D communications. IEEE Trans. Green Commun. Netw. 2018, 2, 1–13. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).