Finding Patterns in Signals Using Lossy Text Compression
Abstract
1. Introduction
1.1. Motivation: Autonomous Toy Robots
1.2. Run Length Encoding (RLE)
1.3. Our Contribution
- Defining recursive run-length-encoding (RRLE) which extends the classic RLE and is natural for strings with repeated patterns such as in communication protocols.
- An algorithm that computes the optimal (smallest) RRLE compression of any given string S in time polynomial in the length of S. See Theorem 4.
- An algorithm that recovers an unknown string S from its noisy version in polynomial time. The only assumption is that S has a corresponding RRLE tree of levels. See Definition 1 for details. The running time is polynomial in , and the result is optimal for a given trade-off cost function (compression rate versus replaced characters). See Theorem 6.
- -approximation for the above algorithms, that takes time for every constant , and can be run on streaming signals and in parallel, using existing core-sets for signals. See Section 4.
- Preliminary experimental results on synthetic and real data that support the guarantees of the theoretical results. See Section 6.
- An open-source and home-made system for automatic reverse-engineering of remote controllers. The system was used to hack dozens of radio (PWM) and IR remote controllers in our lab. We demonstrated it on three micro air-vehicles that were bought from Amazon for less than $30 each. See [4] for more results, code, and discussions.
1.4. Related Work
2. Problem Statement
2.1. Basic Notations
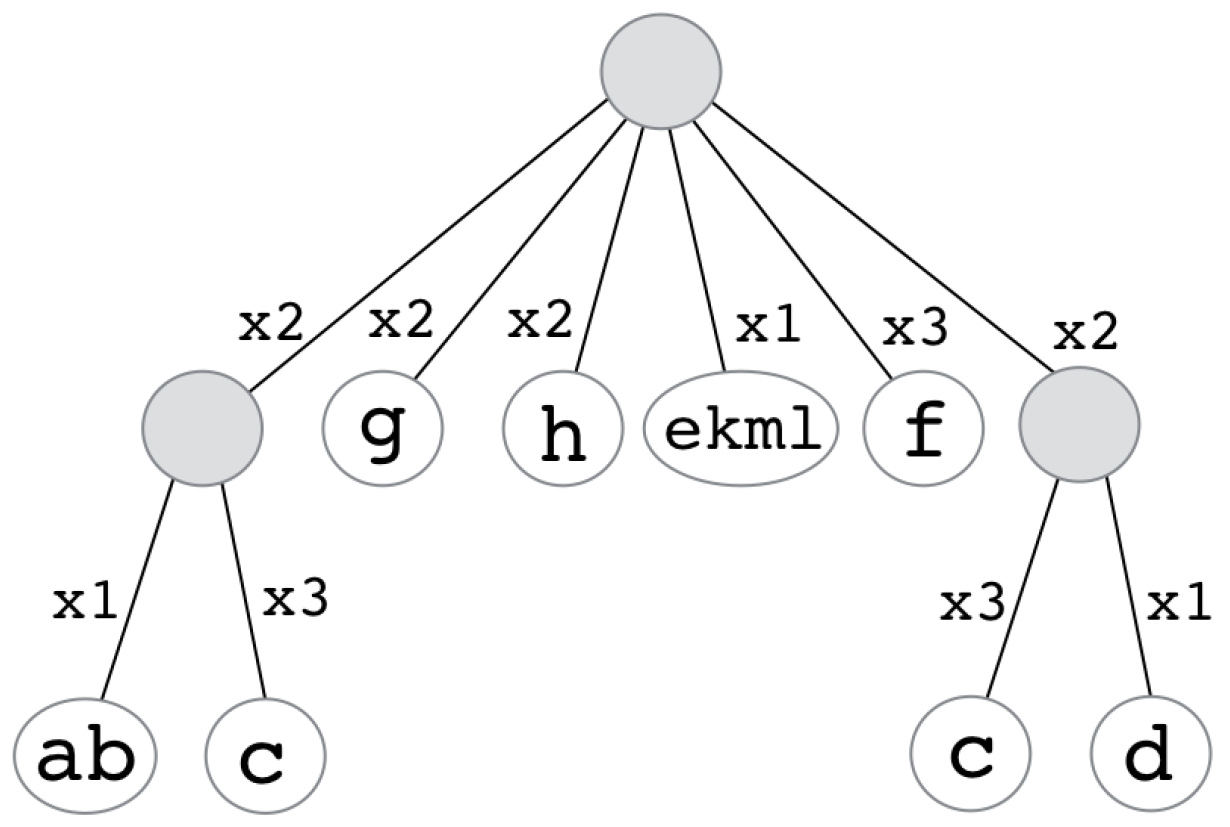
2.2. Recursive Run-Length Encoding (RRLE)
2.3. Lossy Compression
3. Algorithms for Exact and Lossy RRLE Compression
3.1. Warm Up: Exact RRLE Compression
| Algorithm 1: Exact(Q); see Theorem 4 |
 |
3.2. Lossy RRLE Compression
- The minimum cost of modifying Q to be r-periodic, over every possible period length r. Formally, this is the minimal +1, over every string and factor r of n.
- The minimum over all possible partitioning options of Q.
- The cost of representing Q as is, with no compression.
| Algorithm 2:; see Theorem 6. |
 |
- Computing for every possible r takes + the time for computing D for .
- Computing the second value in the equation takes .
- Computing the third value in the equation takes .
4. Linear-Time, Streaming, and Parallel Computation
5. The Reverse Engineering System
5.1. Example of a Protocol: The SYMA G107 Helicopter
5.2. The System
5.3. After Learning the Protocol
- Recording analog signals. In the case of IR signals, we use an IR decoder (sensor) that receives the signals from the remote controller. The IR decoder gets its power from the a micro-computer (Arduino), and is connected to a logic-analyzer.
- Converting Analog signals to binary signals. The logic analyzer converts the analog voltage signal into a digital binary signal that has value “A” or “B” in each time unit.
- Transmitting the binary stream to a laptop via a USB port.
- Running reverse engineering algorithm to learn the protocol.
- Producing commands to the robot using the mini-computer that is connected to a transmitter or a few IR (Infra-Red) LEDs.
6. Reverse Engineering Experiments
6.1. Experiments on Toy Robots
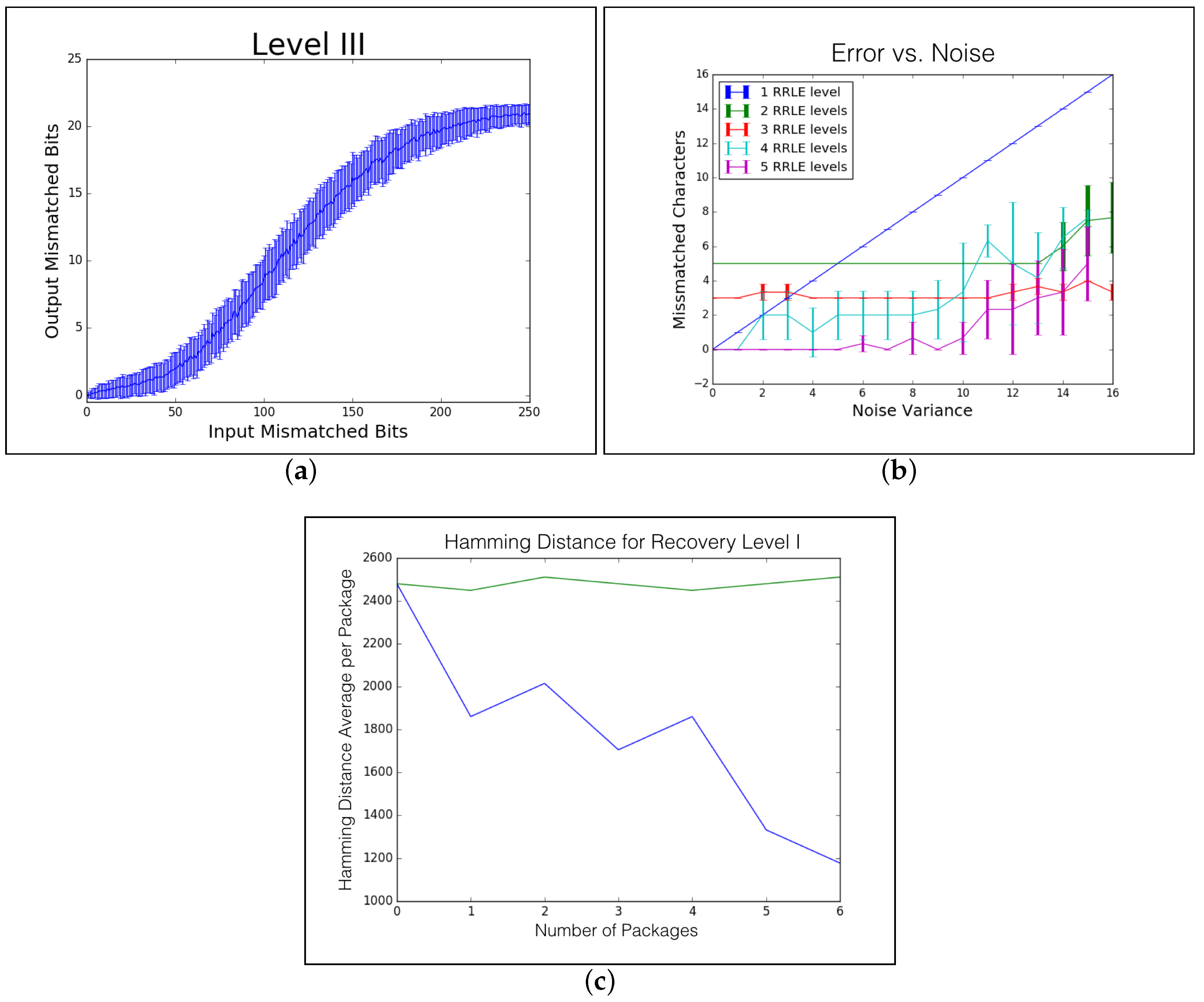
6.2. De-Noising Level I
6.3. De-Noising Level II
6.4. De-Noising Level III
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nasser, S.; Barry, A.; Doniec, M.; Peled, G.; Rosman, G.; Rus, D.; Volkov, M.; Feldman, D. Fleye on the car: big data meets the internet of things. In Proceedings of the 14th International Conference on Information Processing in Sensor Networks, Washington, DC, USA, 14–16 April 2015; pp. 382–383. [Google Scholar]
- D’Ausilio, A. Arduino: A low-cost multipurpose lab equipment. Behav. Res. Methods 2012, 44, 305–313. [Google Scholar] [CrossRef] [PubMed]
- Pi, R. Raspberry pi. Raspberry Pi 2012, 1, 1. [Google Scholar]
- Robotics and Big Data Laboratory, University of Haifa. Available online: https://sites.hevra.haifa.ac.il/rbd/about/ (accessed on 9 December 2019).
- Iliopoulos, C.S.; Moore, D.; Smyth, W.F. A Characterization of the Squares in a Fibonacci String. Theor. Comput. Sci. 1997, 172, 281–291. [Google Scholar] [CrossRef]
- Kolpakov, R.M.; Kucherov, G. Finding Maximal Repetitions in a Word in Linear Time. In Proceedings of the 40th Annual Symposium on Foundations of Computer Science, New York, NY, USA, 17–19 October 1999; pp. 596–604. [Google Scholar]
- Crochemore, M.; Hancart, C.; Lecroq, T. Algorithms on Strings; Cambridge University Press: Cambridge, UK, 2007; 392p. [Google Scholar]
- Main, M.G. Detecting Leftmost Maximal Periodicities. Discret. Appl. Math. 1989, 25, 145–153. [Google Scholar] [CrossRef]
- Crochemore, M. Recherche linéaire d’un carré dans un mot. CR Acad. Sci. Paris Sér. I Math. 1983, 296, 781–784. [Google Scholar]
- Crochemore, M. An Optimal Algorithm for Computing the Repetitions in a Word. Inf. Process. Lett. 1981, 12, 244–250. [Google Scholar] [CrossRef]
- Apostolico, A.; Preparata, F.P. Optimal Off-Line Detection of Repetitions in a String. Theor. Comput. Sci. 1983, 22, 297–315. [Google Scholar] [CrossRef]
- Main, M.G.; Lorentz, R.J. An O(n log n) Algorithm for Finding All Repetitions in a String. J. Algorithms 1984, 5, 422–432. [Google Scholar] [CrossRef]
- Kosaraju, S.R. Computation of Squares in a String. In Annual Symposium on Combinatorial Pattern Matching (CPM); Springer: Berlin, Germany, 1994; pp. 146–150. [Google Scholar]
- Gusfield, D.; Stoye, J. Linear Time Algorithms for Finding and Representing All the Tandem Repeats in a String. J. Comput. Syst. Sci. 2004, 69, 525–546. [Google Scholar] [CrossRef]
- Crochemore, M.; Ilie, L. Computing Longest Previous Factors in Linear Time and Applications. Inf. Process. Lett. 2008, 106, 75–80. [Google Scholar] [CrossRef]
- Amit, M.; Crochemore, M.; Landau, G.M. Locating All Maximal Approximate Runs in a String. In Annual Symposium on Combinatorial Pattern Matching (CPM); Springer: Berlin, Germany, 2013; pp. 13–27. [Google Scholar]
- Landau, G.M.; Schmidt, J.P.; Sokol, D. An Algorithm for Approximate Tandem Repeats. J. Comput. Biol. 2001, 8, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Sim, J.S.; Iliopoulos, C.S.; Park, K.; Smyth, W.F. Approximate Periods of Strings. Lect. Notes Comput. Sci. 1999, 1645, 123–133. [Google Scholar]
- Kolpakov, R.M.; Kucherov, G. Finding Approximate Repetitions under Hamming Distance. Theor. Comput. Sci. 2003, 1, 135–156. [Google Scholar] [CrossRef]
- Amir, A.; Eisenberg, E.; Levy, A. Approximate Periodicity. In Proceedings of the 21st International Symposium on Algorithms and Computation (ISAAC), Jeju Island, Korea, 15–17 December 2010; Volume 6506, pp. 25–36. [Google Scholar]
- Nishimoto, T.; Inenaga, S.; Bannai, H.; Takeda, M. Fully dynamic data structure for LCE queries in compressed space. arXiv 2016, arXiv:1605.01488. [Google Scholar]
- Bille, P.; Gagie, T.; Gørtz, I.L.; Prezza, N. A separation between run-length SLPs and LZ77. arXiv 2017, arXiv:1711.07270. [Google Scholar]
- Babai, L.; Szemerédi, E. On the complexity of matrix group problems I. In Proceedings of the 25th Annual Symposium onFoundations of Computer Science, West Palm Beach, FL, USA, 24–26 October 1984; pp. 229–240. [Google Scholar]
- Storer, J.A.; Szymanski, T.G. Data compression via textual substitution. J. ACM 1982, 29, 928–951. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 1976, 22, 75–81. [Google Scholar] [CrossRef]
- Hamming, R.W. Error detecting and error correcting codes. Bell Syst. Tech. J. 1950, 29, 147–160. [Google Scholar] [CrossRef]
- Knuth, D.E.; Morris, J.H., Jr.; Pratt, V.R. Fast pattern matching in strings. SIAM J. Comput. 1977, 6, 323–350. [Google Scholar] [CrossRef]
- Parikh, R.J. On Context-Free Languages. J. ACM 1966, 13, 570–581. [Google Scholar] [CrossRef]
- Feldman, D.; Sung, C.; Sugaya, A.; Rus, D. idiary: From gps signals to a text-searchable diary. ACM Trans. Sens. Netw. 2015, 11, 60. [Google Scholar] [CrossRef]
- Rosman, G.; Volkov, M.; Feldman, D.; Fisher, J.W., III; Rus, D. Coresets for k-segmentation of streaming data. In Advances in Neural Information Processing Systems; Neural Information Processing Systems Foundation, Inc.: Montreal, QC, Canada, 2014; pp. 559–567. [Google Scholar]
- Stackovervflow. How to Solve an Xord System of Linear Equations. 2016. Available online: https://stackoverflow.com/questions/11558694/how-to-solve-an-xord-system-of-linear-equations (accessed on 15 September 2016).

| Throttle | Role | Pitch | Input to Algorithm 2 (Semantic Package) | Output (RRLE) |
|---|---|---|---|---|
| 25% | 0% | 0% | 01100100100010000001101010011111 | |
| 50% | 0% | 0% | 01001111100010000001101010011001 | |
| 75% | 0% | 0% | 00100011100010000001101010011010 | 0???????10001000000110101001???? |
| 100% | 0% | 0% | 00100011100010000001101010011010 | |
| 100% | −100% | 0% | 01100100111110000001101010010110 | |
| 100% | −50% | 0% | 01100100000110000001101010011000 | |
| 100% | 50% | 0% | 01100100110110000001101010010100 | 01100100????1000000110101001???? |
| 100% | 100% | 0% | 01100100001010000001101010011001 | |
| 100% | 0% | −100% | 01100100100000010001101010010111 | |
| 100% | 0% | 100% | 01100100100011110001101010010110 | 011001001000????000110101001???? |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rozenberg, L.; Lotan, S.; Feldman, D. Finding Patterns in Signals Using Lossy Text Compression. Algorithms 2019, 12, 267. https://doi.org/10.3390/a12120267
Rozenberg L, Lotan S, Feldman D. Finding Patterns in Signals Using Lossy Text Compression. Algorithms. 2019; 12(12):267. https://doi.org/10.3390/a12120267
Chicago/Turabian StyleRozenberg, Liat, Sagi Lotan, and Dan Feldman. 2019. "Finding Patterns in Signals Using Lossy Text Compression" Algorithms 12, no. 12: 267. https://doi.org/10.3390/a12120267
APA StyleRozenberg, L., Lotan, S., & Feldman, D. (2019). Finding Patterns in Signals Using Lossy Text Compression. Algorithms, 12(12), 267. https://doi.org/10.3390/a12120267





