Finding Patterns in Signals Using Lossy Text Compression

Abstract

Whether the source is autonomous car, robotic vacuum cleaner, or a quadcopter, signals from sensors tend to have some hidden patterns that repeat themselves. For example, typical GPS traces from a smartphone contain periodic trajectories such as “home, work, home, work, ⋯”. Our goal in this study was to automatically reverse engineer such signals, identify their periodicity, and then use it to compress and de-noise these signals. To do so, we present a novel method of using algorithms from the field of pattern matching and text compression to represent the “language” in such signals. Common text compression algorithms are less tailored to handle such strings. Moreover, they are lossless, and cannot be used to recover noisy signals. To this end, we define the recursive run-length encoding (RRLE) method, which is a generalization of the well known run-length encoding (RLE) method. Then, we suggest lossy and lossless algorithms to compress and de-noise such signals. Unlike previous results, running time and optimality guarantees are proved for each algorithm. Experimental results on synthetic and real data sets are provided. We demonstrate our system by showing how it can be used to turn commercial micro air-vehicles into autonomous robots. This is by reverse engineering their unpublished communication protocols and using a laptop or on-board micro-computer to control them. Our open source code may be useful for both the community of millions of toy robots users, as well as for researchers that may extend it for further protocols.

1. Introduction

1.1. Motivation: Autonomous Toy Robots

While this paper deals with a natural open problem in string compression and representation (“stringology”), its origin was in our robotics lab. Traditional labs have relatively expensive, potentially dangerous robots, such as heavy quadcopters, crawlers, and humanoids that cost thousands of dollars. However, in recent years it has become easy to order from Amazon or eBay, low-cost “toy” robots that cost a few dozen dollars. More recently, we have seen dozens types of robots in toy stores and malls, including helicopters, quadcopters, cars, small humanoids, and even combinations such as quadcopters with wheels. Due to their price, size, and plastic material, such robots can be used safely indoors (e.g., home, school, or university), are more resistant to crashes, and it is easy to fix or replace their parts.

However, these toy robots are usually not autonomous due to two main problems: (i) they have no “eyes”: sensors such as GPS allow them to know their location and position; and (ii) they are controlled via a remote controller (RC) that is supposed to be operated by a human. These commercial remote controllers usually have no published communication protocol. While a few of them might be found in the internet, they change frequently from model to model.

Unfortunately, most commercial, low-cost (<$50) toy robots (cars, quadcopters and humanoids), do not have published protocols. Moreover, their protocols frequently change over time without notice. In fact, many times we ordered a few copies of exactly the same toy robot from Amazon.com and each one of them had a different protocol. This was also the case with toy helicopters in our experimental results section.

Our goal in this study was to take these toy robots and make them autonomous. To this end, we had to solve the to above-mentioned problems. Problem (i) was already handled by developing low-cost tracking systems based on web-cameras, or on-board analog cameras [1]. In this paper we handle Problem (ii): how to automatically reverse engineer the communication protocol of the robot.

Once this protocol is known, we can imitate the remote control by producing the commands using a mini-computer, such as Arduino [2] or Raspberry Pi [3] that is connected to a transmitter or a few IR (Infra-Red) LEDs. Instead of a human with a remote control, an algorithm can then send hundreds of commands per second to the robot to result in a much more stable and autonomous robot. Such robotic, low-cost systems, that are based on this paper, can be found, e.g., in [1].

Compression or learning? As explained above, the motivation for this study was to learn a communication protocol based on given recording of sampled signals. That is, to reverse-engineer the protocol. However, this problem in principle is very related to the problem of compressing signals. This is because an efficient compression algorithm for a specific protocol is expected to use the repeated format of this protocol. For example, machine learning is used to extract a small (compressed) predictive model from a large sample data, which is used in, e.g., video compression protocols to compress real-time video, where the decoder is expected to predict the next frame via the model, and only the differences (the fitting errors of the model) are being sent by the encoder. Similarly, the results in this paper can be used to learn a protocol, to compress a message efficiently based on a given protocol, or for noise removal. The theoretical optimization problem is very similar, as explained in the next sections.

1.2. Run Length Encoding (RLE)

Given a string S, which represents a signal, our goal is to compress S such that the optimal compression will allow us to resolve the protocol behind that signal. The compression scheme we present in this paper is called recursive run-length encoding (RRLE), and is a natural generalization of run-length-encoding (RLE), but is more suited for semi-periodic strings that are produced by sensors on robots.

RLE is a very simple form of lossless string compression in which runs of letters (that is, sequences in which the same letter occurs in many consecutive elements of the string) are stored as pairs of one count and one single letter, rather than the original run. For example, the string $S=\left(aaaaaaabbbbaaaa\right)$ has three runs and can be represented as the vector $S^{\prime }=(7,a,4,b,4,a)$, which means that string S is consists of seven a’s, followed by four b’s, followed by four a’s. This way the string S can be represented using six letters/integers instead of 15. RLE is most useful on a string that contains many such runs.

In this paper we also use the term run (or period) to denote a periodic string. That is, a string that can be divided into a number of identical adjacent non overlapping substrings. For example, if $S=ababab$, the RLE will be $(3,ab)$ which means that the string $\left(ab\right)$ repeats itself three times in the string S. Similarly, the RLE of $S=ababcb$ is $(2,ab,1,cb)$. In RRLE we recursively define each run (period) so that it may be further compressed using RLE in order to get even better compression as in Figure 1. For a formal definition of RRLE, see Section 2.3.

1.3. Our Contribution

The contributions that are presented in this paper are as follows.

• Defining recursive run-length-encoding (RRLE) which extends the classic RLE and is natural for strings with repeated patterns such as in communication protocols.
• An algorithm that computes the optimal (smallest) RRLE compression of any given string S in time polynomial in the length $n=\left|S\right|$ of S. See Theorem 4.
• An algorithm that recovers an unknown string S from its noisy version $\tilde{S}$ in polynomial time. The only assumption is that S has a corresponding RRLE tree of $O\left(1\right)$ levels. See Definition 1 for details. The running time is polynomial in $\left|S\right|$, and the result is optimal for a given trade-off cost function (compression rate versus replaced characters). See Theorem 6.
• $(1+ϵ)$-approximation for the above algorithms, that takes $O\left(n\right)$ time for every constant $ϵ>0$, and can be run on streaming signals and in parallel, using existing core-sets for signals. See Section 4.
• Preliminary experimental results on synthetic and real data that support the guarantees of the theoretical results. See Section 6.
• An open-source and home-made system for automatic reverse-engineering of remote controllers. The system was used to hack dozens of radio (PWM) and IR remote controllers in our lab. We demonstrated it on three micro air-vehicles that were bought from Amazon for less than $30 each. See [4] for more results, code, and discussions.

1.4. Related Work

Reverse Engineering. There are many systems and applications that suggest imitating remote controllers. For example, a “universal remote controller” can record IR signals and send them again by pressing on the corresponding button of this remote controller. However, such a simple controller with a small number of states, cannot replace the remote controller of, e.g., a common quadcopter with seven channels whose protocol can be used to generate unbounded types of signals.

String Algorithms. The notion of runs and periodicity of strings is at the core of many stringology questions [5,6]. It constitutes a fundamental area of string combinatorics due to important applications of text algorithms, data compression, biological sequences analysis, music analysis, etc. The notion of runs was introduced by Iliopoulos, Moore, and Smyth [5], who showed that Fibonacci words contain only a linear number of runs according to their length. Kolpakov and Kucherov [6] (see also [7], Chapter 8) proved that the property holds for any string and designed an algorithm to compute all runs in a string, which extends previous algorithms [8,9]. Other methods are presented in [7,10,11,12,13,14,15].

All of the above mentioned works have focused on exact runs; i.e., runs that include exactly the same repeated period. Other works focused on approximate runs. For example, when a string S is a concatenation of a non-empty substrings, by the modification of at most k letters, they form an exact run. This problem was widely researched [16,17,18,19,20]. However, none of these previous works have focused on recursive runs, as defined in this paper.

The RRLE compression presented in this paper is a novel definition of recursive approximate runs. Informally, our problem is an optimization problem that looks for approximate runs that include a period that may be a run by autonomously. In addition to run length encoding, RRLE is also closely related to run-length straight line program (RLSLP) compression scheme, which is an extension of straight line programs (SLPs) [21,22].

There are many other compression schemes of strings, such as SLP [23], macro schemes [24], and LZ77 [25], that might be even more useful than the RRLE suggested in this paper. However, the main goal of the study was not to simply compress strings, but actually extract patterns from noisy strings. This was the motivation for the approximation algorithm that is our main result in Section 3.

In the case of communication protocols, the idea of using recursive trees of patterns is important and more relevant than pointers that are more relevant to text documents. In addition, RRLE is not based on the longest repeated factor (substring), but rather based on finding repeated substrings that are well compressed by themselves.

This version of finding recursive approximate runs is challenging, since most known techniques for finding exact or approximate runs cannot be used here without introducing exponential running time. To the best of our knowledge, there are no known efficient (polynomial time) algorithms for the RRLE problem.

Roadmap: In Section 2, we provide the basic stringology notation needed for the algorithms, and a full definitions of the problem we are solving. In Section 3, we present our reverse engineering algorithms, which are the algorithms for exact and lossy text compression. In Section 4 we explain how we can apply these algorithms on our system. Then, in Section 5, we give an example of a protocol, and present in detail our reverse engineering system. Finally, in Section 7 we conclude this paper, and discuss some interesting directions for future work.

2. Problem Statement

In this section we define the RRLE problem and the required notation for the rest of the paper.

2.1. Basic Notations

Let $\Sigma$ denote a set called alphabet, where each item in $\Sigma$ is called a letter. A string is a vector $P\in {\Sigma }^n$, where $n\ge 1$ denotes its length. For simplicity we remove the commas and replace $P=(p_1,\cdots ,p_n)$ by $(p_1\cdots p_n)$. For an integer $j\in [i,n]=\left\{i,i+1,\cdots ,n\right\}$, the string $P^{\prime }=P[i..j]$ is called a substring of P. The empty string is also considered a substring of P. If $i=1$, then $P^{\prime }$ is a prefix of P, and if $j=n$, then $P^{\prime }$ is a suffix of P. The concatenation of two strings P of length n and Q of length m, is denoted by $PQ=P[1..n]Q[1..m]$. For an integer $k\ge 1$, we denote $P^k=P_1\cdots P_k$, where $P_i=P$ for every $i\in [1..k]$.

An integer $r\in [1..n]$ is a factor of n $(nmodr)=0$; i.e., there is an integer $x\ge 1$ such that $rx=n$. The string P is r-periodic (or periodic in r) if $P[1..r]=P[r+1..2r]=\cdots =P[n-r+1..n]$; i.e., $P=P{[1..r]}^{\frac{n}{r}}$. Hence, every string of length n is n-periodic. The string $P[1..r]$ is the smallest period of P if there is no $r^{\prime }\in [1..r-1]$ such that P is $r^{\prime }$-periodic.

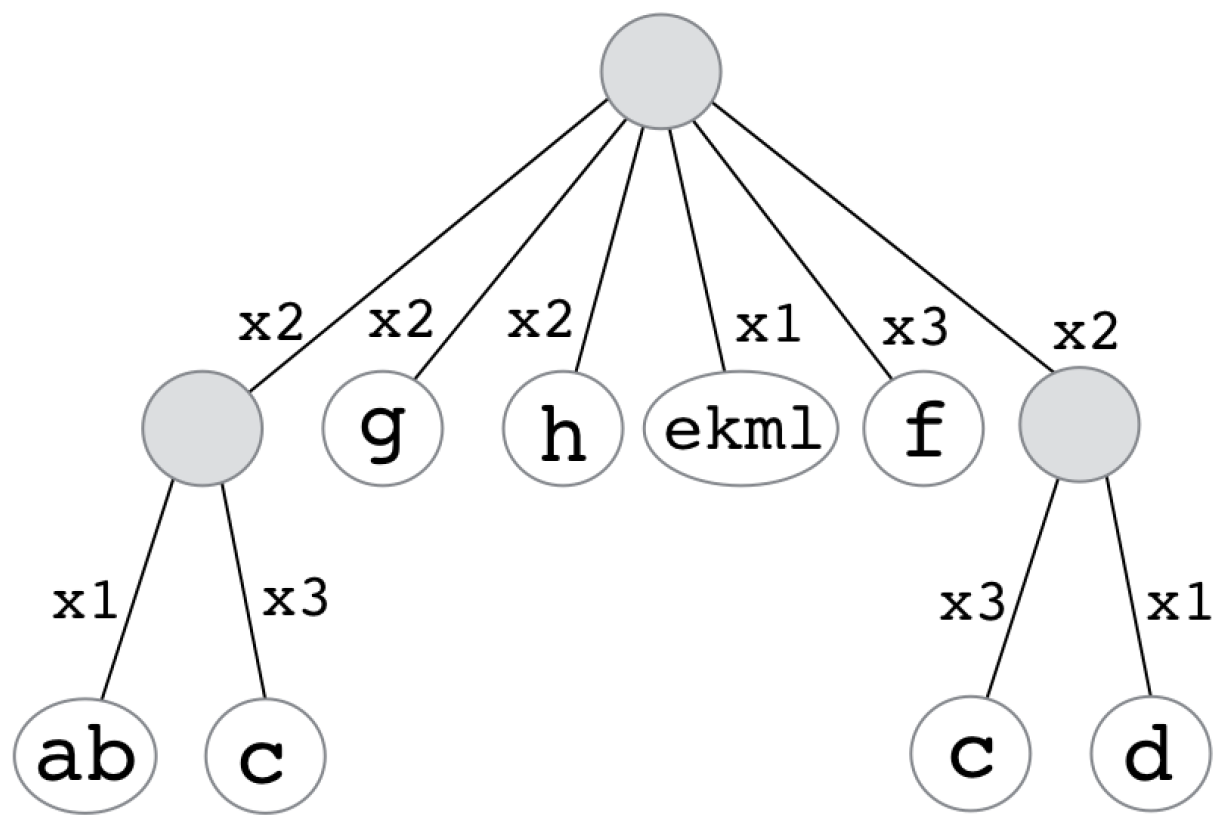
2.2. Recursive Run-Length Encoding (RRLE)

In this subsection we suggest a novel generalization of the classic run-length encoding compression, called recursive run-length-encoding (RRLE) which is more suitable to our applications.

Definition 1

(Recursive run-length encoding (RRLE)). An RRLE $s=(t_1,s_1,\cdots ,t_k,s_k)$ is defined recursively as a $2k$-tuple, where $k\ge 1$ is an integer, $t_i\ge 1$ is an integer, and $s_i$ is either a string or an RRLE, for every $i\in [1..k]$. The size $\left|s\right|$ of s is recursively defined as $k+{\sum }_{i=1}^k\left|s_i\right|$. Similarly, $S\left(s\right)={u_1}^{t_1}\cdots {u_k}^{t_k}$ where $u_i=s_i$ if $s_i$ is a string, and $u_i=S\left(s_i\right)$; otherwise, for every $i\in [1..k]$, if $S\left(s\right)=Q$, then s is RRLE of the string Q. We define $\mathrm{rcost}\left(Q\right)$ to be the size of the smallest RRLE of Q, $\mathrm{rcost}\left(Q\right)={min}_{\left\{s\mid S\left(s\right)=Q\right\}}\left|s\right|$. Such an RRLE is called an optimal RRLE of Q and is denoted by $s^{*}\left(Q\right)$.

For example, consider the string $M=\left(aaabbaaabb\right)$. One RLE of M is $(3,a,2,b,3,a,2,b)$. Another one is $(2,aaabb)$. A possibly shorter description of the string may be as a couple of repetitions of the string $aaabb=(3,a,2,b)$. This gives the recursive description, $\left(aaabbaaabb\right)=(2,aaabb)=(2,S(3,a,2,b\left)\right)$.

A less trivial example is the string

$$\begin{array}{c}abcccabcccgghhekmlfffcccdcccd=\hfill \\ S(2,abccc,2,g,2,h,1,ekml,3,f,2,cccd)=\hfill \\ S(2,S(1,ab,3,c),2,g,2,h,1,ekml,3,f,2,S(3,c,1,d\left)\right).\hfill \end{array}$$

While the last expression seems longer than the first one, it can actually be represented efficiently using a RRLE tree, which is a tree, where each edge corresponds to a counter (number of repetitions), and each of its leaves corresponds to a string; see Figure 1.

A natural problem statement that follows Definition 1 is: how to compute the optimal compression of a given string.

Problem 2.

Given a string Q, compute the optimal RRLE $s^{*}\left(Q\right)$ of Q. That is, $s^{*}\left(Q\right)$ is the tuple that minimizes $\left|s\right|$ over every tuple s which is a compression of Q; i.e., $S\left(s\right)=Q$ and $\left|s\right|=\mathrm{rcost}\left(Q\right)$. Here, $S\left(s\right)$ is the string that corresponds to s as in Definition 1.

2.3. Lossy Compression

The previous subsection discussed exact (non-lossy) compression. However, given a string P, our goal is intuitively to compute a string Q which is a “lossy compression” of P in the sense that: (a) Q is similar (not necessarily identical) to P, and (b) Q takes less space in memory than P.

Of course, we can trivially define $Q=P$ so that the similarity of P and Q will be maximized, but then there will be no compression or memory saving at all. On the other hand, we can define $Q=1^n$, which will minimize the compression cost of Q (since it is just n occurrences of the digit 1), then the similarity cost to P will be very high. In other words, there is a trade-off between these two costs or goals. For a proper lossy compression problem we thus need to define, in addition to the compression cost of the previous section, a similarity and overall cost functions as follows.

Similarity cost. Such a function $\mathrm{scost}(·,·)$ maps every pair of strings P and Q of the same length into a score (real number) $\mathrm{scost}(P,Q)$ that measures how much the strings are different; i.e., how much Q is a good approximation to p. In this paper, $\mathrm{scost}(P,Q)$ will be the number of indices $i\in \left\{1,\cdots ,n\right\}$ which has a different corresponding letter in P and Q, also known as the Hamming distance [26] between P and Q. For example, if $P=ababcb$ and $Q=ababab$, then $\mathrm{scost}(P,Q)=\mathrm{scost}(ababcb,ababab)=1$ since only the 5th letter is different: “c” for P and “a” for Q.

An overall cost function. This function $\mathrm{cost}(·,·)$ assigns an overall score for a pair of string that measures the trade-off between the similarity rate $\mathrm{scost}(P,Q)$ and the compression rate $\mathrm{ccost}\left(Q\right)$. For simplicity, we use the natural goal of minimizing the sum of similarity cost and compression cost,

$$\mathrm{cost}(P,Q)=\mathrm{scost}(P,Q)+\mathrm{rcost}\left(Q\right).$$

For example, if $P=ababcb$ and $Q=ababab$, then the overall cost is

$$\mathrm{cost}(P,Q)=\mathrm{scost}(P,Q)+\mathrm{rcost}\left(Q\right)=1+3=4,$$

compared to the original cost

$$\mathrm{cost}(P,P)=\mathrm{scost}(P,P)+\mathrm{rcost}\left(Q\right)=0+6=6.$$

The second problem statement is then: given S, how can one compute a lossy compression that is both small and decompressed to a similar string as the given one.

Problem 3.

Given a string P, compute a string Q that minimizes

$$\mathrm{cost}(P,Q)=\mathrm{scost}(P,Q)+\mathrm{rcost}\left(Q\right),$$

over every string Q. Here $\mathrm{rcost}\left(Q\right)$ is the (optimal) RRLE compression cost of Q as in Definition 1, and $\mathrm{scost}(P,Q)$ is the similarity (Hamming) cost.

3. Algorithms for Exact and Lossy RRLE Compression

In this section, we define and provide algorithms for the exact and lossy RRLE compression Problems 2 and 3. In the exact version of the problem, the input is a string Q that represents the signal, and the output is $\mathrm{rcost}\left(Q\right)$, which is the size of the smallest RRLE s of Q; see Definition 1. Hence, the similarity cost is $\mathrm{scost}(Q,S(s\left)\right)=0$, and the overall cost is $\mathrm{ccost}(Q,S(s\left)\right)=\mathrm{rcost}\left(Q\right)$.

In the lossy version we aim to “clean” the noise from the input signal Q and extract the hidden repeated patterns by finding a similar string P which minimizes $\mathrm{cost}(Q,P)$; see Problem 3. The motivation for both of the problems is that the input signal is assumed to have periodic patterns (exactly or approximately). By finding these periods we can either compress the signal efficiently, or reverse engineer the hidden protocol that is generated as it is in our experimental results. From the partition of the input string into periodic substrings, we can conclude the format of the protocol, including constant bits and the substring that is responsible for each button. see Section 5.

3.1. Warm Up: Exact RRLE Compression

We now describe Algorithm 1 for computing the smallest RLE of an input string Q and proves its correctness. For simplicity, the algorithm only computes the length of the smallest RLE but the RLE itself can be easily extracted by following the chosen indices during the recursive calls. This solves Problem 2.

Algorithm 1: Exact(Q); see Theorem 4

Overview of Algorithm 1: Given a string Q of length n, the algorithm computes a matrix $D[1..n][1..n]$, such that $D\left[i\right]\left[j\right]=\mathrm{rcost}\left(Q\right[i..j\left]\right)$. In particular, $D\left[1\right]\left[n\right]=\mathrm{rcost}\left(Q\right)$. The matrix D is computed for substrings of increasing length; i.e., we first compute all substrings of length one, then all substrings of length two, and so on until the full string of length n is evaluated. We initialize the matrix on the main diagonal $D\left[i\right]\left[i\right]=2$ for $1\le i\le n$. Then we compute $\mathrm{rcost}\left(Q\right[i..j\left]\right)$ for all $1\le i<j\le n$ using a recursive definition of $D\left[i\right]\left[j\right]=\mathrm{rcost}\left(Q\right[i..j\left]\right)$. This is the minimum between the following three values: (i) $\mathrm{rcost}\left(Q\right[i..i+r-1\left]\right)$ if $Q[i..j]$ is r-periodic, where r is as small as possible, (ii) leaving $Q[i..j]$ as a whole which takes 1 counter and $j-i+1$ letters, and (iii) the smallest $\mathrm{rcost}$ that can be obtained by partitioning $Q[i..j]$ into two consecutive substrings $Q[i..k-1]$ and $Q[k..j]$, over every integer $k\in [i+1,j-i+1]$.

We now prove that the output of Algorithm 1 is indeed the optimal compression $\mathrm{rcost}\left(Q\right)$ of its input Q, which solves Problem 2.

Theorem 4.

Let Q be a string of length n. Let $D\left[1\right]\left[n\right]$ be the output of a call to $Exact\left(Q\right)$; see Algorithm 1. Then $D\left[1\right]\left[n\right]=\mathrm{rcost}\left(Q\right)$ is the size of the smallest RRLE of Q and can be computed in $O\left(n^3\right)$ time.

Proof. 

We prove a more general claim, that the theorem holds for any substring $Q[i..j]$ of Q. The proof is by induction on the length $\ell =j-i+1$ of $Q[i..j]$. For $\ell =1$, we have $D\left[i\right]\left[i\right]=\mathrm{rcost}\left(Q\right[i\left]\right)=2$, for storing the letter $Q\left[i\right]$ and its length counter 1. For $\ell \ge 2$, inductively assume that the theorem holds for any substring of $Q[i..j]$. Let $s=(t_1,s_1,\cdots ,t_m,s_m)$ be the smallest RRLE of $Q[i..j]$. The rest of the proof corresponds to the three possible evaluations of $D\left[i\right]\left[j\right]$ in Algorithm 1.

If $m=1$ and $Q[i..j]$ are r-periodic for $r<\left|Q\right[i..j\left]\right|=j-i+1$, then $t_1\ge 2$ denotes the number of periodic runs. Hence, $s_1=Q[i..i+r-1]$ is the RRLE of each run and $\left|s\right|=1+\left|Q\right[i..i+r-1\left]\right|=D\left[i\right][i+r-1]$.

If $m=1$ and $t_1=1$, then $s_1=Q[i..j]$ and $Q[i..j]$ are $r=j-i+1$ periodic (otherwise we could have better compression rate for $t_1>1$ and shorter string $s_1$). In this case, $D\left[i\right]\left[j\right]=1+\left|Q\right[i..j\left]\right|=1+(j-i+1)=j-i+2$.

If $m\ge 2$, then we can split it into a pair of RRLEs $Q[i..k-1]=S(t_1,s_1,\cdots ,t_j,s_j)$ and $Q[k..j]=S(t_{j+1},s_{j+1},\cdots ,t_m,s_m)$. By the inductive assumption and the definition of the size $\left|s\right|$ of s,

$$\left|s\right|=|(t_1,s_1,\cdots ,t_j,s_j)|+|(t_{j+1},s_{j+1},\cdots ,t_m,s_m)|=D\left[i\right][k-1]+D\left[k\right]\left[j\right].$$

Time Complexity: the algorithm runs $O\left(n^2\right)$ iterations over the pair of “for” loops. For each such iteration, it computes the smallest period, if any, of a string of length $O\left(n\right)$, which takes linear time using the preprocessing of the Knuth–Morris–Pratt (KMP) algorithm [27]. Then, the corresponding entry in D is computed using the $O\left(n\right)$ precomputed values. Hence, the total time complexity of the algorithm is $O\left(n^3\right)$. □

3.2. Lossy RRLE Compression

In this section we solve Problem 3; i.e., compute a lossy good compression of an input string Q. Formally, given such a string Q of length n, the goal of our algorithm is to compute the minimum $\mathrm{cost}(Q,P^{\prime })$ over every string $P^{\prime }\in {\Sigma }^n$; see Section 2.3 for the definition of $\mathrm{cost}$. Of course, one can simply compute $\mathrm{cost}(Q,P^{\prime })$ using $\mathrm{rcost}\left(P^{\prime }\right)=Exact\left(P^{\prime }\right)$ for all possible strings $P^{\prime }$ and output the one whose $\mathrm{cost}(Q,P^{\prime })$ is minimized. However, the time complexity of such a solution is $O\left(\right|\Sigma {|}^n{n}^3)$.

In order to reduce the time complexity, we propose a dynamic programming algorithm, which generalizes Algorithm 1 as follows. In Algorithm 1, if a substring $Q[i..j]$ is not periodic, we check two possible evaluations of $D\left[i\right]\left[j\right]$: partitioning $Q[i..j]$ or leaving it as is. Here, even if $Q[i..j]$ is not periodic, we may change it to be periodic by finding a periodic string $Q^{\prime }$ of length $i-j+1$, and “paying” the similarity cost $\mathrm{scost}$ between $Q[i..j]$ and $Q^{\prime }$ for this change.

Hence, the final $\mathrm{cost}$ of $Q[i..j]$ is defined recursively as the minimum between the following three values:

• The minimum cost of modifying Q to be r-periodic, over every possible period length r. Formally, this is the minimal $\mathrm{cost}(Q,q^{\frac{n}{r}})$+1, over every string $q\in {\Sigma }^r$ and factor r of n.
• The minimum $\mathrm{rcost}$ over all possible partitioning options of Q.
• The cost of representing Q as is, with no compression.

To efficiently implement the above algorithm, we define the r-Parikh Matrix of a given string and its factor r, which we use throughout the algorithm. Intuitively, we define the string $Q_{i,1}$ to be the same as the input string Q except that we change every rth letter of Q to ${\Sigma }_i$. Hence, we changed at most $n/r$ letters. More generally, in $Q_{i,j}$ we do the same where j denotes the offset or first letter we change (beginning of count). The r-Parikh Matrix of Q contains the corresponding mismatching cost (Hamming distance) $\mathrm{scost}\left(Q_{i,j}\right)$ in its $(i,j)$ entry. Examples will follow the definition.

Definition 5

(Parikh Matrix [28]). Let $Q\in {\Sigma }^n$ be a string over an alphabet $\Sigma =\left\{{\Sigma }_1,\cdots ,{\Sigma }_{|\Sigma |}\right\}$. Let $r\ge 1$ be a factor of n. For every $i\in [\Sigma ]$ and $j\in \left[r\right]$, let $Q_{i,j}\in {\Sigma }^n$ denote the string whose letters in the entries $k\in \left\{j,j+r,j+2r,\dots \right\}$ are replaced by ${\Sigma }_i$; i.e., for every $k\in \left[n\right]$ we have

$$Q_{i,j}^r\left[k\right]=Q_{i,j}\left[k\right]=\left\{\begin{array}{cc}{\Sigma }_i\hfill & if(kmodr)=j\hfill \\ Q\left[k\right]\hfill & otherwise\hfill \end{array}\right..$$

The r-Parikh Matrix $M=M^r\left(Q\right)\in {\left\{0,1,\cdots ,n/r\right\}}^{|\Sigma |\times r}$ of Q is the matrix such that

$$M\left[i\right]\left[j\right]=\mathrm{scost}\left(Q_{i,j}\right).$$

For example, let $Q=\left(ababac\right)$ be a string over $\Sigma =\left\{a,b,c\right\}$. If $r=1$, then $j\in \left[r\right]=\left\{1\right\}$, and therefore $j=1$. That is, the period of changing a letter is 1 and thus all the letters will be modified. Indeed, for every $k\in \left[n\right]$ we have $(kmodr)=(kmod1)=0=j-1$. Hence, $Q_{i,j}=Q_{i,1}={\Sigma }_i^n$ consists of n copies of the letter ${\Sigma }_i$. We obtain $Q_{1,1}=\left(aaaaaa\right)$, $Q_{2,1}=\left(bbbbbb\right)$, and $Q_{3,1}=\left(cccccc\right)$. There are 3 corresponding mismatches of $Q_{1,1}=\left(aaaaaa\right)$ compared to $Q=\left(ababac\right)$, in indices $k\in \left\{2,4,6\right\}$. Hence, $M\left[1\right]\left[1\right]=3$. Similarly, $M\left[2\right]\left[1\right]=3$ and $M\left[3\right]\left[1\right]=5$. The 1-Parikh matrix of Q is, thus, $M(Q,1)={(3,3,5)}^T$.

If $r=2$, then $j\in \left\{1,2\right\}$. That is, we start the count with the first letter $j=1$, which means in the above example that we change the letters in indices $k\in \left\{1,3,5\right\}$. We obtain $Q_{1,1}=\left(\mathbf{a}b\mathbf{a}b\mathbf{a}c\right)$, $Q_{2,1}=\left(\mathbf{b}b\mathbf{b}b\mathbf{b}c\right)$, and $Q_{3,1}=\left(\mathbf{c}b\mathbf{c}b\mathbf{c}c\right)$. Counting the corresponding mismatches compared to $Q=\left(ababac\right)$, we get that $M\left[1\right]\left[1\right]=0$, $M\left[2\right]\left[1\right]=3$, and $M\left[3\right]\left[1\right]=3$. In a similar way, for $j=2$, we obtain $Q_{1,2}=\left(a\mathbf{a}a\mathbf{a}a\mathbf{a}\right)$, $Q_{2,2}=\left(a\mathbf{b}a\mathbf{b}a\mathbf{b}\right)$, and $Q_{3,2}=\left(a\mathbf{c}a\mathbf{c}a\mathbf{c}\right)$. Hence, $M\left[1\right]\left[2\right]=3$, $M\left[2\right]\left[2\right]=1$, and $M\left[3\right]\left[2\right]=2$. The 2-Parikh Matrix of Q is then $\left(\begin{array}{cc}0& 3\\ 3& 1\\ 3& 2\end{array}\right)$.

Finally, if $r=n$ then $M\left[i\right]\left[j\right]=0$ if the jth letter of Q equals ${\Sigma }_i$, and $M\left[i\right]\left[j\right]=1$ otherwise. Hence, the 6-Parikh Matrix of $Q=\left(ababac\right)$ is $\left(\begin{array}{cccccc}0& 1& 0& 1& 0& 1\\ 1& 0& 1& 0& 1& 1\\ 1& 1& 1& 1& 1& 0\end{array}\right)$.

For the r-Parikh matrix $M^r$ of a string Q, we it denote by $M_{min}^r\left(j\right)={min}_{i\in \left[\right|\Sigma \left|\right]}{M}^r\left[i\right]\left[j\right]$, the smallest entry in the jth column of $M^r$. Suppose that its row is $i^{*}$; i.e., $M_{min}^r\left(j\right)=M^r\left[i^{*}\right]\left[j\right]$. Therefore, if we wish to fix Q to be r-periodic with an offset j, by paying the smallest Hamming distance $\mathrm{scost}$, then we should change the corresponding letters $Q\left[j\right],Q[j+r],\cdots$ to the letter ${\sigma }_{i^{*}}$. This is also the motivation for using this matrix in Algorithm 2.

Algorithm 2:$\mathrm{L}\mathrm{OSSY}(M,\ell )$; see Theorem 6.

Overview of Algorithm 2: The input to the algorithm is a n-Parikh matrix M of a string Q of size n over $\Sigma$, and an integer ℓ that denotes the maximum RRLE tree level of the compression, as explained below. Note that both Q and n can extracted from this Parikh matrix. We use dynamic programming to compute the matrix $D[1..n][1..n]$, in which $D\left[i\right]\left[j\right]=\mathrm{cost}(Q[i..j],P^{\prime })$ is the (optimal) compression cost of the sub string $Q[i..j]$. The loops are over the length m of the substring (from 1 to n), and then from the starting index i. The last index is denoted by $j=i+m-1$.

We first compute the optimal cost of modifying a substring of length 1 in the ith index. This is $Mmin\left(i\right)$ by definition, so $D\left[i\right]\left[i\right]=1+Mmin\left(i\right)$ for $1\le i\le n$. Next, we compute $D\left[i\right]\left[j\right]=\mathrm{cost}(Q[i..j],P^{\prime })$ for every $1\le i<j\le n$ using recursive exhaustive search over the following three options.

The first option is to modify the substring $Q[i..j]$ in order to get r-periodic substring for some factor r. This costs 1 for the number of reputations and the total compression of the first r letters of Q.

The second option is to partition the substring into a pair of substrings: the left and right side of the original string. The overall cost is then the sum of these two costs.

The last option is simply to keep the substring as is. This takes m letters which is the size of the substring.

Looking at the resulting RLE tree, the first case means we can compress the string by adding the node new single child which represents a period of length r. The edge to this new child is marked with $\frac{n}{r}$. The second case means add k new children which represent the partition of the string. In this case, all k new edges are marked with 1. And the third case means the string itself is a leaf.

For computing the first value, we need to compute the r-Parikh matrix $M^r$, for every possible period length r, and then recursively fill it. However, we bound this recursion by a constant number ℓ, which is the maximal levels in the RLE tree, by keeping for each call to Algorithm 2 its level in the recursion, and if we reach ℓ we only compute the third value. The algorithm also stops when the input Parikh matrix is of size $|\Sigma |\times 1$, and returns $Mmin\left(1\right)$.

The time complexity of computing $D[1..n][1..n]$, is $n^2$ times (for each $i,j$) the following:

• Computing $M^r$ for every possible r takes $O\left(\right|\Sigma \left|n^2\right)$ + the time for computing D for $M^r$.
• Computing the second value in the equation takes $O\left(n\right)$.
• Computing the third value in the equation takes $O\left(\right|\Sigma \left|n\right)$.

Each call takes $O\left(\right|\Sigma \left|n^4\right)$-time, and since we bound the recursive calls to ℓ, the total time complexity is $O\left(\right|\Sigma \left|n^{4\ell }\right)$.

The pseudocode of the algorithm is presented in Algorithm 2. For simplicity, the algorithm output is $\mathrm{cost}(Q,P)$; however, it can be easily modified to include the string P as well.

Theorem 6.

Let Q be a string of length n over Σ, and let x be the output of a call to $\mathrm{L}\mathrm{OSSY}(M,\ell )$, where M is the n-Parikh matrix of Q. Then x is the minimum $\mathrm{cost}(Q,P^{\prime })$ over every string $P^{\prime }\in {\Sigma }^n$ whose recursive depth is ℓ.

Proof. 

To prove the correctness of the algorithm recall that there are two options for a string Q: it is either periodic or not. If Q is not periodic we can partition it to smaller consecutive substrings and compress them, or we can leave it as is. These options are covered by the algorithm in the second and third values, respective of the equation of computing $D\left[i\right]\left[j\right]$.

If Q is periodic, or modified to be periodic, the algorithm checks all possible period lengths r. For each such period length r it computes the r-Parikh matrix $M^r$. The only thing we need to prove is that $M^r$ represents all possible substrings $q\in {\Sigma }^r$, and the corresponding value of $\mathrm{scost}\left(Q\right[1..r],q)$. If this is true, it means that the algorithm considers all possible solution strings.

Let us look at the string Q of size n, and its n-Parikh matrix $M[1..|\Sigma \left|\right][1..n]$. By definition, the cell $M\left[\sigma \right]\left[j\right]$ equals 0, if $Q\left[j\right]=\sigma$, and 1, otherwise. Hence, computing ${\displaystyle \sum _{j=1}^{n}Mmin\left(j\right)}$ gives us the minimum $\mathrm{scost}(Q,P)$ over all strings $P\in {\Sigma }^n$.

The last thing left to prove is that computing the minimum $\mathrm{scost}(Q,P)$ is sufficient in order to get $\mathrm{cost}(Q,P)$ in the case of periodicity. If Q is periodic in r, then, by definition, $\mathrm{cost}(Q,P)=r+1+scost(Q,P)$. Hence, minimizing $\mathrm{scost}(Q,P)$ for a specific r is sufficient to compute the minimum $\mathrm{cost}(Q,P)$ for this r. Since the algorithm computes this value for every possible $1\le r\le \frac{n}{2}$, it will find the correct solution string P. □

4. Linear-Time, Streaming, and Parallel Computation

The algorithms in the previous sections are optimal but take polynomial time in the input (length of string). However, their running time can be easily reduced to be linear in the input, by running them on core-sets for segmentation [29,30]. Roughly speaking, core-set is a problem-dependent reduction of the input, such that running the existing algorithm for solving the problem on the core-set, would yield a provable approximation compared to the result of running the algorithm on the complete data. In fact, using traditional merge-reduce trees, core-sets can be computed on streaming data, when we allow them to have only one pass over the input string, and use memory and update time per new letter, that are only poly-logarithmic in the input. Similarly, we can compute core-sets in parallel, either on few M threads, or on distributed data over M machines on the network (“cloud”), and reduce the running time by a factor of M.

More formally, for the problem in this paper, we use core-set construction for segmentation. This algorithm gets an ordered set of n points over time, and returns an ordered set C of constant size with appropriate weights in $O\left(n\right)$ time. The sum of distances from the original set to every signal that consists of a constant number of k linear segments, is approximated by C, up to $(1+\epsilon )$ multiplicative factor, where $\epsilon \in (0,1)$ is constant. More generally, the core-set time has roughly quadratic dependency on k and $1/ϵ$; see [29,30] for details. Unlike many solutions in machine or PAC-learning, in this and most core-sets there are no special assumptions on the size of input or its distribution (i.e., worse case input is assumed).

To apply Algorithms 1 and 2 on this core-set, we consider the input string to be a signal over integers that represent the letters. We also assume that the optimal RRLE has at most k leaves (more generally, has length of at most k), so that every relevant RRLE candidate will be approximated by the core-set C. This assumption is natural, e.g., in our system, since the number k of patterns in the protocol is significantly smaller than the length n of the highly sampled signal.

5. The Reverse Engineering System

5.1. Example of a Protocol: The SYMA G107 Helicopter

Example Protocol: The SYMA G107 helicopter supports a communication of three channels that represent the current state (level) of each button in the remote controller: throttle, pitch, and yaw of the helicopter. As in most of our RCs, the communication protocol is defined by a multi-layer language. For the special case of SYMA G107, the protocol is as follows.

Level I: A/B (switches). The IR signal is essentially a stream of binary numbers that corresponds to the IR light (on or off) that can be be changed every 13 microseconds. Light on for 13 microseconds represents in our notation the letter “A”; otherwise, the letter is “B”. The letters “A” and “B” are called switches.

Level II: 0/1/H/F (letters). The letter “0” is represented by the sequence of switches “0=ABABABABABBBBBBBBBBB”. That is, five pairs of “AB” followed by ten “B” letters. We encode the last sentence as a sequence of pairs “0” = $(5,AB,10,B)$, known as run-length-encoding (RLE); see Definition 3. Similarly, we define the letters “1” = $(5,AB,23,B)$, “H” = $(75,AB,72,B)$ (called header, and “F” = $S(10,AB,47,B)$ (called footer).

Level III: word. A word in the SYMA G107 protocol is defined by the followings sequence of letters:

$$\begin{array}{cc}\mathrm{word}=\hfill & (1,H,1,“0”,1,yaw,1,“0”,1,pitch,\hfill \\ & 1,“0”,1,serial,1,throttle,1,“0”,1,trim,1,F),\hfill \end{array}$$

where: H and F were defined in Level II above, “serial” is the letter “0” or “1” (Helicopter 0 or 1) that allows the support of two helicopters by a single RC. Each term yaw/pitch/throttle/trim is an integer between 0 and 255. Each integer is represented by a binary word that consists of 8 bits, where a bit is represented by the letter “0” or “1” above. In real-time, a continuous stream of such words is sent from the transmitter (RC) to the receiver of the helicopter that decodes these words.

5.2. The System

Given a remote controller of a toy robot, such as the one of SYMA G107 described above, our goal is to learn its protocol. That is, to reveal from the long recorded stream of analog signals, what is the exact sequence of switches that define each letter in the protocol. Once this is known, we can imitate the remote controller using a mini-computer. This is where the stringology steps in. The algorithm we present below allows us to identify, in this long sequence of “AB” switches, the exact letters of a protocol.

5.3. After Learning the Protocol

After learning the desired protocol using our reverse engineering algorithm, we send the signals that are generated by the controller algorithm using a low-cost set of IR LEDs. The amplifier receives the binary commands from the Arduino code and turns them into on/off commands to the LEDs array. The algorithm that controls the robot runs on a laptop or a mini-computer and generates words according to the learned protocol. These commands are sent to the Arduino through the USB port.

The whole system works as follows:

• Recording analog signals. In the case of IR signals, we use an IR decoder (sensor) that receives the signals from the remote controller. The IR decoder gets its power from the a micro-computer (Arduino), and is connected to a logic-analyzer.
• Converting Analog signals to binary signals. The logic analyzer converts the analog voltage signal into a digital binary signal that has value “A” or “B” in each time unit.
• Transmitting the binary stream to a laptop via a USB port.
• Running reverse engineering algorithm to learn the protocol.
• Producing commands to the robot using the mini-computer that is connected to a transmitter or a few IR (Infra-Red) LEDs.

See Figure 2 for steps 1–3. Note that since the logic analyzer is relatively expensive compared to the other parts of our system, we can use the Arduino board not only as a power provider, but also as a converter from the IR signal to the USB port. An Arduino code that implements this conversion is provided as part of the open source of our system.

6. Reverse Engineering Experiments

We ran experimental results on both synthetic and real data to test Algorithm 2.

We first ran the following experiment on synthetic data to measure the robustness of the recovery of Algorithm 2; i.e., to get some sense of the signal-to-noise (SNR) ratio. Intuitively, we assume that user Alice sends a periodic string over a known alphabet $\Sigma [1..4]$ to another user Bob, through a noisy channel. Bob then tries to recover the original string from the received noisy string over the alphabet of real numbers ${\Sigma }^{\prime }=R$.

The input data was a set $\mathcal{M}$ of $48=16·3$ strings $\left\{M_{i,k}\mid i\in [1..16],k\in [1..3]\right\}$ in $\Sigma$. Each string M in this set was constructed as the sum “$M=M^{*}+N$” of a fixed matrix $M^{*}$ with additional random noise N that were defined as follows. Let $V=S(4{,}^{\prime }{12}^{\prime },4{,}^{\prime }{3}^{\prime },3{,}^{\prime }{4}^{\prime })=121212123333444$, and let $M^{*}=V^3$ be a string from the alphabet $\Sigma$. For $\sigma >0$, let $N_{\sigma }$ denote a string in ${\Sigma }^{\prime }$ of length $\left|N\right|=|M^{*}|$, where $N\left[j\right]\sim \mathcal{N}(0,{\sigma }^2)$ is a random variable from a Gaussian distribution with zero mean and variance ${\sigma }^2$ for every $j\in [1..|N\left|\right]$. To obtain a finite alphabet and Parikh Matrix, we scale and round each letter $N\left[j\right]$ to its nearest integer. We then define ${\sigma }_i=0.05i$ and $M_i=M^{*}+N_{{\sigma }_i}$; i.e., $M_i\left[j\right]=M^{*}\left[j\right]+N_{0.05i}\left[j\right]$, for every $i\in [0..16]$ and $j\in [1..|N\left|\right]$. We repeat this construction of $M_i$ three times to obtain the string $M_{i,1},M_{i,2},M_{i,3}$, with different random noise $N_{{\sigma }_i}$ from the same distribution. The result is then the input set $\mathcal{M}$ of matrices above in the real alphabet ${\Sigma }^{\prime }$.

The experiment is a list of $255=17\times 3\times 5$ calls $O_{i,j,k}=\mathrm{L}\mathrm{OSSY}(M_{i,k},j)$ to Algorithm 2 with the string $M_{i,k}$ and j, over every variance level $i\in [1..17]$, repetition (try) $k\in [1..3]$, and $j\in [1..5]$. The cost error for this call is the weighted number of mismatched letters (i.e., dissimilarity or distance) between the output recovered string $O_{i,j,k}$ and the original de-noised string $M^{*}$,

$$\mathrm{error}(i,j,k)=\sum _{z=1}^{|M^{*}|}|M^{*}\left[z\right]-O_{i,j,k}\left[z\right]|.$$

The results are shown in Figure 3. The x-axis represents the integer level $i={\sigma }_i/0.05$ of the noise variance as defined above. The color of each of the five curves corresponds to different RRLE levels $j\in [1..5]$ that were used in Algorithm 2. The height y of the jth curve in the ith variance level is the mean error over the 3 errors $\mathrm{error}\left(\right(i,j,1)+(i,j,2)+(i,j,3\left)\right)/3$, together with its variance.

Conclusion.Figure 3 shows that the algorithm is more robust to noise as the number of the levels in the tree increases.

6.1. Experiments on Toy Robots

In this section we show experimental results on real data strings. These strings were obtained by recording communication signals from the remote controllers (RC) of a pair of toy robots: (i) The IR-UFO helicopter, which communicates through a 3-channel IR signal (yaw, pitch, and throttle). Such a remote controller contains two sticks: a one that can be rotated to four directions (higher/lower pitch, and higher/lower yaw) and another stick that can be rotated (only left and right for higher/lower throttle). (ii) The Lutema Avatar Hovercraft that has similar RC, but different communication protocol than the IR-UFO.

The ground truth. After using our system, we verified the following protocol of IR-UFO which has a structure that is similar to the SYMA S107, as defined in Section 1, with the following changes. Level I: The IR light changes every 13 microseconds. Level II: $“0”=(175,A,200,B),“1”=(350,A,375,B), \mathrm{and} H=(2,(360,A,240,B\left)\right)$. Level III: A stream of binary words, each consists of 30 bits followed by a list of 4000 “A” bits. The format of a word is

$$\begin{array}{cc}\hfill & \mathrm{package}(throttle,yaw,pitch,channel)\hfill \\ \hfill =& (1,H,2,“0”,1,throttle,1,“1”,1,channelOne,1,\hfill \\ \hfill & yaw,1,channelTwo,1,“0”,1,pitch,1,“0”,1,checksum),\hfill \end{array}$$

(1)

where “throttle”, “yaw”, and “pitch” are integers in $[0,127]$ that are represented using 7 bit words; “channelOne” and “channelTwo” are the left and right bit respectively that represents the integer $channel\in [0,3]$; “checksum”: 4 bits that represent a checksum of all the previous 24 bits of the message. These bits are partitioned into six binary strings $S_1,\cdots ,S_6$, each of length four.

Checksum is

$$checksum=1111\oplus S_1\oplus \cdots \oplus S_6,$$

(2)

where $x\oplus y$ is a bit-wise xor on the corresponding bits in x and y. Once the bits of the checksum field are recovered using our algorithm, it is easy to extract its generating formula, as in (2), by simply solving a system of linear equations over the $F_2$ field. See e.g., [31].

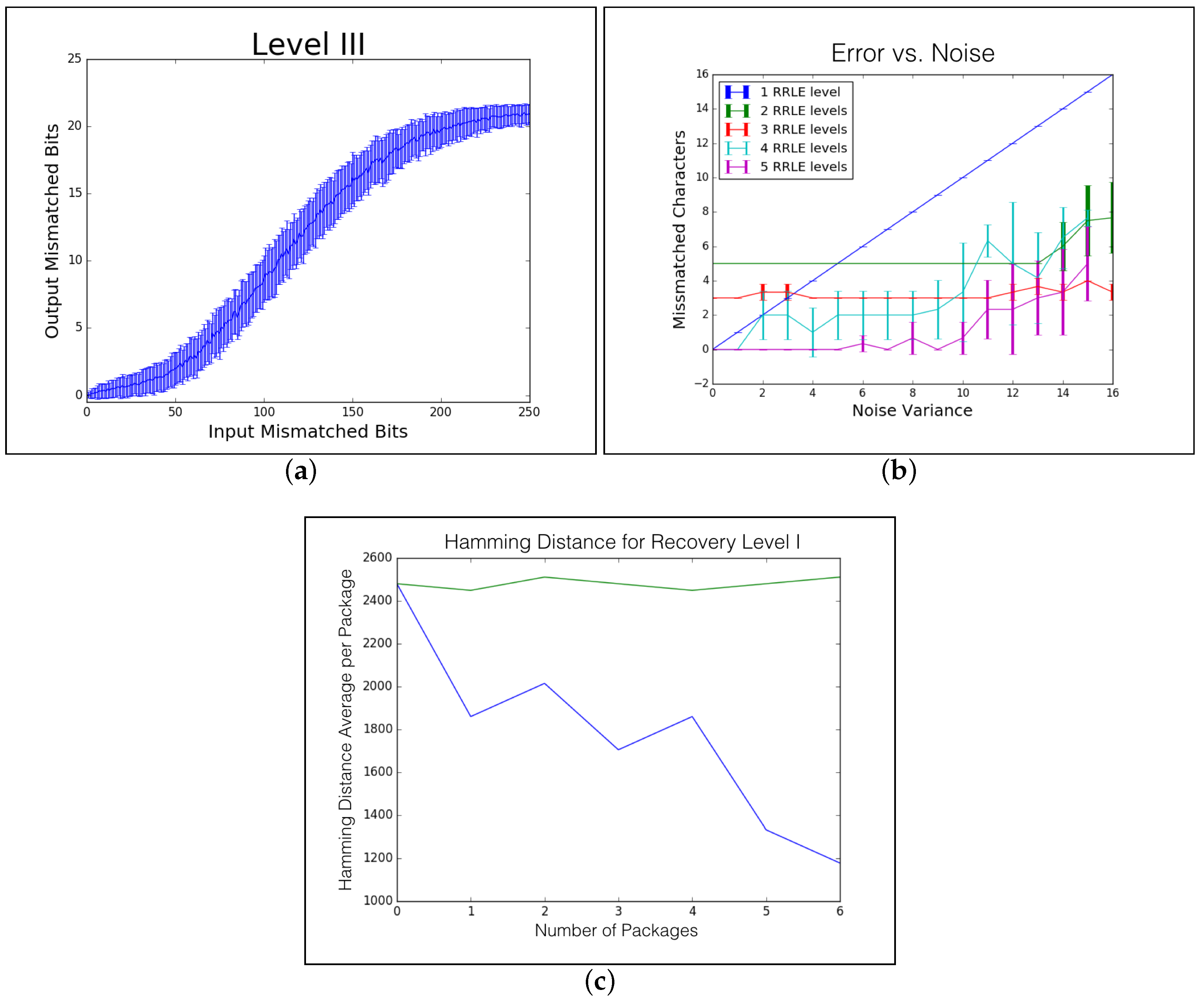
6.2. De-Noising Level I

The purpose of the first experiment is to recognize the repeated letters in the first level, e.g., “0” and “1”, using the raw light signal “A” and “B”.

The experiment. An IR signal was generated from the remote controller (RC). The “throttle” stick on the RC was pushed to its maximum level (100%) which produces repetitions of $W=S\left(\mathrm{package}\right(127,50,50,0\left)\right)$; see (1). Using the recording part of our system (see Figure 2), we recorded a signal of 6 seconds to obtain the Level I string

$$V=S(t_1,“\mathrm{A}”,t_2,“\mathrm{B}”,t_3,“\mathrm{A}”,t_4,“\mathrm{B}”,\cdots ),$$

(3)

for some integers $t_1,t_2,\dots$.

Recovery Error. We partitioned the recorded string V into separate packages $P_1,P_2,\cdots$. This was easy since each package was separated from the following package by a continuous sequence of thousands “A” letters. Hence, we simply removed from V any consecutive sequence of at least 500 “A” letters. The string between each resulting gap was defined to be a package, so we obtained the list of m packages $W_1,W_2,\cdots ,W_m$. We denote by $V_j=W_1{W}_2\cdots W_j$ the string that consists of the first j packages, for every $j\in [1..m]$.

The expected value of $W_i$ for every $i\in [1..m]$, i.e., with no noise, $W_i=W^{*}$ and there is no recovery error. In practice this never occurs, but the length of each package is the same, $|W_i|=|W^{*}|$, for every $i\in [1..m]$. We thus define the error between the transmitted word $W^{*}$ to the received word $W_i$ by their Hamming distance $\mathrm{hamm}(W_i,W)$; i.e., number of corresponding bits that are not the same. The average Hamming distance of the first $j\le m$ packages is then

$$\mathrm{error}\left(j\right):=\mathrm{hamm}(W^j,V_j)=\frac{1}{j}\sum _{i=1}^j\mathrm{hamm}(W,W_j).$$

In practice, this error is proportional to the distance of the IR receiver sensor and the RC in Figure 2.

The error plots are shown in Figure 3. The green curve shows the average Hamming distance $\mathrm{error}\left(j\right)$ in the y-axis, over different number j of words (x-axis), together with its variance.

Recovery using Algorithm 2. We run Algorithm 2 m times using a call to $Lossy(M_j,\mathrm{levels})$, where $M_j$ is the Parikh matrix of $V_j$ and $\mathrm{levels}=2$, and $R_j$ is the output RRLE for each $j=[1..m]$. Without noise, $V_j=W^j$, and the output is $R_j=(j,s^{*}\left(W^{*}\right))$ that corresponds to the string $W^j=V_j=S(j,s^{*}\left(W^{*}\right))$. In practice, $V_j$, unlike $W_j$ is not periodic, but $R_j$ (the recovered output signal) is expected to be j-periodic. The average error of the recovered string $S\left(R_j\right)$ is then

$$\mathrm{ourerror}\left(j\right):=\mathrm{hamm}(W^j,S\left(R_j\right)).$$

Results of Algorithm 2 are shown in Figure 3. The blue curve shows the average Hamming distance $\mathrm{ourerror}\left(j\right)$ in the y-axis, over different number j of words (x-axis). Since $R_j$ is always periodic, the variance error between the recovered packages is zero.

Conclusions: In Figure 3 we see, as expected by the analysis, that the recovery error decreases as Algorithm 2 is given more packages to learn from. On the contrary, the error of the “memory-less” thresholding approach does not reduce over time.

6.3. De-Noising Level II

After we identified $“0”=(175,A,200,B)$ and $“1”=(350,A,375,B)$, we used it to recover Level II of the protocol from each package P. Identifying P as consecutive m sequences

$P=S(a_1,“\mathrm{A}”,b_1,“\mathrm{B}”,\cdots ,a_m,“\mathrm{A}”,b_m,“\mathrm{B}”,\cdots )$. Without noise, either $(a_1,b_1)=(175,200)$, or $(a_1,b_1)=(350,375)$. Otherwise, we define semantic package$L=L\left[1\right]L\left[2\right]\cdots$ of the package P to be

$$L\left[i\right]=\left\{\begin{array}{cc}“0”\hfill & \mathrm{if}|a_i-175|+|b_i-200|>|a_i-350|+|b_i-375|\hfill \\ “1”\hfill & \mathrm{Otherwise},\hfill \end{array}\right.$$

for $i\in [1..m]$. The error is defined to be the Hamming distance between L and the expected semantic package $\mathrm{package}(127,50,50,0)$. We repeat this experiment for each package P.

The results were very similar to the results in Figure 3. By this and the fact that Algorithm 2 is not needed in this level, they were omitted and can be find in [4].

6.4. De-Noising Level III

In Level III, we are given the semantic package of “0” and “1” and need to split it into semantic words as in (1).

In the first experiment we repeated the experiment from the previous section, where in the package P we used different values of $throttle$. That is, the “throttle” stick on the RC was pushed to random levels, from 1% to 100%, which ideally produces a repetitions of the semantic package $L=S\left(\mathrm{package}\right(throttle,50,50,0\left)\right)$ where the value of $throttle$ is then a random integer in $[0..127]$. The checksum field in L was also changed in each package. Let $M=L_1{L}_2,\cdots$ denote the concatenation of these semantic packages.

Our goal was to identify the bits in M that correspond to the throttle field. To that end, we ran Algorithm 2 with the Parikh matrix for the string M with an additional row matrix that corresponded to a wildcard letter: “?”. Each entry in this row will have a (cost) value of $1/2$. The reason is that this wildcard will be used only on the variable “throttle” bits. The other bits are expected to be almost periodic and the cost of using wildcard on them will be too expensive.

Ideally, the algorithm will output the input string M where the “throttle” bits are replaced by wildcards. We repeat this experiment where “throttle” was replaced by “role” and “pitch”.

The results are shown in

Table 1. Example experimental results on a toy helicopter. The three leftmost columns tells which RC button was pressed. The input is the recorded communication bits from the RC for a long repeated signal. The output on the rightmost column is the output of our algorithm. It is the common “intersection” of input signals. Wildcards represent unstable character due to the different throttle, role or pitch values (in bold). From the output we can conclude the format of the message, including constant bits and the sub-string that is responsible for each button. See Section 6.4 for details.

Throttle	Role	Pitch	Input to Algorithm 2 (Semantic Package)	Output (RRLE)
25%	0%	0%	01100100100010000001101010011111
50%	0%	0%	01001111100010000001101010011001
75%	0%	0%	00100011100010000001101010011010	0???????10001000000110101001????
100%	0%	0%	00100011100010000001101010011010
100%	−100%	0%	01100100111110000001101010010110
100%	−50%	0%	01100100000110000001101010011000
100%	50%	0%	01100100110110000001101010010100	01100100????1000000110101001????
100%	100%	0%	01100100001010000001101010011001
100%	0%	−100%	01100100100000010001101010010111
100%	0%	100%	01100100100011110001101010010110	011001001000????000110101001????

. The first 4 lines of Table 1 correspond to 4 semantic packages $M=L_1{L}_2{L}_3{L}_4$ while the throttle is changed and the pitch/roll sticks remain unchanged. The fourth column of the ith row shows $L_i$ for $i\in [1..4]$. The “throttle” bits were marked manually (by us) in bold. The first row in the fifth column contains the output of Algorithm 2 on M, where the throttle field, as well as the checksum, were indeed identified by wildcards.

To recover the complete protocol of IR-UFO, we scanned the two sticks over 20 positions, where each position was recorded for roughly a second. Our system plotted the desired Level III words as defined in (1) after a couple of hours. We expect that using core-sets the running time will reduce to minutes; see Section 4.

In the second experiment the goal was to see how Algorithm 2 is robust to noise that may occur in previous levels. To this end, we added synthetic noise to the input (column 4 from the left in Table 1) for the string M with the variable “throttle” field above. For each $x\in [1..250]$ we changed x bits in M to obtain $M_x$ and run Algorithm 2 with $M_x$ as described in the previous experiment. We then define $y\left(x\right)$ to be the wrong letters in the output, compared to the desired string (rightmost column of first row in Table 1) over 100 experiments. Figure 3 describes the average error y in the output (y-axis) and its variance, for the values of x (in the x-axis).

Conclusions:Figure 3 shows that roughly $90\%$ of the noisy bits in the input were recovered. When the input string is completely noisy, the output string consists of only wild cards, which is correct for few bits but wrong for the other (approximately 20) bits.

7. Conclusions

Novel algorithms for lossy text compression with provable guarantees on running time and optimality were provided. We demonstrated them by providing an open-source, home-made system for automatic reverse-engineering of toy robots, with experimental results on synthetic data and real communication signals. Clearly, there are many other applications of our algorithms such as compressing and recovering XML/Http or other protocols that are made of repeated similar blocks, or finding similar scenes in video/GPS streams.

We focused on IR signals, but similar results were obtained from radio (PWM) signals that used similar protocols; see [1]. Further work includes turning our off-line system into a real-time system that can be used to get control over dangerous quadcopters, e.g., in airports, by learning their protocols. Core-sets seems like a promising way to do this, maybe using a network (“cloud”).