A Pareto-Based Hybrid Whale Optimization Algorithm with Tabu Search for Multi-Objective Optimization

Abstract

Multi-Objective Problems (MOPs) are common real-life problems that can be found in different fields, such as bioinformatics and scheduling. Pareto Optimization (PO) is a popular method for solving MOPs, which optimizes all objectives simultaneously. It provides an effective way to evaluate the quality of multi-objective solutions. Swarm Intelligence (SI) methods are population-based methods that generate multiple solutions to the problem, providing SI methods suitable for MOP solutions. SI methods have certain drawbacks when applied to MOPs, such as swarm leader selection and obtaining evenly distributed solutions over solution space. Whale Optimization Algorithm (WOA) is a recent SI method. In this paper, we propose combining WOA with Tabu Search (TS) for MOPs (MOWOATS). MOWOATS uses TS to store non-dominated solutions in elite lists to guide swarm members, which overcomes the swarm leader selection problem. MOWOATS employs crossover in both intensification and diversification phases to improve diversity of the population. MOWOATS proposes a new diversification step to eliminate the need for local search methods. MOWOATS has been tested over different benchmark multi-objective test functions, such as CEC2009, ZDT, and DTLZ. Results present the efficiency of MOWOATS in finding solutions near Pareto front and evenly distributed over solution space.

1. Introduction

Currently, real-life problems share a common aspect, which have multiple objectives to be optimized. Problems, such as recommender systems [1], industry [2] and bioinformatics [3] have many objectives that need to be optimized simultaneously to reach an effective solution. These objectives are often contradictory, so optimizing one objective deteriorates the degree of optimization of other objectives. Solving Multi-Objective Problems (MOPs) needs multiple solutions to vary the degree of optimization of each objective [4]. Choosing the appropriate solution can be specified by a decision-maker.

Population-based meta-heuristic methods mimic the intelligent behavior of organisms that live in groups [5]. They use a set of solutions to cover solution space, which makes them suitable for solving MOPs. Population-based meta-heuristic methods can be simply classified into Swarm Intelligence (SI) and Evolutionary Algorithmic (EA) methods [6]. SI methods have been first proposed to solve MOPs by Schaffer [7]. They represent each solution to the MOP by a swarm member. They use intelligent intensification and diversification techniques to cover solution space economically. The quality of solutions is assessed using objective functions of the MOP. To identify best solutions regarding multiple objectives, a sophisticated method is needed. Pareto Optimization (PO) has been one of the main techniques used in solving MOPs [8]. It aims to optimize the whole objectives simultaneously. PO generates a set of best solutions called “non-dominated” solutions or “Pareto Front” (PF) [8]. These solutions represent the best solutions to the problem, which cannot be further optimized. Many population-based methods have been combined with PO to solve MOPs, see for example Non-dominated Sorting Genetic Algorithm (NSGA) [9], NSGA-II [10], Multi-Objective Particle Swarm Optimization (MOPSO) [11], Multi-Objective Cat Swarm Optimization (MOCSO) [12], and Multi-Objective Grey Wolf Optimizer (MOGWO) [13], to name a few.

Yet although SI methods presented a good performance in solving MOPs, they have their own drawbacks. Focusing on methods, such as Particle Swarm Optimization (PSO) and its rivals, these methods share common drawbacks such as selecting the swarm leader [14], getting trapped in local optima [15], and obtaining solutions that are not evenly distributed over solution space [15]. These problems result from the lack of mature memory elements, since only a single best solution within the search space is kept, which limits their capabilities to cover the whole solution space. Even when those methods use an external archive to store best solutions, they do not use these solutions to guide swarm members. This limits their ability to search promising regions thoroughly and increases their probability to get trapped in local optima. Also, PSO and its rivals tend to move with big steps to explore different regions of the search space without focusing on exploring neighbors of swarm members, which increases their need to local search methods.

Combining PSO or one of its rivals with mature memory elements can enhance its effectiveness. Tabu Search (TS) is a well-known single-point meta-heuristic method, proposed by Glover [16]. In TS, an Elite List (EL) is used to store the best solutions, and a Tabu List (TL) is used to store pre-visited solutions. These memory elements enable TS to identify promising regions to be searched thoroughly and remembering pre-visited regions to be avoided.

Whale Optimization Algorithm (WOA) is a recent SI method, proposed by Mirjalili et al. [17]. It mimicked the behavior of the humpback whales to heuristically locate the extreme points of arbitrary functions. WOA was tested over multiple engineering optimization problems and presented a good performance [17]. Also, it was successfully used in solving the scheduling problem of a single robot used to transport raw materials within an intelligent manufacturing system [18]. The WOA is a simple method as it uses a small number of parameters to control the search process, which makes it a good candidate for new modifications.

In this paper, we propose combining the WOA [17] with TS for fast computation of almost optimal solutions of MOPs (MOWOATS). MOWOATS is proposed to find solutions of MOPs that are very near the true PF of the problems and evenly distributed over the solution space. This comes as a result from using the mature memory elements of TS to provide a better guidance to swarm members while covering the solution space. Another technique is proposed to overcome the drawbacks of PSO and its rivals, which is the new diversification method that is used to improve the coverage of solution space. MOWOATS uses the crossover operator inspired form Genetic Algorithm (GA) [19] to improve the diversity of the population. These modifications ensure that MOWOATS can cover solution space and obtain high-quality solutions for MOPs in real time.

MOWOATS uses EL to store the non-dominated solutions about the search space. Then, these solutions are used to guide the search by the swarm members to escape from local extreme points. This technique avoids the MOWOATS to get trapped in local optima as it selects the best solution randomly each time from solutions stored in EL. To ensure covering the promising regions in search space, MOWOATS applies a crossover operator among swarm members and solutions in EL. MOWOATS, too, is a modified diversification step that positions the swarm members in their vicinity rather than the vicinity of the prey. This technique provides a better coverage of search space and eliminates the need to local search methods. The crossover operator is also applied among swarm members to improve the diversity of the population. The contributions of this paper can be summarized into:

• Design a simple and hybrid multi-objective optimization algorithm that attains more accurate solutions than common SI-based optimization heuristics. It uses the EL memory component to store non-dominated solutions. These solutions are used to guide swarm members during the search process, which eliminates the need for local search methods.
• A new diversification step is proposed to ensure an effective coverage of search space. The method ensures the balance between local optima and global optimization.
• Since SI methods need to enhance the diversity of swarm members [7,10], MOWOATS uses a crossover operator to broaden the diversity of swarm members. Crossover is also used to enhance the evolution of swarm members by applying it over solutions kept in the EL.
• MOWOATS uses the Pareto dominance criterion to evaluate the solutions. This method allows MOWOATS to optimize the whole objectives simultaneously and ensures obtaining solutions that are evenly distributed over solution space.
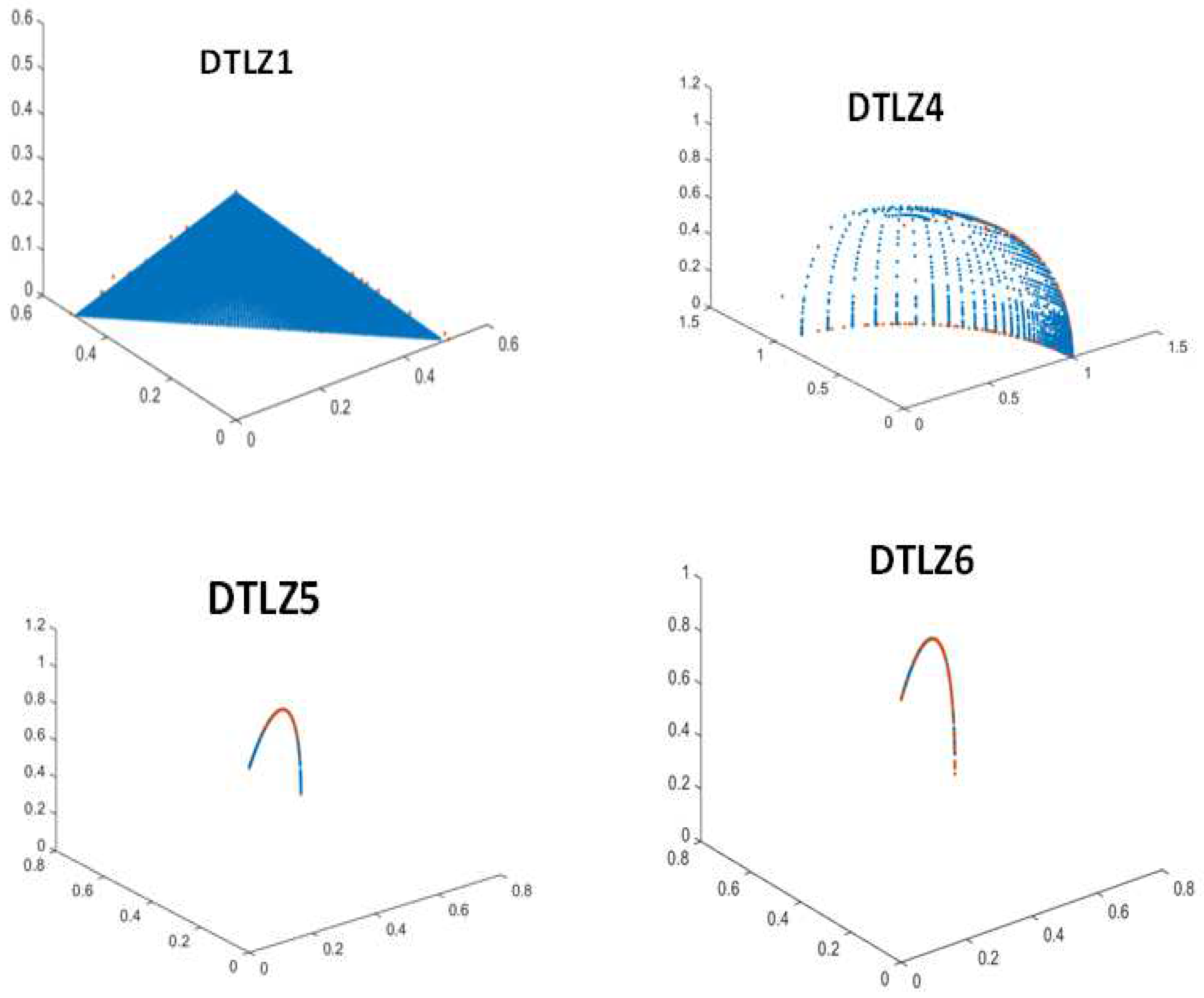
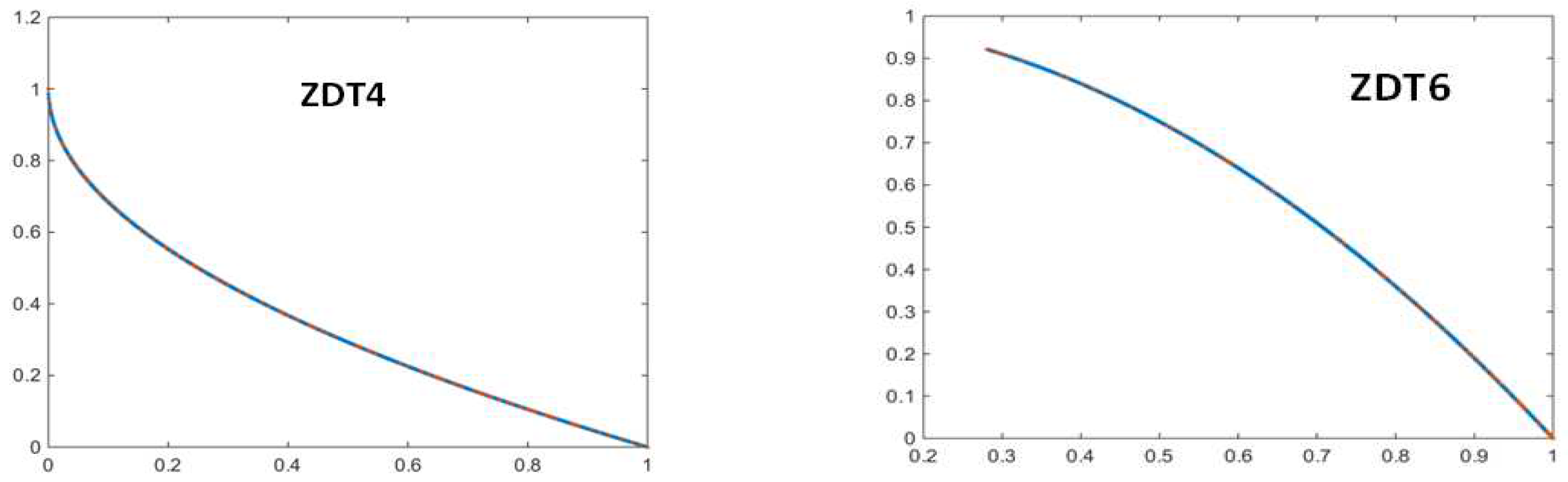
• MOWOATS is tested over different benchmark multi-objective test functions, such as Zitzler-Deb Thiele (ZDT) [20] test functions proposed by Zitzler et al., Deb-Thiele-Laumanns Zitzler (DTLZ) [20] test functions proposed by Deb et al., and CEC2009 test functions proposed by Zhang et al. [21]. The Inverted Generational Distance (IGD) metric [13] is used for the comparison.

The paper is organized as follows. Section 2 presents previous methods proposed to solve MOPs. Section 3 presents a mathematical description of MOPs and provides a short description for both WOA and TS algorithms. Section 4 describes the proposed algorithm and explains in detail some of its major components. Section 5 reports a performance analysis for MOWOATS. Section 6 summarizes the main points of our work and future work.

2. Related Work

There have been three main methods to solve MOPs. First method converts the MOP into a single objective one by aggregating the objectives and giving them different weights according to their importance [22]. Second method orders the objectives according to their importance (lexicographic approach), and tries to optimize objectives according to their order [22]. Third method is PO, which optimizes the whole objectives simultaneously [8]. It generates a non-dominated set of solutions that represent the best solutions to the problem [8]. PO can be used as an effective way to evaluate the goodness of multi-objective solutions, which is needed for multi-objective optimization methods.

SI methods are population-based meta-heuristic methods, which simulate the behavior of natural organisms that live into groups in their strategies to cover a large search space economically [5]. SI methods transform the solutions of a MOP into a M-dimensional solution space, trying to cover the feasible space effectively for finding the best solutions. Since they were first proposed to solve MOPs [7], many meta-heuristic methods have been proposed to solve MOPs [9,10,23]. One of these is NSGA [9], an evolutionary algorithm which combines a genetic algorithm with PO to find non-dominated solutions. Its main goal is to diversify the population over the whole PF. This eliminates the biasness of resulted non-dominated solutions towards specific regions in the search space. Based on these ideas, NSGA-II [10], which is an improved version, has become one of the most popular evolutionary computing techniques for addressing MOPs. The changes included the addition of an EL to store the best solutions found during the search process. This modification enhanced the quality of generated non-dominated solutions and reduced the execution time of the algorithm via parallel candidate paths.

An alternative approach to tackle MOPs is to decompose the original difficult problem into simpler subproblems, and solve them independently but coupling their solutions, in such a way that each subproblem is optimized by using information from its neighboring ones. This was tested successfully by Zhang et al. [23], who used NSGA-II for solving the subproblems and demonstrated better results over NSGA-II alone in different benchmark tests.

SI methods have been combined with PO to solve MOPs. An example is [11] (MOPSO, Multi-Objective Particle Swarm Optimization), where the PSO meta-heuristic is employed to explore the solution space. MOPSO keeps track of the non-dominated solutions during its execution (in an external archive), and in doing so it exhibits the advantages of using enough memory during the search process, especially when dealing with MOPs. Some further improvements in the accuracy of the solutions to MOPs can be achieved by replacing PSO method with other variants of PSO, either for accuracy or for reducing the time complexity. For instance, using Cat Swarm Optimization as in [12], or using information from the neighbor particles, as in Quantum-behaved Multi-Objective Particle Swarm Optimization (MOQPSO) [24], which applies the rules of cultural evolution to control how swarm members evolve. Here, particles in the swarm depend on the other particles in their vicinity, and not only on their own previous positions, to determine their next location. This highlights the importance of performing a local search around the current state so that SI methods can discover better solutions and ultimately converge to a near optimum point, as [24] shows. Another variation appears in [14], where the authors propose a different nature-inspired swarm behavior, the Grey Wolf (GW) social hierarchy, to run the dynamics of the SI-based solver. The paper shows that the multi-objective solver based on a simulated GW society can find better non-dominated solutions in reduced time, compared to other SI algorithms.

Since a multi-objective solver can find several PFs simultaneously, some forms of assessing the relative quality of PFs is usually applied to output a final decision. The hypervolume [25] and the R2 [26] indicators are two recommended approaches. The work in [15] follows this idea, and presents a hybrid multi-objective optimization algorithm which combines PSO with R2. It turns out that this achieves a better performance than using the meta-heuristics alone.

The good search capabilities of the WOA led Kumawat et al. [27] to use it as a multi-objective optimizer. The method complemented the WOA with an external grid archive to store the best optimization values, found so far, for each objective. This heuristic achieves high convergence rates in short number of iterations. However, even though the method exploits the search capabilities of WOA, it does not propose any enhancements for the WOA search capabilities. Specifically, the memory element in [27] was used to store non-dominated solutions, but no other solutions are further explored to add more diversity to the dynamics of the swarm members. Another version of WOA was combined with the Simulated Annealing (SA) heuristic to be applied for feature selection [28]. The method used the SA for the intensification phase, which presents the need for WOA for more enhancements. Another modification was proposed by Abdel-Basset et al. [29]. They proposed combining a local search strategy with WOA for the permutation flow shop scheduling problem. This clarifies the correctness of our analysis for the WOA and its need for a local search method.

To sum up, although WOA exhibits a good performance in solving single objective and multi-objective problems, it still has some drawbacks. First, it is common that only a single best solution is recorded over the whole search space, thus increasing the probability to fall into convergence toward a local optimum. Secondly, despite adding an external archive to store multiple best solutions when solving MOPs, but these solutions are not always used to guide the future evolution of swarm members. Finally, the WOA diversification technique is not efficient enough, so it was enhanced by adding a local search strategy as proposed by Abdel-Basset et al. [29].

From previous work, the novelty of the proposed MOWOATS algorithm is emphasized. The hybridization of WOA and TS for MOPs is new and has not been proposed before.

The next section contains a brief mathematical description of MOPs and gives a presentation about both TS and WOA and how they can be combined for solving a MOP.

3. Background

3.1. Multi-Objective Problems

MOPs can be found in multiple fields, such as engineering [27] and bioinformatics [3]. They have multiple objectives to be optimized. A MOP can be described mathematically over a search space that consists of n variables as:

$${X_i}^l\le X_i\le X_i^u;i=1,\dots ,n,$$

(1)

where n is the number of variables, l and u represent the lower and upper bounds of variable i respectively. A MOP can be described as a set of functions that need to be minimized or maximized. A mathematical representation of a MOP can be described as:

$$F=min[f_1,f_2,\dots ,f_o],$$

(2)

where o stands for the number of objective functions in the problem. The constraint functions are either equalities or inequalities, which can be described as below [4]:

$$\begin{array}{c}{H}_i\left(x\right)=0;i=1,\dots ,k,\end{array}$$

(3)

$$\begin{array}{c}{G}_j\left(x\right)\le 0;j=1,\dots ,m,\end{array}$$

(4)

where the functions H represent the equality functions, the G functions represent the inequality functions, and m stands for the number of inequalities. These functions evaluate the quality of solutions and measure the objective values of each solution.

PO identifies whether a solution y dominates a solution x, if all objectives in y are as good as in x, and at least one objective in y is better than the same objective in x. This can be described mathematically according to:

$$\begin{array}{c}{f}_i\left(y\right)\le f_i\left(x\right);\forall iϵ[1,o]\hfill \\ f_i\left(y\right)<f_i\left(x\right);\exists iϵ[1,o],\hfill \end{array}$$

(5)

where x, y are two different solutions, and o represents the number of objectives. These two rules must hold to ensure that solution y dominates solution x.

3.2. Tabu Search

TS is a single-point meta-heuristic method, which mimics human thinking [16]. It was first proposed by Glover [16] as a global optimizer. It uses memory elements, such as EL to store the best solutions, those that are used to identify promising regions to be searched thoroughly, whereas TL stores pre-visited regions to ensure avoiding revisiting them in the future. These memory elements allow TS to explore and exploit search space economically.

The main drawback of TS is its usage of a single point to explore search space, so this technique is suitable for single objective problems rather than MOPs. Also, a single point does not provide an effective exploration for search space in real time. TS can be combined with a SI method to use mature memory elements of TS to enhance search methodology of the SI method.

3.3. Whale Optimization Algorithm

WOA is a recent SI method, proposed by Mirjalili et al. [17]. The method mimics the social behavior of the humpback whale to ensure a fast exploration of search space. In addition, WOA mimics the bubble-net technique to ensure an effective exploitation of promising regions. The heuristic has been tested over multiple optimization and engineering problems and has proved itself as a global optimizer [17].

Let us describe how the basic algorithm operates. In the intensification phase, the WOA sets the prey to be the best solution overall the search space ${\overrightarrow{X}}^{\ast }\left(t\right)$ and swarm members applies the bubble-net technique to surround the prey. Mathematically, the helix-shaped path taken by each whale $\overrightarrow{X}\left(t\right)$ to the prey can be computed as:

$$\begin{array}{c}\overrightarrow{D}=|{\overrightarrow{X}}^{\ast }\left(t\right)-\overrightarrow{X}\left(t\right)|,\end{array}$$

(6)

$$\begin{array}{c}\overrightarrow{X}(t+1)=\overrightarrow{D}·e^{bl}·cos\left(2\pi l\right)+\overrightarrow{X^{\ast }}\left(t\right),\end{array}$$

(7)

where b stands for a constant that represents the logarithmic spiral shape, l is a random number in the range of $[-1,1]$, and $\overrightarrow{X^{\ast }}\left(t\right)$ stands for the best solution. Considering the diversification phase, the WOA uses two exploration methods to cover search space. These methods simulate the social behavior of the humpback whale. The first diversification method is based on selecting a random whale ${\overrightarrow{X}}_{rand}\left(t\right)$ from the current swarm to be the prey. Then, the swarm members reposition themselves according to:

$$\begin{array}{c}a=2-t\ast (2/Max\_Iteration),\end{array}$$

(8)

$$\begin{array}{c}A=2\ast a\ast r-a,\end{array}$$

(9)

$$\begin{array}{c}C=2\ast r,\end{array}$$

(10)

$$\begin{array}{c}\overrightarrow{D}=|C·{\overrightarrow{X}}_{rand}\left(t\right)-\overrightarrow{X}\left(t\right)|.\end{array}$$

(11)

$$\begin{array}{c}\overrightarrow{X}(t+1)={\overrightarrow{X}}_{rand}\left(t\right)-A·\overrightarrow{D},\end{array}$$

(12)

where r represents a random number, C and A are controlling coefficients, t represents the current iteration number, $Max\_Iteration$ represents the maximum number of iterations, and $(·)$ represents element by element multiplication. The second diversification method was setting the prey to be the best solution ${\overrightarrow{X}}^{\ast }\left(t\right)$. Swarm members update their new positions according to:

$$\begin{array}{c}\overrightarrow{D}=|C·{\overrightarrow{X}}^{\ast }\left(t\right)-\overrightarrow{X}\left(t\right)|.\end{array}$$

(13)

$$\begin{array}{c}\overrightarrow{X}(t+1)={\overrightarrow{X}}^{\ast }\left(t\right)-A·\overrightarrow{D}.\end{array}$$

(14)

The choice between the two diversification methods is controlled by the value of A parameter. In starting iterations $\left(\right|A|<1)$, so WOA focuses on discovering the whole search space by computing the new positions of swarm members according to Equation (12). The value of $\left|A\right|$ decreases with the increase in number of iterations, which makes WOA computes new positions of swarm members according to Equation (14). This mechanism improves the search efficiency of WOA by exploring the whole search space in starting iterations and exploiting promising regions in the final ones.

Choosing between the exploration and the exploitation phases is done randomly according to the random parameter p. WOA uses a $50\%$ value to provide the balance between intensification and diversification methods. The following equation describes the selection criteria of WOA [13]:

$$\overrightarrow{X}(t+1)=\{\begin{array}{cc}\overrightarrow{X^{\ast }}\left(t\right)-A·\overrightarrow{D}\hfill & ifp<0.5,\\ \overrightarrow{D}·e^{bl}·cos\left(2\pi l\right)+\overrightarrow{X^{\ast }}\left(t\right)\hfill & ifp\ge 0.5\end{array}$$

(15)

where p is a random number in range of $[0,1]$. Next section discusses the computational representation of hybridizing WOA with TS.

4. Methodology

4.1. Multi-Objective Whale Optimization Algorithm Combined with Tabu Search (MOWOATS)

MOWOATS is a hybrid algorithm that combines WOA with TS to provide an effective exploration of search space. As pointed above, a good search method is critical for MOP solvers, since MOPs can have multiple solutions and need to evaluate several of them according to the situation of the problem. As expected, MOWOATS transforms the solutions of a MOP into a solution space and tries to find the PF solutions to the problem. For this, it combines the search capabilities of the WOA heuristic with the TS principle, implementing the exploitation phase exactly as proposed in the original WOA (Equation (7)). Next, we describe the basic search procedure. As already stated, WOA simulates the hunting technique of humpback whales. It sets the prey to be the best solution overall the search space. On the other hand, the main difference is MOWOATS chooses the prey ${\overrightarrow{X}}^{\ast }\left(t\right)$ randomly from non-dominated solutions stored in EL, which eliminates the possibility of getting trapped in local optima. Selecting a random non-dominated solution each time improves MOWOATS ability to escape local optima.

In the exploration phase, MOWOATS proposes a different diversification method, which depends on repositioning swarm members in their neighborhood instead of the prey’s neighborhood. This provides a better exploration for search space and eliminates the need for a local search method. In the first diversification method, MOWOATS selects a random whale ${\overrightarrow{X}}_{rand}\left(t\right)$ from swarm members to be the prey. Swarm members reposition themselves according to:

$$\begin{array}{c}\overrightarrow{D}=|C·{\overrightarrow{X}}_{rand}\left(t\right)-\overrightarrow{X}\left(t\right)|.\end{array}$$

(16)

$$\begin{array}{c}\overrightarrow{X}(t+1)=\overrightarrow{X}\left(t\right)+(A/4)·\overrightarrow{D},\end{array}$$

(17)

where $\overrightarrow{X}\left(t\right)$ represents the position of the current whale. In the second diversification method, MOWOATS selects a random non-dominated solution from EL to be the prey ${\overrightarrow{X}}^{\ast }\left(t\right)$. Swarm members compute their new positions as:

$$\begin{array}{c}\overrightarrow{D}=|C·{\overrightarrow{X}}^{\ast }\left(t\right)-\overrightarrow{X}\left(t\right)|.\end{array}$$

(18)

$$\begin{array}{c}\overrightarrow{X}(t+1)=\overrightarrow{X}\left(t\right)+(A/4)·\overrightarrow{D}.\end{array}$$

(19)

The algorithm chooses between the two diversification methods according to the value of A parameter as proposed in the original WOA [13].

The second main modification in MOWOATS to cope with MOPs is changing the selection value between intensification and diversification phases of p parameter. The original method WOA used a $50\%$ value to provide balance between the two methods. On the other hand, MOWOATS uses $80\%$ for diversification and $20\%$ for intensification. Because MOPs do not have a single best solution, MOWOATS tends to increase the probability of diversification to ensure finding non-dominated solutions that are evenly distributed over solution space. This eliminates the need to use crowd detection methods to maintain diversity of non-dominated solutions [10]. Also, the usage of PO ensures covering both concave and convex regions of PF solutions [8,30].

A block diagram of the main steps of the algorithm is given in Figure 1 for reference.

4.2. The Algorithm and Its Components

This section presents the details of MOWOATS main components, such as intensification by crossover and diversification by crossover procedures. A complete description of the algorithm is given at the end of this section.

4.2.1. Intensification by Crossover

The intensification by crossover function (Algorithm 1) aims to improve the quality of solutions in current swarm S by combining swarm members with a random solution from the EL. The function merges two solutions according to a crossover operator inspired by GA [19]. This technique is effective in speeding up the convergence rates, while simultaneously providing a random jump to a test point possibly not in the neighborhood of the current exploration point. After the procedure stops, it returns the updated swarm S.

Algorithm 1 Intensification_Crossover(S, $EL$)

Select $\eta$ solutions randomly from the swarm S. for$m=1,\dots ,\eta$do  Select a random solution ${\overrightarrow{X}}_{rand}$ from EL.  Update $\alpha$ random features in current whale ${\overrightarrow{X}}_m$ with $\alpha$ features selected from ${\overrightarrow{X}}_{rand}$. end for Return the updated swarm S.

4.2.2. Diversification by Crossover

This diversification procedure (Algorithm 2) uses the crossover to generate new and different solutions. It selects one whale randomly from the current swarm and, for each selected whale, another whale is randomly chosen to combine them according to the crossover operator [19]. The new solutions will be generated in a different form that differs from the original ones, with the purpose of increasing the diversity of swarm members. After the procedure stops, it returns the updated swarm S.

Algorithm 2 Diversification_Crossover(S)

Select $\eta$ solutions randomly from the swarm S. for$m=1,\dots ,\eta$do  Select a random solution ${\overrightarrow{X}}_{rand}$ from the current swarm other than current whale ${\overrightarrow{X}}_m$.  Update $\alpha$ random features in the current whale ${\overrightarrow{X}}_m$ with the $\alpha$ random features selected from ${\overrightarrow{X}}_{rand}$. end for Return the updated swarm S.

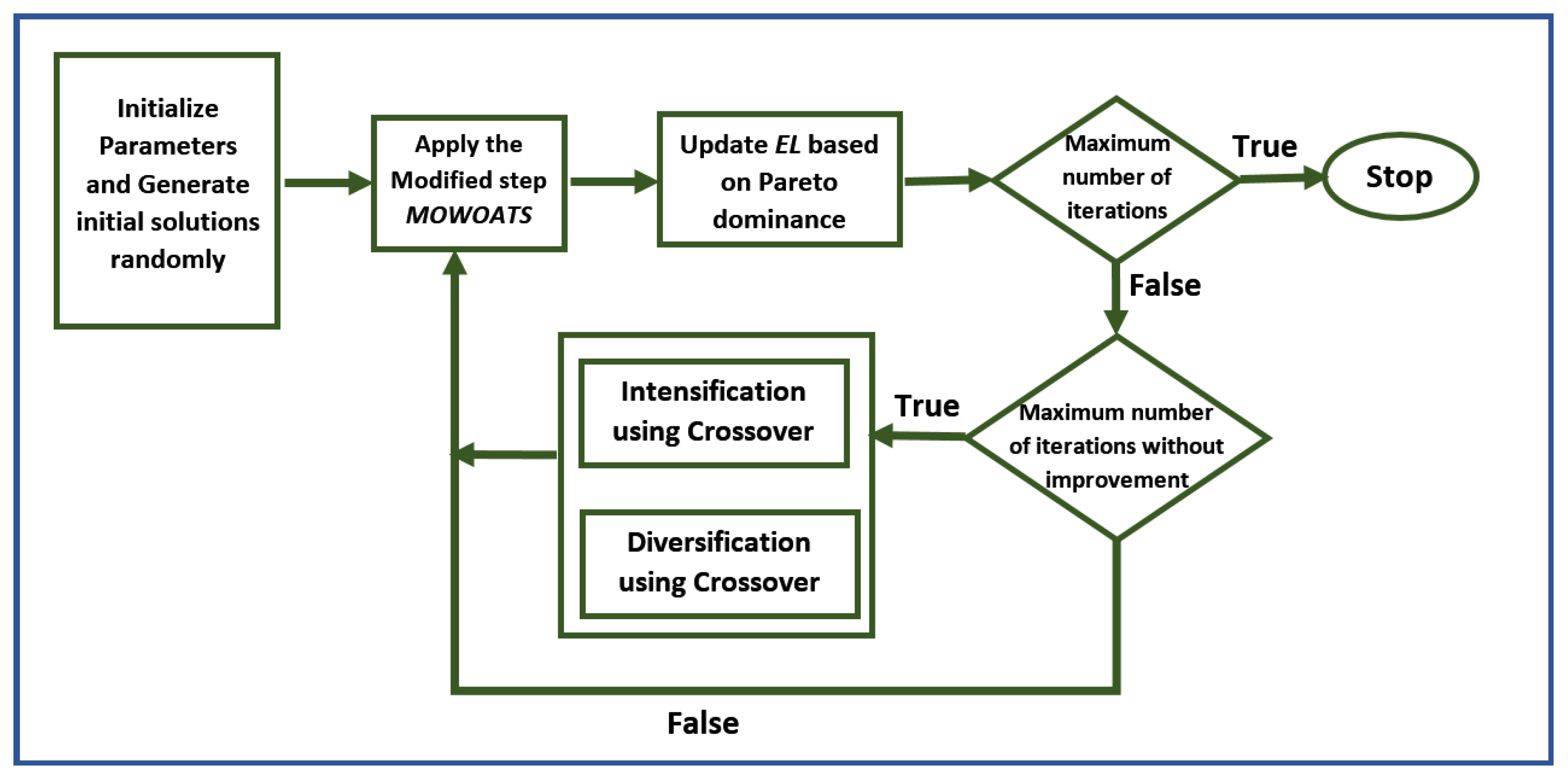
4.2.3. MOWOATS Algorithm

MOWOATS (see Algorithm 3) starts with setting the main parameters of WOA and an empty EL. First, a population is generated randomly from the dataset. Objective values are computed according to the mathematical description of the problem. Then, MOWOATS updates the EL with the best solutions in the initial population according to Pareto dominance criterion. According to the value of p, the algorithm chooses whether to apply intensification or diversification on the swarm. Therefore, it increases the chances of diversification to ensure that generated solutions are uniformly distributed over PF. Furthermore, the solutions in the EL are used to guide the evolution of the swarm members during both the intensification and the diversification phases.

In case that the number of iterations without improvement exceeds $Max\_NonImprove$, MOWOATS applies randomly either $Intensification\_Crossover$ procedure (Algorithm 1) or $Diversification\_Crossover$ procedure (Algorithm 2), to prevent getting trapped in local optima. At the end of the algorithm, the algorithm returns the non-dominated solutions stored in EL.

Algorithm 3 Pseudocode for MOWOATS algorithm

Initialization. Set of particles in swarm $Np$, number of features of each object d, empty $EL$, set $Max\_NonImprove$ to be maximum number of iterations without improvement, and initialize the whale algorithm parameters. for$i=1,\dots ,Np$do  Generate initial solutions randomly from the dataset.  Compute the objective value of current solution according to objective functions that describe the problem.  Update solutions in $EL$ according to Pareto dominance criterion. end for Main Loop. for$t=1,\dots ,MaxIt$do  for $i=1,\dots ,Np$ do   Update WOA parameters $a,A,C,l,p$.   if $(p>0.2)$ then    if $\left(\right|A|<1)$ then     Select a random whale ${\overrightarrow{X}}^{\ast }\left(t\right)$ from EL.     Update position of the current whale ${\overrightarrow{X}}_i\left(t\right)$ applying next equation. $$\overrightarrow{D}=|C·{\overrightarrow{X}}^{\ast }\left(t\right)-\overrightarrow{X}\left(t\right)|.$$ (20) $$\overrightarrow{X}(t+1)=\overrightarrow{X}\left(t\right)+(A/4)·\overrightarrow{D}.$$ (21)    else if $\left(\right|A|\ge 1)$ then     Select a random whale ${\overrightarrow{X}}_{rand}\left(t\right)$ from current swarm.     Update position of current whale ${\overrightarrow{X}}_i\left(t\right)$ applying next equation. $$\overrightarrow{D}=|C·{\overrightarrow{X}}_{rand}\left(t\right)-\overrightarrow{X}\left(t\right)|.$$ (22) $$\overrightarrow{X}(t+1)=\overrightarrow{X}\left(t\right)+(A/4)·\overrightarrow{D}$$ (23)    end if   else if $(p\le 0.2)$ then    Select a random whale ${\overrightarrow{X}}^{\ast }\left(t\right)$ from EL.    Update position of current whale ${\overrightarrow{X}}_i\left(t\right)$ applying next equation $$\overrightarrow{D}=|{\overrightarrow{X}}^{\ast }\left(t\right)-\overrightarrow{X}\left(t\right)|,$$ (24) $$\overrightarrow{X}(t+1)=\overrightarrow{D}·e^{bl}·cos\left(2\pi l\right)+\overrightarrow{X^{\ast }}\left(t\right)$$ (25)   end if   Compute the objective value of current whale ${\overrightarrow{X}}_i\left(t\right)$ according to the objective functions that describe the problem.   Update solutions in $EL$ according to Pareto dominance criterion.  end for  if (number of iterations without improvement ≥$Max\_NonImprove$) then   Set $\tau$ to a random value.   if $(\tau <0.5)$ then    Apply intensification procedure Intensification_Crossover(S,EL) (Algorithm 1).   else    Apply diversification procedure Diversification_Crossover(S) (Algorithm 2).   end if  end if end for Return non-dominated solutions stored in EL

5. Numerical Experiments

The algorithm was implemented in a virtual machine using a Linux environment (UBUNTU 16.04 distribution). Datasets were stored in files and the code was programmed in Scala [31]. This work will be extended to run over a Hadoop computing cluster to handle Multi-Objective (MO) Big Data problems [32]. Working over computing clusters minimizes processing time and permits MOWOATS to process massive datasets in real time. MOWOATS was tested on a Core-i3 processor and 16 GB of memory. It was tested over multiple benchmark datasets. Several numerical experiments have been reported and discussed in this section. We report the main parameter values of MOWOATS method, and the performance of its main components. In addition, comparisons with different meta-heuristic methods are presented to show the efficiency of MOWOATS algorithm.

5.1. Parameters Setting

Table 1. Main Parameter values of MOWOATS.

Parameter	Definition	Value
MaxIt	Maximum number of iterations	1000
Np	Population size	100
Max_NonImprove	Maximum number of iterations without improvement	15
max_EL	Maximum number of solutions stored in elite list	100

presents the values of important parameters used by MOWOATS. These parameters are used to adjust the performance of the algorithm. The $MaxIt$ parameter controls the maximum number of iterations. The value of the $MaxIt$ parameter was chosen to be the least value that ensures the stability of the algorithm. $Np$ parameter represents the number of whales in each swarm. This parameter also was set to the least value that can maintain the stability of the algorithm. Minimizing the values of $MaxIt$ and $Np$ parameters contributes to minimize the running time of the algorithm. The $Max\_NonImprove$ parameter stands for the maximum number of iterations without improvement. The $Max\_NonImprove$ value was set after different number of runs to ensure obtaining high-quality solutions by the algorithm. The $max\_EL$ parameter represents the maximum number of non-dominated solutions that can be stored in EL. This parameter was also set to be as minimum as possible to minimize the time needed when adding new solutions to the EL as the algorithm needs to loop over all the solutions stored in EL to eliminate dominated ones.

MOWOATS starts with a set of random solutions generated from solution space. Then, it applies both intensification and diversification techniques to explore and exploit search space. After running the algorithm, if the number of iterations with no improvement equals $Max\_NonImprove$, then either intensification or diversification by crossover are executed to amplify the diversity of swarm members. After the number of iterations equals $MaxIt$, the algorithm terminates and returns the best solutions stored in EL.

5.2. Results and Discussion

To assess the efficiency of MOWOATS as a multi-objective optimizer, MOWOATS is tested on multiple benchmark problems, which include both bi-objective and tri-objective problems. We use the ZDT [20], DTLZ [20], and CEC2009 [21] benchmark test functions. These test functions are considered to be examples of the most challenging MOPs, for they generate search spaces with different shapes of PF, such as convex, non-convex, discontinuous, and multi-modal shapes.

Evaluating the quality of generated solutions is made by comparing them with respect to the true PF of the problem. There are two main characteristics that can efficiently evaluate the generated solutions: convergence to the true PF and the distribution of solutions over the solution space. The IGD metric is used to evaluate both the convergence of solutions to the true PF and the spread of solutions over solution space [33].

First, the performance of MOWOATS algorithm is compared with several alternate algorithms: MOGWO [13], MOPSO, and a Multi-Objective EA based on Decomposition (MOEA/D) over the CEC2009 test functions according to IGD metric, defined as:

$$IGD=\frac{\sqrt{{\sum }_{i=1}^n{d}_i^2}}{n},$$

(26)

where n represents the number of true PF, $d_i$ corresponds to the Euclidean distance between the ith solution in PF and generated solutions from MOWOATS.

Table 2. IGD statistical results for the CEC2009 test functions $UF1$ to $UF10$.

	UF1(bi-objective)				UF2(bi-objective)
IGD	MOWOATS	MOGWO	MOPSO	MOEA/D	MOWOATS	MOGWO	MOPSO	MOEA/D
Average	0.002318	0.1144	0.1370	0.1871	0.002213	0.0582	0.0604	0.1223
Median	0.002299	0.113	0.1317	0.1828	0.0021	0.0577	0.0483	0.1201
STD	0.0001827	0.0195	0.0441	0.0507	0.0004524	0.0073	0.0276	0.0107
Worst	0.002549	0.1577	0.2278	0.2464	0.003084	0.0732	0.1305	0.14369
Best	0.00212	0.0802	0.0899	0.1265	0.001783	0.0498	0.0369	0.1048
	UF3(bi-objective)				UF4(bi-objective)
IGD	MOWOATS	MOGWO	MOPSO	MOEA/D	MOWOATS	MOGWO	MOPSO	MOEA/D
Average	0.009766	0.2556	0.3139	0.2886	0.001829	0.0586	0.1363	0.0681
Median	0.009917	0.2509	0.3080	0.2892	0.001828	0.0586	0.1343	0.0684
STD	0.0004257	0.0807	0.0447	0.0159	4.0192 × 10${}^{-\mathbf{5}}$	0.0004	0.0073	0.0021
Worst	0.01021	0.3678	0.3773	0.3129	0.001894	0.0593	0.1518	0.0703
Best	0.009194	0.1295	0.2564	0.2634	0.001781	0.0579	0.1273	0.0646
	UF5(bi-objective)				UF6(bi-objective)
IGD	MOWOATS	MOGWO	MOPSO	MOEA/D	MOWOATS	MOGWO	MOPSO	MOEA/D
Average	0.07289	0.7970	2.2023	1.2914	0.01039	0.2793	0.6475	0.6881
Median	0.08149	0.6994	2.1257	1.3376	0.0106	0.2443	0.5507	0.6984
STD	0.03034	0.3785	0.5530	0.1348	0.001497	0.1044	0.2661	0.0553
Worst	0.09776	1.7385	3.0383	1.4674	0.01175	0.5504	1.2428	0.7401
Best	0.01682	0.4679	1.4647	1.1230	0.007643	0.1934	0.3793	0.5524
	UF7(bi-objective)				UF8(tri-objective)
IGD	MOWOATS	MOGWO	MOPSO	MOEA/D	MOWOATS	MOGWO	MOPSO	MOEA/D
Average	0.002116	0.1603	0.3539	0.4552	0.003607	2.0577	0.5367	NA
Median	0.002123	0.0734	0.3873	0.4377	0.003225	2.3359	0.5364	NA
STD	0.0001523	0.1391	0.2044	0.1898	0.0008838	1.1455	0.1825	NA
Worst	0.002331	0.4014	0.6151	0.677	0.005344	3.8789	0.7964	NA
Best	0.001889	0.0628	0.054	0.029	0.003021	0.4613	0.2453	NA
	UF9(tri-objective)				UF10(tri-objective)
IGD	MOWOATS	MOGWO	MOPSO	MOEA/D	MOWOATS	MOGWO	MOPSO	MOEA/D
Average	0.001473	0.1917	0.4885	NA	0.005116	3.5945	1.6372	NA
Median	0.001406	0.166	0.4145	NA	0.005558	2.8255	1.5916	NA
STD	0.0002609	0.0925	0.1445	NA	0.0008621	3.4882	0.2988	NA
Worst	0.001814	0.4479	0.7221	NA	0.005628	12.9564	2.1622	NA
Best	0.001133	0.1291	0.3336	NA	0.003464	$1.0431\times 4$	1.22008	NA

presents the average, median, standard deviation, worst, and best IGD values computed from 30 independent runs. Results in Table 2 show the superiority of MOWOATS over those competitor algorithms for the whole set of test functions, consistently. It reaches high convergence rates to the true PF for all the functions, and the low values of the standard deviation of the results are a consequence of the stability of the algorithm.

Next, a comparison among MOWOATS, the cultural MOQPSO, and other modified EAs [24] is presented in

Table 3. Mean of IGD values for MOWOATS, Cultural MOQPSO, and some population-based algorithms over CEC2009 test problems.

	UF1	UF2	UF3	UF4	UF5	UF6	UF7	UF8	UF9	UF10
GDE3	5.34 × 10${}^{-2}$	1.20 × 10${}^{-2}$	1.06 × 10${}^{-1}$	2.65 × 10${}^{-2}$	3.93 × 10${}^{-2}$	2.51 × 10${}^{-1}$	2.52 × 10${}^{-2}$	2.49 × 10${}^{-1}$	8.25 × 10${}^{-2}$	4.33 × 10${}^{-1}$
MOEADGM	6.20 × 10${}^{-3}$	6.40 × 10${}^{-3}$	4.90 × 10${}^{-2}$	4.76 × 10${}^{-2}$	1.79	5.56 × 10${}^{-1}$	7.60 × 10${}^{-3}$	2.45 × 10${}^{-1}$	1.88 × 10${}^{-1}$	5.65 × 10${}^{-1}$
MTS	6.46 × 10${}^{-3}$	6.15 × 10${}^{-3}$	5.31 × 10${}^{-2}$	2.36 × 10${}^{-2}$	1.49 × 10${}^{-2}$	5.92 × 10${}^{-2}$	4.08 × 10${}^{-2}$	1.13 × 10${}^{-1}$	1.14 × 10${}^{-1}$	5.53 × 10${}^{-1}$
DMOEA-DD	1.04 × 10${}^{-2}$	6.79 × 10${}^{-3}$	3.34 × 10${}^{-2}$	4.27 × 10${}^{-2}$	3.15 × 10${}^{-1}$	6.67 × 10${}^{-2}$	1.03 × 10${}^{-2}$	6.84 × 10${}^{-2}$	4.90 × 10${}^{-2}$	3.22 × 10${}^{-1}$
NSGA-II-LS	1.15 × 10${}^{-2}$	1.24 × 10${}^{-2}$	1.06 × 10${}^{-1}$	5.84 × 10${}^{-2}$	5.66 × 10${}^{-1}$	3.10 × 10${}^{-1}$	2.13 × 10${}^{-2}$	8.63 × 10${}^{-2}$	7.19 × 10${}^{-2}$	8.45 × 10${}^{-1}$
OWMOsaDE	1.22 × 10${}^{-2}$	8.10 × 10${}^{-3}$	1.03 × 10${}^{-1}$	5.13 × 10${}^{-2}$	4.30 × 10${}^{-1}$	1.92 × 10${}^{-1}$	5.85 × 10${}^{-2}$	9.45 × 10${}^{-2}$	9.83 × 10${}^{-2}$	7.43 × 10${}^{-1}$
Clustering MOEA	2.99 × 10${}^{-2}$	2.28 × 10${}^{-2}$	5.49 × 10${}^{-2}$	5.85 × 10${}^{-2}$	2.47 × 10${}^{-1}$	8.71 × 10${}^{-2}$	2.23 × 10${}^{-1}$	2.38 × 10${}^{-1}$	2.93 × 10${}^{-1}$	4.11 × 10${}^{-1}$
AMGA	3.59 × 10${}^{-2}$	1.62 × 10${}^{-2}$	7.00 × 10${}^{-2}$	4.06 × 10${}^{-2}$	9.41 × 10${}^{-2}$	1.29 × 10${}^{-1}$	5.71 × 10${}^{-2}$	1.71 × 10${}^{-1}$	1.89 × 10${}^{-1}$	3.24 × 10${}^{-1}$
MOEP	5.96 × 10${}^{-2}$	1.89 × 10${}^{-2}$	9.90 × 10${}^{-2}$	4.27 × 10${}^{-2}$	2.25 × 10${}^{-1}$	1.03 × 10${}^{-1}$	1.97 × 10${}^{-2}$	4.23 × 10${}^{-1}$	3.42 × 10${}^{-1}$	3.62 × 10${}^{-1}$
OMOEA-II	8.56 × 10${}^{-2}$	3.06 × 10${}^{-2}$	2.71 × 10${}^{-1}$	4.62 × 10${}^{-2}$	1.69 × 10${}^{-1}$	7.34 × 10${}^{-2}$	3.35 × 10${}^{-2}$	1.92 × 10${}^{-1}$	2.32 × 10${}^{-1}$	6.28 × 10${}^{-1}$
Cultural	1.11 × 10${}^{-2}$	2.15 × 10${}^{-2}$	3.75 × 10${}^{-2}$	5.98 × 10${}^{-2}$	1.23 × 10${}^{-1}$	1.66 × 10${}^{-1}$	1.13 × 10${}^{-2}$	1.18 × 10${}^{-1}$	1.16 × 10${}^{-1}$	8.29 × 10${}^{-1}$
MOQPSO
MOWOATS	2.32 × 10${}^{-\mathbf{3}}$	2.21 × 10${}^{-\mathbf{3}}$	9.77 × 10${}^{-\mathbf{3}}$	1.83 × 10${}^{-\mathbf{3}}$	7.29 × 10${}^{-2}$	1.04 × 10${}^{-\mathbf{2}}$	2.12 × 10${}^{-\mathbf{3}}$	3.61 × 10${}^{-\mathbf{3}}$	1.47 × 10${}^{-\mathbf{3}}$	5.12 × 10${}^{-\mathbf{3}}$

and

Table 4. Mean of IGD values for MOWOATS, Cultural MOQPSO, and some population-based algorithms over (ZDT, DTLZ) test problems.

	F1(ZDT1)	F2(ZDT2)	F3(ZDT3)	F4(ZDT4)	F5(ZDT6)	F6(DTLZ1)	F7(DTLZ2)	F8(DTLZ4)
Sigma MOPSO	6.07 × 10${}^{-1}$	5.00 × 10${}^{-1}$	5.50 × 10${}^{-1}$	2.64 × 10${}^1$	2.88 × 10${}^{-3}$	2.23 × 10${}^1$	2.84 × 10${}^{-1}$	7.49 × 10${}^{-1}$
Cluster MOPSO	9.03 × 10${}^{-3}$	9.19 × 10${}^{-2}$	2.92 × 10${}^{-1}$	9.89	6.24 × 10${}^{-3}$	1.39	1.43 × 10${}^{-1}$	8.93 × 10${}^{-1}$
MOPSO-CD	1.30 × 10${}^{-1}$	6.60 × 10${}^{-3}$	3.07 × 10${}^{-1}$	1.53 × 10${}^1$	2.93 × 10${}^{-3}$	2.80	9.86 × 10${}^{-2}$	6.18 × 10${}^{-1}$
MOQPSO	2.17 × 10${}^{-2}$	4.25 × 10${}^{-2}$	1.87 × 10${}^{-1}$	8.81	3.92 × 10${}^{-1}$	1.38 × 10${}^1$	6.94 × 10${}^{-2}$	1.02 × 10${}^{-1}$
Preference-order	6.94 × 10${}^{-3}$	4.75 × 10${}^{-1}$	1.90 × 10${}^{-1}$	2.08	5.86 × 10${}^{-3}$	1.39 × 10${}^1$	2.29 × 10${}^{-1}$	2.91 × 10${}^{-1}$
based QPSO
Cultural	6.13 × 10${}^{-3}$	4.87 × 10${}^{-3}$	1.89 × 10${}^{-1}$	5.26 × 10${}^{-3}$	5.38 × 10${}^{-3}$	4.70 × 10${}^{-2}$	6.51 × 10${}^{-2}$	6.70 × 10${}^{-2}$
MOQPSO
MOWOATS	1.30 × 10${}^{-\mathbf{3}}$	7.32 × 10${}^{-\mathbf{4}}$	2.87 × 10${}^{-\mathbf{3}}$	2.85 × 10${}^{-\mathbf{4}}$	8.92 × 10${}^{-\mathbf{4}}$	3.76 × 10${}^{-\mathbf{4}}$	9.73 × 10${}^{-\mathbf{4}}$	1.28 × 10${}^{-\mathbf{3}}$

for the following benchmark test functions: bi-objective ZDT, tri-objective DTLZ, and CEC2009 test problems. Table 3 and Table 4 report results computed according to IGD Equation (26) [24]. Again, the obtained results in Table 3 show that MOWOATS outperforms the other algorithms for all test functions except $UF5$, where it reaches only the third best result, just behind MTS and GDE3. However, the results are far better for the rest test functions, thus giving strong support to the claim that our algorithm works better for most classes of MOPs. Likewise, results in Table 4 compare MOWOATS to the cultural MOQPSO, and to some EAs according to the IGD metric over bi-objective ZDT [20], and tri-objective DTLZ [20] test functions. For these benchmarks, our algorithm has always produced better IGD indices than the others for every test function.

Figure 2 presents the distribution of the obtained solutions from MOWOATS with respect to the true PF points for some DTLZ test functions. The figure shows the symmetry of the obtained solutions with respect to the true PF solutions. It also presents the diversity of the obtained solutions over the whole solution space. This corroborates the low IGD values obtained by MOWOATS. Figure 3 presents a depiction of the solutions obtained from MOWOATS with respect to the true PF solutions for some ZDT test functions. The figure shows the symmetry of the obtained solutions with respect to the true PF solutions, too, and it also clarifies the coverage of obtained solutions across the whole solution space.

We also conducted a specific comparison of our algorithm with Archive-guided memory to MPSO (AgMOPSO) [14] just to see the performance gains achievable over an algorithm that, as with AgMOPSO, applies decomposition of the original problem into subproblems to search the solution space of a MOP.

The results (IGD metric) are listed in

Table 5. Mean of IGD values for MOWOATS, AgMOPSO, and some population-based algorithms over (ZDT, DTLZ) test problems, averaged for 30 different runs.

Problem		MOWOATS	AgMOPSO	MMOPSO	${\mathit{D}}^2$MOPSO	EAG-MOEA/D	NSGA-II
ZDT1	mean	1.303 × 10${}^{-\mathbf{3}}$	3.701 × 10${}^{-3}$	3.936 × 10${}^{-3}$	1.038 × 10${}^{-2}$	3.757 × 10${}^{-3}$	4.976 × 10${}^{-3}$
	std	7.450 × 10${}^{-4}$	2.83 × 10${}^{-\mathbf{5}}$	3.4.56 × 10${}^{-5}$	6.07 × 10${}^{-3}$	1.02 × 10${}^{-4}$	1.73 × 10${}^{-4}$
ZDT2	mean	7.318 × 10${}^{-\mathbf{4}}$	3.828 × 10${}^{-3}$	2.414 × 10${}^{-2}$	4.904 × 10${}^{-1}$	2.113 × 10${}^{-2}$	5.102 × 10${}^{-3}$
	std	2.955 × 10${}^{-4}$	3.15 × 10${}^{-\mathbf{5}}$	1.11 × 10${}^{-1}$	2.45 × 10${}^{-1}$	8.19 × 10${}^{-2}$	1.79 × 10${}^{-4}$
ZDT3	mean	2.872 × 10${}^{-\mathbf{3}}$	4.367 × 10${}^{-3}$	4.413 × 10${}^{-3}$	1.404 × 10${}^{-2}$	3.142 × 10${}^{-2}$	6.408 × 10${}^{-3}$
	std	2.691 × 10${}^{-3}$	5.23 × 10${}^{-5}$	4.28 × 10${}^{-\mathbf{5}}$	4.34 × 10${}^{-3}$	3.73 × 10${}^{-2}$	5.41 × 10${}^{-3}$
ZDT4	mean	2.850 × 10${}^{-\mathbf{4}}$	7.942 × 10${}^{-3}$	2.342 × 10${}^{-2}$	3.203	2.357 × 10${}^{-2}$	7.654 × 10${}^{-3}$
	std	7.729 × 10${}^{-\mathbf{5}}$	2.23 × 10${}^{-2}$	4.42 × 10${}^{-2}$	2.06	3.18 × 10${}^{-2}$	2.45 × 10${}^{-3}$
ZDT6	mean	8.922 × 10${}^{-\mathbf{4}}$	2.997 × 10${}^{-3}$	3.635 × 10${}^{-3}$	1.423 × 10${}^{-2}$	3.132 × 10${}^{-3}$	9.088 × 10${}^{-3}$
	std	3.476 × 10${}^{-4}$	9.51 × 10${}^{-\mathbf{5}}$	2.31 × 10${}^{-4}$	8.14 × 10${}^{-3}$	2.13 × 10${}^{-4}$	1.00 × 10${}^{-3}$
DTLZ1	mean	3.760 × 10${}^{-\mathbf{4}}$	2.183 × 10${}^{-2}$	2.754 × 10${}^{-2}$	1.515	2.582 × 10${}^{-2}$	2.544 × 10${}^{-2}$
	std	2.735 × 10${}^{-\mathbf{5}}$	1.229 × 10${}^{-4}$	2.56 × 10${}^{-2}$	2.22	3.14 × 10${}^{-3}$	3.02 × 10${}^{-3}$
DTLZ2	mean	9.731 × 10${}^{-\mathbf{4}}$	5.133 × 10${}^{-2}$	6.354 × 10${}^{-2}$	6.078 × 10${}^{-2}$	5.93 × 10${}^{-2}$	6.725 × 10${}^{-2}$
	std	7.122 × 10${}^{-\mathbf{5}}$	2.50 × 10${}^{-4}$	1.82 × 10${}^{-3}$	1.53 × 10${}^{-3}$	1.73 × 10${}^{-3}$	2.74 × 10${}^{-3}$
DTLZ3	mean	2.242 × 10${}^{-\mathbf{3}}$	3.619 × 10${}^{-1}$	1.929	4.505 × 10${}^1$	1.505 × 10${}^{-1}$	1.525 × 10${}^{-1}$
	std	6.181 × 10${}^{-\mathbf{4}}$	5.79 × 10${}^{-1}$	1.61	2.49 × 10${}^1$	1.78 × 10${}^{-1}$	2.52 × 10${}^{-1}$
DTLZ4	mean	1.286 × 10${}^{-\mathbf{3}}$	3.304 × 10${}^{-2}$	6.325 × 10${}^{-2}$	6.261 × 10${}^{-2}$	1.872 × 10${}^{-1}$	6.181 × 10${}^{-2}$
	std	1.325 × 10${}^{-\mathbf{4}}$	4.63 × 10${}^{-4}$	4.55 × 10${}^{-3}$	3.36 × 10${}^{-3}$	1.47 × 10${}^{-1}$	6.24 × 10${}^{-3}$
DTLZ5	mean	4.365 × 10${}^{-\mathbf{5}}$	3.868 × 10${}^{-3}$	3.825 × 10${}^{-3}$	6.072 × 10${}^{-3}$	3.876 × 10${}^{-3}$	5.217 × 10${}^{-3}$
	std	1.507 × 10${}^{-\mathbf{5}}$	8.12 × 10${}^{-5}$	9.45 × 10${}^{-5}$	1.12 × 10${}^{-3}$	8.97 × 10${}^{-5}$	2.69 × 10${}^{-4}$
DTLZ6	mean	1.858 × 10${}^{-\mathbf{4}}$	3.670 × 10${}^{-3}$	3.756 × 10${}^{-3}$	1.392 × 10${}^{-2}$	3.730 × 10${}^{-3}$	1.733 × 10${}^{-2}$
	std	1.400 × 10${}^{-4}$	1.653 × 10${}^{-4}$	1.57 × 10${}^{-4}$	2.06 × 10${}^{-3}$	1.05 × 10${}^{-\mathbf{4}}$	1.38 × 10${}^{-2}$
DTLZ7	mean	2.751 × 10${}^{-\mathbf{3}}$	7.712 × 10${}^{-2}$	3.756 × 10${}^{-3}$	8.312 × 10${}^{-2}$	4.100 × 10${}^{-1}$	7.405 × 10${}^{-2}$
	std	6.663 × 10${}^{-4}$	4.40 × 10${}^{-3}$	1.57 × 10${}^{-\mathbf{4}}$	5.29 × 10${}^{-3}$	2.49 × 10${}^{-1}$	3.00 × 10${}^{-3}$

for the comparison of MOWOATS against AgMOPSO, MMOPSO, $D^2$MOPSO, and EAG-MOEA/D, obtained from 30 independent runs [14]. These experiments were performed on tri-objective DTLZ and CEC2009 benchmark test functions.

Here, the results show once again that MOWOATS achieves the best mean and standard deviation values for all test functions except (ZDT1, ZDT2, ZDT3, ZDT6, DTLZ6, and DTLZ7) test functions. The second-best standard deviation values are attained by our algorithm for ZDT2 and DTLZ6, and the third best results for ZDT3 and ZDT6. While not uniformly better, these results indicate that even when it is not the best, MOWOATS yields results with comparable quality to the best SI-based algorithms proposed in the literature, and that its variability across the different MOPs is small.

Another feature which strains the quality of solutions computed by a MOP solver occurs when the PF exhibits an irregular shape. There have been some works in the literature that address this issue in particular, such as the Clustering-based Adaptive Multi-Objective EA (CA-MOEA) by Hua et al. [34], who suggested using a clustering-based method to overcome those problems with irregular PF shapes. The use of clustering helps to diversify the tentative solutions. We also did an experimental comparison of this algorithm and other relatives/variants with the ours. MOWOATS is compared with this method according to IGD metric, computed as [34]:

$$IGD=\frac{{\sum }_{i=1}^{\left|P\right|}d\left(P_i,P^{\ast }\right)}{\left|P\right|},$$

(27)

where P represents the true PF solutions, $P^{\ast }$ stands for the optimal solutions generated from the algorithm, and $\left|P\right|$ is the number of the true PF.

Specifically,

Table 6. A comparison among MOWOATS, CA-MOEA and some multi-objective evolutionary computing methods over ZDT and DTLZ test functions according to IGD criterion.

PF Shape	Problem	Obj.	MOWOATS	CA-MOEA	MOEA/D	EMyO/C	RVEA*	NSGA-II	NSGA-III
Irregular	DTLZ4	3	1.286 × 10${}^{-3}$	5.4805 × 10${}^{-3}$	3.385 × 10${}^{-1}$	5.617 × 10${}^{-2}$	2.942 × 10${}^{-1}$	1.119 × 10${}^{-1}$	1.275 × 10${}^{-1}$
			1.325 × 10${}^{-4}$	6.98 × 10${}^{-4}$	3.14 × 10${}^{-1}$	7.04 × 10${}^{-4}$	2.85 × 10${}^{-1}$	1.96 × 10${}^{-1}$	1.78 × 10${}^{-1}$
	DTLZ5	3	1.834 × 10${}^{-4}$	4.426 × 10${}^{-3}$	3.369 × 10${}^{-2}$	4.583 × 10${}^{-3}$	6.891 × 10${}^{-3}$	5.754 × 10${}^{-3}$	1.267 × 10${}^{-2}$
			1.360 × 10${}^{-4}$	8.96 × 10${}^{-5}$	8.32 × 10${}^{-5}$	6.03 × 10${}^{-5}$	3.91 × 10${}^{-4}$	2.28 × 10${}^{-4}$	1.58 × 10${}^{-3}$
	DTLZ6	3	2.038 × 10${}^{-4}$	4.2269 × 10${}^{-3}$	3.381 × 10${}^{-2}$	4.619 × 10${}^{-3}$	7.146 × 10${}^{-3}$	5.891 × 10${}^{-3}$	1.868 × 10${}^{-2}$
			1.653 × 10${}^{-4}$	4.09 × 10${}^{-5}$	1.74 × 10${}^{-4}$	1.32 × 10${}^{-4}$	5.55 × 10${}^{-4}$	5.11 × 10${}^{-4}$	3.31 × 10${}^{-3}$
	DTLZ7	2	2.751 × 10${}^{-3}$	4.7253 × 10${}^{-3}$	1.631 × 10${}^{-1}$	6.312 × 10${}^{-3}$	4.852 × 10${}^{-2}$	5.324 × 10${}^{-3}$	6.903 × 10${}^{-3}$
			1.663 × 10${}^{-3}$	8.78 × 10${}^{-5}$	2.14 × 10${}^{-1}$	3.47 × 10${}^{-4}$	1.35 × 10${}^{-1}$	2.47 × 10${}^{-4}$	1.21 × 10${}^{-4}$
	DTLZ7	3	6.314 × 10${}^{-2}$	5.8727 × 10${}^{-2}$	1.416 × 10${}^{-1}$	7.861 × 10${}^{-2}$	8.952 × 10${}^{-2}$	1.263 × 10${}^{-1}$	7.546 × 10${}^{-2}$
			5.678 × 10${}^{-3}$	1.41 × 10${}^{-3}$	9.73 × 10${}^{-4}$	6.44 × 10${}^{-2}$	9.04 × 10${}^{-2}$	1.70 × 10${}^{-1}$	2.34 × 10${}^{-3}$
	UF6	2	5.970 × 10${}^{-2}$	1.1464 × 10${}^{-1}$	4.468 × 10${}^{-1}$	1.673 × 10${}^{-1}$	3.052 × 10${}^{-1}$	1.643 × 10${}^{-1}$	1.441 × 10${}^{-1}$
			5.135 × 10${}^{-2}$	9.11 × 10${}^{-2}$	1.51 × 10${}^{-1}$	1.03 × 10${}^{-1}$	1.45 × 10${}^{-1}$	9.00 × 10${}^{-2}$	8.67 × 10${}^{-2}$
	UF9	3	2.885 × 10${}^{-2}$	1.143 × 10${}^{-1}$	2.515 × 10${}^{-1}$	9.055 × 10${}^{-2}$	2.272 × 10${}^{-1}$	2.539 × 10${}^{-1}$	2.016 × 10${}^{-1}$
			2.193 × 10${}^{-2}$	0.0427	1.36 × 10${}^{-2}$	3.52 × 10${}^{-2}$	8.32 × 10${}^{-2}$	1.18 × 10${}^{-1}$	8.25 × 10${}^{-2}$
Regular	DTLZ1	2	2.065 × 10${}^{-5}$	1.8936 × 10${}^{-3}$	1.811 × 10${}^{-3}$	2.057 × 10${}^{-3}$	1.893 × 10${}^{-3}$	2.231 × 10${}^{-3}$	1.800 × 10${}^{-3}$
			5.054 × 10${}^{-6}$	1.80 × 10${}^{-5}$	5.21 × 10${}^{-5}$	7.75 × 10${}^{-5}$	2.76 × 10${}^{-5}$	7.02 × 10${}^{-5}$	2.33 × 10${}^{-5}$
	DTLZ1	3	3.760 × 10${}^{-4}$	2.0269 × 10${}^{-2}$	2.060 × 10${}^{-2}$	2.097 × 10${}^{-2}$	2.119 × 10${}^{-2}$	2.728 × 10${}^{-2}$	2.057 × 10${}^{-2}$
			2.735 × 10${}^{-5}$	1.23 × 10${}^{-4}$	5.06 × 10${}^{-5}$	3.44 × 10${}^{-4}$	2.27 × 10${}^{-4}$	1.34 × 10${}^{-3}$	1.67 × 10${}^{-5}$
	DTLZ2	2	1.244 × 10${}^{-4}$	4.2168 × 10${}^{-3}$	3.966 × 10${}^{-3}$	4.473 × 10${}^{-3}$	4.133 × 10${}^{-3}$	5.032 × 10${}^{-3}$	3.969 × 10${}^{-3}$
			5.449 × 10${}^{-5}$	6.48 × 10${}^{-5}$	2.95 × 10${}^{-7}$	6.54 × 10${}^{-5}$	3.06 × 10${}^{-5}$	1.84 × 10${}^{-4}$	6.95 × 10${}^{-6}$
	DTLZ2	3	9.731 × 10${}^{-4}$	5.3461 × 10${}^{-2}$	5.447 × 10${}^{-2}$	5.640 × 10${}^{-2}$	5.534 × 10${}^{-2}$	6.887 × 10${}^{-2}$	5.448 × 10${}^{-2}$
			7.122 × 10${}^{-5}$	3.21 × 10${}^{-4}$	2.75 × 10${}^{-6}$	5.65 × 10${}^{-4}$	3.65 × 10${}^{-4}$	2.73 × 10${}^{-3}$	1.43 × 10${}^{-5}$
	DTLZ3	2	2.406 × 10${}^{-4}$	4.7153 × 10${}^{-3}$	4.391 × 10${}^{-3}$	4.950 × 10${}^{-3}$	4.345 × 10${}^{-3}$	5.193 × 10${}^{-3}$	4.195 × 10${}^{-3}$
			1.010 × 10${}^{-4}$	4.17 × 10${}^{-4}$	4.61 × 10${}^{-4}$	1.23 × 10${}^{-3}$	2.12 × 10${}^{-4}$	2.63 × 10${}^{-4}$	2.74 × 10${}^{-4}$
	DTLZ3	3	7.847 × 10${}^{-3}$	5.7776 × 10${}^{-2}$	5.487 × 10${}^{-2}$	5.611 × 10${}^{-2}$	5.548 × 10${}^{-2}$	6.836 × 10${}^{-2}$	5.4833 × 10${}^{-2}$
			2.989 × 10${}^{-3}$	4.00 × 10${}^{-3}$	7.43 × 10${}^{-4}$	7.69 × 10${}^{-4}$	5.92 × 10${}^{-4}$	3.97 × 10${}^{-3}$	2.84 × 10${}^{-4}$
	DTLZ4	2	2.374 × 10${}^{-4}$	4.1222 × 10${}^{-3}$	3.362 × 10${}^{-1}$	4.497 × 10${}^{-3}$	7.793 × 10${}^{-2}$	7.879 × 10${}^{-2}$	3.983 × 10${}^{-3}$
			1.531 × 10${}^{-4}$	1.65 × 10${}^{-1}$	3.77 × 10${}^{-1}$	9.98 × 10${}^{-5}$	2.27 × 10${}^{-1}$	2.27 × 10${}^{-1}$	5.48 × 10${}^{-5}$
	DTLZ5	2	6.643 × 10${}^{-4}$	4.2387 × 10${}^{-3}$	3.385 × 10${}^{-3}$	4.461 × 10${}^{-3}$	4.132 × 10${}^{-3}$	5.128 × 10${}^{-3}$	3.968 × 10${}^{-3}$
			2.612 × 10${}^{-4}$	3.08 × 10${}^{-3}$	3.14 × 10${}^{-1}$	9.99 × 10${}^{-5}$	5.18 × 10${}^{-5}$	1.77 × 10${}^{-4}$	1.22 × 10${}^{-6}$
	DTLZ6	2	2.752 × 10${}^{-4}$	4.2160 × 10${}^{-3}$	3.966 × 10${}^{-3}$	4.434 × 10${}^{-3}$	4.060 × 10${}^{-3}$	5.730 × 10${}^{-3}$	3.966 × 10${}^{-3}$
			7.603 × 10${}^{-5}$	2.17 × 10${}^{-5}$	4.66 × 10${}^{-7}$	8.91 × 10${}^{-5}$	3.57 × 10${}^{-5}$	3.08 × 10${}^{-4}$	4.74 × 10${}^{-4}$

contains a comparison among MOWOATS, CA-MOEA, MOEA/D, EMyO/C, RVEA*, NSGA-II, and NSGA-III according to IGD metric computed according to Equation (27) [34]. The results confirm that MOWOATS reaches the lowest mean values of the IGD metric for all test functions, except for DTLZ73, for which it yields the second rank. Therefore, we can confirm that MOWOATS is able to handle MOPs even if they have solutions with quite irregular solution spaces.

Finally, we compare MOWOATS with hybrid variants of SI-based optimizers that use the R2 indicator to assess the quality of the solutions regarding the PF. We chose (R2HMOPSO, $R2$ indicator combined with MOPSO), R2HMOPSO1, MOEA/D, NSGA-II, dMOPSO, and R2MOPSO and, as in previous cases, computed the IGD (27) after solving the problems in the benchmarks ZDT (two objectives) and DTLZ (three-objective functions) [15]. The values appear in

Table 7. IGD statistical results for the ZDT and DTLZ test functions.

Problem		MOWOATS	R2HMOPSO	R2HMOPSO1	MOEA/D	NSGA-II	dMOPSO	R2MOPSO
ZDT1	mean	1.849 × 10${}^{-3}$	3.904 × 10${}^{-3}$	3.943 × 10${}^{-3}$	7.544 × 10${}^{-3}$	4.929 × 10${}^{-3}$	3.899 × 10${}^{-3}$	3.928 × 10${}^{-3}$
	std	2.648 × 10${}^{-3}$	6.209 × 10${}^{-5}$	8.593 × 10${}^{-5}$	8.473 × 10${}^{-4}$	2.043 × 10${}^{-4}$	3.839 × 10${}^{-5}$	1.091 × 10${}^{-4}$
ZDT2	mean	8.951 × 10${}^{-4}$	3.834 × 10${}^{-3}$	2.260 × 10${}^{-1}$	2.503 × 10${}^{-2}$	4.900 × 10${}^{-3}$	6.442 × 10${}^{-2}$	3.825 × 10${}^{-3}$
	std	1.549 × 10${}^{-3}$	4.907 × 10${}^{-6}$	2.969 × 10${}^{-1}$	1.104 × 10${}^{-1}$	2.074 × 10${}^{-4}$	1.849 × 10${}^{-1}$	3.336 × 10${}^{-5}$
ZDT3	mean	5.586 × 10${}^{-3}$	6.123 × 10${}^{-2}$	8.460 × 10${}^{-3}$	1.212 × 10${}^{-2}$	7.254 × 10${}^{-3}$	1.064 × 10${}^{-2}$	1.017 × 10${}^{-2}$
	std	3.631 × 10${}^{-3}$	1.583 × 10${}^{-1}$	6.058 × 10${}^{-4}$	5.585 × 10${}^{-3}$	7.634 × 10${}^{-3}$	7.098 × 10${}^{-4}$	6.508 × 10${}^{-4}$
ZDT4	mean	9.756 × 10${}^{-5}$	4.518 × 10${}^{-3}$	5.093 × 10${}^{-1}$	2.452 × 10${}^{-1}$	8.420 × 10${}^{-3}$	5.972	8.374 × 10${}^{-2}$
	std	4.180 × 10${}^{-5}$	3.733 × 10${}^{-3}$	2.356 × 10${}^{-1}$	1.571 × 10${}^{-1}$	2.731 × 10${}^{-3}$	4.477	9.787 × 10${}^{-2}$
ZDT6	mean	9.519 × 10${}^{-4}$	1.888 × 10${}^{-3}$	1.868 × 10${}^{-3}$	1.892 × 10${}^{-3}$	2.696 × 10${}^{-3}$	1.879 × 10${}^{-3}$	1.865 × 10${}^{-3}$
	std	6.917 × 10${}^{-4}$	4.334 × 10${}^{-5}$	2.227 × 10${}^{-5}$	1.179 × 10${}^{-5}$	4.111 × 10${}^{-5}$	8.549 × 10${}^{-6}$	3.484 × 10${}^{-5}$
DTLZ1	mean	3.760 × 10${}^{-4}$	1.994 × 10${}^{-2}$	1.724	1.842 × 10${}^{-2}$	1.935 × 10${}^{-2}$	1.529 × 10${}^1$	1.745 × 10${}^1$
	std	2.735 × 10${}^{-5}$	2.080 × 10${}^{-3}$	9.906 × 10${}^{-1}$	4.773 × 10${}^{-4}$	6.011 × 10${}^{-4}$	1.180 × 10${}^1$	3.133
DTLZ2	mean	9.731 × 10${}^{-4}$	4.368 × 10${}^{-2}$	5.555 × 10${}^{-2}$	4.597 × 10${}^{-2}$	5.315 × 10${}^{-2}$	4.716 × 10${}^{-2}$	2.250 × 10${}^{-1}$
	std	7.122 × 10${}^{-5}$	1.203 × 10${}^{-3}$	3.302 × 10${}^{-3}$	1.218 × 10${}^{-3}$	2.373 × 10${}^{-3}$	1.489 × 10${}^{-3}$	1.526 × 10${}^{-2}$
DTLZ4	mean	1.286 × 10${}^{-3}$	5.198 × 10${}^{-2}$	2.505 × 10${}^{-1}$	5.160 × 10${}^{-2}$	5.417 × 10${}^{-2}$	1.175 × 10${}^{-1}$	4.343 × 10${}^{-1}$
	std	1.325 × 10${}^{-4}$	2.011 × 10${}^{-3}$	1.262 × 10${}^{-1}$	1.948 × 10${}^{-3}$	1.727 × 10${}^{-3}$	7.627 × 10${}^{-2}$	5.111 × 10${}^{-2}$
DTLZ7	mean	6.314 × 10${}^{-2}$	7.036 × 10${}^{-2}$	6.459 × 10${}^{-2}$	1.271 × 10${}^{-1}$	7.129 × 10${}^{-2}$	1.265 × 10${}^{-1}$	8.729 × 10${}^{-2}$
	std	5.678 × 10${}^{-3}$	8.439 × 10${}^{-3}$	9.521 × 10${}^{-3}$	5.106 × 10${}^{-3}$	5.101 × 10${}^{-2}$	6.728 × 10${}^{-3}$	8.431 × 10${}^{-3}$

. Please note that although R2HMOPSO, for instance, uses R2 indicator to improve the diversity of MOPSO, MOWOATS still gets better results for all test functions. This can be explained by the introduction of the new diversification step and memory elements in guiding swarm members during the search process, confirming that both procedures contribute to the improvement of solutions.

From previous discussion, we can see that MOWOATS revealed its superiority over many enhanced SI methods. This presents the correctness of our analysis for PSO and its rivals regarding their need for mature memory elements. The new diversification technique employed in MOWOATS allowed it to cover the whole solution space. It also enhanced its capability to solve MOPs.

MOWOATS results showed that it can find solutions very near the true PF of test functions. Also, solutions generated from MOWOATS are distributed evenly over the solution space. This presents the superiority of MOWOATS and qualifies it to be used for real-life MOPs, such as bioinformatics, engineering, and manufacturing.

6. Conclusions and Future Work

MOWOATS is a modified hybrid population-based algorithm, useful to solve Multi-Objective Problems (MOPs). It merges the Whale Optimization Algorithm (WOA) with Tabu Search (TS) method, and enhances the diversification capability of WOA by embedding a new diversification step. MOWOATS stores the non-dominated set of solutions in an Elite List to use them in the crossover of swarm members and in guiding how swarm members shift their state. These modifications have experimentally proven themselves to be very efficient in producing high-quality solutions to MOPs. Our results, obtained after extensive tests over diverse benchmark sets, show that MOWOATS attains more accurate results than many other evolutionary and SI-based methods. We also have observed a fast convergence to the true Pareto front solutions, and checked that the distribution of solutions generated from MOWOATS is highly concentrated around its mean. Overall MOWOATS seems to be a good computational procedure to solve complex MOPs. In the future, we intend to extend it to solve multi-objective real-life Big Data problems by adapting it and running it over computing clusters.