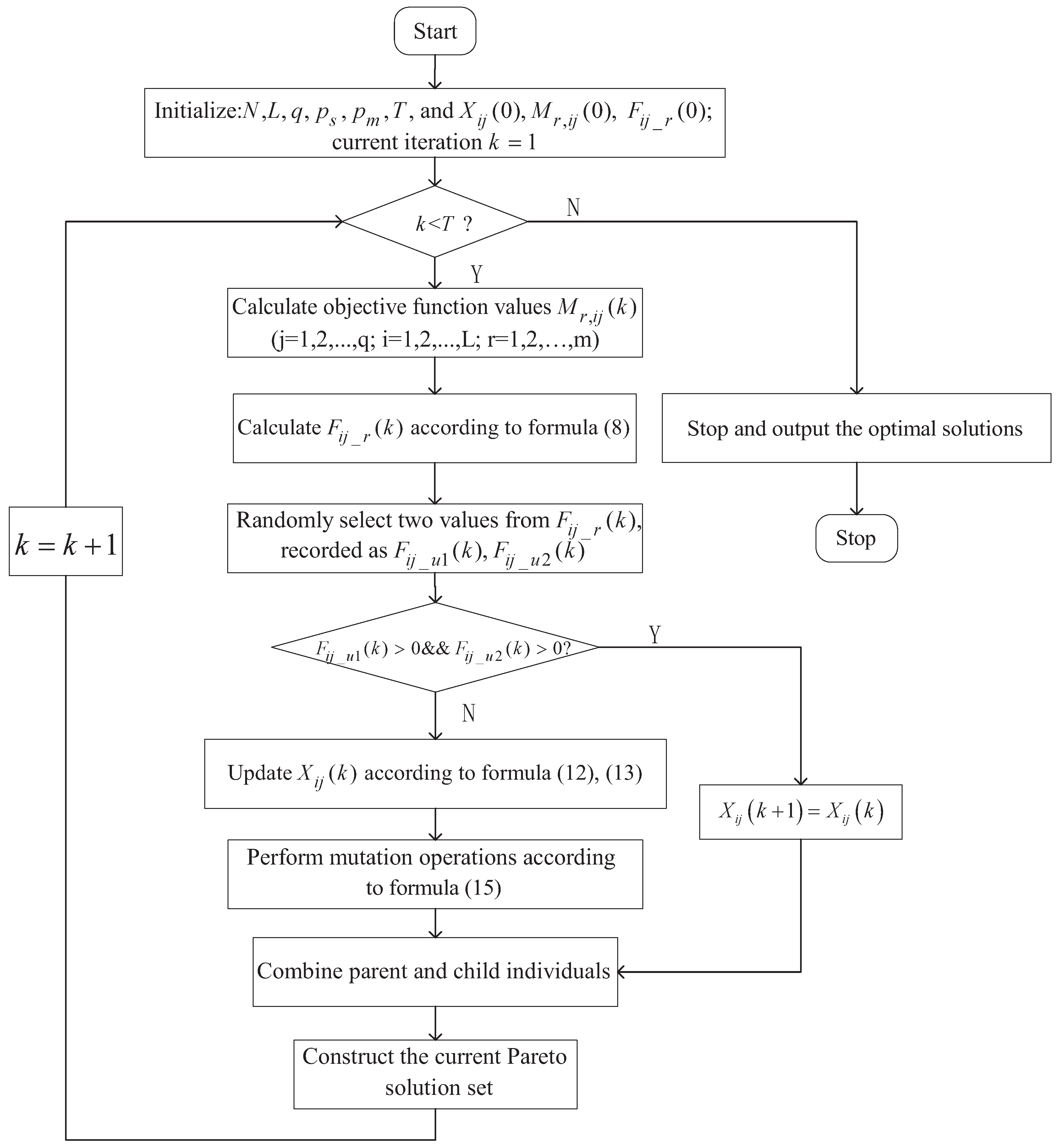
In this section, we first compare the parameters of the proposed MOFECO algorithm, including number of cycles
q and number of elements
L in each cycle, update condition
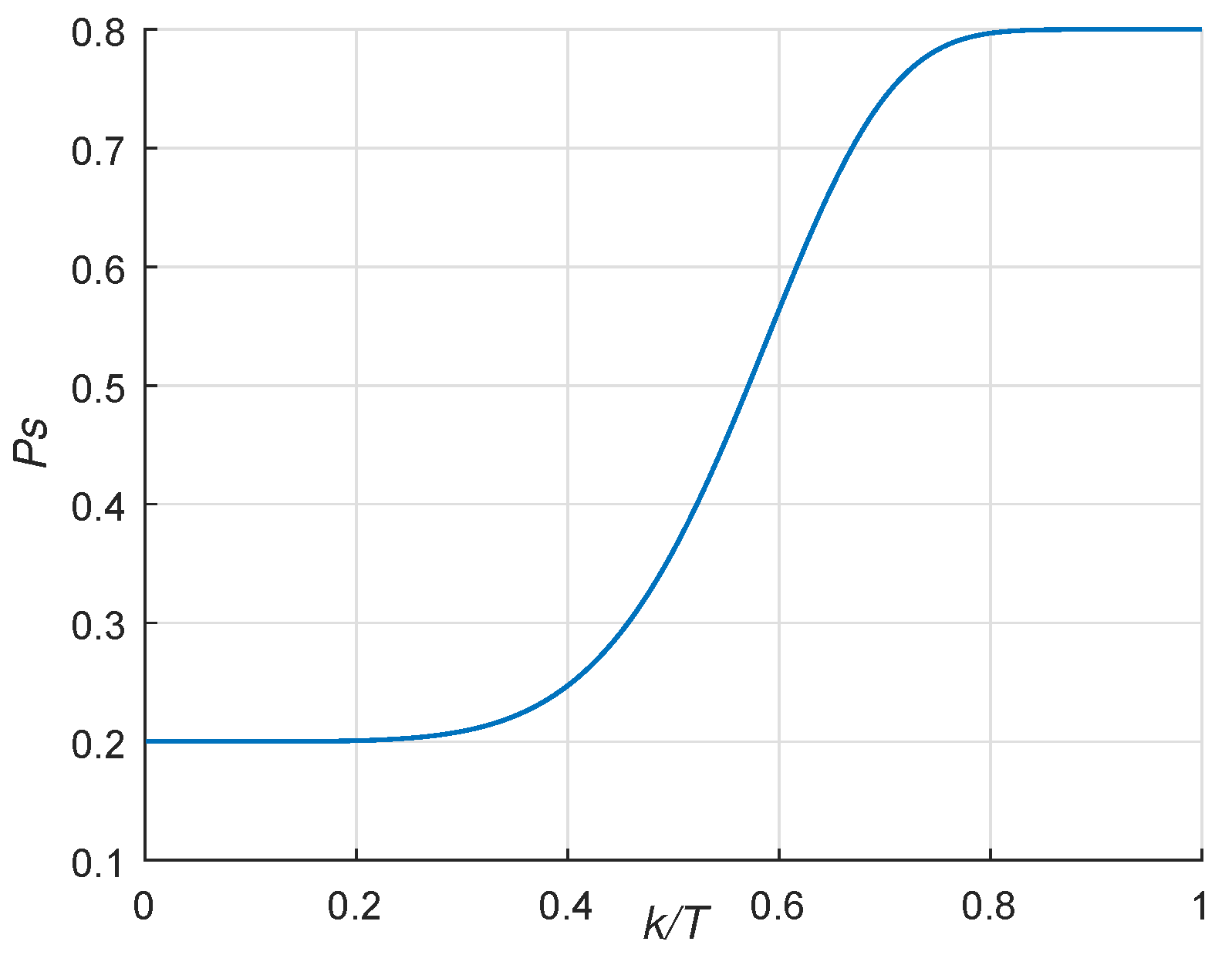
, the local-global probability
and the mutation methods. Secondly, we analyze the performance of MOFECO by empirically comparing it with three classic MOEAs, namely, NSGA-II [
5], MOPSO [
12], PESA-II [
11] and the two latest algorithms KnEA [
2] and NSLS [
15]. The experiments were performed on 15 test problems, which were taken from four widely used test benchmarks suites the Zitzler et al’s Test suite (ZDT) [
37], the Deb et al’s Test suite (DTLZ) [
38], the Walking Fish Group (WFG) [
39] and the Many objective Function (MaF) [
40]. Among them, the ZDT series are bi-objective functions and the DTLZ series are tri-objective functions and we set the MaF and WFG series as four-objective functions. In terms of experimental configuration, all the implementations are done on a 2.39 GHz Intel(R) Xeon(R) CPU with 32 GB RAM under Microsoft Window 10. MOFECO has been implemented in MATLAB R2016a and for the NSGA-II, MOPSO, PESA-II, KnEA and NSLS, the programs are derived from the platEMO provided by the literature [
41].
5.2. Performance Metrics
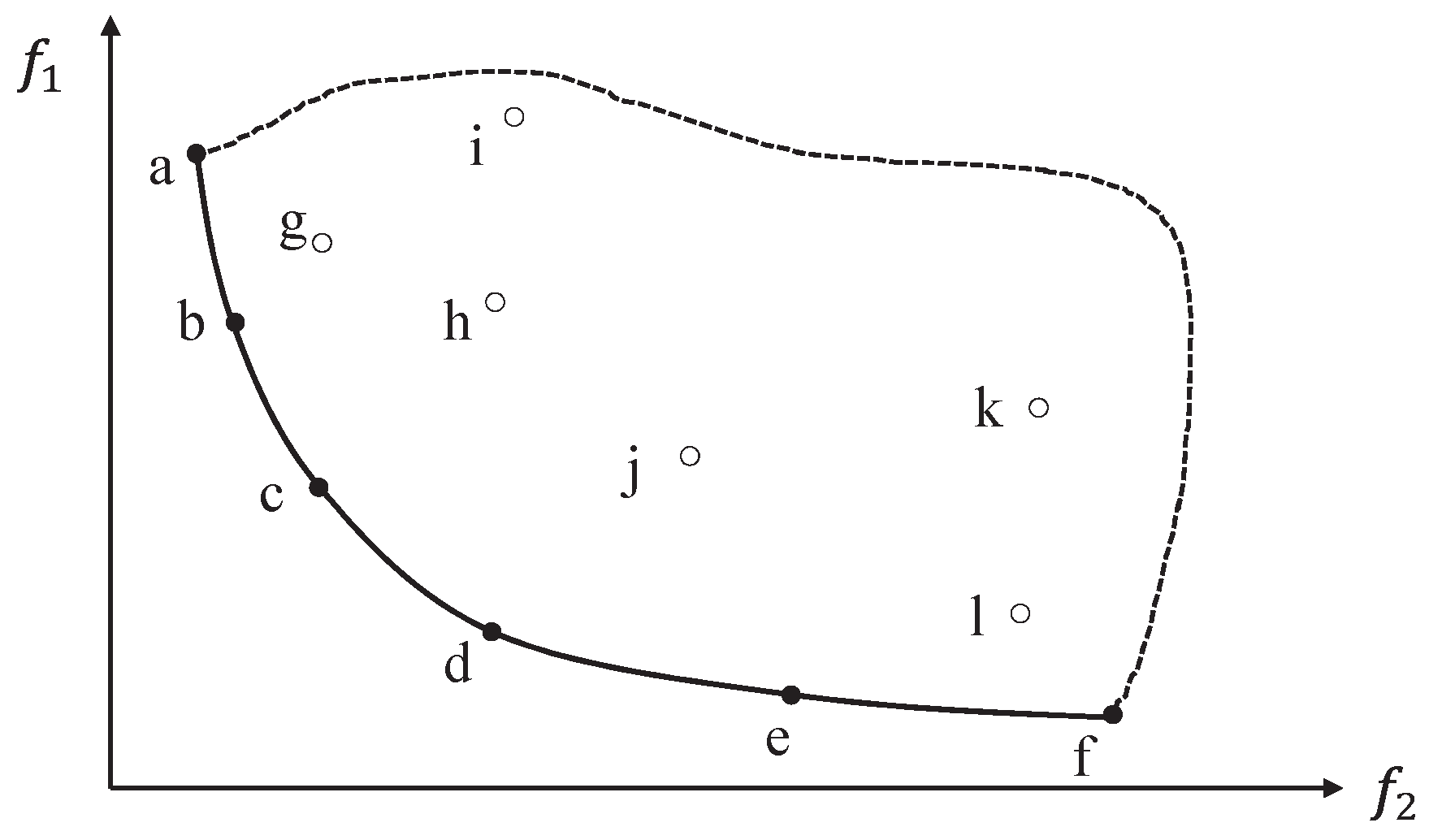
Performance metrics are often used to measure the effectiveness of an algorithm for MOO problems. As we know, the basic aim of multi-objective optimization is to obtain a Pareto set with better convergence, distribution and diversity of the Pareto set. According to whether the performance metrics can measure the convergence, the diversity or both of a solution set, they can be divided into three categories [
42], and the following part describes some commonly used performance metrics of the three categories. Here we suppose the true Pareto optimal front is known as
.
(1) Generational Distance (
):
is used to evaluate the convergence of a solution set, the concept of
was proposed by Veldhuizen and Lamont [
43]. It measures the distance between the obtained non-dominated front
P and the true Pareto set
as:
where
represents the minimum Euclidean distance between the obtained solution
and the solutions in
, and
is the number of the obtained optimal solutions.
measures how far these non-dominated solutions
X are from those in the true Pareto optimal front
. The smaller the
value, the closer the Pareto solution set is to the real Pareto frontier and the better convergence the solution set has. If
, the solution set is on the real Pareto front, which is the most ideal situation.
(2) Spacing metric (
): The spatial evaluation method
[
44] proposed by Schott is used to evaluate the distribution of individuals in the objective space. The function is defined as follows:
where
is the average of all
and
represents the size of Pareto solutions. A smaller value of
demonstrates a better distribution of the obtained solution set. Here,
when the algorithm obtained optimal solutions which are completely evenly distributed in the target space.
(3) Spread indicator (
): Wang et al. [
42] proposed the spread metric
, which is used for independently evaluating the breadth and the spread of the non-dominated solutions.
can be defined mathematically as:
where
P is optimal solution set,
m represents the number of objectives,
are
m extreme solutions, which belongs to the set of true Pareto front. As can be seen, a smaller
means the optimal solution set has a better spread.
(4) Pure diversity (
):
is used for measuring the diversity of species, it is defined as follows [
45]:
where
Here, represents the dissimilarity d from one species to a community X. The larger the value, the better the diversity of the solution set.
(5) Hypervolume (
):
indicator [
46] has become a popular evaluation index because of its good theoretical support. It evaluates the comprehensive performance of MOEAs by calculating the hypervolume value of the space enclosed by the non-dominated solution set and the reference point. The calculation formula is:
where
represents the Lebesgue measure,
represents the hypervolume formed by the reference point and the non-dominated individual and
P represents the optimal solution set. Note that a larger
denotes a better performance of the algorithm.
(6) Inverted Generational Distance (
): The
[
47] is defined as:
where
denotes the uniformly distributed true solutions along the Pareto front.
P represents an approximation to the Pareto front.
denotes the minimum Euclidean distance between the solution
X and the solutions in
P. we can see that the smaller the
value is, the better convergence and diversity of the Pareto optimal set has.
5.4. Comparison with Other Optimization Algorithms
In this section, the performances of MOFECO were verified by empirically comparing it with three classic MOEAs NSGA-II [
5], MOPSO [
12], PESA-II [
11], and two latest algorithms KnEA [
2] and NSLS [
15]. For a fair-minded comparison, we adopt the consistent parameters of population size
and termination condition
for all the six algorithms. The other parameters of MOFECO are shown in
Table 2. For the other parameters used in NSGA-II, MOPSO, PESA-II, KnEA and NSLS, they are consistent with the parameters in their original study [
2,
5,
11,
12,
15]. The detailed parameters configuration for the five compared algorithms are shown in
Table 15.
In the EAreal operator, is the probability of implementing crossover operation, is the expectation of polynomial mutation, represents the distribution index of simulated binary crossover, and represent the distribution index of polynomial mutation. In PESA-II, is the number of divisions in each objective. In KnEA, represents the rate of knee points in the population. In MOPSO, represents the weight factor, and in the NSLS operator, the is the mean value of the Gaussian distribution and is the standard deviation of the Gaussian distribution.
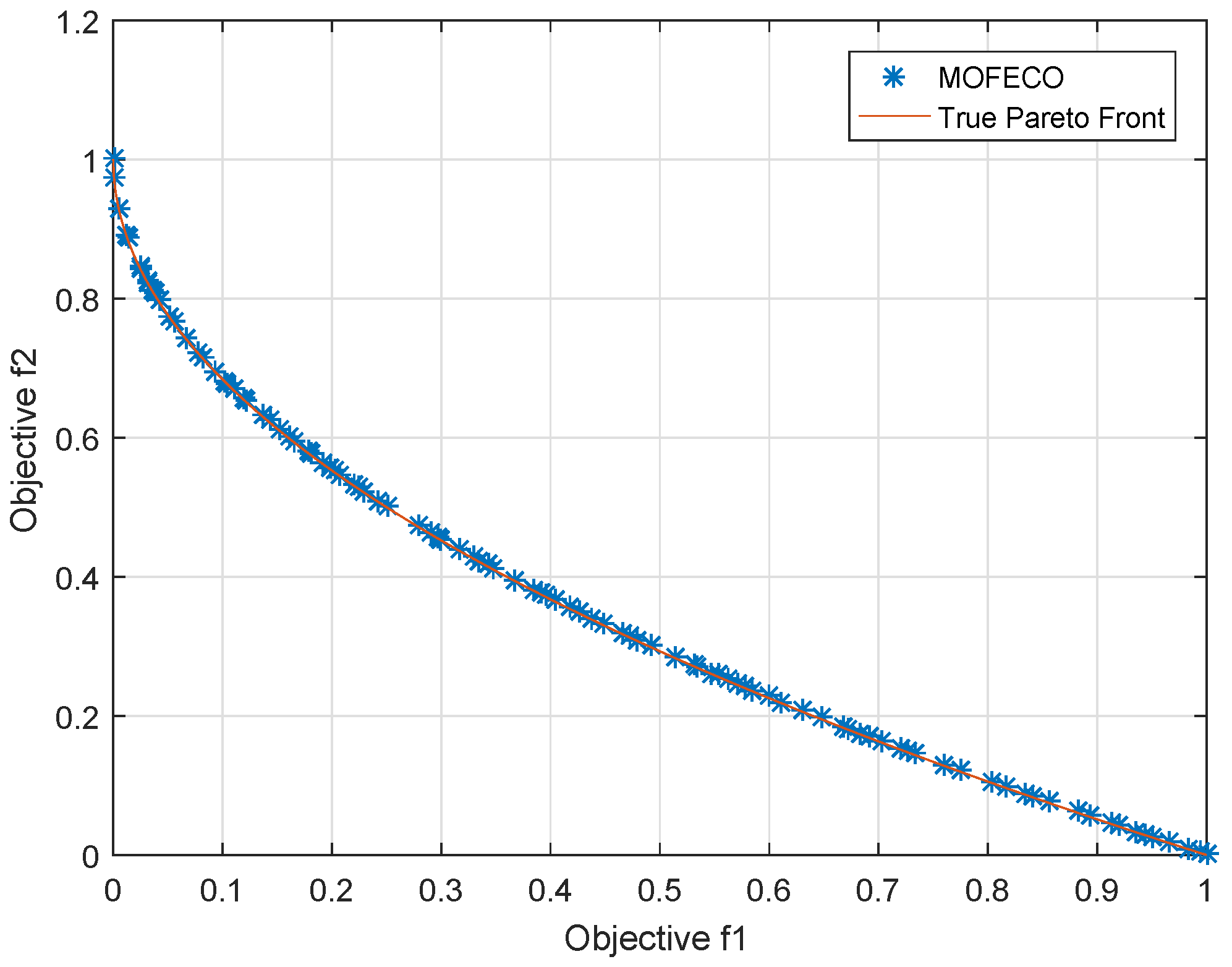
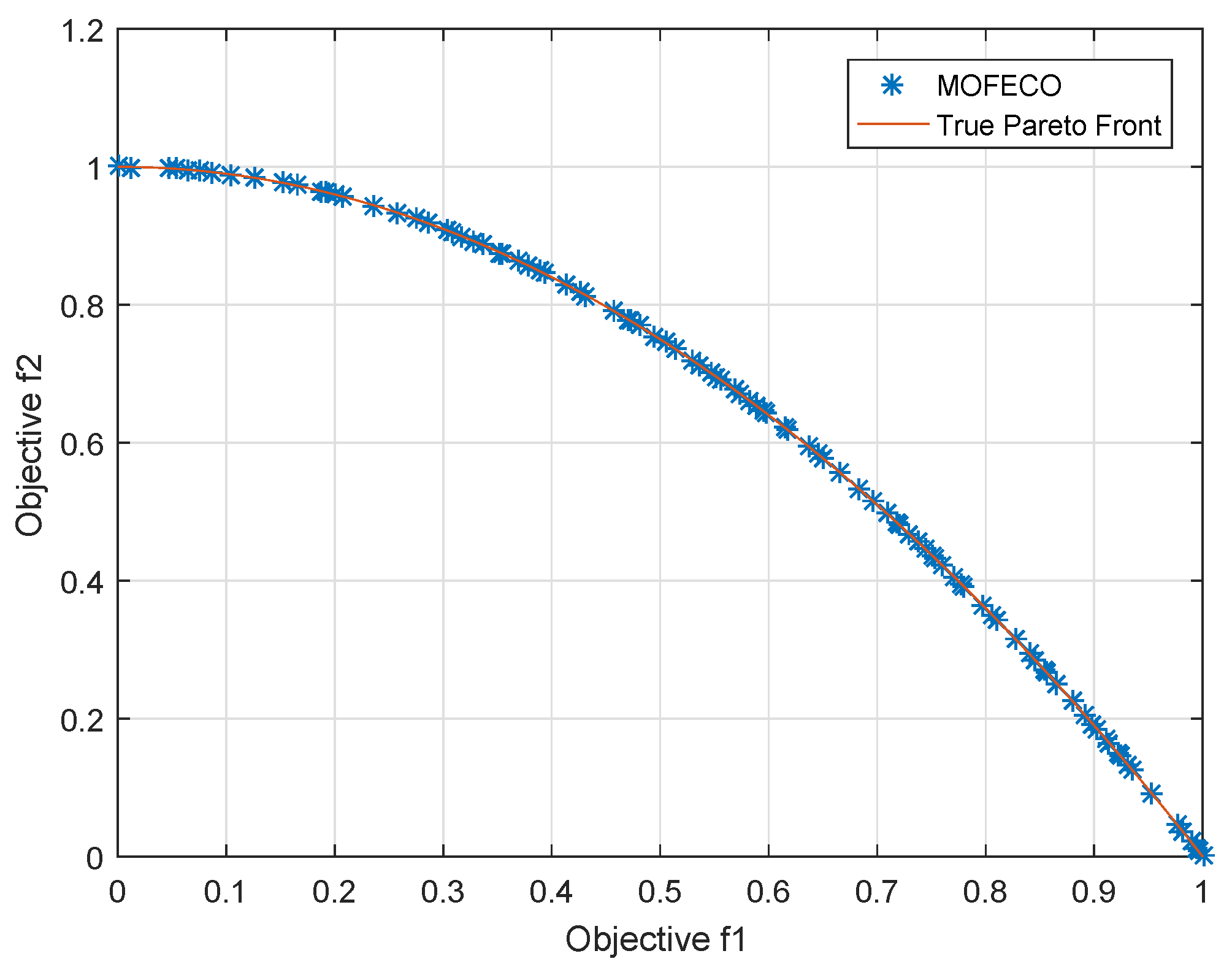
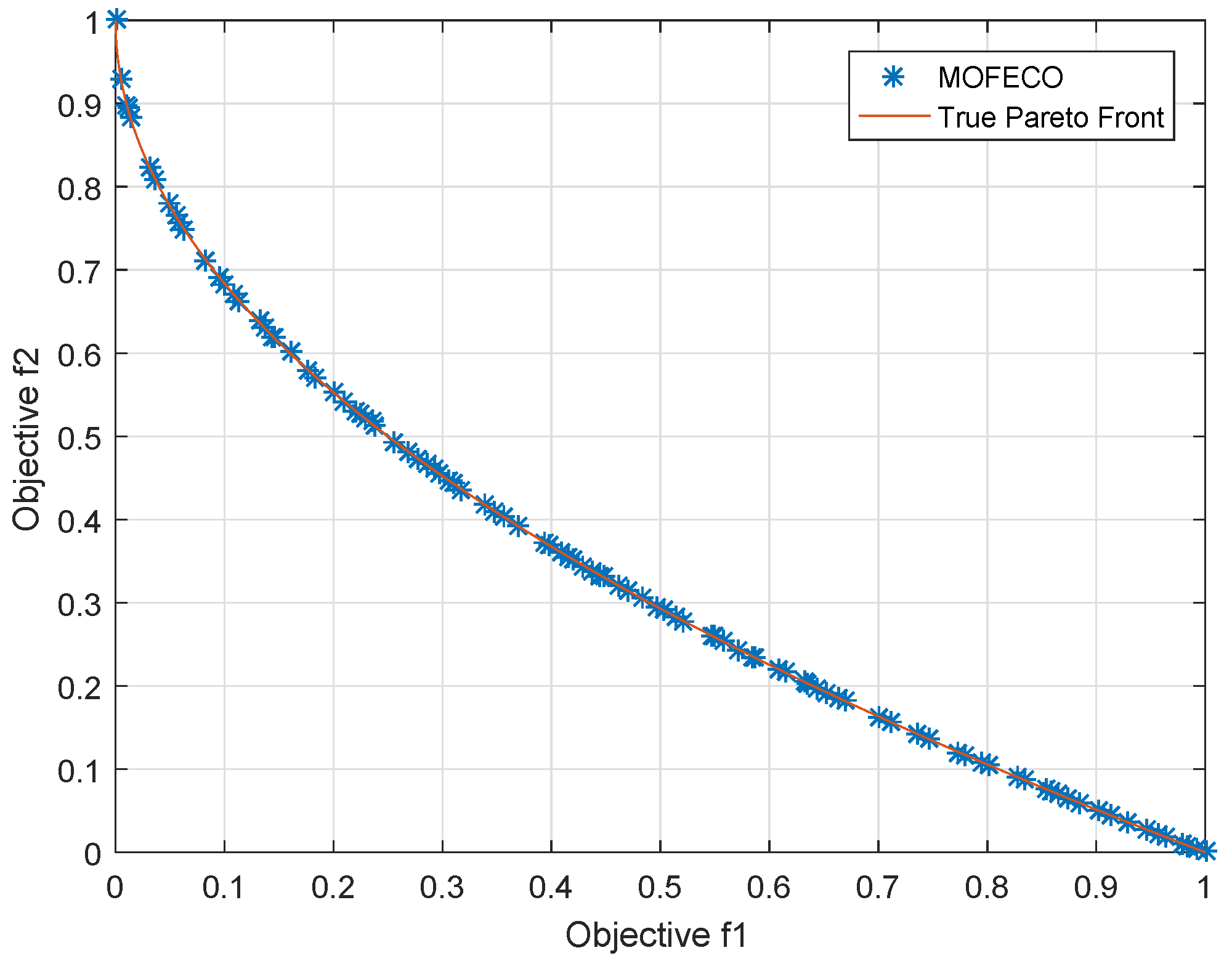
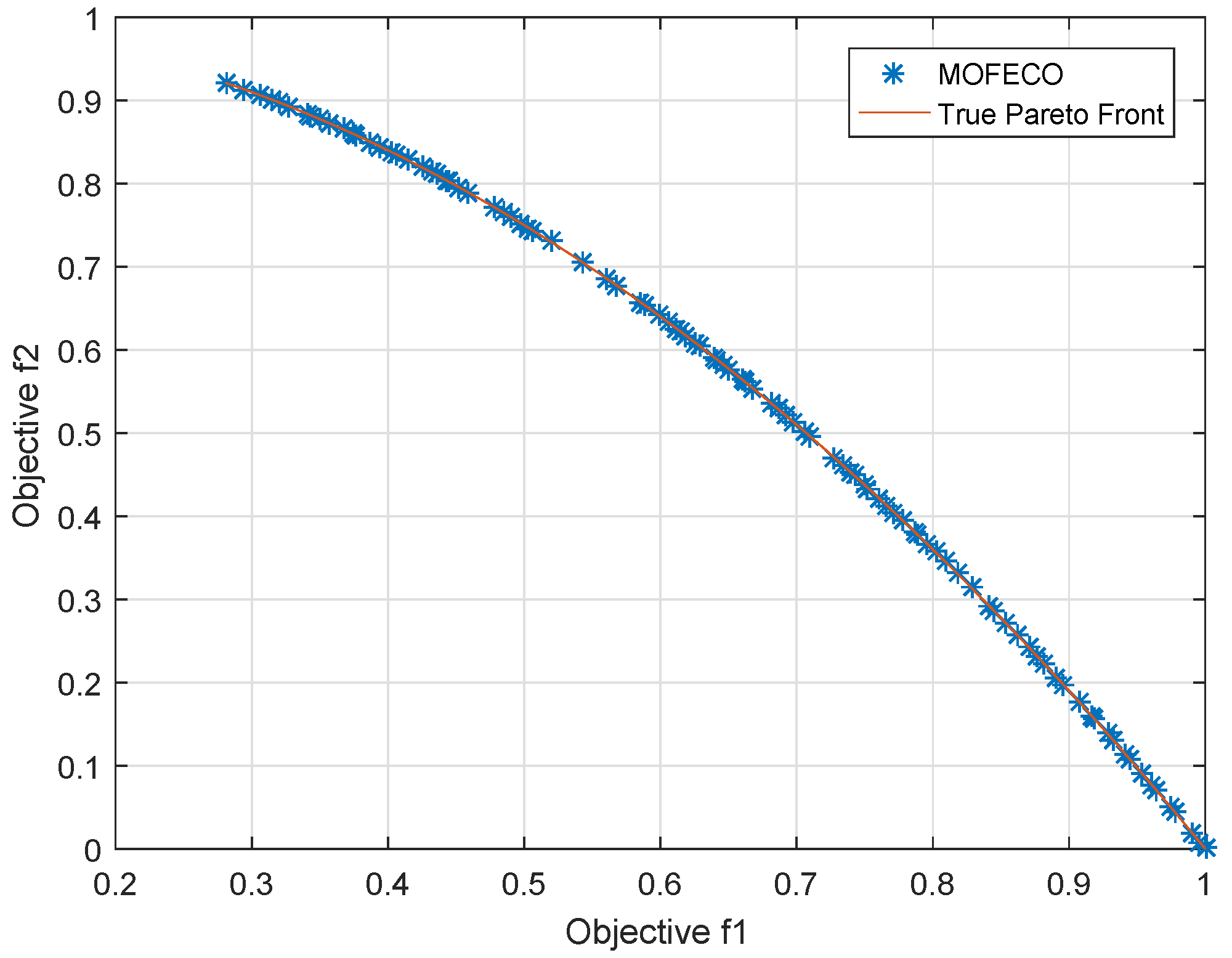
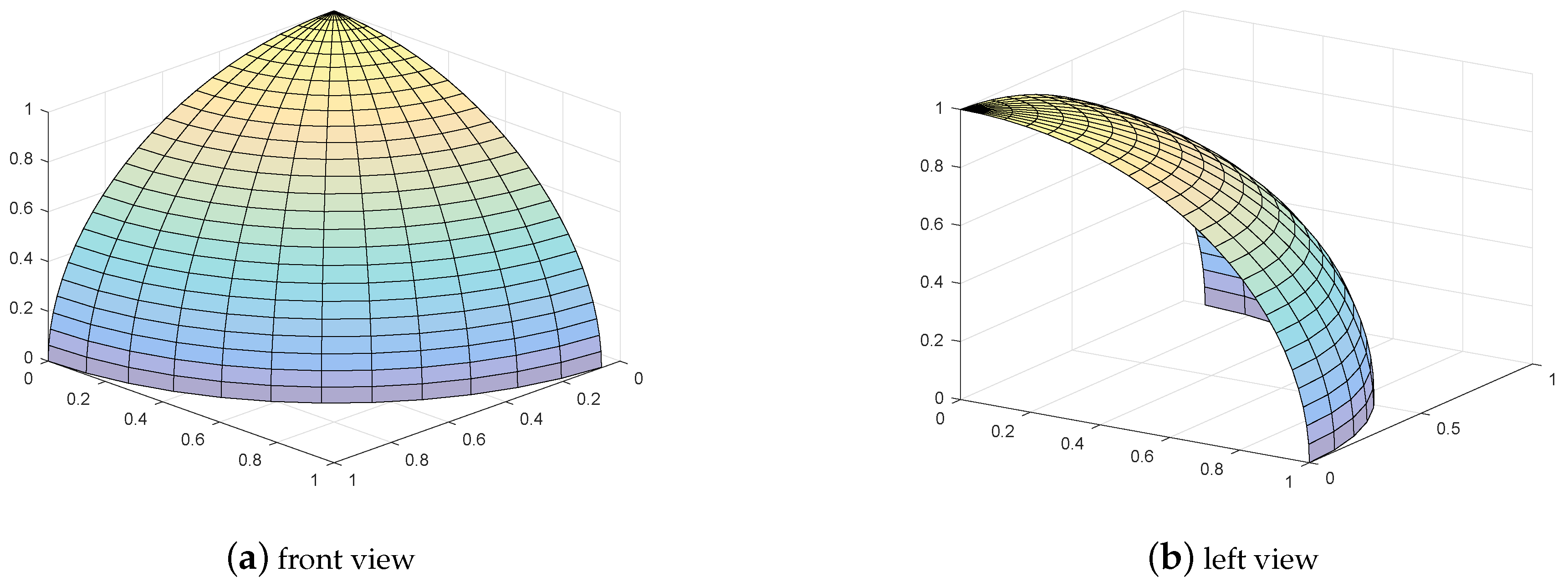
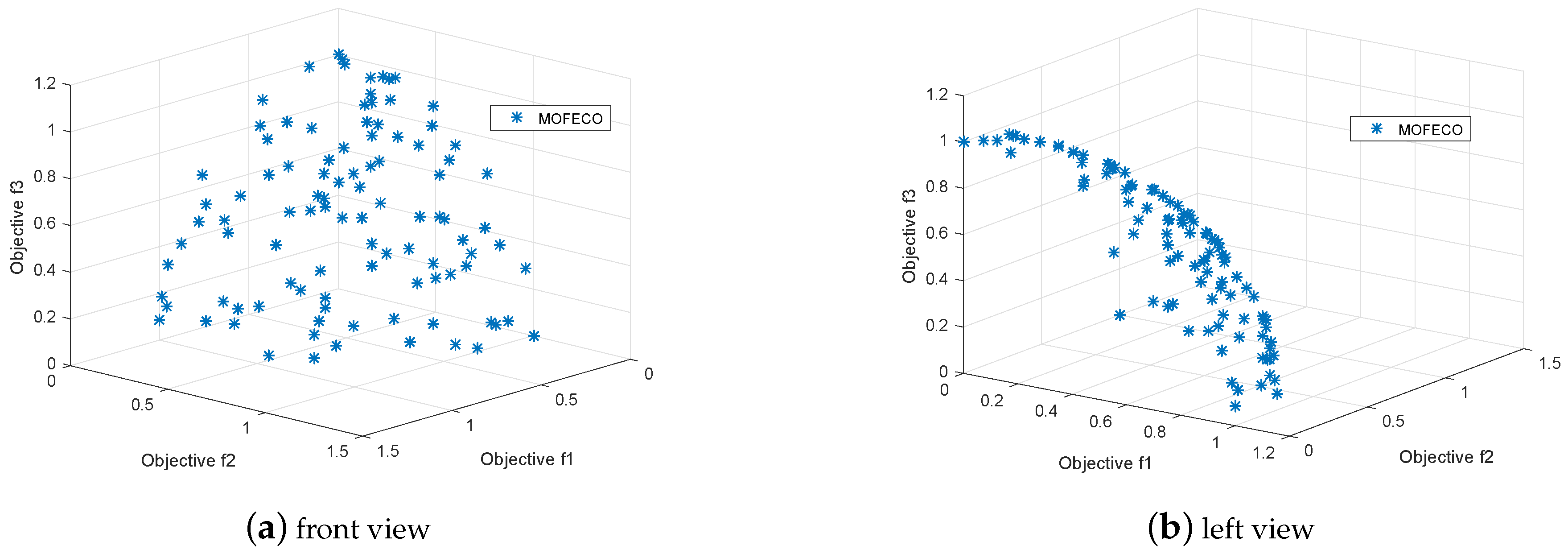
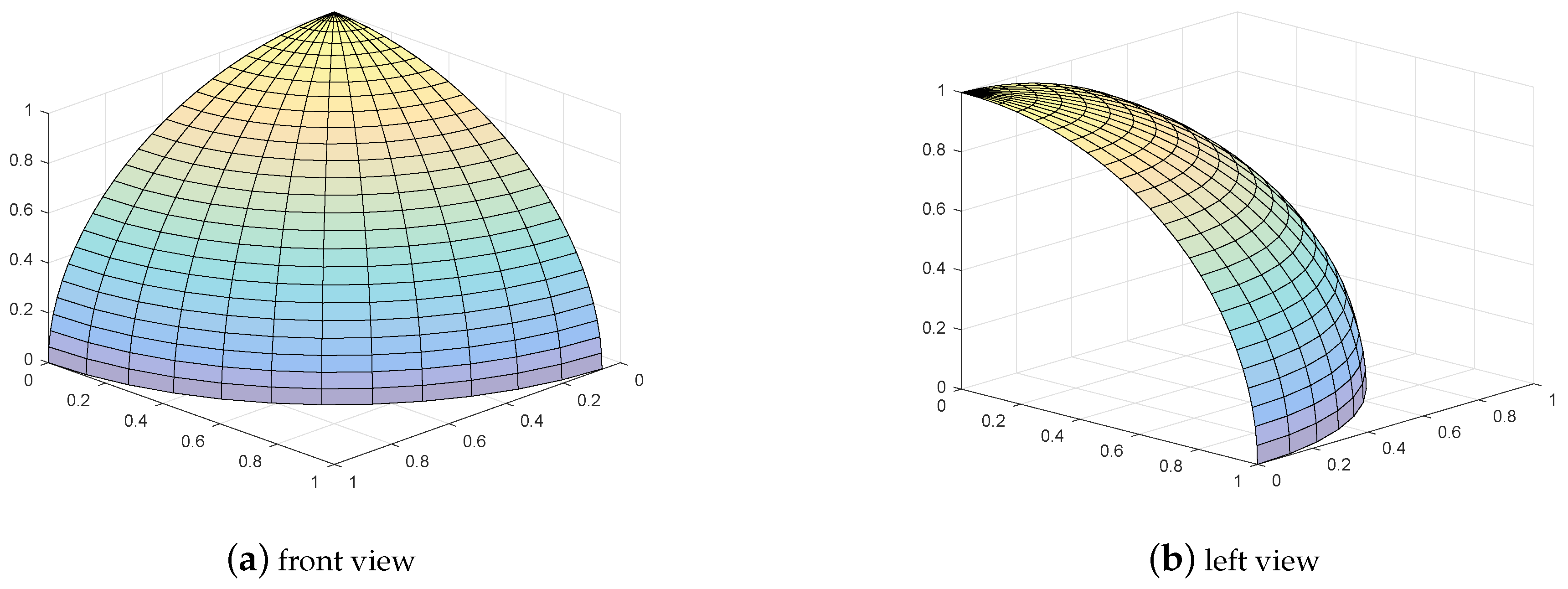
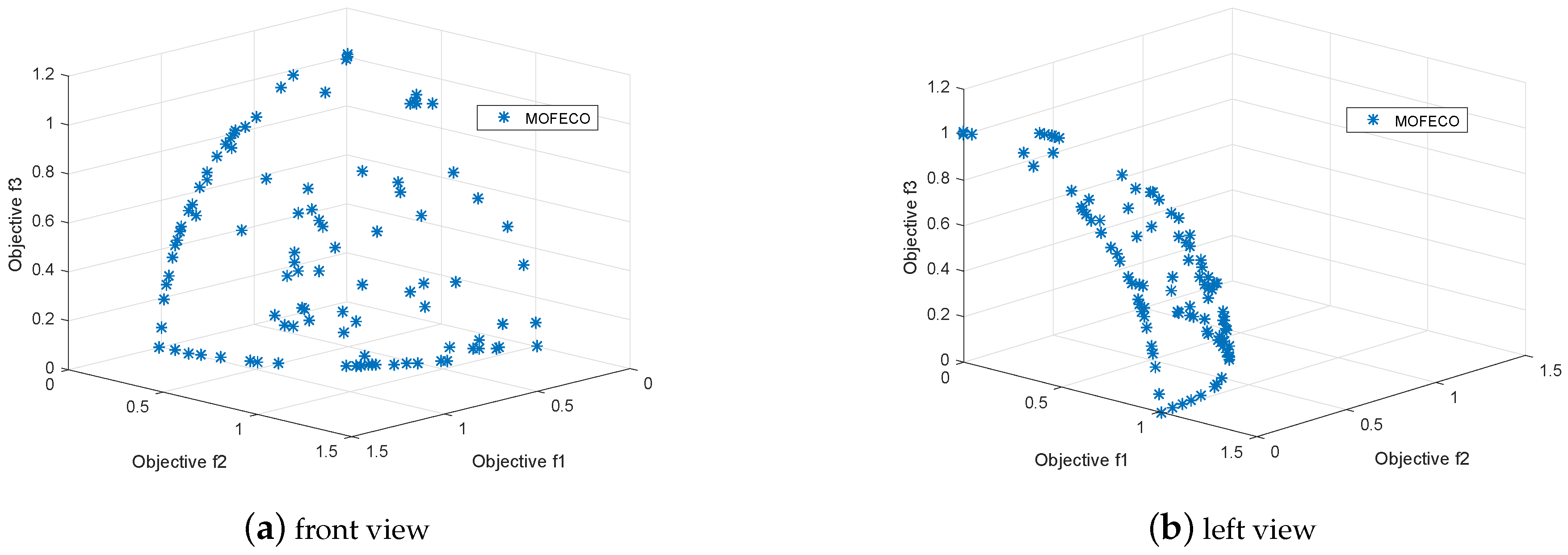
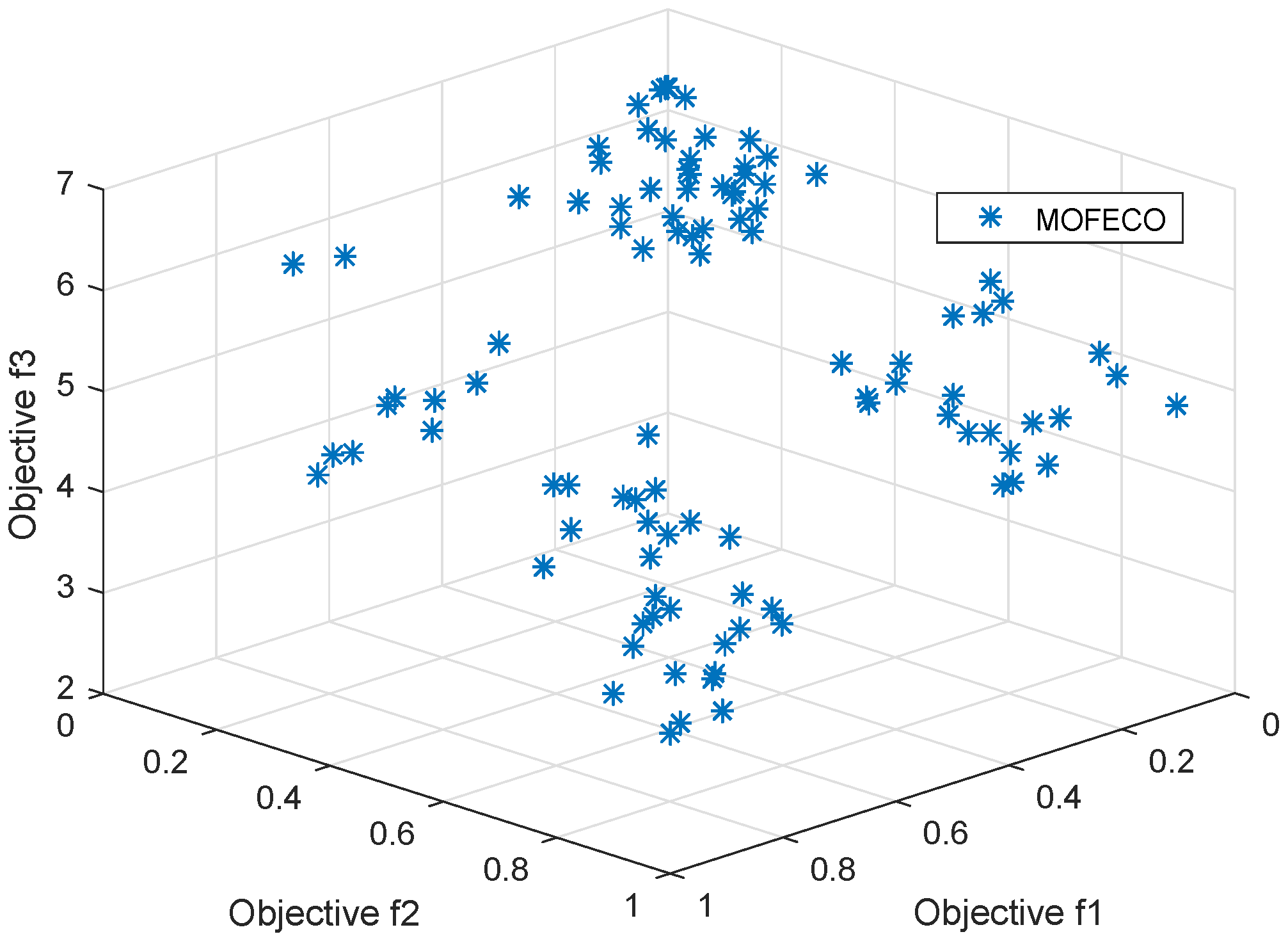
We use the proposed MOFECO algorithm to optimize 15 test functions selected from the ZDT, DTLZ, MaF and WFG series in the aforementioned environment, and the obtained Pareto front by MOFECO and the true Pareto front are shown in
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12,
Figure 13,
Figure 14,
Figure 15,
Figure 16,
Figure 17,
Figure 18,
Figure 19,
Figure 20,
Figure 21,
Figure 22,
Figure 23,
Figure 24,
Figure 25,
Figure 26,
Figure 27,
Figure 28 and
Figure 29.
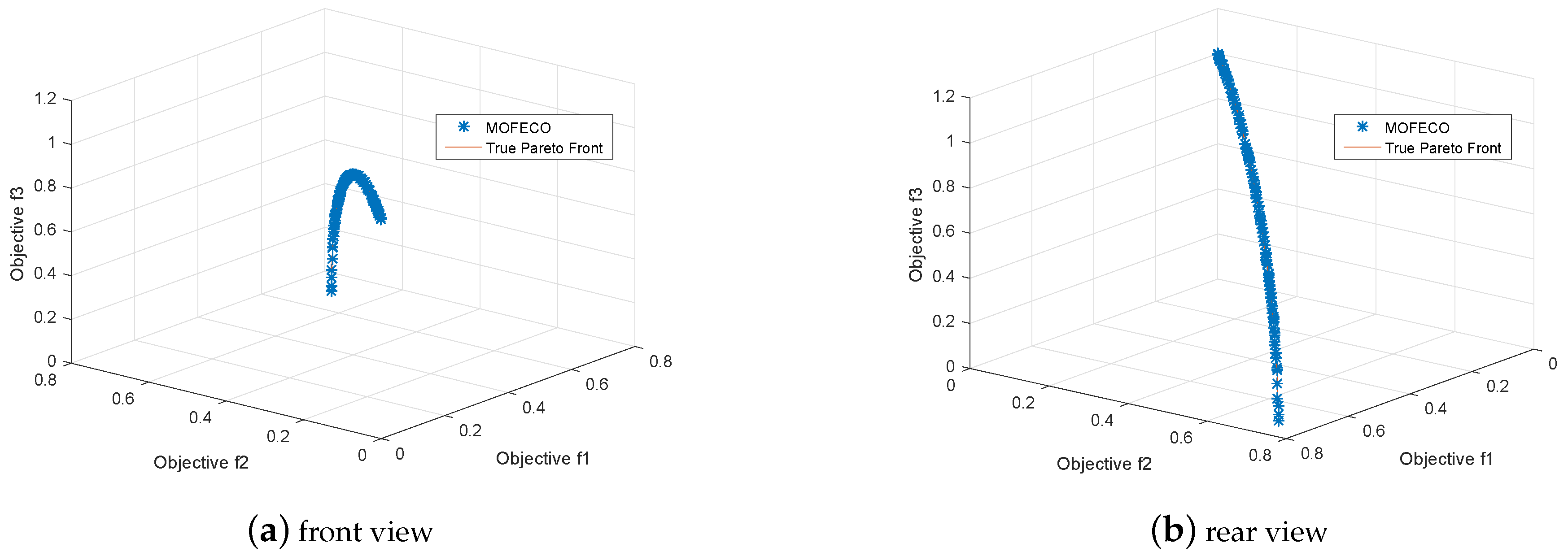
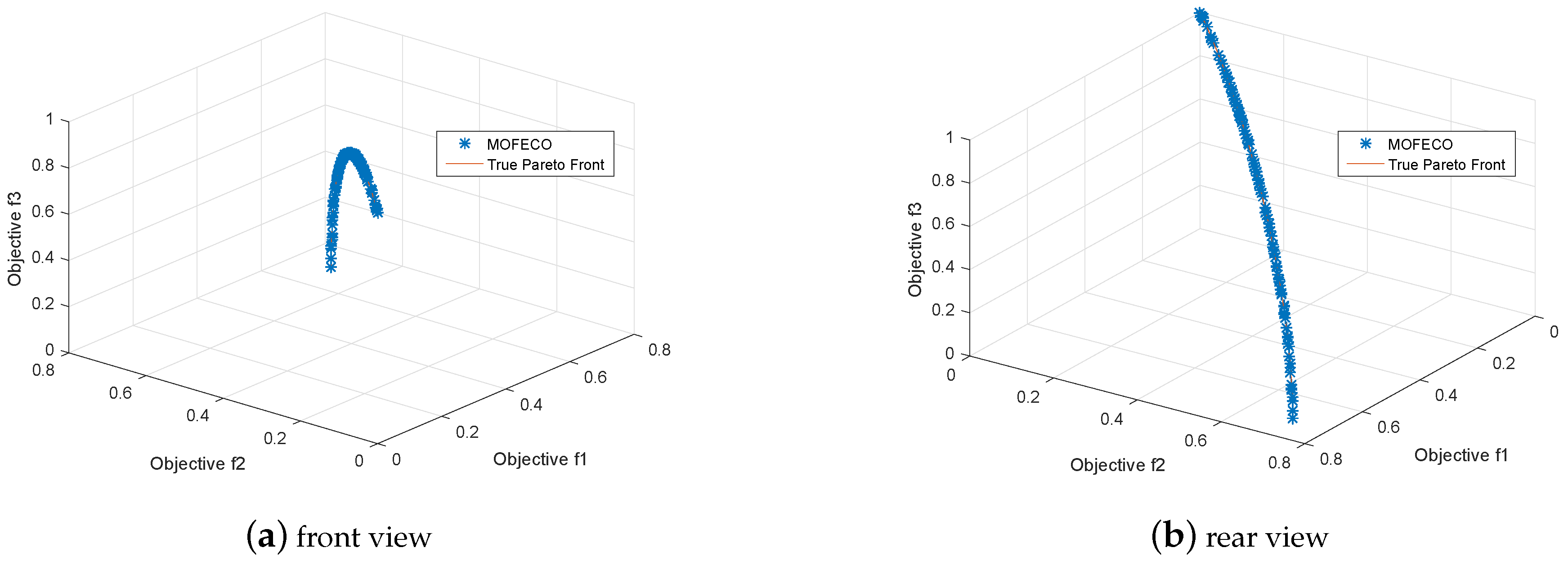
Figure 10 and
Figure 12 shows the true Pareto front of the test function DTLZ2 and DTLZ4, and each of the plots from
Figure 10,
Figure 11,
Figure 12,
Figure 13,
Figure 14 and
Figure 15 has two subgraphs, respectively representing the front and left or rear view of the optimized Pareto front in problems DTLZ2, DTLZ4, DTLZ5 and DTLZ6.
From
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10,
Figure 11,
Figure 12,
Figure 13,
Figure 14,
Figure 15,
Figure 16,
Figure 17,
Figure 18,
Figure 19,
Figure 20,
Figure 21,
Figure 22,
Figure 23,
Figure 24,
Figure 25,
Figure 26,
Figure 27,
Figure 28 and
Figure 29, we can see that the obtained Pareto front by using the proposed MOFECO can evenly distribute on the true Pareto front, which shows that the algorithm can converge to the optimal solution set and is effective in solving MOO problems.
For quantitative analysis,
Table 16,
Table 17,
Table 18,
Table 19 and
Table 20 show the results of convergence (
), diversity (
), comprehensive performance (
) and distribution (
,
) on different test functions by using MOFECO and the other five MOEAs, where “+” means that the MOFECO is better than the comparison algorithms; “-” denotes that the MOFECO algorithm is inferior to the comparison algorithms, and “∼” means that the MOFECO algorithm is similar to the comparison algorithms. At the end of each table, the number of test functions obtained by MOFECO which are better than, inferior to, and equal to the comparison algorithms are listed. In order to eliminate the effects of various random factors on the experimental results, all algorithms run independently for 30 times on each test problem and the average results are recorded.
The
values are used to measure the convergence of a Pareto solution set. From the
Table 16, it can be seen that the proposed MOFECO performed well on ZDT, DTLZ, MaF and WFG test problems. In terms of
indicator, the proposed MOFECO is better than NSGA-II, MOPSO, PESA-II, KnEA and NSLS on more than 10 test functions among the 15 test functions. Specifically, among the four ZDT test problems, MOFECO can achieve the smallest
values on the ZDT test problems except for ZDT1 compared with other algorithms. Among the five DTLZ test problems, MOFECO can achieve the smallest
values on DTLZ2, DTLZ5 and DTLZ6 compared with NSGA-II, MOPSO, PESA-II and KnEA, while MOFECO does not work well on DTLZ4 and DTLZ7. Among the three MaF and three WFG test problems, MOFECO can achieve the smallest
values on all the MaF test problems, and the smallest
values on MaF2 and MaF12. These experimental results indicate that MOFECO is competitive in solving ZDT, DTLZ, WFG and MaF test problems with better convergence.
The
values are used to measure the diversity of the Pareto solution set. Generally speaking, large
values represent good diversity of solution sets. It can be seen from
Table 17 that MOFECO can obtain the largest
values on at least 10 test functions compared with the other five algorithms, particularly, it achieves a good performance on all the four ZDT test problems with two objectives in terms of
. While on the five DTLZ test functions, the PD values obtained by MOFECO on DTLZ2 and DTLZ7 are slightly worse than those obtained by NSGA-II and MOPSO. But on all the five DTLZ test problems, MOFECO can show good performance compared with KnEA and NSLS. Among the four-objective test functions (WFG2, WFG3, WFG4, MaF1, MaF2 and MaF12), MOFECO can achieve the largest
values except for WFG3 compared with NSGA-II, MOPSO, PESA-II, KnEA and NSLS. From those empirical results, we can confirm that the proposed MOFECO algorithm is promising in solving MOO problems, and it has advantages in maintaining the diversity of obtained Pareto solution sets, because of its novel characteristics, such as dividing the population into several independent cycles, relating the new solutions generated in the update process to the optimal solution in each cycle, and the differences in the optimal solutions obtained between different cycles, etc.
As mentioned earlier,
is one of the indicators to measure the comprehensive performance of a Pareto solution set. Generally, the larger the
value is, the better the comprehensive performance of an algorithm has. From
Table 18, we can find that MOFECO can shows the largest
values on all the four ZDT test functions compared with NSGA-II, MOPSO, PESA-II, KnEA and NSLS. On the five DTLZ test functions, MOFECO can achieve larger or equal
values on DTLZ4 to DTLZ6 compared with the other five algorithms, while on DTLZ2 and DTLZ7, MOFECO performs slightly worse. Among the four-objective test functions (WFG2, WFG3, WFG4, MaF1, MaF2 and MaF12), MOFECO has the largest
values on at least five test functions compared with MOPSO, PESA-II and NSLS, but it performs worse compared with NSGA-II and KnEA. Overall, the experimental results show that proposed MOFECO can obtain better
values on 9 test functions approximately among the 15 test functions compared with the other five algorithms, which confirms that the proposed MOFECO has a good characteristic in terms of the comprehensive performance of the Pareto solution set.
and
are indicators for measuring the distribution and distribution breadth of a solution set. The smaller the
and
values are, the better the distribution and breadth a solution set has. It is clear from
Table 19 that the MOFECO has better
values on all the four ZDT test functions except for ZDT1 compared with NSGA-II, MOPSO and PESA-II but on the ZDT6 test function, MOFECO has the smallest
values compared with the other five algorithms. Among the five tri-objective test functions of DTLZ, the MOFECO performs better on metric
on at least four test functions compared with NSGA-II, MOPSO and KnEA, while it performs slightly worse in NSLS algorithm. On the four-objective test functions (WFG2, WFG3, WFG4, MaF1, MaF2 and MaF12), MOFECO achieves the smallest
values on at least four test functions compared with all the other five algorithms and MOFECO can even obtain the smallest
values on all the 6 four-objective test functions compared with NSGA-II and KnEA. From these empirical results, we can confirm that the proposed MOFECO has good performance on solving MOO problems with the objective numbers of 2 to 4, and can obtain better distribution of Pareto solution sets.
According to
Table 20, we can see that on the four bi-objective test functions of ZDT, the
values obtained by MOFECO are revealed to be superior to those obtained by MOPSO, PESA-II and KnEA. While on the five tri-objective test functions of DTLZ, MOFECO performs worse compared with NSLS algorithm, the possible reason of which is that in NSLS, a new method, which combines the non-dominated sorting and the farthest candidate approach, was chosen to generate a new population for improving diversity, while in MOFECO, we only use the crowded comparison mechanism presented in NSGA-II to maintain diversity. Among the six four-objective test functions of the WFG and MaF series, MOFECO shows better
values for at least five test functions compared with NSGA-II, MOPSO, PESA-II and KnEA. These empirical results show that the proposed MOFECO has superiority in solving MOO problems and can obtain solution sets with better spread on Pareto front. But when comparing with the NSLS algorithm, MOFECO performs slightly worse.
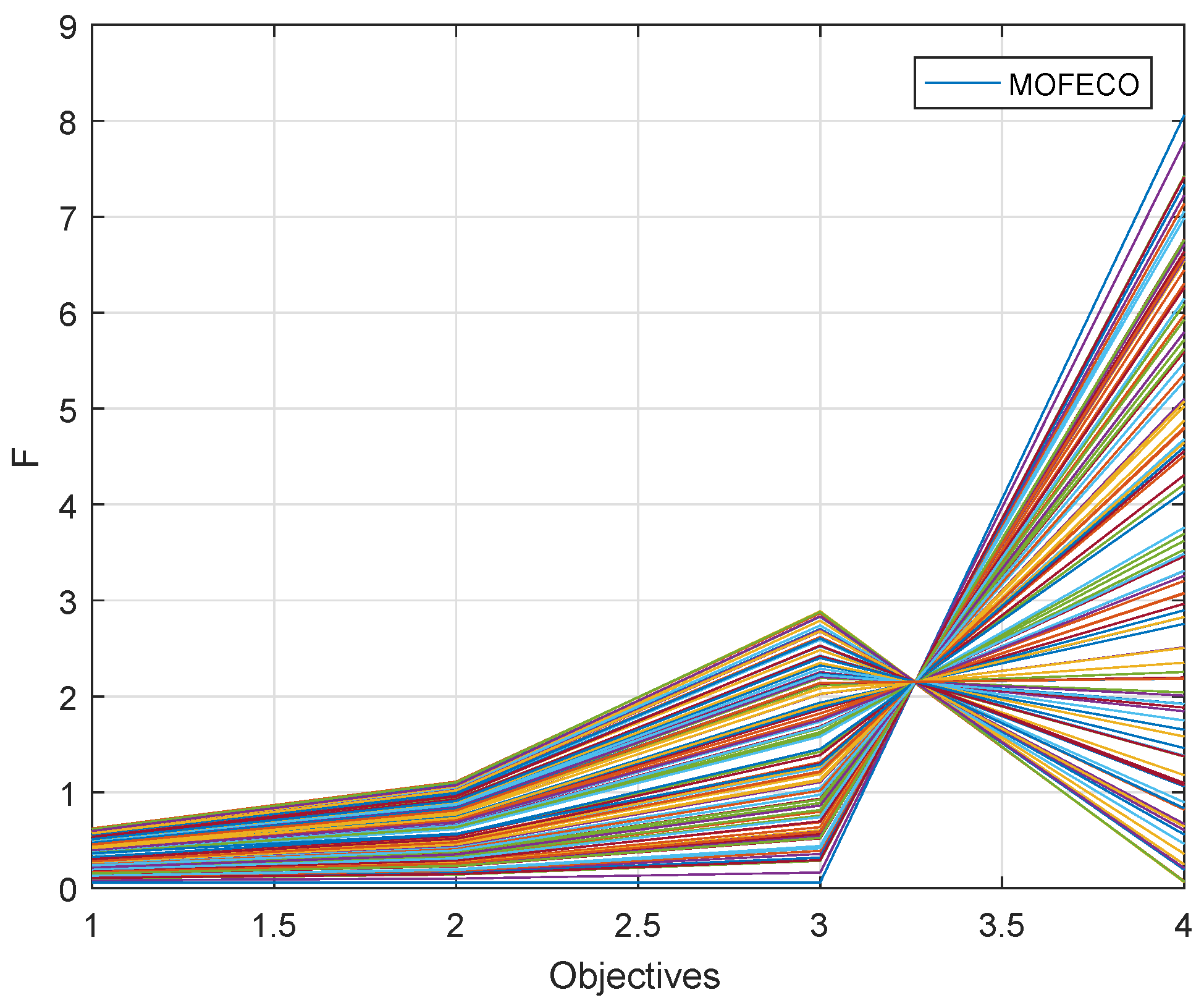
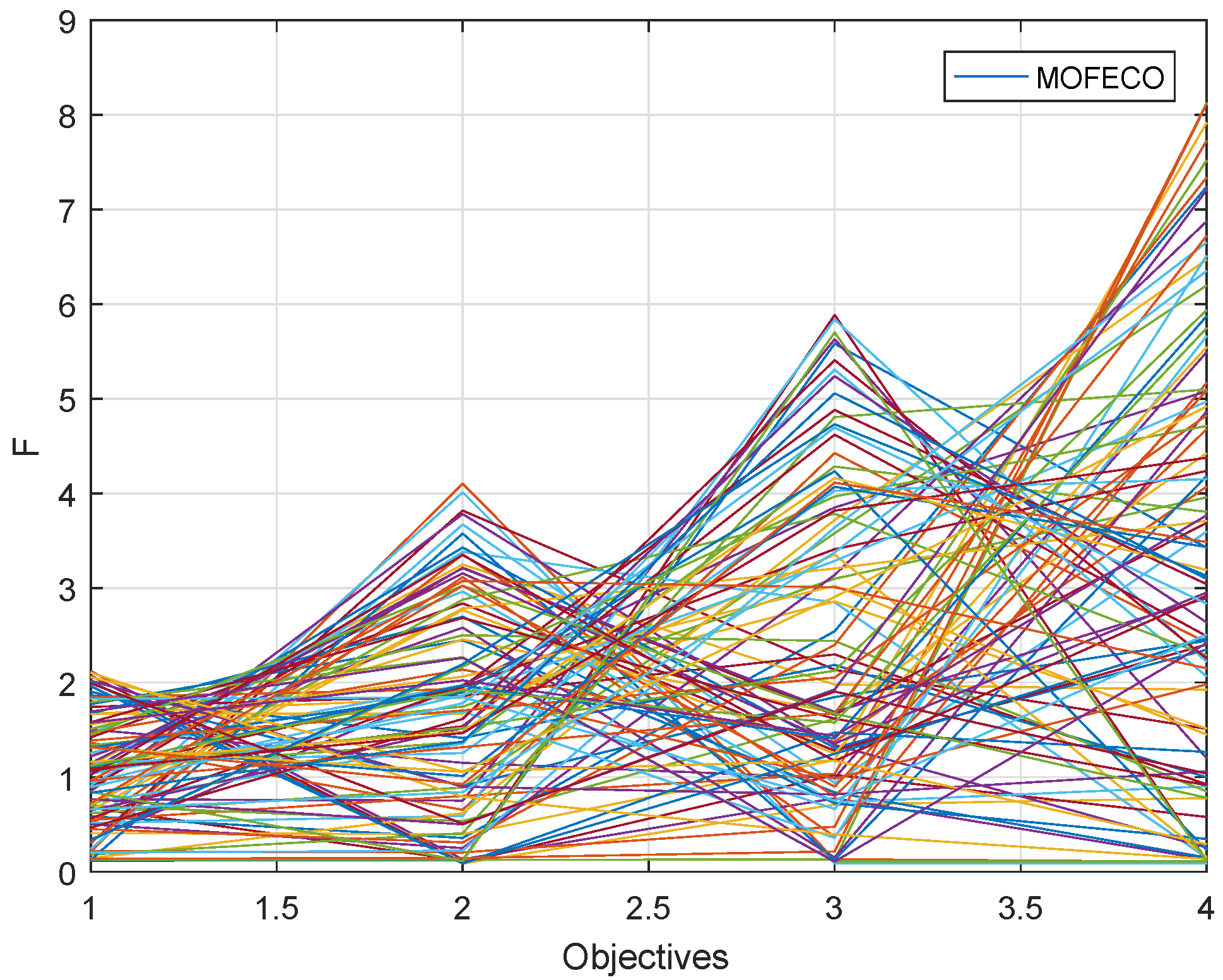
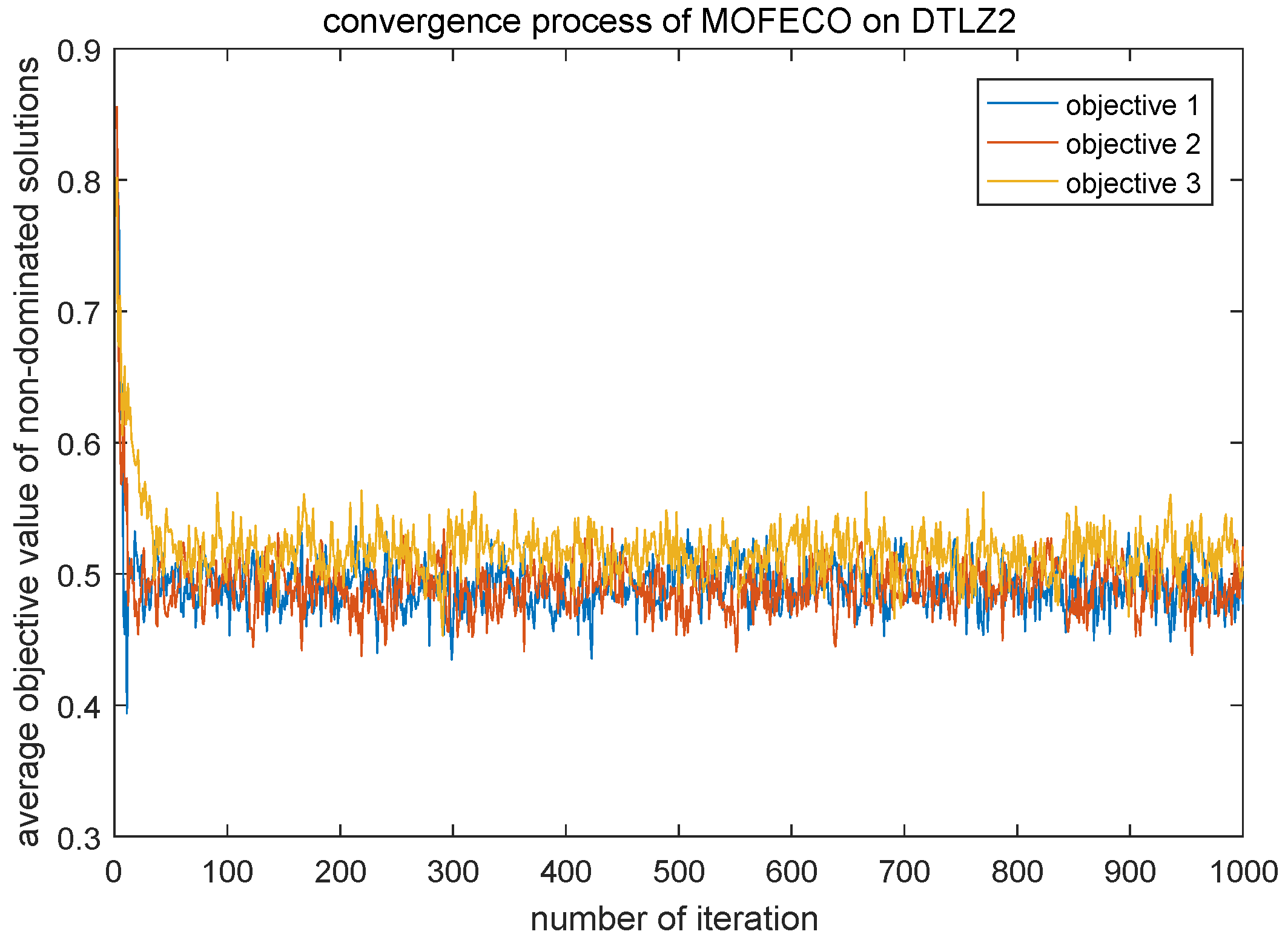
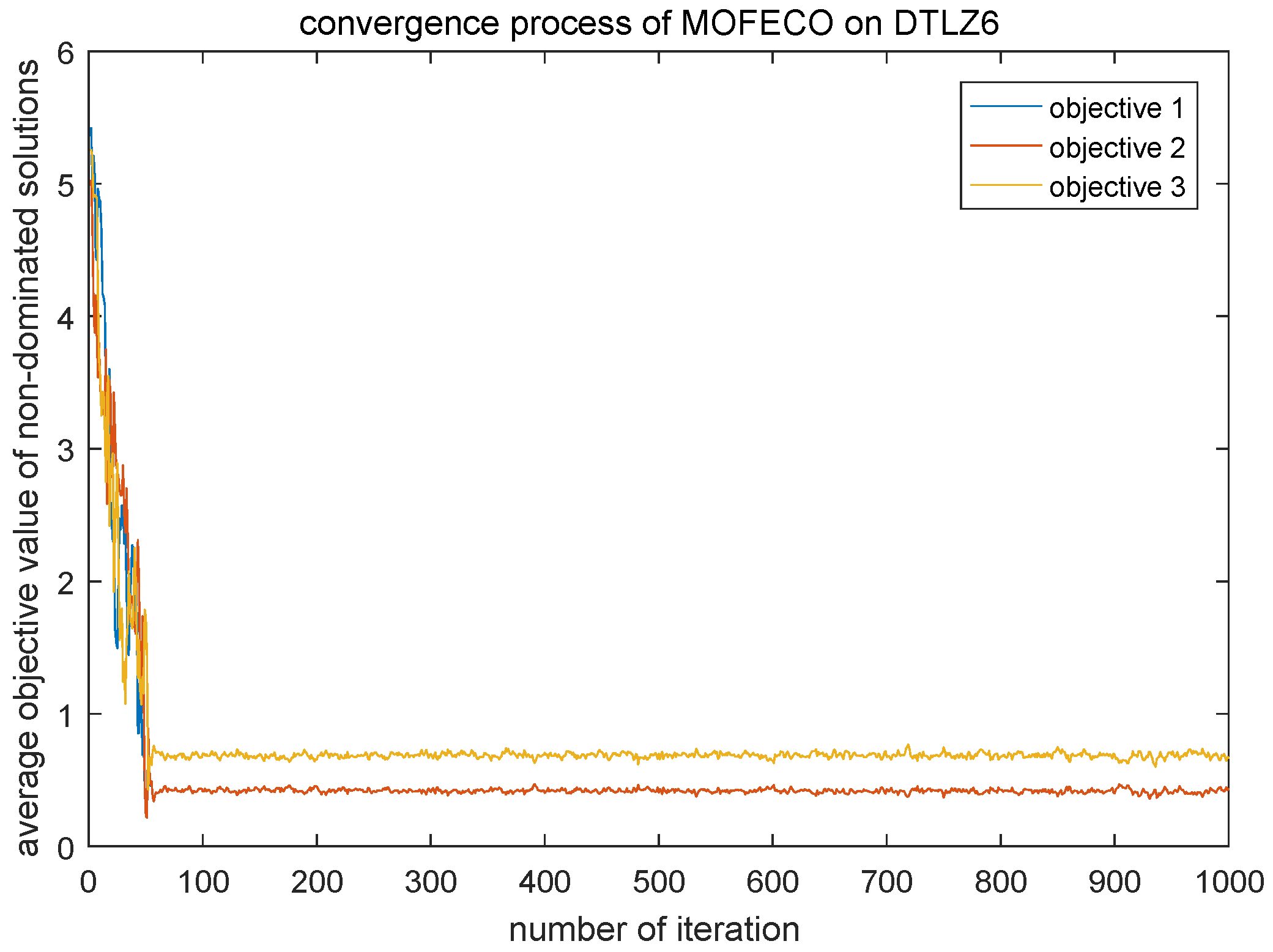
In order to more visually show the performance of the MOFECO algorithm, a detailed convergence process increasing the number of iterations is discussed. Here we choose two test problems DTLZ2 and DTLZ6 to show the convergence process. Experimental results are shown in
Figure 30 and
Figure 31. The abscissa represents the number of iterations and the ordinate represents the average objective function value of the non-dominated solutions in each iteration.
As can be seen from
Figure 30 and
Figure 31, the population obtained by MOFECO converges rapidly in every objective of DTLZ2 and DTLZ6, which reflect the good convergence of the proposed MOFECO algorithm.
Overall, the proposed MOFECO performs better than NSGA-II, MOPSO, PESA-II and KnEA on most of the test functions used in the above experiments in terms of metrics , , , and , which indicates that MOFECO algorithm has better convergence and diversity in solving MOO problems. But MOFECO performs slightly worse on indicator compared with NSLS, which will be one of the problems we need to investigate in the follow-up research.