1. Introduction
There are many problems that make use of the eigenvalue or eigenvector of a matrix in their solution. Because of this, it is often beneficial to be able to calculate the Jacobians of eigenvalues and eigenvectors with respect to the elements of the matrix from which they were computed. For example, eigenvalue and eigenvectors are used throughout finite-element analysis (FEA) solutions to vibration problems, where the goal is often to minimize a structure’s sensitivity to various parameters through the use of eigenvalue/eigenvector derivatives [
1]. As a second example, there are many instances in which the solution for the optimal estimate of a parameter vector takes the form of an eigenvalue problem—such as quaternion-based spacecraft attitude estimation [
2,
3] or ellipse fitting in computer vision [
4]. For these types of problems, it is often important to understand the uncertainty in the optimal estimate, which requires knowledge of the eigenvector Jacobian. Other examples abound, such as direction-of-arrival of plane waves [
5], epipolar geometry in computer vision [
6], pose estimation in robotics [
7], spacecraft optical navigation [
8], or infectious disease epidemiology [
9]. In all of these problems, and in many others, it can be useful (or, in some cases, necessary) to have an analytic expression for the Jacobians of eigenvalues and eigenvectors with respect to the entries in their parent matrix.
Because of the popularity of problems requiring the calculation of eigenvalues, eigenvectors, and their Jacobians, much work has already been devoted to these topics. The prior work on eigenvalue and eigenvector Jacobians can largely be grouped into three basic categories: modal expansion techniques, direct techniques, and techniques based on Nelson’s method. Modal techniques mimic the idea of modal expansion used in FEA, whereby the eigenvector Jacobian is expressed as a linear combination of the other eigenvectors of the system [
10,
11,
12,
13,
14,
15,
16,
17]. Direct solutions find the Jacobians through the solution of a linear system of equations [
18,
19,
20,
21,
22,
23,
24,
25]. Solutions based on Nelson’s method find the Jacobians by considering a homogeneous and particular solution [
26,
27,
28,
29,
30,
31,
32,
33]. Finally, there is a grouping of solutions that are not easily fit into the above categories [
34,
35,
36,
37,
38,
39]. For a more thorough discussion of this literature, see [
39].
In light of the extensive literature already available on the topic, it may not be clear why more work is needed. After careful review, however, a few limitations are apparent with the existing methods. First, the majority of the above literature only presents solutions for the derivatives of the eigenvalues and eigenvectors with respect to a single element of the parent matrix. While these single element derivatives may be assembled to create a Jacobian, their use is cumbersome and the expressions are not compact. In the literature reviewed by these authors, expressions for the full Jacobians of the eigenvalues and eigenvectors only appear once and only for the special case of a symmetric parent matrix [
34]. Second, in the majority of the literature, the derivatives are found using both the left and right eigenvectors of the system or by simultaneously solving a system of equations for both derivatives at once. While it is straightforward to find both the left and right eigensystems, calculating the left eigenvector in order to find the Jacobian of the right eigenvector is an unnecessary extra step that we seek to circumvent. Finally, much of the literature on this topic is only valid when the parent matrix and its eigenvalues and eigenvectors are real due to the choice of the normalization of the eigenvectors.
Due to these observed deficiencies, the authors of this paper proposed a new method in [
39] that did not involve the left eigenvector, did not require the simultaneous solution of both the eigenvector and eigenvalue derivatives, provided the full Jacobian matrices with respect to every element of the parent matrix, and provided a solution capable of handling any matrix with real or complex elements and real or complex eigenvalues and eigenvectors. This new method found the eigenvalue Jacobian by considering the characteristic equation and solved for the eigenvector Jacobian by using the results of the eigenvalue Jacobian along with the normalization condition for the eigenvector.
While the method introduced in [
39] addressed the deficiencies described above, it did produce some new issues—namely that the calculation of the eigenvalue Jacobian was computationally expensive. Additionally, the eigenvector Jacobian relied on the computation of the eigenvalue Jacobian, which could lead to numerical stability issues in large matrices (
).
This paper introduces novel improvements to [
39] that address both of these shortcomings. Specifically, the present work introduces a much simpler solution that addresses all of the original deficiencies in the eigenvalue and eigenvector derivative literature and also addresses the new issues associated with the technique in [
39]. The simpler solution leads to an efficient, compact, and intuitive algorithm. The compact results presented for an arbitrary real or complex matrix (with real or complex eigenvalues and eigenvectors) are found to collapse even further for special cases and to reveal new insight into the structure of this fascinating problem. Thus, the novel approach for computing eigenvalue and eigenvector Jacobians introduced in this manuscript is exceedingly general, is applicable to a wide range of problems, and represents a significant improvement to earlier methods.
This paper is organized as follows. First, a brief discussion on the analyticity of eigenvector normalizations is presented. Then, a review of the solution proposed in [
39] is presented. Next, these results are modified to arrive at the new technique, which is efficient to compute and is valid for general complex matrices. This general result is then shown to collapse to known relations from the literature for the special cases of real symmetric matrices and real diagonal matrices. The new derivatives are then validated numerically through comparison with forward finite differencing. Finally, the execution time on a digital computer is compared for the technique proposed in [
39] and for the new technique proposed this paper.
2. Existence of Eigenvalue and Eigenvector Jacobians
The standard algebraic eigenvalue problem is defined as
where
is a
square matrix,
is an eigenvector of the system, and
is an eigenvalue of the system. As should be apparent, each eigenvalue and eigenvector pair is only implicitly defined according to
It is well known that eigenvectors corresponding to simple eigenvalues are only unique when a constraint is placed on their norm (i.e., “length”). In addition, the eigenvector normalization can be expressed implicitly as
where
is a row vector formed by choosing a column normalization vector and transposition method and
is a normalization constant. Although the choice of
is arbitrary, we often choose
. These two implicit vector functions can be combined to form a single implicit vector equation:
where
. To determine if eigenvalue and eigenvector derivatives exist with respect to the elements of
, we must determine if both
and
can be expressed as an explicit function of
. The implicit function theorem can be used to test if this is possible.
The implicit function theorem states that as long as the determinant of the Jacobian of
with respect to
can be found and is nonzero, then
can be expressed as an explicit function of
. Therefore, consider the Jacobian of
as defined in Equation (
4):
where
will be a
row vector from the rules of matrix vector calculus. Recognizing the block structure of the Jacobian, it can be shown that the determinant is given by
Therefore, in order to evaluate the determinant of the Jacobian, we must evaluate for the specific normalization described by the row vector . The following subsections discuss two potential eigenvector normalizations.
2.1. Constraining the Eigenvectors to the Unit Hypersphere
Begin with the most commonly used normalization for the standard eigenvalue/eigenvector problem,
. Substitution into Equation (
3) leads to:
which constrains the eigenvector to lie on the hypersphere of radius
. As usual, the superscript of
H indicates the Hermitian (conjugate) transpose (
). Expressing this normalization in terms of the elements of
gives
where
is the
element of the eigenvector
and
is the complex conjugate of •.
We proceed by attempting to determine the partial derivative of this normalization with respect to the eigenvector in a domain around the eigenvector. First, since the eigenvector may be complex requiring a complex partial derivative, we need to check that the normalization equation is analytic in a region around the eigenvector. This is done by using the Cauchy–Riemann equations. Since the partial derivative and summation operators are linear, the required partial derivatives for checking the Cauchy–Riemann equations are
and
where
takes the real component of • and
takes the imaginary component of •. Now, using the Cauchy–Riemann equations, it is easy to see that this function is differentiable only when
and
are 0 and is analytic nowhere. In addition, this shows that this normalization is only differentiable when
, which is not generally a valid eigenvector. Therefore, this normalization cannot be used when the eigenvectors are complex because the normalization is not differentiable or analytic for valid eigenvectors. We do note, however, that when
there are no issues with using this normalization.
2.2. Constraining the Eigenvectors to a Hyperplane
Now, consider an eigenvector normalization which constrains the length of the projection of
onto an arbitrary vector,
(so long as
, where we stress here that
is not functionally dependent on
,
, or
.) Such a normalization occurs when
and constrains
to lie on a hyperplane. Therefore, substituting this into Equation (
3) leads to:
Specifically, note that the eigenvector
is now constrained to lie on a hyperplane tangent to the hypersphere of radius
at the point
. Expressing this normalization in the terms of the elements of
and
gives
where
is as defined before and
is the
element of
.
As before, since we are seeking a complex partial derivative, the Cauchy–Riemann equations are used to check if the partial derivative of the normalization is analytic in a region around the eigenvector. The partial derivatives with respect to the components of the
elements of the eigenvector are
and
which satisfy the Cauchy–Riemann equations for any choice of
and
indicating that the normalization is analytic in all of
. Since the Cauchy–Riemann equations are satisfied, the vector form of the partial derivative of the eigenvector normalization constraint with respect to the eigenvector is given as
using the rules of matrix vector calculus.
This allows the implicit function theorem to be used to check to see if the eigenvalues and eigenvectors are guaranteed to be analytic functions of
on some domain centered at their nominal values. Substituting Equation (
19) into Equation (
6) gives
which is guaranteed to be full rank and have a non-zero determinant if
is a simple eigenvalue (defined as an eigenvalue with a multiplicity of 1). Therefore, using the implicit function theorem with this normalization, it is guaranteed that the eigenvectors and eigenvalues are analytic functions of
in some domain around their nominal values for simple eigenvalues. Due to this, the rest of this paper will use the normalization
and the case when the eigenvalue is simple.
3. Previous Work
In [
39], the authors of this paper presented a new technique for calculating the eigenvalue and eigenvector Jacobians. This technique allows the calculation of the full Jacobian matrices for both the eigenvalues and eigenvectors using just the eigenvalue and eigenvector being considered. Some key results from this prior work are now reviewed.
Begin with the standard eigenvalue problem
where
is a simple eigenvalue of
and
is its corresponding eigenvector. Now, take the partial derivative of this relation with respect to the vectorized version of the matrix
to get
where
is formed by stacking the columns of
into a column vector and ⊗ indicates the Kronecker product. This results in a single equation with two unknowns,
and
, and thus a second equation is needed. As described in [
39], the eigenvalue derivative can be calculated by considering the characteristic equation for the matrix
. The characteristic equation for
can be expressed using the notation of exterior algebra [
40] as
where
n is the dimension of
,
indicates the determinant,
is the
exterior power of
, and [
41]
With the above expression for the characteristic equation, the solution for the eigenvalue Jacobian is easy to find:
where
Now, with the independent equation for the eigenvalue Jacobian, return to Equation (
22) to solve for the eigenvector Jacobian. While it would appear simple to calculate the derivative of the eigenvectors directly from Equation (
22), remember that the term
is rank deficient (by the definition of an eigenvalue) and is therefore not invertible. In order to solve this problem, we must make use of a normalization condition to make the eigenvectors unique. As discussed in the preceding section (and [
34]), it is important to ensure that the normalization chosen makes the eigenvector an analytic function of
; therefore, choose the normalization
where
is any non-zero vector that is not orthogonal to
and
is any real non-zero scalar value. In practice, it is usually chosen that numerically
, as this gives rise to a more intuitive interpretation (as we discuss later); however, even when this is the case, it is still important to remember that
is not a function of
or
.
In addition to making the eigenvectors analytic, Equation (
30) also leads to another important relation. Consider the derivative of Equation (
30) with respect to
,
which shows that the normalization vector
is orthogonal to the column space of the eigenvector Jacobian.
Using the above normalization condition and its derivative, perform a rank-one update to the matrix on the lefthand side of Equation (
22) with the so-called
null space matrix,
, in order to make
invertible. This approach is discussed further in [
39]. This allows for the solution of the eigenvector derivative as
where
is the Null Space Matrix and
is a scaling term chosen to make
approximately the same order as
(it is usually sufficient to let the scale be
). Including the Null Space Matrix, as in Equation (
33), is the same as adding a zero vector due to the relation in Equation (
31). Note, of course, that a similar end objective may accomplished by using the pseudoinverse of
instead of including a Null Space Matrix (an example of this alternative approach may be found in [
34]).
The term
is rank deficient with a null space in the direction of
. Additionally, the rank one Null Space Matrix only contains information in the direction of
. Thus, because
is required to not be orthogonal to
, the quantity
is guaranteed to be full rank. For further discussion of the use of the Null Space Matrix and its properties, refer to [
39].
This concludes the review of the technique proposed in [
39] and attention is now turned to the simplification of these methods.
4. Compact Expressions for Eigenvalue and Eigenvector Jacobians
Using the insights from [
39], it is now possible to arrive at a simpler and more efficient solution. Beginning again with Equation (
21), left multiply by
in order to form a new equation:
Recall that, while it is common to set
,
is not a function of
. Taking the derivative of Equation (
34) leads to
through simple application of the chain rule and identities pertaining to the vectorization of a matrix. Note again that a superscript of
T indicates a standard transpose while a superscript of
H indicates the Hermitian (or conjugate) transpose. Now, recalling Equation (
31), the right most term of Equation (
35) vanishes. Thus, after incorporating Equation (
30) and a few simple rearrangements, one finds
which expresses the eigenvalue Jacobian as a function of
,
,
,
, and
.
We now turn our attention to finding a compact expression for the eigenvector Jacobian. Observe that Equations (
22) and (
36) create a system of two equations with two unknowns. Therefore, substituting Equation (
36) into Equation (
22),
which can be arranged to give
as an equation that isolates the eigenvector derivative. This expression can be simplified to
by manipulating the Kronecker products.
4.1. Eigenvector Jacobian
The objective is now to solve Equation (
39) for
. Unlike the result from [
39], there is no need to incorporate a Null Space Matrix (or to use a pseudoinverse) since the term
is already full rank and invertible as long as the eigenvalue under consideration is non-zero. This fact is straightforward to show by considering the column space of the term
, which will generally be rank
(assuming
is simple and
is full rank). Specifically,
spans
with a null space in the direction of
. Now, consider the column space of the term
, which is rank one and spans only
. Therefore, by adding
to
, the resulting column space spans all of
, making the overall term full rank and invertible.
In light of this fact, the solution for the eigenvector Jacobian for a non-zero eigenvalue is given by
which is a function of only
,
,
,
, and
. Additionally, manipulating the Kronecker products allows for a final form of
In the case where it is necessary to find the eigenvector Jacobians when the eigenvalue is zero, the Null Space Matrix can be used as discussed in [
39] to make the left-hand side invertible, resulting in
4.2. Eigenvalue Jacobian
Now, consider how the eigenvector Jacobian may be used to find the eigenvalue Jacobian. Substitute the result of Equation (
41) into Equation (
36) and collect like terms
For the zero-eigenvalue case, the equivalent expression for the eigenvalue Jacobian becomes
Focusing on the general case from Equation (
43), we observe that further simplification is possible. Begin simplification by recognizing that the following are true:
and, therefore,
Applying this result, the intermediate term in Equation (
43) may be simplified
which, upon substitution into Equation (
43), leads to
providing a concise expression for
only in terms of the right eigenvector and the chosen normalization convention,
.
Intuitively, however, we expect the eigenvalue Jacobian to be unrelated to the choice of eigenvector normalization. Indeed, we find
to be the same for any choice of
, so long as
. We may show this by rewriting Equation (
49) without the use of
or
, although doing so does require consideration of the left eigenvector. Specifically, let
be the left eigenvector corresponding to the eigenvalue
(which also has a right eigenvector
),
Observe, therefore, that
Substituting this result into Equation (
49) produces the following compact form that is independent of the choice of eigenvector normalization
This result leads to a few important observations about the sensitivity of
to perturbations in
. First, this demonstrates that the eigenvalue Jacobian from Equation (
49) is indeed the same for any choice of
other than
. Second, Equation (
49) shows the eigenvalue Jacobian in terms of only the right eigenvector, whereas Equation (
53) shows the same eigenvalue Jacobian in terms of both the right and left eigenvectors. Thus, in cases where only the right eigenvector is known (and it is not desirable to compute the corresponding left eigenvector), the result of Equation (
49) provides a compact means of computing the eigenvalue Jacobian. Third, and, finally, observe the division by
on Equation (
53). In general, this suggests eigenvalues will be most stable when their corresponding left and right eigenvectors are colinear (as happens in a Hermitian matrix) and become unstable as the angle between
and
increases (
).
5. On the Choice of a Normalization Vector
As mentioned earlier, the choice of
is arbitrary, so long as
. While this is true, the choice of
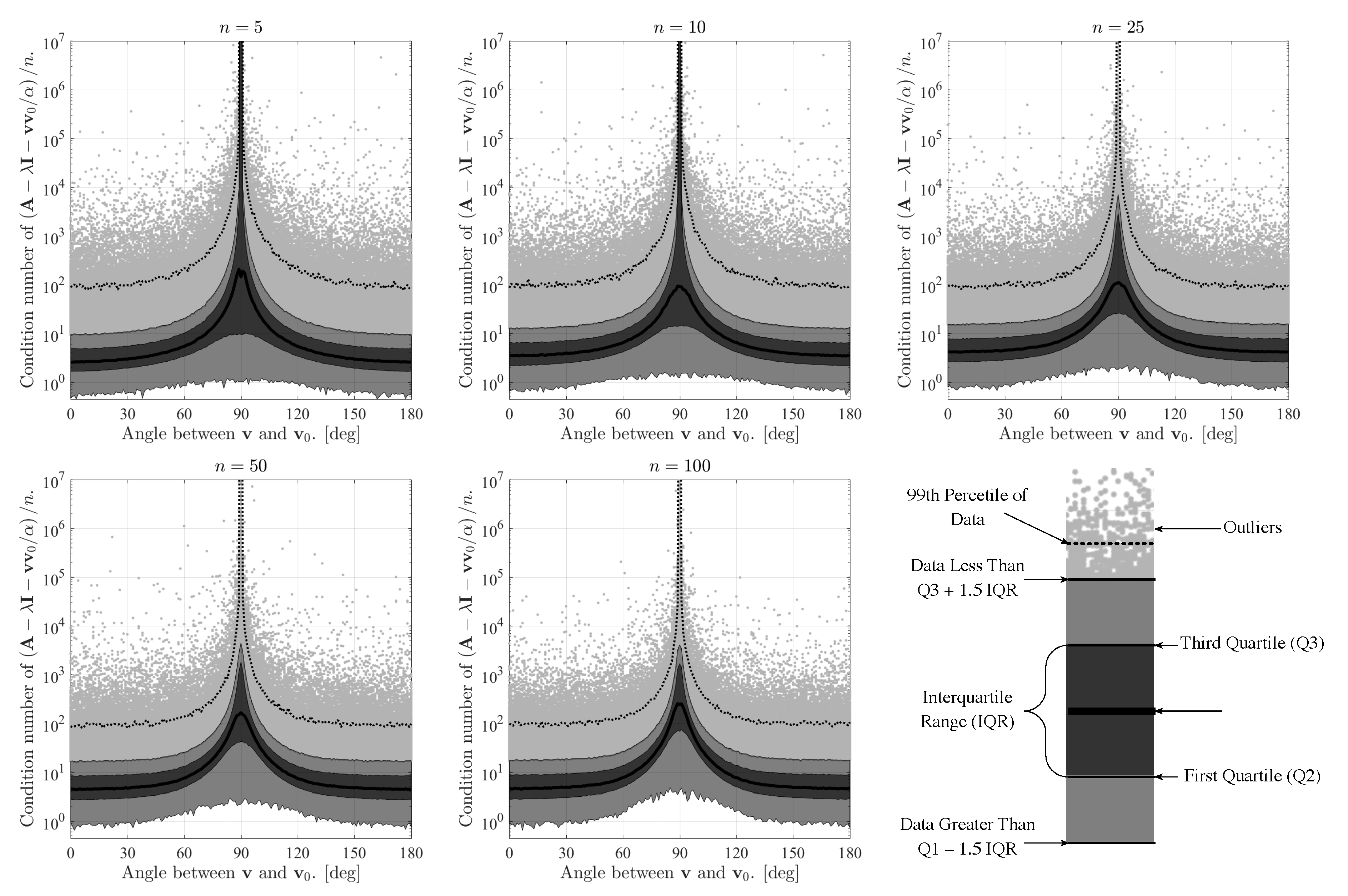
can play an important role in the numerical stability of the system in finite precision computing. In particular, the closer the normalization vector gets to being orthogonal to the eigenvector, the more numerically unstable the system becomes. To demonstrate this phenomena consider
Figure 1, which shows the condition number of the term
normalized by the number of dimensions,
n, as a function of the angle between
and
. A higher condition number indicates a more poorly conditioned matrix prone to issues in finite precision computing.
The samples were generated by producing 10,000 random matrices for each integer value in degrees for the angle between
and
.
Figure 1 shows matrices whose elements are real values which are normally distributed with zero mean and unit variance. In these experiments, the eigenvector,
, for each matrix is randomly selected. Since
and/or
may be complex, the angle between the vectors is computed using
Figure 1 indicates that the probability of poor matrix conditioning is greatest when
and
are nearly orthogonal. Presuming they are are in random directions, as
n increases, it becomes highly probable that
and
will be nearly orthogonal.
Therefore, it is clear that choosing the normalization vector (leading to an angle of 0 deg; or, equivalently, leading to an angle of 180 deg) will ensure the best conditioning for the system and will usually lead to the most intuitive solution. The worst conditioning occurs as (angle of 90 deg). This is why is often chosen in practice, unless there is a compelling reason to choose otherwise.
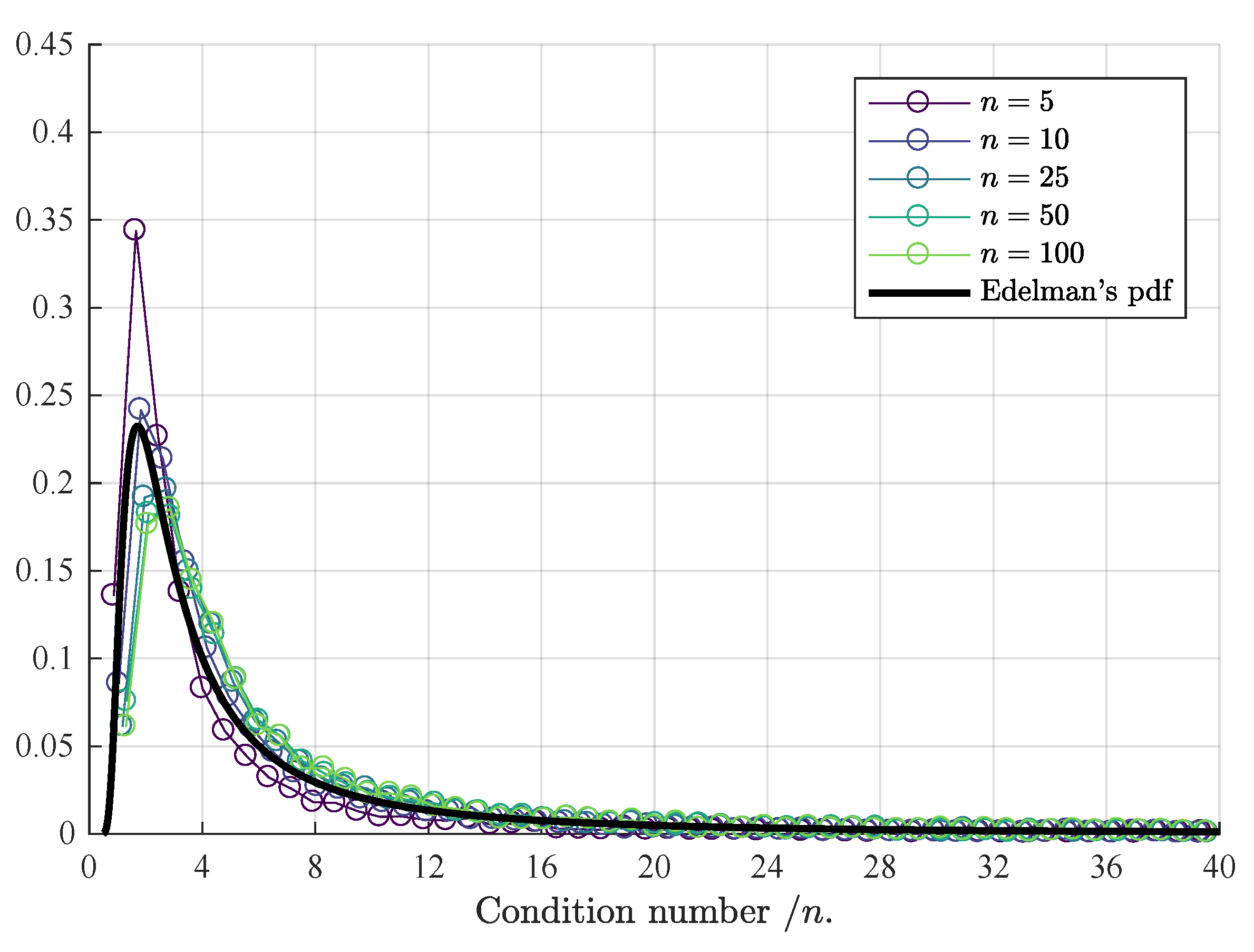
Note that selecting
causes the condition number of
to share many of the statistical properties of the condition number of
. This is especially true for large values of the condition number. Edelman [
42] developed probability density functions for the condition number of
normalized by
n when the elements of
are real values with zero mean and unit variance,
Likewise, for the case where
is composed of complex elements with real and imaginary parts which are each normally distributed with zero mean and unit variance,
Histograms for when
are overlaid with Edelman’s probability density functions in
Figure 2. These figures show that the probability of large condition numbers occurring are well described by Edelman’s result. Unfortunately, Edelman’s density function does not work as well for small condition numbers, but these are of little consequence.
In light of the above discussion, we stress again that
is not the same as
. These results simply demonstrate that the best numerical performance is achieved when the values of the arbitrary vector
are set to be the same as
. Consequently, one may wonder how the usual normalization choice of
(instead of the
normalization suggested in this paper) affects the Jacobians. Observation of the problem geometry reveals that the normalization proposed in Equation (
30) (
) serves as a good approximation for the usual normalization of
when
is well conditioned and the values of
are set to that of
. This is because the usual normalization constrains the eigenvectors to fall on the hypersphere of radius
, while the normalization from Equation (
30) constrains the perturbed eigenvectors to fall on the hyperplane tangent to the hypersphere of radius
at
. Therefore, as long as the perturbation of
leaves the perturbed eigenvector near the original eigenvector, the proposed normalization approximates the normalization constraining the eigenvectors to the hypersphere to first order. Furthermore, when
is chosen to be
, the difference between the usual normalization and Equation (
30) rarely needs to be considered in practice except in very rare situations, such as when attempting to numerically verify the analytic expressions as was done in the “Numerical Validation” section of this paper.
With these observations in mind, additional remarks are necessary regarding the expressions in the literature that rely on the normalization . Recall from our earlier discussion that using does not result in a valid expression for the eigenvector derivatives because the normalization is not analytic. Despite this, the numerical results produced by these methods will be equivalent to the numerical results of the expressions developed in this paper when is chosen to be . While the expressions for the derivatives are numerically equivalent, the derivatives from the existing literature are not valid for the normalization employed. This means that that the derivatives in the existing literature cannot be used to predict the perturbations caused to eigenvectors by perturbations to when the eigenvectors are complex. The derivatives and normalization in this paper are valid for all complex eigenvectors and can be used to predict the perturbation caused to the eigenvectors by the perturbations to .
7. Numerical Validation
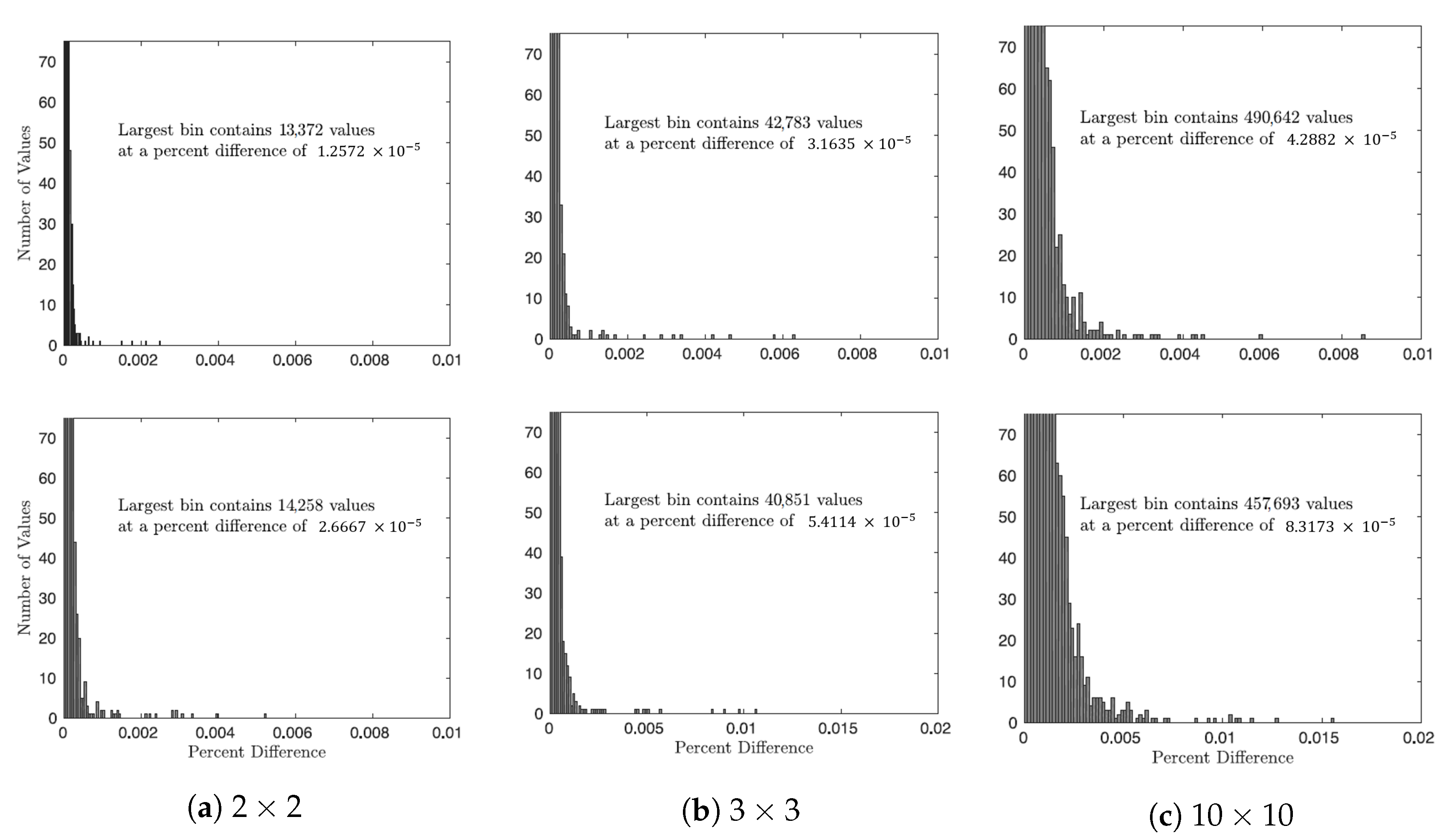
Forward finite differencing was used to validate the formulation of the new eigenvalue and eigenvector Jacobians presented in this manuscript. This provides a numerical approximation of the Jacobians which may be compared with the analytic expressions developed in this paper.
The forward finite differencing was performed by perturbing each element of the parent matrix individually in order to calculate each element of the Jacobians. The analytic derivatives from Equations (
40) and (
49) were then compared with the finite differences and the percent differences were calculated as
This was performed for 5000 randomly generated complex matrices of size
, 5000 randomly generated complex matrices of size
, and 5000 randomly generated complex matrices of size
. The results for both the eigenvalue and eigenvector derivatives are shown in the histograms in
Figure 3. Note that, due to finite precision issues, matrices had to be ignored where the smallest component of the eigenvector derivatives was less than the perturbation size used in the finite differencing. As can be seen in the figure, the new method performed well in every instance, well below
difference for each and every element of the eigenvalue and eigenvector Jacobians. In addition, the output from the techniques derived in this paper matched to within machine precision the outputs from [
39].
8. Comparison of Performance
The primary goal of the derivations presented in this paper was to decrease the computational complexity of those presented in [
39]. An examination of the two formulations indicates that both techniques are
due to the
by
multiplication in Equation (
40) and the
term in Equation (25) (assuming that the technique used to calculate the determinant is faster than
, as this is the case in most modern linear algebra libraries). Despite the fact that both these formulations have the same upper limit on their computational complexity, it should be clear that the new formulation is much simpler, both in terms of operations performed (the formulation from [
39] has two operations that are of order
as opposed to one for the formulations proposed here) and in terms of memory use.
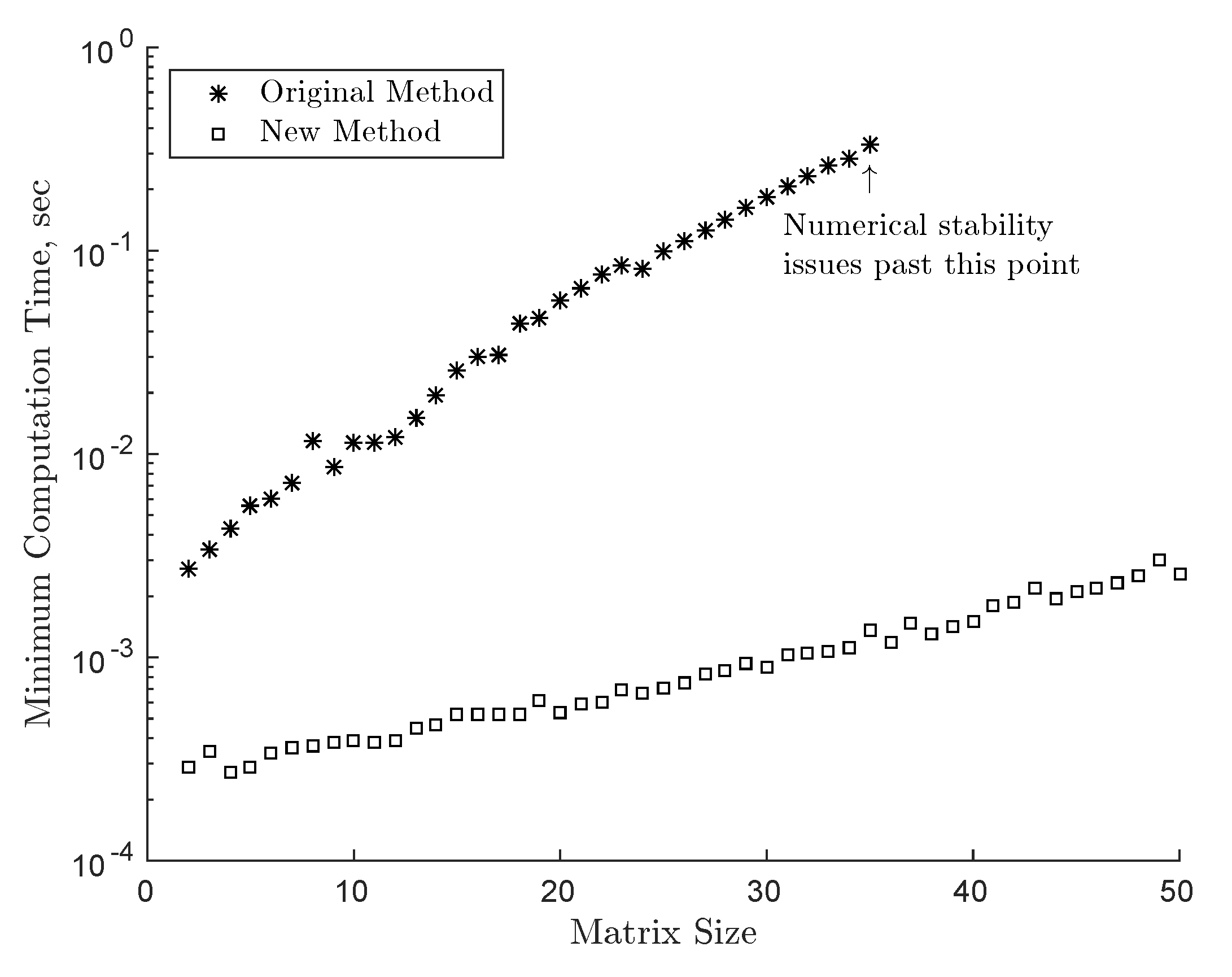
A simulation was run in an attempt to detail the increase in computational efficiency from the technique in [
39] to the technique presented in this paper. The simulation was performed by applying each technique in turn to 50 randomly generated matrices (the same 50 matrices for each technique) at matrix sizes varying from 2 to 50. For each run, the computation time of each method was recorded. Finally, the minimum computation time for each matrix size was chosen for each method, and the results are shown in
Figure 4. As can be seen in the figure, the new method is at minimum an order of magnitude faster and the distance between the performance of the two methods increases as the matrix size increases. In addition, note that the new method is less susceptible to numerical precision issues, as is evidenced by the cut-off of the results for the method from [
39].
These simulations were performed by the authors on the campus of West Virginia University (WVU) in Morgantown, WV in 2016, using an Intel Core i7-3770 processor at 3.4 GHz, and executed within the Matlab programming language (version R2015b).
9. Conclusions
A new formulation is derived for the complete Jacobians of eigenvalues and eigenvectors with respect to the elements of their parent matrix. The new solution relies on only the eigenvalue and eigenvector being considered and is valid for any unitary complex eigenvalue/eigenvector pair. Furthermore, the parent matrix may contain complex entries and need not be symmetric. As a result, the method presented here is extremely general with applications to finite-element analysis (FEA) solutions to vibration problems, fitting of an ellipse to scattered data points, quaternion-based attitude estimation, and a host of other important scientific and engineering problems.
The new eigenvalue and eigenvector Jacobians developed in this manuscript are shown to collapse to well-known results if the parent matrix is either (1) real and symmetric or (2) real and diagonal. This new method may also be reinterpreted to gain a deeper understanding of perturbations of the eigenspace.
Finally, the new eigenvalue and eigenvector Jacobians are validated by comparison with forward finite differencing. The computational performance speed of this new technique was shown to be better by a factor of 10 (or greater for large matrices) when compared with the performance of the technique proposed in [
39].