Comparison and Interpretation Methods for Predictive Control of Mechanics
Abstract
:1. Introduction
A key contribution is the design of predictive controllers that are designed using optimization as the very first step, including a formulation of state feedback for robustness in the same optimization while a subsequent step converts the optimal solution from time-parameterization to state-parameterization allowing proportional-derivative gains to be expressed as exact functions of the optimal solution. Thus, feedback errors are de facto expressed exactly in terms of the solutions to the original optimization problem and errors are, thereby, optimally rejected. This notion permits the reader to use only this predictive, optimal feedback controller by itself and also together with the optimal feedforward. Lastly, comparing the optimal feedforward to the predictive optimal feedback control permits expression of a proposed controller called “2DOF” to imply the twice-invocation of the original optimization problem. This proposed 2DOF topology achieves near-machine precision target tracking errors while using near-minimal costs.
2. Materials and Methods
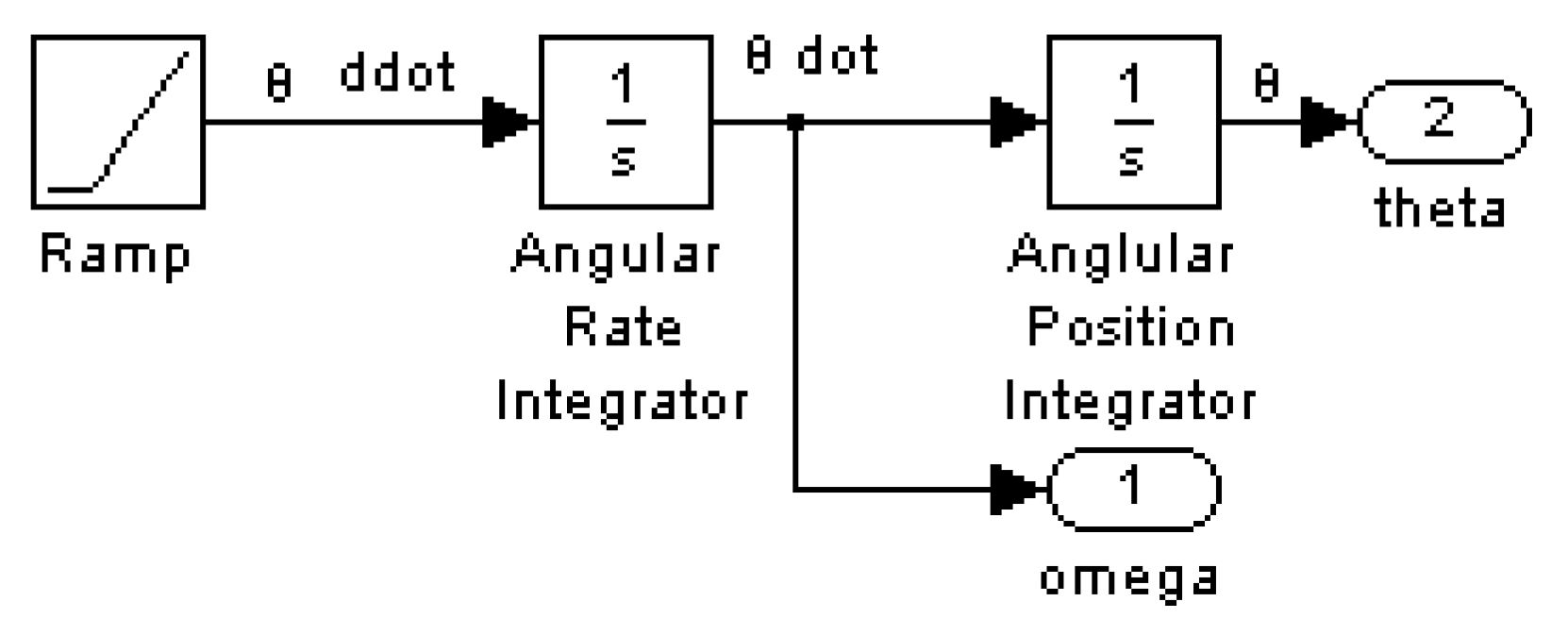
2.1. Open Loop Optimum Controller
- Write the control Hamiltonian.
- Implement the Hamiltonian Minimization Condition for the static problem of Equation (8).This is a constrained minimization problem, so use Equations (9) and (10) where is the Lagrange multiplier associated with the co-state.Confirm optimality by verifying the convexity condition in Equation (11).The result: once we find the co-state, we will have optimum control. Notice Karush-Kuhn-Tucker conditions often used with inequality constraints are not necessary here.
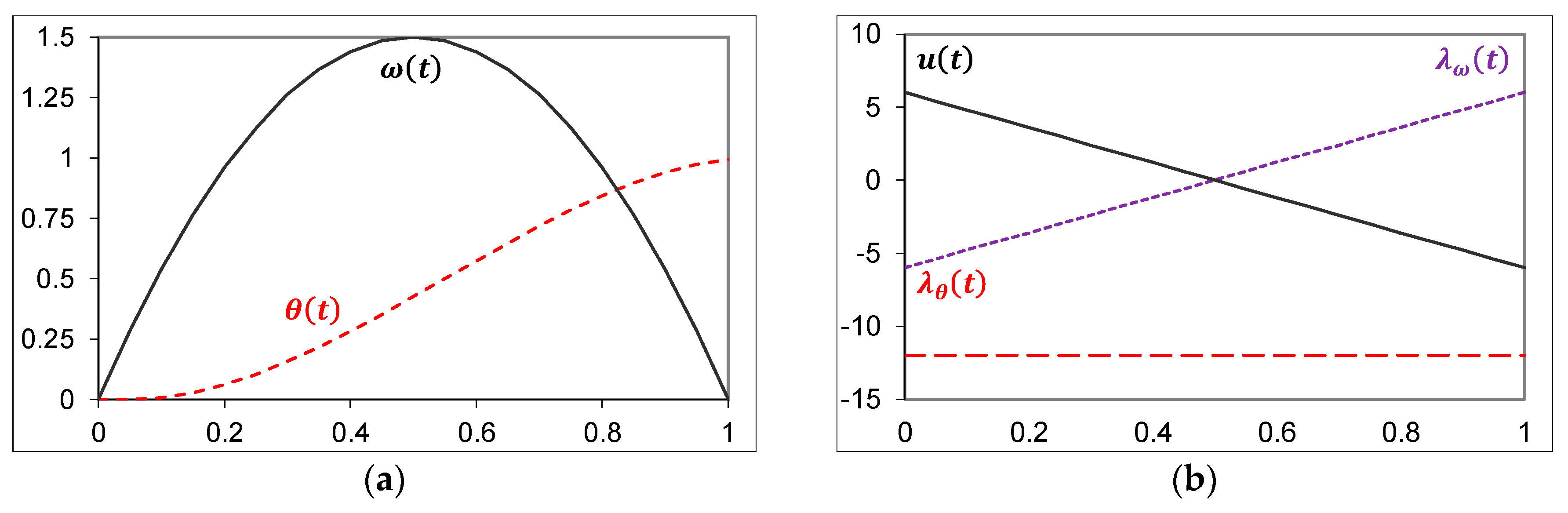
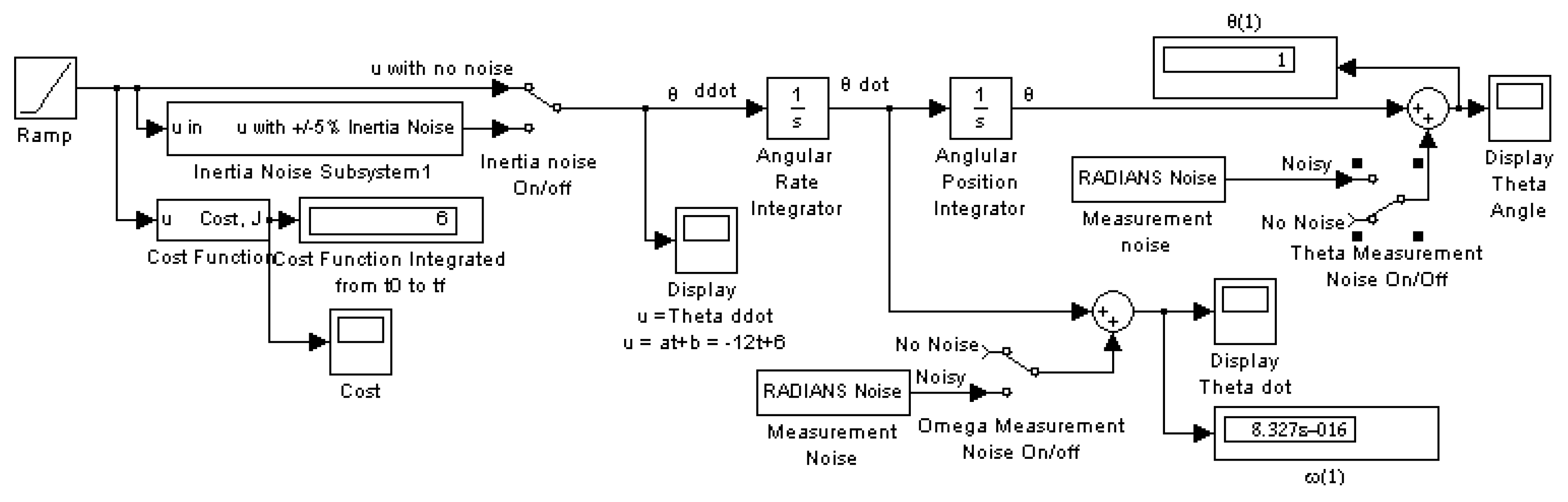
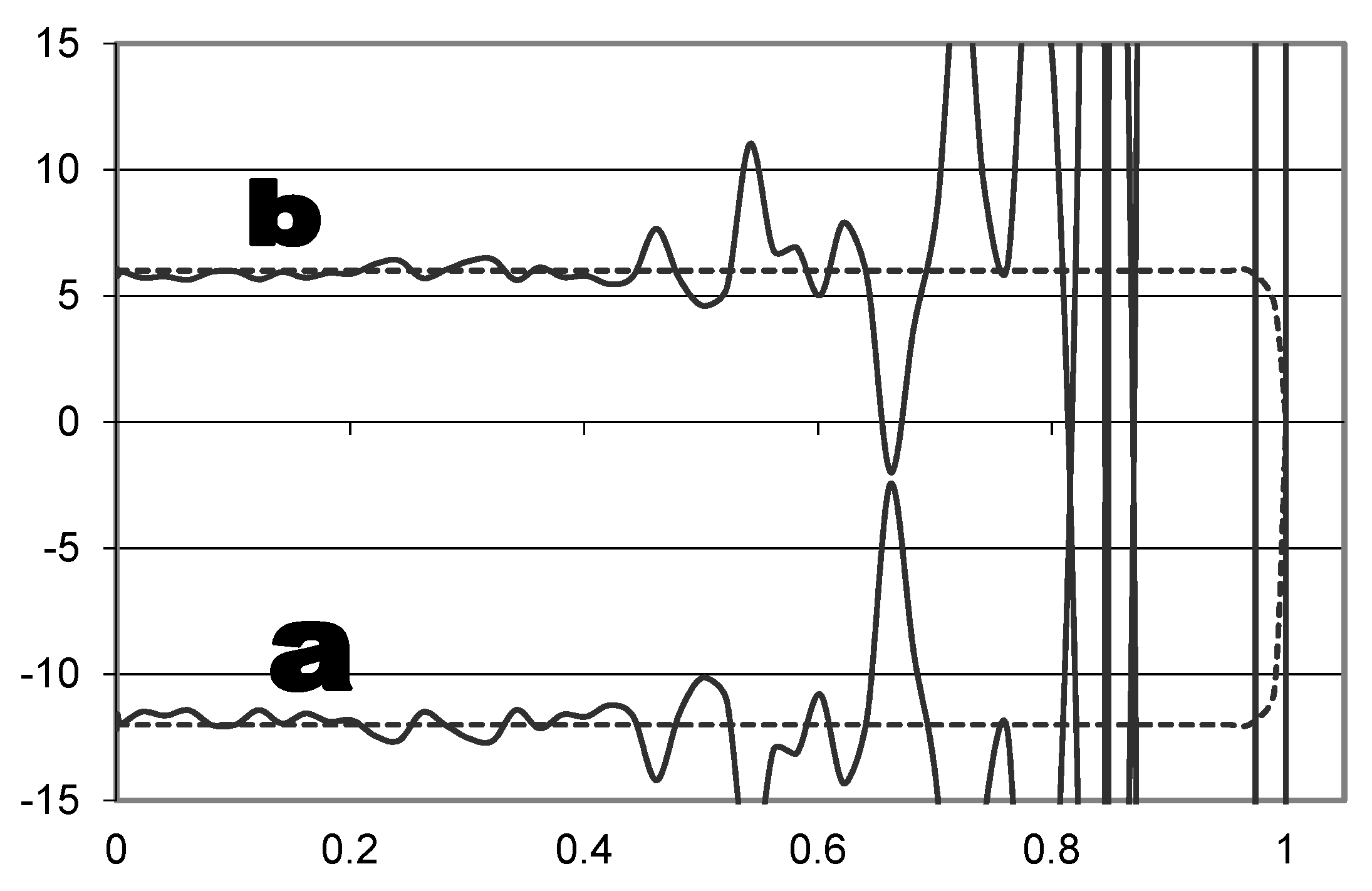
- Apply the Adjoint Equations per Equations (12) and (14), which result in Equations (13) and (15), respectively, and are plotted in Figure 1b.Integrating (14)
- Rewrite the Hamiltonian Minimization Condition in Equation (8) by substituting Equation (9).
- Substituting Equation (15) into Equation (16) produces Equation (17).
ASIDE: We’ll see in the next section how to implement the more general optimum control and solve for constants a and b as time, t progresses. That controller is referred to as the continuous predictive optimal closed-loop controller.
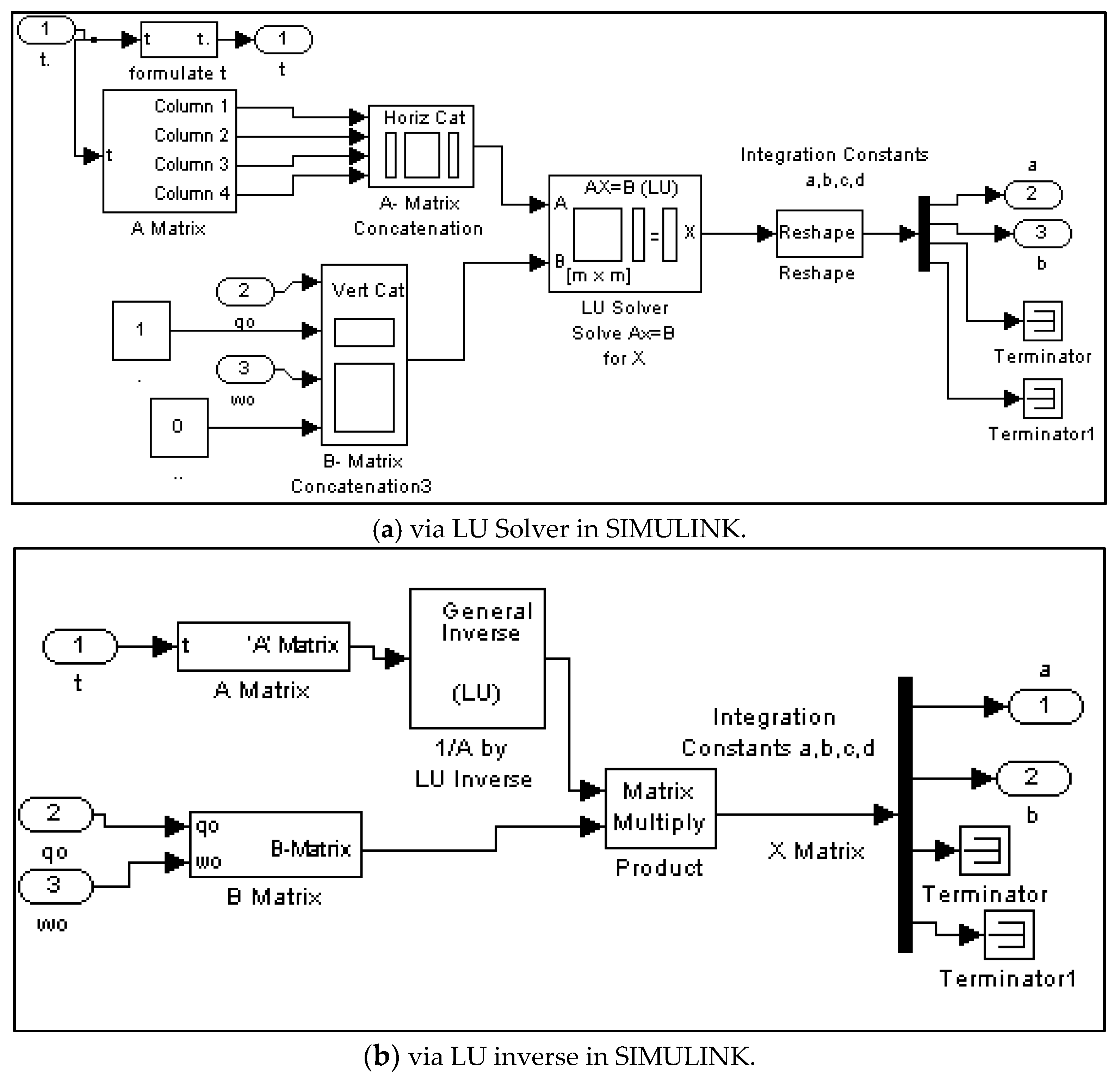
2.2. Continuous Predictive Closed Loop Optimum Controller
- Recall Equations (18)–(20) where yields:
- Set up a matrix equation in the form simulated in Figure 3.
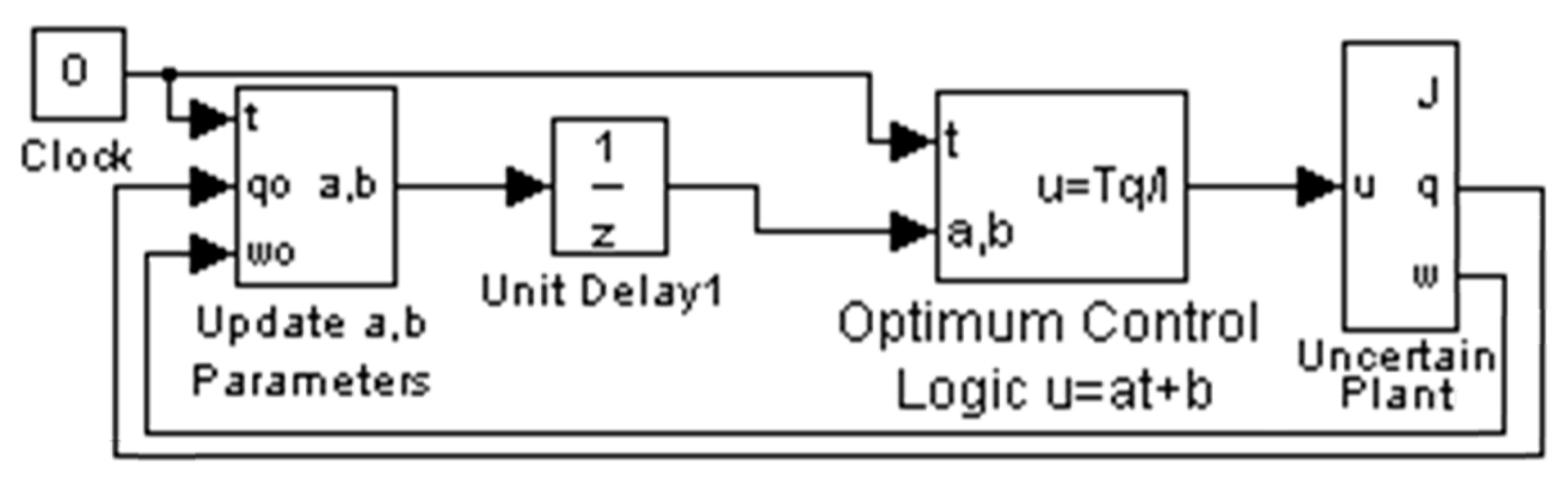
2.3. Sampled-Data Predictive Optimum Controller
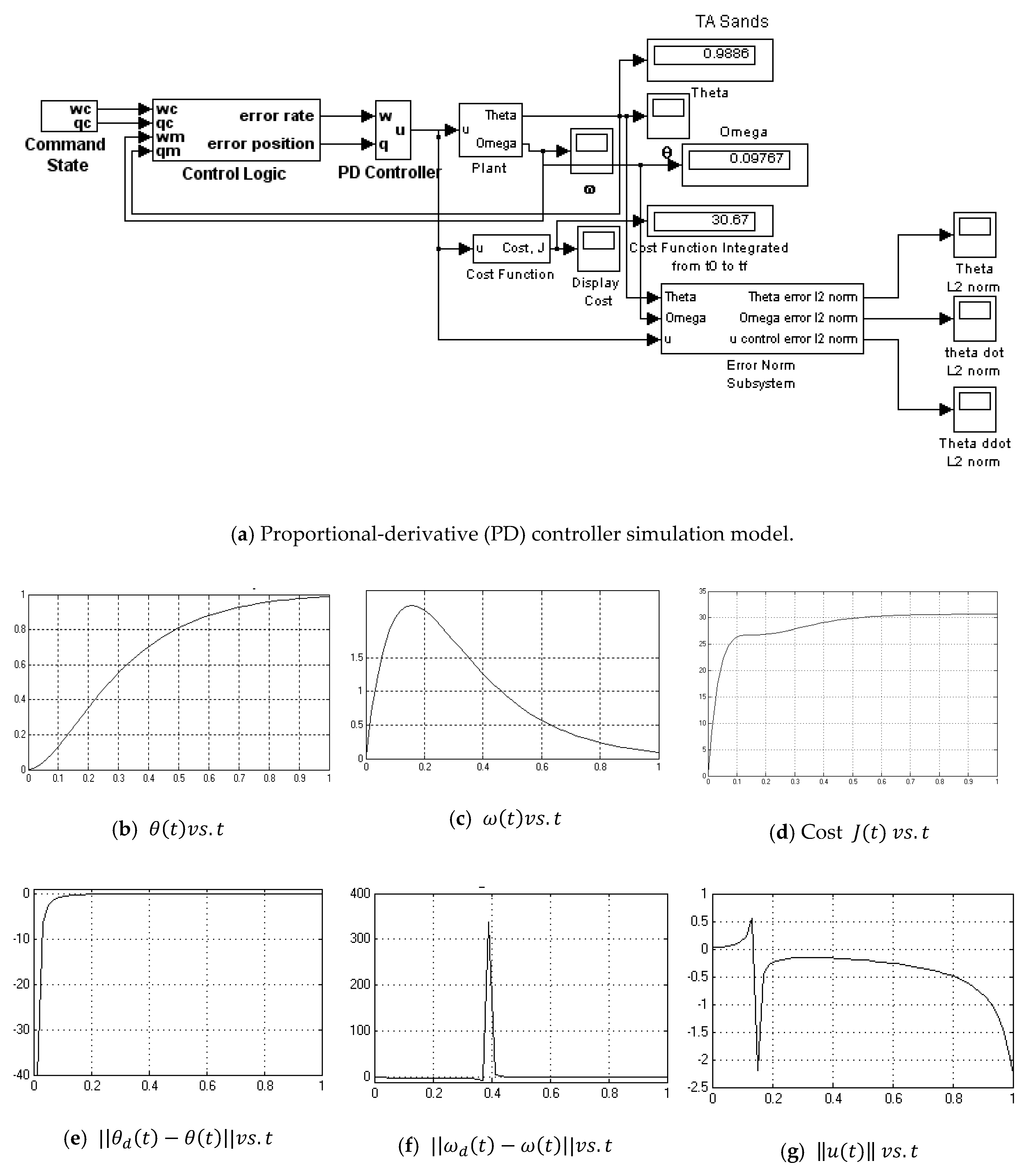
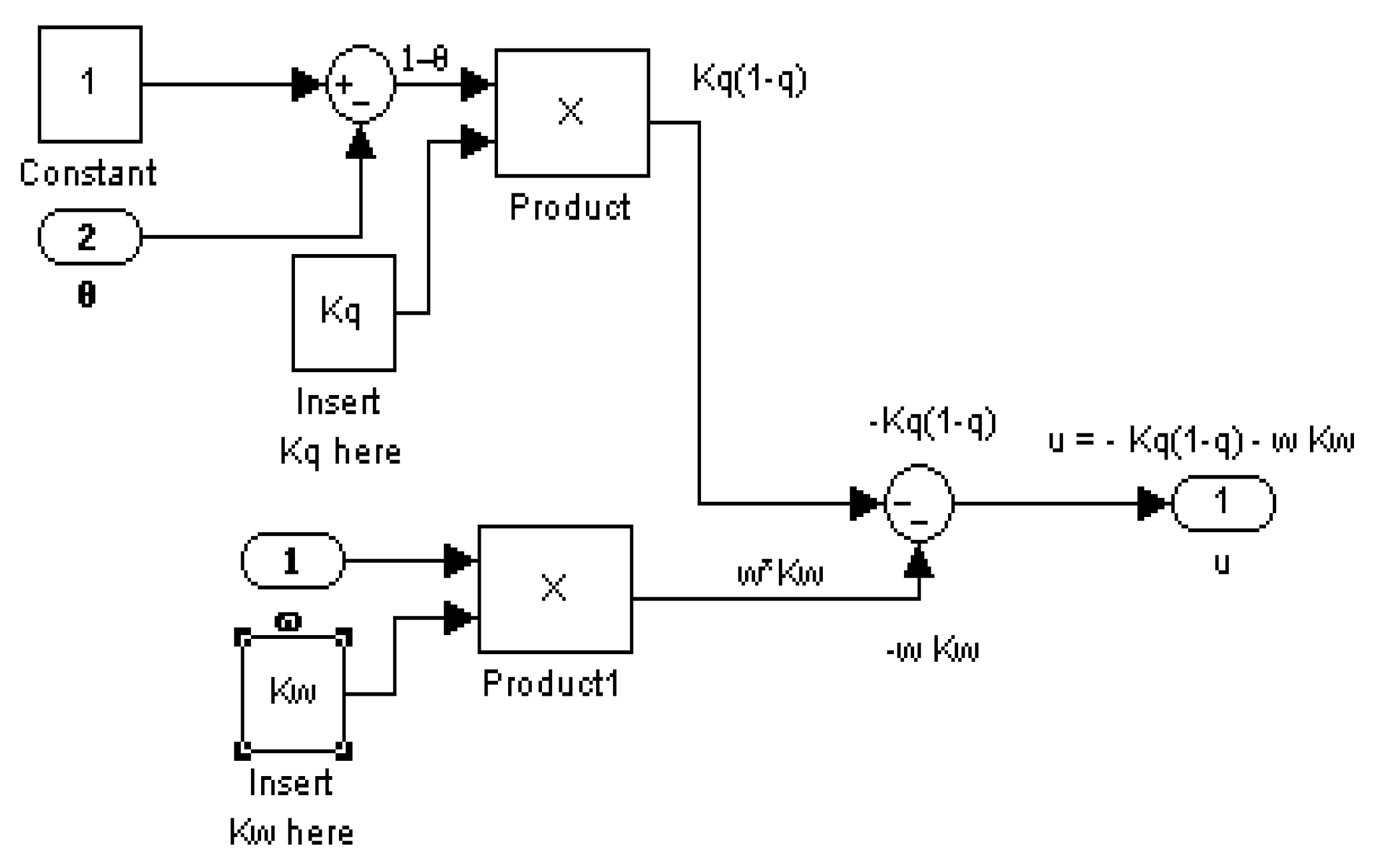
2.4. Proportional Plus Derivative (PD) Controller Derived Foremost from an Optimization Problem
Definingand, the optimum controlas a function of the time may be written as a function of states:where the K’s are feedback gains that are functions of the θ and ω error.
2.5. Feedforward/Feedback PD Controller
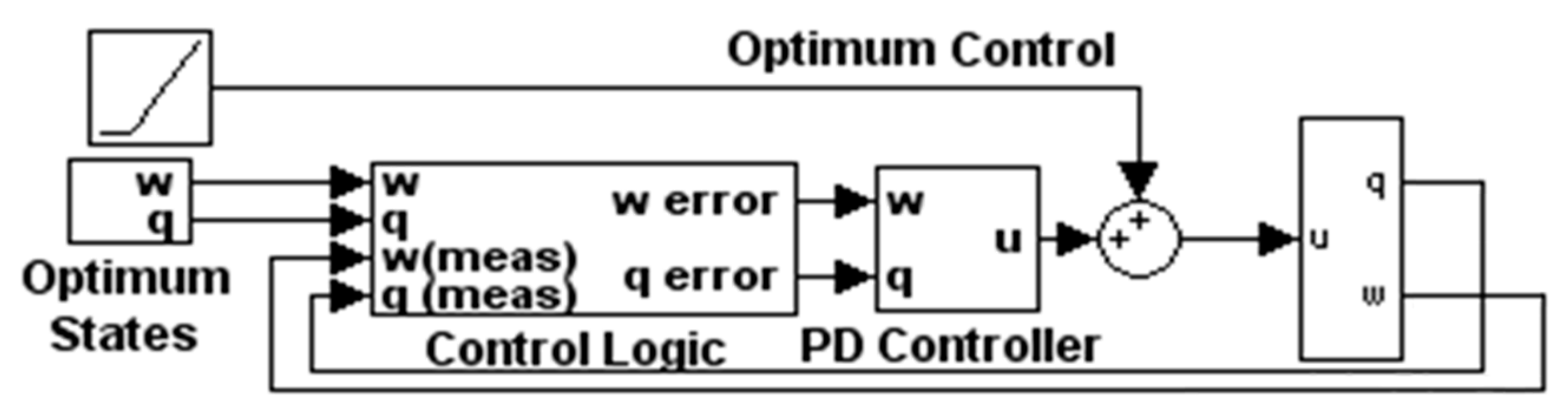
2.6. Two-DOF Controller: Optimal Control Augmented with Feedback Errors Calcuated with Optimal States
3. Results
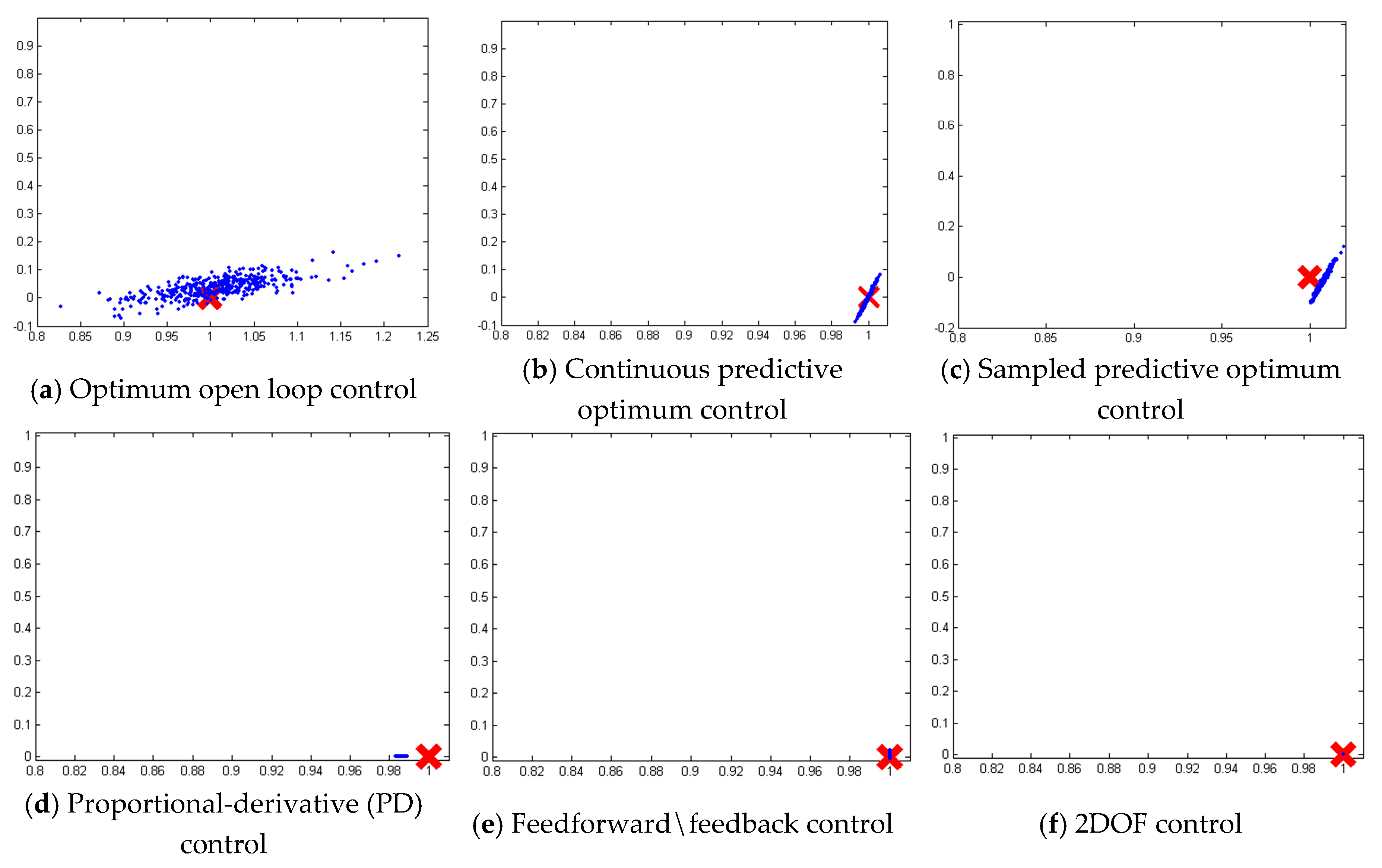
3.1. Monte Carlo Analysis on a Deterministic Plant with Noise
3.2. Open Loop Optimal Controller
3.3. Continuous-Update Optimal Controller
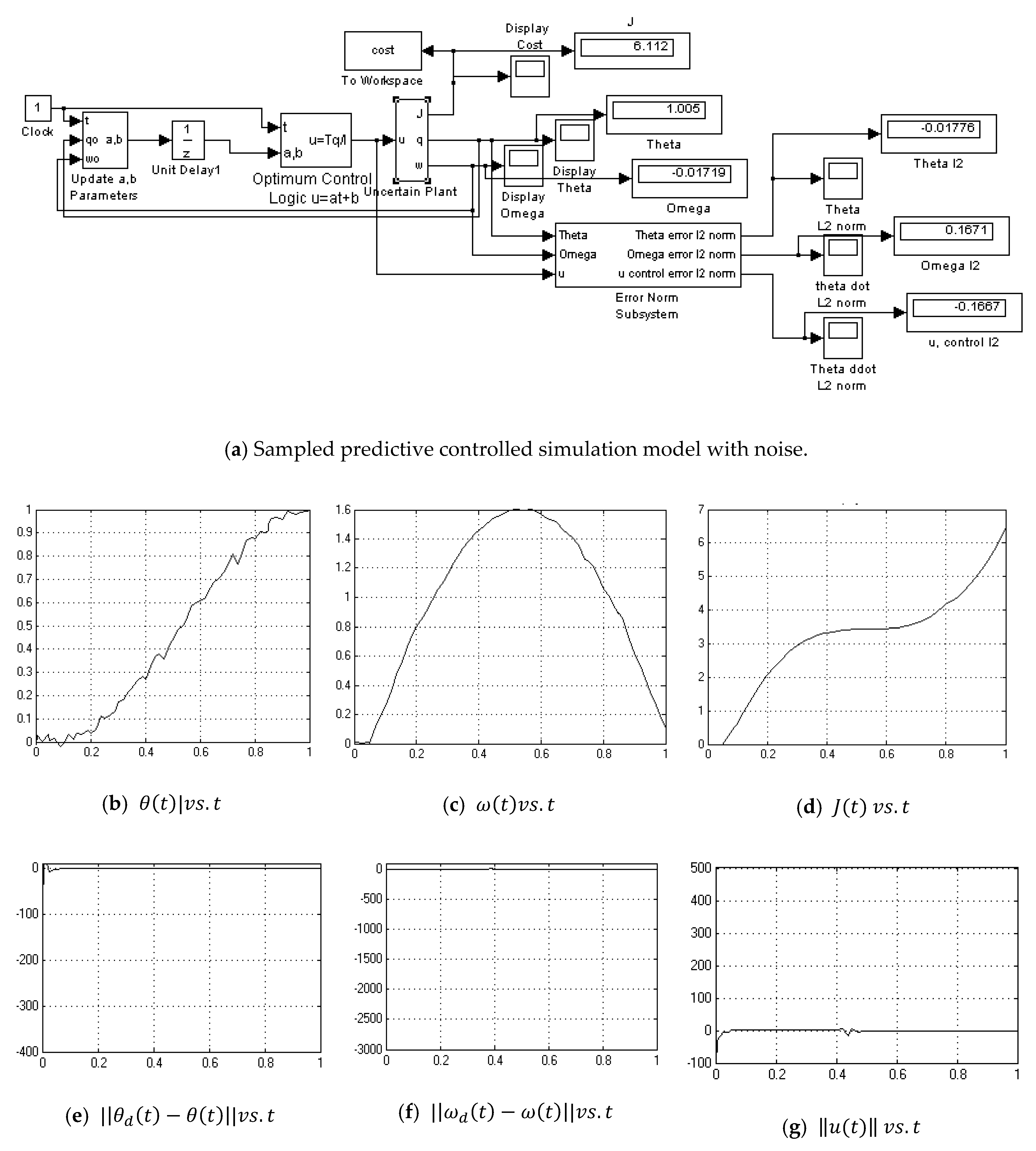
3.4. Sample-Predictive Optimum Controller
3.5. PD Control Derived Foremost from an Optimization Problem
3.6. Feedforward/Feedback PD Controller
3.7. Two-DOF Controller: Optimal Control Augmented with Feedback Errors Calcuated with Optimal States
3.8. Monte Carlo Analysis on a Mismodeled Plant with Noise
4. Discussion
Proposed 2DOF control designed foremost as an optimization problem: The open-loop optimal control is used as a feedforward, while the optimal states derived from a time-parameterized optimal control are compared to the feedback signal to generate the error fed to the feedback controller whose gains are a reparameterization of the optimal solution.
5. Future Works
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- Optimum Open Loop no noise (Figure A1)
- Optimum Open Loop with noise (Figure A2)
- PD Controller no noise (Figure A3)
- PD Controller with noise (Figure A4)
- Continuous Predictive Optimum no noise (Figure A5)
- Continuous Predictive Optimum with noise (Figure A6)
- Feedforward/Feedback PD no noise (Figure A7)
- Feedforward/Feedback PD with noise (Figure A8)
- 2DOF PD Controller no noise (Figure A9)
- 2DOF PD Controller with noise (Figure A10)
- Sampled Predictive Controller without Noise (Figure A11)
- Sampled Predictive Controller with Noise (Figure A12)
- Mis-modeled Plant (Figure A13)
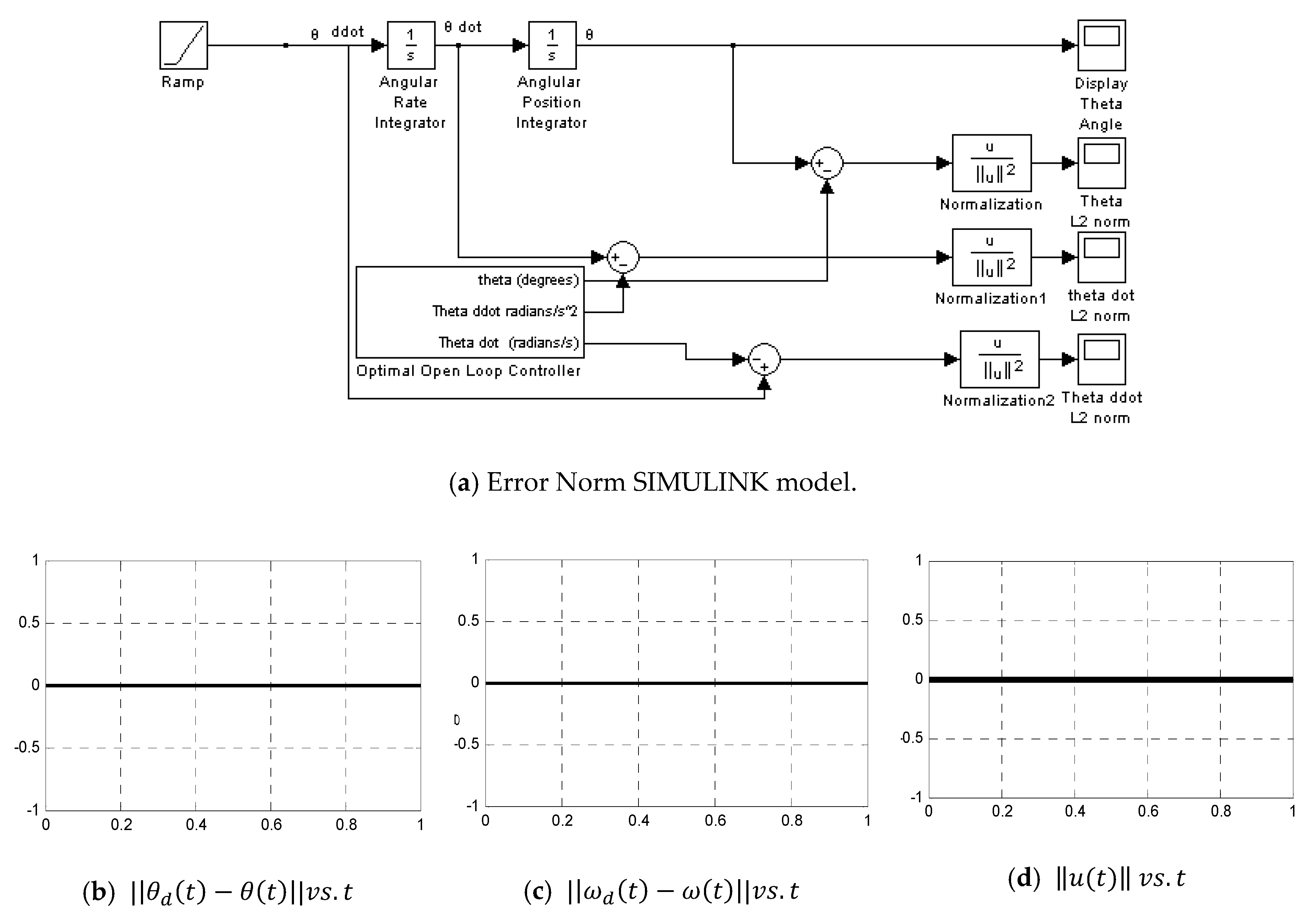
- Error Norms (Figure A14)
Appendix A.1. Optimum Open Loop Controller-No Noise
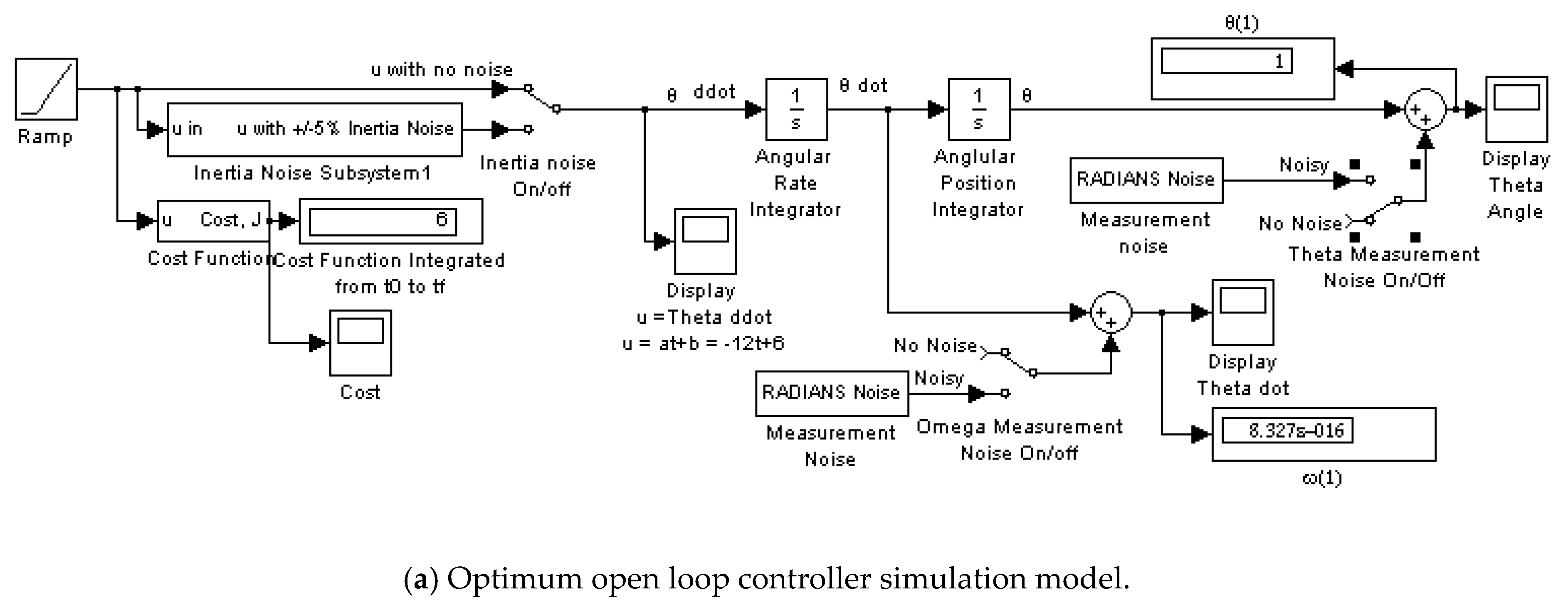
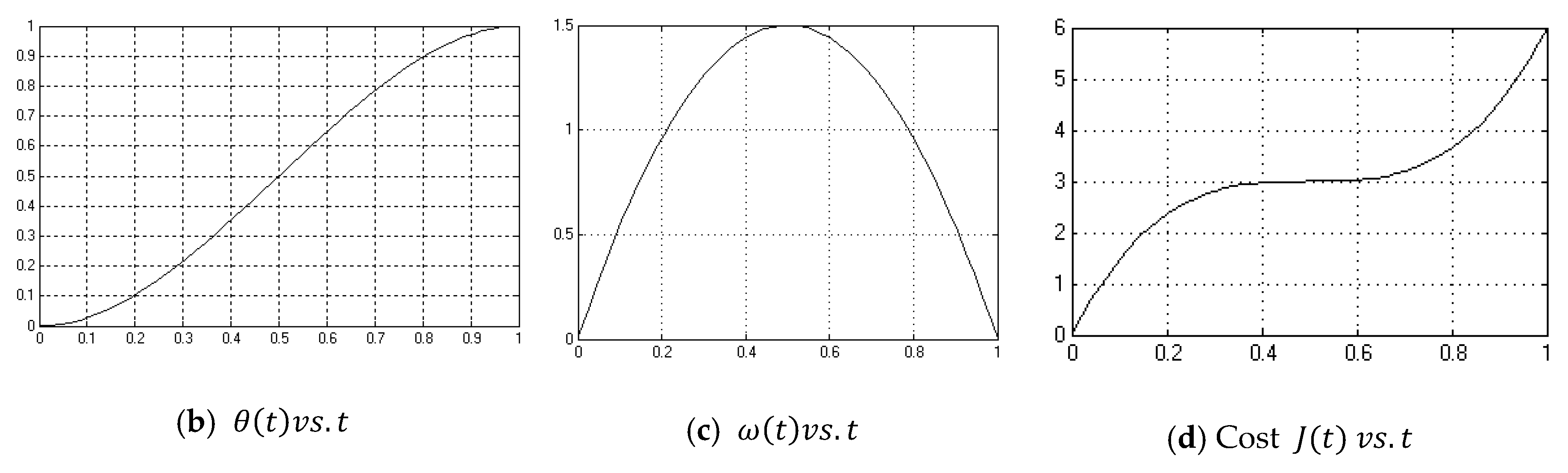
Appendix A.2. Optimum Open Loop Controller-with Noise
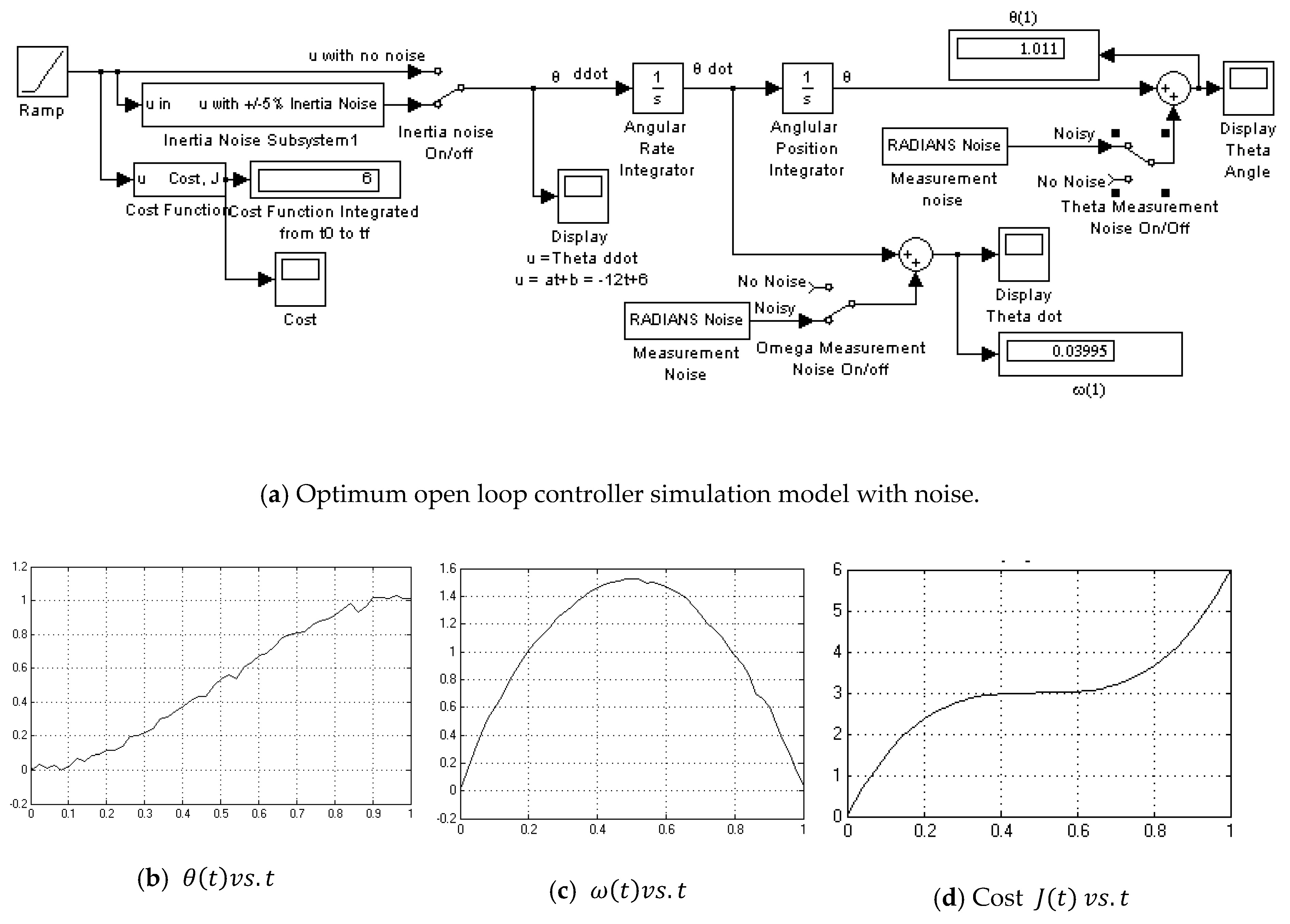
Appendix A.3. PD Controller No Noise
Appendix A.4. PD Controller with Noise
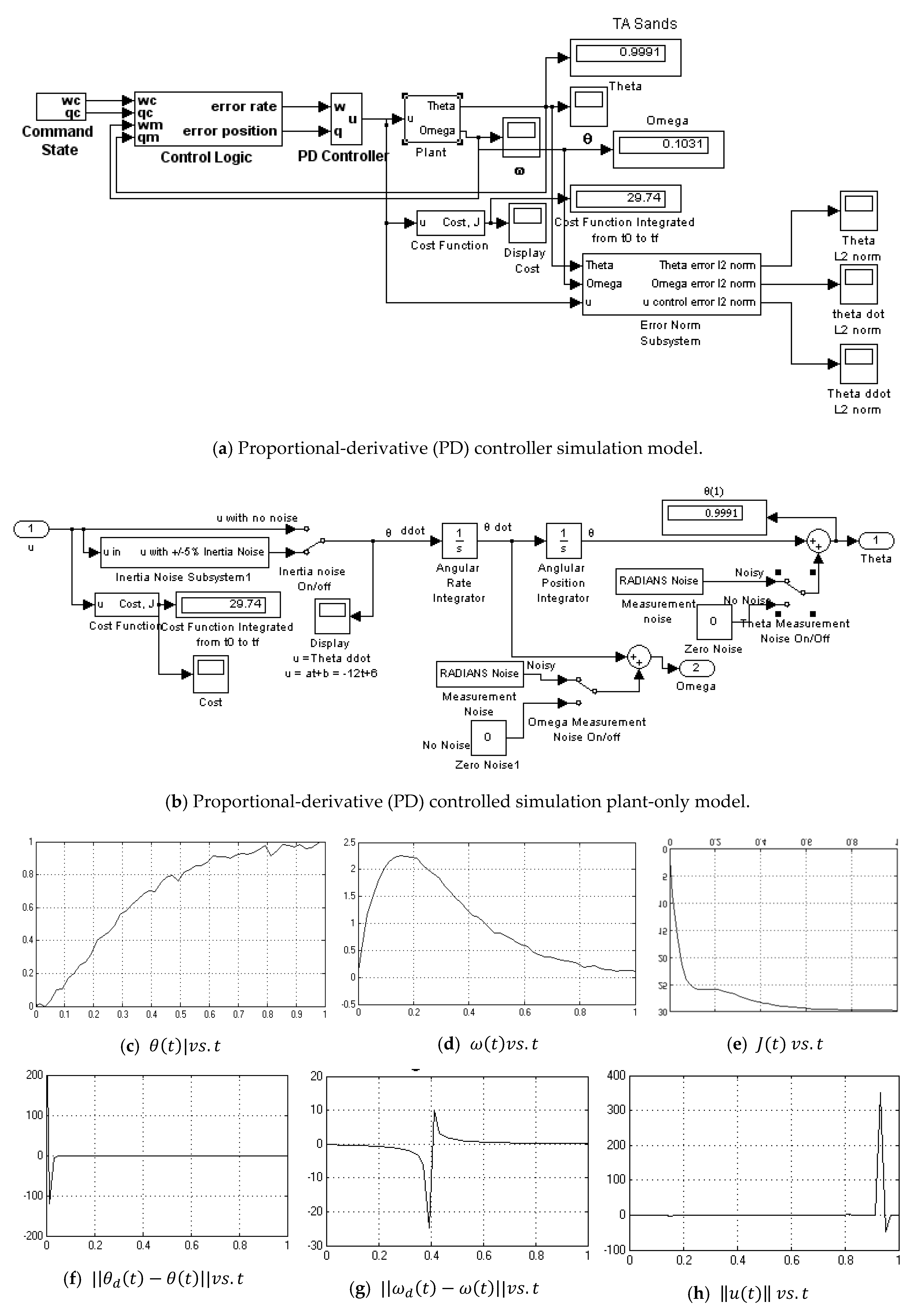
Appendix A.5. Continuouse Predictive Optimum Controller-No Noise
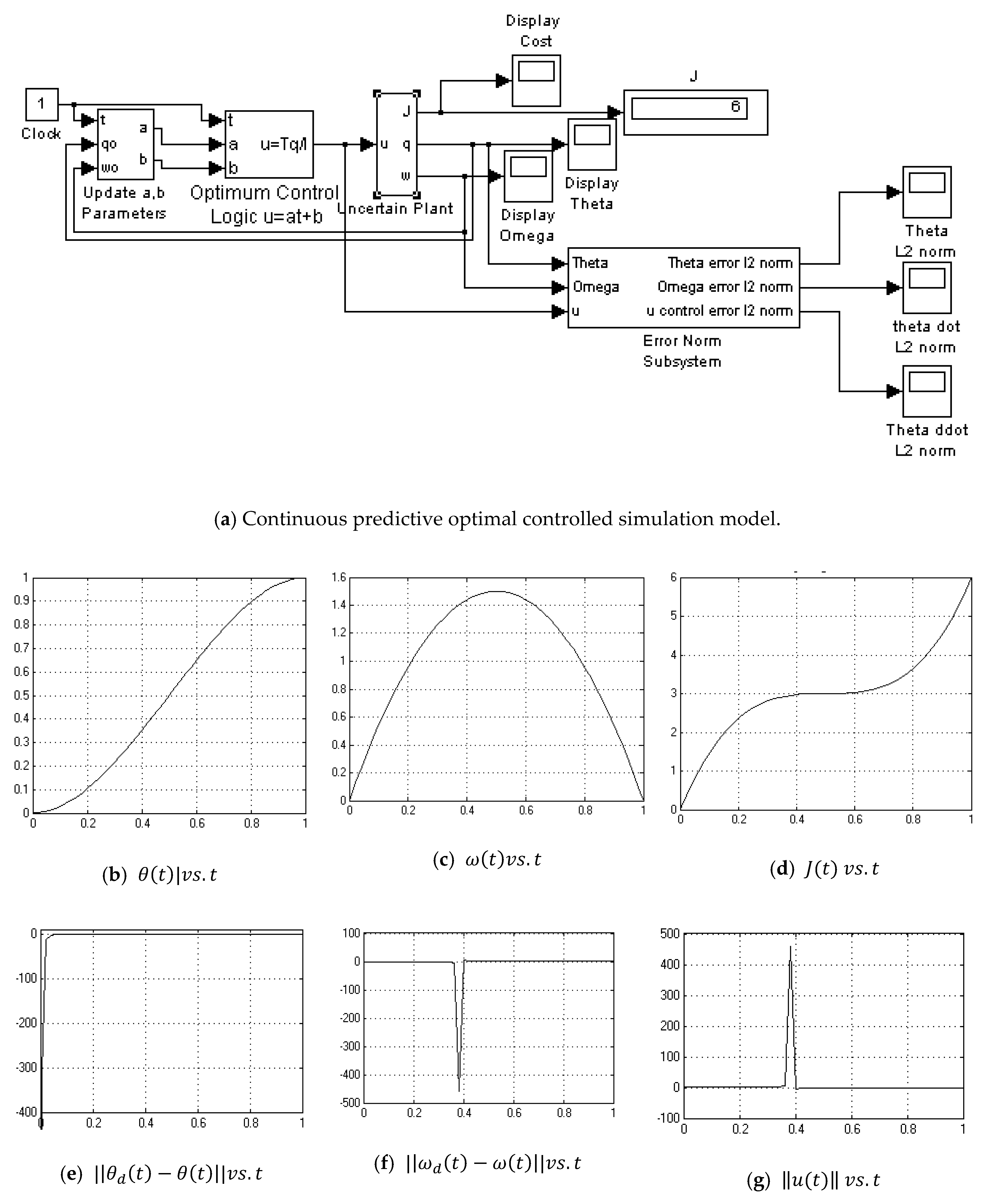
Appendix A.6. Continuouse Predictive Optimum Controlle-with Noise
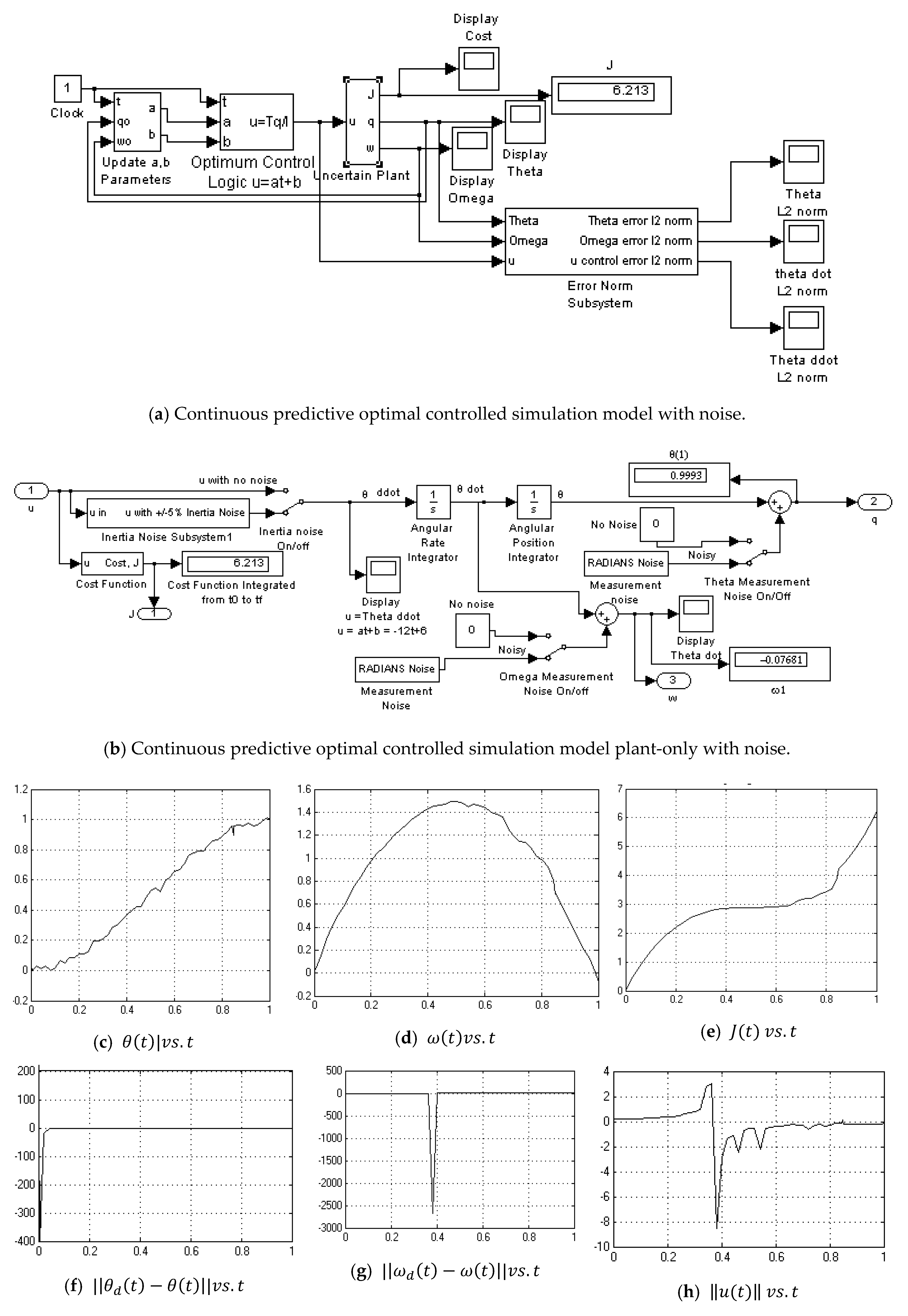
Appendix A.7. Feedforward/Feedback PD Controller-No Noise
Appendix A.8. Feedforward/Feedback PD Controlle-with Noise
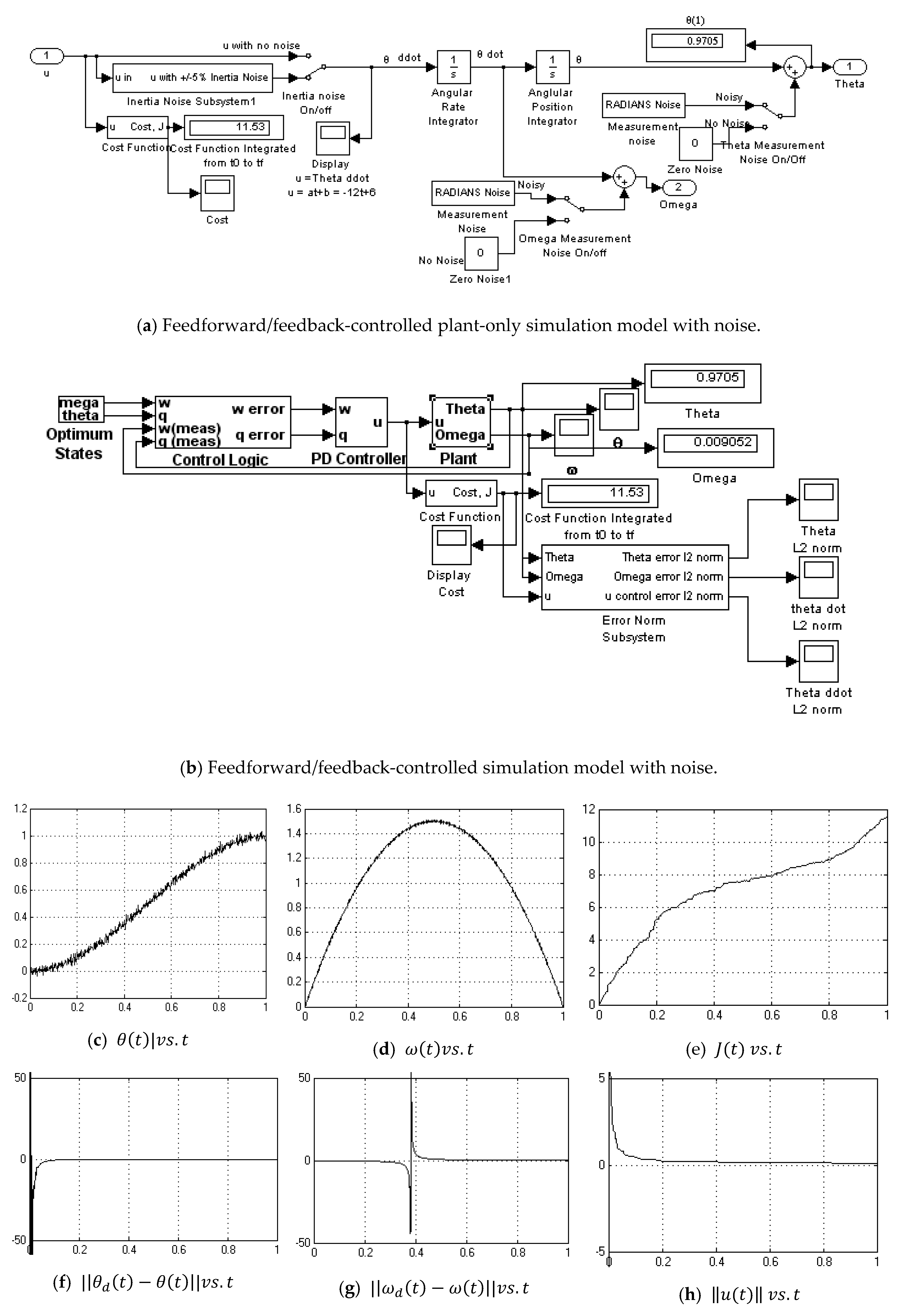
Appendix A.9. 2DOF PD Controller-No Noise
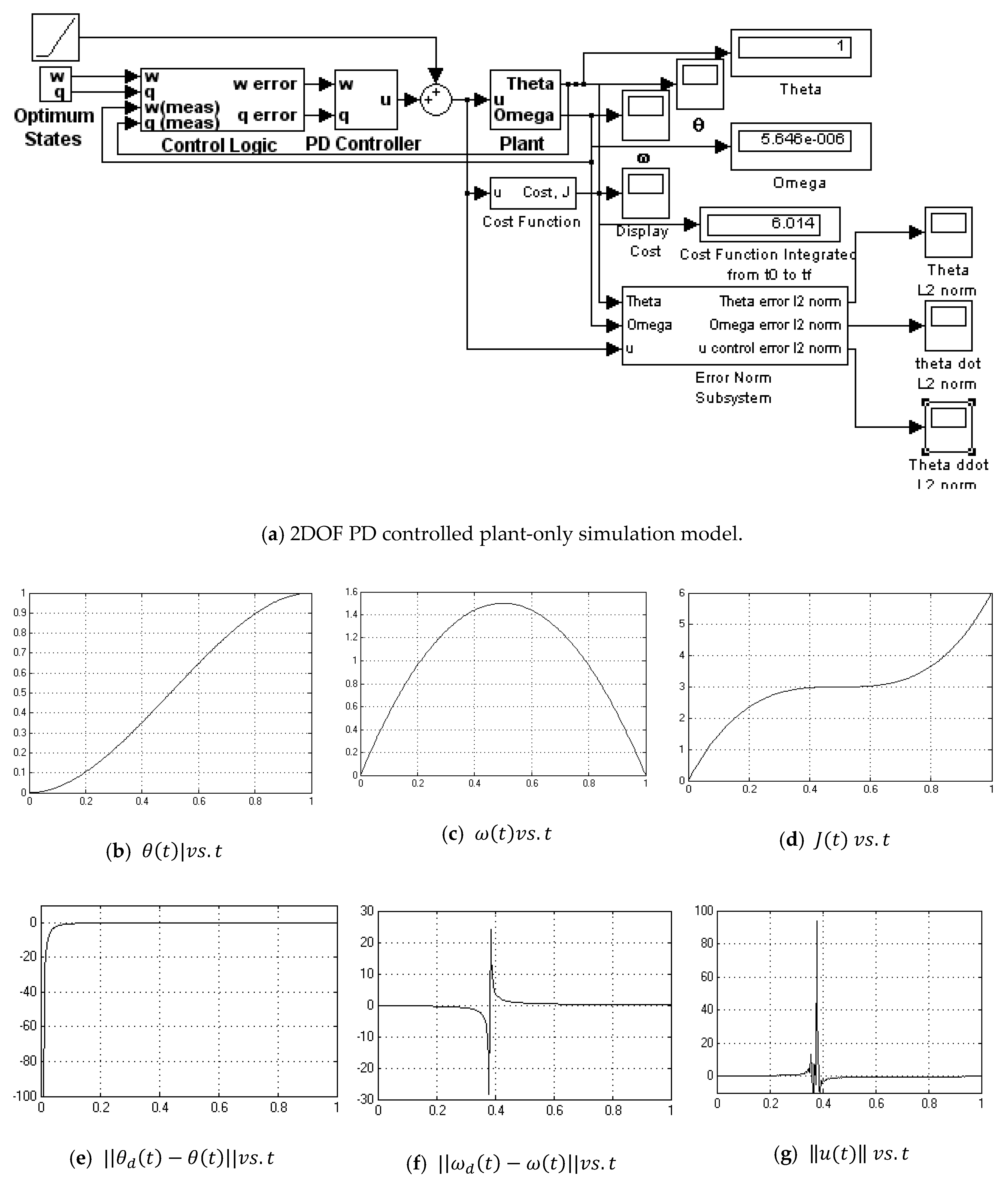
Appendix A.10. 2DOF PD Controller-with Noise
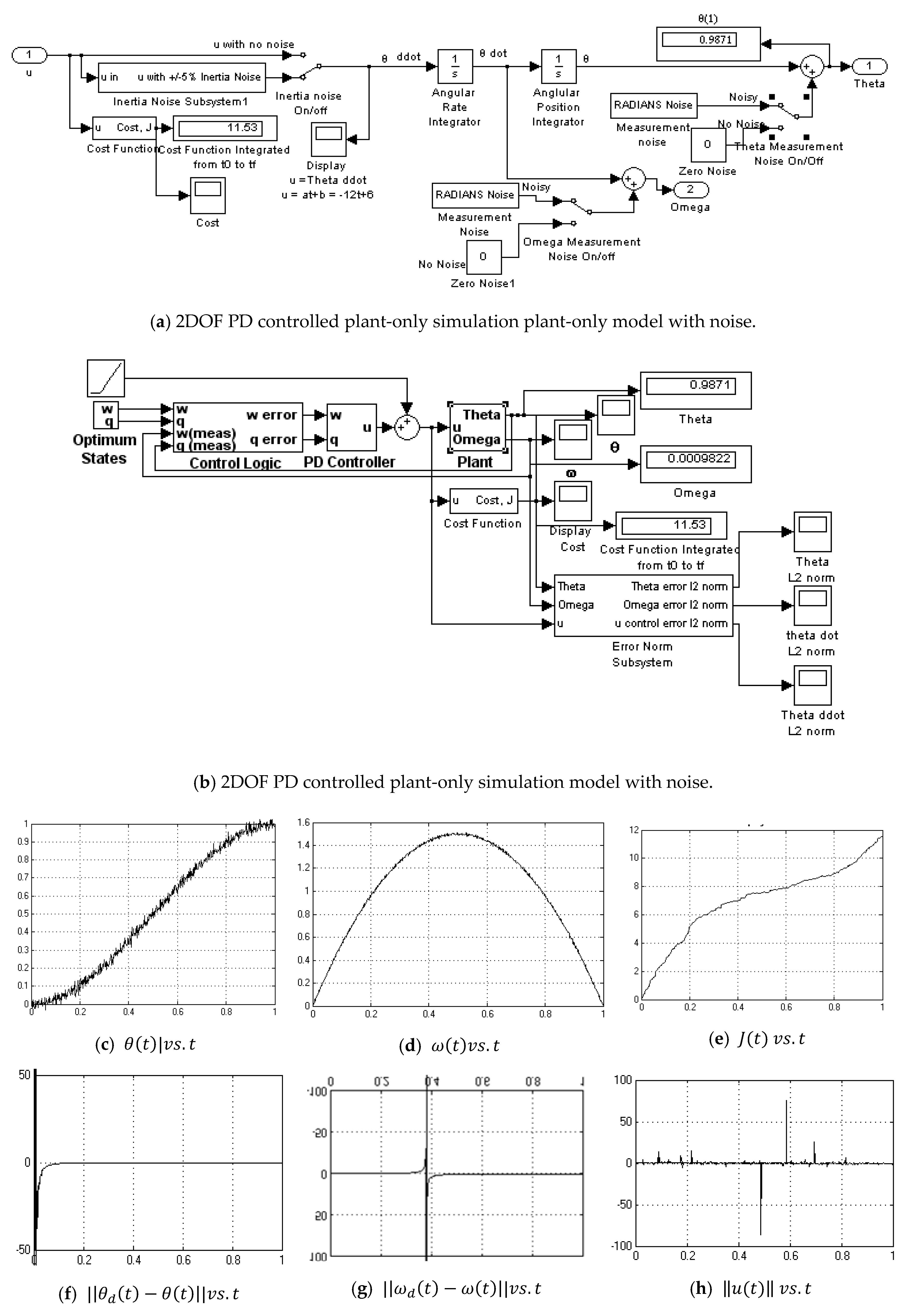
Appendix A.11. Sampled Predictive Controller-without Noise
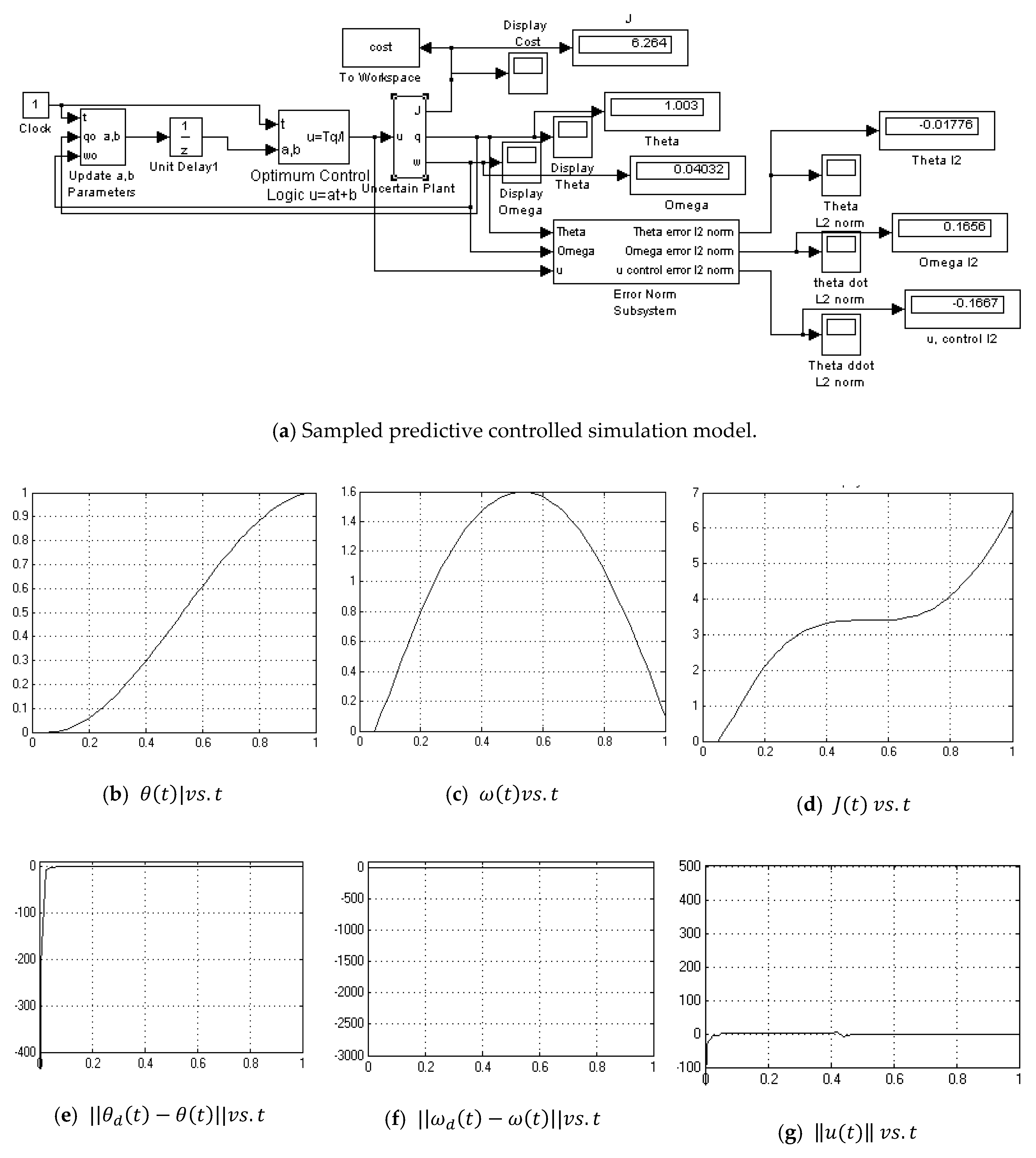
Appendix A.12. Sampled Predictive Controller-with Noise
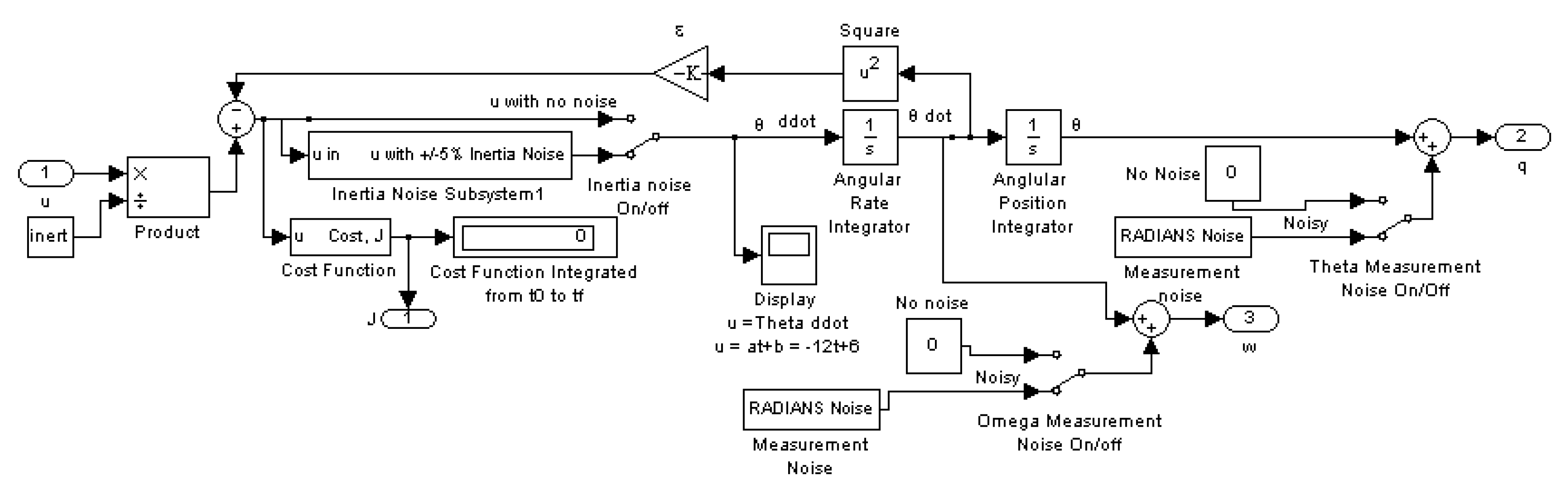
Appendix A.13. Mismodeled Plant
Appendix A.14. Error Norms
References
- Chasles, M. Note sur les propriétés générales du système de deux corps semblables entr’eux. Bull. Sci. Math. Astron. Phys. Chem. 1830, 14, 321–326. (In French) [Google Scholar]
- Euler, L. Formulae Generales pro Translatione Quacunque Corporum Rigidorum (General Formulas for the Translation of Arbitrary Rigid Bodies. Novi Comment. Acad. Sci. Petropolitanae 1776, 20, 189–207. Available online: https://math.dartmouth.edu/~euler/docs/originals/E478.pdf (accessed on 2 November 2019).
- Newton, I. Principia, Jussu Societatis Regiæ ac Typis Joseph Streater; Cambridge University Library: London, UK, 1687. [Google Scholar]
- Turner, A.J. The Time Museum. I: Time Measuring Instruments; Part 3: Water-Clocks, Sand-Glasses, Fire-Clocks; The Museum: Rockford, IL, USA, 1984; ISBN 0-912947-01-2. [Google Scholar]
- Lewis, F.L. Applied Optimal Control and Estimation; Prentice-Hall: Upper Saddle River, NJ, USA, 1992. [Google Scholar]
- Raol, J.; Ayyagari, R. Control Systems: Classical, Modern, and AI-Based Approaches; CRC Press, Taylor and Francis: Boca Raton, FL, USA, 2020. [Google Scholar]
- Wiener, N. Extrapolation, Interpolation, and Smoothing of Stationary Time Series; Wiley: New York, NY, USA, 1949; ISBN 978-0-262-73005-1. [Google Scholar]
- Bellman, R.E. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957; ISBN 0-486-42809-5. [Google Scholar]
- Pontryagin, L.S.; Boltyanskii, V.G.; Gamkrelidze, R.V.; Mischenko, E.F. The Mathematical Theory of Optimal Processes; Neustadt, L.W., Ed.; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Ross, I.M. A Primer on Pontryagin’s Principle in Optimal Control, 2nd ed.; Collegiate Publishers: London, UK, 2015. [Google Scholar]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35. [Google Scholar] [CrossRef]
- Anderson, B.D.O.; Moore, J.B. Optimal Control—Linear Quadratic Methods; Prentice-Hall: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Astrom, K.J.; Bjorn Wittenmark, B. Adaptive Control, 2nd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Slotine, J.J.; Weiping Li, W. Applied Nonlinear Control; Pearson: London, UK, 1991. [Google Scholar]
- Fossen, T.I. Comments on Hamiltonian Adaptive Control of Spacecraft. IEEE Trans. Autom. Control 1993, 38, 671–672. [Google Scholar] [CrossRef]
- Sands, T.; Kim, J.J.; Agrawal, B. Improved Hamiltonian adaptive control of spacecraft. In Proceedings of the Aerospace Conference, Big Sky, MT, USA, 7–14 March 2009; pp. 1–10. [Google Scholar]
- Sands, T. Fine Pointing of Military Spacecraft; Naval Postgraduate School: Monterey, CA, USA, 2007. [Google Scholar]
- Sands, T. Physics-Based Control Methods, Chapter 2, in Advances in Spacecraft Systems and Orbit Determination; InTechOpen: London, UK, 2012. [Google Scholar]
- Sands, T.; Kim, J.J.; Agrawal, B. Spacecraft Adaptive Control Evaluation; Infotech@Aerospace: San Juan, Puerto Rico, 2012. [Google Scholar]
- Sands, T. Improved magnetic levitation via online disturbance decoupling. Phys. J. 2015, 1, 272–280. [Google Scholar]
- Sands, T.; Armani, C. Analysis, correlation, and estimation for control of material properties. J. Mech. Eng. Autom. 2018, 8, 7–31. [Google Scholar]
- Lobo, K.; Lang, J.; Starks, A.; Sands, T. Analysis of deterministic artificial intelligence for inertia modifications and orbital disturbances. Int. J. Control Sci. Eng. 2018, 8, 53–62. [Google Scholar]
- Nakatani, S.; Sands, T. Simulation of spacecraft damage tolerance and adaptive controls. In Proceedings of the Aerospace, Big Sky, MT, USA, 1–8 March 2014; pp. 1–16. [Google Scholar]
- Nakatani, S.; Sands, T. Autonomous damage recovery in space. Int. J. Autom. Control Intell. Syst. 2016, 2, 23–36. [Google Scholar]
- Sands, T. Nonlinear-Adaptive mathematical system identification. Computation 2017, 5, 47. [Google Scholar] [CrossRef]
- Cooper, M.; Heidlauf, P.; Sands, T. Controlling chaos—Forced van der pol equation. Mathematics 2017, 5, 70. [Google Scholar] [CrossRef]
- Sands, T. Space system identification algorithms. J. Space Explor. 2017, 6, 138. [Google Scholar]
- Sands, T. Phase lag elimination at all frequencies for full state estimation of spacecraft attitude. Phys. J. 2017, 3, 1–12. [Google Scholar]
- Nakatani, S.; Sands, T. Battle-Damage tolerant automatic controls. Electr. Electron. Eng. 2018, 8, 23. [Google Scholar]
- Baker, K.; Cooper, M.; Heidlauf, P.; Sands, T. Autonomous trajectory generation for deterministic artificial intelligence. Electr. Electron. Eng. 2018, 8, 59–68. [Google Scholar]
- Sands, T.; Bollino, K. Autonomous Underwater Vehicle Guidance, Navigation, and Control, chapter in Autonomous Vehicles; InTechOpen: London, UK, 2018; Available online: https://www.intechopen.com/online-first/autonomous-underwater-vehicle-guidance-navigation-and-control (accessed on 2 November 2019). [CrossRef]
- Sands, T.; Bollino, K.; Kaminer, I.; Healey, A. Autonomous Minimum Safe Distance Maintenance from Submersed Obstacles in Ocean Currents. J. Mar. Sci. Eng. 2018, 6, 98. [Google Scholar] [CrossRef]
- Sidhu, H.S.; Siddhamshetty, P.; Kwon, J.S. Approximate Dynamic Programming Based Control of Proppant Concentration in Hydraulic Fracturing. Mathematics 2018, 6, 132. [Google Scholar] [CrossRef]
- Gao, S.; Zheng, Y.; Li, S. Enhancing Strong Neighbor-Based Optimization for Distributed Model Predictive Control Systems. Mathematics 2018, 6, 86. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, R.; Bao, J. A Novel Distributed Economic Model Predictive Control Approach for Building Air-Conditioning Systems in Microgrids. Mathematics 2018, 6, 60. [Google Scholar] [CrossRef]
- Xue, D.; El-Farra, N.H. Forecast-Triggered Model Predictive Control of Constrained Nonlinear Processes with Control Actuator Faults. Mathematics 2018, 6, 104. [Google Scholar] [CrossRef]
- Wong, W.C.; Chee, E.; Li, J.; Wang, X. Recurrent Neural Network-Based Model Predictive Control for Continuous Pharmaceutical Manufacturing. Mathematics 2018, 6, 242. [Google Scholar] [CrossRef]
- Sands, T.; Kenny, T. Experimental piezoelectric system identification. J. Mech. Eng. Autom. 2017, 7, 179–195. [Google Scholar]
- Sands, T. Deterministic Artificial Intelligence; InTechOpen: London, UK, 2019; ISBN 978-1-78984-111-4. [Google Scholar]
- Sands, T. Optimization Provenance of Whiplash Compensation for Flexible Space Robotics. Aerospace 2019, 6, 93. [Google Scholar] [CrossRef]
- Lee, J.H.; Ricker, N.L. Extended Kalman Filter Based Nonlinear Model Predictive Control. In Proceedings of the American Control Conference, San Francisco, CA, USA, 2–4 June 1993. [Google Scholar]
- Wang, C.; Ohsumi, A.; Djurovic, I. Model Predictive Control of Noisy Plants Using Kalman Predictor and Filter. In Proceedings of the IEEE TECON, Beijing, China, 28–31 October 2002. [Google Scholar]
- Sørensenog, K.; Kristiansen, S. Model Predictive Control for an Artificial Pancreas. Bachelor’s Thesis, Technical University of Denmark, Lyngby, Denmark, 2007. [Google Scholar]
- Huang, R.; Patwardhan, S.C.; Biegler, L.T. Robust stability of nonlinear model predictive control with extended Kalman filter and target setting. Int. J. Rob. Nonlinear Control 2012, 23, 1240–1264. [Google Scholar] [CrossRef]
- Hong, M.; Cheng, S. Model Predictive Control Based on Kalman Filter for Constrained Hammerstein-Wiener Systems. Math. Probl. Eng. 2013, 6, 2013. [Google Scholar] [CrossRef]
- Ikonen, E. Model Predictive Control and State Estimation; University of Oulu: Oulu, Finland, 2013; Available online: http://cc.oulu.fi/~iko/SSKM/SSKM2016-MPC-SE.pdf (accessed on 2 November 2019).
- Binette, J.-C.; Srinivasan, B. On the Use of Nonlinear Model Predictive Control without Parameter Adaptation for Batch Processes. Processes 2016, 4, 27. [Google Scholar] [CrossRef]
- Cao, Y.; Kang, J.; Nagy, Z.K.; Laird, C.D. Parallel Solution of Robust Nonlinear Model Predictive Control Problems in Batch Crystallization. Processes 2016, 4, 20. [Google Scholar] [CrossRef]
- Ganesh, H.S.; Edgar, T.F.; Baldea, M. Model Predictive Control of the Exit Part Temperature for an Austenitization Furnace. Processes 2016, 4, 53. [Google Scholar] [CrossRef]
- Jost, F.; Sager, S.; Le, T.T.-T. A Feedback Optimal Control Algorithm with Optimal Measurement Time Points. Processes 2017, 5, 10. [Google Scholar] [CrossRef]
- Xu, K.; Timmermann, J.; Trächtler, A. Nonlinear Model Predictive Control with Discrete Mechanics and Optimal Control. In Proceedings of the IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017. [Google Scholar]
- Suwartadi, E.; Kungurtsev, V.; Jäschke, J. Sensitivity-Based Economic NMPC with a Path-Following Approach. Processes 2017, 5, 8. [Google Scholar] [CrossRef]
- Vaccari, M.; Pannocchia, G. A Modifier-Adaptation Strategy towards Offset-Free Economic MPC. Processes 2017, 5, 2. [Google Scholar] [CrossRef]
- Kheradmandi, M.; Mhaskar, P. Data Driven Economic Model Predictive Control. Mathematics 2018, 6, 51. [Google Scholar] [CrossRef]
- Durand, H. A Nonlinear Systems Framework for Cyberattack Prevention for Chemical Process Control Systems. Mathematics 2018, 6, 169. [Google Scholar] [CrossRef]
- Tian, Y.; Luan, X.; Liu, F.; Dubljevic, S. Model Predictive Control of Mineral Column Flotation Process. Mathematics 2018, 6, 100. [Google Scholar] [CrossRef]
- Wu, Z.; Durand, H.; Christofides, P.D. Safeness Index-Based Economic Model Predictive Control of Stochastic Nonlinear Systems. Mathematics 2018, 6, 69. [Google Scholar] [CrossRef]
- Liu, S.; Liu, J. Economic Model Predictive Control with Zone Tracking. Mathematics 2018, 6, 65. [Google Scholar] [CrossRef]
- Bonfitto, A.; Castellanos Molina, L.M.; Tonoli, A.; Amati, N. Offset-Free Model Predictive Control for Active Magnetic Bearing Systems. Actuators 2018, 7, 46. [Google Scholar] [CrossRef]
- Godina, R.; Rodrigues, E.M.G.; Pouresmaeil, E.; Matias, J.C.O.; Catalão, J.P.S. Model Predictive Control Home Energy Management and Optimization Strategy with Demand Response. Appl. Sci. 2018, 8, 408. [Google Scholar] [CrossRef]
- Khan, H.S.; Aamir, M.; Ali, M.; Waqar, A.; Ali, S.U.; Imtiaz, J. Finite Control Set Model Predictive Control for Parallel Connected Online UPS System under Unbalanced and Nonlinear Loads. Energies 2019, 12, 581. [Google Scholar] [CrossRef]
- Yoo, H.-J.; Nguyen, T.-T.; Kim, H.-M. MPC with Constant Switching Frequency for Inverter-Based Distributed Generations in Microgrid Using Gradient Descent. Energies 2019, 12, 1156. [Google Scholar] [CrossRef]
- Zhang, J.; Norambuena, M.; Li, L.; Dorrell, D.; Rodriguez, J. Sequential Model Predictive Control of Three-Phase Direct Matrix Converter. Energies 2019, 12, 214. [Google Scholar] [CrossRef]
- Baždarić, R.; Vončina, D.; Škrjanc, I. Comparison of Novel Approaches to the Predictive Control of a DC-DC Boost Converter, Based on Heuristics. Energies 2018, 11, 3300. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z. Suppression Research Regarding Low-Frequency Oscillation in the Vehicle-Grid Coupling System Using Model-Based Predictive Current Control. Energies 2018, 11, 1803. [Google Scholar] [CrossRef]
- Maxim, A.; Copot, D.; Copot, C.; Ionescu, C.M. The 5W’s for Control as Part of Industry 4.0: Why, What, Where, Who, and When—A PID and MPC Control Perspective. Inventions 2019, 4, 10. [Google Scholar] [CrossRef]

| Controller | Deviation, | Mean Error, | Deviation, | Mean Error, | Mean Cost, J |
|---|---|---|---|---|---|
| Optimal open loop | 0.0328 | 0.0439 | 0.03 | 0.045 | 5.9787 |
| Continuous predictive | 0.0015 | 0.002 | 0.0192 | 0.0251 | 6.0117 |
| Sampled predictive | 0.0031 | 0.0074 | 0.0249 | 0.0321 | 6.1137 |
| Proportional-derivative (PD) | 9.66 × 10−4 | 1.41 × 10−2 | 3.14 × 10−16 | 1.02 × 10−15 | 59.6885 |
| Feedforward + feedback | 7.86 × 10−16 | 9.83 × 10−16 | 0.0058 | 0.0087 | 8.4507 |
| 2DOF | 7.07 × 10−16 | 1.02 × 10−15 | 1.89 × 10−15 | 2.51 × 10−15 | 8.619 |
| Controller | Deviation, | Mean Error, | Deviation, | Mean Error, | Mean Cost, J |
|---|---|---|---|---|---|
| Optimal open loop | 0.034 | 0.044 | 0.0283 | 0.0484 | 6.004 |
| Continuous predictive | 0.0015 | 0.0019 | 0.02 | 0.025 | 6.0137 |
| Sampled predictive | 0.0029 | 0.007 | 0.0222 | 0.0307 | 6.0183 |
| Proportional-derivative (PD) | 9.89 × 10−4 | 0.014 | 3.12 × 10−16 | 1.02 × 10−15 | 59.3244 |
| Feedforward + feedback | 7.36 × 10−16 | 9.69 × 10−16 | 0.0058 | 0.0086 | 8.9637 |
| 2DOF | 6.42 × 10−16 | 9.02 × 10−16 | 1.90 × 10−15 | 2.56 × 10−15 | 7.8284 |
| Controller | Benefits | Weakness |
|---|---|---|
| Optimal open loop | Establishes optimal case | Not realistically implementable |
| Continuous predictive * | Good cost and position | High rate error and deviation |
| Sampled predictive * | Good cost and position | High rate error and deviation |
| Proportional-derivative (PD) * | Best rate control | Worst cost |
| Feedforward + feedback | Best position control | Slight rate error and deviation |
| 2DOF * | All-around good | Slightly higher cost than optimal |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sands, T. Comparison and Interpretation Methods for Predictive Control of Mechanics. Algorithms 2019, 12, 232. https://doi.org/10.3390/a12110232
Sands T. Comparison and Interpretation Methods for Predictive Control of Mechanics. Algorithms. 2019; 12(11):232. https://doi.org/10.3390/a12110232
Chicago/Turabian StyleSands, Timothy. 2019. "Comparison and Interpretation Methods for Predictive Control of Mechanics" Algorithms 12, no. 11: 232. https://doi.org/10.3390/a12110232
APA StyleSands, T. (2019). Comparison and Interpretation Methods for Predictive Control of Mechanics. Algorithms, 12(11), 232. https://doi.org/10.3390/a12110232





