Abstract
The characteristic of the satellite repeat shift time can reflect the status of the satellite operation, and is also one of the key factors of the sidereal filtering multipath correction. Although some methods have been developed to calculate the repeat shift time, few efforts have been made to analyze and compare the performance of this feature for the GPS (Global Positioning System), BDS (BeiDou System), and Galileo in depth. Hence, three methods used for calculating the repeat shift time are presented, and used to compare and analyze the three global systems in depth, named the broadcast ephemeris method (BEM), correlation coefficient method (CCM), and aspect repeat time method (ARTM). The experiment results show that the repeat shift time of each satellite is different. Also, the difference between the maximum and minimum varies from different systems. The maximum difference is about 25 s for the BDS IGSO (Inclined Geosynchronous Orbit) and the minimum is merely 10 s for the GPS system. Furthermore, for the same satellite, the shift time calculated by the three methods is almost identical, and the maximum difference is only about 7 s between the CCM and the ARTM method for the BDS MEO (Medium Earth Orbit) satellite. Although the repeat shift time is different daily for the same satellite and the same method, the changes are very small. Moreover, in terms of the STD (Standard Deviation) of the BS (between satellites) and MS (mean shift for the same satellite), the GPS system is the best, the performance of the BDS system is medium, and the Galileo performs slightly worse than the GPS and BDS.
1. Introduction
For global navigation systems, the satellite has the characteristic of a repeat period, which means that the satellite will appear in the same position with a period for the ground static user. Not only can this feature of the satellite be used to predict the satellite position, but it can also mitigate multipath errors and observation noise effectively. Besides, the repeat period characteristic of the satellite can also reflect the status of satellite operation and assess the stability of the whole system operation to a certain extent.
In order to calculate the orbital repeat shift time of the satellite, some effective methods have been proposed in the literature. The satellite repeat shift time was first pointed out by Genrich et al. [1] which was mainly used to reduce multipath disturbance. After that, authors [2,3,4,5] also used the satellite repeat shift time to reduce the noise for long baselines or isolate signals from multipath error. However, all of them assumed that the shift time between two consecutive days for the same satellite was about 4 min for a GPS satellite. Seeber et al. [6] pointed out that the satellite repeat shift time of the GPS satellite is slightly different for each satellite between 240 and 256 s instead of the assumed 236 s, but the calculation process was not given. Choi et al. [7] adopted broadcast ephemeris values and Kepler’s third law to estimate the satellite repeat period of the GPS satellite, and the results showed that the repeat periods of the satellites are not precisely a sidereal day and are distinct from each satellite. This method was also adopted by Wu and Hsieh [8] and Ye et al. [9]. Moreover, Wang et al. [10] and Chen et al. [11] used the broadcast ephemeris to analyze the satellite repeat shift time for the Beidou satellite. Su et al. [12] analyzed the GPS satellite by applying the broadcast ephemeris method, which showed that the mean shift time of each satellite is different. Particularly, for a satellite undergoing a maneuver, the mean shift time is significantly different from that of other satellites.
Taking advantage of the correlation method, Ge et al. [13] observed the repeat shift time by the correlation coefficient method for the GPS satellite first. Ragheb et al. [14] proposed the use of the auto-correlation technique to determine the repeat shift time for a GPS satellite. Wang et al. [15] analyzed the repeat shift time of a Beidou GEO satellite by utilizing the Fourier transform, correlation, and wavelet transform methods. The results indicated that the satellite repeat shift time ranges from 220 to 270 s. Similarly, Ning et al. [16] employed correlation analysis, Fourier transformation, and wavelet decomposition methods to estimate the repeat shift time for Beidou IGSO and MEO satellites. Larson et al. [17] developed the cross-correlation method to determine the repeat shift time for the GPS satellite. Furthermore, Zhao et al. [18] also introduced this method to analyze the characteristics of the Beidou satellite’s orbit.
Moreover, Agnew and Larson [19] proposed the aspect repeat time method to determine the repeat shift time for the GPS satellite, and the experiment results indicated that the mean repeat shift time calculated by this method is 246 s and the fluctuations through the day are as much as 2.5 s at high latitudes. Larson et al. [17] utilized the aspect repeat time method to estimate time-varying and site-dependent shifts for the GPS satellite. Fang [20] compared the broadcast ephemeris method with the aspect repeat time method. Wang et al. [21] also used the aspect repeat time method to calculate the repeat shift time for the Galileo satellite. In addition, Wang et al. [22] compared the three methods by using the GPS satellite, and the results showed that the differences between the repeat shift time from the three methods are less than 1.2 s on average, the broadcast ephemeris method has the lowest computation, and the aspect repeat time method is optimal for real-time applications.
As discussed above, most of the related research has focused on the global GPS and BDS systems based on the broadcast ephemeris strategy. In addition, they have mainly used the characteristic of the satellite repeat shift time to mitigate multipath error or observation noise, but they have not carried out an analysis and systematic study itself. Meanwhile, few efforts have been made to analyze the characteristics of the Galileo system, nor to compare the performance between the three global systems. Therefore, this paper aims to gain more insights into the characteristics of the satellite repeat shift time itself. Furthermore, this characteristic between the global GPS, BDS, and Galileo systems is also compared and analyzed. Since the GLONASS system broadcast ephemeris is different from the other systems, it is not discussed in this article. Finally, the results are discussed and concluded.
2. Two Models for Calculating the Satellite Repeat Period
Prior to the introduction of these two models, the definition of the satellite repeat period, satellite operation period, and the satellite repeat shift time are given. First, the satellite repeat period refers to when the satellite returns to the same position on the sky after a period of running, denoted as TSRP. Since the ground track repeats for a circle in this process, it is also named the revisiting period [23]. As for the satellite operation period, it means the period when the satellite moves around the orbit of itself once in time, denoted as TSOP [19]. Lastly, the satellite repeat shift time is the interval between the precise satellite repeat period and the approximate satellite repeat period by solar days, denoted as TSRST [3].
In terms of the approximate satellite repeat period united in solar days, mainly two methods are used to calculate it: One is based on the orbit offset coefficient model [24] and the other is based on the simplest fraction model [23]. The specific algorithms are given as following.
2.1. Orbit Offset Coefficient Method
The satellite operation period must be obtained before calculating the satellite repeat period. The satellite operation period means the period of the satellite around the orbit of itself one time. Based on Kepler’s third law, the operation period can be determined as:
where GM (=3.986005 × 1014 m3/s2) is Earth’s gravitational constant, R denotes the mean radius of Earth, and H is the height of the satellite from the ground. Then, the number laps of the satellite around the Earth for one solar day can be calculated by:
where TSOP is counted in minutes, and the 24 × 60 means the time of a solar day united in minutes. Thus, the approximate satellite repeat period united in solar days can be obtained by:
where nint = Integer(n). D means the approximate days of the satellite repeat period and united in solar days. Additionally, d denotes the coefficient of orbit offset, which is the orbital offset relative to the previous day [24]. In the practical calculation, if the satellite orbital offset is westward, the value of d is negative. If the offset is eastward, the value of d is positive. Since the value of d is only given by satellite designers and is unknown for users, another method is adopted to calculate the approximate satellite repeat period.
2.2. Simplest Fraction Method
Similarly, the simplest fraction method is also necessary to calculate the satellite operation period, which is expressed as TSOP. The calculation method is same as the description in Section 2.1. Then, based on the simplest fraction method, the simplest fractions, N and D, can satisfy the following equation:
which means that, after D solar days, the satellite operates N laps, and the satellite orbital ground trajectory begins to repeat. Te is the time interval of the orbit revolving around the Earth one time, which is named the sidereal day. Since TSOP can be calculated by the broadcast ephemeris, the concrete values of N and D can be determined by the search and test process [23]. Similarly, D also means the approximate days of the satellite repeat period united in solar days.
3. Three Methods for Calculating Satellite Repeat Shift TTime
Theoretically, there are mainly three methods to determine the satellite repeat shift time, which include the satellite-based broadcast ephemeris method [7], receiver-based correlation coefficient method [13], and satellite receiver-based aspect repeat time method [19]. In particular, for the correlation coefficient method, it can be further divided into several methods from the correlation type and correlation quantity, such as auto-correlation and cross-correlation. These three methods will be elaborated in the following.
3.1. Broadcast Ephemeris Method
The broadcast ephemeris provides the relevant parameters of the satellite, which includes the semi-major axis of the orbit and the correction to the mean motion of the satellite. Hence, the effective mean motion is obtained by a small correction to the third Kepler law, which is expressed by:
where is the Earth’s universal gravitational constant (1.996498 × 107 in SI units), a denotes the semi-major axis of the orbit ellipse, and Δn denotes the correction to the mean motion, which is the difference between the mean motion of the satellite calculated by the precise ephemeris and the mean motion obtained by the given parameters (rad/s). Therefore, the accurate satellite operation period, TSOP, in inertial space can be expressed by:
Hence, the satellite repeat shift time, TSRFT, can be defined as:
where D is the approximate solar days of the satellite repeat period, which is calculated in Section 2. TMSD is the duration of a mean solar day in seconds. N denotes the number of laps of the satellite operations around the orbit of itself in D solar days. TSOP is the precise satellite repeat period in seconds, which is obtained by Equations (5) and (6).
Although the orbit operation period of GNSS satellites are roughly the same, their satellite repeat period varies largely. As for the GPS system, in the reference frame on the rotating Earth, since the satellite repeat time of the satellite relative to a static position in the ground is two times more than its satellite operation period, the precise satellite repeat period, TGSRP, for GPS satellites is given by:
However, unlike the GPS system, the satellite repeat period of other navigation systems has its own characteristics. For example, as for the Galileo system satellite, the repeat period of the satellite relative to the ground is 17 times its orbit operation period during 10 sidereal days. Then, the repeat period TGASRP for Galileo satellites is determined by:
Similarly, the repeat period of BDS satellites can also be derived, and is summarized as follows:
where TBSRP and TBMSRP denote the repeat period of BDS GEO/IGSO and MEO satellites, respectively.
Then, the satellite repeat shift time of the same satellite can be determined by:
where TGSRFT and TGASRFT mean the repeat shift time of the GPS and Galileo satellite, respectively. Additionally, TBSRFT and TBMSRFT denote the repeat shift time of the BDS GEO/IGSO and BDS MEO satellite, respectively.
3.2. Correlation Coefficient Method
Essentially, the correlation coefficient method is a mathematical analysis algorithm, which is mainly used to analyze the correlation between variables. Let X(n) and Y(n) be random variables, and n is the dimension of each variable. The correlation coefficient of the two variables is given as:
where Cov(X,Y) is the co-variance of the two variables, and Var[X] and Var[Y] are the variance of the variable X and Y, respectively. If X and Y are two groups of data of the consecutive observations for the same satellite, the satellite repeat shift time (TS) can be estimated by:
where Ft is the sampling of the observations, and τm is the epoch of the correlation coefficient that keeps the maximum. In order to calculate the repeat shift time accurately, the sample rate of the observation data must be 1 Hz. It is only in this way that the shift time can reach the seconds level.
It is worth noting that, from the correlation coefficient aspect, the repeat period of the satellite can be estimated by different quantities, such as the residuals of the single difference in the observation domain and the residuals of the position in the coordinate domain. Both of them can achieve the shift time of the repeat period for the same satellite by this method, and there is not much difference between them.
3.3. Aspect Repeat Time Method
For the static receiver on the ground, what we are most interested in is the repeat period of the satellite in the same vector direction of the receiver to satellite. Assume that the unit vector of the receiver to satellites is x0(t0) on the epoch t0 in the reference day for the first time it is observed, and the other vector is x1(t1) on the epoch t1 in the subsequent day for the second time it is observed after a repetition period. It is noted that, the epochs t0 and t1 are counted from zero for every solar day. If the angle between the two unit vectors x0(t0) and x1(t1) reaches the minimum value, the satellite repeat shift time can be determined:
where Ft is the sampling of the observations and t1 is the epoch of the second time it is observed. The process of the calculation involves the following steps and is presented in Figure 1:
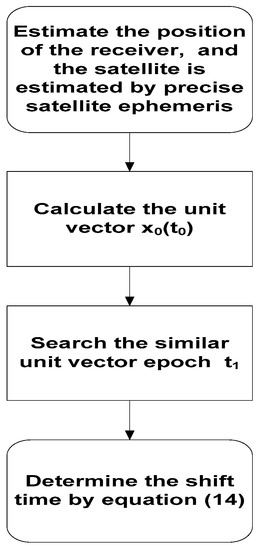
Figure 1.
Flowchart of the aspect repeat time method.
1) Estimate the receiver position, and the satellite position is also estimated by the precise satellite ephemeris on the given reference epoch t0;
2) Calculate the unit vector of the receiver to satellite at the epoch t0, and express it as x0(t0);
3) Search the epoch t1, which has a similar unit vector x1(t1) to the initial vector x0(t0) during the repeat period; and
4) Determine the satellite repeat shift time of this epoch by Equation (14).
4. Experiments and Analysis
In order to analyze and compare the characteristic of the satellite repeat shift time for current global systems more comprehensively, all three methods were used to calculate the shift time. Multi-GNSS data collected from 10 to 30 June 2018 at two stations in the Asia-Pacific region were collected. The two stations are located in Australia, named CUT0 and CUT2, respectively. The sampling rate of the dataset was 1 Hz and the mask angle was 15°. It should be noted that the use of the quantity of the CCM method is the single-difference observations between receivers, and the observations were denoised by a filter.
4.1. Performance Analysis for the GPS System
Figure 2 demonstrates the results of the mean satellite repeat shift time for the GPS system by three methods during DOY (Day of Year): 161–181, 2018. The blue, red, and green line denote the results calculated by the BEM, CCM, and ARTM methods, respectively. From Figure 2, it can be seen that the mean shift time of the three methods are almost same for most satellites, and the average of the difference between the three methods for all satellites is only 2 s. In addition, the maximum difference between the CCM and the ARTM methods appeared in G32, which is about 4 s. Moreover, for the same method, the mean shift time of each satellite is also different, and the difference between the maximum and minimum reached about 10 s. Statistically, the STD (Standard Deviation) of the satellite repeat shift time between all the satellites for the three algorithms is 2.74 for BEM, 2.68 for CCM, and 2.67 for ARTM.
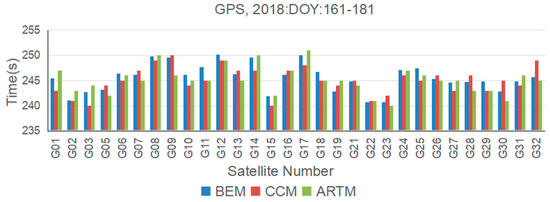
Figure 2.
The mean shift time for GPS satellites calculated by the three methods during DOY: 161–181, 2018.
In order to assess the performance of the fluctuation of the satellite repeat shift time, the STD of the three methods for each satellite is also presented in Figure 3. It is obvious that the STD of the three methods for each satellite is less than 0.5, which is very small. These results indicate that, for the same satellite and calculation method, although the satellite repeat shift time is different every day, the fluctuation is very small. However, the STD of the satellite repeat shift time varies for different satellites. For example, the STD of the G05 satellite is slightly higher than other satellites, and the G08 satellite is more stable than other satellites for all three methods. In addition, for some satellites, the STD performance of the different methods is significantly different, such as the G11 and G27 satellites. Generally, in terms of fluctuation, the performance of the BEM and ARTM methods is more similar for all the satellites.
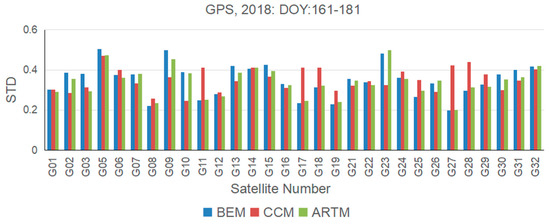
Figure 3.
The STD of the satellite repeat shift time for the three methods for each satellite during the period DOY:161–181, 2018.
It should be noted that in both Figure 2 and Figure 3, the G04 and G20 satellite information is not included. Since G04 is invalid during this period, there is no observation. Additionally, G20 is in the state of maneuvering during this period and the mean repeat shift time is markedly different from other satellites, which is about 187 s during DOY:161–172 and is about 246 s during DOY:173–181 for the BEM method. The STD of these two periods is about 0.56 for the period DOY:161–172 and nearly 0.81 for DOY:173–181, respectively. This phenomenon indicates that the satellite repeat shift time fluctuates more obviously when the satellite is undergoing an orbit maneuver.
4.2. Performance Analysis for the BDS System
Considering the fact that the BDS system includes three types of orbital satellites, they were compared and analyzed separately. First, Figure 4 presents the results of the satellite repeat shift time by the three methods for BDS GEO during DOY:161–181, 2018. Consistent with the theoretical derivation, the mean shift time of the GEO satellites is about 236 s. For the same satellite, the difference between the three methods performs in different ways, and the maximum difference is found in the C04 satellite between the CCM and ARTM, which is about 4 s. However, for the C05 satellite, the results are almost identical to the three methods. In addition, for the same method, the difference of the mean shift time between satellites is not significant, and the maximum difference is only 4 s, which appeared between C04 and C01 for CCM.
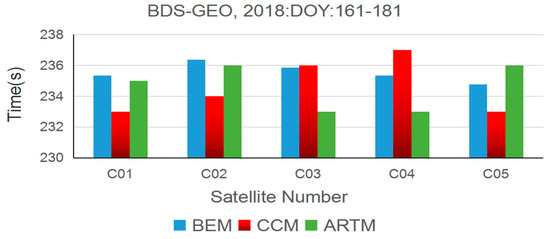
Figure 4.
The mean shift time for BDS GEO satellites calculated by the three methods during DOY: 161–181, 2018.
Similarly, Figure 5 demonstrates the STD of the repeat shift time of the three methods for each satellite during DOY:161–181, 2018. Obviously, the STD of each BDS GEO satellite is relatively high, and the values of the STD are more than 6 for all satellites and methods. This phenomenon indicates that the satellite repeat shift time of GEO satellites obviously fluctuates during this period. In addition, comparing the three methods, it is clear that the STD of CCM is higher than the other two methods for most satellites. This is mainly because the change of the elevation and azimuth is not obvious, since the GEO satellite is almost stationary relative to the ground user.
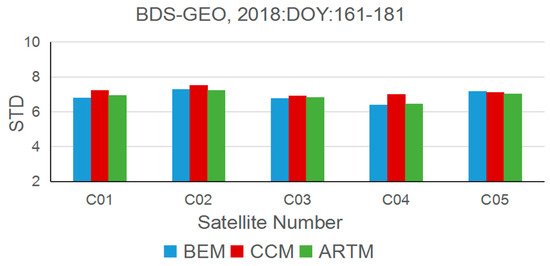
Figure 5.
The STD of the satellite repeat shift time for the three methods for each satellite during the period DOY:161–181, 2018.
Although the GEO and IGSO satellites have similar repeat periods, their orbital operation track is different. Hence, the characteristic of the satellite repeat shift time for IGSO is also different from the GEO satellite. From Figure 6, it is apparent that the mean repeat shift time for the BEM, CCM, and ARTM is almost similar for the same satellite during this period. On the contrary, the mean shift time varies with different satellites, such as C08 and C10; the maximum difference between them is approximately 25 s. In particular, the mean shift time of C08 is much shorter than other IGSO satellites, which is only 225 s during these days.
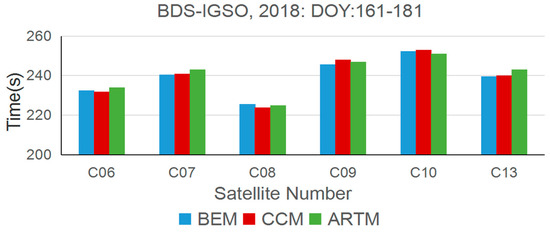
Figure 6.
The mean shift time for BDS IGSO satellites calculated by the three methods during DOY: 161–181, 2018.
Figure 7 demonstrates the results of the STD of the three methods, which was used to evaluate the fluctuation of the BDS IGSO satellites. It is obvious that although the STD of the CCM method is slightly higher than those of the other two methods, the difference is negligible. In addition, compared to the BDS GEO satellite, the STD of IGSO is much smaller, which is only about 2. This result indicates that the fluctuation of the satellite repeat shift time of IGSO is more stable than GEO satellites.
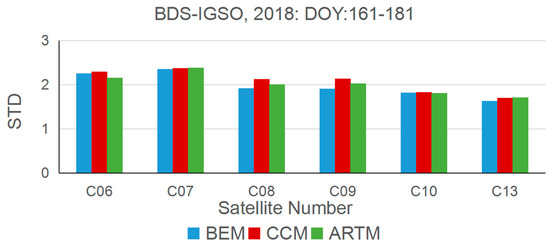
Figure 7.
The STD of the satellite repeat shift time for the three methods for each satellite during the period DOY:161–181, 2018.
The BDS MEO satellite operation track is also different from the IGSO satellite, whose satellite repeat period is about 7 days and the satellite repeat shift time is about 1700 s. Figure 8 presents the results of the mean shift time of the three methods for the three MEO satellites. From Figure 8, it can be seen that for the same satellite, the mean shift time of the three methods is not much different, especially for the C11 satellite. The maximum difference between the BEM and CCM for C14 is about 4 s. However, for different satellites, the mean shift time is also different. Additionally, the maximum difference is about 7 s, such as the C12 and C14 for the CCM and ARTM methods.
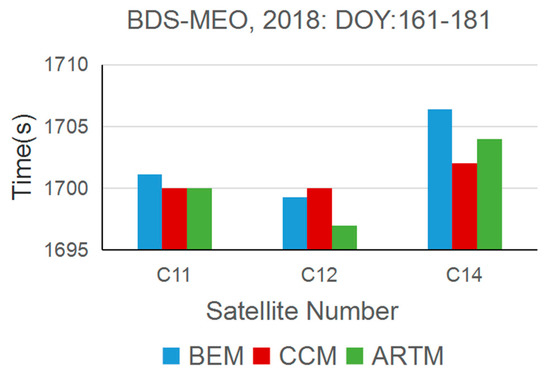
Figure 8.
The mean shift time for BDS MEO satellites calculated by the three methods during DOY: 161–181, 2018.
The STD of the satellite repeat shift time of the three methods is demonstrated in Figure 9. From the figure, it can be found that the STD of C14 is higher than the other two satellites, which almost reaches 3. However, although the STD of the C14 satellite is higher than the other MEO satellites and IGSO satellites, it is still much smaller than the GEO satellite relatively. As for the C11 and C12 satellites, the STD of the three methods performs similar to the IGSO satellite, which is only about 2. In addition, the STD of the three methods does not appear to be much different for the same satellite, which indicates the performance of the three methods is almost identical.
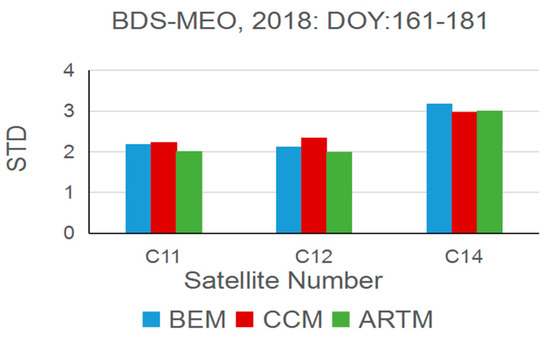
Figure 9.
The STD of the satellite repeat shift time for the three methods for each satellite during the period DOY:161–181, 2018.
4.3. Performance Analysis for the Galileo System
Actually, for most Galileo satellites, including the IOV (in-orbit validation) and FOC (full operational capability) types, have a satellite repeat period of about 10 days [25]. However, as for the E18 and E14 satellites, their satellite repeat period is about 20 days. This is mainly because that they were launched into incorrect orbits in 2014 and 2015, respectively [26,27]. Therefore, in this experiment, the dataset collected during DOY:161–191, 2018 was used to assess the performance of the satellite repeat shift time of the three methods for Galileo satellites.
Figure 10 demonstrates the results of the mean shift time of the three methods for most Galileo satellites, for which the satellite repeat period is about 10 days. From Figure 10, it is obvious that the mean shift time calculated by the three methods performs almost similarly for the same satellite. The maximum difference between the three methods is only 5 s, which appeared in E12 for BEM and CCM. In addition, it is clear that the shift time of the satellites is roughly divided into two categories, one around 2430 s and the other at about 2020 s. Therefore, it also indicates that the mean shift time of the different satellites is different, and the maximum difference reaches about 12 s between the E04 and E30 for CCM.
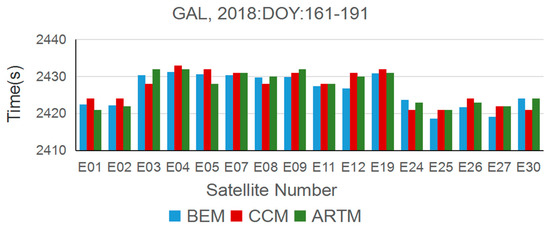
Figure 10.
The mean shift time for GAL(Galileo) satellites calculated by the three methods during DOY: 161–191, 2018.
Similarly, Figure 11 presents the STD of the three methods to evaluate the fluctuation of the shift time for the satellite. Apparently, there is no significant difference in the STD among the three methods for the same satellite, and most of the STD values are higher than 4. However, as for the E11, E12, and E26 satellites, the fluctuation of the shift time is relatively stable compared to other satellites during this period. In addition, compared to the GPS and BDS systems as a whole, it is clear that the GAL satellite STD is almost greater than the GPS, BDS IGSO, and BDS MEO but is still smaller than the BDS GEO satellite.
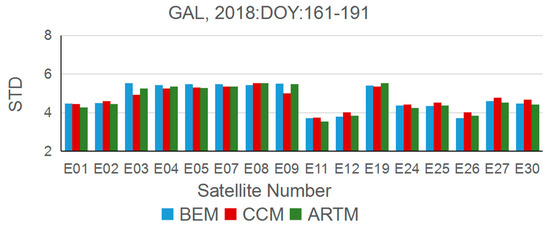
Figure 11.
The STD of the satellite repeat shift time for the three methods for each satellite during the period DOY:161–191, 2018.
Since only two satellites have the special satellite repeat period, Table 1 presents the characteristics of the mean shift time and the corresponding STD of the three methods for each satellite. From Table 1, it can be seen that the shift time is different from the above satellites, and the mean shift time is more than double that of the normal orbital satellites. This is consistent with the theoretical derivation. Furthermore, it is obvious that the mean shift time for the same satellite is significantly different among the three methods, and this is different from other satellites. This phenomenon is perhaps due to the characteristic of the long repeat period, which leads to the error accumulation varying with the different methods.

Table 1.
The mean shift time and STD for GAL E14 and E18 satellites, which was calculated by the three methods during DOY:161–191, 2018.
Moreover, from the STD of the three methods, it is also found that the fluctuation of the shift time performs higher than other satellite during this period. Numerically, the STDs of these methods are all greater than 30, which is markedly different from other system satellites. It may be mainly affected by three reasons. The first reason is that these two satellites are in the incorrect orbit due to the fault of the launching calculation; this may cause the satellite to be in an unstable state. The second reason is that these two satellites have longer satellite repeat periods, which is about 20 solar days. In addition, the satellite will repeat 37 times in the 20 solar days. Therefore, the longer satellite repeat period may lead to the accumulation of errors, resulting in a larger standard deviation of the shift time. Lastly, based on the broadcast ephemeris of the Galileo navigation system, it is obvious that the eccentricities of these two satellites are higher than other satellites. This may also lead to larger standard deviations for E14 and E18. However, since these two satellites are in the incorrect orbit, this phenomenon is also not universal for the Galileo system.
4.4. Comparison and Analysis Among Systems
To further analyze and compare the characteristic of the repeat period for GPS, BDS, and GAL systems, the STD between the satellites (BS) of the same system is presented in Table 2. For convenience of comparison, the mean STD (MS) of all the satellites for each method is also presented. Furthermore, the STD of the BDS system was calculated for different orbital types separately. For the Galileo system, only the normal orbit satellites were counted.

Table 2.
The STD of the GPS, BDS, and GAL systems, which was calculated by the three methods. BS denotes the STD between the satellites for the same system, and MS denotes the STD of the mean shift time for the same satellite.
It is interesting to note that although the MS of the BDS GEO satellite is very high for each method, the STD between the GEO satellites appears to be much smaller than the other satellite types, which is only 0.59 for the BEM method. This is mainly because the GEO satellites are relatively stationary, and the mean shift time for different satellites is almost identical. On the contrary, as for the BDS IGSO satellite, although the MS for each method is very small, the BS of the satellite performs much greater than other system satellites. This result indicates that the shift time of the IGSO satellite is stable for each satellite, but the fluctuation is more serious between the inter-satellites.
At the same time, the MS of the BDS MEO satellites shows little difference with the IGSO satellites. These results demonstrate that the performance of the BDS satellite orbital repeat track is representative of the whole BDS system. Moreover, it can be seen that the MS of the three methods for the GPS system is much smaller than the other systems. Even for the BS, the GPS system also performs better than the BDS IGSO, BDS MEO, and GAL systems.
Based on the above analysis, in terms of the system as a whole, the mean shift time of the GPS system is more stable than the other systems. Additionally, the BS and MS of the GAL system are significantly greater than the GPS and BDS MEO satellites. However, it should be noted that the characteristics of the shift time can only be used to evaluate the performance of the orbital track of the satellite but does not reflect other aspects of the performance for the satellite or system.
5. Conclusions
The satellite repeat shift time can be used to mitigate the multipath for GNSS static applications, and the stability of satellite operation can also be reflected to some extent. Two methods were introduced to estimate the approximate satellite repeat period in solar days, named the orbit shift coefficient method and the simplest fraction method. After that, three methods for calculating the satellite repeat shift time were also demonstrated. The recent GNSS observations collected from two stations in Australia were used to evaluate the characteristics of the shift time of the three global systems: GPS, BDS, and GAL.
The experimental results indicated that the satellite repeat shift time calculated by the three methods is almost identical for the same satellite. It was shown that all three methods can be applied to sidereal filtering multipath correction without much difference. However, for the same method, the mean shift time of each satellite was obviously different. Concretely, the maximum difference between satellites was about 10 s for the GPS system, 25 s for the BDS system IGSO satellite, and 12 s for the GAL system, respectively. Moreover, the STD of the shift time for the satellite and the inter-systems was also estimated to investigate the fluctuation of the satellite and systems. In addition, the mean STD of the ARTM was more stable than the other two methods, which is mainly due to the fact that the ARTM method adopts the precise ephemeris to estimate the shift time.
Considering the characteristic of the satellite repeat shift time as a whole, the GPS system is more stable than the BDS and GAL systems. Both the BS (the STD between the satellites for the same system) and MS (the STD of the mean shift time for the same satellite) of the GPS system were much smaller than the other two systems, which indicates that the fluctuation of the satellite orbit track is more stable and the stability of the whole system is also much better than the other systems. In addition, since the broadcast ephemeris of the GLONASS system is different from other global systems, the characteristics of the satellite repeat shift time of the GLONASS system need to be further investigated in the future.
Author Contributions
Conceptualization, Y.Y. and M.S.; Methodology, J.J.; Software, M.S.; Validation, Y.Y.; Formal analysis, Y.Y.; Investigation, Y.Y.; Resources, Y.Y.; Data curation, Y.Y.; Writing—original draft preparation, Y.Y.; Writing—review and editing, Y.Y.; Visualization, M.S.; Supervision, M.S.; Project administration, J.J.; Funding acquisition, J.J.
Funding
This research was funded by the National Key Research and Development Program of China, grant number 2018YFB0505200 and 2018YFB0505201 and funded by the Fundamental Research Funds for the Central Universities, grant number 2042018kf0253, and also funded by National Natural Science Foundations of China, grant number 41704154.
Acknowledgments
Authors would like to thank the editor and the reviewers for their constructive suggestions and comments. This work is supported by the National Key Research and Development Program of China (2018YFB0505200 and 2018YFB0505201), and in part by the Fundamental Research Funds for the Central Universities (2042018kf0253), and the National Natural Science Foundations of China under grant No. 41704154.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Genrich, J.F.; Bock, Y. Rapid resolution of crustal motion at short ranges with the global positioning system. J. Geophys. Res. Space Phys. 1992, 97, 3261–3269. [Google Scholar] [CrossRef]
- Elosegui, P.; Davis, J.L.; Jaldehag, R.T.K.; Johansson, J.M.; Niell, A.E.; Shapiro, I.I. Geodesy using the Global Positioning System: The effects of signal scattering on estimates of site position. J. Geophys. Res. Space Phys. 1995, 100, 9921–9934. [Google Scholar] [CrossRef]
- Bock, Y.; Nikolaidis, R.M.; De Jonge, P.J.; Jonge, P.J.; Bevis, M. Instantaneous geodetic positioning at medium distances with the Global Positioning System. J. Geophys. Res. Space Phys. 2000, 105, 28223–28253. [Google Scholar] [CrossRef]
- Nikolaidis, R.M.; Bock, Y.; De Jonge, P.J.; Shearer, P.; Agnew, D.C.; Van Domselaar, M. Seismic wave observations with the Global Positioning System. J. Geophys. Res. Space Phys. 2001, 106, 21897–21916. [Google Scholar] [CrossRef]
- Park, K.-D.; Elosegui, P.; Davis, J.L.; Jarlemark, P.O.J.; Corey, B.E.; Niell, A.E.; Normandeau, J.E.; Meertens, C.E.; Andreatta, V.A. Development of an antenna and multipath calibration system for Global Positioning System sites. Radio Sci. 2004, 39, RS5002. [Google Scholar] [CrossRef]
- Seeber, G.; Menge, F.; Völksen, C.; Wübbena, G.; Schmitz, M. Precise GPS Positioning Improvements by Reducing Antenna and Site Dependent Effects. In Proceedings of the International Symposium on Advancing Geodesy in a Changing World; Springer Science and Business Media LLC: Berlin, Germany, 1998; Volume 118, pp. 237–244. [Google Scholar]
- Choi, K.; Bilich, A.; Larson, K.M.; Axelrad, P. Modified sidereal filtering: Implications for high-rate GPS positioning. Geophys. Res. Lett. 2004, 31, L22608. [Google Scholar] [CrossRef]
- Wu, J.; Hsieh, C. Statistical modeling for the mitigation of GPS multipath delays from day-to-day range measurements. J. Geod. 2010, 84, 223–232. [Google Scholar] [CrossRef]
- Ye, S.S.; Chen, D.; Liu, Y.; Jiang, P.; Tang, W.; Xia, P. Carrier phase multipath mitigation for BeiDou navigation satellite system. GPS Solut. 2015, 19, 545–557. [Google Scholar] [CrossRef]
- Wang, X.; Liu, W.; Li, B.; Sun, G. A modified sidereal filtering for mitigating the code measurement multipath effects of BeiDou GEO satellites. Surv. Rev. 2016, 49, 428–436. [Google Scholar] [CrossRef]
- Chen, D.; Ye, S.; Xia, J.; Liu, Y.; Xia, P. A geometry-free and ionosphere-free multipath mitigation method for BDS three-frequency ambiguity resolution. J. Geod. 2016, 90, 703–714. [Google Scholar] [CrossRef]
- Su, M.; Zheng, J.; Yang, Y.; Wu, Q. A new multipath mitigation method based on adaptive thresholding wavelet denoising and double reference shift strategy. GPS Solut. 2018, 22, 40. [Google Scholar] [CrossRef]
- Ge, L.; Han, S.; Rizos, C. GPS Multipath Change Detection in Permanent GPS Stations. Surv. Rev. 2002, 36, 306–322. [Google Scholar] [CrossRef]
- Ragheb, A.; Clarke, P.; Edwards, S. GPS sidereal filtering: Coordinate and carrier-phase -level strategies. J. Geod. 2007, 81, 325–335. [Google Scholar] [CrossRef]
- Wang, G.; de Jong, K.; Zhao, Q.; Hu, Z.; Guo, J. Multipath analysis of code measurements for BeiDou geostationary satellites. GPS Solut. 2015, 19, 129–139. [Google Scholar] [CrossRef]
- Ning, Y.; Yuan, Y.; Chai, Y.; Huang, Y. Analysis of the Bias on the Beidou GEO Multipath Combinations. Sensors 2016, 16, 1252. [Google Scholar] [CrossRef] [PubMed]
- Larson, K.M.; Bilich, A.; Axelrad, P. Improving the precision of high-rate GPS. J. Geophys. Res. Space Phys. 2007, 112, 51–70. [Google Scholar] [CrossRef]
- Zhao, Q.; Wang, G.; Liu, Z.; Hu, Z.; Dai, Z.; Liu, J. Analysis of BeiDou Satellite Measurements with Code Multipath and Geometry-Free Ionosphere-Free Combinations. Sensors 2016, 16, 123. [Google Scholar] [CrossRef] [PubMed]
- Agnew, D.; Larson, K. Finding the repeat times of the GPS constellation. GPS Solut. 2007, 11, 71–76. [Google Scholar] [CrossRef]
- Fang, R. High-Rate GPS Data Non-Difference Precise Processing and Its Application on Seismology. Ph.D. Thesis, Wuhan University, Wuhan, China, 2010. [Google Scholar]
- Wang, K.; Khodabandeh, A.; Teunissen, P.J.G. Five-frequency Galileo long-baseline ambiguity resolution with multipath mitigation. GPS Solut. 2018, 22, 75. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J.; Dong, D.; Li, H.; Han, L.; Chen, W. Comparison of Three Methods for Estimating GPS Multipath Repeat Time. Remote Sens. 2018, 10, 6. [Google Scholar] [CrossRef]
- Yang, J. Spacecraft Orbit Dynamics and Control; China Astronautic Publishing House: Beijing, China, 1995; pp. 196–197. [Google Scholar]
- Sun, J. Principles and Applications of Remote Sensing; Wuhan University Press: Wuhan, China, 2009; pp. 31–32. [Google Scholar]
- Zandbergen, R.; Dinwiddy, S.; Hahn, J.; Breeuwer, E.; Blonski, D. Galileo orbit selection. In Proceedings of the 17th International Technical Meeting of the Satellite Division of the Institute of Navigation ION GNSS 2004, Long Beach, CA, USA, 21–24 September 2004; pp. 616–623. [Google Scholar]
- ESA. Galileo Satellite Recovered and Transmitting Navigation Signals. European Space Agency, Our Activities, Navigation. Galileo Satellite Recovered and Transmitting Navigation Signals. European Space Agency, Our Activities, Navigation. Available online: http://www.esa.int/Our_Activities/Navigation/ Galileo_ satellite recovered and_ transmitting navigation signals (accessed on 3 December 2014).
- ESA. Sixth Galileo satellite reaches corrected orbit. European Space Agency, our activities, navigation, Galileo, Galileo Launches. Available online: http://www.esa.int/Our_Activities/ Navigation/Galileo/Galileo_ Launches/Sixth Galileo satellite reaches corrected orbit (accessed on 9 November 2015).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).