A Reinforcement Learning Method for a Hybrid Flow-Shop Scheduling Problem
Abstract
1. Introduction
2. Literature Review
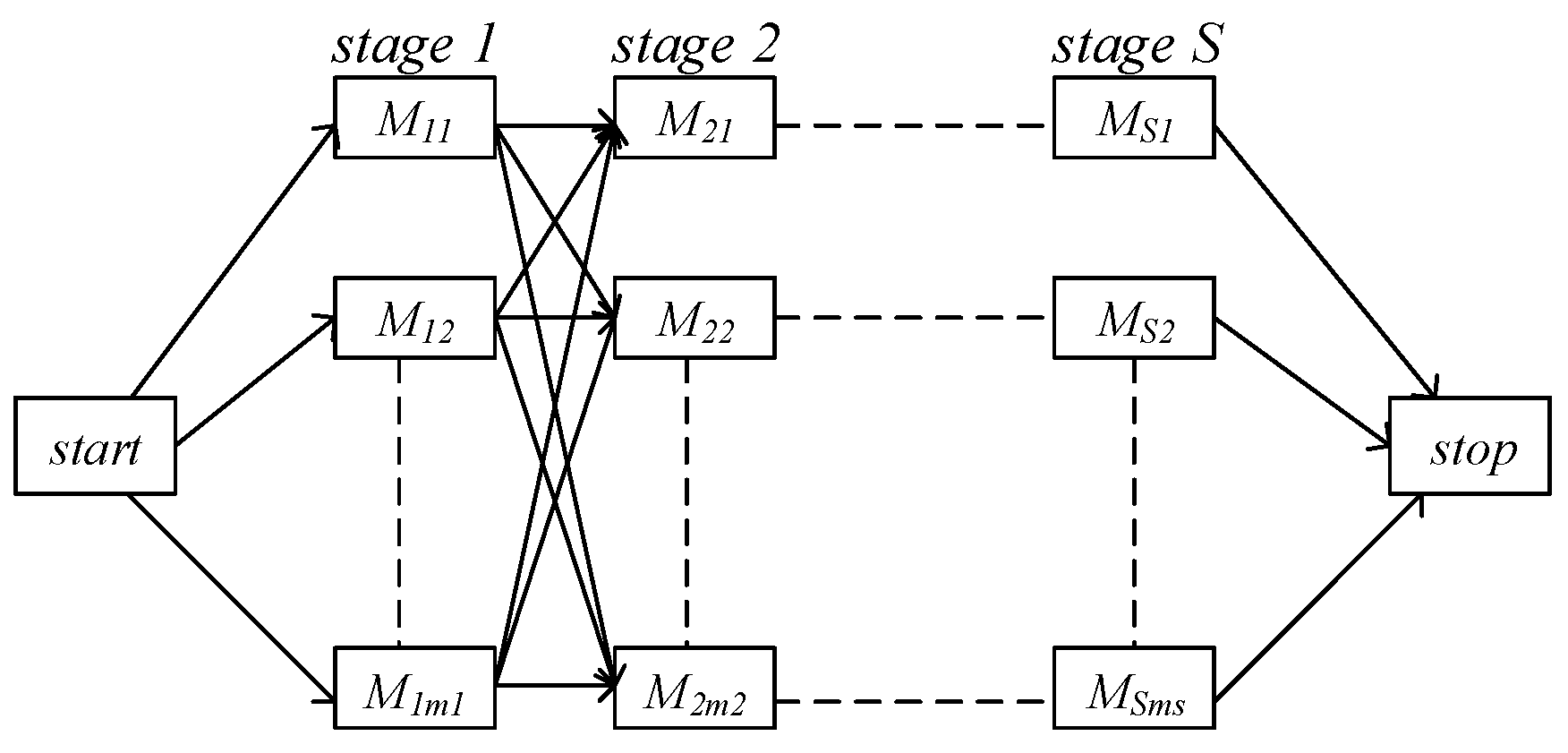
3. Description of the Hybrid Flow-Shop Scheduling Problem
4. MDP Framework for HFSP
4.1. Description of MDP
4.2. Abstraction of State and Action for HFSP
4.3. Exploration and Exploitation
4.3.1. Improved -Greedy Policy
4.3.2. Boltzmann Exploration Policy
4.4. Reward Function Representation Based on Machining Time
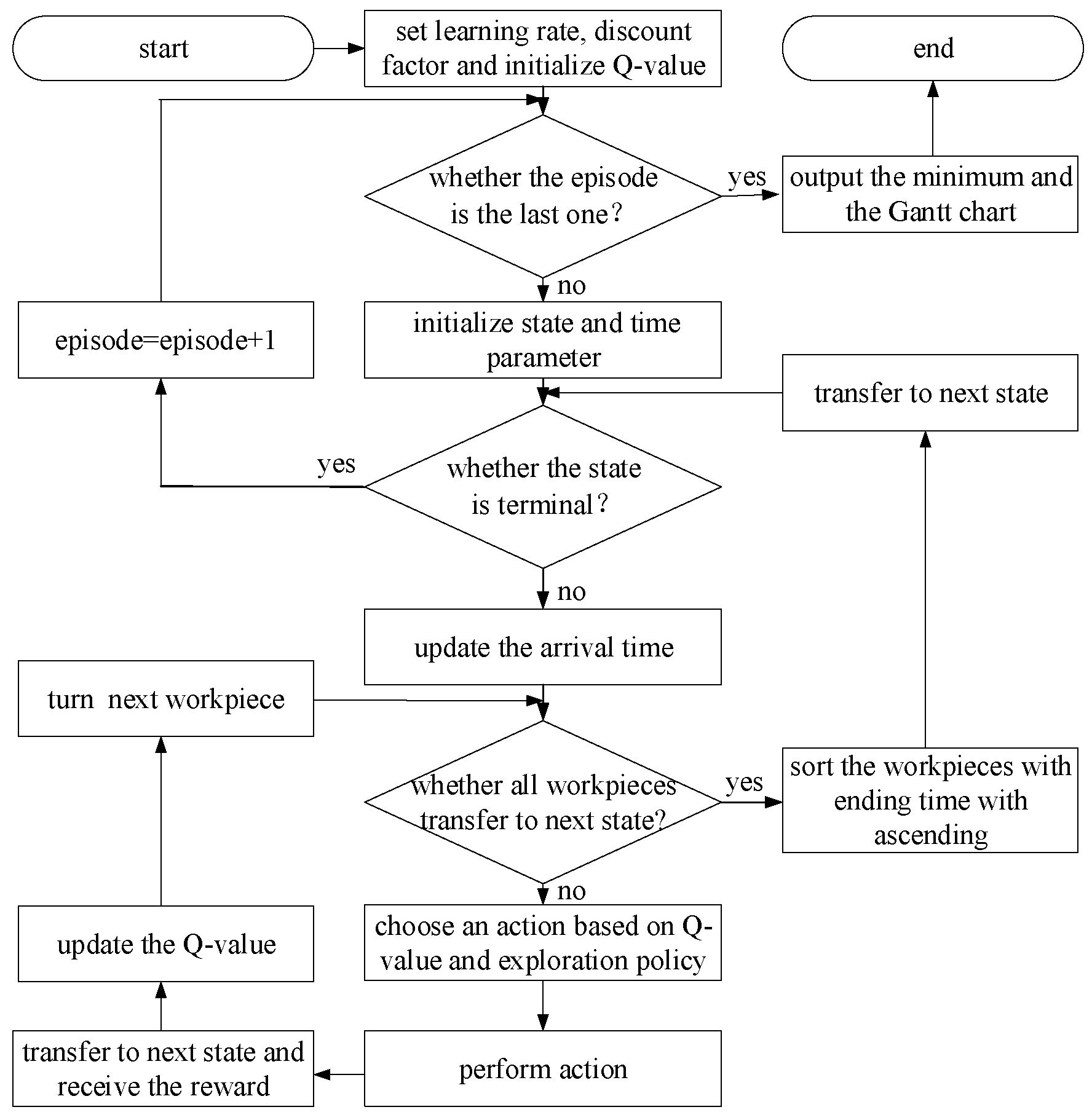
4.5. Reinforcement Learning Process for HFSP
| Algorithm 1. The Reinforcement Learning Method for HFSP |
|
5. Case Validation
5.1. Case Description
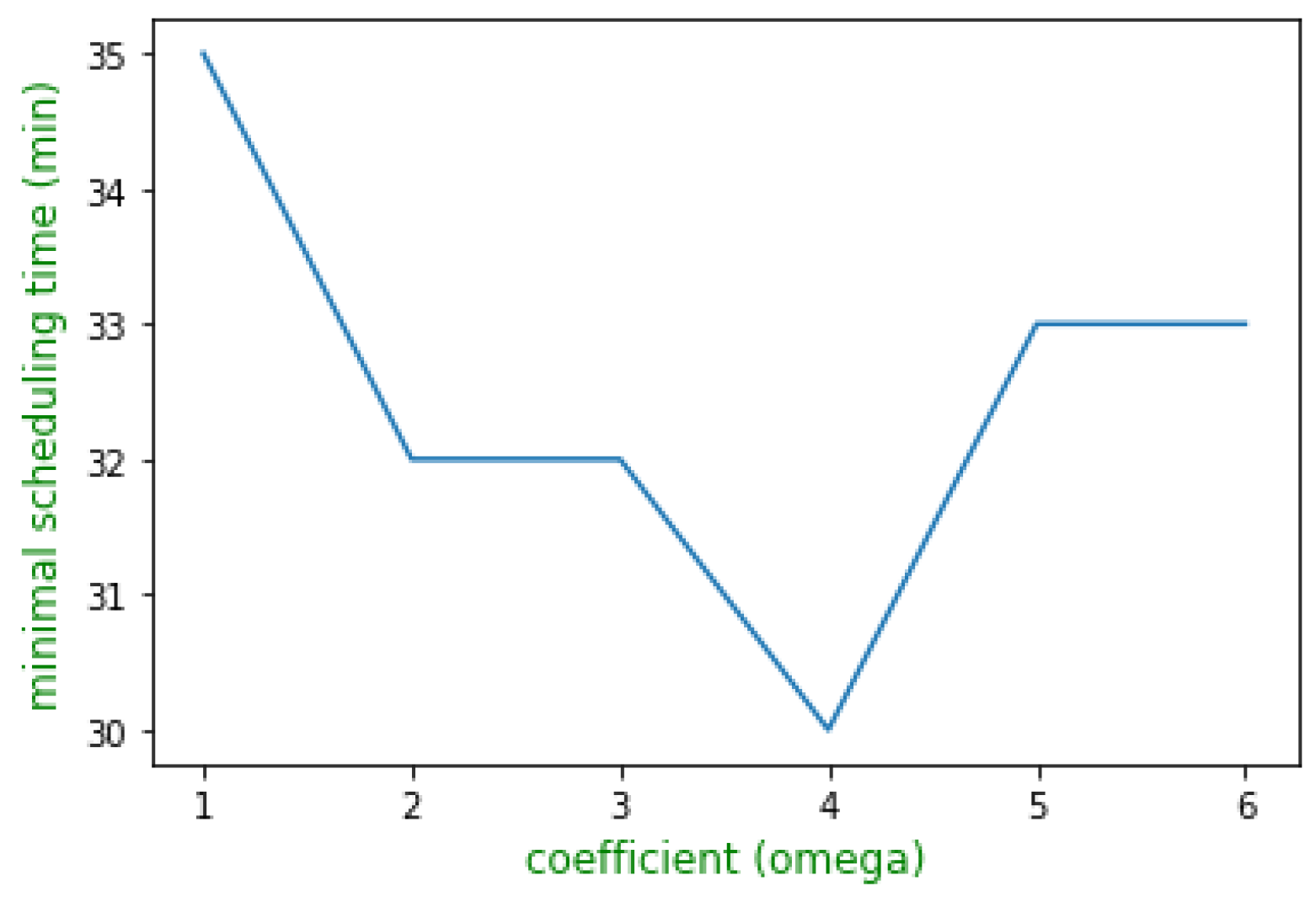
5.2. Parameters Setting
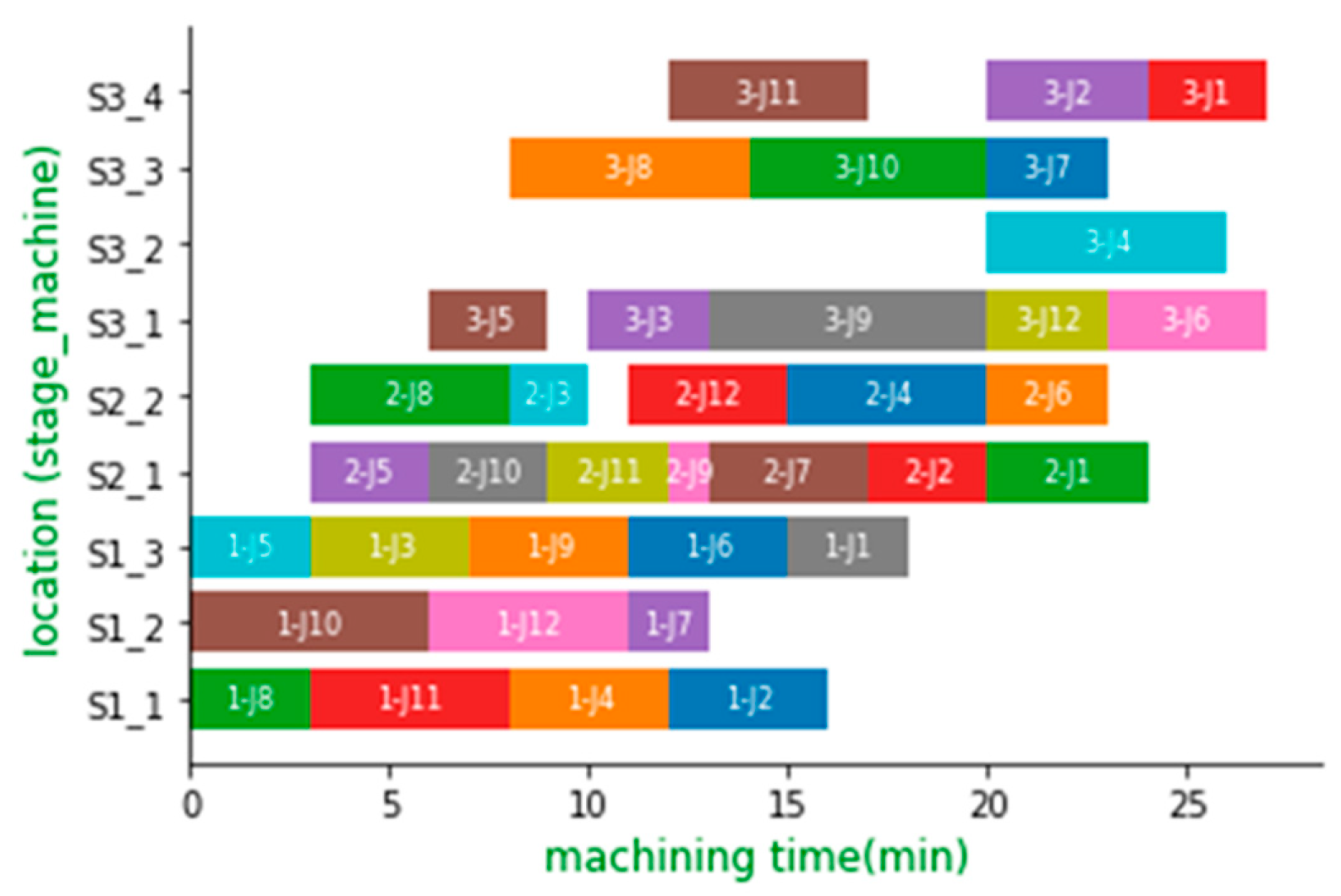
5.3. Case Results
5.4. Results Discussion
6. Application
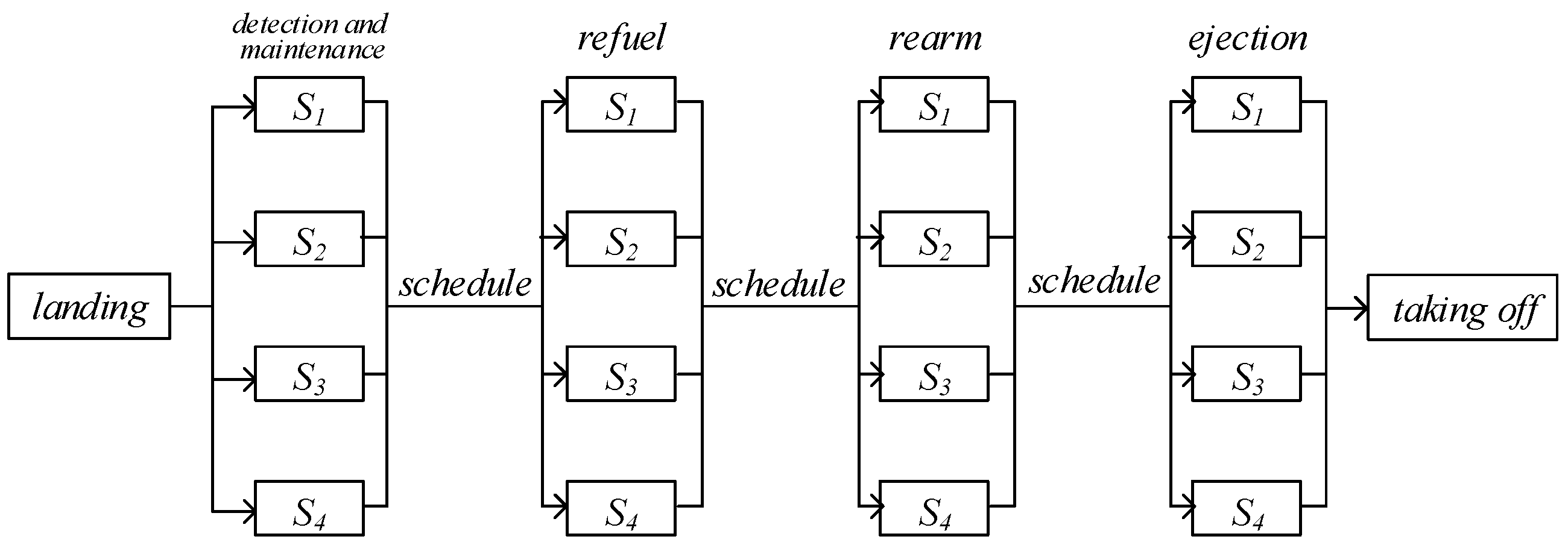
6.1. Description of Carrier Aircraft Deck Operations Problem
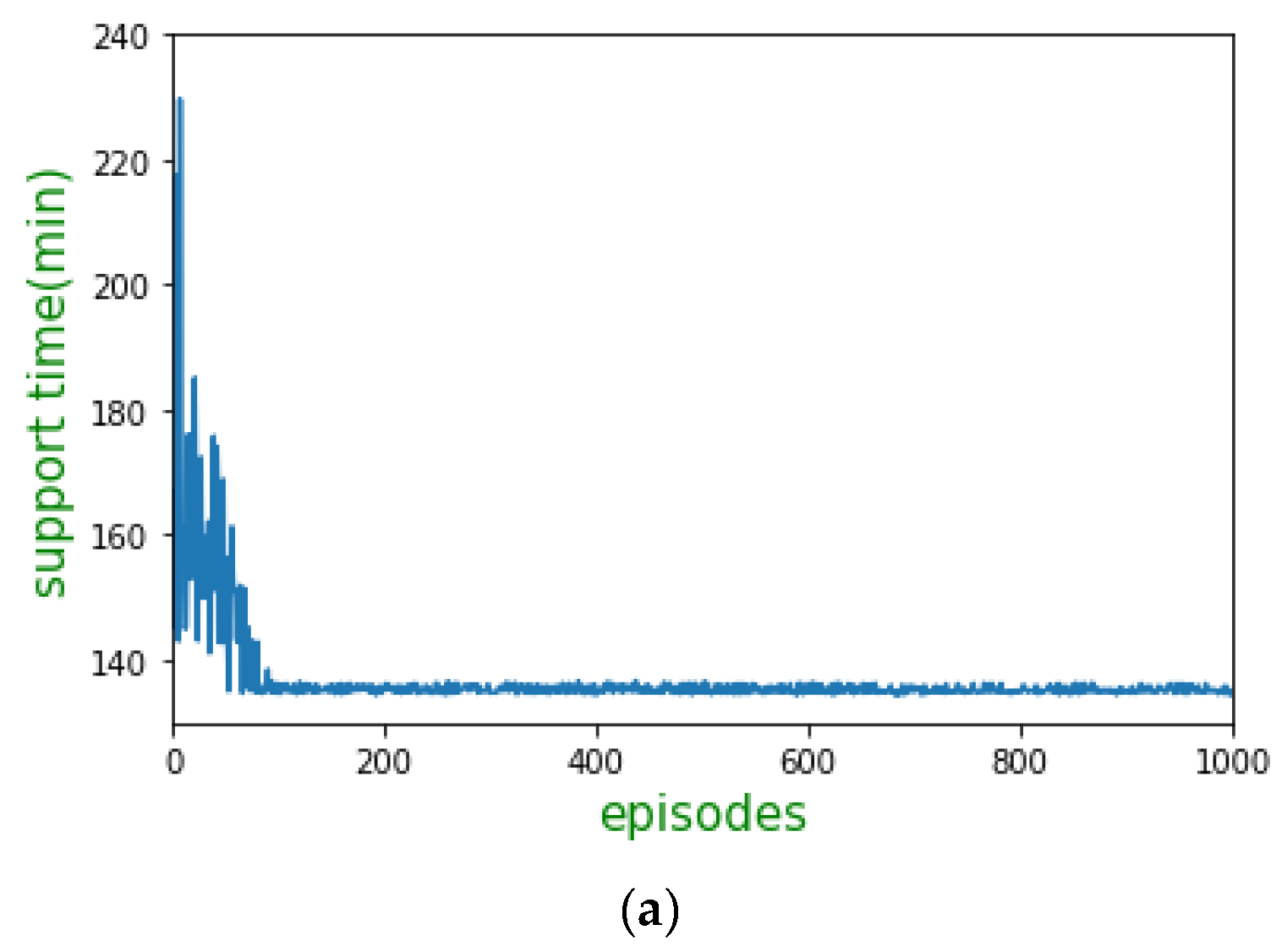
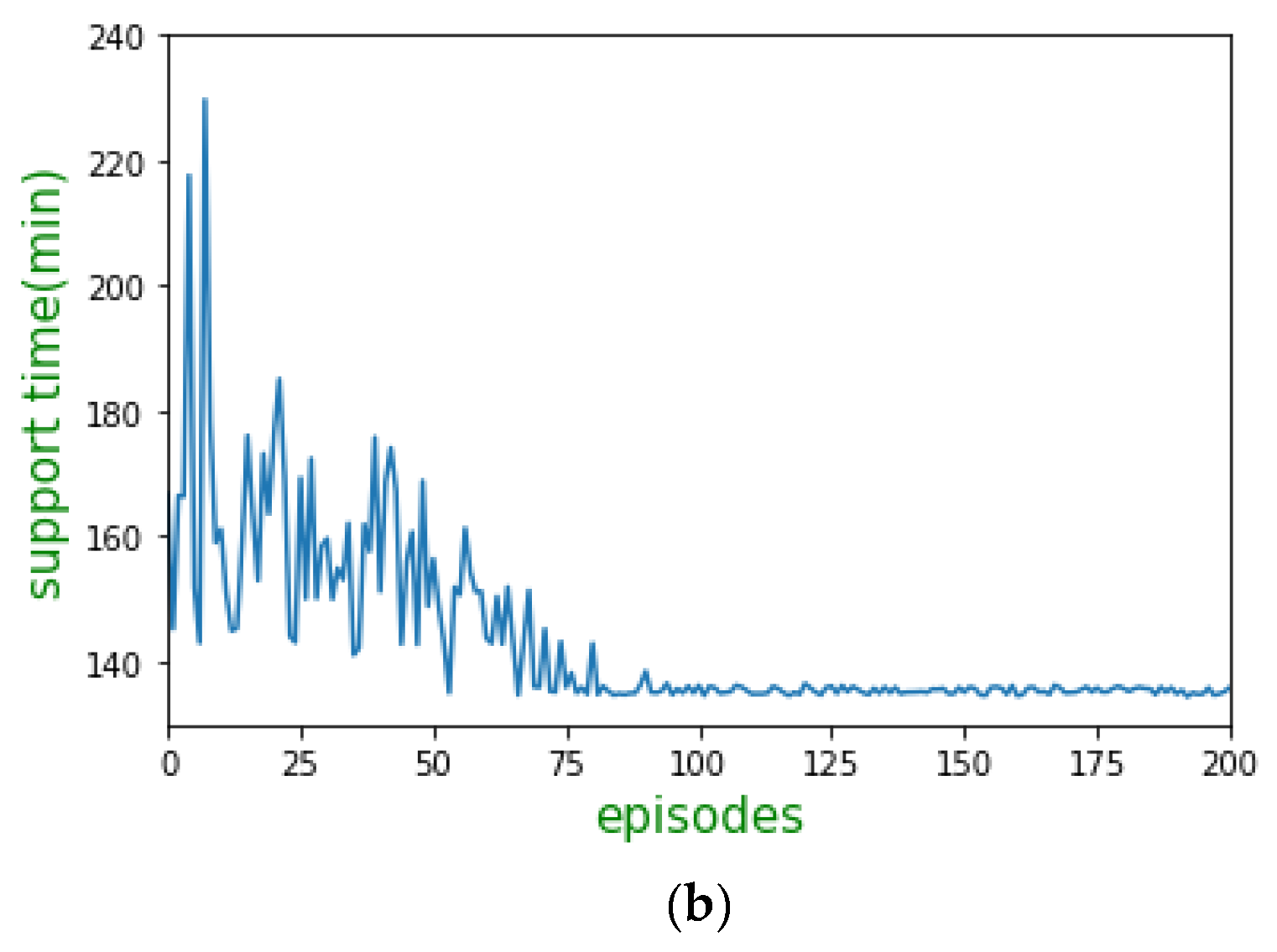
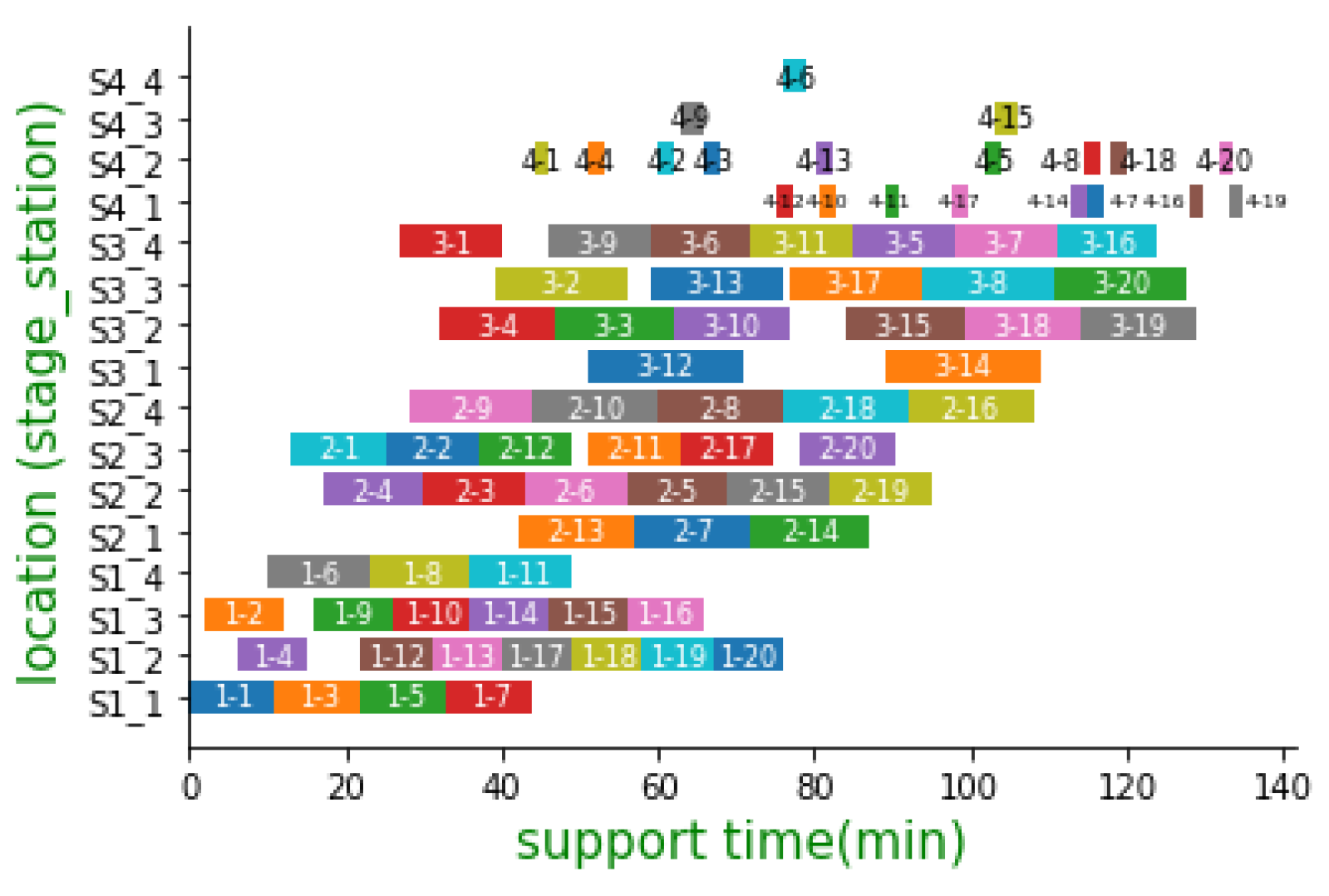
6.2. Simulation Results
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tian, Y.; Liu, D.Y. A Hybrid Particle Swarm Optimization Method for Flow Shop Scheduling Problem. Acta Electron. Sinica 2011, 39, 1087–1093. [Google Scholar]
- Ciavotta, M.; Meloni, C.; Pranzo, M. Speeding up a Rollout algorithm for complex parallel machine scheduling. Int. J. Prod. Res. 2016, 54, 4993–5009. [Google Scholar] [CrossRef]
- Ciavotta, M.; Meloni, C.; Pranzo, M. Scheduling dispensing and counting in secondary pharmaceutical manufacturing. AIChE J. 2009, 55, 1161–1170. [Google Scholar] [CrossRef]
- Hoogeveen, J.A.; Lenstra, J.K.; Veltman, B. Preemptive scheduling in a two-stage multiprocessor flow shop is NP-hard. Eur. J. Oper. Res. 1996, 89, 172–175. [Google Scholar] [CrossRef]
- Wang, S.; Wang, L.; Xu, Y. An Estimation of Distribution Algorithm for Solving Hybrid Flow-shop Scheduling Problem. Acta Autom. Sin. 2012, 38, 437–443. [Google Scholar] [CrossRef]
- Sawik, T. An Exact Approach for Batch Scheduling in Flexible Flow Lines with Limited Intermediate Buffers. Math. Comput. Model. 2002, 36, 461–471. [Google Scholar] [CrossRef]
- Sawik, T.; Schaller, A.; Tirpak, T.M. Scheduling of Printed Wiring Board Assembly in Surface Mount Technology Lines. J. Electron. Manuf. 2002, 11, 1–17. [Google Scholar] [CrossRef]
- Ruiz, R.; Vazquez-Rodriguez, J.A. The Hybrid Flow Shop Scheduling Problem. Eur. J. Oper. Res. 2010, 205, 1–18. [Google Scholar] [CrossRef]
- Xiao, W.; Hao, P.; Zhang, S.; Xu, X. Hybrid Flow Shop Scheduling Using Genetic Algorithms. In Proceedings of the 3rd World Congress on Intelligent Control and Automation, Hefei, China, 26 June–2 July 2000; IEEE Press: Piscataway Township, NJ, USA, 2000; pp. 537–541. [Google Scholar]
- Low, C. Simulated Annealing Heuristic for Flow Shop Scheduling Problems with Unrelated Parallel Machines. Comput. Oper. Res. 2005, 32, 2013–2025. [Google Scholar] [CrossRef]
- Oğuz, C.; Zinder, Y.; Janiak, A.; Lichtenstein, M. Hybrid Flow-shop Scheduling Problems with Multiprocessor Task Systems. Eur. J. Oper. Res. 2004, 152, 115–131. [Google Scholar] [CrossRef]
- Gao, Y.; Zhou, R.Y.; Wang, H.; Cao, Z.X. Study on an average reward reinforcement learning algorithm. Chin. J. Comput. 2007, 30, 1372–1378. [Google Scholar]
- Qi-Ming, F.; Quan, L.; Hui, W.; Fei, X.; Jun, Y.; Jiao, L. A novel off policy Q(λ) algorithm based on linear function approximation. Chin. J. Comput. 2014, 37, 677–686. (In Chinese) [Google Scholar]
- Kober, J.; Peters, J. Reinforcement learning in robotics: A survey. Int. J. Robot. Res. 2013, 32, 1238–1274. [Google Scholar] [CrossRef]
- Wei, Y.Z.; Zao, M.Y. A reinforcement learning-based approach to dynamic job-shop scheduling. Acta Autom. Sin. 2005, 31, 765–771. (In Chinese) [Google Scholar]
- Ipek, E.; Mutlu, O.; Martínez, J.F.; Caruana, R. Self-optimizing memory controllers: A reinforcement learning approach. Comput. Archit. 2008, 36, 39–50. [Google Scholar] [CrossRef]
- Tesauro, G. TD-Gammon, a self-teaching backgammon program, achieves master-level play. Neural Comput. 1994, 6, 215–219. [Google Scholar] [CrossRef]
- Kocsis, L.; Szepesvári, C. Bandit based Monte-Carlo planning. In Machine Learning: ECML 2006, Proceedings of the 17th European Conference on Machine Learning, Berlin, Germany, 18–22 September 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 282–293. [Google Scholar]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Haouar, I.M.; Hidr, I.L.; Gharb, I.A. Optimal Scheduling of a Two-stage Hybrid Flow Shop. Math. Methods Oper. Res. 2006, 64, 107–124. [Google Scholar] [CrossRef]
- Hua, X.; Lixin, T. Lagrangian Relation Algorithm for Real-time Hybrid Flow-shop Scheduling with No-wait in Process. Control Decis. 2006, 21, 376–380. [Google Scholar]
- Riane, F.; Artiba, A.; Elmaghraby, S.E. Sequencing a Hybrid Two-stage Flow Shop with Dedicated Machines. Int. J Prod. Res. 2002, 40, 4353–4380. [Google Scholar] [CrossRef]
- Low, C.Y.; Hsu, C.Z.; Su, C.T. A Two-stage Hybrid Flow-shop Scheduling Problem with a Function Constraint and Unrelated Alternative Machines. Comput. Oper. Res. 2008, 35, 845–853. [Google Scholar] [CrossRef]
- Hong, T.P.; Wang, T.T.; Wang, S.L. A Palmer-based Continuous Fuzzy Flexible Flow-shop Scheduling Algorithm. Soft Comput. 2001, 5, 426–433. [Google Scholar] [CrossRef]
- Ying, K.C.; Lin, S.W. Multiprocessor Task Scheduling in Multistage Hybrid Flow-shops: An Ant Colony System Approach. Int. J Prod. Res. 2006, 44, 3161–3177. [Google Scholar] [CrossRef]
- Wang, X.; Tang, L. A Tabu Search Heuristic for the Hybrid Flow-shop Scheduling with Finite Intermediate Buffers. Comput. Oper. Res. 2008, 36, 907–918. [Google Scholar] [CrossRef]
- Alaykyran, K.; Engin, O.; Doyen, A. Using Ant Colony Optimization to Solve Hybrid Flow Shop Scheduling Problems. Int. J. Adv. Manuf. Technol. 2007, 35, 541–550. [Google Scholar] [CrossRef]
- Tseng, C.T.; Liao, C.J. A Particle Swarm Optimization Algorithm for Hybrid Flow-shop scheduling with Multiprocessor Tasks. Int. J. Prod. Res. 2008, 46, 4655–4670. [Google Scholar] [CrossRef]
- Wu, J.H.; Yang, T. Improved grey wolf optimization algorithm for flexible shop scheduling problem. Manuf. Autom. 2019, 41, 107–111. (In Chinese) [Google Scholar]
- Meng, G.J.; Yang, D.C.; Tao, X.P. Study on multi-objective flexible Job-Shop scheduling problem based on hybrid artificial bee colony algorithm. Appl. Res. Comput. 2019, 36, 18–20, 25. (In Chinese) [Google Scholar]
- Liu, F.; Zhang, X.P.; Zou, F.X.; Zeng, L.L. Immune clonal selection algorithm for hybrid flow-shop scheduling problem. In Proceedings of the Chinese Control and Decision Conference, Guilin, China, 17–19 June 2009; pp. 2605–2609. [Google Scholar]
- Wang, Q.B.; Zhang, W.X.; Wang, B.L.; Wu, Z.X. Research on Agent-based Hybrid Flow Shop Dynamic Scheduling Problem. J. Comput. Appl. 2017, 37, 2991–2998. (In Chinese) [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. arXiv 2018, arXiv:1801.01290. [Google Scholar]
- Haarnoja, T.; Pong, V.; Zhou, A.; Dalal, M.; Abbeel, P.; Levine, S. Composable deep reinforcement learning for robotic manipulation. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 6244–6251. [Google Scholar]
- Gao, Y.; Lin, J.; Yu, F.; Levine, S.; Darrell, T. Reinforcement learning from imperfect demonstrations. arXiv 2018, arXiv:1802.05313. [Google Scholar]
- Gu, S.; Lillicrap, T.; Sutskever, I.; Levine, S. Continuous deep q-learning with model-based acceleration. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; Volume 48, pp. 2829–2838. [Google Scholar]
- O’Donoghue, B.; Munos, R.; Kavukcuoglu, K.; Mnih, V. Combining policy gradient and Q-learning. arXiv 2016, arXiv:1611.01626. [Google Scholar]
- Bertsekas, D.P. Dynamic Programming and Optimal Control; Athena Scientific: Belmont, MA, USA, 2005; Volume 1. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.L.; Yao, M.H.; Wu, Y.G.; Wu, Q. Hybrid flow-shop scheduling approach based on genetic algorithm. J. Syst. Simul. 2002, 14, 863–865. [Google Scholar]
- Su, X.C.; Li, C.Y.; Chen, Z.G. Hybrid differential evolution algorithm for sortie scheduling of carrier aircraft. Comput. Simul. 2015, 32, 74–78. (In Chinese) [Google Scholar]
| Workpiece | J1 | J2 | J3 | J4 | J5 | J6 | J7 | J8 | J9 | J10 | J11 | J12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| lathing | M1 | 2 | 4 | 6 | 4 | 4 | 6 | 5 | 3 | 2 | 3 | 5 | 6 |
| M2 | 2 | 5 | 5 | 3 | 5 | 5 | 2 | 5 | 5 | 6 | 2 | 5 | |
| M3 | 3 | 4 | 4 | 4 | 3 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| planing | M1 | 4 | 3 | 4 | 6 | 3 | 2 | 4 | 7 | 1 | 3 | 3 | 5 |
| M2 | 5 | 4 | 2 | 5 | 1 | 3 | 6 | 5 | 2 | 4 | 5 | 4 | |
| grinding | M1 | 2 | 3 | 3 | 3 | 3 | 4 | 3 | 3 | 7 | 4 | 6 | 3 |
| M2 | 3 | 4 | 4 | 6 | 4 | 3 | 4 | 3 | 8 | 8 | 7 | 4 | |
| M3 | 2 | 5 | 2 | 5 | 6 | 9 | 3 | 6 | 6 | 6 | 6 | 7 | |
| M4 | 3 | 4 | 5 | 8 | 5 | 5 | 5 | 4 | 5 | 7 | 5 | 5 | |
| Times | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| AIS | 27 | |||||||||
| GA | 29 | 30 | 29 | 29 | 29 | 31 | 29 | 29 | 29 | 30 |
| RL | 27 | 28 | 28 | 28 | 27 | 28 | 28 | 27 | 28 | 28 |
| Method | AIS [31] | GA [40] | RL |
|---|---|---|---|
| parameter values | N = 40, EG = 100, S = 3, n = 12 | N = 30, EG = 100, S = 3, n = 12 | IS = 100, E = 200, S = 3, n = 12 |
| complexity | O(|N||EG||S||n|) | O(|N||EG||S||n|) | O(|IS||E||S||n|) |
| optimal scheduling time | 27 min | 29 min | 27 min |
| computing time | -- | -- | 19 to 21 s |
| Stage | Detection and Maintenance | Refuel | Rearm | Ejection |
|---|---|---|---|---|
| station 1 | 11 | 15 | 20 | 2 |
| station 2 | 9 | 13 | 15 | 2 |
| station 3 | 10 | 12 | 17 | 3 |
| station 4 | 13 | 16 | 13 | 3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, W.; Guo, F.; Su, X. A Reinforcement Learning Method for a Hybrid Flow-Shop Scheduling Problem. Algorithms 2019, 12, 222. https://doi.org/10.3390/a12110222
Han W, Guo F, Su X. A Reinforcement Learning Method for a Hybrid Flow-Shop Scheduling Problem. Algorithms. 2019; 12(11):222. https://doi.org/10.3390/a12110222
Chicago/Turabian StyleHan, Wei, Fang Guo, and Xichao Su. 2019. "A Reinforcement Learning Method for a Hybrid Flow-Shop Scheduling Problem" Algorithms 12, no. 11: 222. https://doi.org/10.3390/a12110222
APA StyleHan, W., Guo, F., & Su, X. (2019). A Reinforcement Learning Method for a Hybrid Flow-Shop Scheduling Problem. Algorithms, 12(11), 222. https://doi.org/10.3390/a12110222





