Freeway Traffic Congestion Reduction and Environment Regulation via Model Predictive Control
Abstract
1. Introduction
2. Literature Review
3. Traffic Flow Models
3.1. METANET Model
3.2. Integrating METANET Model with VT-micro Model
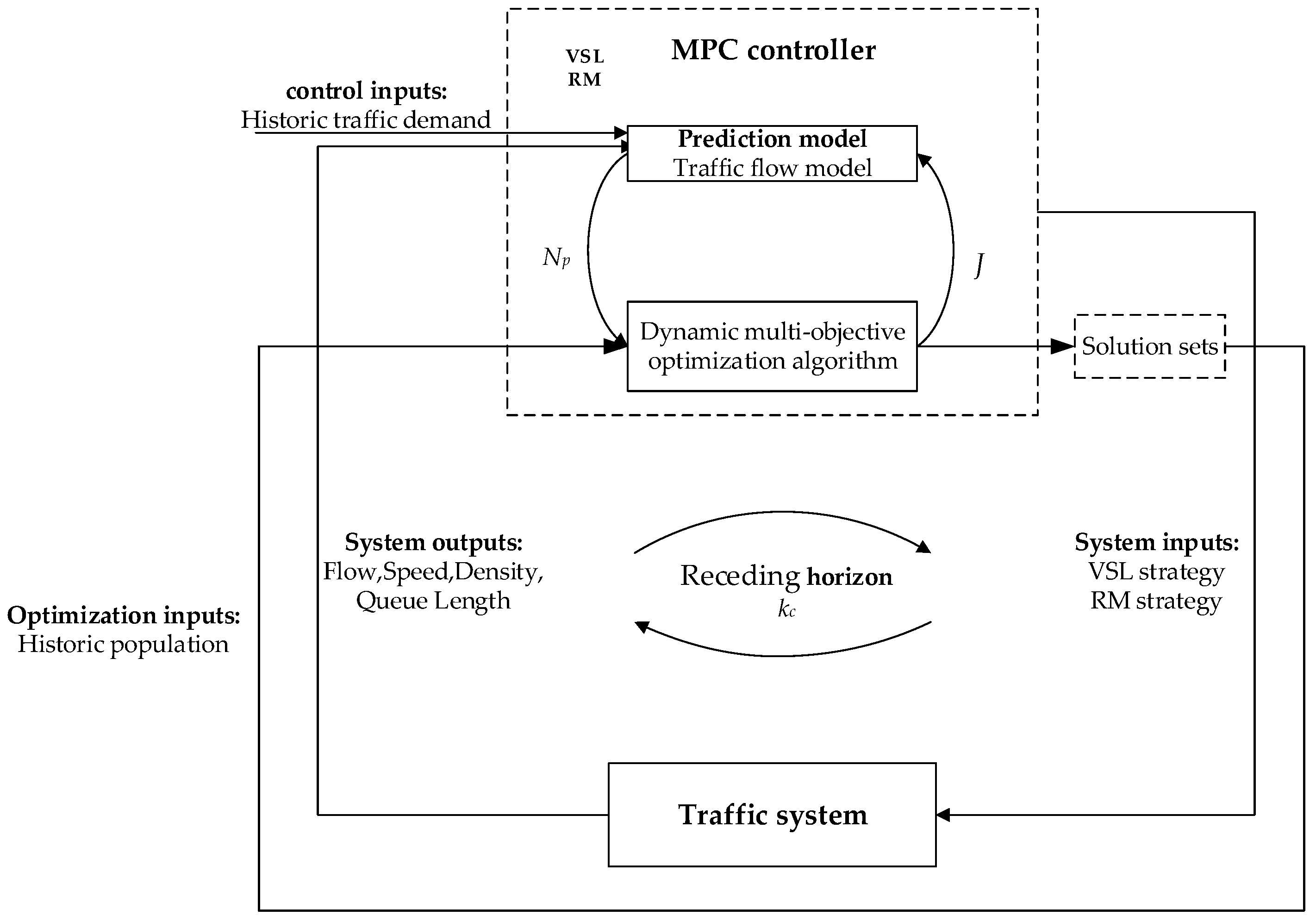
4. The Proposed Algorithm: MPC_CPDMO-NSGA-II
4.1. Framework of MPC_CPDMO-NSGA-II
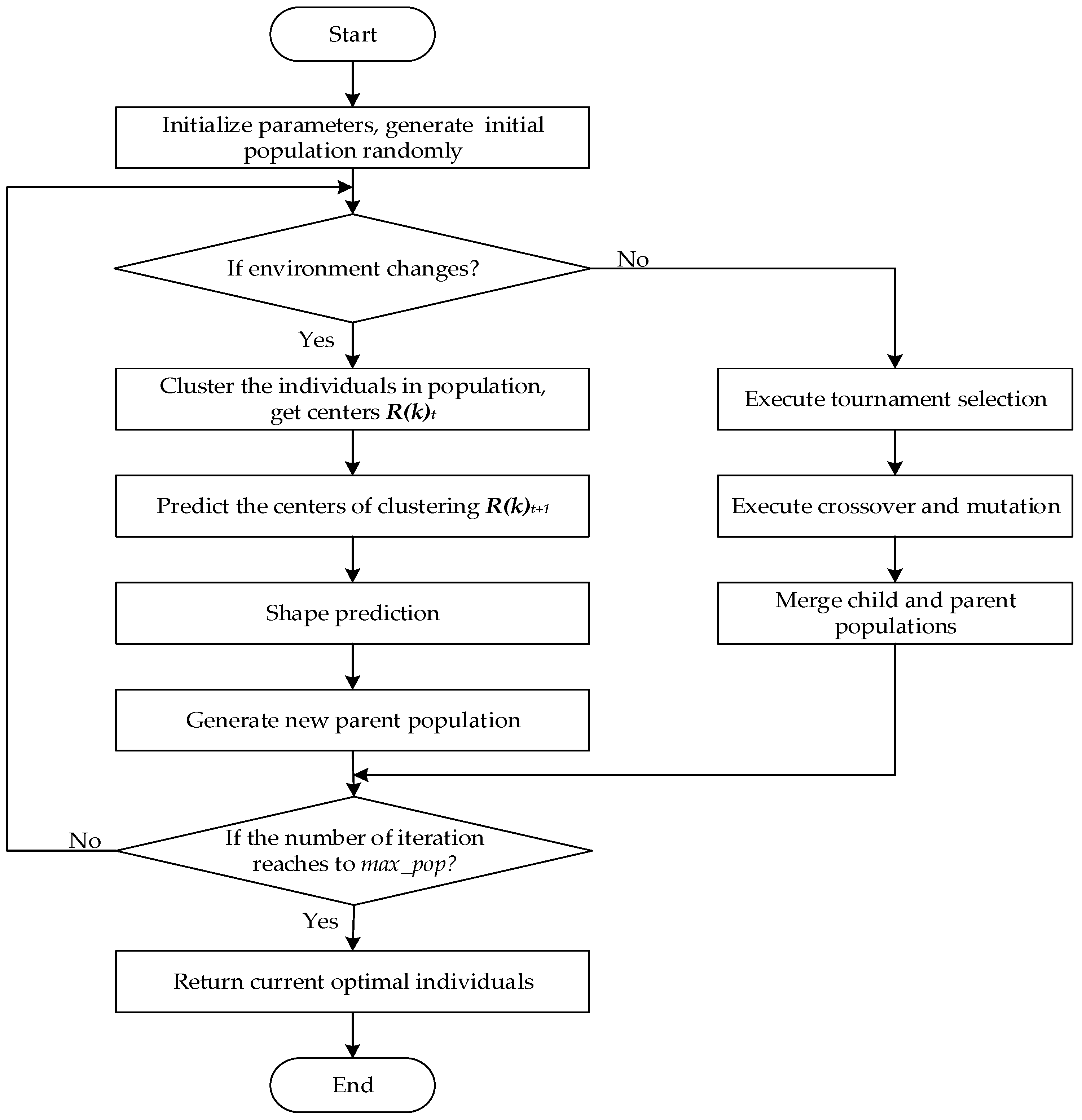
4.2. CPDMO-NSGA-II
4.2.1. Description of CPDMO-NSGA-II
4.2.2. Environmental Detection
4.2.3. Prediction Strategy
5. Problem Formulation
6. Simulation Research
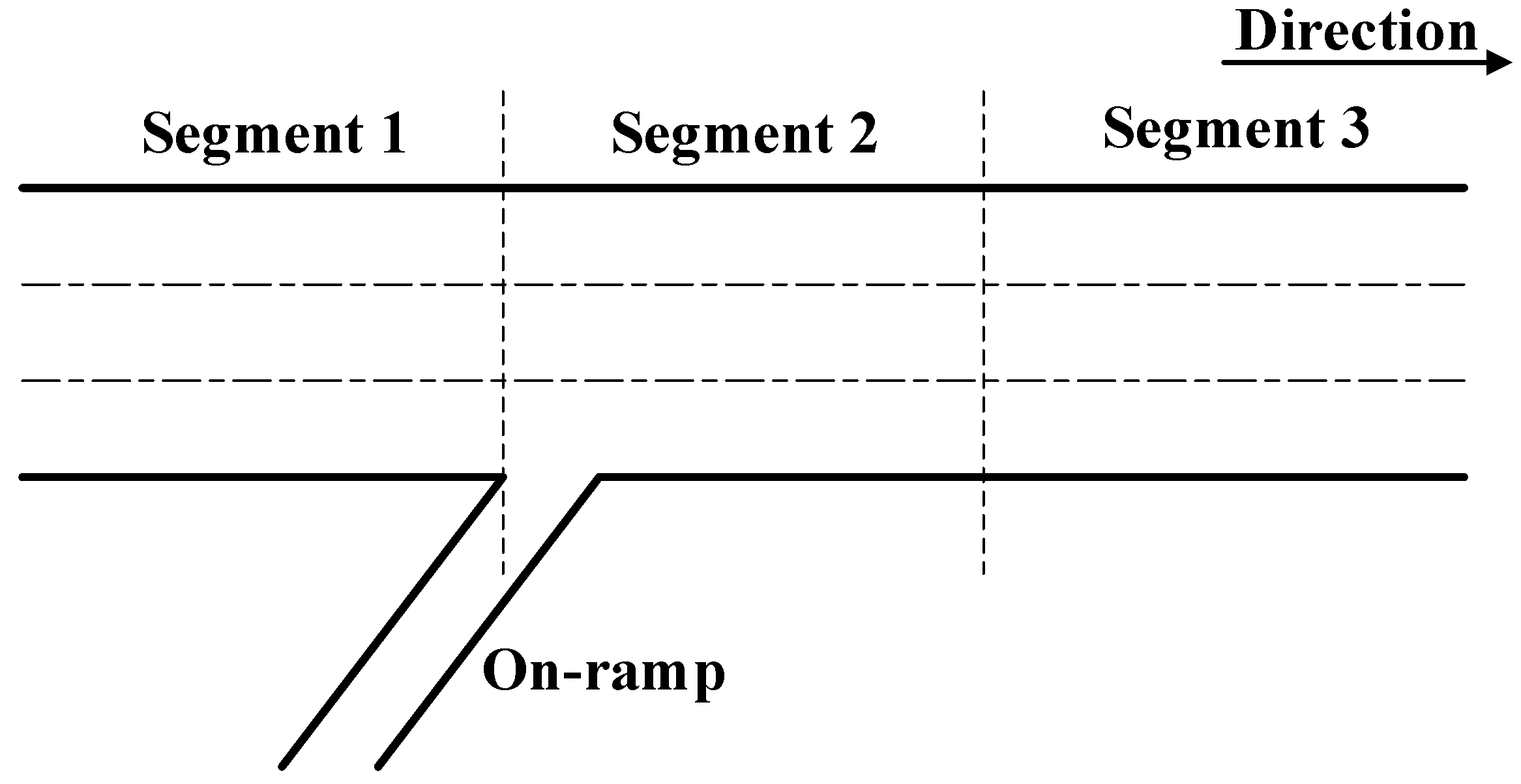
6.1. Simulation Network
6.2. Simulation Results
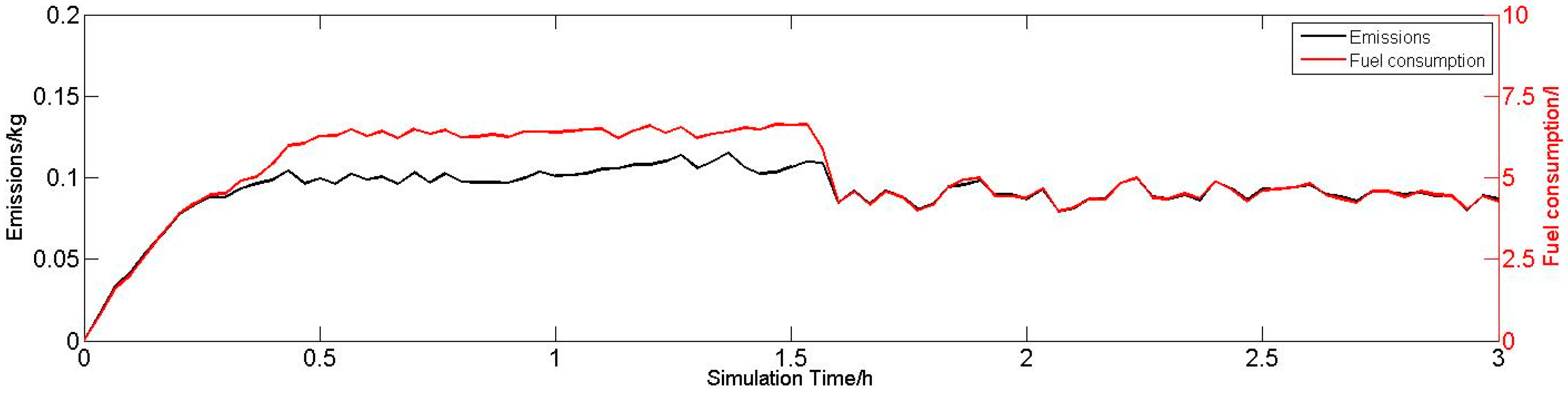
6.2.1. Results of Traffic Condition, Emissions and Fuel Consumption of the Freeway with Fixed Speed Limit
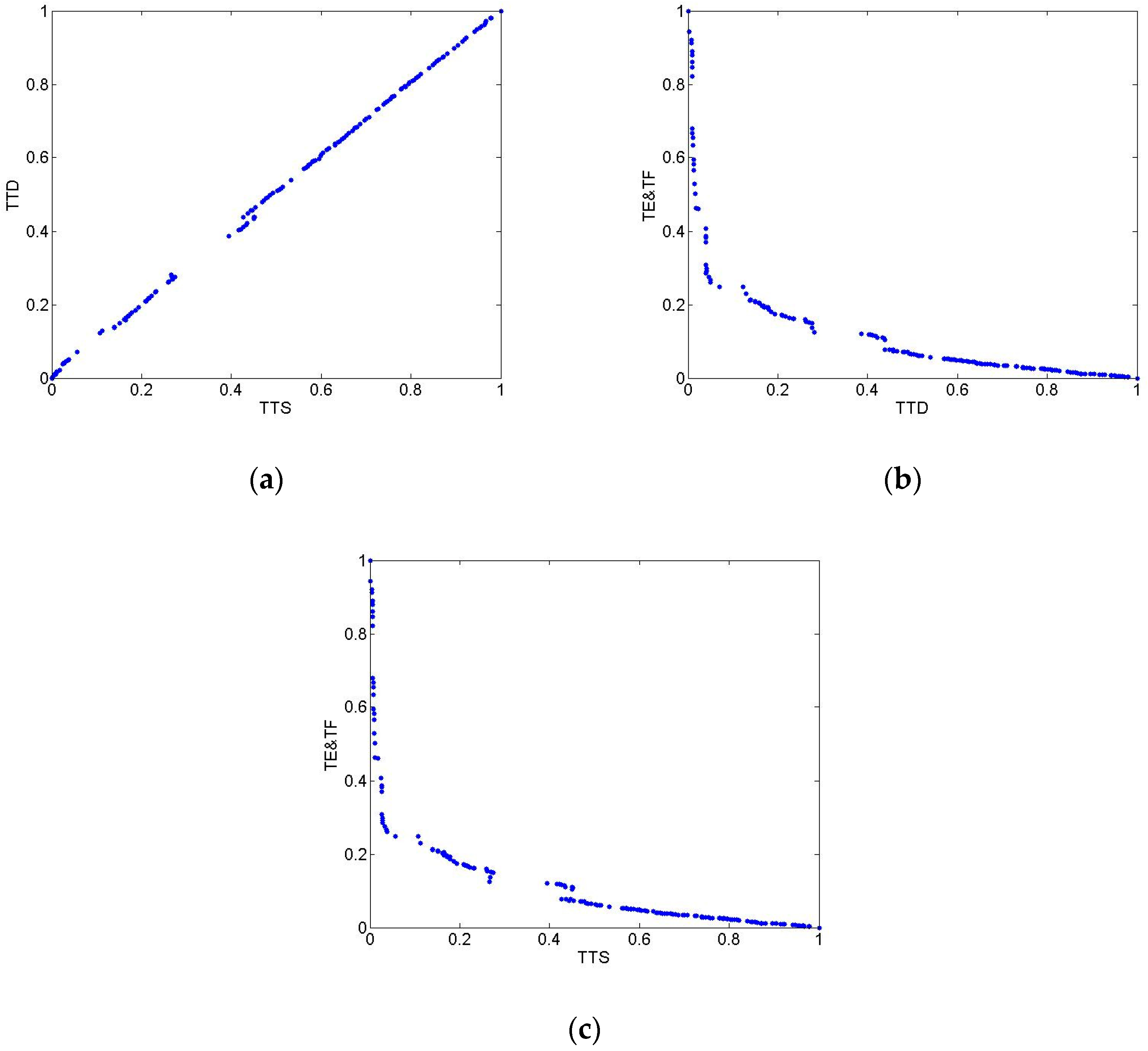
6.2.2. Pareto Fronts Obtained by MPC_CPDMO-NSGA-II Algorithm
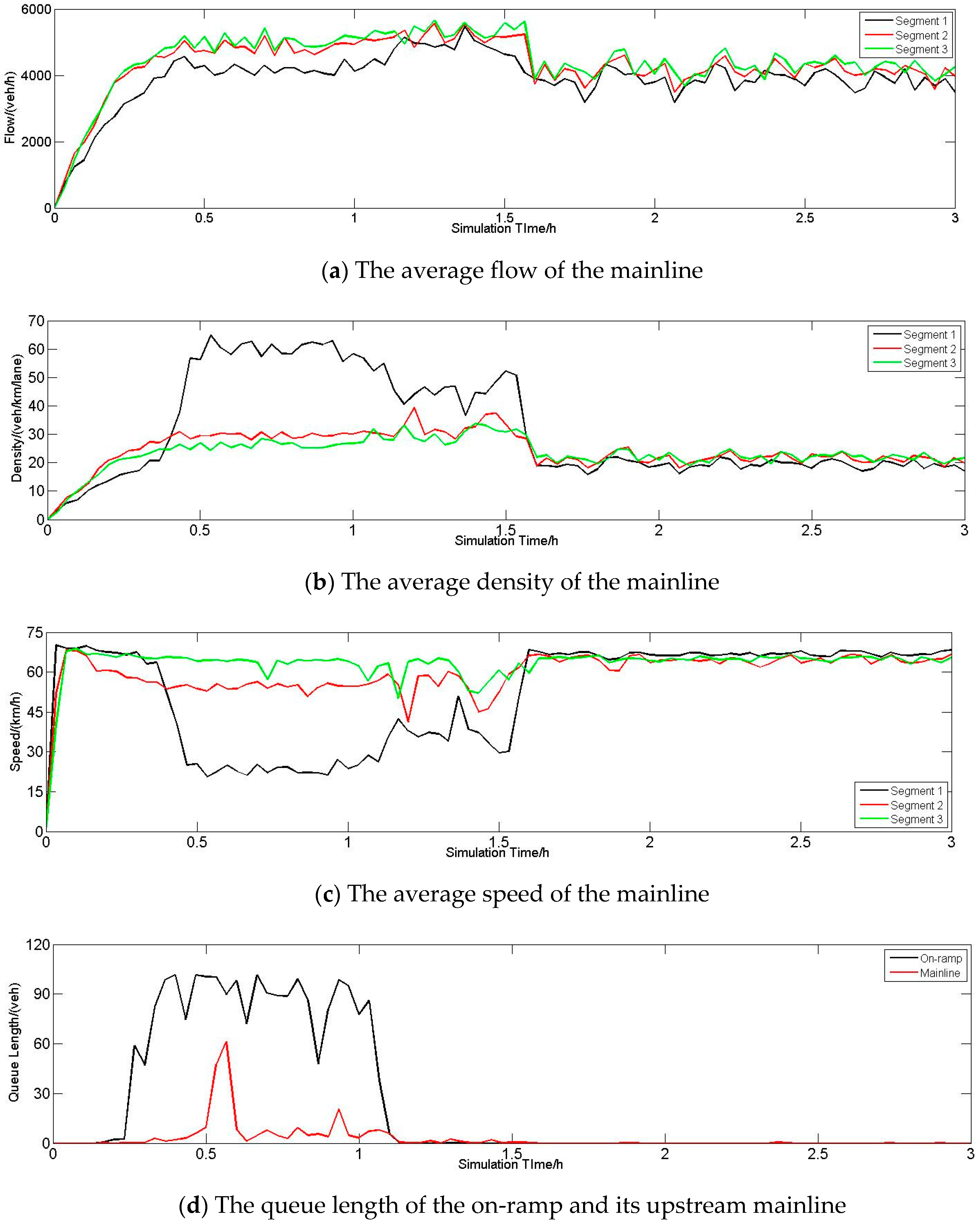
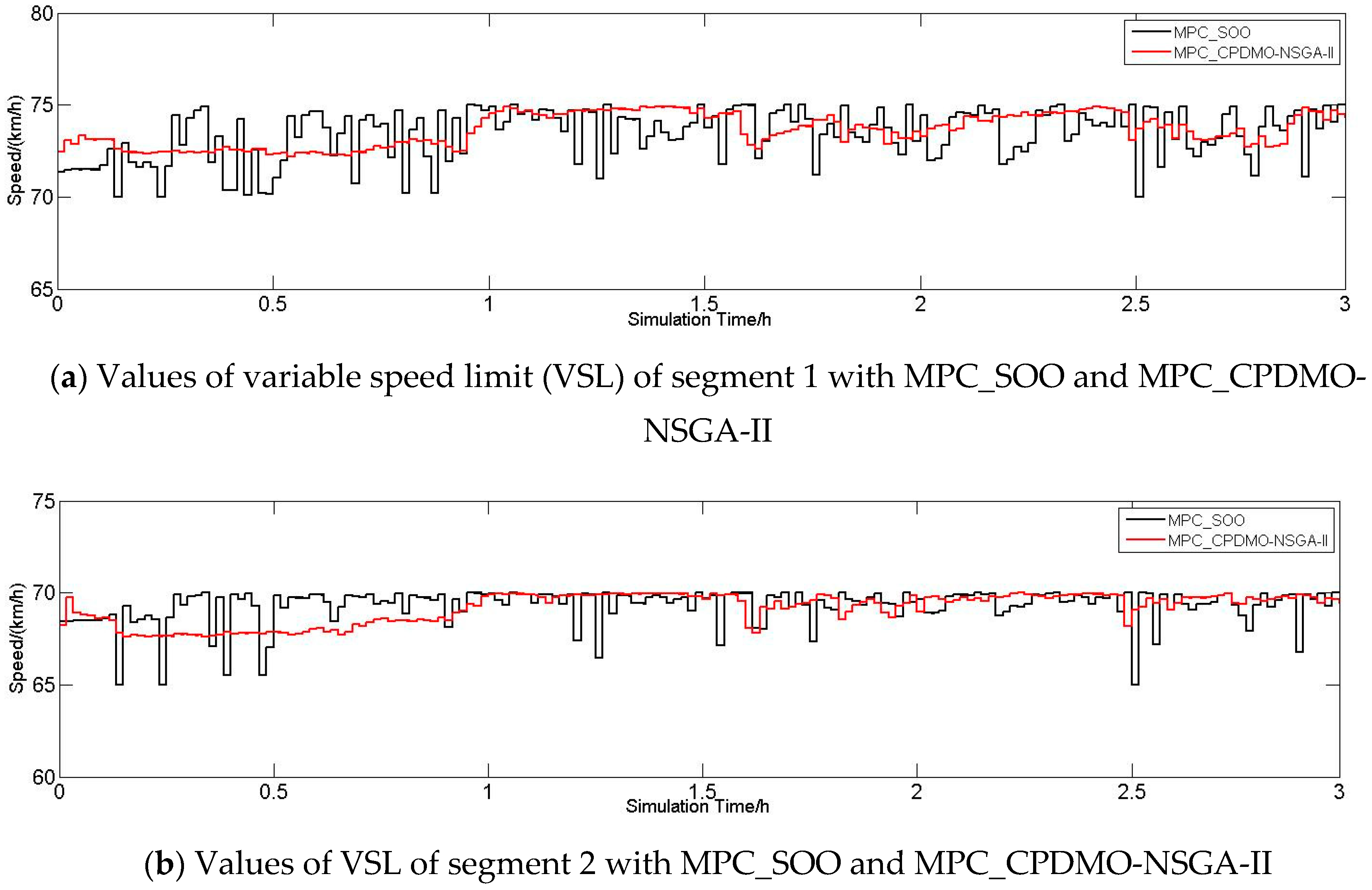
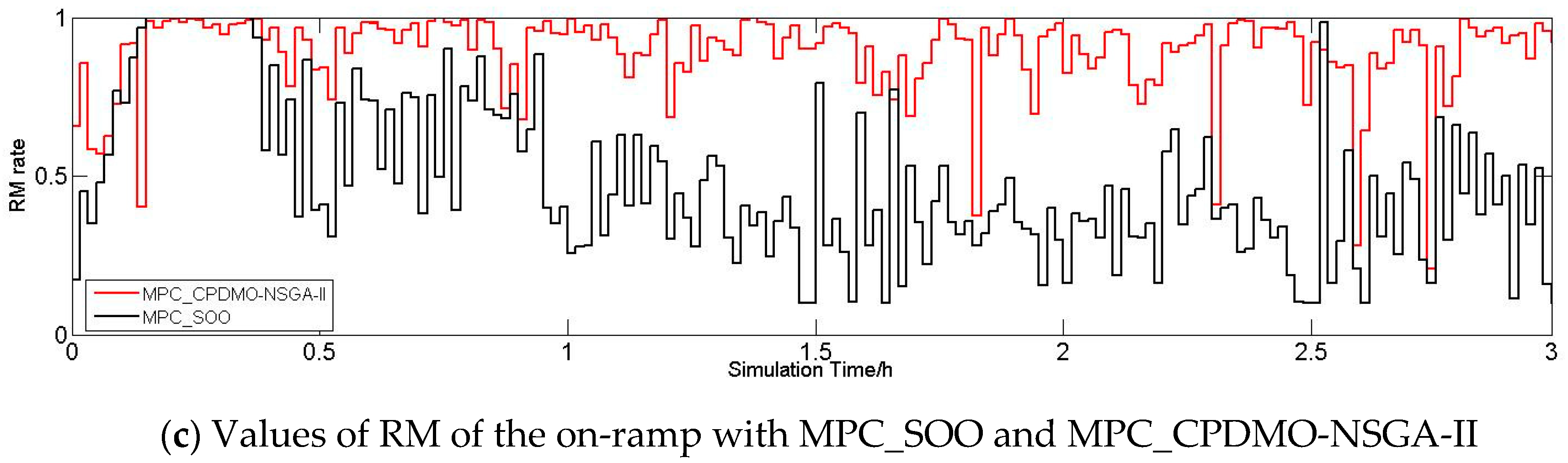
6.2.3. Performance of the Freeway
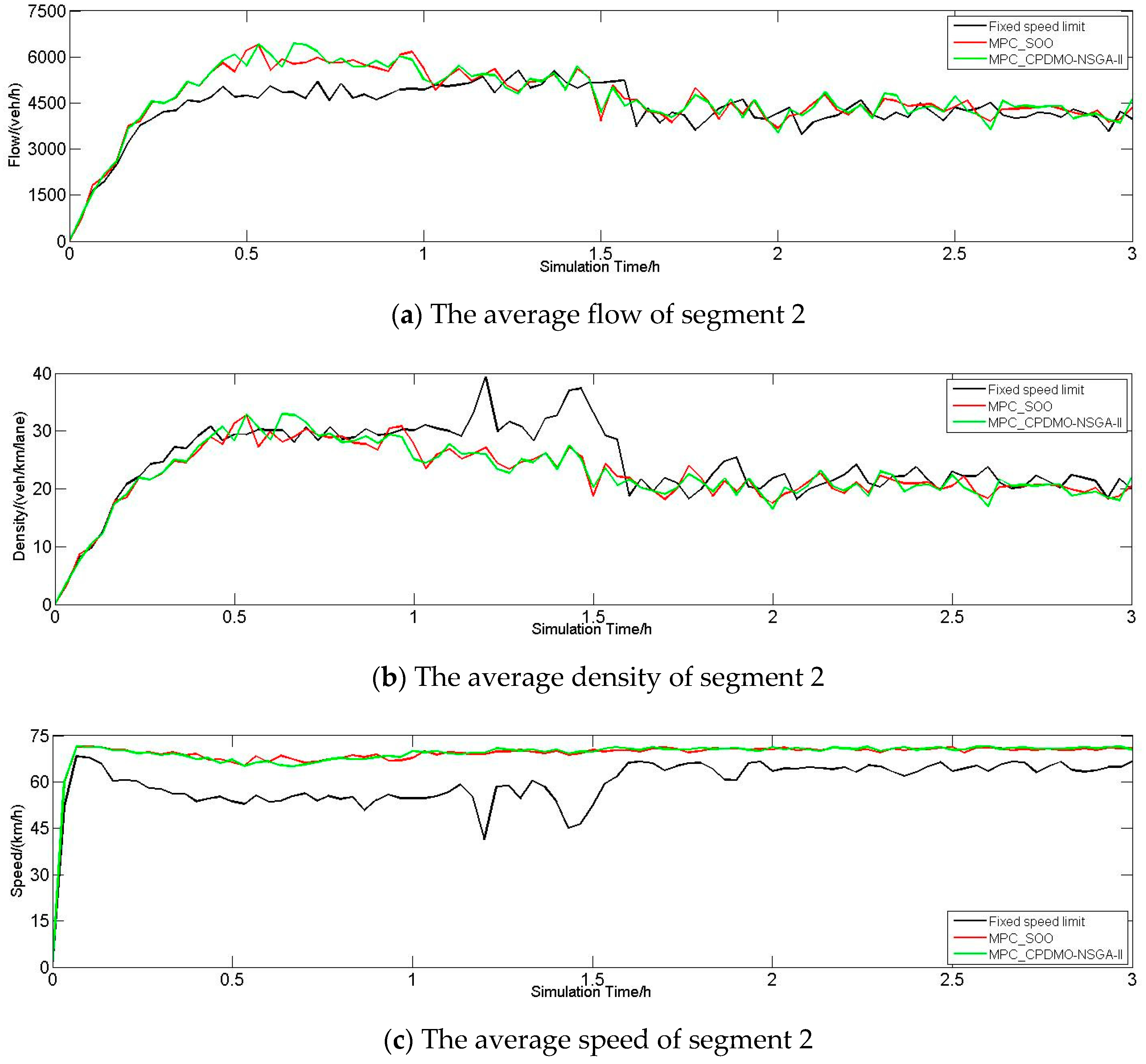
6.2.4. Discussion about Traffic Conditions
7. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Acronym List
| Acronym List | |
| English Abbreviations | English Full Name |
| MPC | model predictive control |
| NSGA-II | a fast and elitist multi-objective genetic algorithm |
| CPDMO-NSGA-II | dynamic multi-objective optimization algorithm based on clustering and prediction with NSGA-II |
| MPC_CPDMO-NSGA-II | model predictive control based on CPDMO-NSGA-II |
| TOPSIS | Technique for Order Preference by Similarity to an Ideal Solution |
| VSL | variable speed limit |
| RM | ramp metering |
| AR, VAR | Autoregressive, Vector (multivariate) Autoregressive |
| RND, VAR, PRE, V&P | Random, Variation, Prediction, Variation and Prediction |
| CPM_DMOEA | clustering prediction model based dynamic multi-objective evolutionary algorithm |
| TTS | Total Time Spend |
| TTT | Total travel time |
| TWT | Total waiting time |
| TTD | Total Travel Distance |
| TE | Total Emissions |
| TF | Total Fuel Consumption |
| MPC_SOO | model predictive control based on single-objective optimization algorithm |
References
- Zegeye, S.K.; De Schutter, B.; Hellendoorn, J.; Breunesse, E.A.; Hegyi, A. Integrated macroscopic traffic flow, emission, and fuel consumption model for control purposes. Transp. Res. Part C Emerg. Technol. 2013, 31, 158–171. [Google Scholar] [CrossRef]
- Frejo, J.R.D.; Núñez, A.; De Schutter, B.; Camacho, E.F. Hybrid model predictive control for freeway traffic using discrete speed limit signals. Transp. Res. Part C Emerg. Technol. 2014, 46, 309–325. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Bellemans, T.; Schutter, B.D.; Moor, B.D. Model predictive control for ramp metering of motorway traffic: A case study. Control Eng. Pract. 2006, 14, 757–767. [Google Scholar] [CrossRef]
- Frejo, J.R.D.; Núnez, A.; De Schutter, B.; Camacho, E.F. Model predictive control for freeway traffic using discrete speed limit signals. In Proceedings of the 2013 Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 4033–4038. [Google Scholar]
- Ding, H.F.; Liu, S.Z.; Qin, Z. Coordinated Traffic Control for Urban Expressway Based on Model Predictive Control. J. Highw. Transp. Res. Dev. 2016, 33, 111–117. [Google Scholar]
- Hu, L.; Sun, W.; Wang, H. An extended model predictive control approach to coordinated ramp metering. In Proceedings of the 2013 10th IEEE International Conference on Control and Automation (ICCA), Hangzhou, China, 12–14 June 2013. [Google Scholar]
- Long, K.J.; Yun, M.P.; Zheng, J.L.; Yang, X. Model predictive control for variable speed limit in freeway work zone. In Proceedings of the 2008 27th Chinese Control Conference, Kunming, China, 16–18 July 2008; pp. 488–493. [Google Scholar]
- Zheng, T.; Wu, G.; Liu, G.H.; Ling, Q. Multi-Objective Nonlinear Model Predictive Control: Lexicographic Method. In Model Predictive Control; InTechOpen: London, UK, 2010. [Google Scholar]
- Zegeye, S.K.; De Schutter, B.; Hellendoorn, H.; Breunesse, E. Reduction of travel times and traffic emissions using model predictive control. In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 5392–5397. [Google Scholar]
- Liu, S.; Hellendoorn, H.; Schutter, B.D. Model Predictive Control for Freeway Networks Based on Multi-Class Traffic Flow and Emission Models. IEEE Trans. Intell. Transp. Syst. 2017, 18, 306–320. [Google Scholar] [CrossRef]
- Zegeye, S.K.; De Schutter, B.; Hellendoorn, J.; Breunesse, E.A. Nonlinear MPC for the improvement of dispersion of freeway traffic emissions. IFAC Proc. Vol. 2011, 44, 10703–10708. [Google Scholar] [CrossRef]
- Luo, L.; Ge, Y.E.; Zhang, F.; Ban, X.J. Real-time route diversion control in a model predictive control framework with multiple objectives: Traffic efficiency, emission reduction and fuel economy. Transp. Res. Part D Transp. Environ. 2016, 48, 332–356. [Google Scholar] [CrossRef]
- Li, G.; Xie, B.L. Intelligent Integrated Control System of Expressway Based on MPC; Academy Edition; China Public Security: Beijing, China, 2017. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Muruganantham, A.; Zhao, Y.; Gee, S.B.; Qiu, X.; Tan, K.C. Dynamic multiobjective optimization using evolutionary algorithm with Kalman filter. Procedia Comput. Sci. 2013, 24, 66–75. [Google Scholar] [CrossRef]
- Hatzakis, I.; Wallace, D. Dynamic multi-objective optimization with evolutionary algorithms: A forward-looking approach. In Proceedings of the Conference on Genetic and Evolutionary Computation, Washington, DC, USA, 8–12 July 2006; pp. 1201–1208. [Google Scholar]
- Zhou, A.; Jin, Y.; Zhang, Q. Prediction-Based Population Re-Initialization for Evolutionary Dynamic Multi-Objective Optimization. In Evolutionary Multi-Criterion Optimization; Springer: Berlin/Heidelberg, Germany, 2007; pp. 832–846. [Google Scholar]
- Wu, Y.; Liu, X.X.; Chi, C.Z. Predictive multiobjective genetic algorithm for dynamic multiobjective problmes. Control Decis. 2013, 28, 677–682. [Google Scholar]
- Zhou, J.; Wang, G.H.; Zhao, Y.L. A Dynamic Multi-Objective Evolutionary Algorithm Based on Cluster Prediction Model. J. Nat. Sci. Hunan Norm. Univ. 2014, 37, 56–61. [Google Scholar]
- Xu, Z.S. Uncertain Multiple Attribute Decision Making: Methods and Applications; Tsinghua University Press: Beijing, China, 2004. [Google Scholar]
- Ahn, K.; Trani, A.A.; Rakha, H.; Van Aerde, M. Microscopic fuel consumption and emission models. In Proceedings of the 78th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 10–14 January 1999. CD-ROM. [Google Scholar]
- Pinto, G. Using the Relationship between Vehicle Fuel Consumption and CO2 Emissions to Illustrate Chemical Principles. J. Chem. Educ. 2008, 85, 218–220. [Google Scholar] [CrossRef]
- Jin, L.D.; Cui, E.Y.; Li, P.C.; Tian, Y.C. Dynamic Multi-Objective Optimization Algorithm Based on Reference Point Prediction. Acta Autom. Sin. 2017, 43, 313–320. [Google Scholar]
- Ishibuchi, H.; Masuda, H.; Tanigaki, Y.; Nojima, Y. Difficulties in specifying reference points to calculate the inverted generational distance for many-objective optimization problems. In Proceedings of the 2014 IEEE Symposium on Computational Intelligence in Multi-Criteria Decision-Making (MCDM), Orlando, FL, USA, 9–12 December 2015; pp. 170–177. [Google Scholar]
- Zhang, C.B.; Zhang, P.L.; Yan, X.P.; Jiang, Z. Variable Speed Limit for Freeway under Rain Weather Based on Cell Transmission Model. J. Transp. Syst. Eng. Inf. Technol. 2014, 14, 221–226. [Google Scholar]
- Sun, J.; Zhang, S.; Tang, K. Online evaluation of an integrated control strategy at on-ramp bottleneck for urban expressways in Shanghai. IET Intell. Transp. Syst. 2014, 8, 648–654. [Google Scholar] [CrossRef]
- Deb, K. An efficient constraint handling method for genetic algorithms. Comput. Methods Appl. Mech. Eng. 2000, 186, 311–338. [Google Scholar] [CrossRef]





| Name | Value | Unit | Name | Value | Unit |
|---|---|---|---|---|---|
| 18 | s | 33.5 | veh/km/lane | ||
| 40 | veh/km/lane | 0.012 | - | ||
| 60 | km2/h | 1.636 | - | ||
| 180 | veh/km/lane | 110 | km/h |
| Name | Value |
|---|---|
| Simulation time | 3 h |
| Sampling period (Ts) | 10 s |
| Control period | 1 min |
| Prediction horizon | 15 min |
| Control horizon | 10 min |
| Indicators | TTS (h) | TTD (km) | TE (kg) | TF (l) | |
|---|---|---|---|---|---|
| Methods | |||||
| Fixed speed limit | 554.217 | 29,228.58 | 99.554 | 5493.556 | |
| MPC_SOO | 465.8766 (−15.9%) | 30,564.13 4.6% | 38.687 (−61.1%) | 1775.608 (−67.7%) | |
| MPC_CPDMO-NSGA-II | 459.8024 (−17%) | 30,653.24 4.9% | 38.576 (−61.3%) | 1767.215 (−67.8%) | |
| Methods | Fixed Speed Limit | MPC_SOO | MPC_CPDMO-NSGA-II | |
|---|---|---|---|---|
| Traffic Conditions | ||||
| Flow (veh/h) | Segment 1 | 3942.02 | 4124.11 4.6% | 4121.85 4.6% |
| Segment 2 | 4360.05 | 4682.84 7.4% | 4704.81 7.9% | |
| Segment 3 | 4489.31 | 4652.83 3.6% | 4670.68 4.0% | |
| Density (veh/km/lane) | Segment 1 | 31.55 | 18.73 (−40.6%) | 18.72 (−40.7%) |
| Segment 2 | 24.70 | 22.56 (−8.7%) | 22.62 (−8.4%) | |
| Segment 3 | 23.60 | 21.35 (−9.5%) | 21.40 (−9.3%) | |
| Speed (km/h) | Segment 1 | 52.37 | 73.49 40.3% | 73.52 40.4% |
| Segment 2 | 60.07 | 69.55 15.8% | 69.63 15.9% | |
| Segment 3 | 63.67 | 72.62 14.0% | 72.70 14.2% |
| Location | Mainline(veh) | On-ramp(veh) | |
|---|---|---|---|
| Methods | |||
| Fixed Speed Limit | 3 | 24 | |
| MPC_SOO | 0 (−100%) | 13 (−45.8%) | |
| MPC_CPDMO-NSGA-II | 0 (−100%) | 0 (−100%) | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Yu, Y.; Guo, Q. Freeway Traffic Congestion Reduction and Environment Regulation via Model Predictive Control. Algorithms 2019, 12, 220. https://doi.org/10.3390/a12100220
Chen J, Yu Y, Guo Q. Freeway Traffic Congestion Reduction and Environment Regulation via Model Predictive Control. Algorithms. 2019; 12(10):220. https://doi.org/10.3390/a12100220
Chicago/Turabian StyleChen, Juan, Yuxuan Yu, and Qi Guo. 2019. "Freeway Traffic Congestion Reduction and Environment Regulation via Model Predictive Control" Algorithms 12, no. 10: 220. https://doi.org/10.3390/a12100220
APA StyleChen, J., Yu, Y., & Guo, Q. (2019). Freeway Traffic Congestion Reduction and Environment Regulation via Model Predictive Control. Algorithms, 12(10), 220. https://doi.org/10.3390/a12100220





