Data-Driven Predictive Modeling of Neuronal Dynamics Using Long Short-Term Memory
Abstract
1. Introduction
2. Neural Network Architecture, Algorithm and Approach
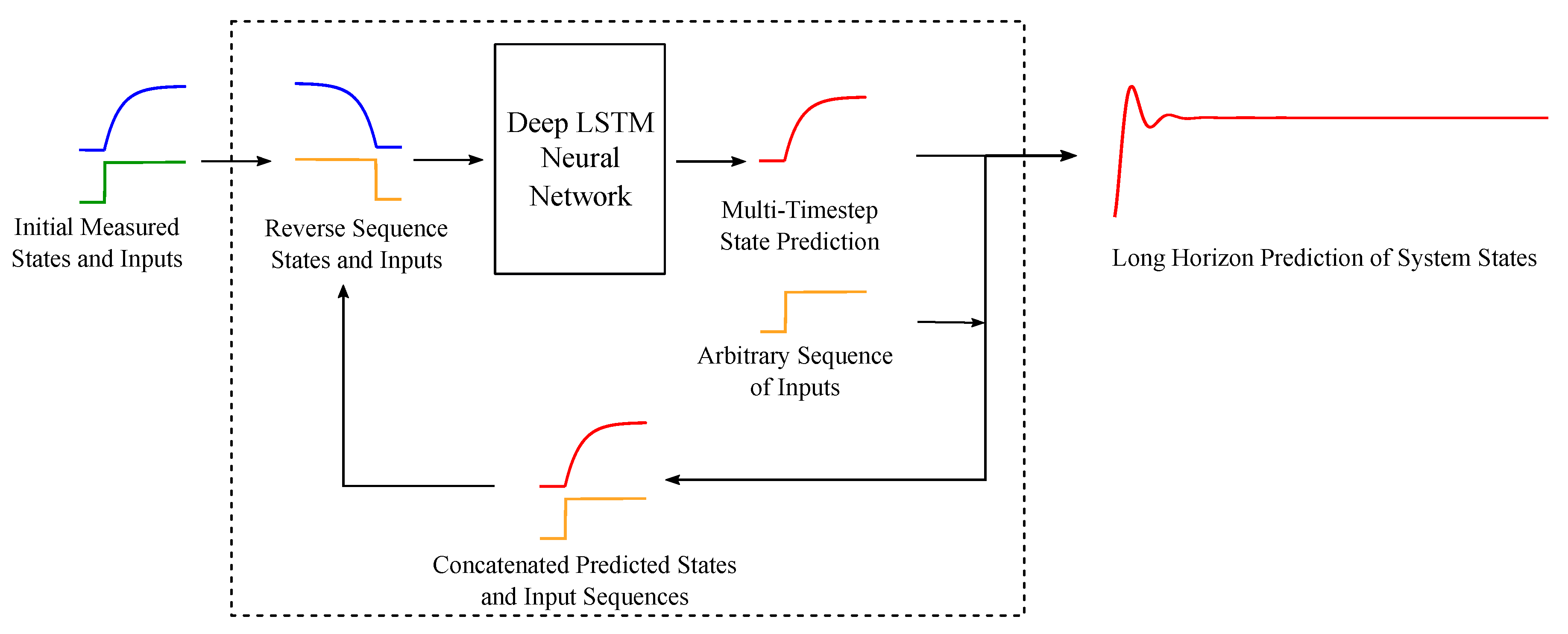
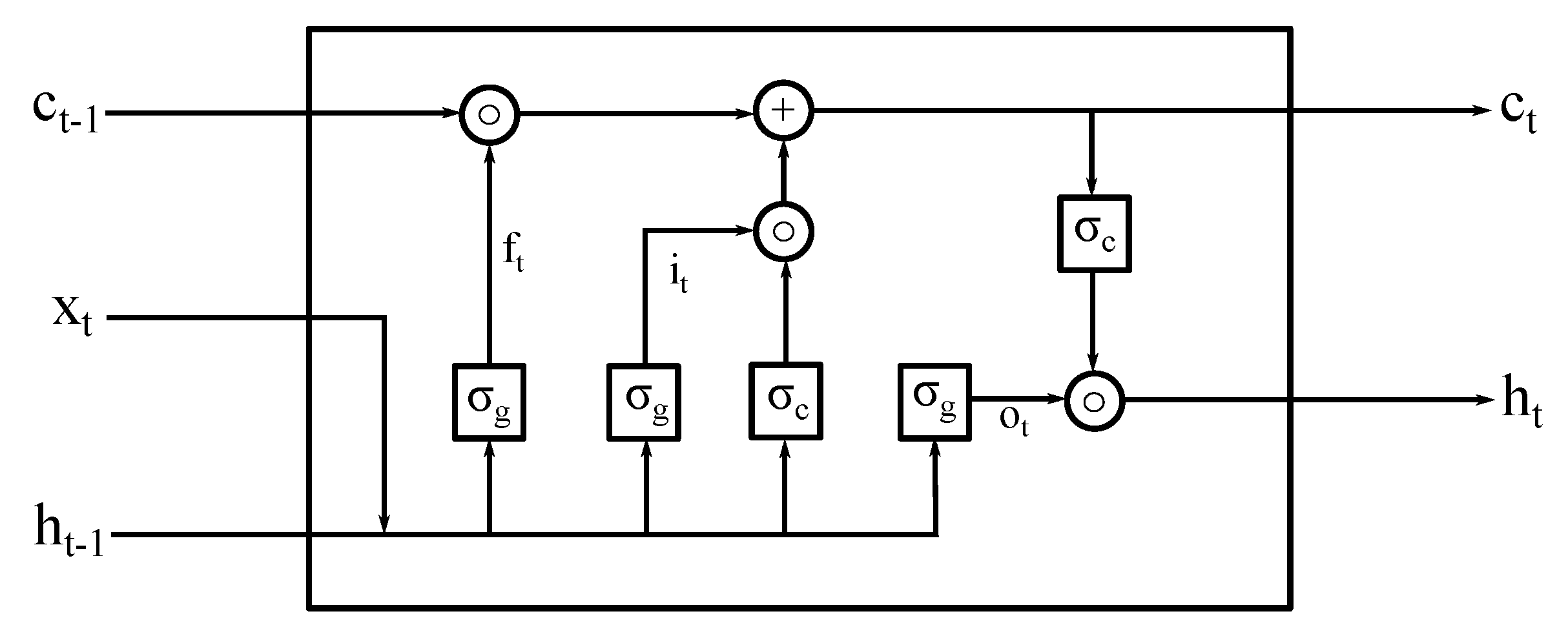
2.1. Deep LSTM Neural Network Architecture
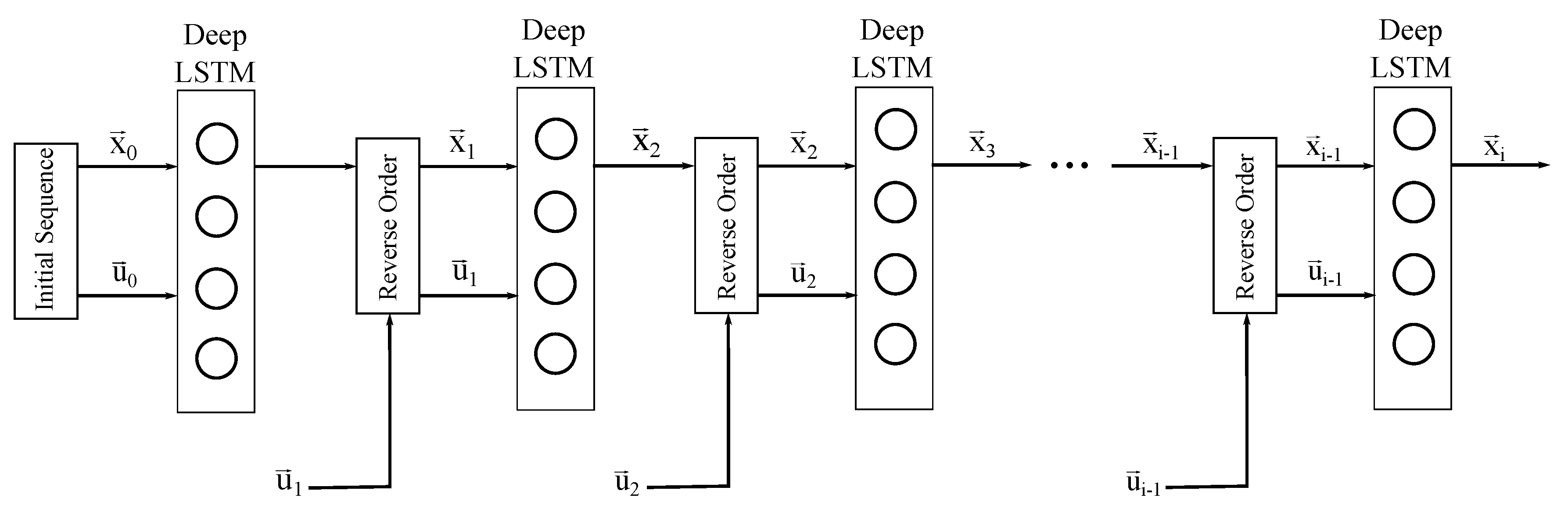
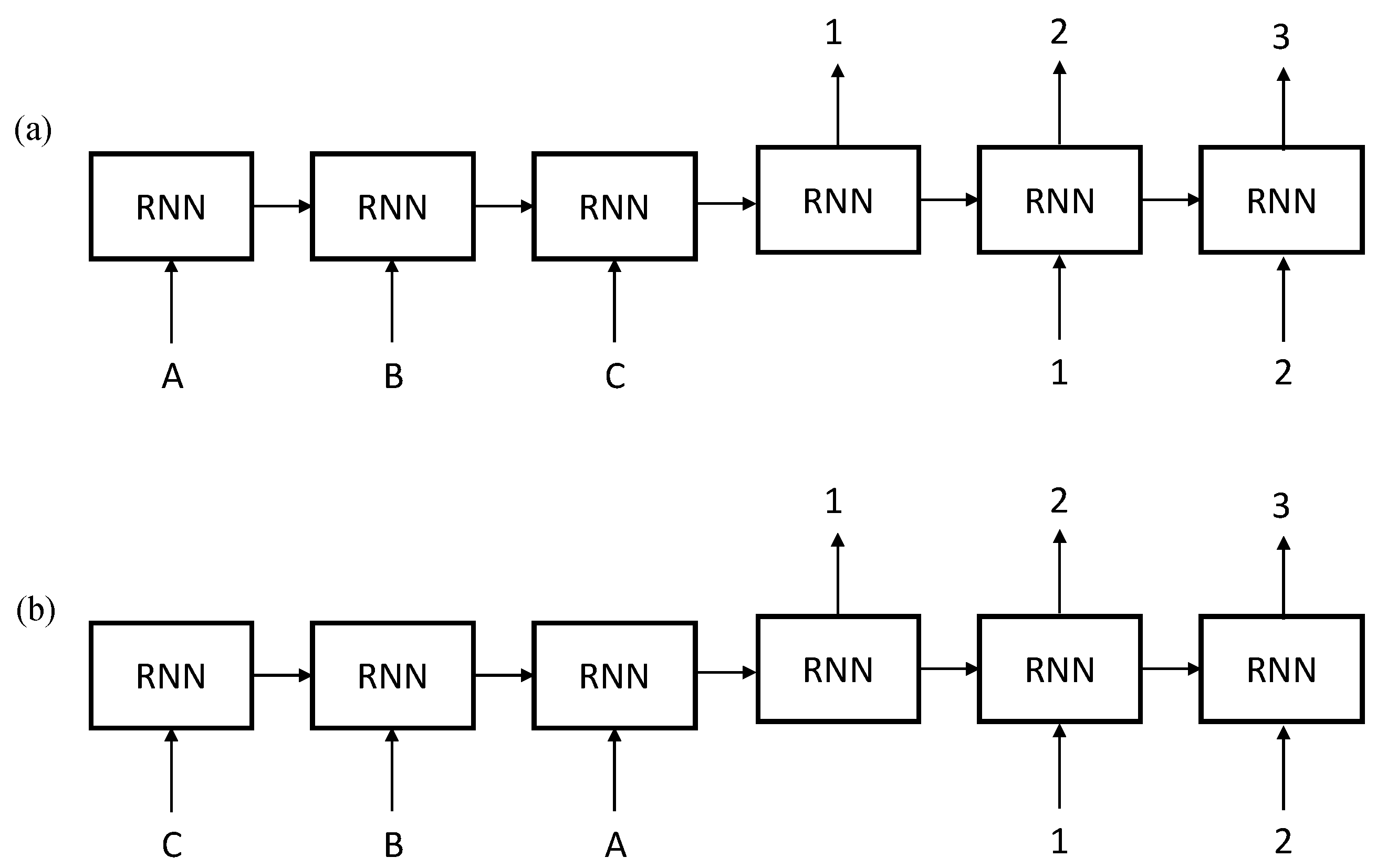
2.2. Sequence to Sequence Mapping with Neural Networks
2.3. Synthetic Data
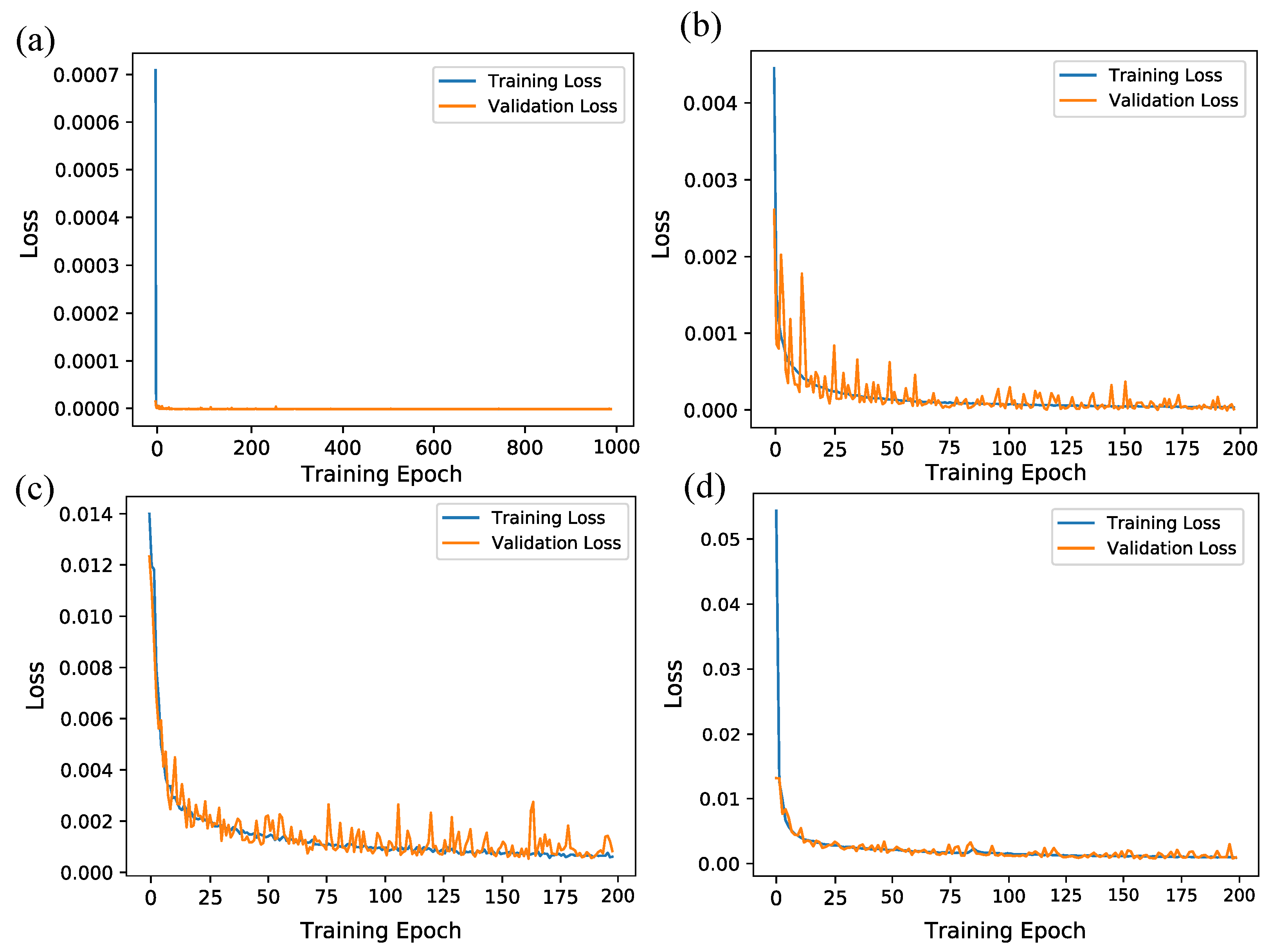
2.4. Network Training
3. Simulation Results
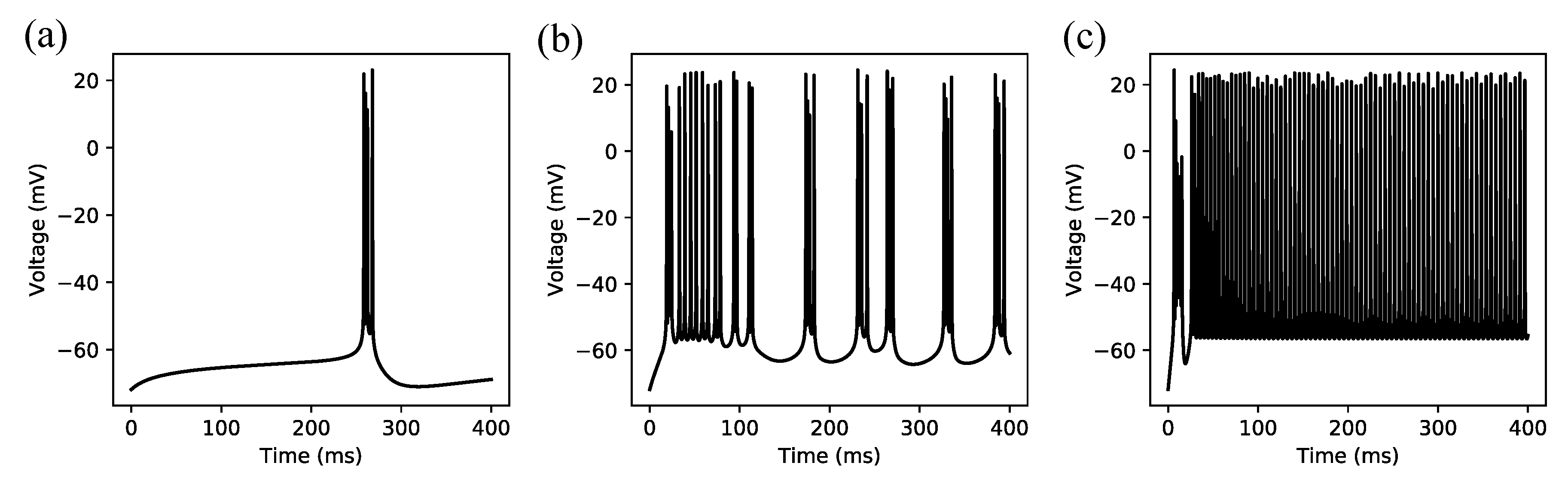
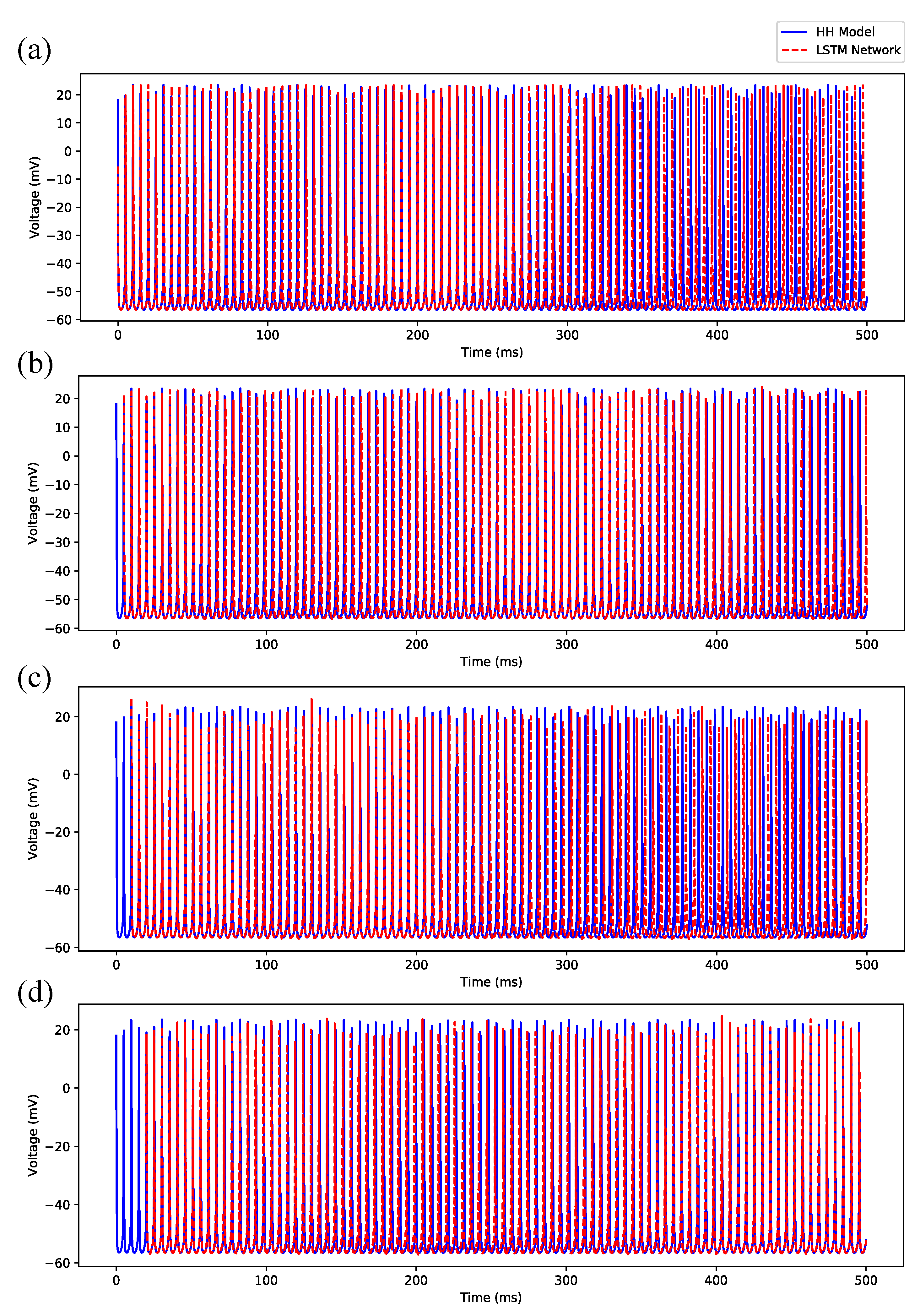
3.1. Regular Spiking
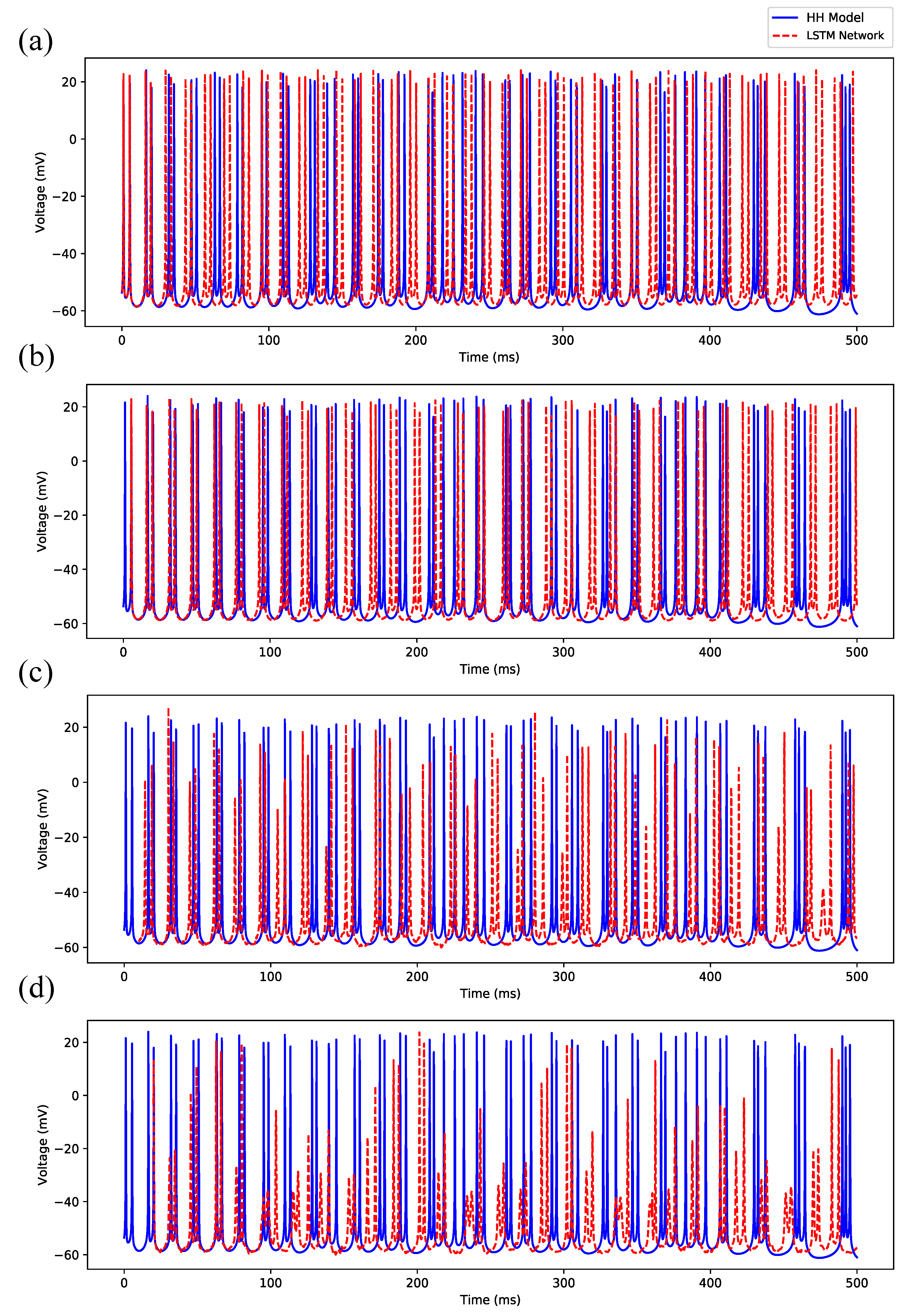
3.2. Irregular Bursting
3.3. Regular Bursting
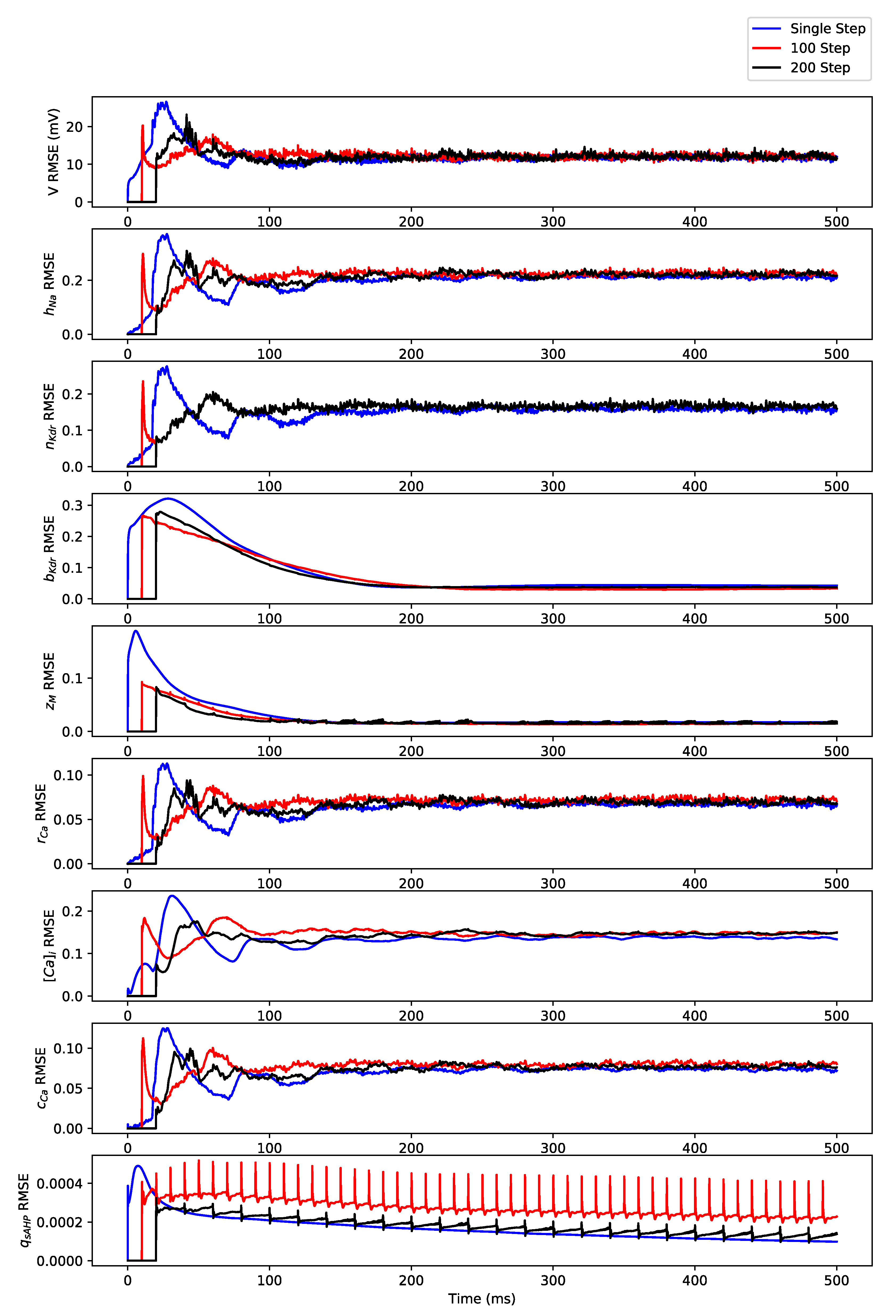
4. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. Hodgkin-Huxley Model of CA1 Pyramidal Neuron Dynamics
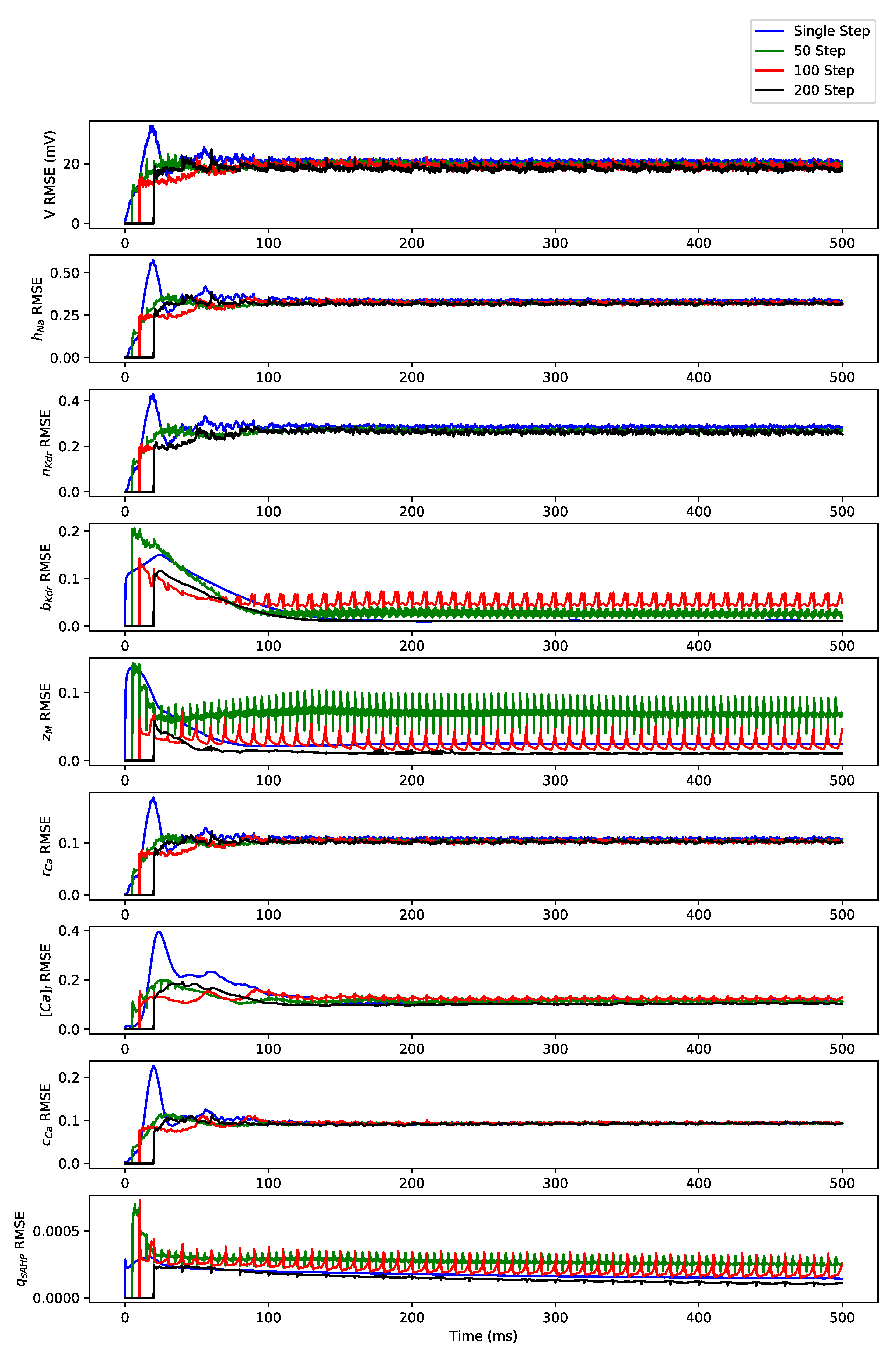
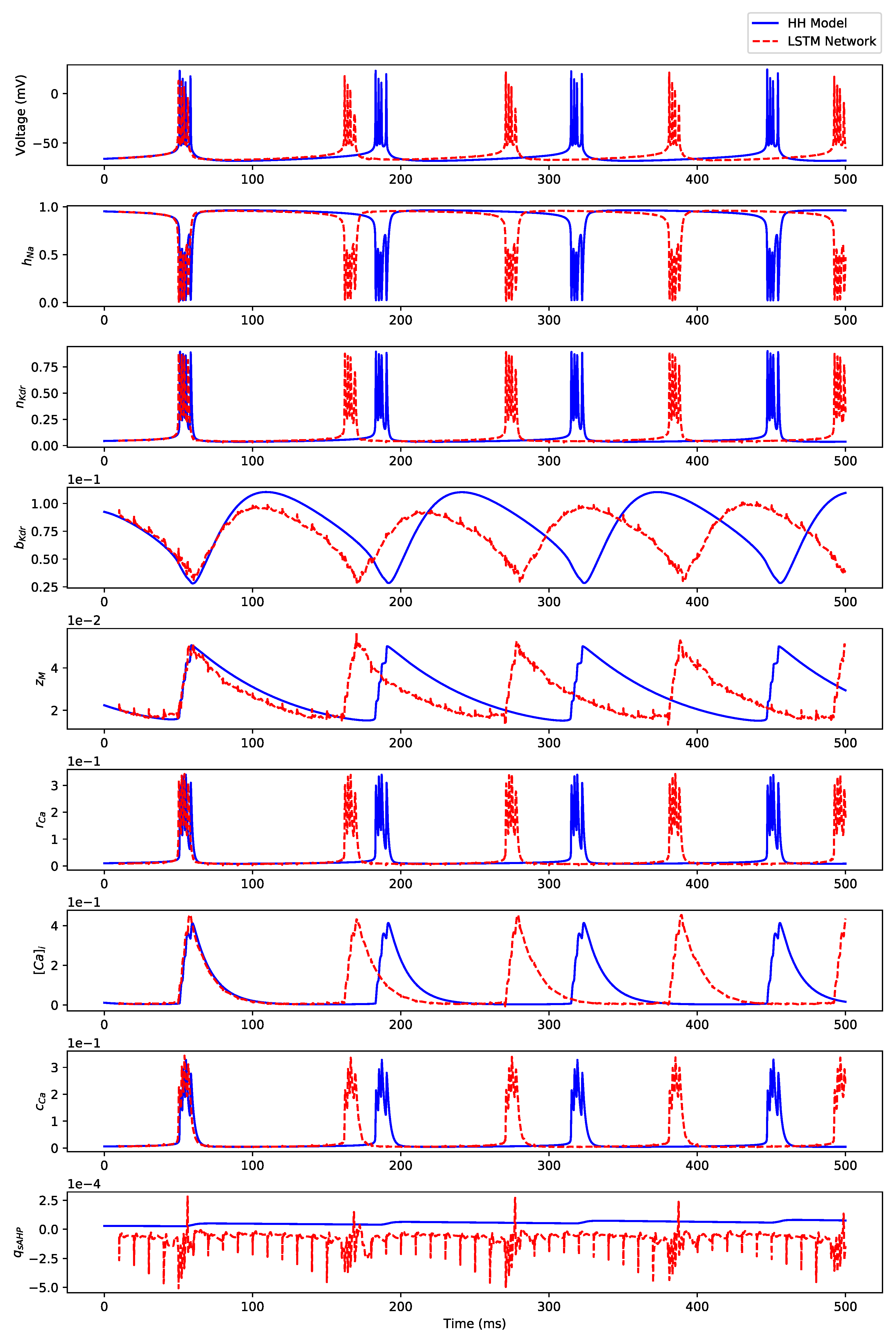
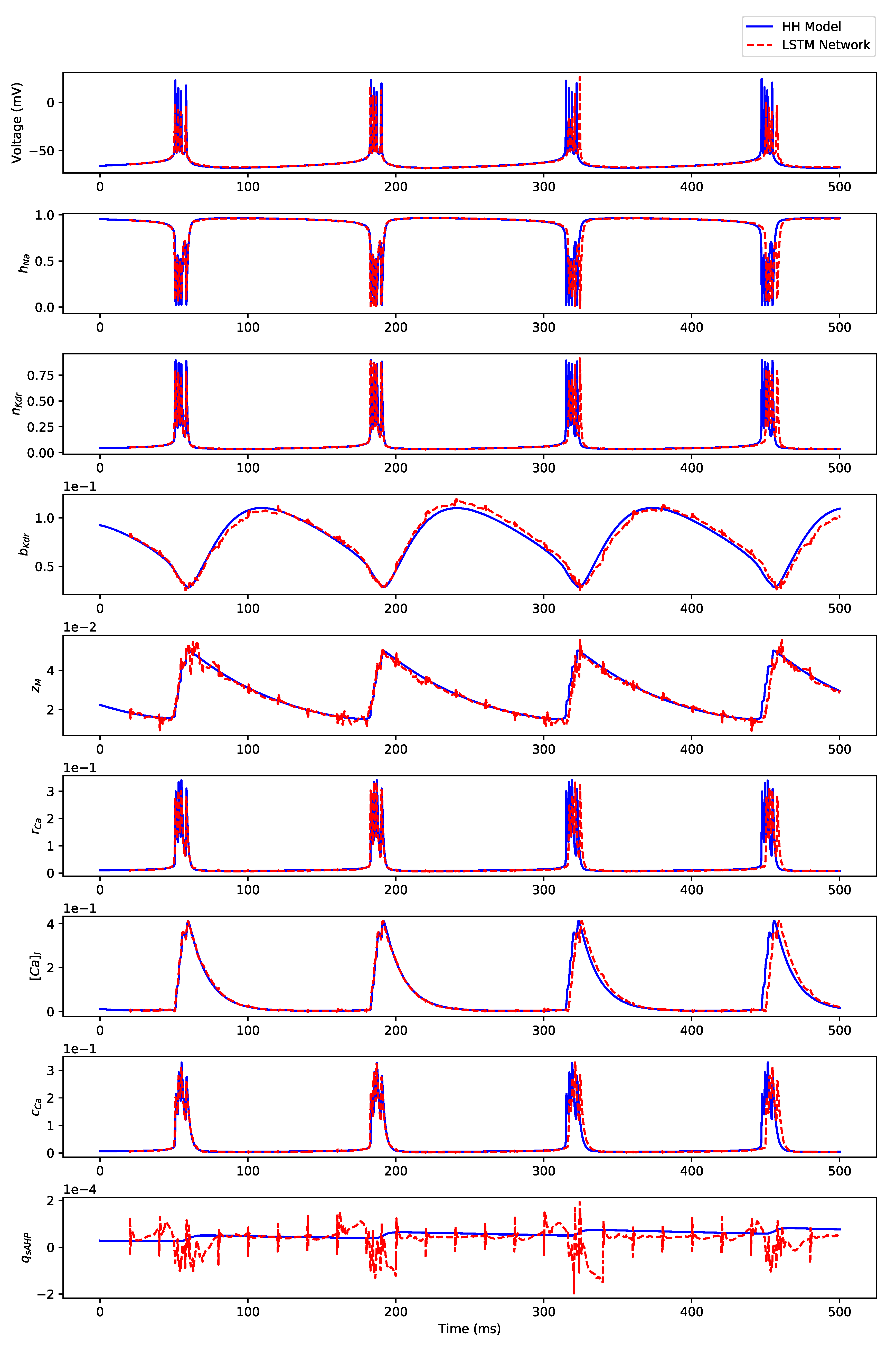
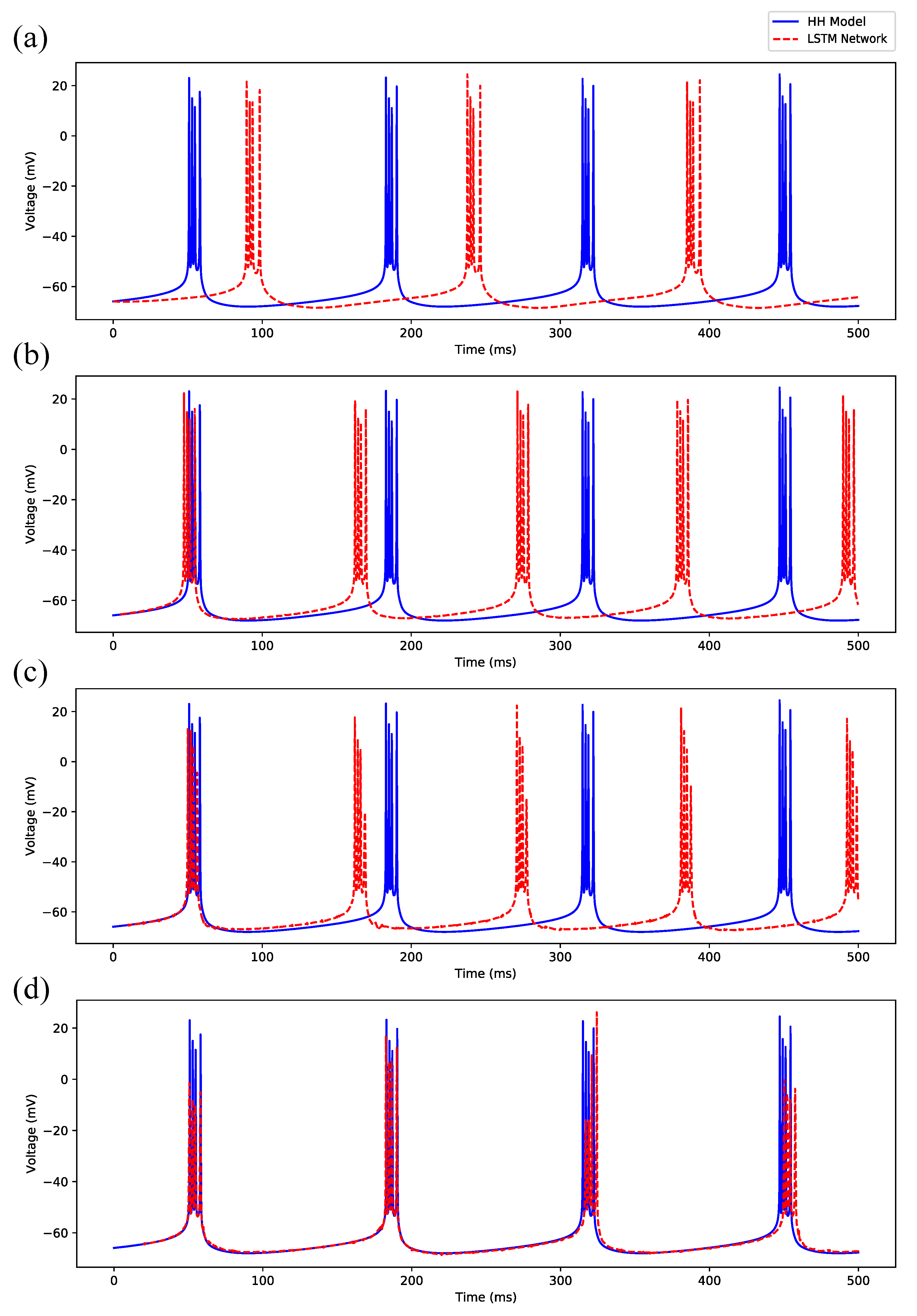
Appendix B. Simulation Results on Full State Predictions of Hodgkin-Huxley Model
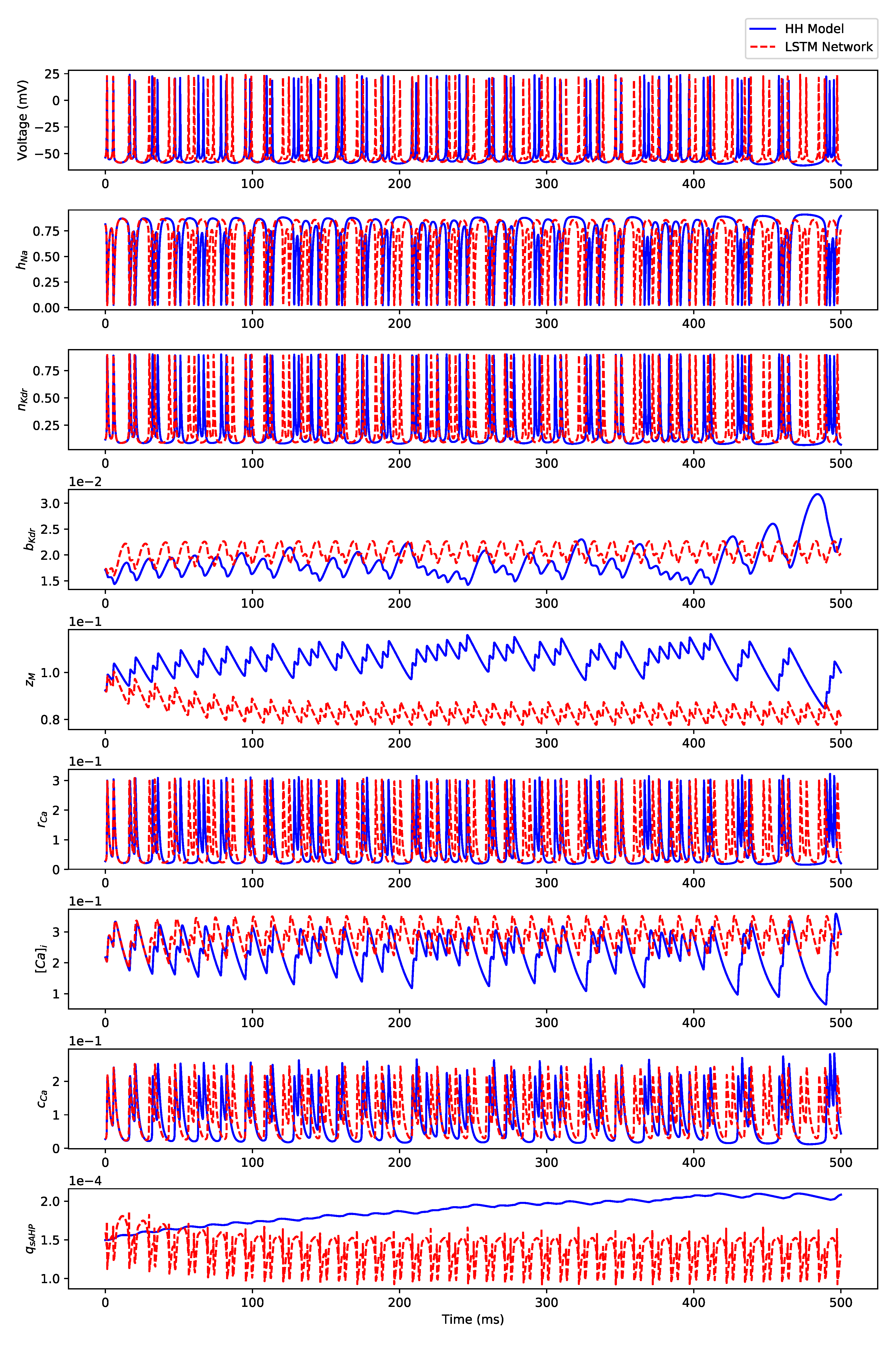
Appendix B.1. Regular Spiking
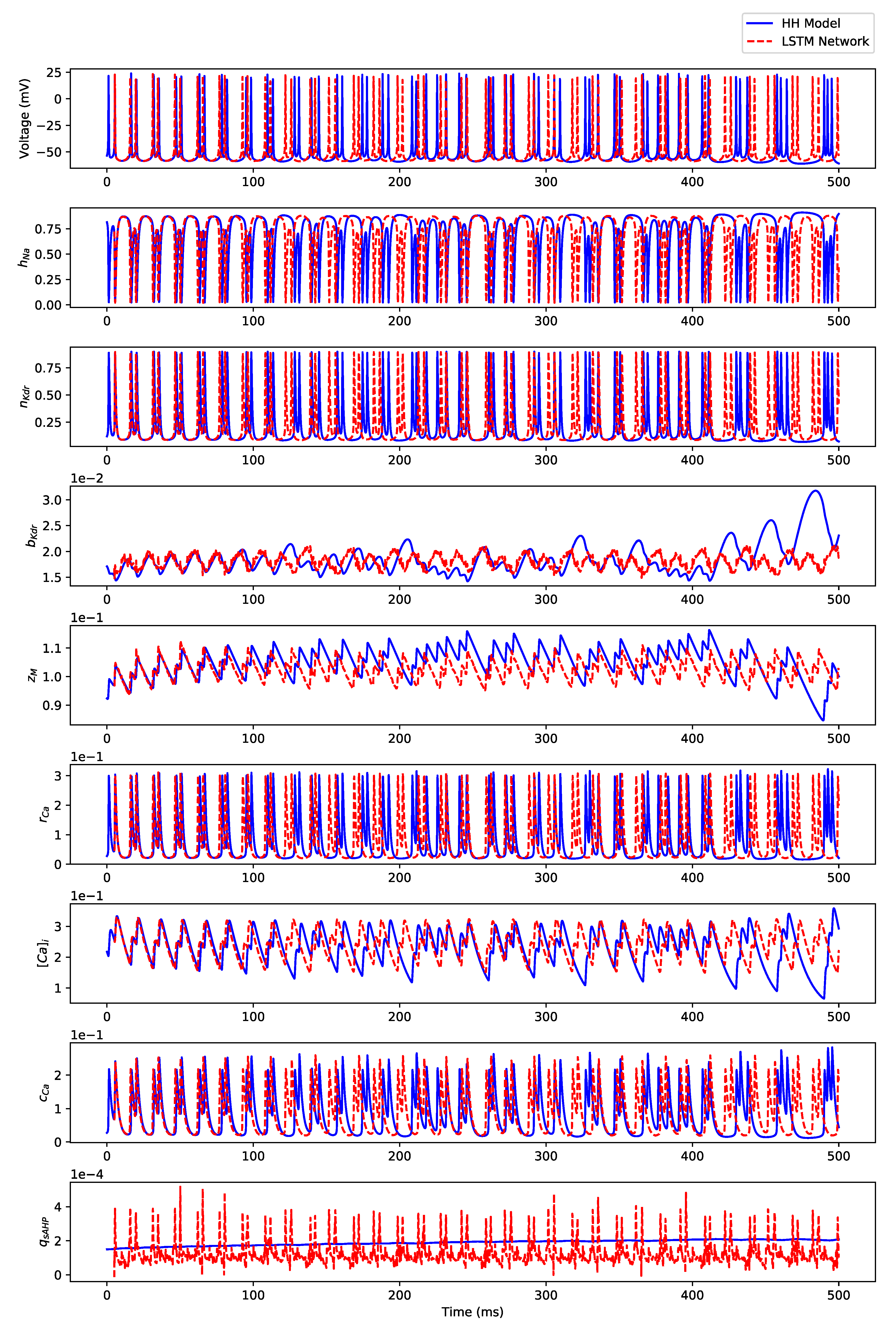
Appendix B.2. Irregular Bursting
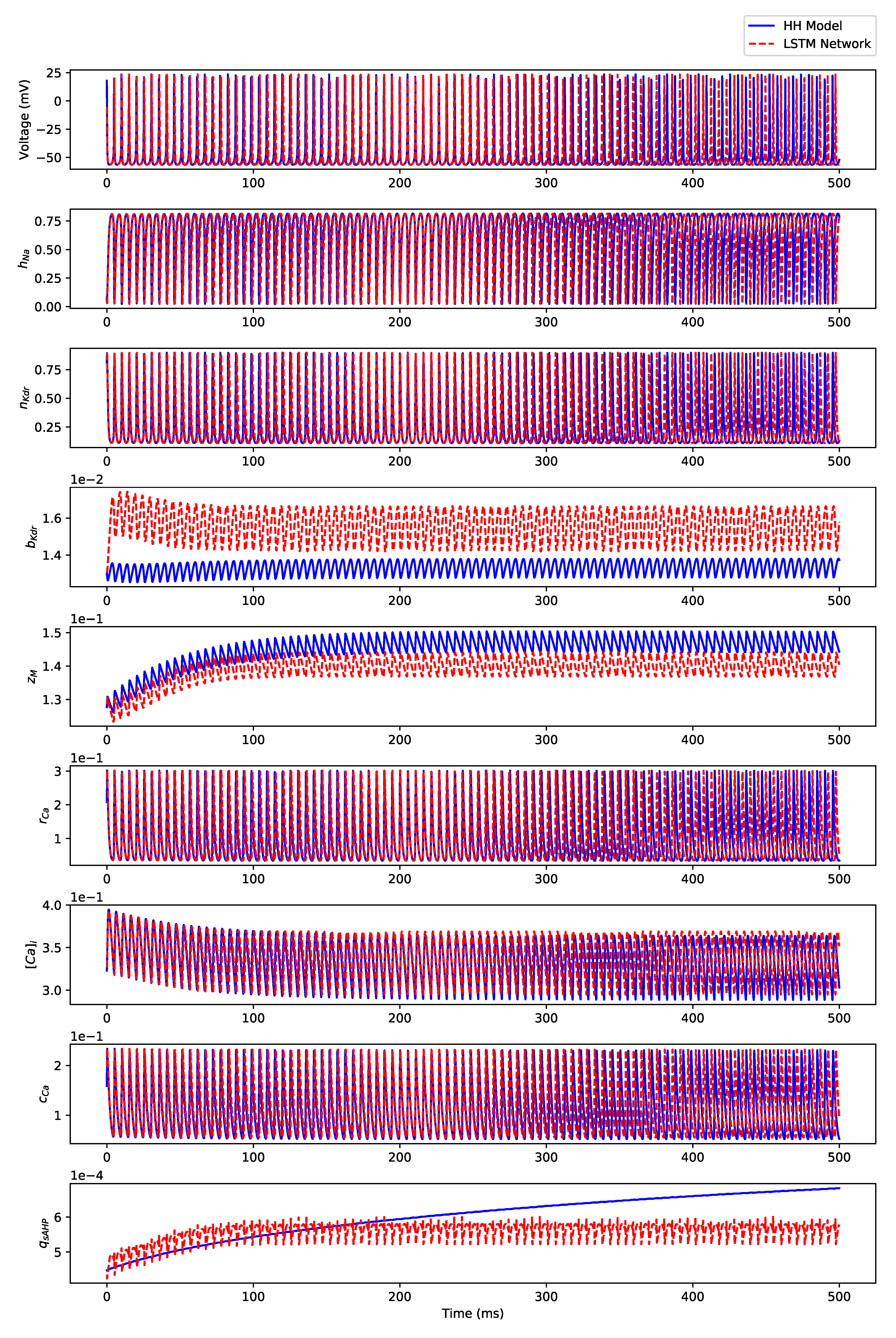
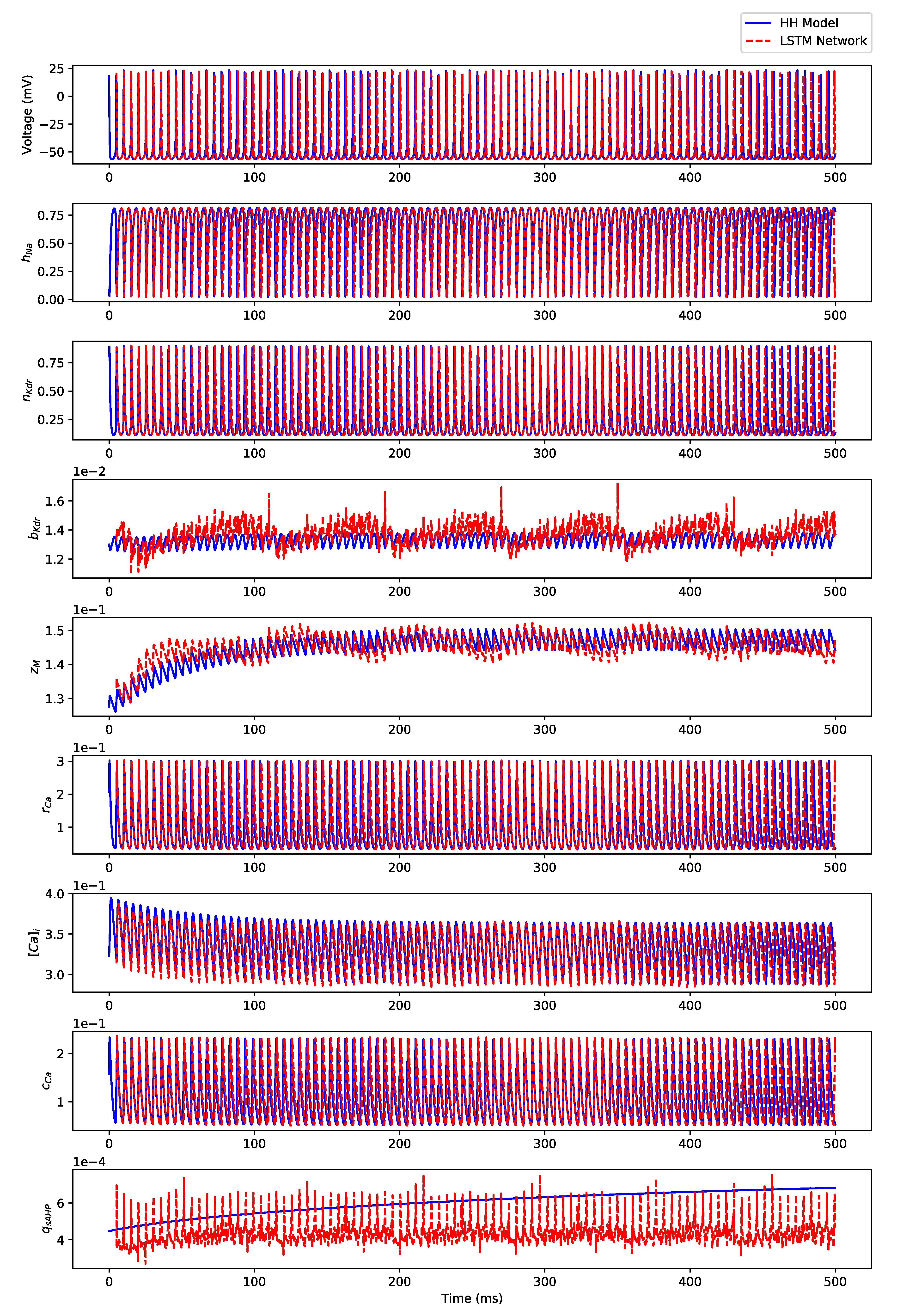
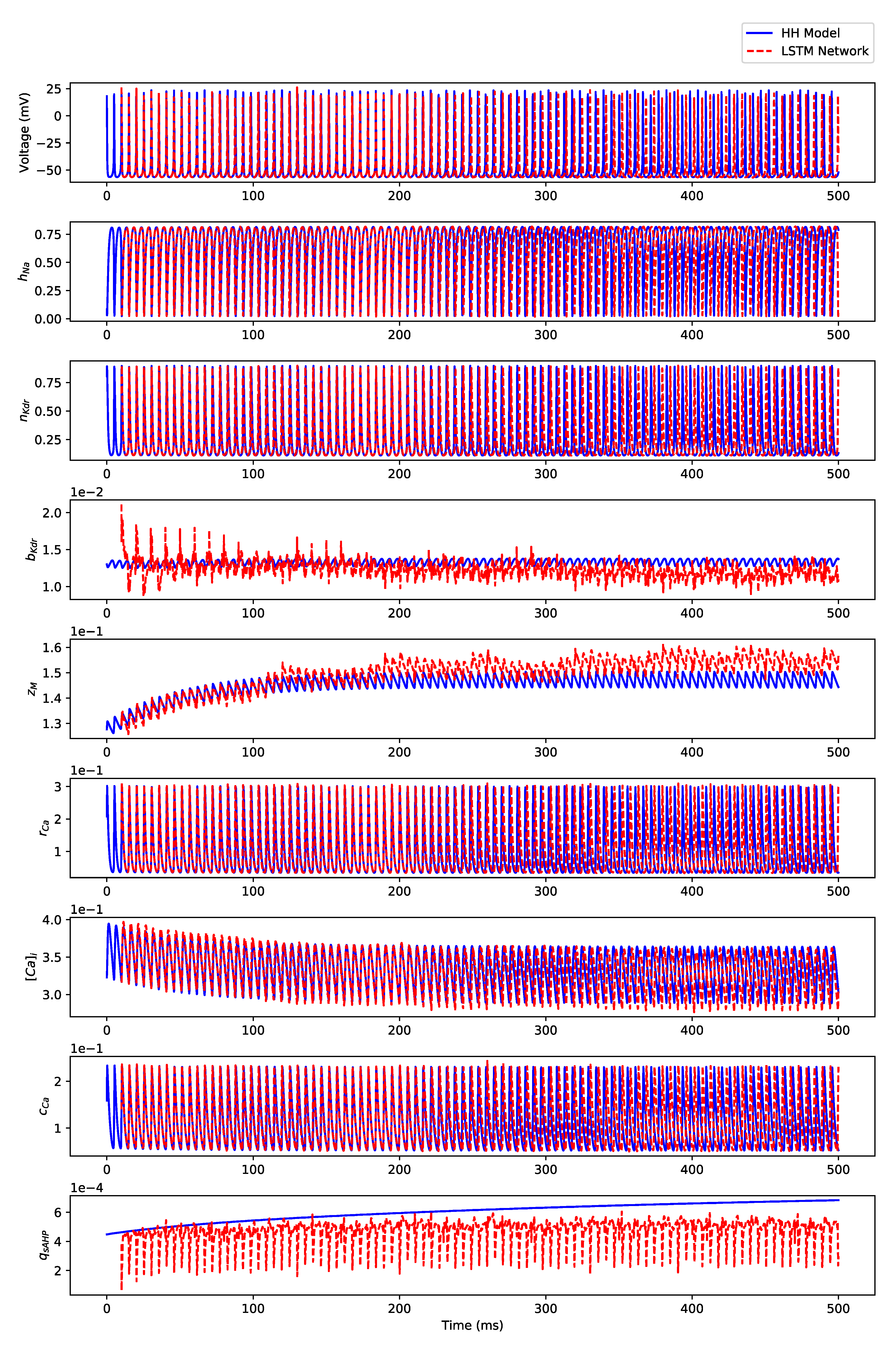
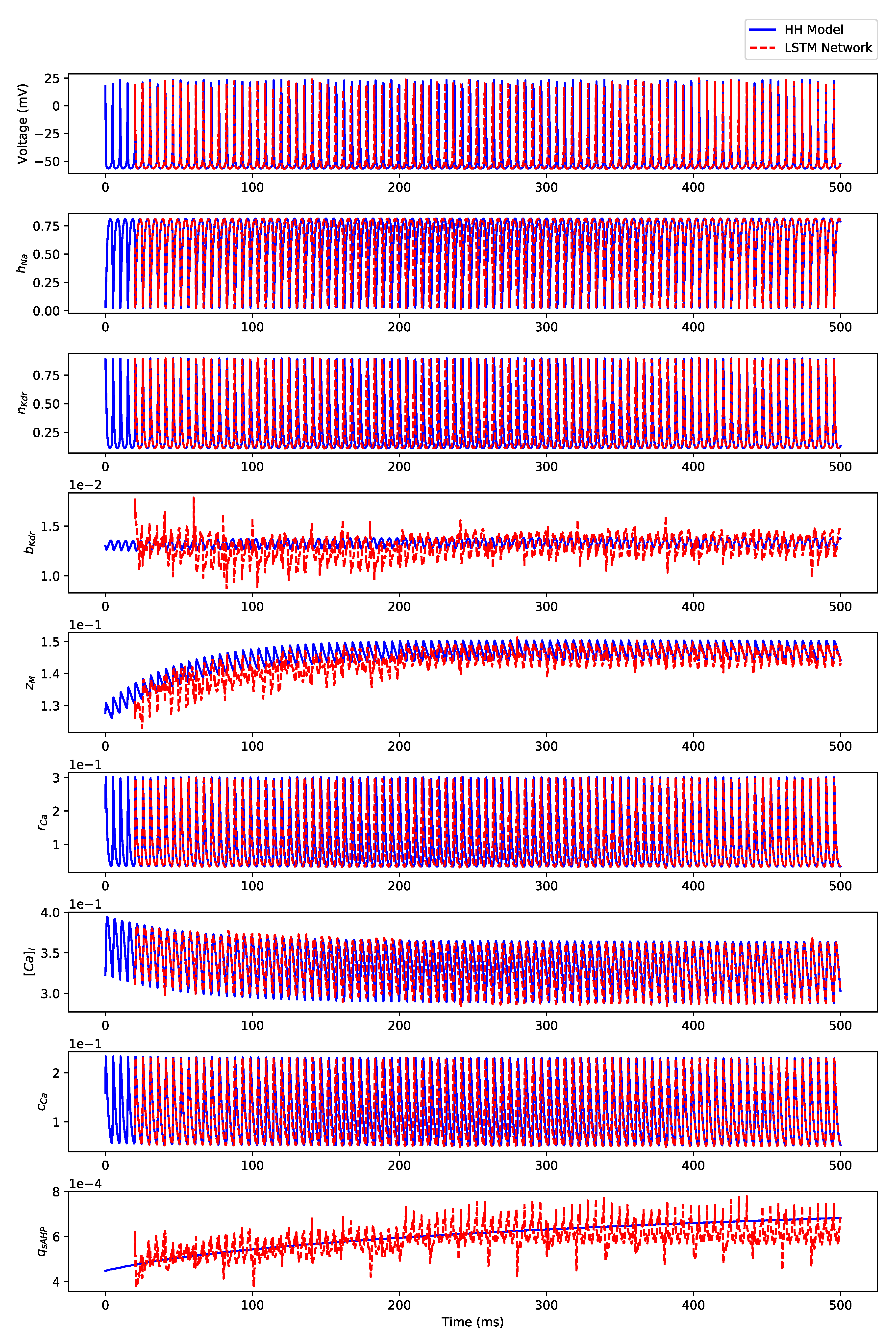
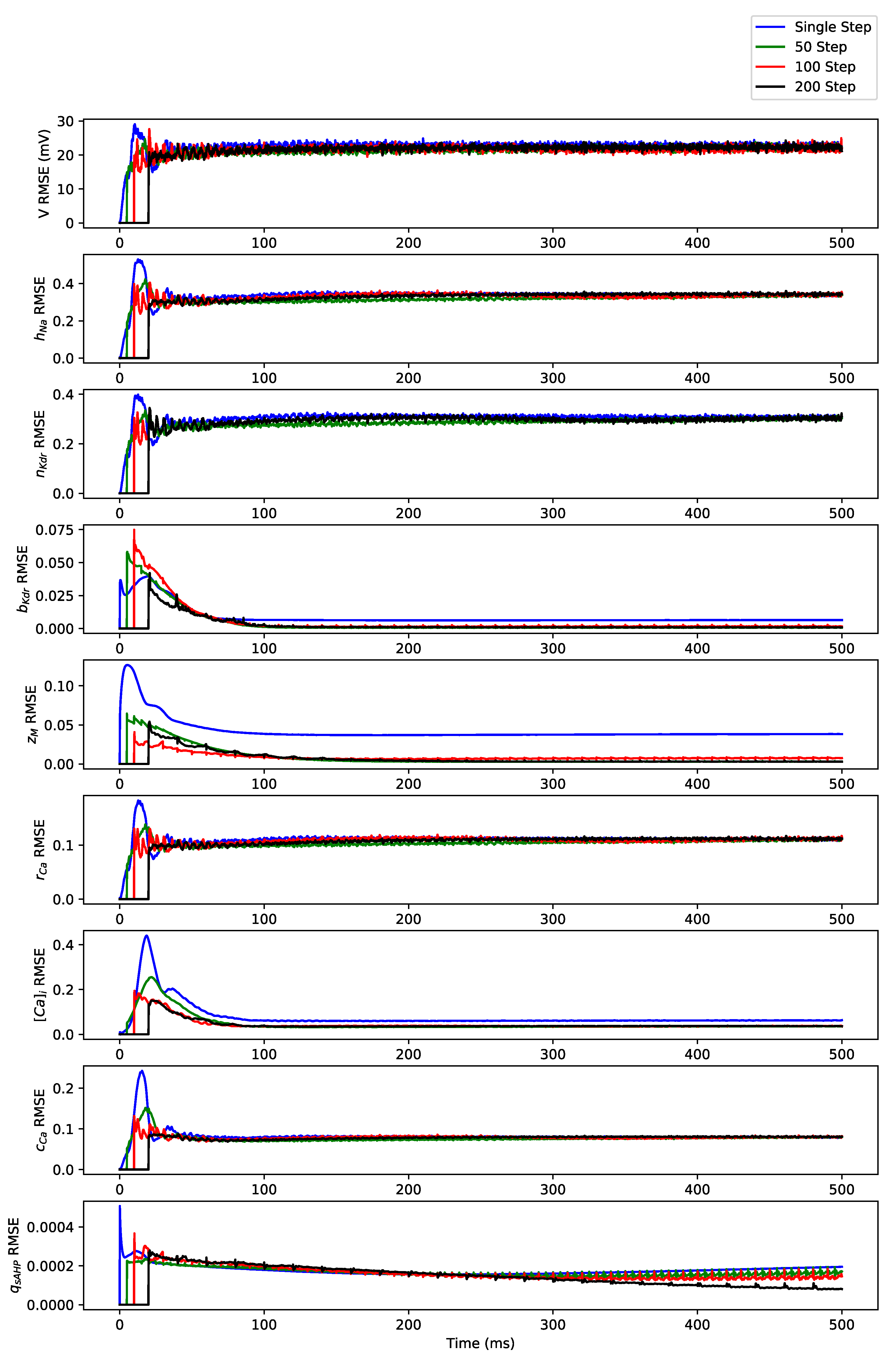
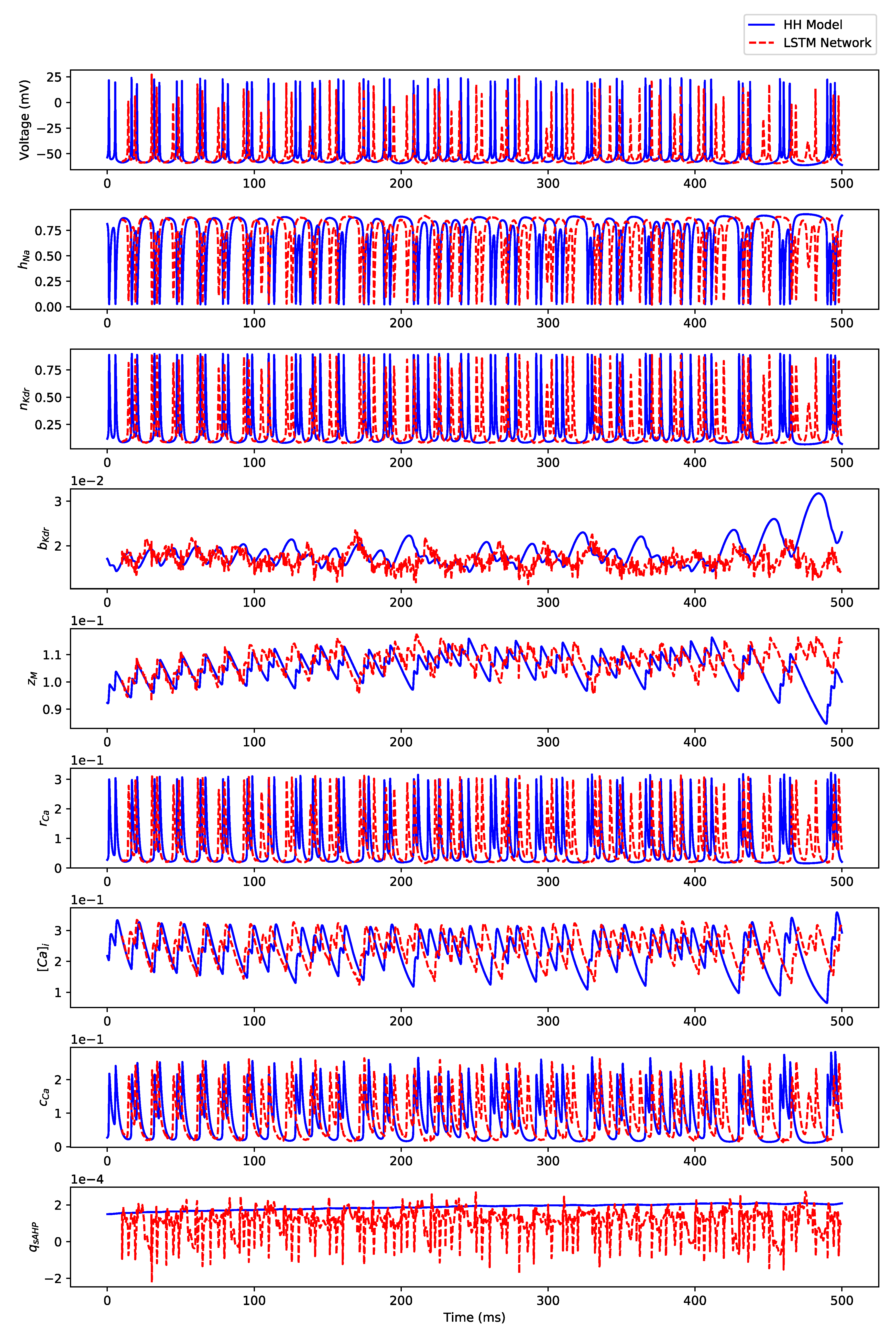
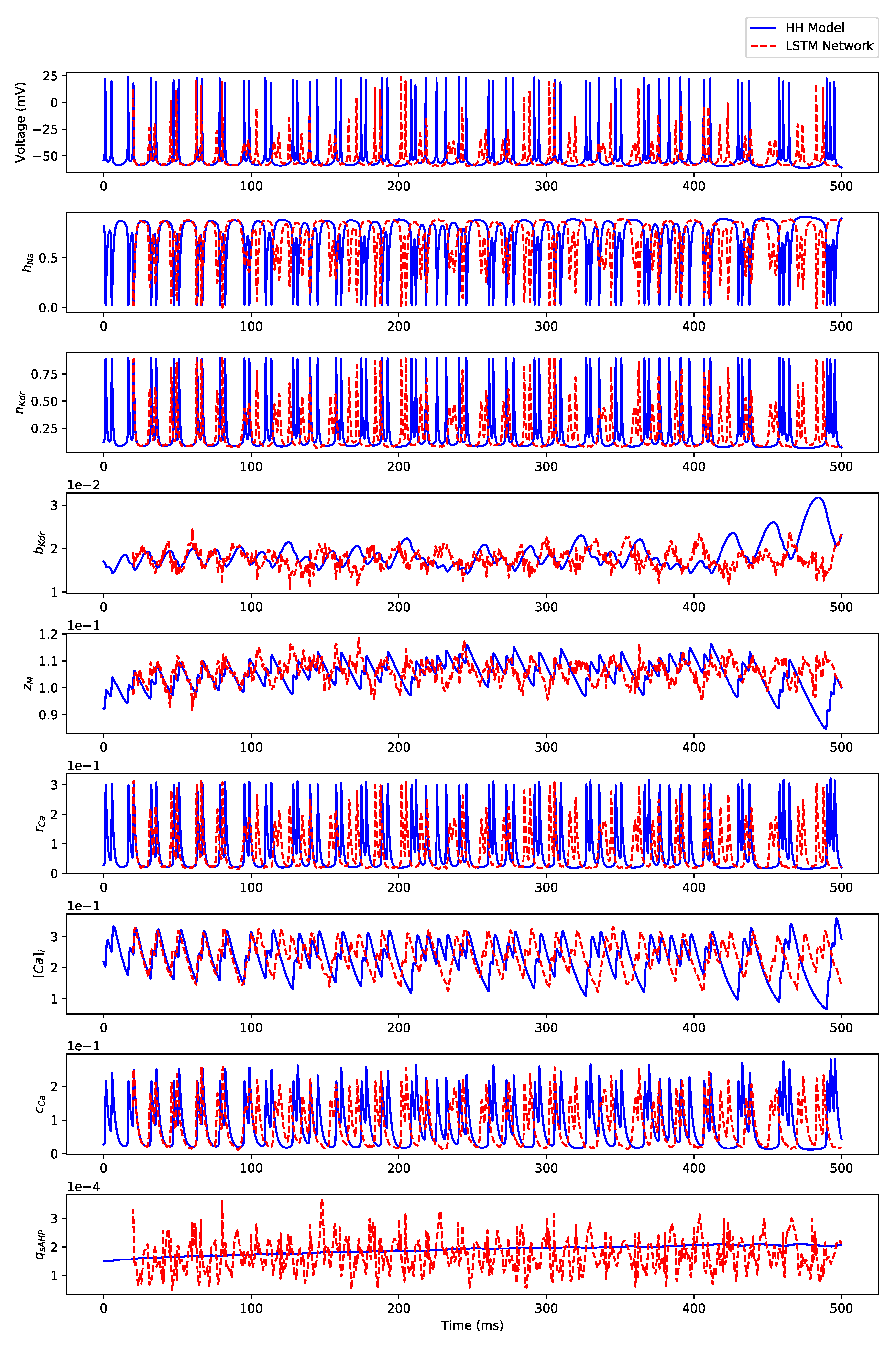
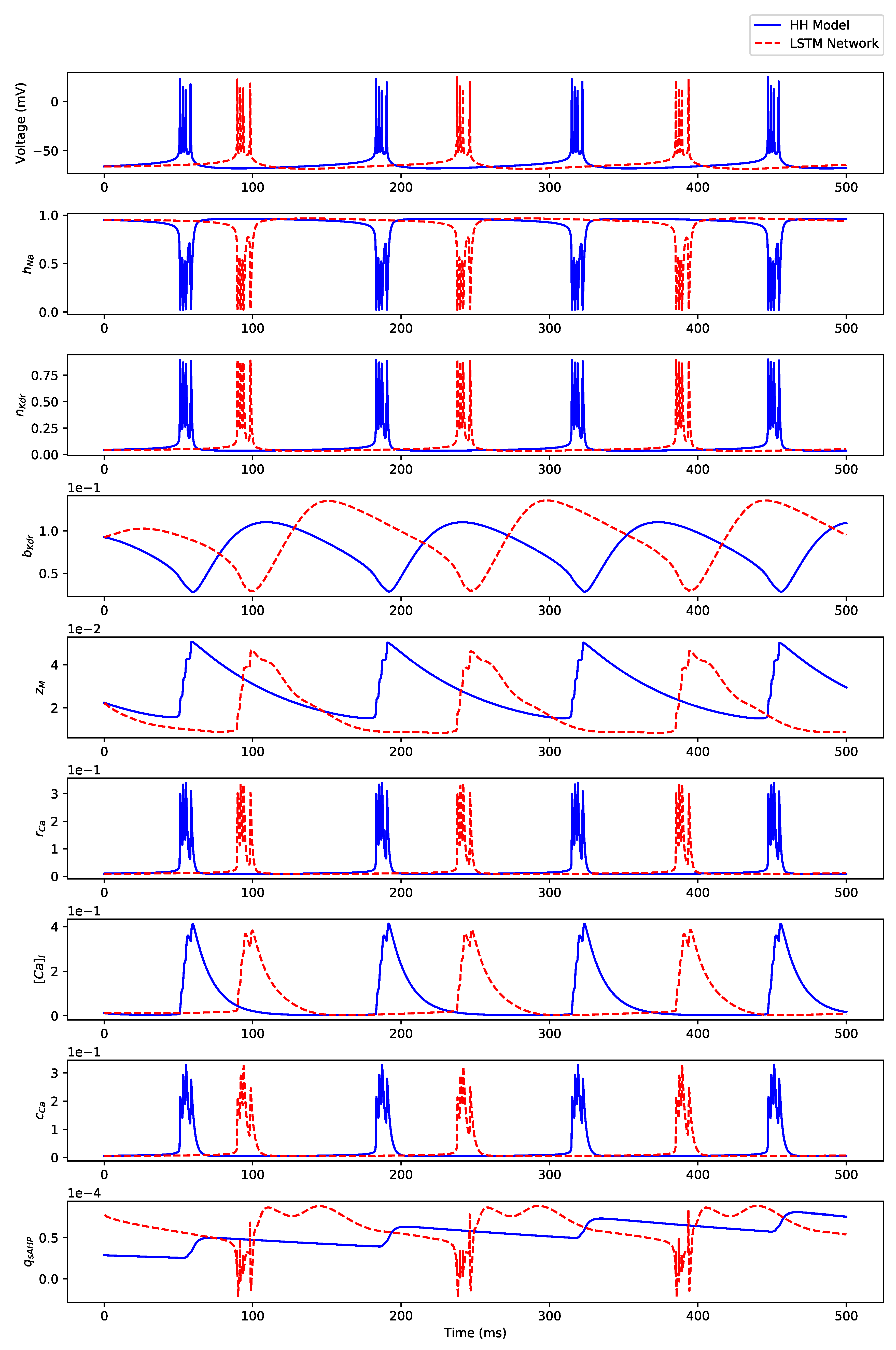
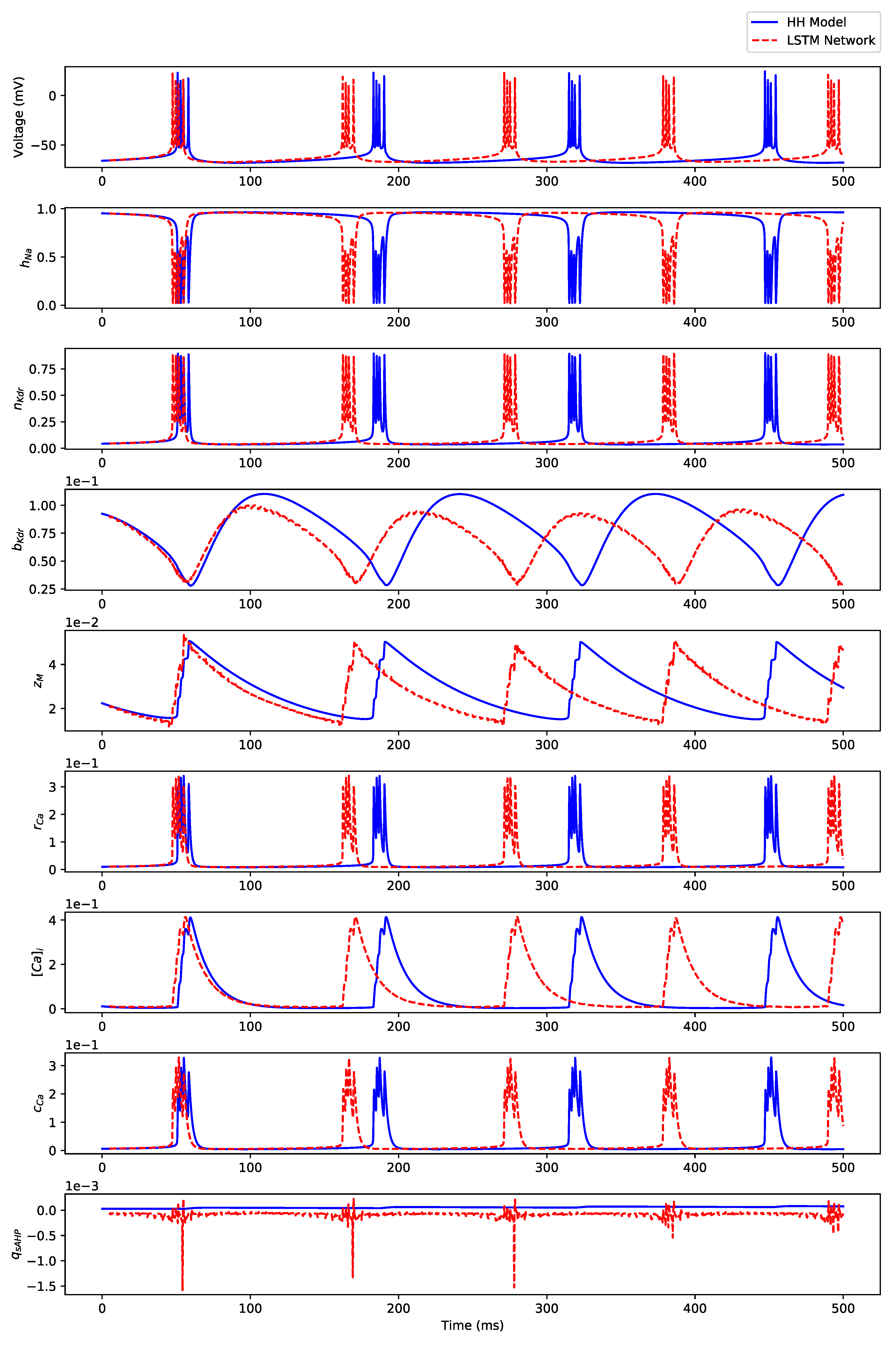
Appendix B.3. Regular Bursting
References
- Salmelin, R.; Hari, R.; Lounasmaa, O.; Sams, M. Dynamics of brain activation during picture naming. Nature 1994, 368, 463. [Google Scholar] [CrossRef] [PubMed]
- Fox, M.D.; Snyder, A.Z.; Vincent, J.L.; Corbetta, M.; Van Essen, D.C.; Raichle, M.E. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc. Natl. Acad. Sci. USA 2005, 102, 9673–9678. [Google Scholar] [CrossRef]
- Kiebel, S.J.; Daunizeau, J.; Friston, K.J. A hierarchy of time-scales and the brain. PLoS Comput. Biol. 2008, 4, e1000209. [Google Scholar] [CrossRef]
- Gerstner, W.; Kistler, W.M.; Naud, R.; Paninski, L. Neuronal Dynamics: From Single Neurons to Networks and Models of Cognition; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Siettos, C.; Starke, J. Multiscale modeling of brain dynamics: From single neurons and networks to mathematical tools. Wiley Interdiscip. Rev. Syst. Biol. Med. 2016, 8, 438–458. [Google Scholar] [CrossRef] [PubMed]
- Breakspear, M. Dynamic models of large-scale brain activity. Nat. Neurosci. 2017, 20, 340. [Google Scholar] [CrossRef] [PubMed]
- Herz, A.V.; Gollisch, T.; Machens, C.K.; Jaeger, D. Modeling single-neuron dynamics and computations: A balance of detail and abstraction. Science 2006, 314, 80–85. [Google Scholar] [CrossRef] [PubMed]
- Gerstner, W.; Naud, R. How good are neuron models? Science 2009, 326, 379–380. [Google Scholar] [CrossRef]
- Chen, S.; Billings, S. Neural networks for nonlinear dynamic system modelling and identification. Int. J. Control 1992, 56, 319–346. [Google Scholar] [CrossRef]
- Purwar, S.; Kar, I.; Jha, A. Nonlinear system identification using neural networks. IETE J. Res. 2007, 53, 35–42. [Google Scholar] [CrossRef]
- Kuschewski, J.G.; Hui, S.; Zak, S.H. Application of feedforward neural networks to dynamical system identification and control. IEEE Trans. Control Syst. Technol. 1993, 1, 37–49. [Google Scholar] [CrossRef]
- Pan, S.; Duraisamy, K. Long-time predictive modeling of nonlinear dynamical systems using neural networks. Complexity 2018, 2018, 4801012. [Google Scholar] [CrossRef]
- Gupta, P.; Sinha, N.K. Modeling robot dynamics using dynamic neural networks. IFAC Proc. Vol. 1997, 30, 755–759. [Google Scholar] [CrossRef]
- Patra, J.C.; Pal, R.N.; Chatterji, B.; Panda, G. Identification of nonlinear dynamic systems using functional link artificial neural networks. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1999, 29, 254–262. [Google Scholar] [CrossRef] [PubMed]
- Nagabandi, A.; Kahn, G.; Fearing, R.S.; Levine, S. Neural network dynamics for model-based deep reinforcement learning with model-free fine-tuning. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 7559–7566. [Google Scholar]
- Jaeger, H.; Haas, H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science 2004, 304, 78–80. [Google Scholar] [CrossRef] [PubMed]
- Bailer-Jones, C.A.; MacKay, D.J.; Withers, P.J. A recurrent neural network for modelling dynamical systems. Netw. Comput. Neural Syst. 1998, 9, 531–547. [Google Scholar] [CrossRef]
- Lenz, I.; Knepper, R.A.; Saxena, A. DeepMPC: Learning deep latent features for model predictive control. In Proceedings of the Robotics: Science and Systems, Rome, Italy, 13–17 July 2015. [Google Scholar]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the difficulty of training recurrent neural networks. In Proceedings of the International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1310–1318. [Google Scholar]
- Mohajerin, N.; Waslander, S.L. Multistep Prediction of Dynamic Systems With Recurrent Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2019. [Google Scholar] [CrossRef] [PubMed]
- Lin, L.; Gong, S.; Li, T.; Peeta, S. Deep learning-based human-driven vehicle trajectory prediction and its application for platoon control of connected and autonomous vehicles. In Proceedings of the Autonomous Vehicles Symposium, San Francisco, CA, USA, 9–12 July 2018; Volume 2018. [Google Scholar]
- Gonzalez, J.; Yu, W. Non-linear system modeling using LSTM neural networks. IFAC-PapersOnLine 2018, 51, 485–489. [Google Scholar] [CrossRef]
- Wang, Y. A new concept using LSTM neural networks for dynamic system identification. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 5324–5329. [Google Scholar]
- Vlachas, P.R.; Byeon, W.; Wan, Z.Y.; Sapsis, T.P.; Koumoutsakos, P. Data-driven forecasting of high-dimensional chaotic systems with long short-term memory networks. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20170844. [Google Scholar] [CrossRef]
- Zenke, F.; Ganguli, S. Superspike: Supervised learning in multilayer spiking neural networks. Neural Comput. 2018, 30, 1514–1541. [Google Scholar] [CrossRef]
- Huh, D.; Sejnowski, T.J. Gradient descent for spiking neural networks. In Proceedings of the Conference on Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 1433–1443. [Google Scholar]
- Pandarinath, C.; O’Shea, D.J.; Collins, J.; Jozefowicz, R.; Stavisky, S.D.; Kao, J.C.; Trautmann, E.M.; Kaufman, M.T.; Ryu, S.I.; Hochberg, L.R.; et al. Inferring single-trial neural population dynamics using sequential auto-encoders. Nat. Methods 2018, 15, 805–815. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- McKiernan, E.C.; Marrone, D.F. CA1 pyramidal cells have diverse biophysical properties, affected by development, experience, and aging. PeerJ 2017, 5, e3836. [Google Scholar] [CrossRef] [PubMed]
- Golomb, D.; Yue, C.; Yaari, Y. Contribution of persistent Na+ current and M-type K+ current to somatic bursting in CA1 pyramidal cells: Combined experimental and modeling study. J. Neurophysiol. 2006, 96, 1912–1926. [Google Scholar] [CrossRef] [PubMed]
- Nowacki, J.; Osinga, H.M.; Brown, J.T.; Randall, A.D.; Tsaneva-Atanasova, K. A unified model of CA1/3 pyramidal cells: An investigation into excitability. Prog. Biophys. Mol. Biol. 2011, 105, 34–48. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, K.A.; Huh, C.Y.; Amilhon, B.; Williams, S.; Skinner, F.K. Simple, biologically-constrained CA1 pyramidal cell models using an intact, whole hippocampus context. F1000Research 2014, 3, 104. [Google Scholar] [CrossRef] [PubMed]
- Poirazi, P.; Brannon, T.; Mel, B.W. Arithmetic of subthreshold synaptic summation in a model CA1 pyramidal cell. Neuron 2003, 37, 977–987. [Google Scholar] [CrossRef]
- Royeck, M.; Horstmann, M.T.; Remy, S.; Reitze, M.; Yaari, Y.; Beck, H. Role of axonal NaV1. 6 sodium channels in action potential initiation of CA1 pyramidal neurons. J. Neurophysiol. 2008, 100, 2361–2380. [Google Scholar] [CrossRef] [PubMed]
- Katz, Y.; Menon, V.; Nicholson, D.A.; Geinisman, Y.; Kath, W.L.; Spruston, N. Synapse distribution suggests a two-stage model of dendritic integration in CA1 pyramidal neurons. Neuron 2009, 63, 171–177. [Google Scholar] [CrossRef]
- Bianchi, D.; Marasco, A.; Limongiello, A.; Marchetti, C.; Marie, H.; Tirozzi, B.; Migliore, M. On the mechanisms underlying the depolarization block in the spiking dynamics of CA1 pyramidal neurons. J. Comput. Neurosci. 2012, 33, 207–225. [Google Scholar] [CrossRef]
- Marasco, A.; Limongiello, A.; Migliore, M. Fast and accurate low-dimensional reduction of biophysically detailed neuron models. Sci. Rep. 2012, 2, 1–7. [Google Scholar] [CrossRef]
- Kim, Y.; Hsu, C.L.; Cembrowski, M.S.; Mensh, B.D.; Spruston, N. Dendritic sodium spikes are required for long-term potentiation at distal synapses on hippocampal pyramidal neurons. Elife 2015, 4, e06414. [Google Scholar] [CrossRef] [PubMed]
- Bezaire, M.J.; Raikov, I.; Burk, K.; Vyas, D.; Soltesz, I. Interneuronal mechanisms of hippocampal theta oscillations in a full-scale model of the rodent CA1 circuit. Elife 2016, 5, e18566. [Google Scholar] [CrossRef] [PubMed]
- Werbos, P.J. Generalization of backpropagation with application to a recurrent gas market model. Neural Netw. 1988, 1, 339–356. [Google Scholar] [CrossRef]
- Werbos, P.J. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef]
- Mozer, M.C. A focused backpropagation algorithm for temporal. In Backpropagation: Theory, Architectures, and Applications; Lawrence Erlbaum Associates: Hillsdale, NJ, USA; Hove, UK, 1995; p. 137. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Naud, R.; Marcille, N.; Clopath, C.; Gerstner, W. Firing patterns in the adaptive exponential integrate-and-fire model. Biol. Cybern. 2008, 99, 335. [Google Scholar] [CrossRef] [PubMed]
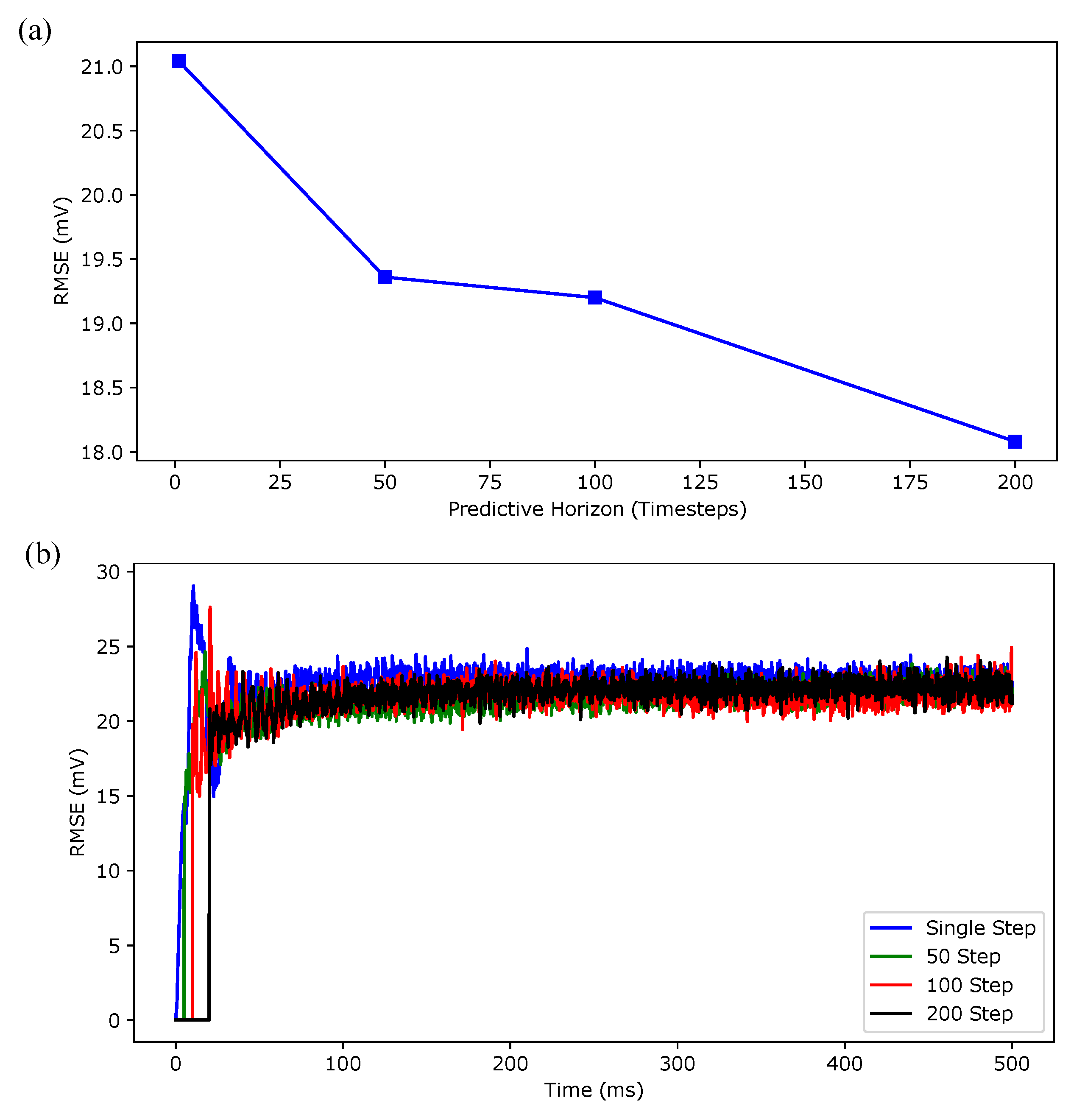
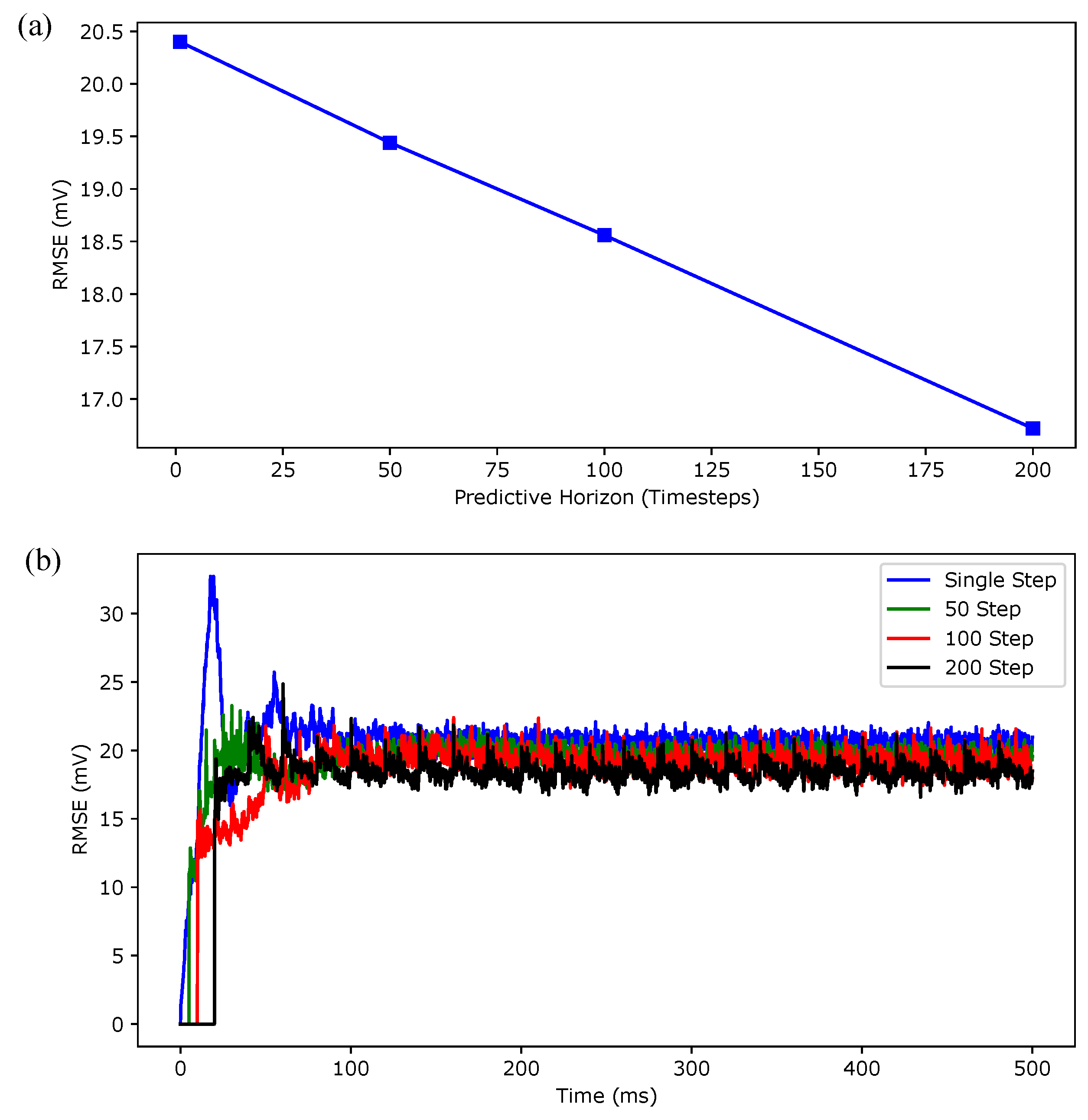

| ( ms) | Prediction Time (ms) | Iterations | On-Line Computation Time (s) | |
|---|---|---|---|---|
| 1 | 500 | 5000 | 8.896 | |
| 50 | 500 | 100 | 3.778 | |
| 100 | 500 | 50 | 3.679 | |
| 200 | 500 | 25 | 3.565 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plaster, B.; Kumar, G. Data-Driven Predictive Modeling of Neuronal Dynamics Using Long Short-Term Memory. Algorithms 2019, 12, 203. https://doi.org/10.3390/a12100203
Plaster B, Kumar G. Data-Driven Predictive Modeling of Neuronal Dynamics Using Long Short-Term Memory. Algorithms. 2019; 12(10):203. https://doi.org/10.3390/a12100203
Chicago/Turabian StylePlaster, Benjamin, and Gautam Kumar. 2019. "Data-Driven Predictive Modeling of Neuronal Dynamics Using Long Short-Term Memory" Algorithms 12, no. 10: 203. https://doi.org/10.3390/a12100203
APA StylePlaster, B., & Kumar, G. (2019). Data-Driven Predictive Modeling of Neuronal Dynamics Using Long Short-Term Memory. Algorithms, 12(10), 203. https://doi.org/10.3390/a12100203





