A Machine Learning Approach to Algorithm Selection for Exact Computation of Treewidth
Abstract
1. Introduction
1.1. The Importance of Treewidth
1.2. Algorithm Selection
1.3. Our Contribution
2. Preliminaries
2.1. Tree Decompositions and Treewidth
- The union of all bags equals V, i.e., every vertex of the original graph G is in at least one bag in the tree decomposition.
- For every edge in G, there exists a bag X that contains both u and v, i.e., both endpoints of every edge in the original graph G can be found together in at least one bag in the tree decomposition.
- If two bags and both contain a vertex v, then every bag on the path between and also contains v.
2.2. Algorithm Selection
- the set of algorithms A,
- the instances of the problem, also known as the problem space P,
- measurable characteristics (features) of a problem instance, known as the feature space F,
- the performance space Y.
3. Methodology
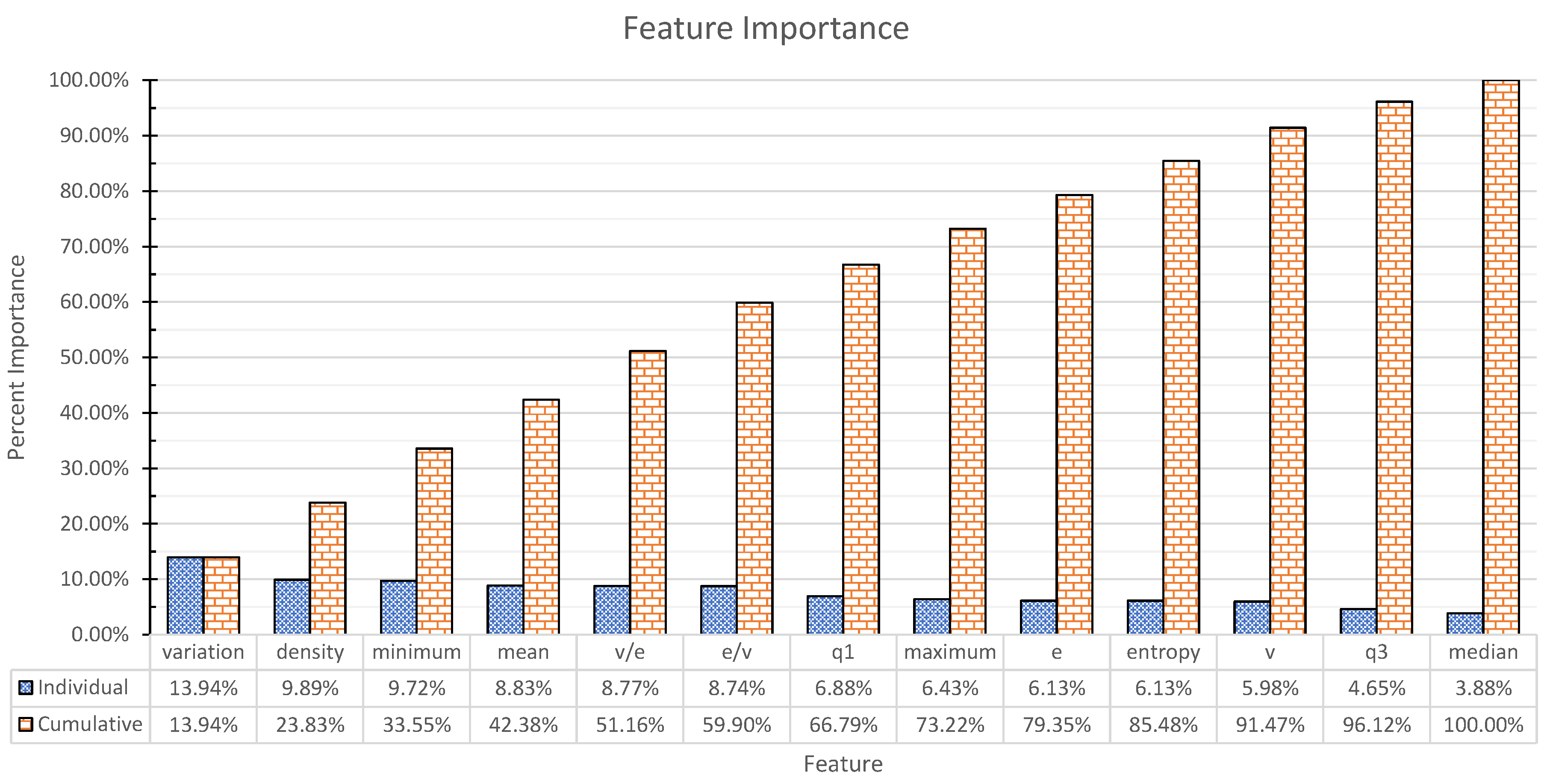
3.1. Features
- 1:
- number of nodes:v
- 2:
- number of edges:e
- 3,4:
- ratio:,
- 5:
- density:
- 6–13:
- degree statistics: min, max, mean, median, , , variation coefficient, entropy.
3.2. Treewidth Algorithms
- tdlib, by Lukas Larisch and Felix Salfelder, referred to as tdlib. This is an implementation of the algorithm that Tamaki proposed [14] for the 2016 iteration of the PACE challenge [15], which itself builds on the algorithm by Arnborg et al. [8]. Implementation available at github.com/freetdi/p17
- Exact Treewidth, by Hisao Tamaki and Hiromu Ohtsuka, referred to as tamaki. Also an implementation of Tamaki’s algorithm [14]. Implementation available at github.com/TCS-Meiji/PACE2017-TrackA
- Jdrasil, by Max Bannach, Sebastian Berndt and Thorsten Ehlers, referred to as Jdrasil [41]. Implementation available at github.com/maxbannach/Jdrasil
3.3. Machine Learning Algorithms
3.4. Reflections on the Choice of Machine Learning Model
4. Experiments and Results
4.1. Datasets
- PACE 2017 treewidth exact competition instances, referred to as ex. Available at github.com/PACE-challenge/Treewidth-PACE-2017-instances
- PACE 2017 bonus instances, referred to as bonus. Available at github.com/PACE-challenge/Treewidth-PACE-2017-bonus-instances
- Named graphs, referred to as named. (These are graphs with special names, originally extracted from the SAGE graphs database). Available at github.com/freetdi/named-graphs
- Control flow graphs, referred to as cfg. Available at github.com/freetdi/CFGs
- PACE 2017 treewidth heuristic competition instances, referred to as he. Available at github.com/PACE-challenge/Treewidth-PACE-2017-instances
- UAI 2014 Probabilistic Inference Competition instances, referred to as uai. Available at github.com/PACE-challenge/UAI-2014-competition-graphs
- SAT competition graphs, referred to as sat_sr15. Available at people.mmci.uni-saarland.de/ hdell/pace17/SAT-competition-gaifman.tar
- Transit graphs, referred to as transit. Available at github.com/daajoe/transit_graphs
- PACE 2016 treewidth instances [15], referred to as pace2016. Available at bit.ly/pace16-tw-instances-20160307
- Asgeirsson and Stein [47]*, referred to as vc. Available at ru.is/kennarar/eyjo/vertexcover.html
- PACE 2019 Vertex Cover challenge instances*, referred to as vcPACE. Available at pacechallenge.org/files/pace2019-vc-exact-public-v2.tar.bz2
- DIMACS Maximum Clique benchmark instances*, referred to as dimacsMC. Available at iridia.ulb.ac.be/~fmascia/maximum_clique/DIMACS-benchmark
4.2. Experimental Setup
4.3. Experimental Results
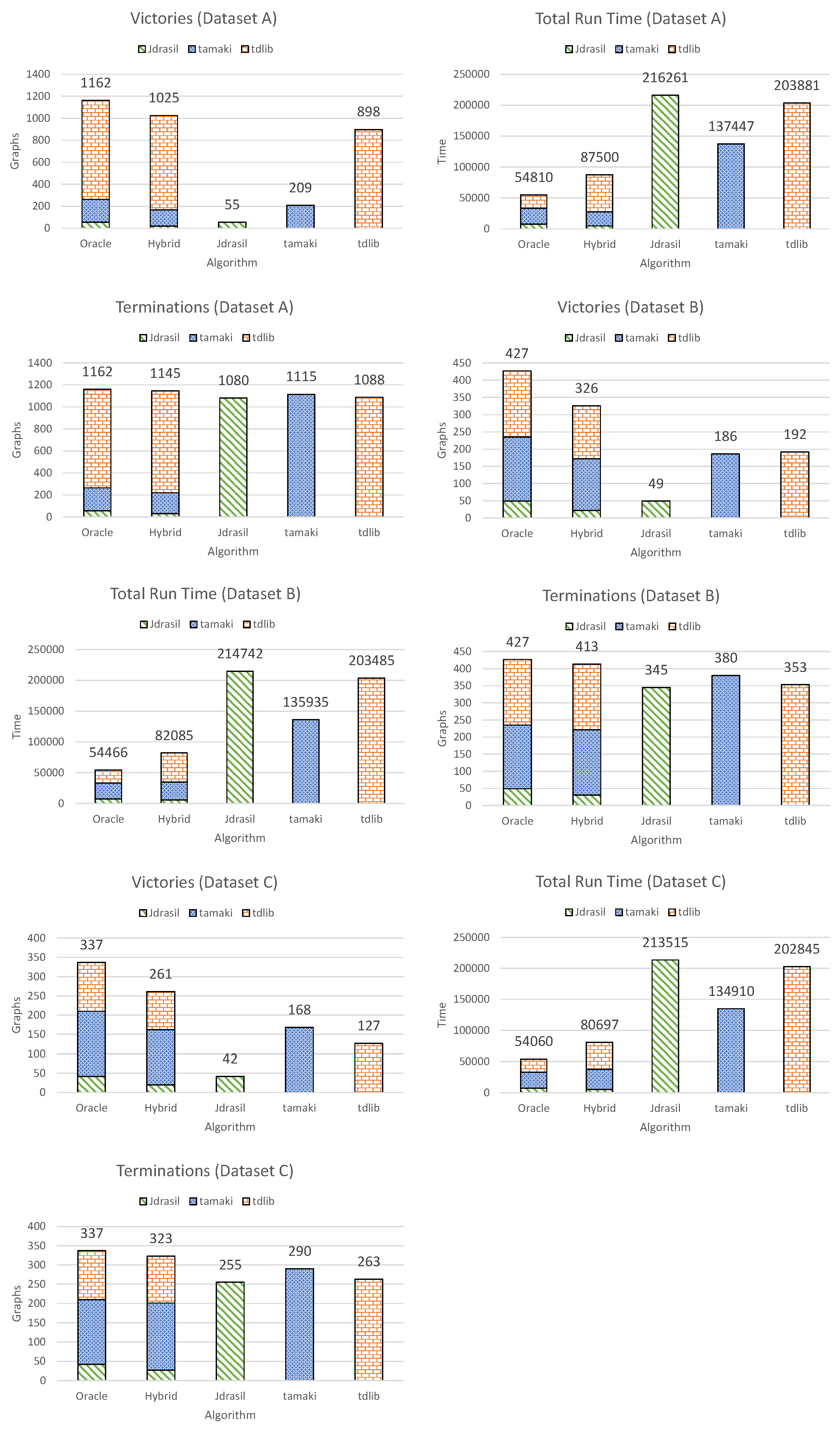
- Victories. A `victory’ is defined as being (or selecting, in the case of the hybrid algorithm or the oracle algorithm) the fastest algorithm for a certain graph.
- Total run time on the entire dataset.
- Terminations. A `termination’ is defined as successfully solving the given problem instance within the given time. No regard is given to the run-time, the only thing that matters is whether the algorithm managed to find a solution at all.
4.3.1. Dataset A
4.3.2. Dataset B
4.3.3. Dataset C
4.3.4. Dataset B—Decision Tree
4.3.5. Dataset B—Principal Component Analysis
5. Analysis
6. Discussion
7. Conclusions and Future Work
7.1. Conclusions
7.2. Future Work
7.3. The Best of Both Worlds
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Diestel, R. Graph Theory (Graduate Texts in Mathematics); Springer: New York, NY, USA, 2005. [Google Scholar]
- Bodlaender, H.L. A tourist guide through treewidth. Acta Cybern. 1994, 11, 1. [Google Scholar]
- Bodlaender, H.L.; Koster, A.M. Combinatorial optimization on graphs of bounded treewidth. Comput. J. 2008, 51, 255–269. [Google Scholar] [CrossRef]
- Cygan, M.; Fomin, F.V.; Kowalik, L.; Lokshtanov, D.; Marx, D.; Pilipczuk, M.; Pilipczuk, M.; Saurabh, S. Parameterized Algorithms; Springer: Cham, Switzerland, 2015; Volume 4. [Google Scholar]
- Bannach, M.; Berndt, S. Positive-Instance Driven Dynamic Programming for Graph Searching. arXiv 2019, arXiv:1905.01134. [Google Scholar]
- Hammer, S.; Wang, W.; Will, S.; Ponty, Y. Fixed-parameter tractable sampling for RNA design with multiple target structures. BMC Bioinform. 2019, 20, 209. [Google Scholar] [CrossRef] [PubMed]
- Bienstock, D.; Ozbay, N. Tree-width and the Sherali–Adams operator. Discret. Optim. 2004, 1, 13–21. [Google Scholar] [CrossRef]
- Arnborg, S.; Corneil, D.G.; Proskurowski, A. Complexity of finding embeddings in a k-tree. SIAM J. Algeb. Discret. Methods 1987, 8, 277–284. [Google Scholar] [CrossRef]
- Strasser, B. Computing Tree Decompositions with FlowCutter: PACE 2017 Submission. arXiv 2017, arXiv:1709.08949. [Google Scholar]
- Van Wersch, R.; Kelk, S. ToTo: An open database for computation, storage and retrieval of tree decompositions. Discret. Appl. Math. 2017, 217, 389–393. [Google Scholar] [CrossRef]
- Bodlaender, H. A Linear-Time Algorithm for Finding Tree-Decompositions of Small Treewidth. SIAM J. Comput. 1996, 25, 1305–1317. [Google Scholar] [CrossRef]
- Bodlaender, H.L.; Fomin, F.V.; Koster, A.M.; Kratsch, D.; Thilikos, D.M. On exact algorithms for treewidth. ACM Trans. Algorithms (TALG) 2012, 9, 12. [Google Scholar] [CrossRef]
- Gogate, V.; Dechter, R. A complete anytime algorithm for treewidth. In Proceedings of the 20th conference on Uncertainty in artificial intelligence, UAI 2004, Banff, AB, Canada, 7–11 July 2004; AUAI Press: Arlington, VA, USA, 2004; pp. 201–208. [Google Scholar]
- Tamaki, H. Positive-instance driven dynamic programming for treewidth. J. Comb. Optim. 2019, 37, 1283–1311. [Google Scholar] [CrossRef]
- Dell, H.; Husfeldt, T.; Jansen, B.M.; Kaski, P.; Komusiewicz, C.; Rosamond, F.A. The first parameterized algorithms and computational experiments challenge. In Proceedings of the 11th International Symposium on Parameterized and Exact Computation (IPEC 2016), Aarhus, Denmark, 24–26 August 2016; Schloss Dagstuhl-Leibniz-Zentrum für Informatik: Wadern, Germany, 2017. [Google Scholar]
- Dell, H.; Komusiewicz, C.; Talmon, N.; Weller, M. The PACE 2017 Parameterized Algorithms and Computational Experiments Challenge: The Second Iteration. In Proceedings of the 12th International Symposium on Parameterized and Exact Computation (IPEC 2017), Leibniz International Proceedings in Informatics (LIPIcs), Vienna, Austria, 6–8 September 2017; Lokshtanov, D., Nishimura, N., Eds.; Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2018; Volume 89, pp. 1–12. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Automated configuration of mixed integer programming solvers. In Proceedings of the International Conference on Integration of Artificial Intelligence (AI) and Operations Research (OR) Techniques in Constraint Programming, Thessaloniki, Greece, 4–7 June 2019; Springer: Cham, Switzerland, 2010; pp. 186–202. [Google Scholar]
- Kruber, M.; Lübbecke, M.E.; Parmentier, A. Learning when to use a decomposition. In Proceedings of the International Conference on AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems, Padova, Italy, 5–8 June 2017; Springer: Cham, Switzerland, 2017; pp. 202–210. [Google Scholar]
- Tang, Y.; Agrawal, S.; Faenza, Y. Reinforcement Learning for Integer Programming: Learning to Cut. arXiv 2019, arXiv:1906.04859. [Google Scholar]
- Smith-Miles, K.; Lopes, L. Measuring instance difficulty for combinatorial optimization problems. Comput. Oper. Res. 2012, 39, 875–889. [Google Scholar] [CrossRef]
- Hutter, F.; Xu, L.; Hoos, H.H.; Leyton-Brown, K. Algorithm runtime prediction: Methods & evaluation. Artif. Intell. 2014, 206, 79–111. [Google Scholar]
- Leyton-Brown, K.; Hoos, H.H.; Hutter, F.; Xu, L. Understanding the empirical hardness of NP-complete problems. Commun. ACM 2014, 57, 98–107. [Google Scholar] [CrossRef]
- Lodi, A.; Zarpellon, G. On learning and branching: A survey. Top 2017, 25, 207–236. [Google Scholar] [CrossRef]
- Alvarez, A.M.; Louveaux, Q.; Wehenkel, L. A machine learning-based approximation of strong branching. INFORMS J. Comput. 2017, 29, 185–195. [Google Scholar] [CrossRef]
- Balcan, M.F.; Dick, T.; Sandholm, T.; Vitercik, E. Learning to branch. arXiv 2018, arXiv:1803.10150. [Google Scholar]
- Bengio, Y.; Lodi, A.; Prouvost, A. Machine Learning for Combinatorial Optimization: A Methodological Tour d’Horizon. arXiv 2018, arXiv:1811.06128. [Google Scholar]
- Fischetti, M.; Fraccaro, M. Machine learning meets mathematical optimization to predict the optimal production of offshore wind parks. Comput. Oper. Res. 2019, 106, 289–297. [Google Scholar] [CrossRef]
- Sarkar, S.; Vinay, S.; Raj, R.; Maiti, J.; Mitra, P. Application of optimized machine learning techniques for prediction of occupational accidents. Comput. Oper. Res. 2019, 106, 210–224. [Google Scholar] [CrossRef]
- Nalepa, J.; Blocho, M. Adaptive guided ejection search for pickup and delivery with time windows. J. Intell. Fuzzy Syst. 2017, 32, 1547–1559. [Google Scholar] [CrossRef]
- Rice, J.R. The algorithm selection problem. In Advances in Computers; Elsevier: Amsterdam, The Netherlands, 1976; Volume 15, pp. 65–118. [Google Scholar]
- Leyton-Brown, K.; Nudelman, E.; Andrew, G.; McFadden, J.; Shoham, Y. A portfolio approach to algorithm selection. In Proceedings of the IJCAI, Acapulco, Mexico, 9–15 August 2003; Volume 3, pp. 1542–1543. [Google Scholar]
- Nudelman, E.; Leyton-Brown, K.; Devkar, A.; Shoham, Y.; Hoos, H. Satzilla: An algorithm portfolio for SAT. Available online: http://www.cs.ubc.ca/~kevinlb/pub.php?u=SATzilla04.pdf (accessed on 12 July 2019).
- Xu, L.; Hutter, F.; Hoos, H.H.; Leyton-Brown, K. SATzilla: Portfolio-based algorithm selection for SAT. J. Artif. Intell. Res. 2008, 32, 565–606. [Google Scholar] [CrossRef]
- Ali, S.; Smith, K.A. On learning algorithm selection for classification. Appl. Soft Comput. 2006, 6, 119–138. [Google Scholar] [CrossRef]
- Guo, H.; Hsu, W.H. A machine learning approach to algorithm selection for NP-hard optimization problems: A case study on the MPE problem. Ann. Oper. Res. 2007, 156, 61–82. [Google Scholar] [CrossRef]
- Musliu, N.; Schwengerer, M. Algorithm selection for the graph coloring problem. In Proceedings of the International Conference on Learning and Intelligent Optimization 2013 (LION 2013), Catania, Italy, 7–11 January 2013; pp. 389–403. [Google Scholar]
- Xu, L.; Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Hydra-MIP: Automated algorithm configuration and selection for mixed integer programming. In Proceedings of the RCRA Workshop on Experimental Evaluation of Algorithms for Solving Problems with Combinatorial Explosion at the International Joint Conference on Artificial Intelligence (IJCAI), Paris, France, 16–20 January 2011; pp. 16–30. [Google Scholar]
- Kerschke, P.; Hoos, H.H.; Neumann, F.; Trautmann, H. Automated algorithm selection: Survey and perspectives. Evol. Comput. 2019, 27, 3–45. [Google Scholar] [CrossRef]
- Abseher, M.; Musliu, N.; Woltran, S. Improving the efficiency of dynamic programming on tree decompositions via machine learning. J. Artif. Intell. Res. 2017, 58, 829–858. [Google Scholar] [CrossRef]
- Bannach, M.; Berndt, S.; Ehlers, T. Jdrasil: A modular library for computing tree decompositions. In Proceedings of the 16th International Symposium on Experimental Algorithms (SEA 2017), London, UK, 21–23 June 2017; Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik: Wadern, Germany, 2017. [Google Scholar]
- Kotsiantis, S.B. Decision trees: A recent overview. Artif. Intell. Rev. 2013, 39, 261–283. [Google Scholar] [CrossRef]
- Li, R.H.; Belford, G.G. Instability of decision tree classification algorithms. In Proceedings of the Eighth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Edmonton, AB, Canada, 23–26 July 2002; ACM: New York, NY, USA, 2002; pp. 570–575. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Bertsimas, D.; Dunn, J. Optimal classification trees. Mach. Learn. 2017, 106, 1039–1082. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ásgeirsson, E.I.; Stein, C. Divide-and-conquer approximation algorithm for vertex cover. SIAM J. Discret. Math. 2009, 23, 1261–1280. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Tsamardinos, I.; Rakhshani, A.; Lagani, V. Performance-estimation properties of cross-validation-based protocols with simultaneous hyper-parameter optimization. Int. J. Artif. Intell. Tools 2015, 24, 1540023. [Google Scholar] [CrossRef]
- Smith-Miles, K.A. Cross-disciplinary perspectives on meta-learning for algorithm selection. ACM Comput. Surv. (CSUR) 2009, 41, 6. [Google Scholar] [CrossRef]
- Bodlaender, H.L.; Jansen, B.M.; Kratsch, S. Preprocessing for treewidth: A combinatorial analysis through kernelization. SIAM J. Discret. Math. 2013, 27, 2108–2142. [Google Scholar] [CrossRef]
- Van Der Zanden, T.C.; Bodlaender, H.L. Computing Treewidth on the GPU. arXiv 2017, arXiv:1709.09990. [Google Scholar]

| Datasets | Unfiltered | A | B | C |
|---|---|---|---|---|
| bonus | 100 | 36 | 36 | 35 |
| cfg | 1797 | 43 | 1 | 0 |
| ex | 200 | 200 | 172 | 137 |
| he | 200 | 26 | 17 | 17 |
| named | 150 | 47 | 14 | 11 |
| pace2016 | 145 | 95 | 16 | 13 |
| toto | 27,123 | 594 | 92 | 53 |
| transit | 19 | 10 | 4 | 4 |
| uai | 133 | 27 | 14 | 43 |
| vc | 178 | 58 | 42 | 38 |
| vcPACE | 100 | 6 | 6 | 6 |
| dimacsMC | 80 | 20 | 13 | 10 |
| sat_sr15 | 115 | 0 | 0 | 0 |
| Total | 30,340 | 1162 | 427 | 337 |
| Unfiltered | Dataset A | Dataset B | Dataset C | |
|---|---|---|---|---|
| Jdrasil | 55 | 55 | 49 | 42 |
| tamaki | 209 | 209 | 186 | 168 |
| tdlib | 29,234 | 898 | 192 | 127 |
| VE | v | e | v/e | e/v | Density | q1 | Median | q3 | Minimum | Mean | Maximum | Variation | Entropy |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.58 | −0.01 | 0.33 | −0.17 | 0.36 | 0.30 | 0.36 | 0.36 | 0.36 | 0.32 | 0.36 | 0.00 | −0.02 | 0.12 |
| 0.25 | 0.55 | 0.09 | 0.15 | 0.00 | −0.07 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.55 | 0.55 | 0.24 |
| 0.08 | −0.14 | 0.21 | 0.63 | 0.05 | −0.44 | 0.07 | 0.06 | 0.04 | 0.02 | 0.05 | −0.18 | −0.17 | 0.52 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slavchev, B.; Masliankova, E.; Kelk, S. A Machine Learning Approach to Algorithm Selection for Exact Computation of Treewidth. Algorithms 2019, 12, 200. https://doi.org/10.3390/a12100200
Slavchev B, Masliankova E, Kelk S. A Machine Learning Approach to Algorithm Selection for Exact Computation of Treewidth. Algorithms. 2019; 12(10):200. https://doi.org/10.3390/a12100200
Chicago/Turabian StyleSlavchev, Borislav, Evelina Masliankova, and Steven Kelk. 2019. "A Machine Learning Approach to Algorithm Selection for Exact Computation of Treewidth" Algorithms 12, no. 10: 200. https://doi.org/10.3390/a12100200
APA StyleSlavchev, B., Masliankova, E., & Kelk, S. (2019). A Machine Learning Approach to Algorithm Selection for Exact Computation of Treewidth. Algorithms, 12(10), 200. https://doi.org/10.3390/a12100200





