An Auto-Adjustable Semi-Supervised Self-Training Algorithm
Abstract
1. Introduction
2. A Review of Semi-Supervised Classification Via Self-Labeled Approach
2.1. Semi-Supervised Classification
2.2. Semi-Supervised Self-Labeled Methods
3. Auto-Adjustable Self-Training Semi-Supervised Algorithm
| Algorithm 1: Auto-Adjustable Self-Training (AAST). |
|
4. Experimental Results
- C4.5 [33] constitutes one of the most effective and efficient classification algorithms for building decision trees. This algorithm induces classification rules in the form of decision trees for a given training set. More analytically, it categorizes instances to a predefined set of classes according to their attribute values from the root of a tree down to a leaf. The accuracy of a leaf corresponds to the percentage of correctly classified instances of the training set.
- JRip [34] is generally considered to be a very effective and fast rule-based algorithm, especially on large samples with noisy data. The algorithm examines each class in increasing size and an initial set of rules for a class is generated using incremental reduced errors. Then, it proceeds by treating all the examples of a particular judgement in the training data as a class and determines a set of rules that covers all the members of that class. Subsequently, it proceeds to the next class and iteratively applies the same procedure until all classes have been covered. What is more, JRip produces error rates competitive with C4.5 with less computational effort.
- kNN [35] constitutes a representative instance-structured learning algorithm based on dissimilarities among a set of instances. It belongs to the lazy learning family of methods [35] which do not build a model during the learning process. According to kNN algorithm, characteristics extracted from classification process by viewing the entire distance among new individuals, should be classified and then the nearest k category is used. As a result of this process, test data belongs to the nearest k neighbor category which has more members in certain class. The main advantages of the kNN classification algorithm is its easiness and simplicity of implementation and the fact that it provides good generalization results during classification assigned to multiple categories.
4.1. Sensitivity of AAST to the Value of Parameter k
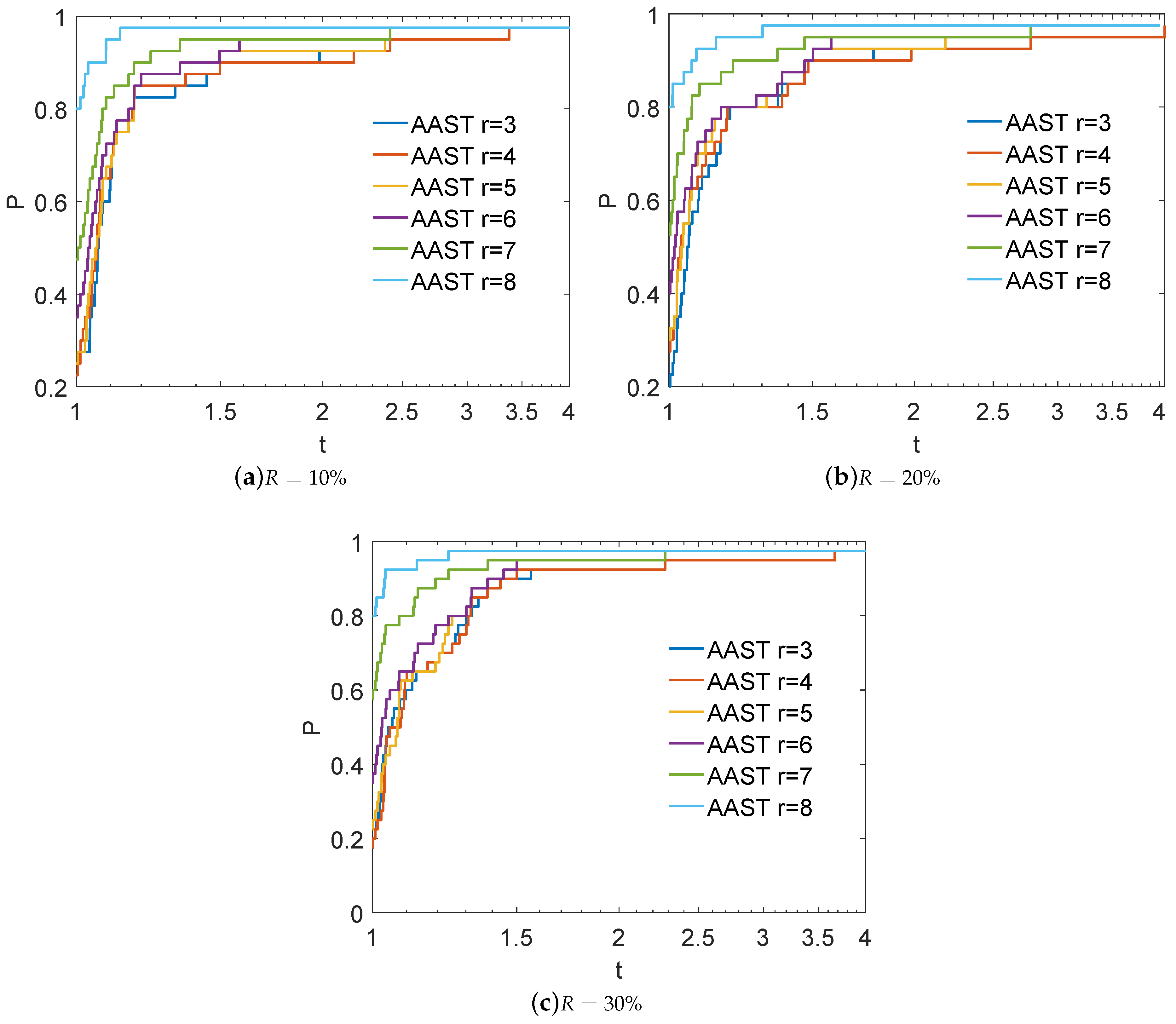
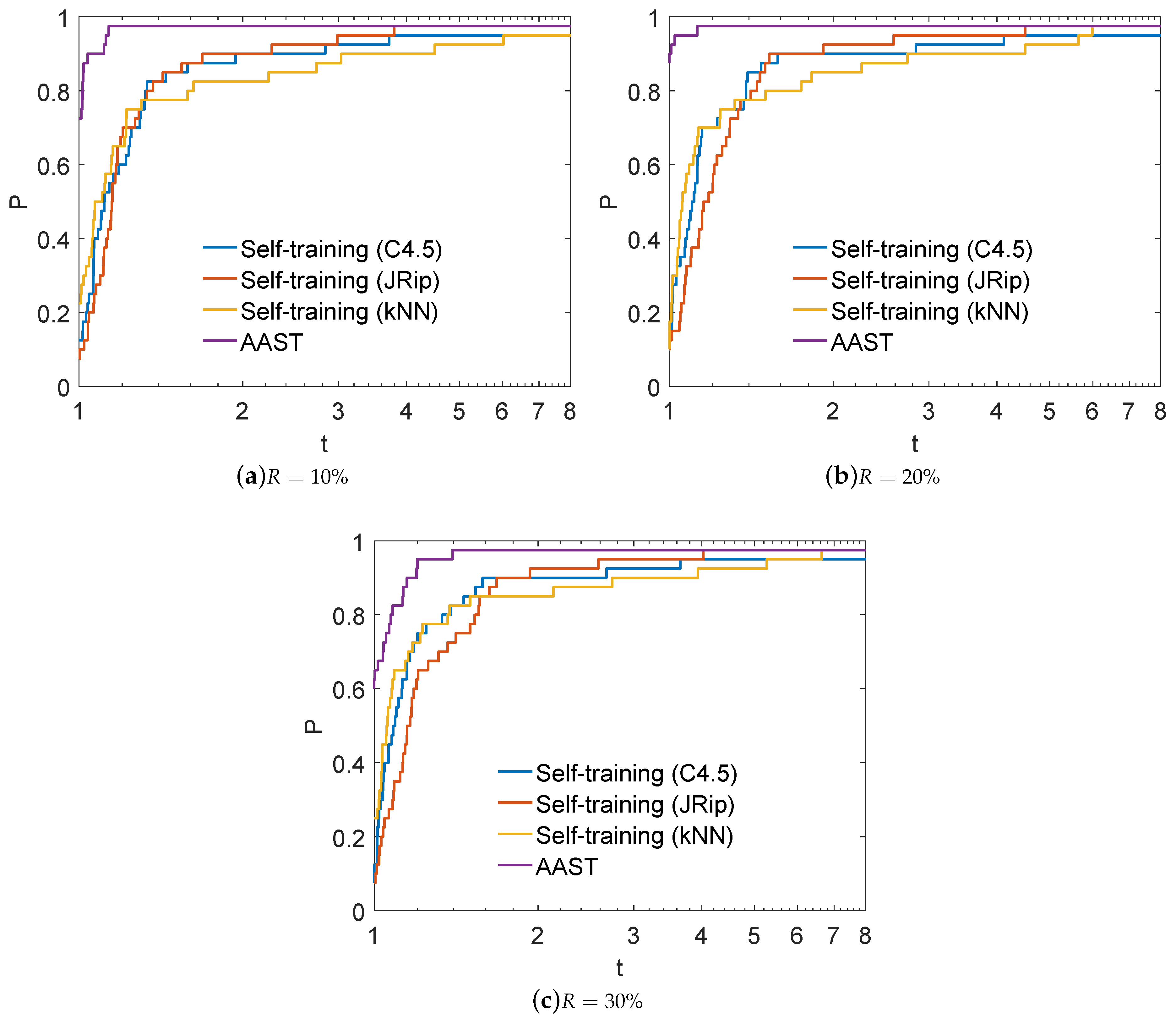
4.2. Performance Evaluation of AAST
4.3. Statistical and Post-Hoc Analysis
5. Conclusions and Future Research
Author Contributions
Funding
Conflicts of Interest
References
- Alpaydin, E. Introduction to Machine Learning, 2nd ed.; The MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Zhu, X.; Goldberg, A. Introduction to semi-supervised learning. Synth. Lect. Artif. Intell. Mach. Learn. 2009, 3, 1–130. [Google Scholar] [CrossRef]
- Zhu, X. Semi-supervised learning. In Encyclopedia of Machine Learning; Springer: Berlin, Germany, 2011; pp. 892–897. [Google Scholar]
- Livieris, I.E.; Drakopoulou, K.; Tampakas, V.; Mikropoulos, T.; Pintelas, P. Predicting secondary school students’ performance utilizing a semi-supervised learning approach. J. Educ. Comput. Res. 2018. [Google Scholar] [CrossRef]
- Sigdel, M.; Dinç, I.; Dinç, S.; Sigdel, M.; Pusey, M.; Aygün, R. Evaluation of semi-supervised learning for classification of protein crystallization imagery. Proc. IEEE Southeastcon 2014, 1–6. [Google Scholar] [CrossRef]
- Keyvanpour, M.; Imani, M. Semi-supervised text categorization: Exploiting unlabeled data using ensemble learning algorithms. Intell. Data Anal. 2013, 17, 367–385. [Google Scholar]
- Hassanzadeh, H.; Keyvanpour, M. A two-phase hybrid of semi-supervised and active learning approach for sequence labeling. Intell. Data Anal. 2013, 17, 251–270. [Google Scholar]
- Borchani, H.; Larrañaga, P.; Bielza, C. Classifying evolving data streams with partially labeled data. Intell. Data Anal. 2011, 15, 655–670. [Google Scholar]
- Chen, M.; Tan, X.; Zhang, L. An iterative self-training support vector machine algorithm in brain-computer interfaces. Intell. Data Anal. 2016, 20, 67–82. [Google Scholar] [CrossRef]
- Laleh, N.; Azgomi, M.A. A hybrid fraud scoring and spike detection technique in streaming data. Intell. Data Anal. 2010, 14, 773–800. [Google Scholar]
- Blum, A.; Chawla, S. Learning from Labeled and Unlabeled Data Using Graph Mincuts. In Proceedings of the 18th International Conference on Machine Learning, Williamstown, MA, USA, 28 June–1 July 2001; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA; pp. 19–26. [Google Scholar]
- Blum, A.; Mitchell, T. Combining labeled and unlabeled data with co-training. In Proceedings of the 11th Annual Conference on Computational Learning Theory, Madison, WI, USA, 24–26 July 1998; ACM: New York, NY, USA, 1998; pp. 92–100. [Google Scholar]
- Triguero, I.; García, S.; Herrera, F. Self-labeled techniques for semi-supervised learning: taxonomy, software and empirical study. Knowl. Inf. Syst. 2015, 42, 245–284. [Google Scholar] [CrossRef]
- Nigam, K.; Ghani, R. Analyzing the effectiveness and applicability of co-training. In Proceedings of the 9th International Conference on Information and Knowledge Management, McLean, VA, USA, 6–11 November 2000; ACM: New York, NY, USA, 2000; pp. 86–93. [Google Scholar]
- Li, M.; Zhou, Z. SETRED: Self-training with editing. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Berlin, Germany, 2005; pp. 611–621. [Google Scholar]
- Tanha, J.; van Someren, M.; Afsarmanesh, H. Semi-supervised selftraining for decision tree classifiers. Int. J. Mach. Learn. Cybern. 2015, 8, 355–370. [Google Scholar] [CrossRef]
- Ghosh, J. Multiclassifier systems: Back to the future. In International Workshop on Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2002; pp. 277–280. [Google Scholar]
- Ng, V.; Cardie, C. Weakly supervised natural language learning without redundant views. In Proceedings of the 2003 Conference of the North American Chapter of the Association for Computational Linguistics on Human Language Technology, Edmonton, AB, Canada, 27 May–1 June 2003; Volume 1, pp. 94–101. [Google Scholar]
- Triguero, I.; Sáez, J.; Luengo, J.; García, S.; Herrera, F. On the characterization of noise filters for self-training semi-supervised in nearest neighbor classification. Neurocomputing 2014, 132, 30–41. [Google Scholar] [CrossRef]
- Zhou, Y.; Goldman, S. Democratic co-learning. In Proceedings of the16th IEEE International Conference on Tools with Artificial Intelligence (ICTAI), Boca Raton, FL, USA, 15–17 November 2004; pp. 594–602. [Google Scholar]
- Li, M.; Zhou, Z. Improve computer-aided diagnosis with machine learning techniques using undiagnosed samples. IEEE Trans. Syst. Man Cybern. A 2007, 37, 1088–1098. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, M. Tri-training: Exploiting unlabeled data using three classifiers. IEEE Trans. Knowl. Data Eng. 2005, 17, 1529–1541. [Google Scholar] [CrossRef]
- Hady, M.; Schwenker, F. Combining committee-based semi-supervised learning and active learning. J. Comput. Sci. Technol. 2010, 25, 681–698. [Google Scholar] [CrossRef]
- Kostopoulos, G.; Livieris, I.; Kotsiantis, S.; Tampakas, V. CST-Voting - A semi-supervised ensemble method for classification problems. J. Intell. Fuzzy Syst. 2018, 35, 99–109. [Google Scholar] [CrossRef]
- Livieris, I.E.; Kanavos, A.; Tampakas, V.; Pintelas, P. An Ensemble SSL Algorithm for Efficient Chest X-ray Image Classification. J. Imaging 2018, 4, 95. [Google Scholar] [CrossRef]
- Livieris, I.E.; Drakopoulou, K.; Tampakas, V.; Mikropoulos, T.; Pintelas, P. An ensemble-based semi-supervised approach for predicting students’ performance. In Research on e-Learning and ICT in Education; Springer: Berlin, Germany, 2018. [Google Scholar]
- Baumgartner, D.; Serpen, G. Large Experiment and Evaluation Tool for WEKA Classifiers. Int. Conf. Data Min. 2009, 16, 340–346. [Google Scholar]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I. The WEKA data mining software: An update. SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Bache, K.; Lichman, M. UCI Machine Learning Repository; University of California Press: Oakland, CA, USA, 2013. [Google Scholar]
- Alcalá-Fdez, J.; Fernández, A.; Luengo, J.; Derrac, J.; García, S.; Sánchez, L.; Herrera, F. Keel data-mining software tool: data set repository, integration of algorithms and experimental analysis framework. J. Mult.-Valued. Log. Soft Comput. 2011, 17, 255–287. [Google Scholar]
- Wang, Y.; Xu, X.; Zhao, H.; Hua, Z. Semi-supervised learning based on nearest neighbor rule and cut edges. Knowl.-Based Syst. 2010, 23, 547–554. [Google Scholar] [CrossRef]
- Wu, X.; Kumar, V.; Quinlan, J.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.; Ng, A.; Liu, B.; Yu, P.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
- Quinlan, J. C4.5: Programs for Machine Learning; Morgan Kaufmann: San Francisco, CA, USA, 1993. [Google Scholar]
- Cohen, W. Fast Effective Rule Induction. In Proceedings of the International Conference on Machine Learning, Tahoe City, CA, USA, 9–12 July 1995; pp. 115–123. [Google Scholar]
- Aha, D. Lazy Learning; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Dolan, E.; Moré, J. Benchmarking optimization software with performance profiles. Math. Program. 2002, 91, 201–213. [Google Scholar] [CrossRef]
- Livieris, I.E.; Pintelas, P. An improved spectral conjugate gradient neural network training algorithm. Int. J. Artif. Intell. Tools 2012, 21, 1250009. [Google Scholar] [CrossRef]
- Livieris, I.E.; Pintelas, P. A new class of nonmonotone conjugate gradient training algorithms. Appl. Math. Comput. 2015, 266, 404–413. [Google Scholar] [CrossRef]
- Finner, H. On a monotonicity problem in step-down multiple test procedures. J. Am. Statist. Assoc. 1993, 88, 920–923. [Google Scholar] [CrossRef]
- García, S.; Fernández, A.; Luengo, J.; Herrera, F. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: Experimental analysis of power. Inform. Sci. 2010, 180, 2044–2064. [Google Scholar] [CrossRef]
- Zhu, X. Semi-Supervised Learning Literature Survey; Technical Report 1530; University of Wisconsin: Madison, WI, USA, 2006. [Google Scholar]
- Bie, T.D.; Cristianini, N. Convex methods for transduction. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2005; pp. 73–80. ISBN 0262195348. [Google Scholar]
- De Bie, T.; Cristianini, N. Semi-supervised learning using semi-definite programming. In Semi-Supervised Learning; The MIT Press: Cambridge, MA, USA, 2006; Volume 32. [Google Scholar]
- Qi, Z.; Tian, Y.; Niu, L.; Wang, B. Semi-supervised classification with privileged information. Int. J. Mach. Learn. Cybern. 2015, 6, 667–676. [Google Scholar] [CrossRef]
- Hou, X.; Yao, G.; Wang, J. Semi-Supervised Classification Based on Low Rank Representation. Algorithms 2016, 9, 48. [Google Scholar] [CrossRef]
- Feng, L.; Yu, G. Semi-Supervised Classification Based on Mixture Graph. Algorithms 2015, 8, 1021–1034. [Google Scholar] [CrossRef]
- Zha, Z.J.; Mei, T.; Wang, J.; Wang, Z.; Hua, X.S. Graph-based semi-supervised learning with multiple labels. J. Vis. Commun. Image Represent. 2009, 20, 97–103. [Google Scholar] [CrossRef]
- Zhou, D.; Huang, J.; Schölkopf, B. Learning from labeled and unlabeled data on a directed graph. In Proceedings of the 22nd International Conference on Machine Learning, Bonn, Germany, 7–11 August 2005; ACM: New York, NY, USA, 2005; pp. 1036–1043. [Google Scholar]
- Pan, F.; Wang, J.; Lin, X. Local margin based semi-supervised discriminant embedding for visual recognition. Neurocomputing 2011, 74, 812–819. [Google Scholar] [CrossRef]
- Li, K.; Zhang, J.; Xu, H.; Luo, S.; Li, H. A semi-supervised extreme learning machine method based on co-training. J. Comput. Inf. Syst. 2013, 9, 207–214. [Google Scholar]
- Huang, G.; Song, S.; Gupta, J.N.; Wu, C. Semi-supervised and unsupervised extreme learning machines. IEEE Trans. Cybern. 2014, 44, 2405–2417. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Wang, R.; Liu, J.; Powers, D.M. A semi-supervised online sequential extreme learning machine method. Neurocomputing 2016, 174, 168–178. [Google Scholar] [CrossRef]
- Nigam, K.; McCallum, A.K.; Thrun, S.; Mitchell, T. Text classification from labeled and unlabeled documents using EM. Mach. Learn. 2000, 39, 103–134. [Google Scholar] [CrossRef]
- Bishop, C. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Platt, J. Using sparseness and analytic QP to speed training of support vector machines. In Advances in Neural Information Processing Systems; Kearns, M., Solla, S., Cohn, D., Eds.; The MIT Press: Cambridge, UK, 1999; pp. 557–563. [Google Scholar]
- Li, S.; Wang, Z.; Zhou, G.; Lee, S.Y.M. Semi-supervised learning for imbalanced sentiment classification. In Proceedings of the IJCAI Proceedings-International Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011; Volume 22, p. 1826. [Google Scholar]
- Jeni, L.A.; Cohn, J.F.; De La Torre, F. Facing imbalanced data—Recommendations for the use of performance metrics. In Proceedings of the 2013 Humaine Association Conference on Affective Computing and Intelligent Interaction, Geneva, Switzerland, 2–5 September 2013; pp. 245–251. [Google Scholar]
- Flach, P.A. The geometry of ROC space: understanding machine learning metrics through ROC isometrics. In Proceedings of the 20th International Conference on Machine Learning (ICML-03), Washington, DC, USA, 21–24 August 2003; pp. 194–201. [Google Scholar]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]

| Dataset | #Instances | #Features | #Classes | Dataset | #Instances | #Features | #Classes |
|---|---|---|---|---|---|---|---|
| appendicitis | 106 | 7 | 2 | magic | 19,020 | 10 | 2 |
| australian | 690 | 14 | 2 | mammographic | 961 | 5 | 2 |
| automobile | 205 | 26 | 7 | mushroom | 8124 | 22 | 2 |
| banana | 5300 | 2 | 2 | page-blocks | 5472 | 10 | 5 |
| breast | 286 | 9 | 2 | phoneme | 5404 | 5 | 2 |
| bupa | 345 | 6 | 2 | ring | 7400 | 20 | 2 |
| chess | 3196 | 36 | 2 | saheart | 462 | 9 | 2 |
| cleveland | 297 | 13 | 5 | satimage | 6435 | 36 | 7 |
| coil2000 | 9822 | 85 | 2 | sonar | 208 | 60 | 2 |
| contraceptive | 1473 | 9 | 3 | spectheart | 267 | 44 | 2 |
| ecoli | 336 | 7 | 8 | splice | 3190 | 60 | 3 |
| flare | 1066 | 9 | 2 | texture | 5500 | 40 | 11 |
| german | 1000 | 20 | 2 | thyroid | 7200 | 21 | 3 |
| glass | 214 | 9 | 7 | tic-tac-toe | 958 | 9 | 2 |
| haberman | 306 | 3 | 2 | twonorm | 7400 | 20 | 2 |
| heart | 270 | 13 | 2 | vehicle | 846 | 18 | 4 |
| hepatitis | 155 | 19 | 2 | vowel | 990 | 13 | 11 |
| housevotes | 435 | 16 | 2 | wisconsin | 683 | 9 | 2 |
| iris | 150 | 4 | 3 | yeast | 1484 | 8 | 10 |
| led7digit | 500 | 7 | 10 | zoo | 101 | 17 | 7 |
| Algorithm | Parameters |
|---|---|
| AAST | = C4.5, = JRip, = kNN. |
| . | |
| C4.5 | Confidence factor used for pruning = 0.25. |
| Minimum number of instances per leaf = 2. | |
| Number of folds used for reduced-error pruning = 3. | |
| Pruning is performed after tree building. | |
| JRip | Number of optimization runs = 2. |
| Number of folds used for reduced-error pruning = 3. | |
| Minimum total weight of the instances in a rule = 2.0. | |
| Pruning is performed after tree building. | |
| kNN | Pruning is performed after tree building. |
| Euclidean distance. |
| Algorithm | Friedman Ranking | Finner Post-Hoc Test | |
|---|---|---|---|
| p-Value | Null Hypothesis | ||
| AAST | 121.575 | − | − |
| Tri-Training (kNN) | 211.613 | 0.003697 | rejected |
| SETRED | 217.300 | 0.002229 | rejected |
| Self-Training (kNN) | 226.250 | 0.000903 | rejected |
| Tri-Training (C4.5) | 235.825 | 0.000316 | rejected |
| Self-Training (C4.5) | 241.613 | 0.000171 | rejected |
| Co-Training (kNN) | 245.275 | 0.000122 | rejected |
| Co-Forest | 267.238 | 0.000006 | rejected |
| Self-Training (JRip) | 273.888 | 0.000002 | rejected |
| Co-Training (C4.5) | 276.400 | 0.000002 | rejected |
| Tri-Training (JRip) | 283.138 | 0.000001 | rejected |
| Co-Training (JRip) | 285.888 | 0.000001 | rejected |
| Algorithm | Friedman Ranking | Finner Post-Hoc Test | |
|---|---|---|---|
| p-Value | Null Hypothesis | ||
| AAST | 115.688 | − | − |
| Tri-Training (kNN) | 202.988 | 0.004883 | rejected |
| SETRED | 208.338 | 0.003097 | rejected |
| Self-Training (kNN) | 221.063 | 0.000831 | rejected |
| Tri-Training (C4.5) | 228.575 | 0.000375 | rejected |
| Self-Training (C4.5) | 238.588 | 0.000117 | rejected |
| Co-Training (kNN) | 256.575 | 0.000010 | rejected |
| Co-Forest | 259.438 | 0.000008 | rejected |
| Tri-Training (JRip) | 274.063 | 0.000001 | rejected |
| Co-Training (C4.5) | 283.413 | 0 | rejected |
| Co-Training (JRip) | 298.275 | 0 | rejected |
| Self-Training (JRip) | 299.000 | 0 | rejected |
| Algorithm | Friedman Ranking | Finner Post-Hoc Test | |
|---|---|---|---|
| p-Value | Null Hypothesis | ||
| AAST | 132.088 | − | − |
| SETRED | 207.063 | 0.015637 | rejected |
| Self-Training (kNN) | 221.413 | 0.004374 | rejected |
| Tri-Training (C4.5) | 224.188 | 0.003645 | rejected |
| Co-Training (kNN) | 229.513 | 0.002314 | rejected |
| Tri-Training (kNN) | 234.775 | 0.001462 | rejected |
| Self-Training (C4.5) | 245.013 | 0.000498 | rejected |
| Co-Forest | 258.463 | 0.000101 | rejected |
| Tri-Training (JRip) | 274.038 | 0.000013 | rejected |
| Co-Training (C4.5) | 277.625 | 0.000010 | rejected |
| Co-Training (JRip) | 281.100 | 0.000009 | rejected |
| Self-Training (JRip) | 300.725 | 0.000001 | rejected |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Livieris, I.E.; Kanavos, A.; Tampakas, V.; Pintelas, P. An Auto-Adjustable Semi-Supervised Self-Training Algorithm. Algorithms 2018, 11, 139. https://doi.org/10.3390/a11090139
Livieris IE, Kanavos A, Tampakas V, Pintelas P. An Auto-Adjustable Semi-Supervised Self-Training Algorithm. Algorithms. 2018; 11(9):139. https://doi.org/10.3390/a11090139
Chicago/Turabian StyleLivieris, Ioannis E., Andreas Kanavos, Vassilis Tampakas, and Panagiotis Pintelas. 2018. "An Auto-Adjustable Semi-Supervised Self-Training Algorithm" Algorithms 11, no. 9: 139. https://doi.org/10.3390/a11090139
APA StyleLivieris, I. E., Kanavos, A., Tampakas, V., & Pintelas, P. (2018). An Auto-Adjustable Semi-Supervised Self-Training Algorithm. Algorithms, 11(9), 139. https://doi.org/10.3390/a11090139







