Multi-Level Elasticity for Wide-Area Data Streaming Systems: A Reinforcement Learning Approach

Abstract

The capability of efficiently processing the data streams emitted by nowadays ubiquitous sensing devices enables the development of new intelligent services. Data Stream Processing (DSP) applications allow for processing huge volumes of data in near real-time. To keep up with the high volume and velocity of data, these applications can elastically scale their execution on multiple computing resources to process the incoming data flow in parallel. Being that data sources and consumers are usually located at the network edges, nowadays the presence of geo-distributed computing resources represents an attractive environment for DSP. However, controlling the applications and the processing infrastructure in such wide-area environments represents a significant challenge. In this paper, we present a hierarchical solution for the autonomous control of elastic DSP applications and infrastructures. It consists of a two-layered hierarchical solution, where centralized components coordinate subordinated distributed managers, which, in turn, locally control the elastic adaptation of the application components and deployment regions. Exploiting this framework, we design several self-adaptation policies, including reinforcement learning based solutions. We show the benefits of the presented self-adaptation policies with respect to static provisioning solutions, and discuss the strengths of reinforcement learning based approaches, which learn from experience how to optimize the application performance and resource allocation.

1. Introduction

Nowadays, sensing devices are widely diffused in our everyday environment, being embedded in human-carried mobile devices, Internet-of-Things (IoT), as well as monitoring systems for public utilities, transportation, and facilities. All these heterogeneous sources continuously produce data streams that can be collected and analyzed by means of Data Stream Processing (DSP) systems to extract valuable information in a near real-time fashion. The extracted knowledge can be then used to realize new intelligent services in many different domains (e.g., health-care, energy management, and Smart City).

A DSP application consists of data sources, operators, and final consumers, which exchange streams and process data on-the-fly (i.e., without storing them). Each operator can be seen as a black-box processing element that continuously receives incoming streams, applies a transformation, and generates new outgoing streams. Aiming to extract information as soon as possible, DSP applications often express strict Quality of Service (QoS) requirements, e.g., in terms of response time (e.g., [1,2]). Moreover, since DSP applications are long-running, these QoS requirements must be satisfied at run-time, despite the variability and the high volume of the incoming workloads.

To deal with operator overloading, a commonly adopted stream processing optimization is data parallelism. It consists in running multiple parallel replicas of the same operator, so that the incoming data flow is split among the different replicas that carry out the computation in parallel [3,4]. Data parallelism (also known as fission [4]) allows processing data in parallel on multiple computing nodes (given that a single machine cannot provide enough processing power). As DSP applications are long-running and subject to highly variable workloads, the application parallelism should be elastically adapted at run-time to match the workload and prevent resource wastage: the number of operator replicas should be scaled-out when then load increases, and scaled-in as the load decreases.

Since the operator replicas run on computing resources, modern DSP systems should be able to dynamically adjust the set of computing resources to satisfy the application resource demand while avoiding costly deployment. It results a complex system which should quickly control elasticity at multiple levels, namely at the application and at the infrastructure level (e.g., [5]). Furthermore, since data sources are usually geographically distributed, recent trends investigate the possibility of decentralizing the execution of DSP applications (e.g., [3]). The very idea is to move DSP applications closer to the data (rather than the other way around), thus reducing the expected application response time. To this end, the ever increasing presence of distributed cloud and fog computing resources can be exploited. Besides the benefits, this new processing environment also poses new challenges which arise from the number and location of the computing resources that will host and execute the DSP application operators.

Most of the approaches proposed in the literature for managing DSP applications have been designed for cluster environments, where a single centralized control component takes deployment decisions by exploiting a global system view (e.g., [5,6,7]). These solutions typically do not scale well in a highly distributed environment, given the spatial distribution, heterogeneity, and sheer size of the infrastructure itself. In fact, modern DSP systems should be able to seamlessly deal with a large number of interconnected small- and medium-sized devices (e.g., IoT devices), which continuously emit and consume data. Moreover, aggregating information from the whole infrastructure to build a global view of the system is a challenging problem on its own. To improve scalability, decentralized management solutions have been proposed in the DSP context (e.g., [8,9,10,11]). However, devising a decentralized self-adaptation policy that only relies on a local system view is, in general, not trivial. Indeed, the inherent lack of coordination of fully decentralized solutions might result in frequent deployment reconfigurations that negatively affect the application performance (e.g., [12]).

Aiming to exploit the strengths of centralized and decentralized solutions, in our previous work [8], we proposed a hierarchical distributed architecture for controlling the elasticity of DSP applications. Building on this solution, we then proposed Multi-Level Elastic and Distributed DSP Framework (E2DF) [13] to include mechanisms for realizing the infrastructure elasticity. E2DF consists of loosely coupled components that interact to realize the multi-level elasticity. In particular, it includes the Application Control System (ACS), which manages the elasticity of DSP applications, and the Infrastructure Control System (ICS), which can dynamically acquire and release computing resource for the framework. The resulting framework provides a unified solution for achieving self-adaptation of DSP systems both at the application-level and the infrastructure-level. The ACS and the ICS can be equipped with different control policies, which determine when and how the E2DF mechanisms should be used to adapt the DSP system both at the application-level and the infrastructure-level.

In this paper, we investigate the E2DF control architecture. As first contribution, we design a novel elasticity policy for the ICS, by resorting on Reinforcement Learning (RL). The proposed solution autonomously learns when and how to acquire and release computing resources to satisfy the applications resource demand and avoid resource wastage. RL refers to a collection of trial-and-error methods by which an agent can learn to make good decisions through a sequence of interactions with a system or environment [14]. As such, RL allows expressing what the user aims to obtain, instead of how it should be obtained (as required by threshold-based policies, which are usually adopted to deal with cloud elasticity). Specifically, to design the ICS elasticity policy, we resort to a model-based solution that instills knowledge about the system dynamics within the learning agent [14]. Differently from the RL-based application-level elasticity policy we proposed in [8], the model-based solution we present in this paper estimates the need of computing resources. In particular, considering active and idle resources, it estimates the ability to satisfy the future application demand. Therefore, in this new model, we deal with a different and larger set of unknown dynamics, due to the possible presence of several running applications, each with an unpredictable workload. To tackle the emerging complexity, we exploit an approximate transition probability formulation.

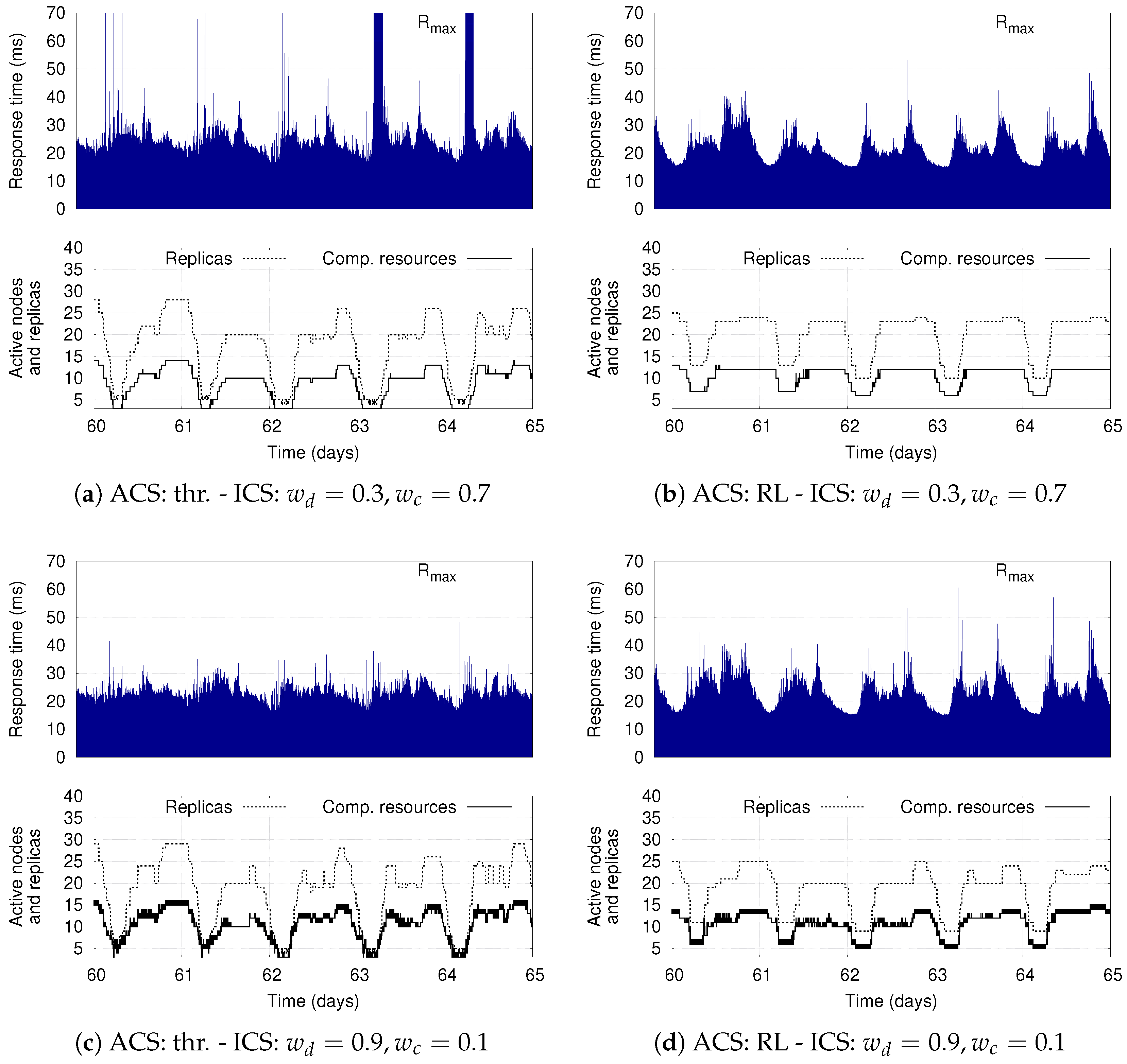
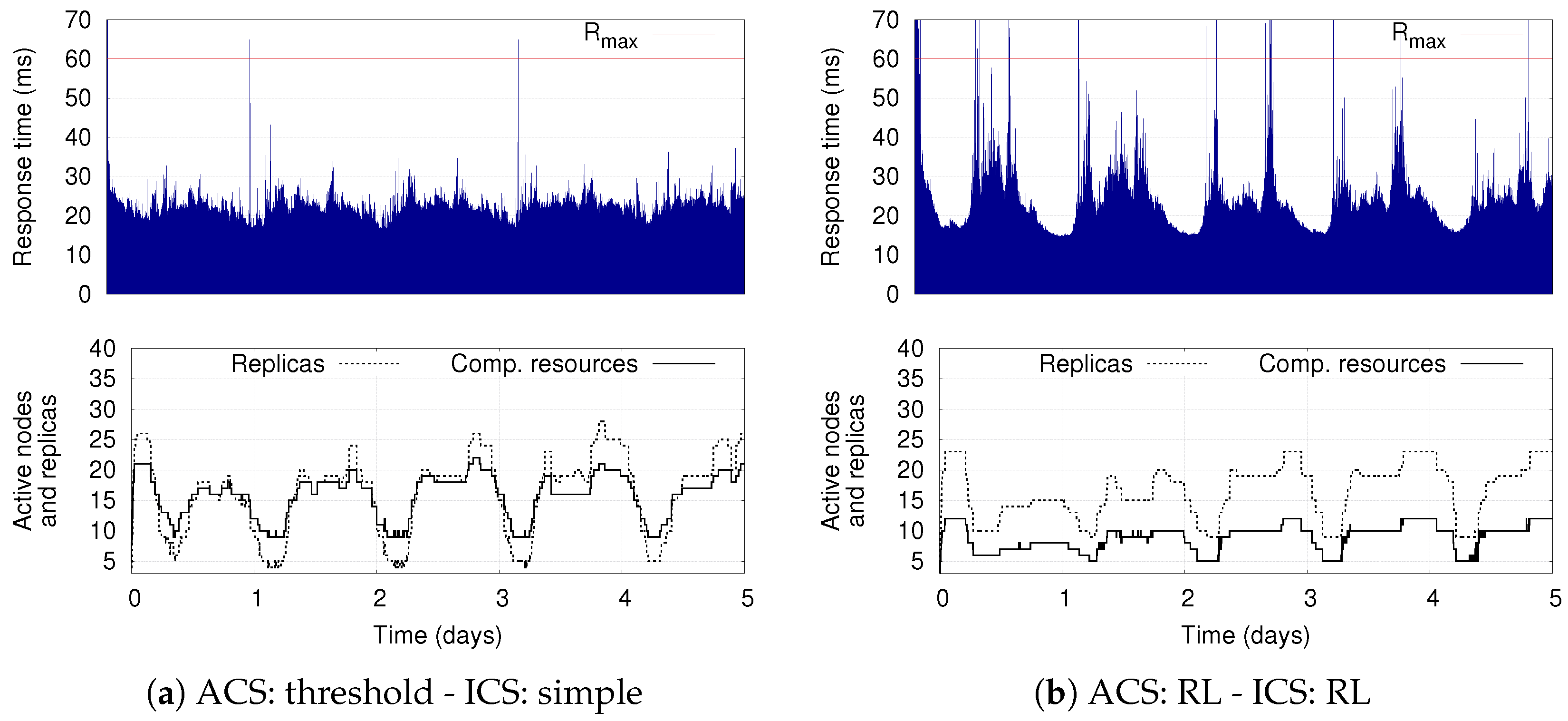
The presence of the ACS and ICS, each of which can be equipped with hierarchical control policies, results in a complex system, whose adaptation capabilities deserve a detailed analysis. Therefore, as second contribution, we extensively investigate benefits and limitations of combining different adaptation policies for the two control systems. For the ICS, we consider a simple policy that preserves a limited pool of ready-to-run computing resources as well as the more sophisticated RL-based solution that we present in this paper. 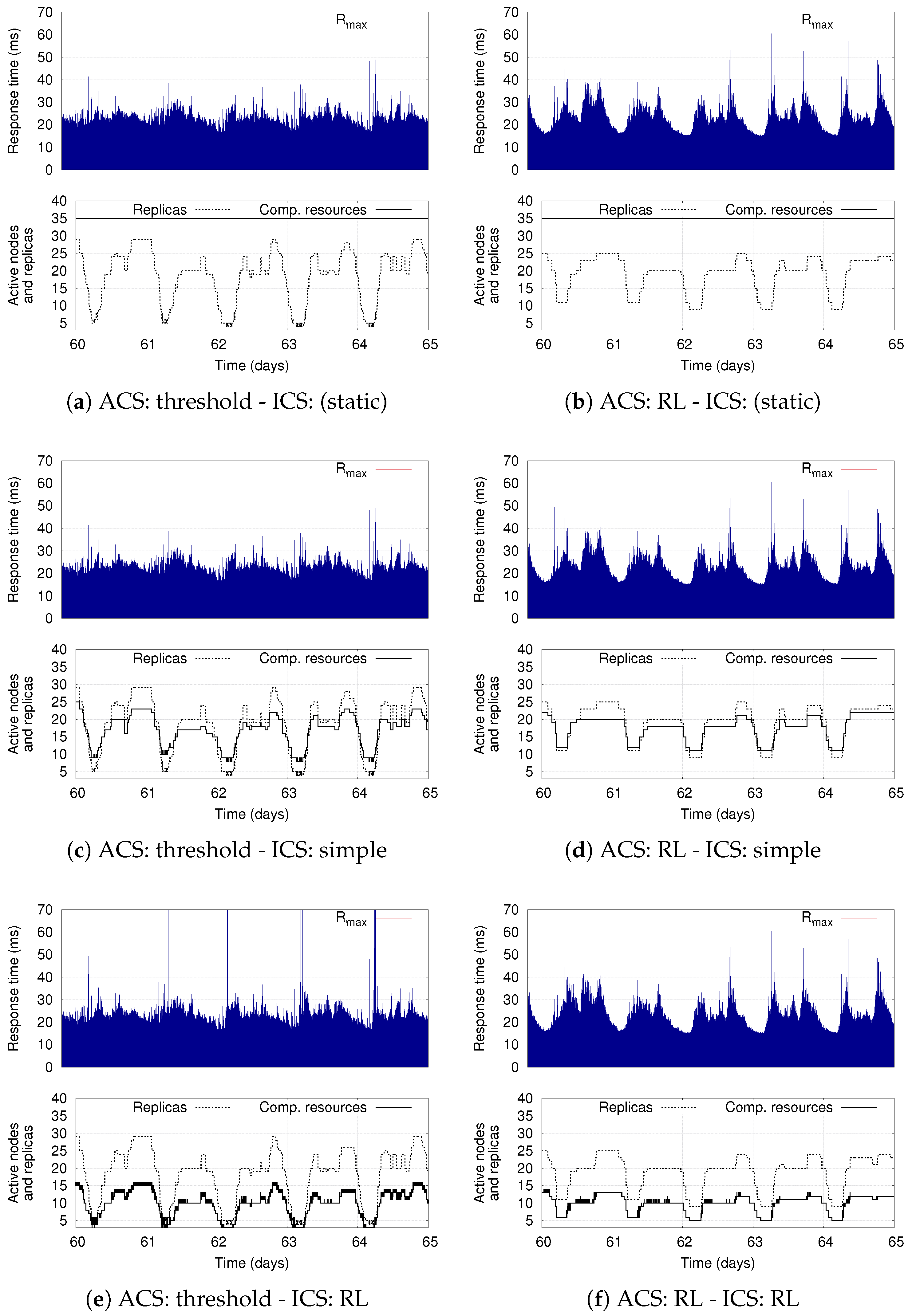For the ACS, we evaluate a simple threshold-based approach as well as the model-based RL solution presented in [8]. The proposed evaluation has a threefold objective. First, to investigate the ability of the ACS and ICS to adapt the application deployment and the computing infrastructure, respectively. Second, to show the flexibility of the proposed RL-based policy for the ICS. Third, to discuss the time experienced by the RL policy to learn a good infrastructure elasticity policy.

Our simulation results show the benefits of having two separate control components that autonomously adapt the deployment of DSP applications on a dynamic set of computing resources. They demonstrate the flexibility of the proposed infrastructure-level policy based on RL, which can be tuned to optimize different deployment objectives while still supporting the application-level elasticity. The results also show that the combination of RL-based solutions for the ICS as well as for the ACS represents the most flexible solution: if conveniently configured, it reduces the average number of used computing resources with respect to the other policies, while also limiting the number of application reconfigurations (thus increasing the application availability).

The rest of this paper is organized as follows. In Section 2. we review related work; in Section 3, we describe the system model and the problem under investigation; and, in Section 4, we present E2DF and its hierarchical control architecture for self-adaptation. To control DSP applications and computing resources, E2DF exploits hierarchical policies (Section 5). For the ICS, we propose novel policies resorting on a simple heuristic and on a RL-based approach (Section 6). To show the multi-level adaptation capabilities of E2DF, we also consider some elasticity policies already proposed in literature, which can conveniently scale the number of operator replicas at run-time (Section 7). Then, by means of simulations, we extensively evaluate the proposed RL-based control policy for the ICS and the resulting self-adaptation capabilities of E2DF (Section 8). Finally, we conclude in Section 9.

2. Related Work

DSP applications are usually long running and expose computational requirements that are usually unknown and, most importantly, can change continuously at run-time. Therefore, in the last years, research and industrial efforts have investigated the run-time adaptation of DSP applications [3], mainly achieved through elastic data parallelism [15]. In this section, we review related work by considering first the system architectures and then the policies that have been proposed to tackle the elasticity of DSP applications.

2.1. System Architectures

Approaches that enable elasticity are often, either explicitly or implicitly, architected as self-adaptive software systems based on the MAPE loop, which is a well known pattern to design self-adaptive systems [16]. Following this model, in response to (observed or predicted) changes, the application deployment is adapted by scaling the number of operator replicas or computing resources or by relocating some operators (or eventually their replicas) onto the computing resources. In the latter case, the set of computing nodes can be also elastically scaled-in/out as needed.

Most of the existing system architectures consider a centralized management solution, where a single coordination entity exploits its global knowledge about the entire system state to plan the proper adaptation actions (e.g., [6,7,17,18,19,20,21]). Although this approach can potentially achieve a global optimum adaptation strategy, it may not be suitable for a wide-area distributed environment, because of the tight coupling among the system components and the fact that a central manager represents a bottleneck in a large-scale system due to monitoring and planning overheads.

Conversely, other solutions rely on decentralized adaptation planners that exploit a limited local view of the system, thus overcoming the scalability issues due to the management of global information. In this case, the vast majority of the proposed approaches rely on a fully decentralized architecture (e.g., [9,10,11,22,23]). Although these decentralized solutions appear to be appealing for wide-area distributed environments, the lack of coordination among the decentralized planning agents may cause frequent reconfiguration decisions, which can cause instability that compromises the DSP application performance, as shown in [12].

Differently from the above approaches, we consider a hierarchical distributed architecture, which can take the best of centralized and fully decentralized architectures, thus improving performance and scalability without compromising stability. A hierarchical control scheme has been previously adopted by Zhou et al. [24] to address the placement and relocation at runtime of the DSP operators. In their solution, there are multiple coordinators organized in a hierarchical tree, and each coordinator is in charge of a subgraph of the DSP application and of the underlying computing network. However, their control knob is based on redistributing the DSP operators, without scaling the number of operator replicas or computing resources. The system architecture we propose in this paper is built on our previous works [8,13], where we presented a hierarchical decentralized architecture to control elasticity first at the DSP application level [8] and then also at the infrastructure level [13]. Here, we propose and evaluate new control policies for the infrastructure elasticity. Moreover, we investigate the benefits of a loosely coupled system architecture for controlling elasticity both at the application and infrastructure level. In particular, we show the the intertwined effects of autonomous policies operating at different levels of the system architecture.

Few solutions have so far explicitly considered the run-time adaptation of DSP applications in fog and cloud distributed environments, where the ever increasing amount of resources at the network periphery can be exploited to improve the application latency. Distributed Storm [12] extends the Apache Storm architecture with decentralized monitoring and planning components to deal with a wide-area distributed operating environment. An extended framework based on Apache Storm and with a centralized planning component that determines the application redeployment to reduce communication latencies has been later presented by Papageorgiou et al. [25]. DRS [19] is a dynamic resource scaling framework for cloud-based DSP applications, which has been integrated with Apache Storm. It provides a layer, organized as a MAPE control loop, that is responsible for application performance monitoring, resource allocation and scaling at the infrastructure level. The proposed solution is based on two greedy algorithms that, exploiting a performance model based on queuing theory, are triggered when the application performance degrades. The first allows determining the minimum number of resources that satisfy the constraint on the mean application response time, while the latter assigns the resources to the DSP operators in such a way to minimize the mean application response time. However, DRS does not support elasticity at the application level. SpanEdge [26] uses a cloud- and fog-based architecture to unify stream processing and adopts a master-worker architecture, also implemented in Apache Storm. Foglets [27] is a fog-specific programming model supporting the migration of application components but it does not focus on elasticity. GigaSight [28] is a hybrid cloud- and edge-based architecture for a specific use case of computer-vision analytics: a federated system of proximal edge nodes filters and processes mobile video streams in near real-time, and sends only the processing results to remote cloud servers. However, this research effort focuses more on on privacy and access controls rather than on system elasticity. A unified cloud-edge data analytics platform based on a serverless stream application model has been presented by Nastic et al. [29]. Finally, Firework [30] is a another recently proposed framework for hybrid cloud-edge analytics, but it supports elasticity only at the infrastructure level.

By explicitly considering wide-area distributed environments, we designed E2DF with a hierarchical distributed architecture that can scale with the number of DSP applications and computing resources that should be efficiently managed. Being adaptation a key feature of modern DSP systems, we focus our efforts on devising efficient elasticity policies that can meet application performance requirements and reduce resource wastage, while avoiding too frequent reconfigurations.

2.2. Elasticity Policies

Several elasticity policies at the DSP application-level have been proposed in the literature; their goal is to automatically adjust the parallelism degree of DSP operators without requiring any human intervention. These policies either consider a static infrastructure environment or assume that the underlying computing infrastructure can elastically scale by its own. The main distinguishing feature of the existing elasticity policies regards their being centralized, fully decentralized, or hybrid. Another characterizing aspect is related to taking into account or not the reconfiguration costs that arise after a scaling-in/out decision as well as a migration from one computing resource to another and are particularly burdensome in case of stateful operators [31].

Some works (e.g., [15,17,32,33,34]) adopt simple decentralized threshold-based policies that use the utilization level of either the system nodes or the operator instances. The basic idea is that, when the node or operator utilization exceeds the threshold, the replication degree of the involved operators is modified accordingly. Different approaches can be identified to define the threshold. A single statically-defined threshold is used (e.g., [17]) to limit load unbalance among computing nodes. Multiple statically-defined thresholds, used for example in [33], allow to customize the behavior of each individual node within the system. A dynamically configured threshold improves the system adaptivity, (e.g., [5,34]).

Other works (e.g., [7,35,36,37,38]) use more complex centralized policies to determine the scaling decisions, exploiting optimization methods that rely on the knowledge of a global model, such as integer linear programming [7], control theory [35], queueing theory [36], and fuzzy logic [37]. In [7], we presented an integer linear programming problem for the run-time elasticity management of DSP applications that takes into account the application reconfiguration costs after scaling operations and aims to minimize them while satisfying the application performance requirements. Lohrmann et al. [36] proposed a strategy that enforces latency constraints by relying on a predictive latency model based on queueing theory. Mencagli et al. [37] presented a two-level adaptation solution that handles workload variations at different time-scales: at a fast time-scale, a control-theoretic approach is used to deal with load imbalance, while, at a slower time-scale, a global controller makes operator scaling decisions employing fuzzy logic. However, their solution is specifically designed for sliding-window preference queries executed on multi-core architectures. While the previously mentioned policies are reactive and cannot thus provision replicas in advance, De Matteis and Mencagli [35] proposed a proactive control-based strategy that takes into account a limited future time horizon to choose the reconfigurations. Centralized heuristic policies have been also proposed in [6,38,39,40]. Liu et al. [6] proposed a stepwise profiling framework that considers both application features and processing power of the computing resources and selectively evaluates the efficiency of several possible configurations of parallelism. Heinze et al. [39] presented a policy that takes into account the reconfiguration costs: the latency spikes caused by operator reallocations are first estimated through a model and then used to define a heuristic placement algorithm which is based on a bin packing heuristic. Stela [38] relies on a throughput-based metric to estimate the impact of each operator towards the application throughput and to identify those operators that need to be scaled. Kotto Kombi et al. [40] proposed an approach to preventively adapt the replication degree of operators according to stream rate fluctuations.

Differently from the above centralized policies, Mencagli [22] presented a fully decentralized game-theoretic approach where the elasticity control logic is distributed on each operator. In [41], we started to study decentralized elasticity policies based on reinforcement learning by considering only a single DSP operator in isolation. We continued this investigation in [8], where we proposed a hierarchical policy to manage the elasticity at the application level, considering a DSP application composed by many interconnected operators. This hierarchical application control policy, which is described in Section 7, combines a decentralized elasticity policy carried out by each operator with a centralized token-bucket solution. Our previous works [8,41] do not consider elasticity at the infrastructure level.

As regards elasticity control policies at the infrastructure level, it has been a hot research topic in cloud computing, as surveyed in [42,43]. Therefore, we review only some works that are most closely related to the RL-based approach we propose in Section 6.

Threshold-based elasticity policies represent the classical and easiest approach for controlling also the auto-scaling of computing resources. For example, they represent the usual choice by cloud providers that offer auto-scaling services (e.g., AWS Auto Scaling and Google Compute Engine Autoscaling). However, they require the user to know how to set the corresponding threshold rules [44]. On the other hand, automatic decision-making approaches, such as RL, allow the user to focus on what he/she aim to obtain, instead of how it should be obtained. The Q-learning algorithm [14] is a classic model-free RL algorithm, which is often considered in literature (e.g., [45,46]). It requires no prior knowledge of the system dynamics, which is rather learned as the system runs. On the negative side, it is slow to converge, also because it does not make efficient use of the data that it gathers as a result of learning. With the goal to free the user from defining scaling thresholds, Jamshidi et al. [44] exploited fuzzy logic, proposing an auto-scaling controller that learns and modifies fuzzy rules at run-time using Q-learning. Tesauro et al. [47] observed that RL approaches can suffer from curse of dimensionality problems, because the lookup table has to store a separate value for every possible state-action pair. Moreover, during the on-line training, performance may be unacceptably poor, due to the absence of domain knowledge or good heuristics. To overcome these issues, they combined RL with a queueing-based system model, which computes the initial deployment decisions and drives the exploration actions. They used the SARSA learning algorithm [14], which however suffers from slow convergence as Q-learning. With the same goal of reducing the state space, Arabnejad et al. [48] combined the classic Q-learning and SARSA RL algorithms with a fuzzy inference system, while Barrett et al. [45] proposed a parallel Q-learning approach. Differently from all these works, in this paper, we consider a model-based RL policy, which exploits knowledge on the estimated system dynamics, so to improve convergence rate and achieve good system performance.

Overall, the works most closely related to our proposal have been presented in [5,6], which consider multi-level elasticity both at the application and infrastructure level in the DSP context. Liu et al. [6] presented a profiling framework that evaluates the efficiency of different combinations of operator parallelism. We share the same goal of avoiding resource wastage; however, they did not propose auto-scaling policies. Lombardi et al. [5] considered at the same time the elasticity at the operator and resource levels, where scaling actions can be executed either in a reactive or proactive fashion. We observe that, differently from us, these proposals have been designed for traditional DSP systems deployed in a clustered environment and therefore could suffer from scalability issues when executed in a wide-area environment. Our E2DF framework is a first step that addresses an explicitly coordinated multi-level elasticity for DSP systems deployed in geo-distributed cloud and fog/ edge environments.

3. System Model and Problem Definition

3.1. DSP Application Model

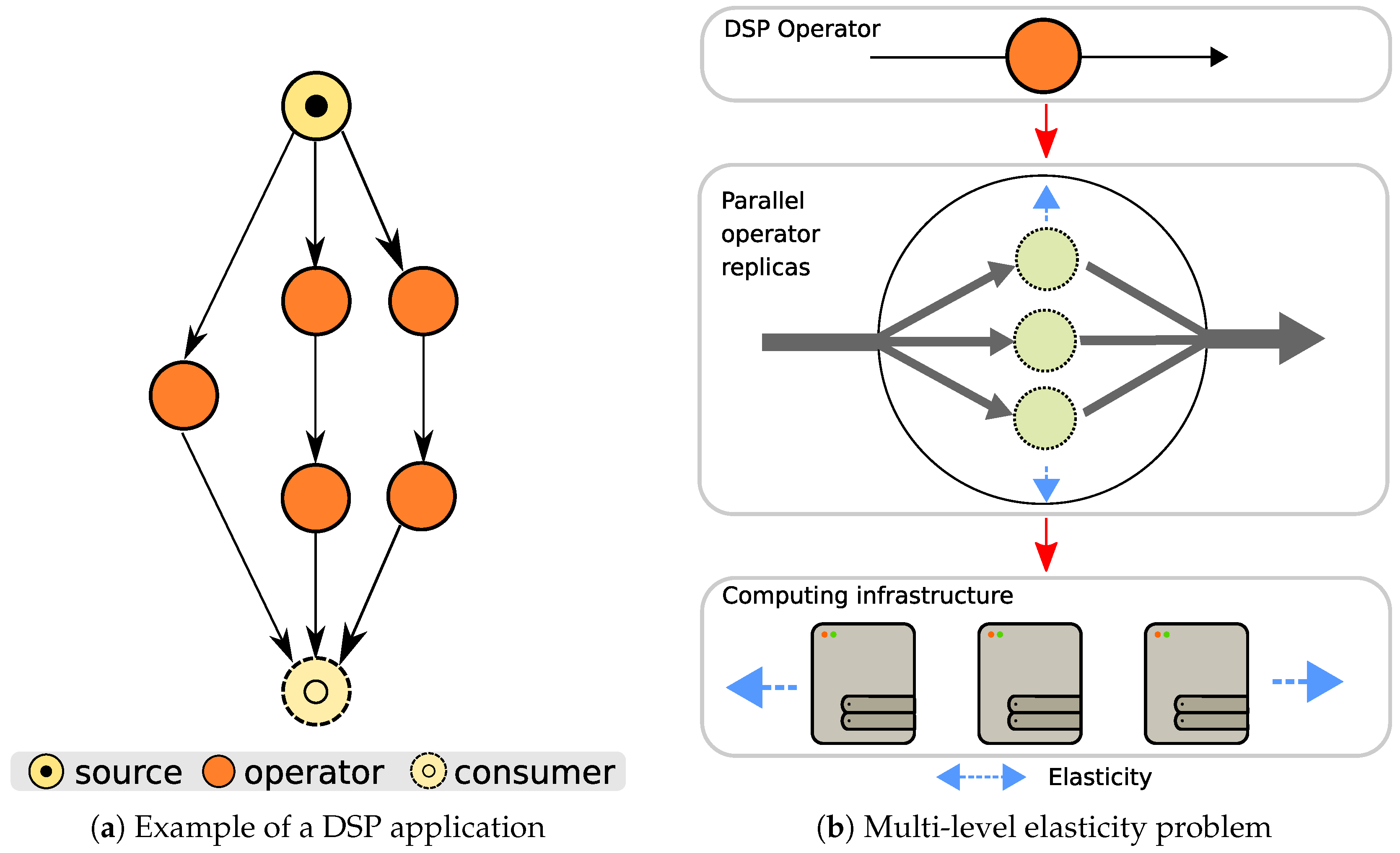
A DSP application can be regarded as a directed acyclic graph (DAG), where data sources, operators, and consumers are connected by streams (see Figure 1a) An operator is a self-contained processing element that carries out a specific operation (e.g., filtering and POS-tagging), whereas a stream is an unbounded sequence of data (e.g., tuples). DSP applications are usually employed in latency-sensitive domains [2,35,36], where reduced response time is required. Although multiple definitions of response time exist in the context of DSP, the widely used one defines it as the overall processing and transmission latency from a data source to a final consumer on the application DAG. In this work, we assume that the DSP application exposes requirements in terms of response time, specifying a target value $R_{max}$ that should not be exceeded.

To improve performance, multiple replicas can be used to run an operator, where each replica processes a subset of the incoming data flow (data parallelism). By partitioning the stream over multiple replicas, running on one or more computing nodes, the load per replica is reduced, and so is the processing latency. Since DSP applications are long-running and subject to workloads that vary over time, the number of replicas should accordingly change at run-time to meet the performance target while avoiding resource wastage (application elasticity).

3.2. Infrastructure Model

For the execution, a DSP application needs to be deployed on computing resources, which will host and execute the operators. In a large-scale environment, multiple cloud data centers and fog micro-data centers provide computing resources on-demand. A DSP system can be deployed over multiple data centers to exploit the geographic distribution of the infrastructure, and acquire resources closer to data sources and consumers. We indicate a data center or a micro-data center as a deployment region (or region, for short). A region contains computing resources that are close to each other, meaning that they can exchange data using local area networks, which result in negligible communication delay. Computing resources belonging to different regions exchange data using wide area networks, with not negligible communication delay.

We assume that a region contains virtual computing resources (i.e., either virtual machines or container running on physical machines), which can be acquired and released as needed, thus enabling infrastructure elasticity. For the sake of simplicity, in this paper, we assume that within the same region the acquired computing resources are homogeneous. Nevertheless, the proposed approach can be extended to consider the case of heterogeneous computing resources within the same region, accounting for different prices and capacities. Each region allows acquiring and release computing resources as needed; nevertheless, in accordance with the limits imposed by nowadays cloud service providers, we assume that the number of virtual resources that can be acquired in a certain time period is limited (e.g., at most 50 new virtual machines can be acquired at once). Regions well model nowadays wide-area distributed computing infrastructures: for example, the large-scale computing infrastructure of a cloud provider can be modeled as a multitude of regions, where each region includes resources of a specific availability zone within a single data center. Considering fog/edge computing scenarios, regions can also model geographically distributed micro-data centers, each one composed by a set of servers placed at network edges.

3.3. Problem Definition

Nowadays, DSP applications are executed by means of a DSP framework. The latter provides an abstraction layer where DSP applications can be more easily developed for and deployed over the distributed computing infrastructure. A DSP framework has to control the application execution to preserve acceptable run-time performance. On the other hand, it has also to control the computing infrastructure, aiming to provide enough computing resources for the execution of its DSP applications.

DSP applications are usually long-running, and their operators can experience changing working conditions (e.g., fluctuations of the incoming workload and variations in the execution environment). To preserve the application performance within acceptable bounds and avoid costly over-provisioning of system resources, the deployment of DSP applications must be conveniently reconfigured at run-time. A scaling operation changes the replication degree of an operator: a scale-out decision increases the number of replicas when the operator needs more computing resources to deal with load spikes, whereas a scale-in decreases the number of replicas when the operator under-uses its resources. Adapting at run-time the application deployment introduces a short-term performance penalty (e.g., downtime), because changing the number of operator replicas involves the execution of management operations aimed to accordingly save the operator internal state and redistribute it across the new number of replicas. Therefore, if applied too often, the adaptation actions negatively impact the application performance.

As regards the computing infrastructure, we observe that, in a static setting, the DSP framework can be executed over a statically defined cluster of nodes. However, modern technologies allow the execution over a dynamic set of resources that can be acquired and released at runtime (e.g., cloud and fog computing). This feature is suitable for addressing the dynamism of DSP applications while avoiding the cost of an over-sized infrastructure. Therefore, modern DSP frameworks should be able to efficiently scale the number of computing resources at run-time with a twofold objective: satisfy the applications’ requirements and avoid resource wastage. Moreover, to efficiently operate over the emerging geo-distributed computing environments (e.g., distributed cloud and fog computing), modern DSP frameworks should be able to seamlessly deal with a large number of resources. In this context, a centralized and monolithic framework will soon suffer from scalability issues. Conversely, despite the increased management complexity, a modular and hierarchically distributed framework allows decentralizing the management responsibilities, thus increasing its ability to oversee a large number of computing resources and DSP applications.

As illustrated in Figure 1b, a modern DSP framework should be able to efficiently deal with the multi-level elasticity problem: at the application level, the framework should adapt the number of operator replicas at run-time, whereas, at the infrastructure level, the framework should acquire and release computing resources as needed.

4. Hierarchical System Architecture

The complexity of the computing environment calls for systems that can autonomously adapt their behavior in face of changing working conditions. The MAPE control cycle is a well-know architectural pattern that organizes the autonomous control of a software system according to four main components (Monitor, Analyze, Plan, and Execute), which are responsible for the primary functions of self-adaptation [16].

When the controlled system is distributed across a large number of computing nodes, a single and centralized MAPE loop may represent a system bottleneck that may compromise the system responsiveness. To overcome the limitations of a centralized control solution, we can efficiently decentralize the MAPE components according to popular design patterns, as described in [49]. Among the different decentralization solutions, the hierarchical control pattern represents a suitable approach to manage wide-area distributed systems. The hierarchical control pattern revolves around the idea of a layered architecture, where each layer works at a different level of abstraction. In this pattern, multiple MAPE control loops work with time scales and concerns separation. Lower levels operate on a shorter time scale and deal with local adaptation. Exploiting a broader view on the system, higher levels steer the overall adaptation by providing guidelines to the lower levels.

To efficiently control the execution of elastic DSP applications in a geo-distributed computing environment, we propose Multi-Level Elastic and Distributed DSP Framework (E2DF). It includes two management systems that are organized according to a two-layered hierarchical pattern: the Application Control System (ACS), which adapts the DSP operators deployment, and the Infrastructure Control System (ICS), which controls the computing resource elasticity. 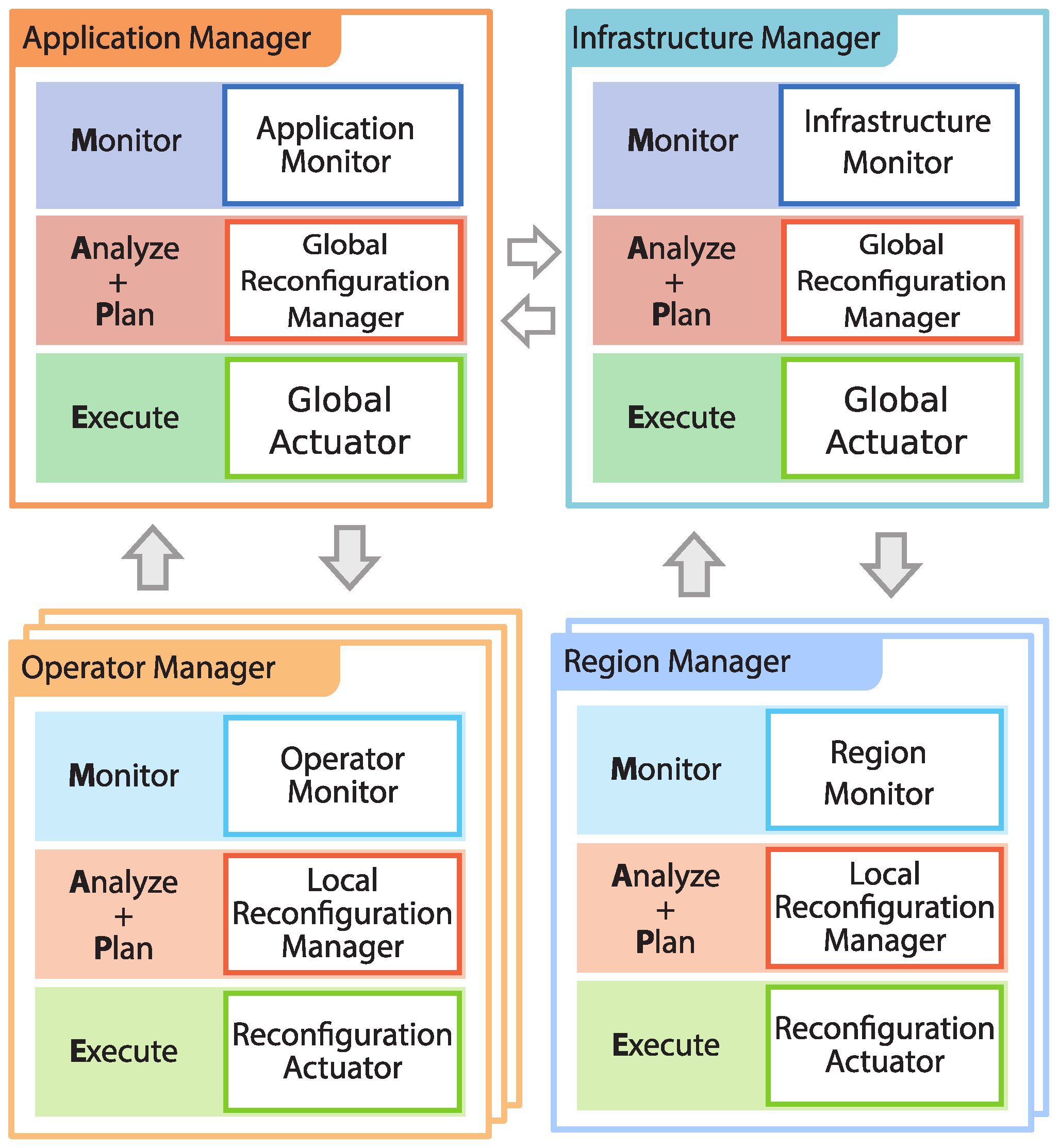Figure 2 illustrates the conceptual architecture of E2DF, highlighting the hierarchy of the multiple MAPE loops and the system components in charge of the MAPE loop phases.

The ICS includes a centralized Infrastructure Manager (IM), which cooperates with multiple decentralized Region Managers (RMs). Similarly, the ACS comprises one centralized Application Manager (AM) and multiple decentralized Operator Managers (OMs). These components oversee the application deployment at run-time, which can be conveniently adapted when improvements of the application performance can be achieved. The IM and AM can work independently one another or can cooperate so as to realize cross-level optimizations. In such a way, the infrastructure can be adapted to better address specific application needs (e.g., to provision resources in advance or to prevent node consolidation). In this paper, we do not consider cross-level optimization, but we mainly focus on adaptation policies for the ICS.

4.1. Infrastructure Control System

When a DSP system is deployed over a large-scale environment, managing resources is not a trivial task: the number of computing resources as well as the network latency among them can introduce prohibitively high delays in managing the DSP system. To address this management challenge, we exploit the concept of deployment region, considering that resources within a single region can be managed independently from other regions. Hence, we introduce, within the DSP system, a two-layered hierarchical control system that resorts on an Infrastructure Manager (IM) and multiple Region Managers (RMs), one per each region.

The Region Manager (RM) is a distributed entity that controls computing resources within a single region. To perform these operations, the RM is organized according to the MAPE loop and realizes the lower level control loop of the ICS. The RM monitors the computing nodes used by E2DF within the region through the Resource Monitor. The latter periodically queries the active nodes to retrieve the number of hosted application operators and the average utilization of its computing and memory resources. Then, through the Local Reconfiguration Manager, it analyzes the monitored data and determines if new resources should be acquired, or leased ones should be released (e.g., to reduce resource wastage). To this end, the Local Reconfiguration Manager is equipped with a local policy, whose details are presented in Section 6. When the RM local policy determines that some adaptation should occur, it issues an adaptation request to the higher layer.

At the higher layer, the Infrastructure Manager (IM) coordinates the resource adaptation among the different computing regions through a global MAPE loop. By means of the Infrastructure Monitor, it collects aggregated monitoring data from the different available regions. Then, through the Global Reconfiguration Manager, the IM analyzes the monitored data and the reconfiguration requests received by the multiple RMs to decide which reconfiguration should be granted. For example, the Global Reconfiguration Manager can decide that it is more convenient to acquire resources from a specific region, so it will inhibit scaling operations proposed for other regions. According to its internal policy (see Section 6.3), the Global Reconfiguration Manager can interact with the AM and accordingly adapt its behavior. For example, it may suggest the AM to consolidate the managed DSP operators on fewer computing nodes (the AM can conveniently accept or deny the request), or it may request to balance load among the deployment regions. Using the Global Actuator, the IM communicates its reconfiguration decisions to each RM, which can, finally, scale the computing infrastructure by means of the their local Reconfiguration Actuators.

4.2. Application Control System

The ACS manages the run-time adaptation of a DSP application. Similar to the ICS, it implements a two-layered hierarchical MAPE loop, where an Application Manager oversees subordinate and decentralized Operator Managers.

At the lower layer, the Operator Manager (OM) controls the reconfiguration of a single DSP operator and proposes reconfiguration requests to the higher level. The OM uses the Operator Monitor to retrieve the resources usage by the operator as well as its performance in terms of response time. By analyzing this information, the Local Reconfiguration Manager determines if any local reconfiguration action is needed. The available actions are scale-out and scale-in, which respectively increase and reduce the number of replicas per operator. When the OM determines that some adaptation should occur, it issues an operator adaptation request to the higher layer.

At the higher layer, the Application Manager (AM) is the centralized entity that coordinates the adaptation request aiming to obtain good overall DSP application performance. By means of the Application Monitor, it oversees the global application behavior. Then, using the Global Reconfiguration Manager, it analyzes the monitored data and the reconfiguration requests received by the multiple OMs. The AM decides which reconfigurations should be granted by using its global policy (Section 7.3). Then, it communicates the adaptation decisions through the Global Actuator to each OM; finally, the latter can execute the operator adaptation actions by means of their local Reconfiguration Actuator. We refer the reader to [8] for further details.

5. Multi-Level Adaptation Policy

The architecture of E2DF identifies different macro-components (i.e., AM-OM and IM-RM) that cooperate to adapt the deployment of DSP applications and infrastructures at run-time. The resulting architecture is general enough to not limit the specific internal policies and goals for these components. By properly selecting the internal policy for each component, the proposed solution can work in different execution contexts, which may encompass applications with different requirements, infrastructures with heterogeneous resources, and different user preferences. As a result, the system components can work under different degree of coupling. To favor decentralization and scalability, we design internal control policies that pursuit a strict separation of concerns among the different system components.

Since the control components (i.e., AM, OMs, IM, and RMs) work at different abstraction layers, we need two-layered control policies as well. Specifically, we consider local policies, associated with each RM and OM, that are concerned about low-layer adaptation actions and exploit a fine-grained view on the controlled entities (i.e., computing resources and DSP operators). The local policies do not directly enact planned adaptation actions, which instead are communicated to the higher level components (i.e., IM or AM). Each of these components is equipped with a global policy that works at the granularity of the whole application/infrastructure and thus exploits a global level view. Based on the overall monitored performance and the application requirements (i.e., its target response time $R_{max}$), the global policies identify the most effective reconfigurations proposed by the decentralized agents, providing an implicit coordination mechanism among the independent local policies.

6. Infrastructure Control Policy

The ICS policies aim to dynamically acquire and release computing resources for E2DF. These strategies result from the cooperation of a global policy for the IM and a local policy for the RMs. The overall adaptation goal is to improve resource utilization (i.e., to reduce wastage), while being able to satisfy the varying demand for resources by the applications.

Each RM has visibility of the computing resources belonging to a single deployment region used by E2DF. To elastically adapt the number and type of these resources, the RM uses a local policy, which in particular implements the planning component of the low-layer MAPE loop. In this paper, we explore two classes of RM policies: the first aims at preserving a limited pool of ready-to-run resources (Section 6.1), and the second is based on a Reinforcement Learning approach (Section 6.2).

The RMs send their reconfiguration request to the IM, which grants reconfiguration according to its global policy. The latter works at the granularity of the whole infrastructure, therefore it can take advantage of a global view on the computing infrastructure. In this paper we mainly focus on local policies for controlling the infrastructure in a decentralized manner, therefore we only present a very simple global policy that coordinates the infrastructure reconfiguration requests (Section 6.3).

6.1. Local Policy: Simple Provisioning Policy

In the simple provisioning policy, the RM preserves a predefined number of computing nodes, $N_{\mathrm{idle}}$, in a completely idle state for the region. An idle node does not host any application component; however, it is up-and-running and ready to receive DSP operator assignments. The main idea behind this policy is to keep a limited set of ready-to-run resources that can be quickly used in case of need (i.e., they can be used without waiting the boot time of new computing resources). When the RM detects a number of idle nodes lower than $N_{\mathrm{idle}}$, it acquires a new resource for E2DF within its region. Conversely, when too many resources are not utilized (i.e., when there are more than $N_{\mathrm{idle}}$ idle nodes), the RM proposes a scale-in operation, which frees the unused computing resources of E2DF. Observe that, since an idle node does not host any application component, it can be turned off without impacting the applications running in E2DF.

6.2. Local Policy: Reinforcement Learning Scaling Policy

Reinforcement learning approaches aim to learn the optimal strategy—in our scenario the RM scaling strategy—through experience and direct interaction with the system [14]. A RL task basically considers an agent who aims to minimize a long-term cost. Considering a sequence of discrete time steps, which models the periodical activation of the local policy, at each step, the agent performs an action, looking at the current state of its environment (i.e., the region). The chosen action causes the payment of an immediate cost, and the transition to a new state. Both the paid cost and the next state transition usually depend on external unknown factors as well, hence are stochastic. To minimize the expected long-term (discounted) cost, the agent keeps the estimates $Q(s,a)$, which represent the expected long-run cost that follows the execution of action a in state s. These estimates constitute the so-called Q-function, and are used by the RM to make decisions. By observing the actual incurred costs, the RM updates these estimates over time, and by so doing, also improves its policy. RL techniques are based on the assumption that the underlying system is stationary and satisfies the Markov property. 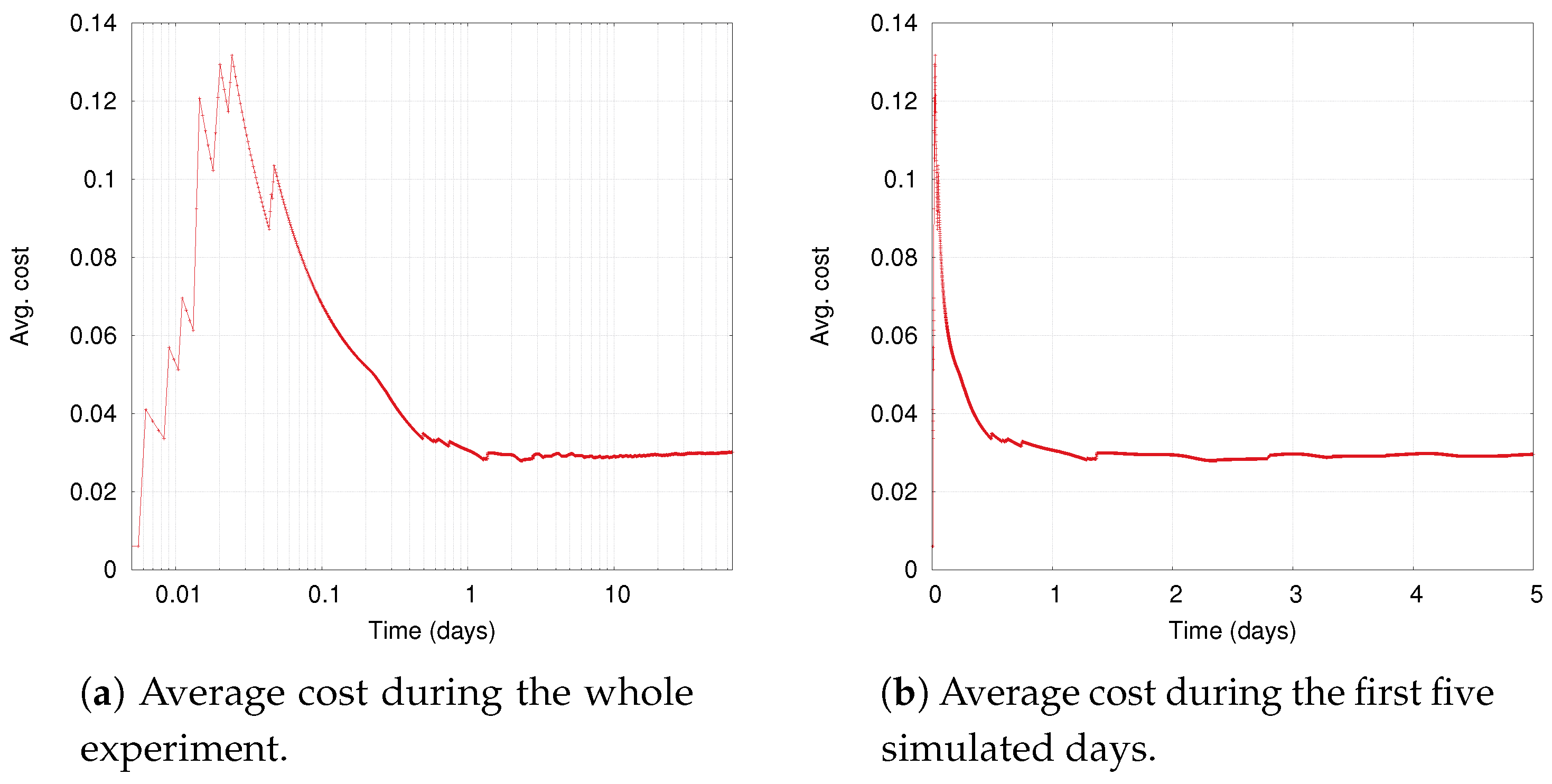Although these properties might not hold true in real systems, RL techniques have been often applied successfully in non-Markovian domains [14]. To cope with the (possible) lack of the stationary property, it is sufficient to use a constant (rather than decreasing) learning rate to let the learned policies adapt over time [14].

We define the state at the beginning of the ith time interval as the triple $s_i=(k_i,u_i,f_i)$, where $k_i$ is the number of active computing nodes, $u_i$ is the average resource utilization for the currently deployed application components, and $f_i\in \left\{0,1\right\}$ signals whether an idle node exists. In general, $u_i$ is a vector containing the utilization of several resources (e.g., CPU, memory, and network bandwidth). For simplicity, in this work, we assume it to be a scalar value, representing the average CPU utilization for the running application replicas. Even though the average utilization is a real number taking values in $[0,1]$, for the sake of analysis, we discretize it by assuming that $u_i\in \{0,\overline{u},\dots ,L_u\overline{u}\}$ where $\overline{u}$ is a suitable quantum. We also assume that $k_i\in \{0,\dots ,K_{max,r}\}$, where $K_{max,r}$ depends on the total amount of resources available in region r, and is statically configured. We will denote by $\mathcal{S}$ the set of all the possible RM states.

For each state $s\in \mathcal{S}$, we have a set of scaling decisions represented by a set of actions $\mathcal{A}\left(s\right)=\{+1,-1,0\}$, where $a=+1$ denotes the decision of launching a new computing node, $a=-1$ the decision of terminating one of the active nodes, and $a=0$ is the do nothing decision. Obviously, not all of the above-mentioned actions are available in those states with $k=0$ or $f=0$, where $\mathcal{A}\left(s\right)=\{+1,0\}$ (there is no node that can be terminated), or with $k=K_{max,r}$, where $\mathcal{A}\left(s\right)=\{-1,0\}$ (we cannot add more computing nodes beyond the maximum available capacity).

To each triple $(s,a,s^{\prime })$, we associate an immediate cost function $c(s,a,s^{\prime })$, which captures the cost of carrying out action a when the system is in state s and transitions into $s^{\prime }$. Since the ICS has a two-fold goal (i.e., satisfying the application resource demand and minimizing the resource usage), in our RL model, we consider two different costs:

• $c_{demand}$ captures a penalty paid whenever the RM cannot satisfy all the resource acquisition requests coming from the application during the next time interval. We simply consider this cost term as a constant penalty, which is paid whatever the number of the unsatisfied resource requests is (i.e., one or more).
• $c_{resource}$ accounts for the cost of the active computing nodes throughout the next time interval. For simplicity, we assume that we have a constant cost per node.

Using the Simple Additive Weighting technique [50], we define single cost function $c(s,a,s^{\prime })$ as the weighted sum of the different costs (normalized in the interval $[0,1]$):

$$\begin{array}{ccc}\hfill c(s,a,s^{\prime })& =& w_d\frac{{𝟙}_{\{M_r>0\}}{c}_{demand}}{c_{demand}}+w_r\frac{(k+a)c_{resource}}{K_{max,r}{c}_{resource}}\hfill \\ & =& w_d{𝟙}_{\{M_r>0\}}+w_r\frac{k+a}{K_{max,r}}\hfill \end{array}$$

(1)

where ${𝟙}_{\{·\}}$ is the indicator function, $M_r$ refers to the number of resource acquisition requests coming from the applications that are unsatisfied, and $w_d$ and $w_r$, with $w_d+w_r=1$, are non-negative weights for the different costs. Intuitively, the cost function allows us to instruct the RM to discriminate between the good system configurations and actions and the bad configurations and actions (the larger the cost, the worse the configuration). As the RM aims at minimizing the incurred cost, it is encouraged by the cost function: (i) to reduce the number of active nodes; and (ii) to avoid rejecting resource acquisition requests coming from the application. The different weights allow us to express the relative importance of each cost term. Differently from the simple solution described in Section 6.1, this policy directly optimizes metrics that represent the ICS objectives. Therefore, by appropriately setting the weights, we expect the the local cost function to guide the agent towards meeting the global performance goals in a decentralized way.

6.2.1. Learning the Optimal Policy

At each decision time i, the RL agent has to decide which action to take. Specifically, being in state s, the agent relies on its policy to pick an action. A policy $\pi :\mathcal{S}\to \mathcal{A}$ is a function that associates each state s with an action $a\in \mathcal{A}\left(s\right)$. Ideally, the agent relies on the optimal policy ${\pi }^{\ast }$, which minimizes the long-term discounted cost, and satisfies the Bellman optimality equations (see [14]). Unfortunately, we cannot explicitly determine the optimal policy without a complete and accurate system model formulation. The presence of unpredictable dynamics in the system forces the agent to learn the policy to use at run-time.

Algorithm 1 illustrates the general RL scheme: the Q functions are first initialized (setting all to zero will often suffices) (Line 1); then, at each step i, the agent chooses an action $a_i$ based on the current estimates of Q (Line 3), observes the incurred cost $c_i$ and the next state $s_{i+1}$ (Line 4), and updates the Q function based on what it just experienced during step i, that is, the tuple $(s_i,a_i,c_i,s_{i+1}$) (Line 5).

Different RL techniques differ for the actual learning algorithm adopted, and on the assumptions about the system. For example, the well-known Q-learning algorithm is a model-free learning algorithm which requires no knowledge of the system dynamics, and only learns by direct experience. By doing so, Q-learning often requires much time for convergence, and thus cannot be easily adopted in real systems, as we also have shown in [41] for the simple case of a single DSP operator in isolation. For this reason, we present a model-based approach, which basically improves its estimates of the entire system dynamic over time, and accordingly updates the Q function.

Algorithm 1 RL-based operator elastic control algorithm.

1: Initialize the Q functions 2: loop 3:     choose a scaling action $a_i$ (based on current estimates of Q) 4:     observe the next state $s_{i+1}$ and the incurred cost $c_i$ 5:     update the $Q(s_i,a_i)$ functions based on the experience 6: end loop

6.2.2. Model-Based Reinforcement Learning

Model-based RL relies on a possibly approximated system model to directly compute the Q-functions. Instead of learning the value of state and actions through experience, in this scenario, the agent uses its experience to improve the system model approximation. In particular, we consider the full backup model-based RL approach (see [14]), which backups the value of each state-action pair at every time step. To update the Q-function for all $s\in \mathcal{S}$ and for all $a\in \mathcal{A}\left(s\right)$, we directly use the Bellman equation [14,51]

$$Q(s,a)=\sum _{s^{\prime }\in \mathcal{S}}p\left(s^{\prime }\right|s,a)\left[c(s,a,s^{\prime })+\gamma \underset{a^{\prime }\in \mathcal{A}}{min}Q(s^{\prime },a^{\prime })\right].$$

We replace the unknown state transition probabilities $p\left(s^{\prime }\right|s,a)=P[s_{i+1}=s^{\prime }|s_i=s,a_i=a]$, and the unknown cost function $c(s,a,s^{\prime })$, $\forall s,s^{\prime }\in \mathcal{S}$ and $a\in \mathcal{A}\left(s\right)$ by their empirical estimates, $\widehat{p}\left(s^{\prime }\right|s,a)$ and $\widehat{c}(s,a,s^{\prime })$. To estimate the transition probabilities $p\left(s^{\prime }\right|s,a)$, we first observe that

$$\begin{array}{ccc}p\left(s^{\prime }\right|s,a)\hfill & =\hfill & P[s_{i+1}=(k^{\prime },u^{\prime },f^{\prime })|s_i=(k,u,f),a_i=a]=\hfill \\ & =\hfill & \left\{\begin{array}{cc}P[u_{i+1}=u^{\prime },f_{i+1}=f^{\prime }|k_i=k,u_i=u,f_i=f,a_i=a]\hfill & k^{\prime }=k+a\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

(2)

Unfortunately, the dynamics of the resource utilization and the presence of idle nodes are not fully captured by our model, as they also depend on the application workload and the adaptation actions carried on by the ACS. Therefore, a naive approach would consist in estimating the transition probabilities on-line by observing the state transition frequencies. However, since these probabilities depend on several state-action variables, the agent would need to learn a large number of parameters, possibly requiring a long transitory phase. Aiming at balancing the model accuracy and the learning velocity, we adopt an approximate probability model that relies on the following assumptions: (i) the resource utilization variations do not depend on the ICS decisions, but they depend only on the application workload changes; and (ii) the presence of an idle computing node in $i+1$ only depends on its presence in i and the latest action $a_i$. Formally, we have

$$p\left(s^{\prime }\right|s,a)\approx {𝟙}_{\{k^{\prime }=k+a\}}P[u_{i+1}=u^{\prime }|u_i=u]P[f_{i+1}=f^{\prime }|f_i=f,a_i=a].$$

(3)

Hereafter, since u takes value in a discrete set, we will write $P_{j,j^{\prime }}^u=P[u_{i+1}=j^{\prime }\overline{u}|u_i=j\overline{u}]$, $j,j^{\prime }\in \{0,\dots ,L_u\}$ for short. Let $n_{i,j{j}^{\prime }}^u$ be the number of times the average resource utilization changes from state $j\overline{u}$ to $j^{\prime }\overline{u}$, in the interval $\{1,\dots ,i\}$, $j,j^{\prime }\in \{1,\dots ,L_u\}$. At time i, the transition probabilities estimates are then

$$\widehat{P_{j,j^{\prime }}^u}=\frac{n_{i,j{j}^{\prime }}^u}{{\sum }_{l=0}^{L_u}{n}_{i,jl}^u}.$$

Analogously, we define the estimated transition probabilities for the variable f, that is $\widehat{P_{x,y}^f},x,y\in \left\{0,1\right\}$. Replacing these probabilities, we derive the estimates $\widehat{p}\left(s^{\prime }\right|s,a)$ via (3).

Besides the state transition probabilities, to compute the Q-function using the Bellman equation, we need an (approximate) formulation of the cost function. To estimate the immediate cost $c(s,a,s^{\prime })$, we first split it into two terms, that we indicate as the known and the unknown costs:

$$c(s,a,s^{\prime })=c_k(s,a)+c_u\left(s^{\prime }\right).$$

(4)

Comparing the expression above with Equation (1), we observe that the known cost $c_k(s,a)$ accounts for the resources costs, thus it only depends on the current state and action. On the other hand, the unknown cost $c_u\left(s^{\prime }\right)$ accounts for the unsatisfied resource demand penalty, which depends on the resource utilization and the application behavior in the next time interval (i.e., it depends on the next state $s^{\prime }$). Since we cannot easily formulate these dynamics, we replace $c_u\left(s^{\prime }\right)$ with its on-line estimate ${\widehat{c}}_u\left(s^{\prime }\right)$. To this end, the agent observes the incurred cost $c_i$ at the end of each time interval i and determines the “unknown” cost paid in the ith time slot, $c_{u,i}$, as

$$c_{u,i}=c_i-c_k(s,a)$$

by simply applying Equation (4). Then, the unknown cost estimate is updated using a simple exponential weighted average:

$${\widehat{c}}_u\left(s^{\prime }\right)\leftarrow (1-\alpha ){\widehat{c}}_u\left(s^{\prime }\right)+\alpha c_{u,i}.$$

(5)

We must note that the cost estimation rule above does not exploit all the a priori knowledge about the system. Indeed, we can heuristically assume that the expected cost due to unsatisfied resource requests is not lower when the amount of nodes is reduced and/or the utilization increases, and it is not higher with more nodes and/or a lower utilization. Therefore, after applying Equation (5) for $s=(k,\lambda )$, we always enforce the following constraints adjusting the estimates for states $s^{\prime }=(k^{\prime },{\lambda }^{\prime })$:

$$\begin{array}{ccc}{\widehat{c}}_{u,i}\left(s\right)\hfill & \hfill \le {\widehat{c}}_{u,i}\left(s^{\prime }\right)& \forall k\ge k^{\prime },u\le u^{\prime }\hfill \\ \hfill {\widehat{c}}_{u,i}\left(s\right)& \ge {\widehat{c}}_{u,i}\left(s^{\prime }\right)\hfill & \hfill \forall k\le k^{\prime },u\ge u^{\prime }.\end{array}$$

The resulting Q-function update step (Line 5 of Algorithm 1) is summarized in Algorithm 2. Given the current estimates $Q(s,a)$, at any step, the RM chooses the greedy action, that is, the action with the minimum long term estimated cost, $arg{min}_{a\in A\left(s_i\right)}Q(s_i,a)$. It is worth noting that, differently from the model-free RL algorithms, with this approach we do not need a mechanism for forcing action space exploration, which is a common issue in RL solutions [14].

Algorithm 2 Full backup model-based learning update.

1: Update estimates $\widehat{P_{j,j^{\prime }}^u}$, $\widehat{P_{x,y}^f}$ and ${\widehat{c}}_{u,i}\left(s_i\right)$ 2: for all$s\in \mathcal{S}$do 3:     for all $a\in \mathcal{A}\left(s\right)$ do 4:         $Q(s,a)\leftarrow {\sum }_{s^{\prime }\in \mathcal{S}}\widehat{p}\left(s^{\prime }\right|s,a)\left[\widehat{c}(s,a,s^{\prime })+\gamma {min}_{a^{\prime }\in \mathcal{A}}Q(s^{\prime },a^{\prime })\right]$ 5:     end for 6: end for

Each learning update step requires iterating over all the states, all the actions, and all the next states. Therefore, the computational complexity is $O\left(\right|\mathcal{S}{|}^2\left|\mathcal{A}\right|)$. Given the limited amount of available actions (two or three) and the fact that many transition probabilities are equal to 0 (see Equation (2)), the complexity reduces to $O(K_{max,r}{\lceil \frac{1}{\overline{u}}\rceil }^2)$, that is, it scales linearly with the number of resources in the region. Storing the Q function in memory requires $O(K_{max,r}\lceil \frac{1}{\overline{u}}\rceil )$, corresponding to $O\left(\right|\mathcal{S}||\mathcal{A}\left|\right)$ space.

6.3. Global Policy

The IM global policy implements the Analyze and Plan steps of the centralized MAPE loop. It coordinates the adaptation actions proposed by the decentralized RMs and can enforce strategies aimed to balance the number of computing resources acquired across different regions of the infrastructure. We design a simple coordination policy that accepts the reconfiguration requests proposed by the different RMs. However, more sophisticated solutions can be devised to better control the way the infrastructure is adapted. For example, the IM could exploit the information coming from the RMs to improve resource utilization by interacting with the AM; to this end, the RM could expose aggregated information on the utilization or price of resources, or on resources that can be consolidated by migrating some of the application operators.

Conceptually, the global policy periodically runs the following steps: (1) reconfiguration request prioritization; (2) acceptance of requests; and (3) post-reconfiguration actions.

In the reconfiguration request prioritization step, the global policy prioritizes the reconfiguration requests proposed by the RMs and determines which are the most worthy to be applied. The prioritization criterion depends on the specific global policy; it can favor resources belonging to a specific region (e.g., for political or economical reasons) or resources with specific quality attributes (e.g., price, availability, and processing capacity).

In the acceptance of requests step, the global policy decides which reconfiguration requests should be granted. The choice ranges from simply accepting all the proposed requests to limit somehow their number. This step allows the global policy to deal with a limited budget for the acquisition of computing resources. We consider this step to be performed by exploiting the sorted list of most worthy reconfiguration requests. In this paper, to design and evaluate decentralized RM policies, our simple global policy grants all the proposed reconfiguration requests.

In the last step, post-reconfiguration actions, the global policy can interact with the AM to propose either migration or consolidation operations. This step can be used by the IM to improve resource efficiency and load balancing, and/or limit resource wastage. For example, if the IM detects that computing resources within a region are under-utilized, it can propose the AM to consolidate its applications on a fewer number of resources, to free and dismiss some of the computing nodes. The IM can also determine that using resources belonging to a specific regions is not convenient anymore, therefore it may undertake actions to free all the used region resources. Our global policy does not currently perform any post-reconfiguration action and we let the exploitation of policies for the interplay between the IM and the AM to future work.

7. Application Control Policy

The ACS manages the DSP applications deployment through a local policy (executed by the OMs) and a global policy (executed by the AM).

The OM local policy implements the Analyze and Plan phases of the decentralized MAPE loop, which controls the execution of a single DSP operator. Running on decentralized components, this policy has only a local view of the system, which consists of the execution status of each operator replica (in terms of response time and resource utilization). We consider two different local policies. The first is a threshold-based policy whereby scaling decisions are based on the replicas CPU utilization compared to predefined threshold values (Section 7.1). The second resorts on a more sophisticated RL solution, where the scaling policy is learned over time by interacting with the system (Section 7.2). Whenever a scale-out decision is taken, the OM places the new operator replica within the same region where the other operator replicas are running. In the case of a scale-in decision, the OM terminates one (randomly selected) operator replica among the available ones.

To accept or reject the reconfiguration actions proposed by the OM, the AM resorts on a global policy, which implements the Analyze and Plan steps of the centralized MAPE loop. Its main goal is to coordinate the reconfiguration actions to satisfy the DSP application requirements, while minimizing the number of used computing resources. We consider a simple global policy that is only aimed to solve reconfiguration conflicts, i.e., it rejects adaptation actions when they try to allocate the same computing resource to multiple operator replicas (Section 7.3). More sophisticated approaches (e.g., based on a token bucket to limit the number of performed reconfigurations) can be proposed as well [8].

In the next section, we present the idea behind the different policies. Nevertheless, their details can be found in [8].

7.1. Local Policy: Threshold-Based Policy

In the threshold-based scaling policy, the OM monitors the CPU utilization of the operator replicas. Let us denote by $U_r$ the utilization of replica r, which measures the fraction of CPU time used by r. When the replica utilization exceeds the target utilization level $U_{\mathrm{s}-\mathrm{out}}\in \left[0,1\right]$, the OM proposes to add a new replica. Conversely, the OM proposes to remove one of the n running replicas (i.e., a scale-in operation), when the average utilization of the remaining replicas would not exceed a fraction of the target utilization, i.e., when ${\sum }_{r=1}^n{U}_r/(n-1)<c{U}_{\mathrm{s}-\mathrm{out}}$, $c\in (0,1)$. This avoids system oscillations with the OM executing a scale-out operation just after a scale-in one.

7.2. Local Policy: Reinforcement Learning Based Policy

To design the RL policy for the OM, we follow a similar approach to the one presented in Section 6.2. In this case, the RL policy learns the optimal strategy for scaling a DSP operator at run-time through experience and direct interaction with the system. The RL agent consider the state of a single DSP operator and performs scaling actions, aiming to minimize a long-term cost.

We define the state of an operator based on the number of running replicas, and the measured average tuple arrival rate at the operator. For each state, we have the following reconfiguration actions: add a new operator replica (i.e., scale-out decision), remove an operator replica (i.e., scale-in decision), and a do nothing decision. We also consider that not all of these actions are available in all the states; indeed, we guarantee that at least one replica should be executed and that the operator has a maximum allowed replication degree.

As for the ICS, the RL agent is driven by a long-term cost, that depends on the immediate cost function. For the DSP operator, the immediate cost function captures three different terms:

• The reconfiguration cost $c_{rcf}\left(a\right)$: Whenever the system carries out scale-out or a scale-in operation, the operator suffers a downtime period during which no tuple is processed.
• The performance penalty $c_{perf}(s,a,s^{\prime })$: This is paid whenever the operator response time exceeds a per-operator bound $R_{max,op}$.
• The resource cost $c_{res}(s,a)$: This accounts for the cost of the computing resources used to run the operator replicas. For simplicity, we assume that we have a constant cost per operator replica.

We combine the different costs into a single cost function as the weighted sum of the costs:

$$\begin{array}{c}\hfill w_{rcf}{c}_{rcf}\left(a\right)+w_{perf}{c}_{perf}(s,a,s^{\prime })+w_{res}{c}_{res}(s,a)\end{array}$$

(6)

where s and $s^{\prime }$ represent the operator state before and after applying the reconfiguration action a, respectively; and $w_{rcf}$, $w_{perf}$, and $w_{res}$, with $w_{rcf}+w_{perf}+w_{res}=1$ are non-negative weights for the different costs. As the OM aims to minimize the incurred cost, the cost function suggests: (i) reducing the number of requested reconfigurations; (ii) keeping the response time within the given bound; and (iii) limiting the resource usage, with the different weights expressing the relative importance of each term.

As regards the definition of the bounds $R_{max,op}$, we observe that they grant a share of the global bound $R_{max}$ to each operator according to their computational weight. They could be set either statically after preliminary profiling, or dynamically estimated and adapted at run-time by the AM.

7.3. Global Policy

The AM global policy implements the Analyze and Plan steps of the centralized MAPE loop. Its main goal is to obtain satisfying application performance, by coordinating the adaptation actions proposed by the decentralized OMs. In this paper, we resort to a simple global policy that coordinates reconfigurations and prevents the enactment of conflicting reconfigurations (e.g., two operators requesting a new replica on the same computing resource).

8. Evaluation

We evaluate the behavior of the presented control policies, and their interplay when combined through simulation. After presenting the experimental setup (Section 8.1), we propose three main sets of experiments. First, we investigate the ability of the ACS and ICS to adapt the application deployment and the computing infrastructure, respectively, when different control policies are adopted (Section 8.2). Second, we evaluate the flexibility of the proposed RL-based policy for infrastructure-level elasticity control; we show how it can control the computing infrastructure when we change the relative importance of avoiding resource wastage with respect to the ability of satisfying the application demand for resources (Section 8.3). Third, we discuss about the learning time experienced by the RL policy to learn a good infrastructure adaptation policy (Section 8.4).

8.1. Simulation Setup

As a reference application, we considered a simple WordCount topology, composed of one (or more) data sources and four processing operators: splitter, filter, counter, and consumer. The data source emits sentences, which are split into words by the first operator; for each tuple coming into the splitter, five new tuples on average are emitted. The next operator is a filter, which drops about $60\%$ of the incoming word stream. The final two operators, i.e., counter and consumer, respectively, keep a count of the frequency of each word, and publish the most frequent ones. To simulate the behavior of a real application [8], we modeled each operator as a M/D/1 queue, with service rate $\mu =330$ tuple/s. Each operator can be executed using up to 20 parallel replicas to keep the total application processing latency within $R_{max}=60$ ms. The data source emission rate ranges from 0 to 600 tuples per second, following the daily pattern shown in Figure 3. We simulated the behavior of the system over $100,000$ min (about two months).

For our evaluation, we considered a wide-area infrastructure that comprises three geographically distributed micro-data centers: dc1, dc2, and dc3. In our framework, each data center is modeled as a region, and thus will be controlled by a RM. We assumed that we can run up to 50 computing nodes for the DSP system within each region. Each node is a virtual machine with two CPU cores, thus can host at most two operator replicas. We simulated the following network latencies between the different regions: $d_{(dc1,dc2)}=2$ ms, $d_{(dc1,dc3)}=2$ ms, and and $d_{(dc2,dc3)}=1$ ms.

In E2DF, the planning components are activated periodically, every minute of simulated time, and we considered that all the adaptation actions enacted by the framework are completed within the next minute. We compared the behavior of the proposed RL policy for the ICS against a baseline strategy, where computing resources are statically provisioned, and against the simple provisioning policy, described in Section 6.1. We used the following values in the RL-based policy: $\gamma =0.99$, $\alpha =0.1$, $\overline{u}=0.1$. In particular, the discount factor $\gamma$, being close to 1, allows the RL agent to act with foresight, while the learning rate $\alpha$ enables the RL-based policies to continuously yet slowly adapt to (possibly) varying system dynamics. The $\overline{u}$ parameter aims to find a good trade-off between model approximation and number of system states; indeed, both these features depend on the utilization quantum $\overline{u}$. We considered different settings for the cost function weights, exploring distinct trade-offs among application requests satisfaction and resource usage. As regards the ACS, we considered two adaptation policies, namely the threshold-based policy (Section 7.1) and the RL-based one (Section 7.2). The threshold-based policy aims to keep the utilization of each operator replica between $50\%$ and $75\%$; therefore, it uses as parameters $U_{s-out}=0.75$ and $c=0.75$. The RL-based policy used by the OMs uses a balanced configuration of weights for the cost function, i.e., $w_{rcf}=w_{perf}=w_{res}=\frac{1}{3}$, meaning that, for the application, it is equally important to not exceed the response time bound and to avoid resource wastage.

8.2. Results with Different Combinations of Policies

We first evaluated E2DF considering different combinations of policies for the ICS and ACS. In these experiments, we used the following weights for the cost function: $w_d=0.7$ and $w_c=0.3$.

Table 1. Results with different combinations of policies for the ICS and the ACS. We report the percentage of time in which the target response time $R_{max}$ is violated, the percentage of time in which the ACS decides to reconfigure the application, the average number of operator replicas, and the average number of used computing nodes.

ICS Policy	ACS Policy	${\mathbf{R}}_{\mathit{m}\mathit{a}\mathit{x}}$ Violations	Reconfigurations	Replicas	Active Nodes
(Static)	Threshold	0.01%	3.21%	17.84	36.00
(Static)	RL	0.15%	1.02%	18.32	36.00
Simple	Threshold	0.01%	3.26%	17.83	16.57
Simple	RL	0.15%	1.04%	18.32	16.82
RL	Threshold	0.17%	3.20%	17.63	9.66
RL	RL	0.17%	1.10%	18.25	9.76

reports several metrics of interest corresponding to the different evaluated scenarios, whereas Figure 4 shows the application response time and the amount of used resources. To show the full potential of the policies, we discuss the E2DF behavior when the RL agents have completed their learning process. We postpone to Section 8.4 considerations on their learning and convergence rate.

Static provisioning. As a baseline scenario, we consider the case in which the number of active nodes in each region is statically defined as 12, and the application elasticity is driven by a simple threshold-based policy. (By preliminary experiments, we verified that this configuration guarantees enough resources to the application.) In this scenario, the application runs $17.8$ operator replicas on average, violating the target response time only for $0.01\%$ of the time, but reconfiguring (thus causing downtime) for $3\%$ of the experiment. The RL-based policy for application-level elasticity is aware of the adaptation cost. Therefore, it allows reducing the reconfigurations to about $1\%$, by increasing the average number of running replicas to $18.3$ and accepting slightly more response time violations (however, they are less than $1\%$). In these experiments, in which the infrastructures is statically provisioned, the total number of active computing resources is equal to 36. Figure 4a,b show the different behavior of the two application-level elasticity policies, with the RL-based one avoiding too frequent oscillations.

Simple ICS provisioning policy. We now consider the simple provisioning policy for the ICS presented in Section 6.1, which aims at avoiding resource wastage. In Figure 4c,d, the overall application behavior is not significantly affected by the ICS policy. In Table 1, we can confirm this insight: with both threshold-based and RL-based policies for the ACS, the application performance is almost identical to the baseline scenario. However, the ICS policy is effective in dramatically reducing the amount of used computing resources; on average, it uses 16 nodes, instead of 36 nodes as in the baseline case.

Reinforcement Learning based ICS policy. We compare the behavior of our RL-based ICS policy to that of the simple provisioning policy and to the baseline static scenario. In Figure 4e,f it seems that the application behavior is not significantly affected. In Table 1, we note that, when using the threshold-based ACS policy, the percentage of time in which the response time requirement is violated is larger. This value is identical in the case of the RL-based ACS policy, which, however, reduces the number of adaptation actions (hence the downtime) by a third. Thus, while the application performance is overall only slightly affected by the RL-based ICS policy, we observe that the number of allocated computing resources is significantly reduced, to about nine. In other words, equipped with this policy, E2DF is able to achieve a $50\%$ reduction in terms of used computing resources without compromising the application performance.

Interestingly, our model-based RL solution at the infrastructure level does not suffer from instability during the learning phase, even when it is coupled with another RL agent at the application level. Moreover, the coupling of the two RL-based policies represents the most promising configuration among the evaluated ones; indeed, the RL-based ACS policy can be further tuned to achieved a different trade-off among the considered metrics to better suit the user’s requirements (see [8] for a more detailed discussion).

8.3. Results with Different Objectives

A classic advantage of RL-based solutions is their ability to determine optimal policies given a specification of what the user wants to achieve, instead of how to achieve it. In this set of experiment, we investigated the flexibility of our RL-based policy in optimizing different trade-offs among resource usage cost and application requirements satisfaction. Specifically, we ran experiments with different configurations of weights for the cost function expressed in (1). For the application-level elasticity, we used both the threshold-based and the RL-based policies.

The results we obtain are reported in

Table 2. Results with different objectives for our RL-based ICS policy. We report the percentage of time in which the target response time $R_{max}$ is violated, the percentage of time in which the ACS decides to reconfigure the application, the average number of operator replicas, and the average number of used computing nodes.

ICS Policy	ACS Policy	${\mathbf{R}}_{\mathit{m}\mathit{a}\mathit{x}}$ Violations	Reconfigurations	Replicas	Active Nodes
$w_d=0.1,w_c=0.9$	Threshold	79.20%	0.91%	6.13	3.14
$w_d=0.3,w_c=0.7$	Threshold	8.45%	2.88%	16.60	8.57
$w_d=0.5,w_c=0.5$	Threshold	1.37%	3.09%	17.35	9.10
$w_d=0.7,w_c=0.3$	Threshold	0.17%	3.21%	17.63	9.66
$w_d=0.9,w_c=0.1$	Threshold	0.01%	3.25%	17.75	10.23
$w_d=0.1,w_c=0.9$	RL	41.52%	0.69%	15.81	8.15
$w_d=0.3,w_c=0.7$	RL	0.72%	1.09%	18.91	9.87
$w_d=0.5,w_c=0.5$	RL	0.20%	1.18%	18.64	9.74
$w_d=0.7,w_c=0.3$	RL	0.17%	1.10%	18.25	9.76
$w_d=0.9,w_c=0.1$	RL	0.16%	1.07%	18.32	10.33

. We first considered an extreme configuration in which we almost only optimize the resource usage cost (i.e., $w_d=0.1,w_c=0.9$). In this setting, E2DF only uses $3.1$ computing nodes on average, but the application performance is really poor: with the threshold-based scaling policy, the target response time is exceeded almost $80\%$ of the time; with the RL-based policy for the ACS, the performance is better but still bad, with the response time constraint violated $40\%$ of the time.

Then, we tried less unbalanced settings, with $w_d=0.3$ and $w_c=0.7$ as well as $w_d=0.7$ and $w_c=0.3$, and the perfectly balanced setting with $w_d=w_c=0.5$. As expected, as the satisfaction of the application demand for resources is weighted more, the number of response time violations quickly decreases, whereas the amount of allocated nodes increases, up to nine. As a final scenario, we used the extreme setting with $w_d=0.9$ and $w_c=0.1$, almost ignoring the resource usage cost. In this case, the amount of allocated nodes is slightly more than 10 on average, but the beneficial effect on the application performance is negligible, as illustrated in Figure 5.

8.4. Considerations on the Initial Learning Phase

From our experiments, the RL-based policies seem to outperform simpler control policies both at the application and infrastructure level. A common issue with RL solutions is the long time often required to learn a good policy, which leads to long initial transitory phases. Model-based approaches try to overcome this issue by exploiting the (partial) available knowledge about the underlying system dynamics [41].

In Figure 6, we compare the behavior of the system at the beginning of our simulations, with and without RL-based policies for the ICS and the ACS. We can observe that indeed the behavior of the RL-based policies at the beginning is not optimal, but quickly improves after the first 2–3 simulated days of operation. This behavior is also shown in Figure 7, which reports the average cost, computed according to Equation (1), incurred by the RL-based RM. Indeed, after the end of the first simulated day we cannot observe significant variations in the average cost.

We should also note that, in practice, we could let E2DF start with a simple policy, and automatically switch to the RL-based one after the initial transitory phase. Therefore, our solution can be used without worrying about the initial learning phase.

9. Conclusions

In this paper, we present and investigate the features of Multi-Level Elastic and Distributed DSP Framework (E2DF), a hierarchical approach for elastic distributed DSP. E2DF aims to enhance DSP systems with self-adaptation capabilities, adjusting both the operators parallelism (application-level elasticity) and the amount of allocated computing resources (infrastructure-level elasticity) at run-time. In particular, E2DF includes an ACS, which adapts the elastic DSP operators deployment, and an ICS, which controls the resource elasticity. These control systems are designed according to a hierarchical decentralized MAPE control pattern, where a centralized manager controls the reconfiguration requests proposed by decentralized managers.

Within this framework, we consider different policies for the hierarchical control. In this paper, we specifically design auto-scaling approaches for the computing infrastructure. We present a first baseline solution that relies on a simple provisioning approach that always keeps a limited pool of ready-to-use idle nodes. Aiming to design a more flexible self-adaptation strategy, we have investigated RL-based approaches, where distributed agents learn which are the most valuable reconfiguration actions to perform. Specifically, we present and evaluate a model-based RL algorithm, which exploits the partially available knowledge about the system dynamics to speedup the learning process. As regards the application elasticity, we consider two existing approaches: a threshold-based scaling policy, which is widely used in the literature, and a RL-based policy, which we presented in a previous work [8].

Our evaluation shows that our multi-level adaptation solution allows significantly reducing resource wastage with respect to statically provisioned infrastructures, with negligible application performance degradation. Interestingly, our results also demonstrate the benefits of RL-based solutions, which provide greater flexibility by autonomously learning how to meet the optimization goals specified by the user.

As future work, we will further investigate the presented hierarchical approach. We plan to design more sophisticated control policies that consider a larger set of constraints and (possibly conflicting) deployment objectives. As regards the global policy, we will explore proactive solutions that can dynamically adapt the local components behavior by providing informative feedback. Moreover, we will also study the multi-agent optimization problem that arises from the interplay between the ACS and ICS, recurring to techniques specifically targeted to this class of problems (e.g., multi-agent RL).