DenseZDD: A Compact and Fast Index for Families of Sets †
Abstract
:1. Introduction
2. Preliminaries
2.1. Succinct Data Structures for Rank/Select
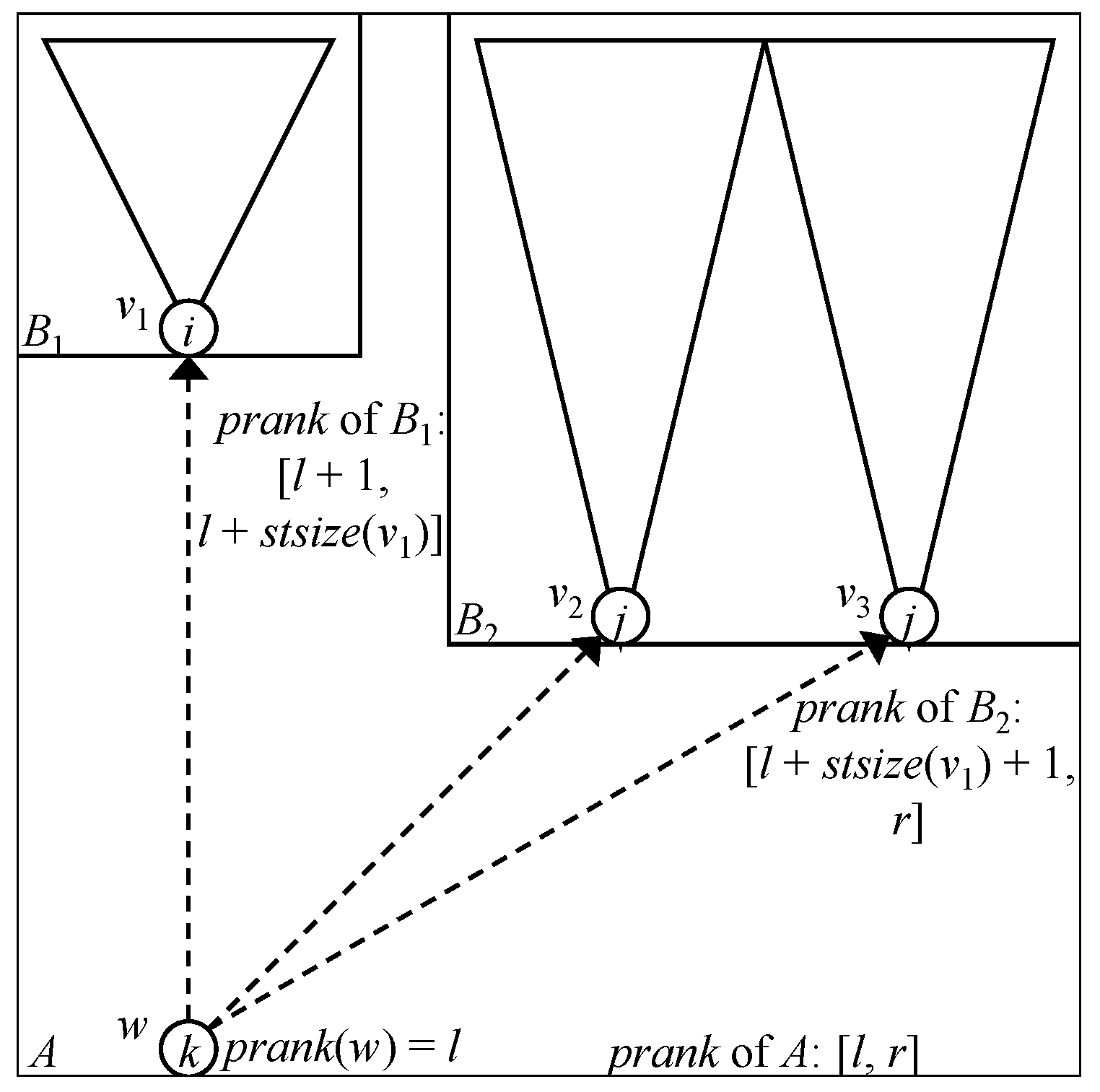
2.2. Succinct Data Structures for Trees
- : the depth of the node at position i. (The depth of a root is 0.)
- : the preorder of the node at position i.
- : the position of the ancestor with depth d of the node at position i.
- : the position of the parent of the node at position i (identical to (P, i, ).
- : the number of children of the node at position i.
- : the d-th child of the node at position i.
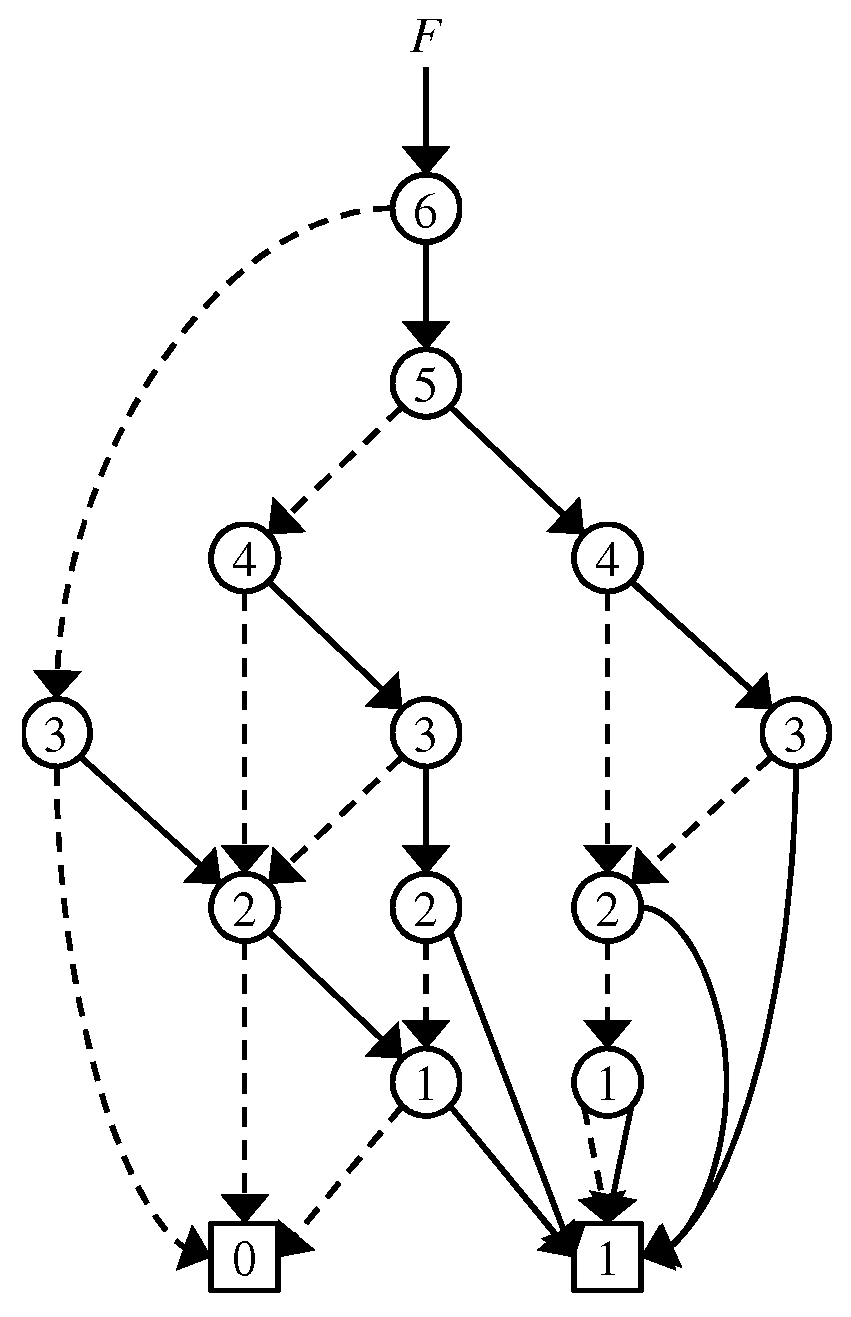
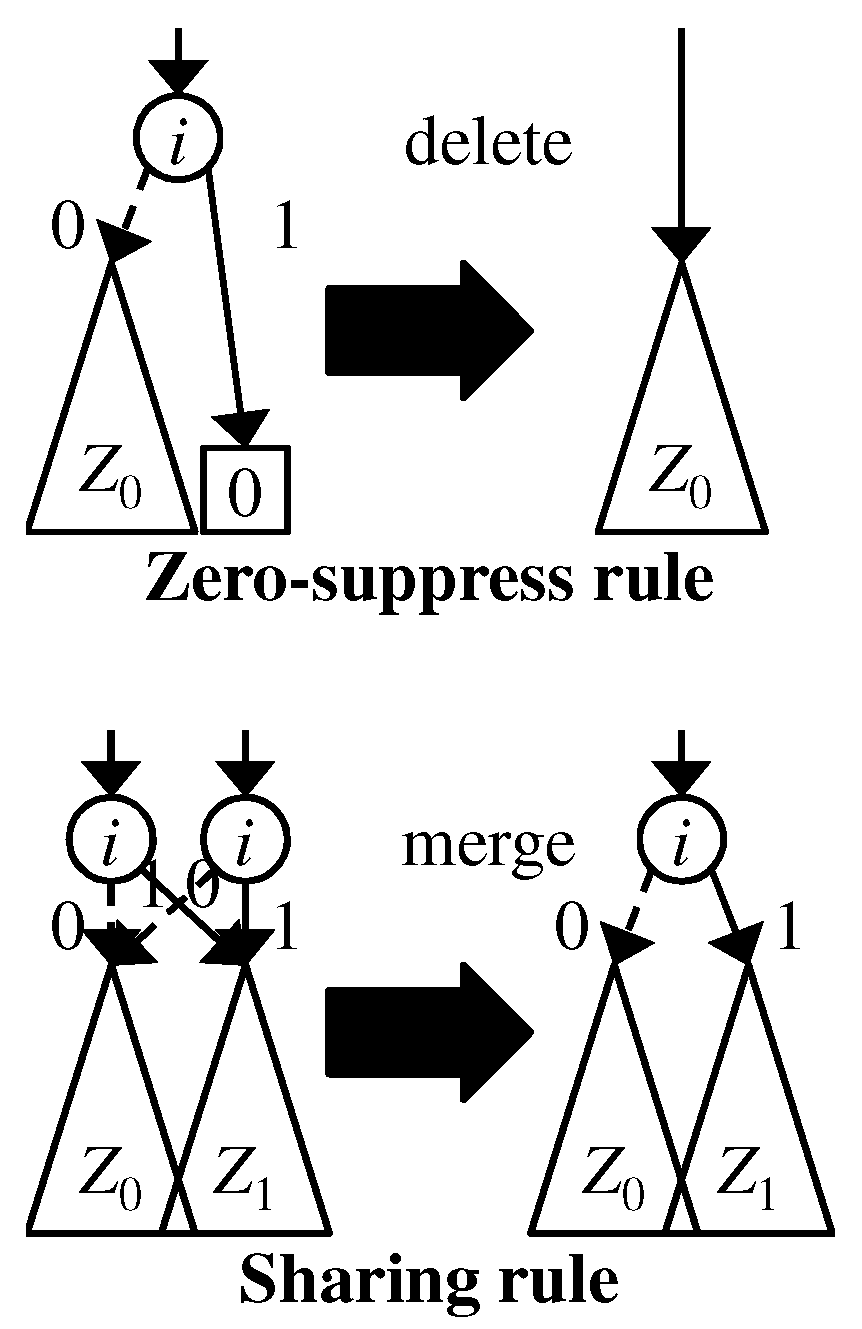
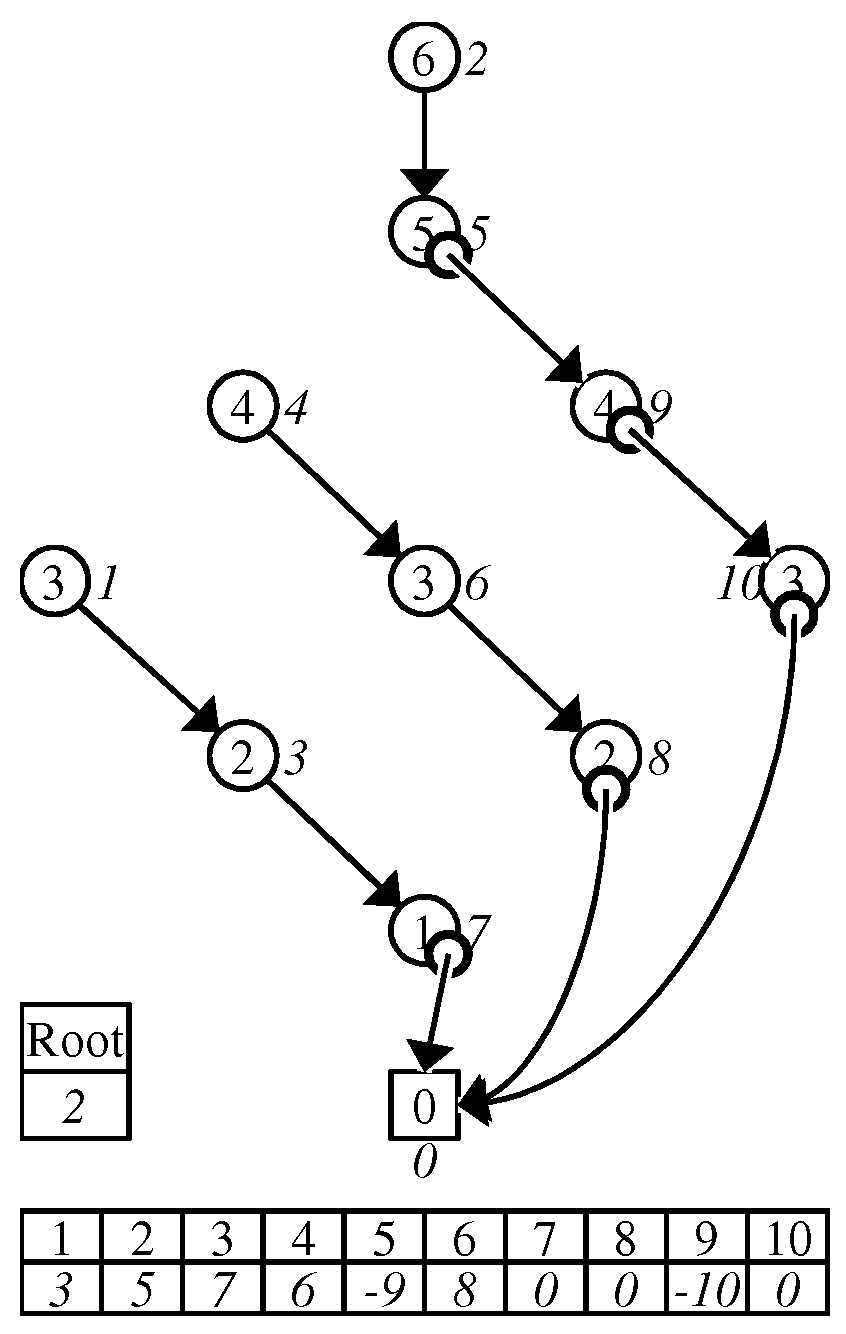
2.3. Zero-Suppressed Binary Decision Diagrams
2.4. Problem of Existing ZDDs
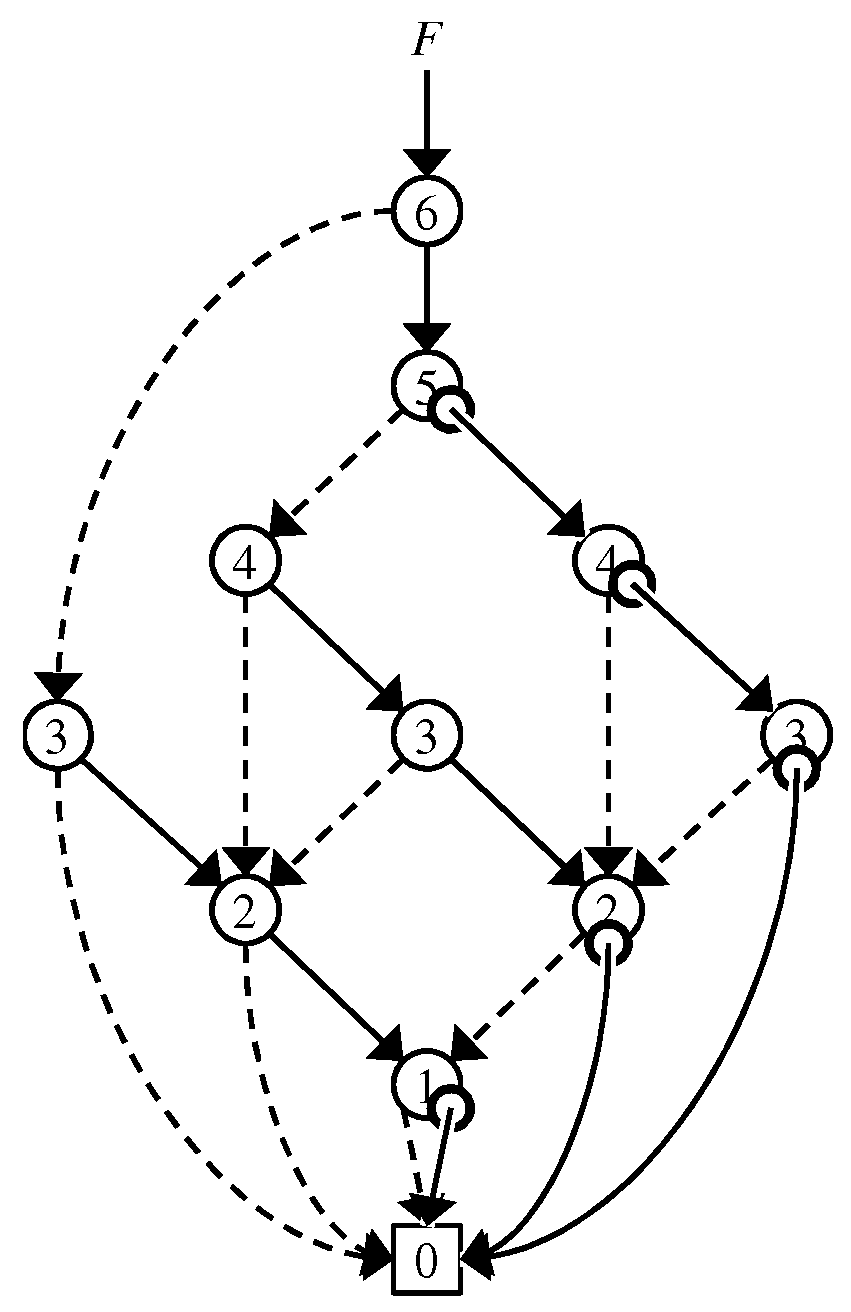
3. Data Structure
3.1. DenseZDD
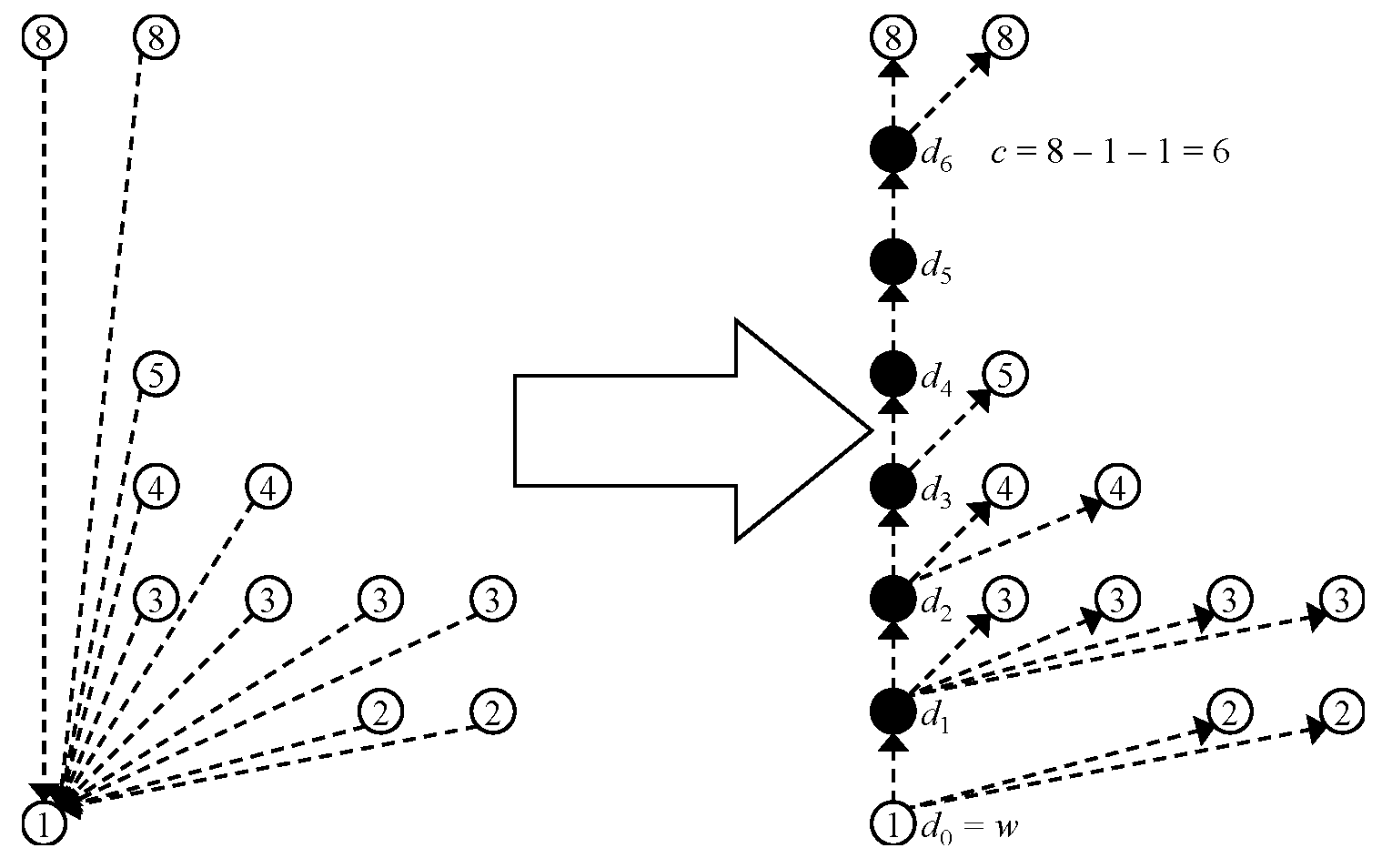
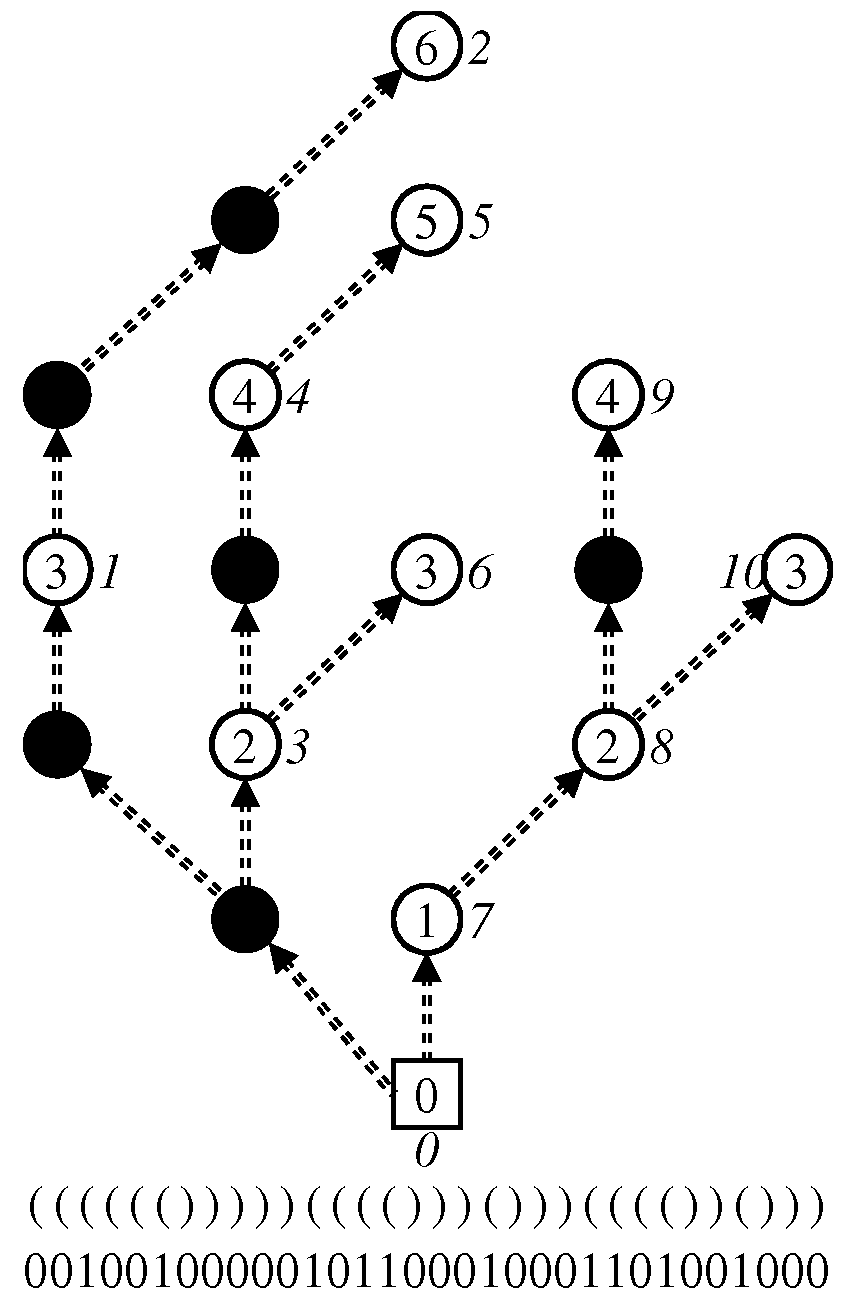
3.1.1. Zero-Edge Tree
3.1.2. Dummy Node Vector
3.1.3. One-Child Array
3.2. Convert Algorithm
| Algorithm 1 Compute_Preorder: Algorithm that computes the preorder rank of each node v. Sets of nodes are implemented by arrays or lists in this code. |
|
| Algorithm 2 Convert_ZDD_BitVectors (): Algorithm for obtaining the BP representation of the zero-edge tree, the dummy node vector, and the one-child array. |
Input: ZDD node v, list of parentheses , list of bits , list of integers
|
| Algorithm 3 Construct_DenseZDD (W: a set of root nodes of ZDD): Algorithm for constructing the DenseZDD from a source ZDD. |
Output: DenseZDD
|
4. ZDD Operations
4.1.
4.2.
4.3.
4.4.
4.5.
4.6.
| Algorithm 4 Count: Algorithm that computes the cardinality of the family of sets represented by nodes reachable from a node i. The cardinalities are stored in an integer array C of length m, where m is the number of ZDD nodes. The initial values of all the elements in C are 0. |
|
| Algorithm 5 Random_naive: Algorithm that returns a set uniformly and randomly chosen from the family of sets that is represented by a ZDD whose root is node i. Assume that Count has already been executed. The argument means whether or not the current family of sets has the empty set. If , this family has the empty set. |
|
| Algorithm 6 Random_bin: Algorithm that returns a set uniformly and randomly chosen from the family of sets represented by the ZDD whose root is node i. This algorithm chooses the index by binary search on nodes linked by 0-edges. |
|
5. Complexity Analysis
6. Hybrid Method
7. Other Decision Diagrams
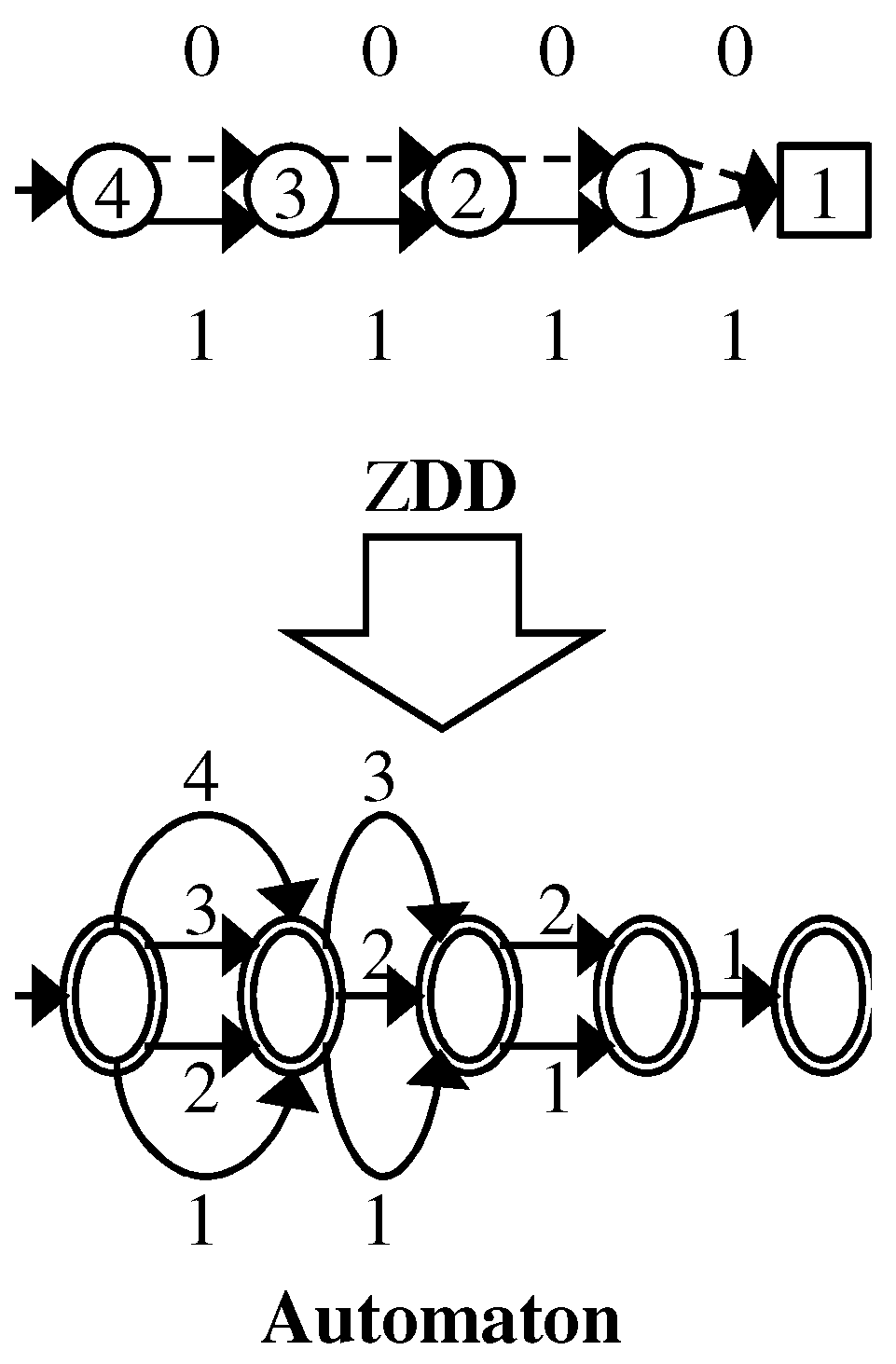
7.1. Sets of Strings
7.2. Boolean Functions
8. Experimental Results
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bryant, R.E. Graph-Based Algorithms for Boolean Function Manipulation. IEEE Trans. Comput. 1986, 100, 677–691. [Google Scholar] [CrossRef]
- Minato, S. Zero-Suppressed BDDs for Set Manipulation in Combinatorial Problems. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 1058–1066. [Google Scholar]
- Minato, S.; Uno, T.; Arimura, H. LCM over ZBDDs: Fast Generation of Very Large-Scale Frequent Itemsets Using a Compact Graph-Based Representation. In Proceedings of the Advances in Knowledge Discovery and Data Mining (PAKDD), Osaka, Japan, 20–23 May 2008; pp. 234–246. [Google Scholar]
- Minato, S.; Arimura, H. Frequent Pattern Mining and Knowledge Indexing Based on Zero-Suppressed BDDs. In Proceedings of the 5th International Workshop on Knowledge Discovery in Inductive Databases (KDID 2006), Berlin, Germany, 18 September 2006; pp. 152–169. [Google Scholar]
- Knuth, D.E. The Art of Computer Programming, Fascicle 1, Bitwise Tricks & Techniques; Binary Decision Diagrams; Addison-Wesley: Boston, MA, USA, 2009; Volume 4. [Google Scholar]
- Minato, S. SAPPORO BDD Package; Division of Computer Science, Hokkaido University: Sapporo, Japan, 2012; unreleased. [Google Scholar]
- Denzumi, S.; Kawahara, J.; Tsuda, K.; Arimura, H.; Minato, S.; Sadakane, K. DenseZDD: A Compact and Fast Index for Families of Sets. In Proceedings of the International Symposium on Experimental Algorithms 2014, Copenhagen, Denmark, 29 June–1 July 2014. [Google Scholar]
- Raman, R.; Raman, V.; Satti, S.R. Succinct indexable dictionaries with applications to encoding k-ary trees, prefix sums and multisets. ACM Trans. Algorithms 2007, 3, 43. [Google Scholar] [CrossRef]
- Navarro, G.; Sadakane, K. Fully-Functional Static and Dynamic Succinct Trees. ACM Trans. Algorithms 2014, 10, 16. [Google Scholar] [CrossRef]
- Minato, S.; Ishiura, N.; Yajima, S. Shared Binary Decision Diagram with Attributed Edges for Efficient Boolean function Manipulation. In Proceedings of the 27th ACM/IEEE Design Automation Conference, Orlando, FL, USA, 24–28 June 1990; pp. 52–57. [Google Scholar]
- Denzumi, S.; Yoshinaka, R.; Arimura, H.; Minato, S. Sequence binary decision diagram: Minimization, relationship to acyclic automata, and complexities of Boolean set operations. Discret. Appl. Math. 2016, 212, 61–80. [Google Scholar] [CrossRef]
- Minato, S. Z-Skip-Links for Fast Traversal of ZDDs Representing Large-Scale Sparse Datasets. In Proceedings of the European Symposium on Algorithms, Sophia Antipolis, France, 2–4 September 2013; pp. 731–742. [Google Scholar]
- Maruyama, S.; Nakahara, M.; Kishiue, N.; Sakamoto, H. ESP-index: A compressed index based on edit-sensitive parsing. J. Discret. Algorithms 2013, 18, 100–112. [Google Scholar] [CrossRef] [Green Version]
- Navarro, G. Compact Data Structures; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Elias, P. Universal codeword sets and representation of the integers. IEEE Trans. Inf. Theory 1975, 21, 194–203. [Google Scholar] [CrossRef]
- Okanohara, D.; Sadakane, K. Practical Entropy-Compressed Rank/Select Dictionary. In Proceedings of the Workshop on Algorithm Engineering and Experiments (ALENEX), New Orleans, LA, USA, 6 January 2007. [Google Scholar]
- Loekito, E.; Bailey, J.; Pei, J. A binary decision diagram based approach for mining frequent subsequences. Knowl. Inf. Syst. 2010, 24, 235–268. [Google Scholar] [CrossRef]
- Inoue, T.; Iwashita, H.; Kawahara, J.; Minato, S. Graphillion: Software library for very large sets of labeled graphs. Int. J. Softw. Tools Technol. Transf. 2016, 18, 57–66. [Google Scholar] [CrossRef]
- Bryant, R.E. Chain Reduction for Binary and Zero-Suppressed Decision Diagrams. In Proceedings of the Tools and Algorithms for the Construction and Analysis of Systems, Thessaloniki, Greece, 14–21 April 2018; pp. 81–98. [Google Scholar]
- Nishino, M.; Yasuda, N.; Minato, S.; Nagata, M. Zero-suppressed Sentential Decision Diagrams. In Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; pp. 272–277. [Google Scholar]
| Returns the index of node v. | |
| Returns the 0-child of node v. | |
| Returns the 1-child of node v. | |
| Generates (or makes a reference to) a node v | |
| with index i and two child nodes and . | |
| Returns a node with the index i reached by traversing only 0-edges from v. | |
| If such a node does not exist, it returns the 0-terminal node. | |
| Returns if , and returns otherwise. | |
| Returns . | |
| Returns a set uniformly and randomly. | |
| Returns u such that . | |
| Returns u such that . | |
| Returns v such that , for . |
| Data Set | n | #roots | #nodes | ||
|---|---|---|---|---|---|
| rect1x10000 | 10,000 | 10,000 | 10,000 | 1 | 10,001 |
| rect5x2000 | 10,000 | 1 | 10,001 | ||
| rect100x100 | 10,000 | 1 | 10,001 | ||
| rect2000x5 | 10,000 | 1 | 10,001 | ||
| rect10000x1 | 10,000 | 1 | 10,000 | 1 | 10,001 |
| randomjoin256 | 32,740 | 1 | 25,743 | ||
| randomjoin2048 | 32,765 | 1 | 375,959 | ||
| randomjoin8192 | 32,768 | 1 | |||
| randomjoin16384 | 32,768 | 1 | |||
| bddqueen13 | 169 | 73,712 | 958,256 | 1 | 204,782 |
| bddqueen14 | 196 | 365,596 | 1 | 911,421 | |
| bddqueen15 | 225 | 1 | |||
| T40I10D100K:0.001 | 925 | 1 | |||
| T40I10D100K:0.0005 | 933 | 1 | |||
| T40I10D100K:0.0001 | 942 | 1 | |||
| accidents:0.1 | 76 | 1 | 36,324 | ||
| accidents:0.05 | 106 | 1 | 183,144 | ||
| accidents:0.01 | 167 | 1 | |||
| chess:0.1 | 62 | 1 | |||
| chess:0.05 | 67 | 1 | |||
| chess:0.01 | 72 | 1 | |||
| connect:0.05 | 87 | 1 | 331,829 | ||
| connect:0.01 | 110 | 1 | |||
| connect:0.005 | 116 | 1 | |||
| 16-adder_col | 66 | 17 | |||
| C1908 | 66 | 25 | 133,379 | ||
| C3540 | 100 | 22 | |||
| C499 | 82 | 32 | 140,932 | ||
| C880 | 120 | 26 | 606,310 | ||
| comp | 64 | 196,606 | 3 | 589,783 | |
| my_adder | 66 | 655,287 | 17 | 884,662 |
| Data Set | Size (byte) | Comp. Ratio | ||||
|---|---|---|---|---|---|---|
| Z | DZ | DZ | DZ | DZ | ||
| rect1x10000 | 320,032 | 14,662 | 10,372 | 0.000 | 0.046 | 0.032 |
| rect5x2000 | 320,032 | 36,947 | 29,227 | 0.444 | 0.115 | 0.091 |
| rect100x100 | 320,032 | 38,014 | 29,648 | 0.498 | 0.119 | 0.093 |
| rect2000x5 | 320,032 | 38,078 | 32,100 | 0.500 | 0.119 | 0.100 |
| rect10000x1 | 320,032 | 38,078 | 34,048 | 0.500 | 0.119 | 0.106 |
| randomjoin256 | 823,760 | 792,703 | 279,719 | 0.978 | 0.962 | 0.340 |
| randomjoin2048 | 0.821 | 0.210 | 0.135 | |||
| randomjoin8192 | 0.424 | 0.139 | 0.115 | |||
| randomjoin16384 | 0.145 | 0.128 | 0.113 | |||
| bddqueen13 | 846,809 | 752,775 | 0.466 | 0.138 | 0.123 | |
| bddqueen14 | 0.510 | 0.153 | 0.136 | |||
| bddqueen15 | 0.558 | 0.171 | 0.151 | |||
| T40I10D100K:0.001 | 0.826 | 0.220 | 0.148 | |||
| T40I10D100K:0.0005 | 0.748 | 0.191 | 0.141 | |||
| T40I10D100K:0.0001 | 0.703 | 0.200 | 0.159 | |||
| accidents:0.1 | 125,440 | 117,714 | 0.083 | 0.108 | 0.101 | |
| accidents:0.05 | 672,553 | 634,169 | 0.079 | 0.115 | 0.108 | |
| accidents:0.01 | 0.089 | 0.135 | 0.128 | |||
| chess:0.1 | 0.098 | 0.127 | 0.120 | |||
| chess:0.05 | 0.098 | 0.131 | 0.124 | |||
| chess:0.01 | 0.118 | 0.135 | 0.127 | |||
| connect:0.05 | 0.206 | 0.122 | 0.112 | |||
| connect:0.01 | 0.204 | 0.133 | 0.124 | |||
| connect:0.005 | 0.202 | 0.133 | 0.124 | |||
| 16-adder_col | 0.124 | 0.127 | 0.122 | |||
| C1908 | 487,434 | 470,422 | 0.027 | 0.114 | 0.110 | |
| C3540 | 0.152 | 0.128 | 0.122 | |||
| C499 | 513,322 | 499,158 | 0.009 | 0.114 | 0.111 | |
| C880 | 0.305 | 0.129 | 0.120 | |||
| comp | 0.234 | 0.127 | 0.119 | |||
| my_adder | 0.399 | 0.133 | 0.122 | |||
| Data Set | Conversion Time (s) | Getnode Time (s) | ||||
|---|---|---|---|---|---|---|
| convert | const. | comp. | Z | DZ | DZ | |
| rect1x10000 | 0.007 | 0.009 | 0.008 | 0.001 | 0.001 | 0.005 |
| rect5x2000 | 0.006 | 0.015 | 0.011 | 0.000 | 0.001 | 0.006 |
| rect100x100 | 0.006 | 0.014 | 0.009 | 0.001 | 0.001 | 0.005 |
| rect2000x5 | 0.006 | 0.016 | 0.012 | 0.000 | 0.001 | 0.005 |
| rect10000x1 | 0.504 | 0.015 | 0.009 | 0.000 | 0.001 | 0.008 |
| randomjoin256 | 0.025 | 0.105 | 0.005 | 0.001 | 0.002 | 0.013 |
| randomjoin2048 | 0.254 | 0.263 | 0.001 | 0.036 | 0.037 | 0.189 |
| randomjoin8192 | 0.946 | 0.526 | 0.000 | 0.156 | 0.164 | 0.710 |
| randomjoin16384 | 1.463 | 0.692 | 0.010 | 0.235 | 0.278 | 1.123 |
| bddqueen13 | 0.175 | 0.087 | 0.003 | 0.009 | 0.017 | 0.159 |
| bddqueen14 | 0.926 | 0.415 | 0.019 | 0.059 | 0.074 | 0.692 |
| bddqueen15 | 6.217 | 2.438 | 0.142 | 0.426 | 0.402 | 3.498 |
| T40I10D100K:0.001 | 0.934 | 0.814 | 0.037 | 0.089 | 0.218 | 0.872 |
| T40I10D100K:0.0005 | 6.006 | 3.958 | 0.175 | 0.771 | 1.088 | 4.706 |
| T40I10D100K:0.0001 | 233.006 | 120.423 | 4.378 | 32.316 | 30.181 | 122.104 |
| accidents:0.1 | 0.026 | 0.040 | 0.023 | 0.002 | 0.005 | 0.033 |
| accidents:0.05 | 0.162 | 0.094 | 0.022 | 0.012 | 0.023 | 0.161 |
| accidents:0.01 | 5.901 | 1.949 | 0.075 | 0.785 | 0.657 | 4.568 |
| chess:0.1 | 1.149 | 0.455 | 0.016 | 0.142 | 0.145 | 1.130 |
| chess:0.05 | 3.319 | 1.263 | 0.085 | 0.471 | 0.414 | 2.895 |
| chess:0.01 | 5.829 | 2.408 | 0.098 | 0.847 | 0.729 | 4.662 |
| connect:0.05 | 0.289 | 0.136 | 0.002 | 0.023 | 0.037 | 0.227 |
| connect:0.01 | 2.287 | 0.945 | 0.033 | 0.297 | 0.268 | 1.625 |
| connect:0.005 | 4.377 | 1.716 | 0.080 | 0.579 | 0.491 | 2.996 |
| 16-adder_col | 1.318 | 0.585 | 0.010 | 0.119 | 0.137 | 1.821 |
| C1908 | 0.085 | 0.070 | 0.016 | 0.006 | 0.011 | 0.147 |
| C3540 | 1.319 | 0.563 | 0.017 | 0.098 | 0.119 | 1.488 |
| C499 | 0.084 | 0.073 | 0.010 | 0.007 | 0.010 | 0.140 |
| C880 | 0.491 | 0.249 | 0.005 | 0.034 | 0.048 | 0.551 |
| comp | 0.445 | 0.232 | 0.002 | 0.032 | 0.046 | 0.683 |
| my_adder | 0.743 | 0.375 | 0.009 | 0.061 | 0.083 | 0.930 |
| Data Set | Traverse Time (s) | Search Time (s) | ||||
|---|---|---|---|---|---|---|
| Z | DZ | DZ | Z | DZ | DZ | |
| rect1x10000 | 0.000 | 0.002 | 0.002 | 4.563 | 0.012 | 0.014 |
| rect5x2000 | 0.000 | 0.002 | 0.002 | 2.082 | 0.014 | 0.015 |
| rect100x100 | 0.000 | 0.001 | 0.002 | 0.092 | 0.009 | 0.011 |
| rect2000x5 | 0.001 | 0.002 | 0.003 | 0.006 | 0.009 | 0.021 |
| rect10000x1 | 0.001 | 0.003 | 0.015 | 0.002 | 0.009 | 0.070 |
| randomjoin256 | 0.001 | 0.004 | 0.005 | 0.470 | 0.013 | 0.013 |
| randomjoin2048 | 0.021 | 0.057 | 0.065 | 3.772 | 0.014 | 0.015 |
| randomjoin8192 | 0.088 | 0.176 | 0.201 | 14.568 | 0.019 | 0.020 |
| randomjoin16384 | 0.144 | 0.269 | 0.306 | 25.244 | 0.016 | 0.016 |
| bddqueen13 | 0.013 | 0.054 | 0.237 | 0.014 | 0.005 | 0.007 |
| bddqueen14 | 0.068 | 0.259 | 0.998 | 0.015 | 0.005 | 0.006 |
| bddqueen15 | 0.420 | 1.421 | 4.778 | 0.016 | 0.005 | 0.006 |
| T40I10D100K:0.001 | 0.054 | 0.222 | 0.298 | 0.003 | 0.002 | 0.003 |
| T40I10D100K:0.0005 | 0.314 | 1.210 | 1.606 | 0.003 | 0.002 | 0.002 |
| T40I10D100K:0.0001 | 11.615 | 42.730 | 55.085 | 0.004 | 0.001 | 0.002 |
| accidents:0.1 | 0.002 | 0.007 | 0.028 | 0.003 | 0.000 | 0.000 |
| accidents:0.05 | 0.011 | 0.038 | 0.150 | 0.003 | 0.000 | 0.000 |
| accidents:0.01 | 0.369 | 1.165 | 4.507 | 0.003 | 0.000 | 0.000 |
| chess:0.1 | 0.075 | 0.251 | 1.000 | 0.003 | 0.000 | 0.000 |
| chess:0.05 | 0.218 | 0.707 | 2.640 | 0.003 | 0.000 | 0.000 |
| chess:0.01 | 0.394 | 1.276 | 3.911 | 0.003 | 0.000 | 0.000 |
| connect:0.05 | 0.022 | 0.069 | 0.169 | 0.003 | 0.000 | 0.000 |
| connect:0.01 | 0.169 | 0.492 | 1.219 | 0.003 | 0.000 | 0.000 |
| connect:0.005 | 0.316 | 0.906 | 2.250 | 0.003 | 0.000 | 0.000 |
| 16-adder_col | 0.090 | 0.340 | 2.054 | 0.053 | 0.002 | 0.018 |
| C1908 | 0.007 | 0.030 | 0.174 | 0.169 | 0.221 | 1.851 |
| C3540 | 0.085 | 0.358 | 2.162 | 0.072 | 0.123 | 1.017 |
| C499 | 0.007 | 0.031 | 0.171 | 0.101 | 0.145 | 0.988 |
| C880 | 0.033 | 0.147 | 0.815 | 0.081 | 0.159 | 1.331 |
| comp | 0.035 | 0.138 | 0.956 | 0.010 | 0.010 | 0.085 |
| my_adder | 0.066 | 0.185 | 0.931 | 0.054 | 0.001 | 0.003 |
| Data Set | Count Time (sec) | Sample Time (sec) | ||||||
|---|---|---|---|---|---|---|---|---|
| D | DZ | DZ | Z | DZ (naive) | DZ (bin) | DZ (naive) | DZ (bin) | |
| rect1x10000 | 0.002 | 0.002 | 0.003 | 5.375 | 4.813 | 0.014 | 5.527 | 0.014 |
| rect5x2000 | 0.001 | 0.002 | 0.003 | 9.125 | 5.126 | 0.063 | 4.825 | 0.062 |
| rect100x100 | 0.002 | 0.003 | 0.003 | 10.150 | 5.155 | 0.816 | 5.176 | 0.812 |
| rect2000x5 | 0.004 | 0.005 | 0.007 | 8.250 | 5.765 | 7.142 | 5.773 | 7.171 |
| rect10000x1 | 0.001 | 0.004 | 0.016 | 0.001 | 0.011 | 0.012 | 0.074 | 0.075 |
| randomjoin256 | 0.003 | 0.007 | 0.007 | 1.035 | 0.535 | 0.036 | 0.564 | 0.035 |
| randomjoin2048 | 0.067 | 0.091 | 0.102 | 7.650 | 4.254 | 0.048 | 4.056 | 0.048 |
| randomjoin8192 | 0.256 | 0.305 | 0.336 | 22.989 | 16.830 | 0.056 | 15.663 | 0.056 |
| randomjoin16384 | 0.393 | 0.455 | 0.508 | 31.561 | 24.036 | 0.058 | 23.357 | 0.059 |
| bddqueen13 | 0.029 | 0.077 | 0.265 | 0.037 | 0.026 | 0.026 | 0.026 | 0.026 |
| bddqueen14 | 0.149 | 0.380 | 1.146 | 0.042 | 0.029 | 0.031 | 0.030 | 0.031 |
| bddqueen15 | 0.876 | 2.226 | 5.664 | 0.047 | 0.033 | 0.035 | 0.034 | 0.035 |
| T40I10D100K:0.001 | 0.187 | 0.339 | 0.418 | 0.947 | 0.338 | 0.047 | 0.323 | 0.045 |
| T40I10D100K:0.0005 | 1.153 | 1.925 | 2.338 | 0.954 | 0.479 | 0.049 | 0.495 | 0.047 |
| T40I10D100K:0.0001 | 36.329 | 67.113 | 79.435 | 0.978 | 0.576 | 0.061 | 0.572 | 0.066 |
| accidents:0.1 | 0.006 | 0.011 | 0.033 | 0.077 | 0.077 | 0.036 | 0.075 | 0.033 |
| accidents:0.05 | 0.031 | 0.059 | 0.175 | 0.108 | 0.106 | 0.040 | 0.105 | 0.040 |
| accidents:0.01 | 0.957 | 2.066 | 5.474 | 0.169 | 0.165 | 0.050 | 0.164 | 0.048 |
| chess:0.1 | 0.208 | 0.413 | 1.181 | 0.062 | 0.061 | 0.050 | 0.061 | 0.050 |
| chess:0.05 | 0.591 | 1.188 | 3.158 | 0.067 | 0.065 | 0.056 | 0.066 | 0.057 |
| chess:0.01 | 1.061 | 2.115 | 4.817 | 0.073 | 0.067 | 0.073 | 0.068 | 0.071 |
| connect:0.05 | 0.059 | 0.108 | 0.212 | 0.088 | 0.085 | 0.066 | 0.084 | 0.064 |
| connect:0.01 | 0.435 | 0.828 | 1.575 | 0.111 | 0.105 | 0.076 | 0.105 | 0.075 |
| connect:0.005 | 0.804 | 1.557 | 2.925 | 0.118 | 0.109 | 0.078 | 0.111 | 0.077 |
| 16-adder_col | 0.224 | 0.505 | 2.260 | 0.167 | 0.246 | 0.474 | 0.246 | 0.483 |
| C1908 | 0.016 | 0.045 | 0.191 | 0.259 | 0.658 | 1.386 | 0.662 | 1.398 |
| C3540 | 0.199 | 0.530 | 2.386 | 0.150 | 0.349 | 0.715 | 0.352 | 0.727 |
| C499 | 0.017 | 0.045 | 0.189 | 0.455 | 1.241 | 2.500 | 1.250 | 2.529 |
| C880 | 0.079 | 0.214 | 0.904 | 0.084 | 0.233 | 0.480 | 0.238 | 0.485 |
| comp | 0.081 | 0.199 | 1.038 | 0.035 | 0.055 | 0.109 | 0.055 | 0.109 |
| my_adder | 0.135 | 0.278 | 1.043 | 0.081 | 0.232 | 0.416 | 0.234 | 0.424 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Denzumi, S.; Kawahara, J.; Tsuda, K.; Arimura, H.; Minato, S.-i.; Sadakane, K. DenseZDD: A Compact and Fast Index for Families of Sets †. Algorithms 2018, 11, 128. https://doi.org/10.3390/a11080128
Denzumi S, Kawahara J, Tsuda K, Arimura H, Minato S-i, Sadakane K. DenseZDD: A Compact and Fast Index for Families of Sets †. Algorithms. 2018; 11(8):128. https://doi.org/10.3390/a11080128
Chicago/Turabian StyleDenzumi, Shuhei, Jun Kawahara, Koji Tsuda, Hiroki Arimura, Shin-ichi Minato, and Kunihiko Sadakane. 2018. "DenseZDD: A Compact and Fast Index for Families of Sets †" Algorithms 11, no. 8: 128. https://doi.org/10.3390/a11080128
APA StyleDenzumi, S., Kawahara, J., Tsuda, K., Arimura, H., Minato, S.-i., & Sadakane, K. (2018). DenseZDD: A Compact and Fast Index for Families of Sets †. Algorithms, 11(8), 128. https://doi.org/10.3390/a11080128




