Sliding Suffix Tree
Abstract
1. Introduction and Related Work
2. Notation and Preliminaries
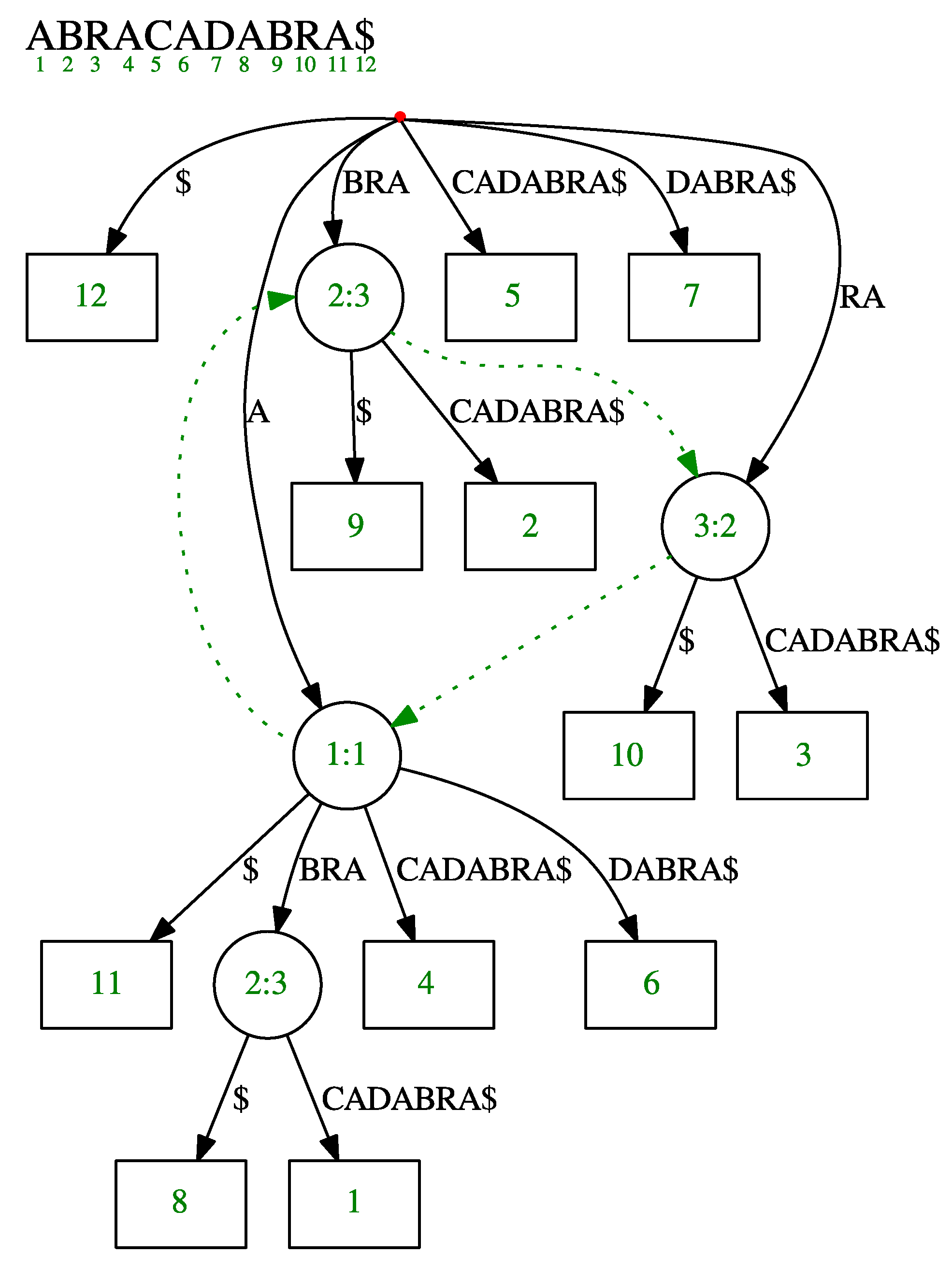
2.1. Suffix Tree
2.2. Ukkonen’s Online Suffix Tree Construction Algorithm
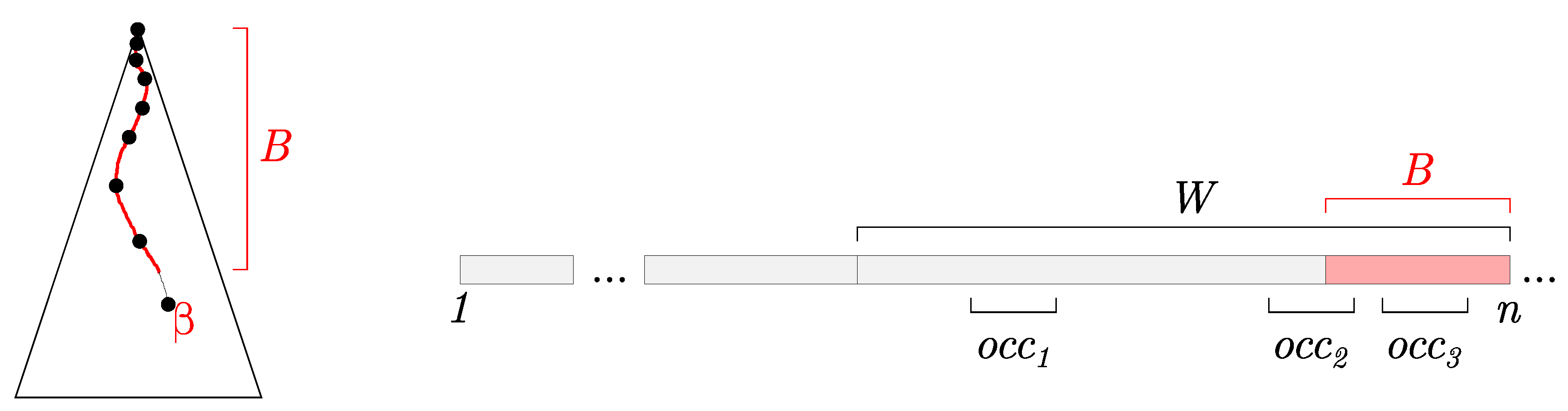
- Implicit buffer B, which corresponds to the longest repeated suffix of the text processed so far,
- the active node , which represents a node where we end up by navigating B in the suffix tree constructed so far, i.e., B is a prefix of a string spelled out by .
- Queries: When performing a query, we need to report the occurrences, both in the partially constructed suffix tree and in B.
- Maintenance: The original Ukkonen’s algorithm supports adding a new character to the indexed text. When a window is shifted, we also remove the oldest (longest) suffix from the text.
3. Sliding Suffix Tree
- find(W, Q) — returns all positions of the query string Q in W (obviously, .
- shift(W, c) — appends a character c to W and removes the oldest character from W.
3.1. Queries
| Algorithm 1: Query procedure in the sliding suffix tree. |
| Input: Query Q, Unfinalized suffix tree , Active node , Buffer B, Current position in a stream n Output: Positions of Q in the window  |
Time Complexity
3.2. Maintenance
Time Complexity
4. Conclusions and Open Problems
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Navarro, G.; Mäkinen, V. Compressed full-text indexes. ACM Comput. Surv. 2007, 39, 2. [Google Scholar] [CrossRef]
- Abouelhoda, M.I.; Kurtz, S.; Ohlebusch, E. Replacing suffix trees with enhanced suffix arrays. J. Discrete Algorithms 2004, 2, 53–86. [Google Scholar] [CrossRef]
- Grossi, R.; Gupta, A.; Vitter, J.S. High-Order Entropy-Compressed Text Indexes. In Proceedings of the 14th Annual ACM-SIAM Symposium on Discrete Algorithms, Baltimore, MD, USA, 12–14 January 2003; Volume 2068, pp. 841–850. [Google Scholar]
- Knuth, D.; Morris, J., Jr.; Pratt, V. Fast Pattern Matching in Strings. SIAM J. Comput. 1977, 6, 323–350. [Google Scholar] [CrossRef]
- Boyer, R.S.; Moore, J.S. A fast string searching algorithm. Commun. ACM 1977, 20, 762–772. [Google Scholar] [CrossRef]
- Karp, R.M.; Rabin, M.O. Efficient randomized pattern-matching algorithms. IBM J. Res. Dev. 1987, 31, 249–260. [Google Scholar] [CrossRef]
- Ergun, F.; Jowhari, H.; Sağlam, M. Periodicity in Streams. In Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques; Serna, M., Shaltiel, R., Jansen, K., Rolim, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 545–559. [Google Scholar]
- Breslauer, D.; Galil, Z. Real-Time Streaming String-Matching. In Combinatorial Pattern Matching; Giancarlo, R., Manzini, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 162–172. [Google Scholar]
- Casey, E. Handbook of Digital Forensics and Investigation, 2nd ed.; Elsevier Academic Press: Burlington, MA, USA, 2009. [Google Scholar]
- Cox, R. Regular Expression Matching: the Virtual Machine Approach. 2009. Available online: https://swtch.com/rsc/regexp/ (accessed on 2nd August 2018).
- Stewart, J.; Uckelman, J. Searching Massive Data Streams Using Multipattern Regular Expressions. In Advances in Digital Forensics VII; Peterson, G., Shenoi, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 49–63. [Google Scholar]
- Agravat, D.; Vaishnav, U.; Swadas, P.B. Modified Ant Miner for Intrusion Detection. In Proceedings of the 2010 Second International Conference on Machine Learning and Computing, Bangalore, India, 9–11 Febuary 2010; pp. 228–232. [Google Scholar]
- Kukielka, P.; Kotulski, Z. Analysis of neural networks usage for detection of a new attack in IDS. Ann. UMCS Inform. 2010, 10, 51–59. [Google Scholar] [CrossRef]
- Fiala, E.R.; Greene, D.H. Data compression with finite windows. Commun. ACM 1989, 32, 490–505. [Google Scholar] [CrossRef]
- McCreight, E.M. A Space-Economical Suffix Tree Construction Algorithm. J. ACM 1976, 23, 262–272. [Google Scholar] [CrossRef]
- Larsson, N.J. Structures of String Matching and Data Compression. Ph.D. Thesis, Lund University, Lund, Sweden, 1999. [Google Scholar]
- Ukkonen, E. On-Line Construction of Suffix Trees. Algorithmica 1995, 14, 249–260. [Google Scholar] [CrossRef]
- Senft, M. Suffix tree for a sliding window: An overview. In Week of Doctoral Students; Šafránková, J., Ed.; Matfyzpress: Prague, Czech Republic, 2005; pp. 41–46. [Google Scholar]
- Blumer, A.; Blumer, J.; Haussler, D.; McConnell, R.; Ehrenfeucht, A. Complete Inverted Files for Efficient Text Retrieval and Analysis. J. ACM 1987, 34, 578–595. [Google Scholar] [CrossRef]
- Inenaga, S.; Hoshino, H.; Shinohara, A.; Takeda, M.; Arikawa, S.; Mauri, G.; Pavesi, G. On-line construction of compact directed acyclic word graphs. Discrete Appl. Math. 2005, 146, 156–179. [Google Scholar] [CrossRef]
- Inenaga, S.; Shinohara, A.; Takeda, M.; Arikawa, S. Compact directed acyclic word graphs for a sliding window. J. Discrete Algorithms 2004, 2, 33–51. [Google Scholar] [CrossRef]
- Ferreira, A.; Oliveira, A.; Figueiredo, M. On the Use of Suffix Arrays for Memory-Efficient Lempel-Ziv Data Compression. In Proceedings of the 2009 Data Compression Conference, Snowbird, UT, USA, 16–18 March 2009; p. 444. [Google Scholar]
- Ferreira, A.; Oliveira, A.; Figueiredo, M. Sliding Window Update Using Suffix Arrays. In Proceedings of the 2011 Data Compression Conference, Snowbird, UT, USA, 29–31 March 2011; p. 456. [Google Scholar]
- Salson, M.; Lecroq, T.; Léonard, M.; Mouchard, L. A four-stage algorithm for updating a Burrows–Wheeler transform. Theor. Comput. Sci. 2009, 410, 4350–4359. [Google Scholar] [CrossRef]
- Farach-Colton, M.; Ferragina, P.; Muthukrishnan, S. On the sorting-complexity of suffix tree construction. J. ACM 2000, 47, 987–1011. [Google Scholar] [CrossRef]
- Barsky, M.; Stege, U.; Thomo, A.; Upton, C. Suffix trees for very large genomic sequences. In Proceeding of the 18th ACM conference on Information and knowledge management - CIKM ’09, Hong Kong, China, 2–6 November 2009; ACM Press: New York, NY, USA, 2009; p. 1417. [Google Scholar]
- Mansour, E.; Allam, A.; Skiadopoulos, S.; Kalnis, P. ERA: Efficient serial and parallel suffix tree construction for very long strings. Proc. VLDB Endow. 2011, 5, 49–60. [Google Scholar] [CrossRef]
- Comin, M.; Farreras, M. Efficient parallel construction of suffix trees for genomes larger than main memory. In Proceedings of the 20th European MPI Users’ Group Meeting on EuroMPI ’13, Madrid, Spain, 15–18 September 2013; ACM Press: New York, NY, USA, 2013; p. 211. [Google Scholar]
- Shun, J.; Blelloch, G.E. A simple parallel cartesian tree algorithm and its application to parallel suffix tree construction. ACM Trans. Parallel Comput. 2014, 1, 1–20. [Google Scholar] [CrossRef]
- Jekovec, M.; Brodnik, A. Parallel Query in the Suffix Tree; Technical Report; University of Ljubljana, Faculty of Computer and Information Science: Ljubljana, Slovenia, 2015. [Google Scholar]
- Christiansen, A.R.; Farach-Colton, M. Parallel Lookups in String Indexes. In Proceedings of the String Processing and Information Retrieval: 23rd International Symposium, SPIRE 2016, Beppu, Japan, 18–20 October 2016; Inenaga, S., Sadakane, K., Sakai, T., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 61–67. [Google Scholar]
- Sadakane, K. Compressed Suffix Trees with Full Functionality. Theory Comput. Syst. 2007, 41, 589–607. [Google Scholar] [CrossRef]
- Brodal, G.S.; Fagerberg, R. Cache-oblivious string dictionaries. In Proceedings of the 17th annual ACM-SIAM symposium on Discrete algorithm, SODA ’06, Miami, Florida, 22–26 January 2006; ACM Press: New York, NY, USA, 2006; pp. 581–590. [Google Scholar]
- Brodnik, A.; Jekovec, M. Sliding Suffix Tree; Technical Report; University of Ljubljana, Faculty of Computer and Information Science: Ljubljana, Slovenia, 2018. [Google Scholar]
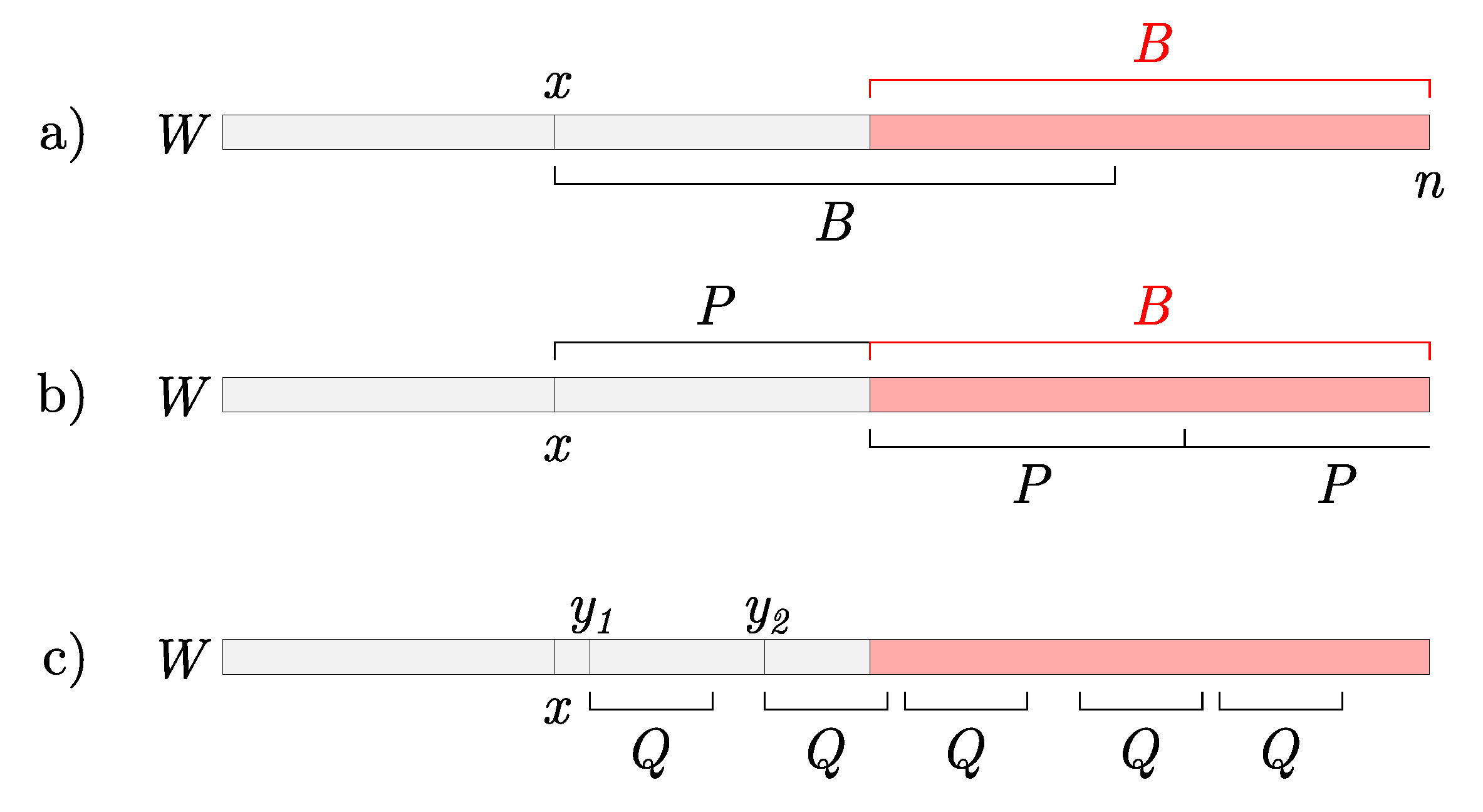

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brodnik, A.; Jekovec, M. Sliding Suffix Tree. Algorithms 2018, 11, 118. https://doi.org/10.3390/a11080118
Brodnik A, Jekovec M. Sliding Suffix Tree. Algorithms. 2018; 11(8):118. https://doi.org/10.3390/a11080118
Chicago/Turabian StyleBrodnik, Andrej, and Matevž Jekovec. 2018. "Sliding Suffix Tree" Algorithms 11, no. 8: 118. https://doi.org/10.3390/a11080118
APA StyleBrodnik, A., & Jekovec, M. (2018). Sliding Suffix Tree. Algorithms, 11(8), 118. https://doi.org/10.3390/a11080118




