Efficient Model-Based Object Pose Estimation Based on Multi-Template Tracking and PnP Algorithms
Abstract
1. Introduction
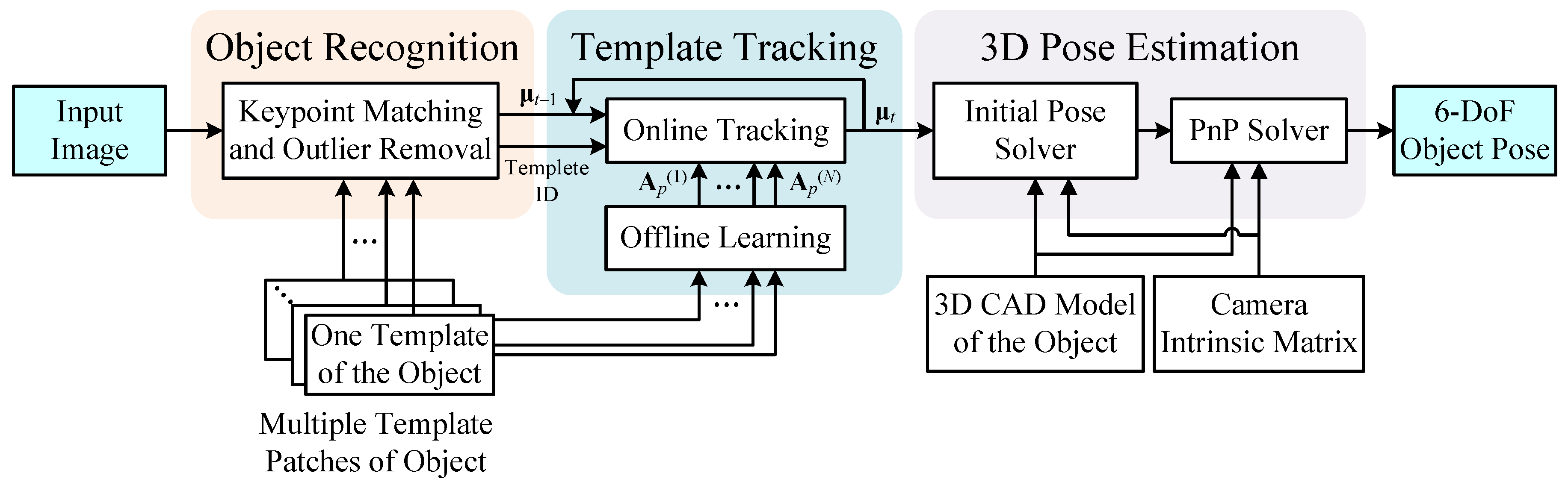
2. System Framework
3. Multi-Template Tracking Algorithm
3.1. Offline Learning
3.2. Online Tracking
4. Model-Based 3D Pose Estimation
4.1. Initial Pose Solver
4.2. PnP Solver
5. Experimental Results
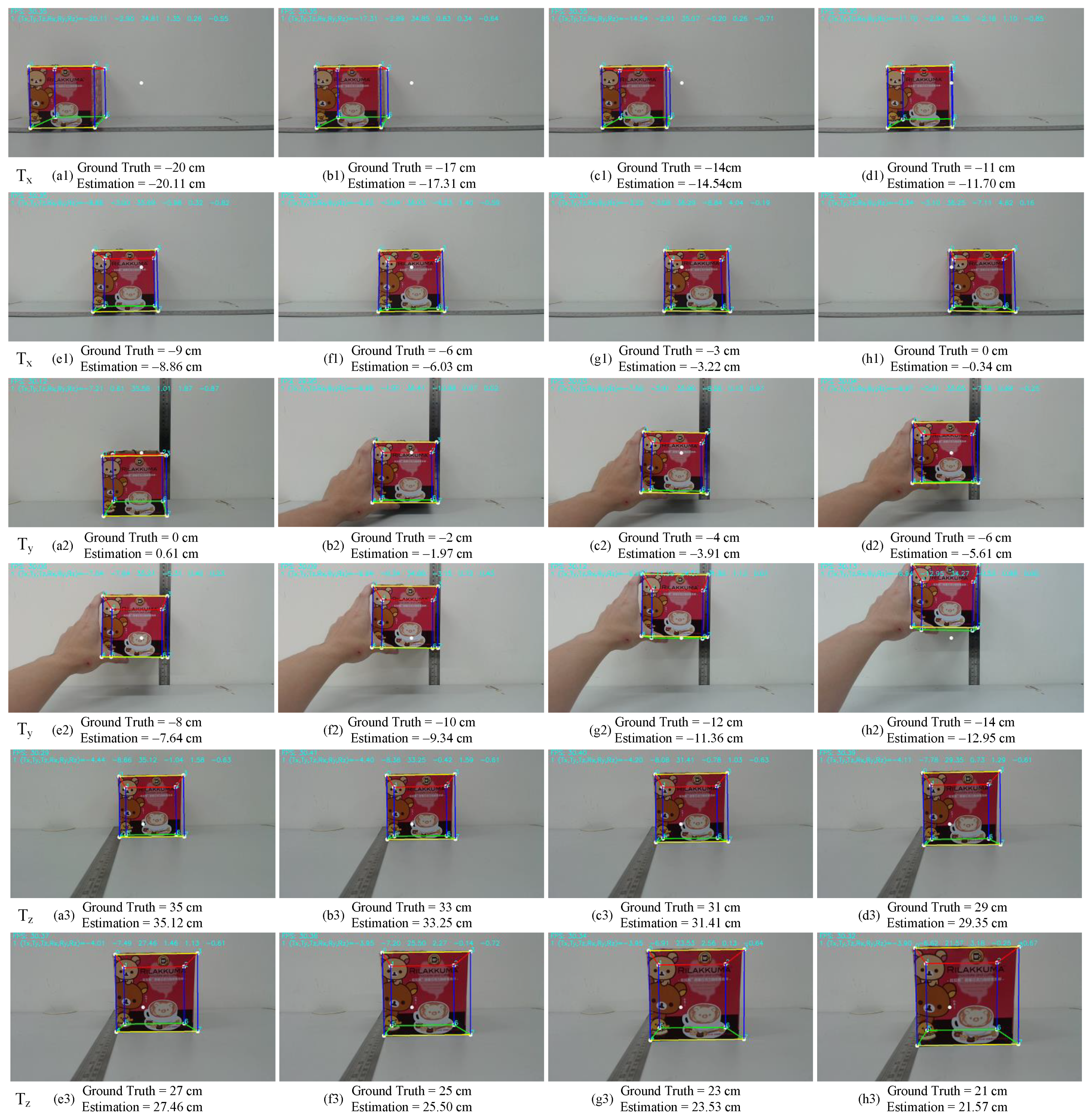
5.1. Pose Estimation Results
5.2. Quantitative Evaluation
5.3. Computational Efficiency
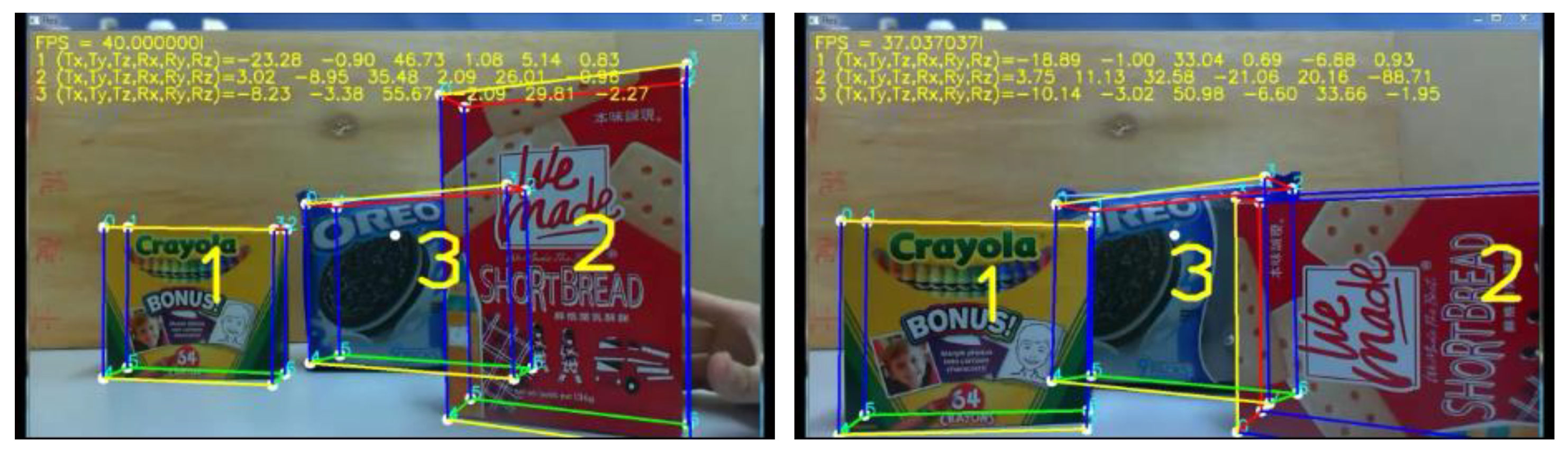
5.4. Multi-Object Pose Tracking
6. Conclusions and Future Work
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Gool, V.L. Speeded-up robust features (SURF). Compu. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Calonder, M.; Lepetit, V.; Özuysal, M.; Trzcinski, T.; Strecha, C.; Fua, P. BRIEF: Computing a local binary descriptor very fast. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1281–1298. [Google Scholar] [CrossRef] [PubMed]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT and SURF. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Lepetit, V.; Lagger, P.; Fua, P. Randomized trees for real-time keypoint recognition. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005. [Google Scholar]
- Lepetit, V.; Fua, P. Keypoint recognition using randomized trees. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1465–1479. [Google Scholar] [CrossRef] [PubMed]
- Decker, P.; Paulus, D. Model based pose estimation using SURF. In Proceedings of the 10th Asian Conference on Computer Vision, Queenstown, New Zealand, 8–12 November 2010. [Google Scholar]
- Choi, C.; Christensen, H.I. Real-time 3D model-based tracking using edge and keypoint features for robotic manipulation. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010. [Google Scholar]
- Harris, C. Tracking with Rigid Objects; MIT Press: Massachusetts, MA, USA, 1992. [Google Scholar]
- Zhang, Y.; Li, X.; Liu, H.; Shang, Y. Probabilistic approach for maximum likelihood estimation of pose using lines. IET Comput. Vis. 2016, 10, 475–482. [Google Scholar] [CrossRef]
- Tsai, C.-Y.; Wang, W.-Y.; Tsai, S.-H. 3D object pose tracking using a novel model-based contour fitting algorithm. ICIC Express Lett. 2016, 10, 563–568. [Google Scholar]
- Tsai, C.-Y.; Tsai, S.-H. Simultaneous 3D object recognition and pose estimation based on RGB-D images. IEEE Access. 2018, 6, 28859–28869. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Sturm, P. Algorithms for plane-based pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hilton Head Island, SC, USA, 15 June 2000. [Google Scholar]
- Collins, T.; Durou, J.-D.; Gurdjos, P.; Bartoli, A. Single-view perspective shape-from-texture with focal length estimation: A piecewise affine approach. In Proceedings of the 5th International Symposium on 3D Data Processing, Visualization, and Transmission, Paris, France, 17–20 May 2010. [Google Scholar]
- Simon, G.; Fitzgibbon, A.W.; Zisserman, A. Markerless tracking using planar structures in the scene. In Proceedings of the IEEE and ACM International Symposium on Augmented Reality, Munich, Germany, 5–6 October 2000. [Google Scholar]
- Hager, G.D.; Belhumeur, P.N. Efficient region tracking with parametric models of geometry and illumination. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1025–1039. [Google Scholar] [CrossRef]
- Buenaposada, J.M.; Baumela, L. Real-time tracking and estimation of plane pose. In Proceedings of the IEEE International Conference on Pattern Recognition, Quebec, QC, Canada, 11–15 August 2002. [Google Scholar]
- Jurie, F.; Dhome, M. Hyperplane approximation for template matching. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 996–1000. [Google Scholar] [CrossRef]
- Zheng, Q.; Wang, Y.; Heng, P.A. Online robust image alignment via subspace learning from gradient orientations. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Tjaden, H.; Schwanecke, U.; Schömer, E. Real-time monocular pose estimation of 3D objects using temporally consistent local color histograms. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Chang, C.-H.; Chou, C.-N.; Chang, E.Y. CLKN: Cascaded Lucas-Kanade networks for image alignment. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Ha, H.; Rameau, F.; Kweon, I.S. 6-DOF direct homography tracking with extended Kalman filter. In Proceedings of the 7th Pacific-Rim Symposium, PSIVT 2015, Auckland, New Zealand, 25–27 November 2015; Bräunl, T., McCane, B., Rivera, M., Yu, X., Eds.; Lecture Notes in Computer Science. Volume 9431, pp. 447–460. [Google Scholar]
- A GPU Implementation of David Lowe’s Scale Invariant Feature Transform. Available online: https://github.com/pitzer/SiftGPU (accessed on 11 August 2018).
- Tsai, C.-Y.; Huang, C.-H.; Tsao, A.-H. Graphics processing unit-accelerated multi-resolution exhaustive search algorithm for real-time keypoint descriptor matching in high-dimensional spaces. IET Comput. Vis. 2016, 10, 212–219. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Holzer, S.; Ilic, S.; Tan, D.; Pollefeys, M.; Navab, N. Efficient learning of linear predictors for template tracking. Int. J. Comput. Vis. 2015, 111, 12–28. [Google Scholar] [CrossRef]
- Crivellaro, A.; Fau, P.; Lepetit, V. Dense Methods for Image Alignment with an Application to 3D Tracking. Available online: https://infoscience.epfl.ch/record/197866/files/denseMethods2014.pdf (accessed on 11 August 2018).
- Collins, T.; Bartoli, A. Infinitesimal plane-based pose estimation. Int. J. Comput. Vis. 2014, 109, 252–286. [Google Scholar] [CrossRef]
- NVIDIA’s Tesla C2050 Board Specification. Available online: http://www.nvidia.com/docs/io/43395/tesla_c2050_board_specification.pdf (accessed on 11 August 2018).
- Experimental Result of 3d Pose Tracking of Multiple Objects. Available online: https://www.youtube.com/watch?v=wBEHEQMFer4 (accessed on 11 August 2018).
- Experimental Result of 3d Pose Tracking of a Single Object. Available online: https://www.youtube.com/watch?v=-uVUbBIPAH4 (accessed on 11 August 2018).
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]



| Estimation Error | ||||||
|---|---|---|---|---|---|---|
| Unit | cm | Degree | ||||
| eTx | eTy | eTz | eRx | eRy | eRz | |
| (a) | 0.0121 | 0.3721 | 0.0144 | 2.1025 | 2.1609 | 0.0100 |
| (b) | 0.0961 | 0.0009 | 0.0625 | 2.9241 | 3.5344 | 0.3844 |
| (c) | 0.2916 | 0.0081 | 0.1681 | 0.0676 | 2.1609 | 0.0225 |
| (d) | 0.4900 | 0.1521 | 0.1225 | 0.2401 | 0.0961 | 0.0144 |
| (e) | 0.0196 | 0.1296 | 0.2116 | 0.0841 | 0.5476 | 0.0729 |
| (f) | 0.0009 | 0.4356 | 0.2500 | 0.1849 | 2.2801 | 0.0729 |
| (g) | 0.0484 | 0.4096 | 0.2809 | 0.4225 | 1.3225 | 0.7744 |
| (h) | 0.1156 | 1.0816 | 0.3249 | 0.4900 | 1.0000 | 0.4225 |
| Average | 0.1343 | 0.3237 | 0.1794 | 0.8145 | 1.6378 | 0.2218 |
| Stage | Object Recognition | Template Tracking | 3D Pose Estimation | ||
|---|---|---|---|---|---|
| Process | Keypoint extraction | Keypoint matching | Tracker initialization | Template tracking | Initial Pose Solver and PnP Solver |
| Average Time | 65 ms | 53 ms | 3.85 ms | 0.39 ms | 0.70 ms |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, C.-Y.; Hsu, K.-J.; Nisar, H. Efficient Model-Based Object Pose Estimation Based on Multi-Template Tracking and PnP Algorithms. Algorithms 2018, 11, 122. https://doi.org/10.3390/a11080122
Tsai C-Y, Hsu K-J, Nisar H. Efficient Model-Based Object Pose Estimation Based on Multi-Template Tracking and PnP Algorithms. Algorithms. 2018; 11(8):122. https://doi.org/10.3390/a11080122
Chicago/Turabian StyleTsai, Chi-Yi, Kuang-Jui Hsu, and Humaira Nisar. 2018. "Efficient Model-Based Object Pose Estimation Based on Multi-Template Tracking and PnP Algorithms" Algorithms 11, no. 8: 122. https://doi.org/10.3390/a11080122
APA StyleTsai, C.-Y., Hsu, K.-J., & Nisar, H. (2018). Efficient Model-Based Object Pose Estimation Based on Multi-Template Tracking and PnP Algorithms. Algorithms, 11(8), 122. https://doi.org/10.3390/a11080122







