Time Series Forecasting Using a Two-Level Multi-Objective Genetic Algorithm: A Case Study of Maintenance Cost Data for Tunnel Fans
Abstract
1. Introduction
2. Materials and Methods
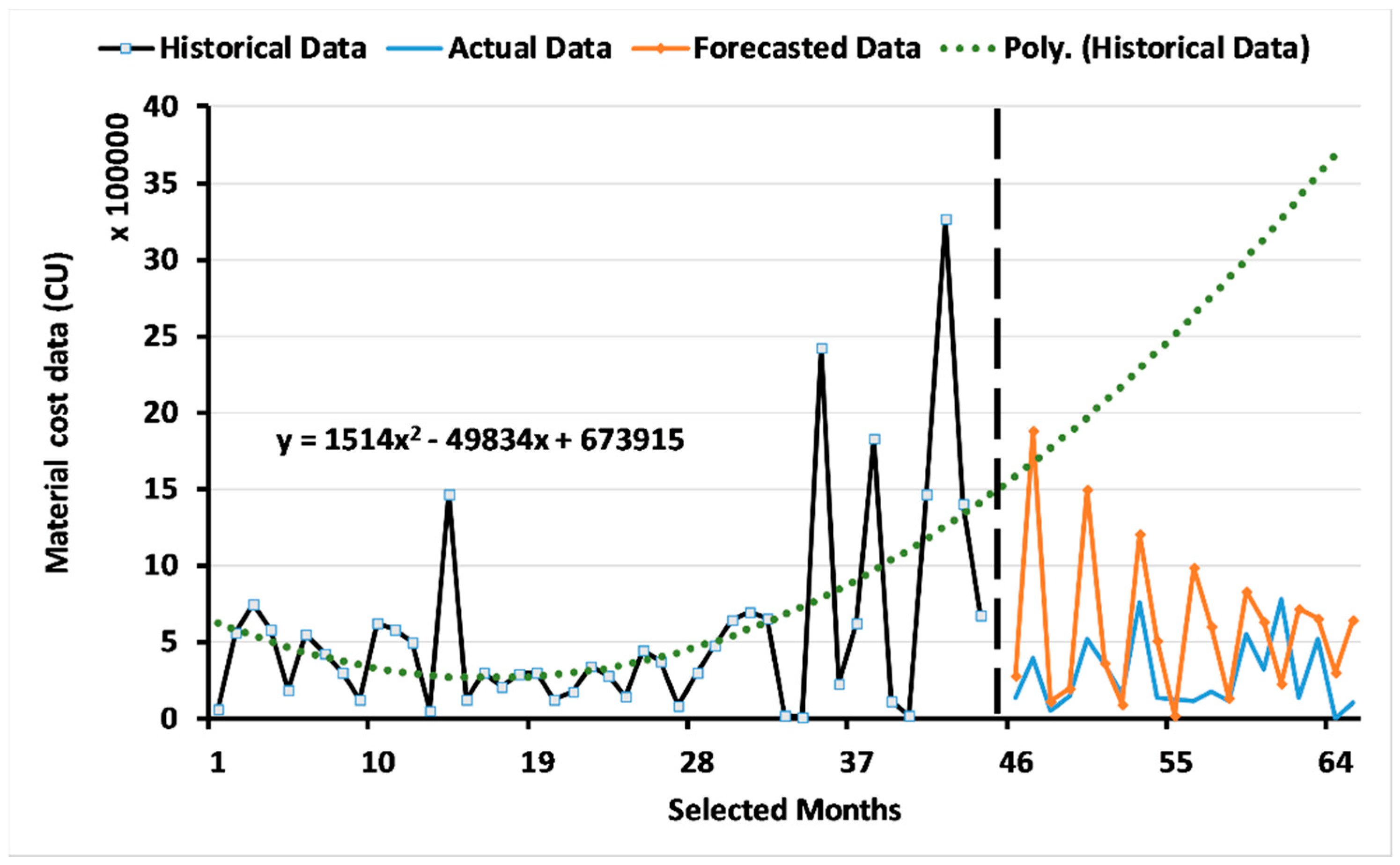
2.1. Data Collection
2.2. The ARIMA Model
- : the actual data over time;
- : the mean value of the time series data;
- : the number of autoregressive cut-off lags;
- : the number of differences calculated with the equation
- : the number of cut-off lags of the moving average process;
- : autoregressive coefficients (AR);
- : moving average coefficients (MA);
- : time
- : the white noise of the time series data.
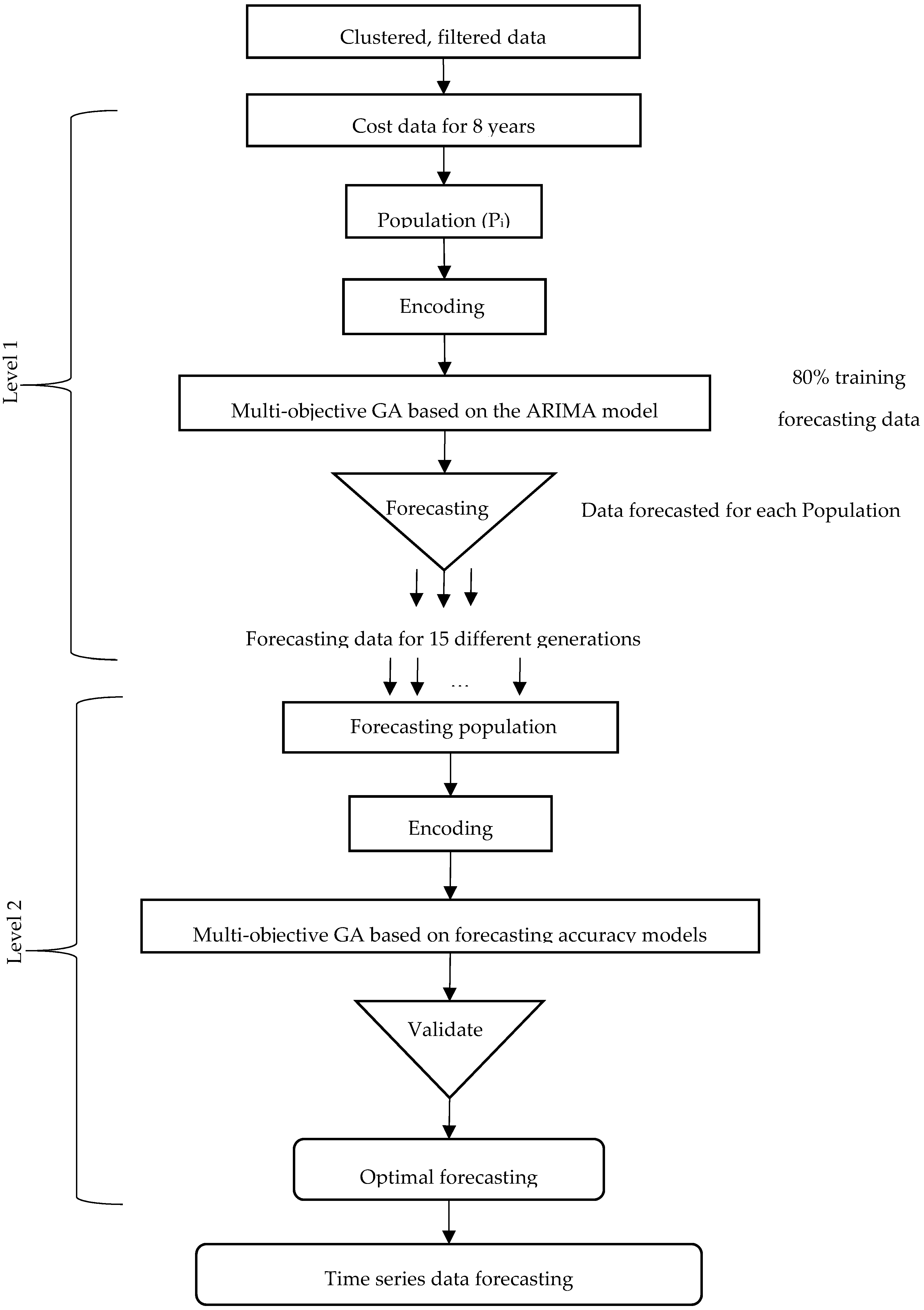
2.3. Two-Level System of Multi-Objective Genetic Algorithms
2.3.1. Level 1: Multi-Objective GA Based on the ARIMA Model
- : the actual data over time;
- : constant estimated value of the time series data;
- : the hypothesis is either = 1 or < 1;
- : time ;
- : the white noise of the time series data.
- : the mean value of the time series data;
- : the number of autoregressive cut-off lags;
- : the number of differences calculated with the equation ;
- : the number of cut-off lags of the moving average process;
- : autoregressive coefficients (AR);
- : moving average coefficients (MA);
- : time ;
- : the white noise of the time series data.
- : months {1, 2, 3,…, }.
2.3.2. Level 2: Multi-Objective GA for Measuring the Forecasting Accuracy
- : time ;
- : the actual data over time;
- : the forecasted data over time.
2.4. Multi-Objective Genetic Algorithms (GAs) Based on the Dynamic Regression Model
- : constant value calculated with the normal equation, where ;
- and : calculated with the normal equation, where ;
- : related to and ;
- : white noise.
2.5. Models Evaluation Method
3. Results and Discussion
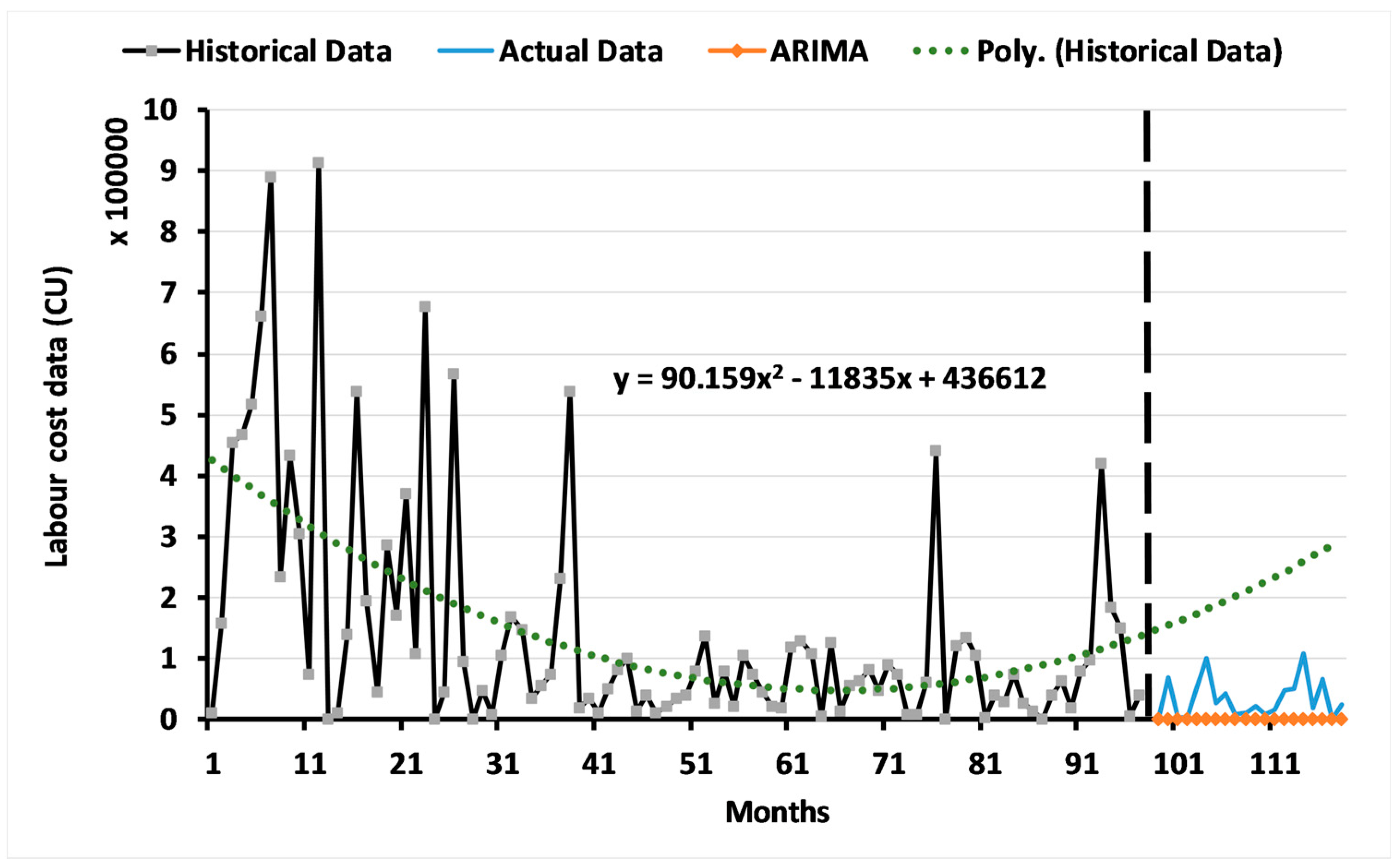
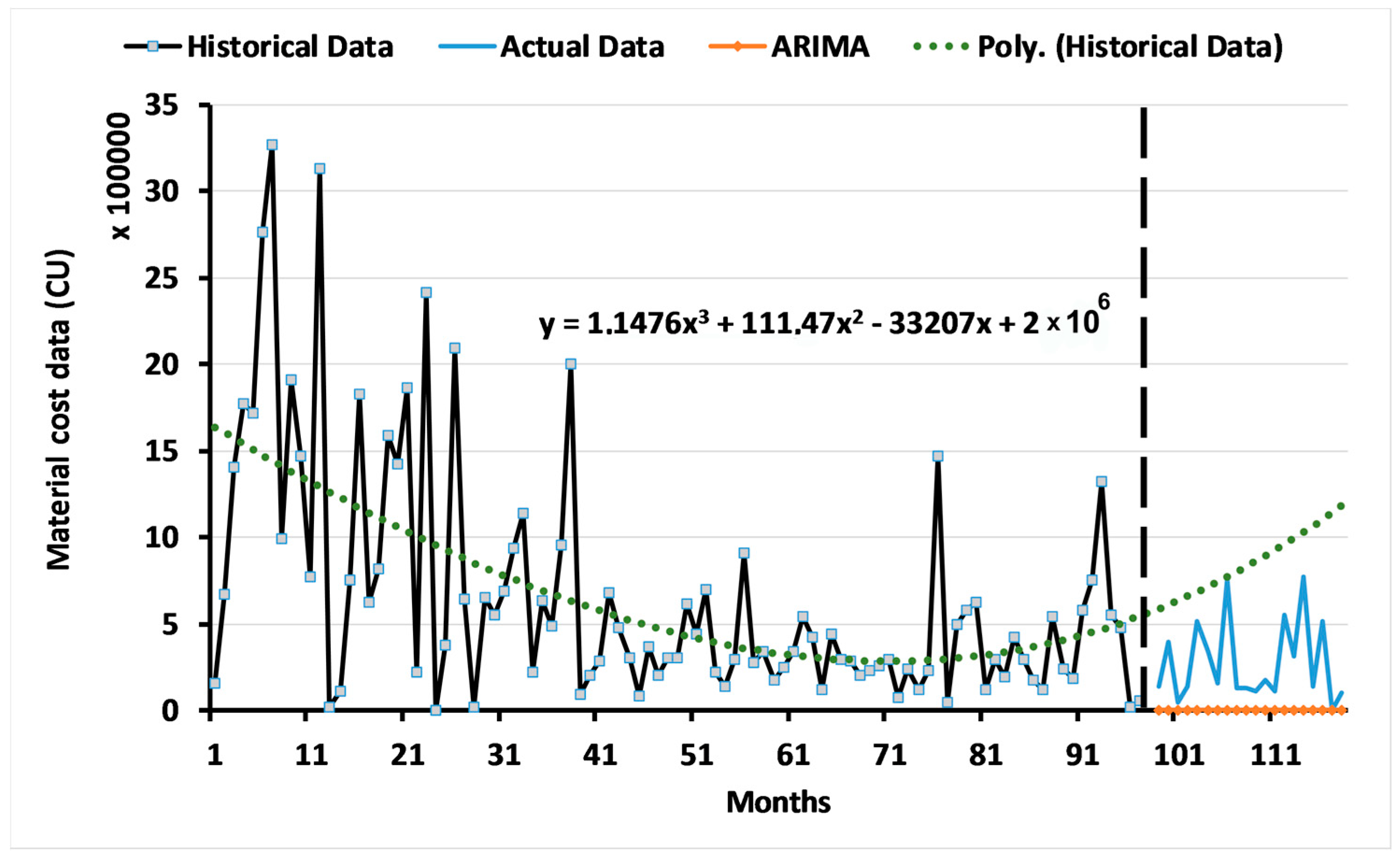
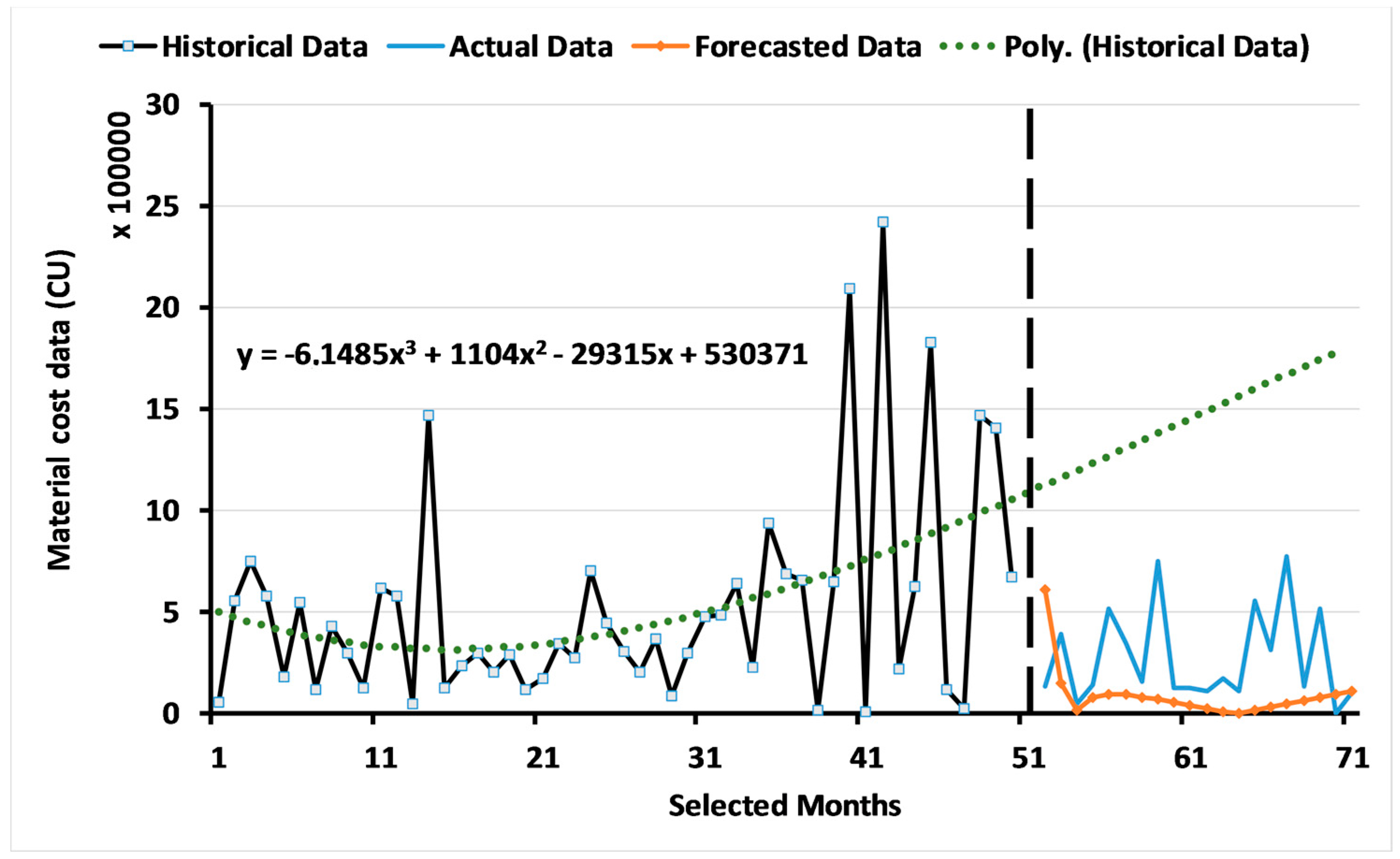
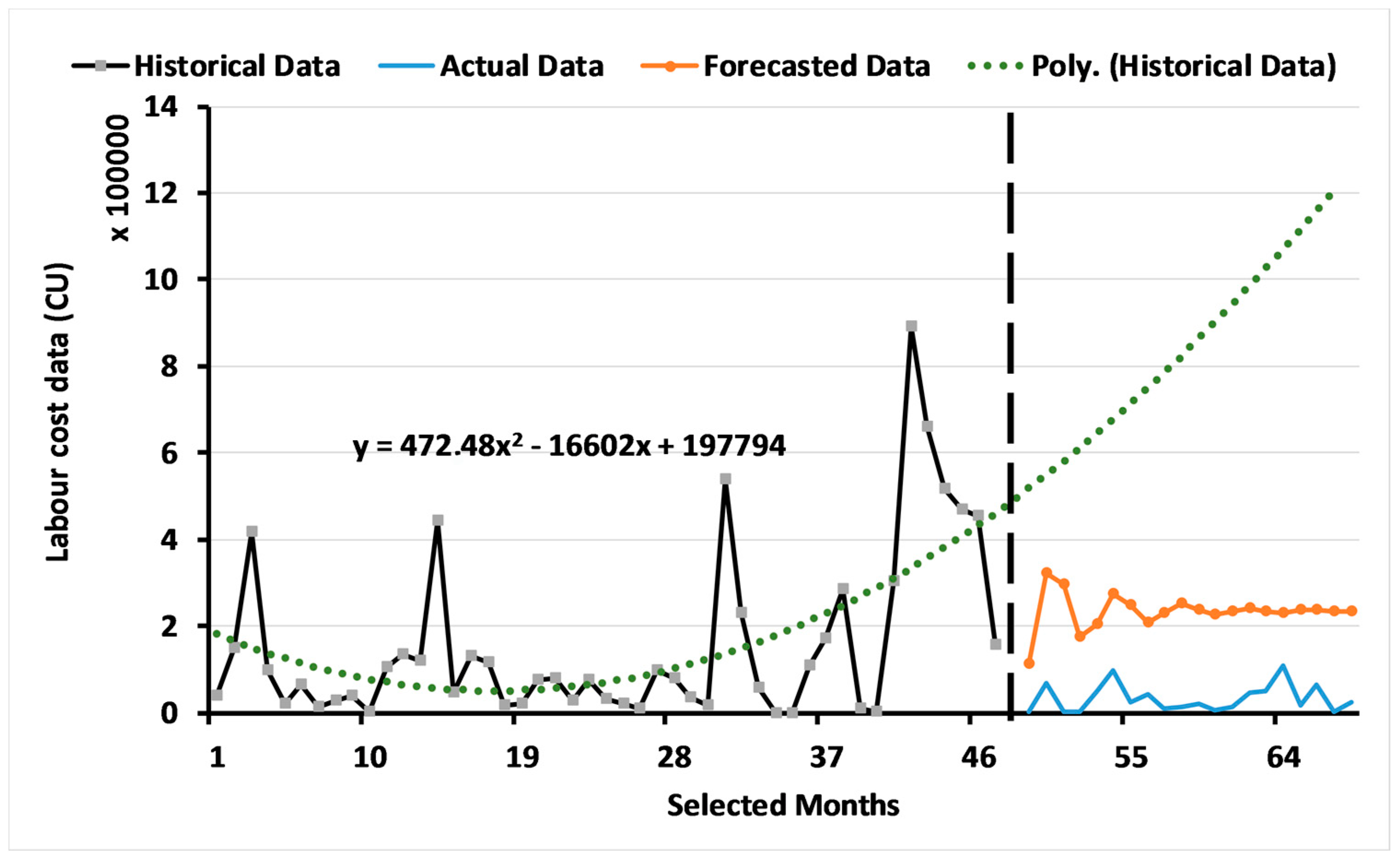
3.1. Results of the ARIMA Model
3.2. Results of the Two-Level System of Multi-Objective GAs
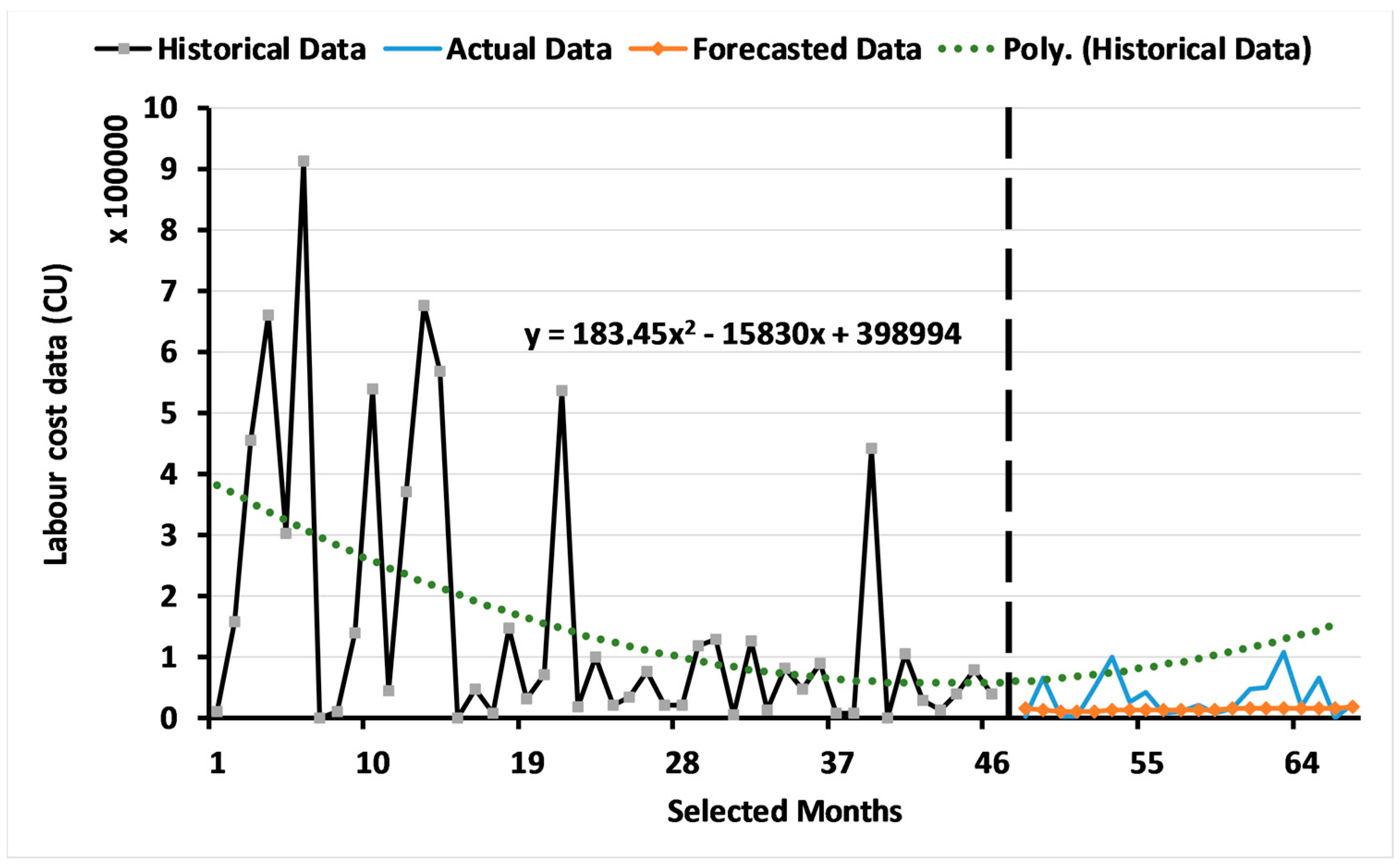
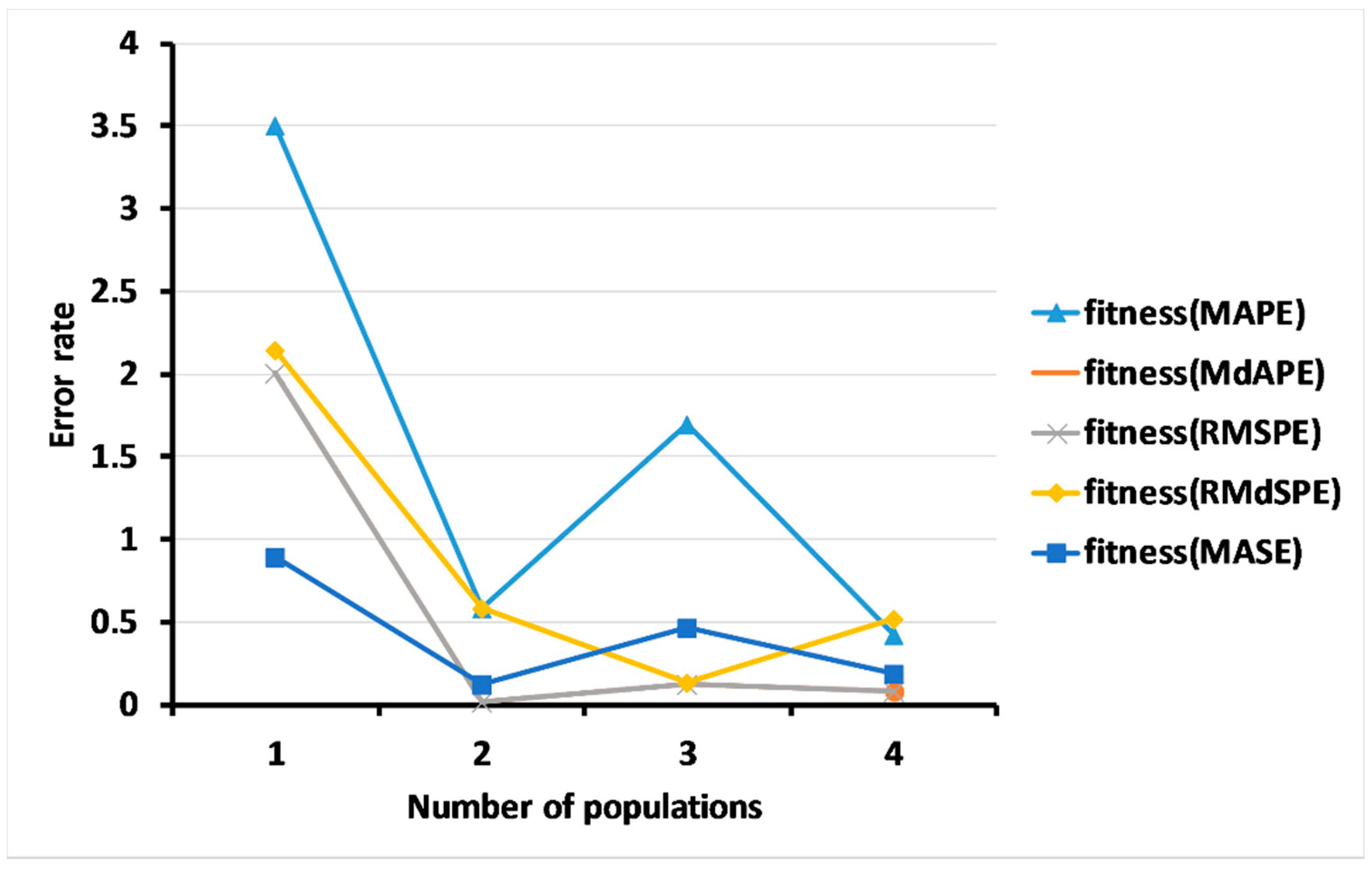
3.2.1. Results for Level 1: Multi-Objective GA Based on the ARIMA Model
3.2.2. Results of Level 2: Multi-Objective GA for Measuring the Forecasting Accuracy
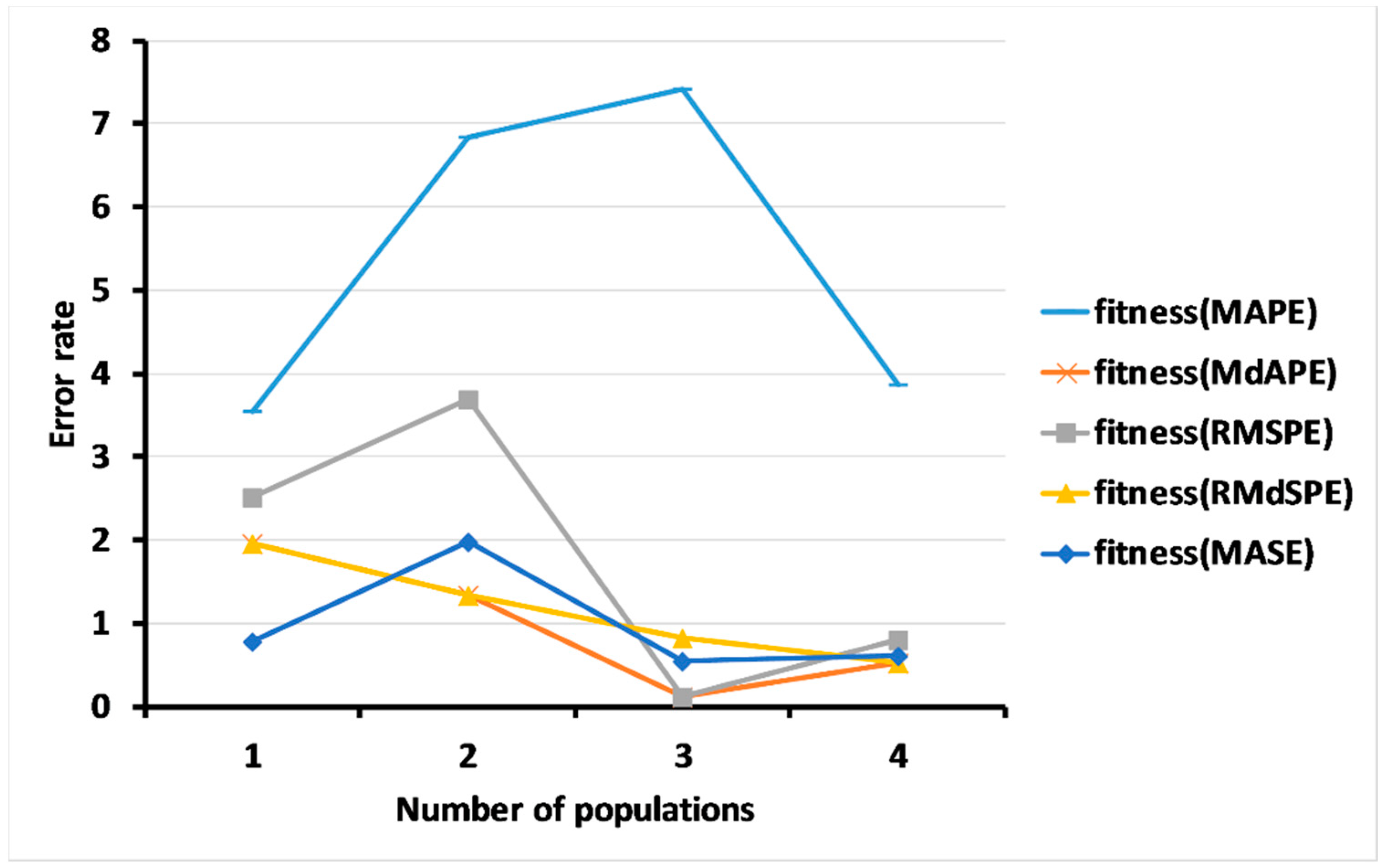
3.3. Results of the Multi-Objective Genetic Algorithms (GAs) Based on the Dynamic Regression Model
3.4. Results of a Comparison of the Methods
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Tyralis, H.; Papacharalampous, G. Variable selection in time series forecasting using random forests. Algorithms 2017, 10, 114. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, B.; Dong, J.; Abraham, A. Time-series forecasting using flexible neural tree model. Inf. Sci. 2005, 174, 219–235. [Google Scholar] [CrossRef]
- Hansen, J.V.; McDonald, J.B.; Nelson, R.D. Time Series Prediction with Genetic-Algorithm Designed Neural Networks: An Empirical Comparison With Modern Statistical Models. Comput. Intell. 1999, 15, 171–184. [Google Scholar] [CrossRef]
- Ramos, P.; Oliveira, J.M. A Procedure for Identification of Appropriate State Space and ARIMA Models Based on Time-Series Cross-Validation. Algorithms 2016, 9, 76. [Google Scholar] [CrossRef]
- Hatzakis, I.; Wallace, D. Dynamic multi-objective optimization with evolutionary algorithms: A forward-looking approach. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, Seattle, WA, USA, 8–12 July 2006; pp. 1201–1208. [Google Scholar]
- Ghaffarizadeh, A.; Eftekhari, M.; Esmailizadeh, A.K.; Flann, N.S. Quantitative trait loci mapping problem: An Extinction-Based Multi-Objective evolutionary algorithm approach. Algorithms 2013, 6, 546–564. [Google Scholar] [CrossRef]
- Herbst, N.R.; Huber, N.; Kounev, S.; Amrehn, E. Self-adaptive workload classification and forecasting for proactive resource provisioning. Concurr. Comput. Pract. Exp. 2014, 26, 2053–2078. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? J. Econ. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Khandakar, Y. Automatic Time Series for Forecasting: The Forecast Package for R; Department of Econometrics and Business Statistics, Monash University: Clayton, VIC, Australia, 2007. [Google Scholar]
- Vantuch, T.; Zelinka, I. Evolutionary based ARIMA models for stock price forecasting. In ISCS 2014: Interdisciplinary Symposium on Complex Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 239–247. [Google Scholar]
- Wang, C.; Hsu, L. Using genetic algorithms grey theory to forecast high technology industrial output. Appl. Math. Comput. 2008, 195, 256–263. [Google Scholar] [CrossRef]
- Ervural, B.C.; Beyca, O.F.; Zaim, S. Model Estimation of ARMA Using Genetic Algorithms: A Case Study of Forecasting Natural Gas Consumption. Procedia-Soc. Behav. Sci. 2016, 235, 537–545. [Google Scholar] [CrossRef]
- Wang, L.; Zeng, Y.; Chen, T. Back propagation neural network with adaptive differential evolution algorithm for time series forecasting. Expert Syst. Appl. 2015, 42, 855–863. [Google Scholar] [CrossRef]
- Zeng, Y.; Zeng, Y.; Choi, B.; Wang, L. Multifactor-influenced energy consumption forecasting using enhanced back-propagation neural network. Energy 2017, 127, 381–396. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Qu, H.; Liu, S. Optimal forecast combination based on neural networks for time series forecasting. Appl. Soft Comput. 2018, 66, 1–17. [Google Scholar] [CrossRef]
- Thomassey, S.; Happiette, M. A neural clustering and classification system for sales forecasting of new apparel items. Appl. Soft Comput. 2007, 7, 1177–1187. [Google Scholar] [CrossRef]
- Ding, C.; Cheng, Y.; He, M. Two-level genetic algorithm for clustered traveling salesman problem with application in large-scale TSPs. Tsinghua Sci. Technol. 2007, 12, 459–465. [Google Scholar] [CrossRef]
- Cordón, O.; Herrera, F.; Gomide, F.; Hoffmann, F.; Magdalena, L. Ten years of genetic fuzzy systems: Current framework and new trends. Fuzzy Sets Syst. 2001, 3, 1241–1246. [Google Scholar]
- Shi, C.; Cai, Y.; Fu, D.; Dong, Y.; Wu, B. A link clustering based overlapping community detection algorithm. Data Knowl. Eng. 2013, 87, 394–404. [Google Scholar] [CrossRef]
- Leybourne, S.J.; Mills, T.C.; Newbold, P. Spurious rejections by Dickey-Fuller tests in the presence of a break under the null. J. Econ. 1998, 87, 191–203. [Google Scholar] [CrossRef]
- Huang, R.; Huang, T.; Gadh, R.; Li, N. Solar generation prediction using the ARMA model in a laboratory-level micro-grid. In Proceedings of the 2012 IEEE Third International Conference on Smart Grid Communications (SmartGridComm), Tainan, Taiwan, 5–8 November 2012; pp. 528–533. [Google Scholar]
- Hyndman, R.J.; Koehler, A.B. Another look at measures of forecast accuracy. Int. J. Forecast. 2006, 22, 679–688. [Google Scholar] [CrossRef]
- Hwang, S. Dynamic regression models for prediction of construction costs. J. Constr. Eng. Manag. 2009, 135, 360–367. [Google Scholar] [CrossRef]
- Date, C.J. An Introduction to Database Systems; Pearson Education India: New Delhi, India, 2006. [Google Scholar]
- Al-Douri, Y.; Hamodi, H.; Zhang, L. Data clustering and imputing using a two-level multi-objective genetic algorithms (GA): A case study of maintenance cost data for tunnel fans. Cogent Eng. 2018. submitted. [Google Scholar]
| DV1 | DV2 | |
|---|---|---|
| ARIMA model | 0.2374 | 1.2169 |
| Multi-objective GA based on the ARIMA model | 0.1192 | 0.3869 |
| Multi-objective GA based on the dynamic regression model | 1.2630 | 6.2324 |
| DV1 | DV2 | |
|---|---|---|
| ARIMA model | 0.4171 | 1.0438 |
| Multi-objective GA based on the ARIMA model | 0.3555 | 0.8477 |
| Multi-objective GA based on the dynamic regression model | 0.5615 | 3.9543 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Douri, Y.K.; Hamodi, H.; Lundberg, J. Time Series Forecasting Using a Two-Level Multi-Objective Genetic Algorithm: A Case Study of Maintenance Cost Data for Tunnel Fans. Algorithms 2018, 11, 123. https://doi.org/10.3390/a11080123
Al-Douri YK, Hamodi H, Lundberg J. Time Series Forecasting Using a Two-Level Multi-Objective Genetic Algorithm: A Case Study of Maintenance Cost Data for Tunnel Fans. Algorithms. 2018; 11(8):123. https://doi.org/10.3390/a11080123
Chicago/Turabian StyleAl-Douri, Yamur K., Hussan Hamodi, and Jan Lundberg. 2018. "Time Series Forecasting Using a Two-Level Multi-Objective Genetic Algorithm: A Case Study of Maintenance Cost Data for Tunnel Fans" Algorithms 11, no. 8: 123. https://doi.org/10.3390/a11080123
APA StyleAl-Douri, Y. K., Hamodi, H., & Lundberg, J. (2018). Time Series Forecasting Using a Two-Level Multi-Objective Genetic Algorithm: A Case Study of Maintenance Cost Data for Tunnel Fans. Algorithms, 11(8), 123. https://doi.org/10.3390/a11080123





