Color-Based Image Retrieval Using Proximity Space Theory
Abstract
1. Introduction
2. Proposed Method
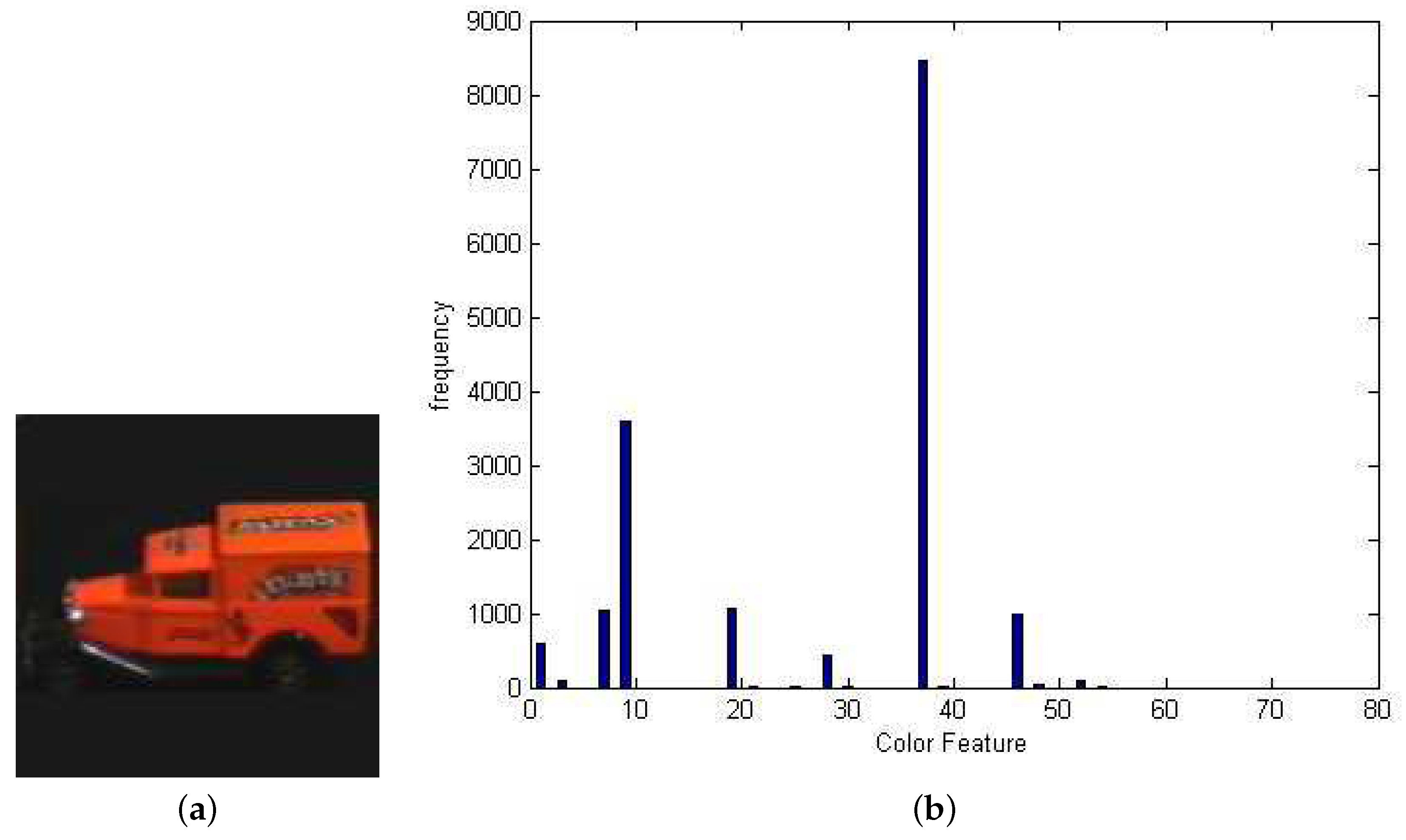
2.1. Feature Extraction
2.2. Similarity Measure Based on Dominance Perceptual Information
| , | , |
2.3. Algorithm Flow Chart
3. Experiment and Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Amores, J.; Sebe, N.; Radeva, P.; Gevers, T.; Smeulders, A. Boosting Contextual Information in Content-Based Image Retrieval. In Proceedings of the 6th ACM SIGMM International Workshop on Multimedia Information Retrieval, New York, NY, USA, 15–16 October 2004; pp. 31–38. [Google Scholar]
- Zhang, Y.P.; Zhang, S.B.; Yan, Y.T. A Multi-view Fusion Method for Image Retrieval. In Proceedings of the International Congress on Image and Signal Processing, BioMedical Engineering and Information, Shanghai, China, 14–16 October 2017; pp. 379–383. [Google Scholar]
- Chen, Y.Y. The Image Retrieval Algorithm Based on Color Feature. In Proceedings of the IEEE International Conference on Software Engineering and Service Science, Beijing, China, 26–28 August 2016; pp. 647–650. [Google Scholar]
- Liang, C.W.; Chung, W.Y. Color Feature Extraction and Selection for Image Retrieval. In Proceedings of the IEEE International Conference on Advanced Materials for Science and Engineering, Tainan, Taiwan, 12–13 November 2016; pp. 589–592. [Google Scholar]
- Li, M.Z.; Jiang, L.H. An Improved Algorithm Based on Color Feature Extraction for Image Retrieval. In Proceedings of the International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 25–26 August 2016. [Google Scholar]
- Alhassan, A.K.; Alfaki, A.A. Color and Texture Fusion-Based Method for Content-Based Image Retrieval. In Proceedings of the International Conference on Communication, Control, Computing and Electronics, Khartoum, Sudan, 16–18 Janary 2017; pp. 1–6. [Google Scholar]
- Gopal, N.; Bhooshan, R.S. Content Based Image Reterieval using Enhanced SURF. In Proceedings of the Fifth National Conference on Computer Vision, Pattern Recognition, Image Processing and Graphics, Patna, India, 16–19 December 2015; pp. 1–4. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Gool, L.V. Speeded-Up Robust Features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Kaur, M.; Sohi, N. A Novel Techinique for Content Based Image Retrieval Using Color, Texture and Edge Features. In Proceedings of the International Conference on Communication and Electronics System, Coimbatore, India, 21–22 October 2016; pp. 1–7. [Google Scholar]
- Chen, Q.S.; Ding, Y.Y.; Li, H.; Wang, X.; Wang, J.; Deng, X. A Novel Multi-Feature Fusion and Sparse Coding Based Framework for Image Retrieval. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics Octobor, San Diego, CA, USA, 5–8 October 2014; pp. 2391–2396. [Google Scholar]
- Kang, L.W.; Hsu, C.Y.; Chen, H.W.; Lu, C.S.; Lin, C.Y. Feature-Based Sparse Representation for Image Similarity Assessment. IEEE Trans. Multimed. 2011, 13, 1019–1030. [Google Scholar] [CrossRef]
- Bakhshali, M.A. Segmentation and Enhancement of Brain MR Images using Fuzzy Clustering Based on Information Theory. Soft Comput. 2016, 21, 6633–6640. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough sets, Proceedings of the 6th ACMSIGMM. Int. J. Comput. Inform. Sci. 1995, 256–341. [Google Scholar]
- Lim, K.Y.; Rajeswari, M. Segmenting Object with Ambiguous Boundary using Information Theoretic Rough Sets. Int. J. Electron. Commun. 2017, 77, 50–56. [Google Scholar] [CrossRef]
- Senthilkumaran, N.; Rajesh, R. Brain Image Segmentation using Granular Rough Sets. Int. J. Arts Sci. 2009, 3, 69–78. [Google Scholar]
- Roy, P.; Goswami, S.; Chakraborty, S.; Azar, A.T.; Dey, N. Image Segmentation using Rough Set Theory: A Review. Int. J. Rough Sets Data Analy. 2014, 1, 62–74. [Google Scholar] [CrossRef]
- Khodaskar, A.A.; Ladhake, S.A. Emphasis on Rough Set Theory for Image Retrieval. In Proceedings of the 6th ACM SIGMM International Conference on Computer Communication and Informatics, Coimbatore, India, 8–10 Janary 2015; pp. 1–6. [Google Scholar]
- Thilagavathy, C.; Rajesh, R. Rough Set Theory and its Applications Image Processing-A Short Review. In Proceedings of the 3rd World Conference on Applied Sciences, Engineering, Technology, Kathmandu, Nepal, 27–29 September 2014; pp. 27–29. [Google Scholar]
- Rocio, L.M.; Raul, S.Y.; Victor, A.R.; Alberto, P.R. Improving a Rough Set Theory-Based Segmentation Approach using Adaptable Threshold Selection and Perceptual Color Spaces. J. Electron. Imag. 2014, 23, 013024. [Google Scholar]
- Wasinphongwanit, P.; Phokharatkul, P. Image Retrieval using Contour Feature with Rough Set Method. In Proceedings of the International Conference on Computer, Mechatronics, Control and Electronic Engineering, Changchun, China, 24–26 August 2010; Volume 6, pp. 349–352. [Google Scholar]
- Peters, J.F. Computational Proximity—Excursions in the Topology of Digital Images; Springe: Berlin, Germany, 2016. [Google Scholar]
- Pták, P.; Kropatsch, W.G. Nearness in Digital Images and Proximity Spaces. In Proceedings of the 9th International Conference on Discrete Geometry, Nantes, France, 18–20 Apirl 2016; pp. 69–77. [Google Scholar]
- Peters, J.F. Visibility in Proximal Delaunay Meshes and Strongerly Near Wallman Proximity. Adv. Math. 2015, 4, 41–47. [Google Scholar]
- Ma, J. Content-Based Image Retrieval with HSV Color Space and Texture Features. In Proceedings of the International Conference on IEEE Web Information Systems and Mining, Shanghai, China, 7–8 November 2009; pp. 61–63. [Google Scholar]
- Yan, Y.; Ren, J.; Li, Y.; Windmill, J.; Ijomah, W. Fusion of Dominant Colour and Spatial Layout Features for Effective Image Retrieval of Coloured Logos and Trademarks. In Proceedings of the IEEE International Conference on Multimedia Big Data, Beijing, China, 20–22 April 2015; Volume 106, pp. 306–311. [Google Scholar]
- Schroder, B.S.W. Ordered Sets: An Introduction; Springer: Berlin, Germany, 2002. [Google Scholar]
- Messing, D.S.; Beek, P.V.; Errico, J.H. The MPEG-7 Colour Struture Descriptor: Image Description using Colour and Local Spatial Information. In Proceedings of the 2001 International Conference on Image Processing, Thessaloniki, Greece, 7–10 October 2001; pp. 670–673. [Google Scholar]
- Shih, J.L.; Chen, L.H. Colour Image Retrieval Based on Primitives of Colour Moments. IEE Proc. Vis. Image Signal Process. 2002, 149, 370–376. [Google Scholar]
- Kasutani, E.; Yamada, A. The MPEG-7 Color Layout Descriptor: A Compact Image Feature Description for High-Speed ImageNideo Segment Retrieval. In Proceedings of the International Conference on Image Processing, Thessaloniki, Greece, 7–10 October 2001; pp. 674–677. [Google Scholar]





| (a) Note: The Results of Enhanced SURF Method. | ||||||||||||||||||||
| Object category | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t |
| 65 | 45 | 24 | 43 | 25 | 65 | 13 | 30 | 54 | 17 | 42 | 49 | 60 | 34 | 21 | 46 | 62 | 35 | 38 | 28 | |
| 238 | 215 | 56 | 92 | 268 | 232 | 31 | 31 | 1087 | 168 | 91 | 762 | 1105 | 57 | 96 | 417 | 184 | 97 | 89 | 77 | |
| Precision | 0.273 | 0.209 | 0.428 | 0.467 | 0.093 | 0.280 | 0.419 | 0.968 | 0.05 | 0.101 | 0.462 | 0.064 | 0.054 | 0.596 | 0.219 | 0.110 | 0.337 | 0.361 | 0.427 | 0.364 |
| Recall | 0.903 | 0.625 | 0.333 | 0.597 | 0.347 | 0.902 | 0.180 | 0.417 | 0.75 | 0.236 | 0.583 | 0.680 | 0.833 | 0.472 | 0.292 | 0.639 | 0.861 | 0.486 | 0.528 | 0.389 |
| (b) Note: The Results of Our Proposed Method. | ||||||||||||||||||||
| Object category | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t |
| 72 | 53 | 55 | 47 | 59 | 72 | 33 | 24 | 72 | 68 | 70 | 72 | 72 | 51 | 59 | 72 | 72 | 65 | 68 | 50 | |
| 247 | 219 | 58 | 95 | 272 | 242 | 33 | 31 | 1116 | 176 | 96 | 788 | 1197 | 59 | 109 | 453 | 194 | 100 | 89 | 77 | |
| Precision | 0.291 | 0.256 | 0.948 | 0.494 | 0.202 | 0.298 | 1 | 0.774 | 0.065 | 0.375 | 0.729 | 0.091 | 0.060 | 0.881 | 0.541 | 0.159 | 0.371 | 0.680 | 0.772 | 0.649 |
| Recall | 1 | 0.778 | 0.763 | 0.652 | 0.764 | 1 | 0.458 | 0.333 | 1 | 0.917 | 0.972 | 1 | 1 | 0.722 | 0.819 | 1 | 1 | 0.944 | 0.958 | 0.694 |
| Category Name | CLD [27] | Color Moment [28] | CSD [29] | Proposed Method | ||||
|---|---|---|---|---|---|---|---|---|
| Precision | Recall | Precision | Recall | Precision | Recall | Precision | Recall | |
| African Tribes | 0.213 | 0.144 | 0.389 | 0.260 | 0.562 | 0.347 | 0.505 | 0.312 |
| Beaches | 0.529 | 0.283 | 0.295 | 0.169 | 0.288 | 0.153 | 0.442 | 0.209 |
| Buildings | 0.341 | 0.157 | 0.382 | 0.211 | 0.553 | 0.341 | 0.664 | 0.397 |
| Buses | 0.255 | 0.113 | 0.580 | 0.319 | 0.447 | 0.258 | 0.703 | 0.435 |
| Dinosaurs | 0.907 | 0.510 | 0.938 | 0.785 | 0.794 | 0.614 | 0.962 | 0.539 |
| Elephants | 0.477 | 0.235 | 0.491 | 0.302 | 0.630 | 0.260 | 0.706 | 0.339 |
| Flowers | 0.700 | 0.288 | 0.679 | 0.360 | 0.537 | 0.253 | 0.733 | 0.300 |
| Horses | 0.980 | 0.703 | 0.747 | 0.401 | 0.641 | 0.338 | 0.885 | 0.549 |
| Mountains | 0.566 | 0.357 | 0.260 | 0.157 | 0.613 | 0.294 | 0.441 | 0.229 |
| Foods | 0.127 | 0.057 | 0.463 | 0.277 | 0.320 | 0.138 | 0.792 | 0.482 |
| Average Precision | 0.509 | 0.285 | 0.522 | 0.324 | 0.627 | 0.354 | 0.683 | 0.379 |
| Query Image | Precision | Query Image | Precision |
|---|---|---|---|
| African Tribes | 46% | Elephants | 59% |
| Beaches | 34% | Flowers | 60% |
| Buildings | 60% | Horses | 83% |
| Buses | 63% | Mountains | 36% |
| Dinosaurs | 92% | Foods | 72% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, L.; Liu, X.; Ren, Y.; Yuan, Y. Color-Based Image Retrieval Using Proximity Space Theory. Algorithms 2018, 11, 115. https://doi.org/10.3390/a11080115
Wang J, Wang L, Liu X, Ren Y, Yuan Y. Color-Based Image Retrieval Using Proximity Space Theory. Algorithms. 2018; 11(8):115. https://doi.org/10.3390/a11080115
Chicago/Turabian StyleWang, Jing, Lidong Wang, Xiaodong Liu, Yan Ren, and Ye Yuan. 2018. "Color-Based Image Retrieval Using Proximity Space Theory" Algorithms 11, no. 8: 115. https://doi.org/10.3390/a11080115
APA StyleWang, J., Wang, L., Liu, X., Ren, Y., & Yuan, Y. (2018). Color-Based Image Retrieval Using Proximity Space Theory. Algorithms, 11(8), 115. https://doi.org/10.3390/a11080115




