A Regional Topic Model Using Hybrid Stochastic Variational Gibbs Sampling for Real-Time Video Mining
Abstract
1. Introduction
2. Related Works
3. Materials and Methods
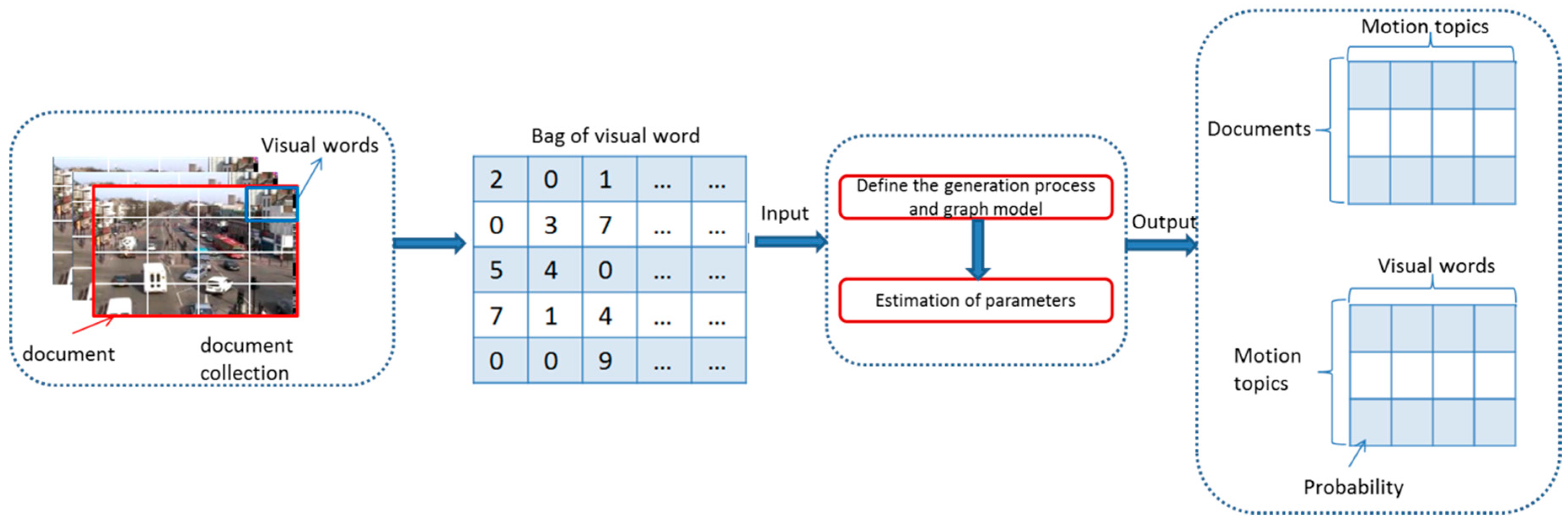
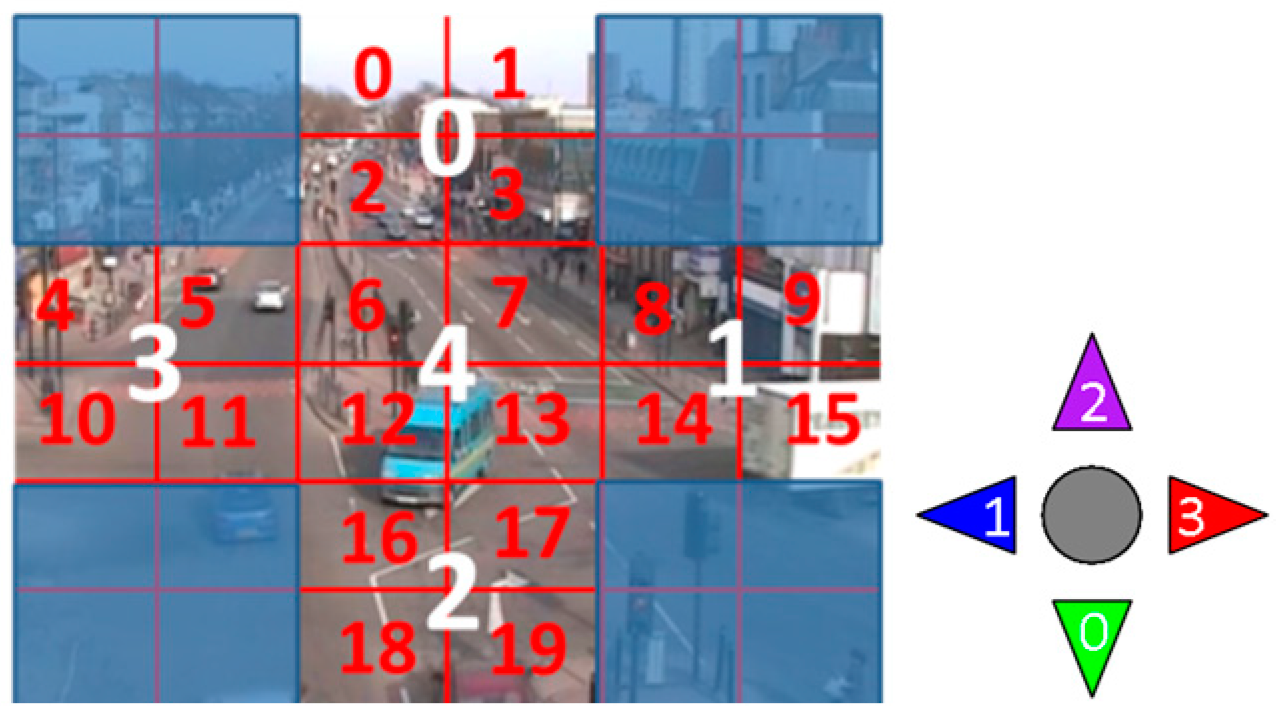
3.1. Video Representation
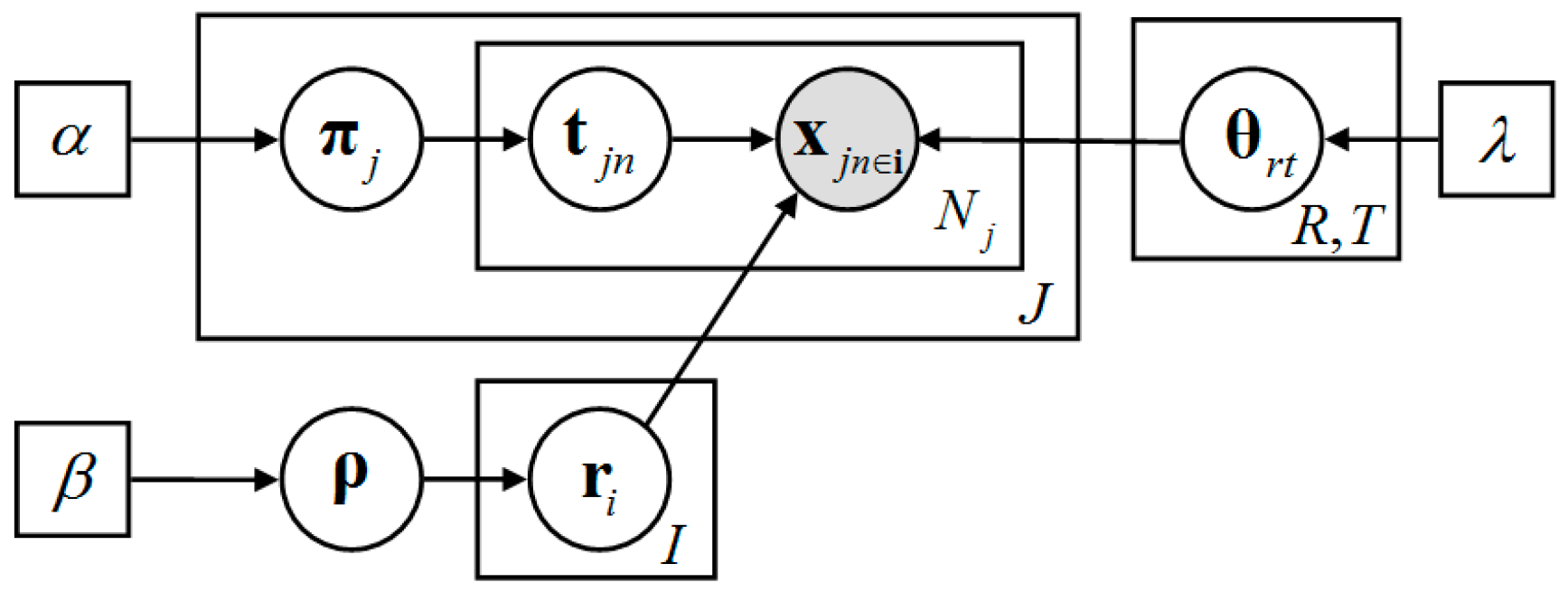
3.2. Regional Topic Model and Its Online Inference Algorithm
| Algorithm 1. HSVG algorithm of RTM model |
| Initialize global variational parameters , and while the number of random iterations do |
| Update iteration step: |
| Import a small batch documents |
| Initialize from , from |
| for do |
| For a sample of document local MCMC inference is adopted |
| end_for |
| end_for |
| times iteration in burn-in time is not processed |
| For converged Markov chain do |
| end_for |
| , where |
| end_while |
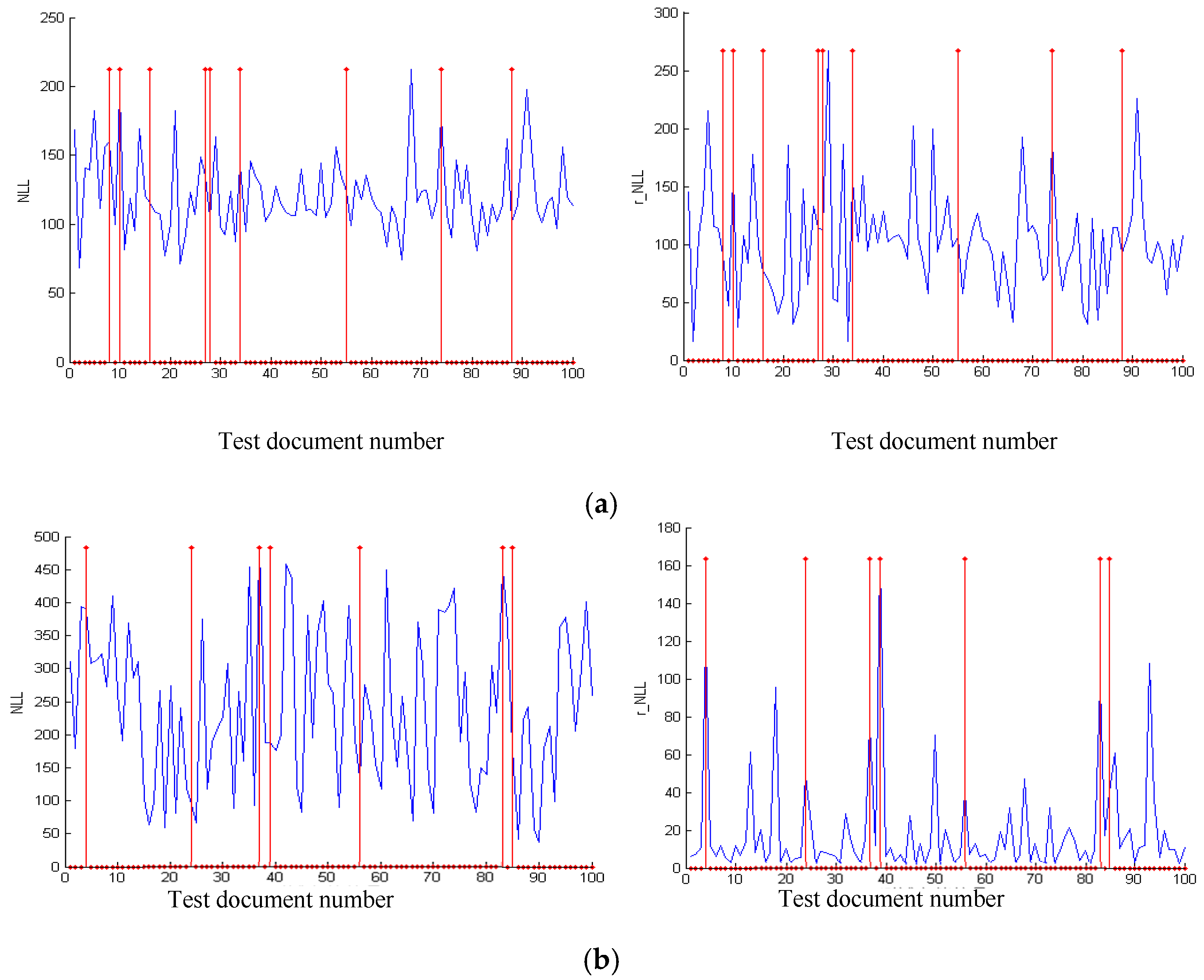
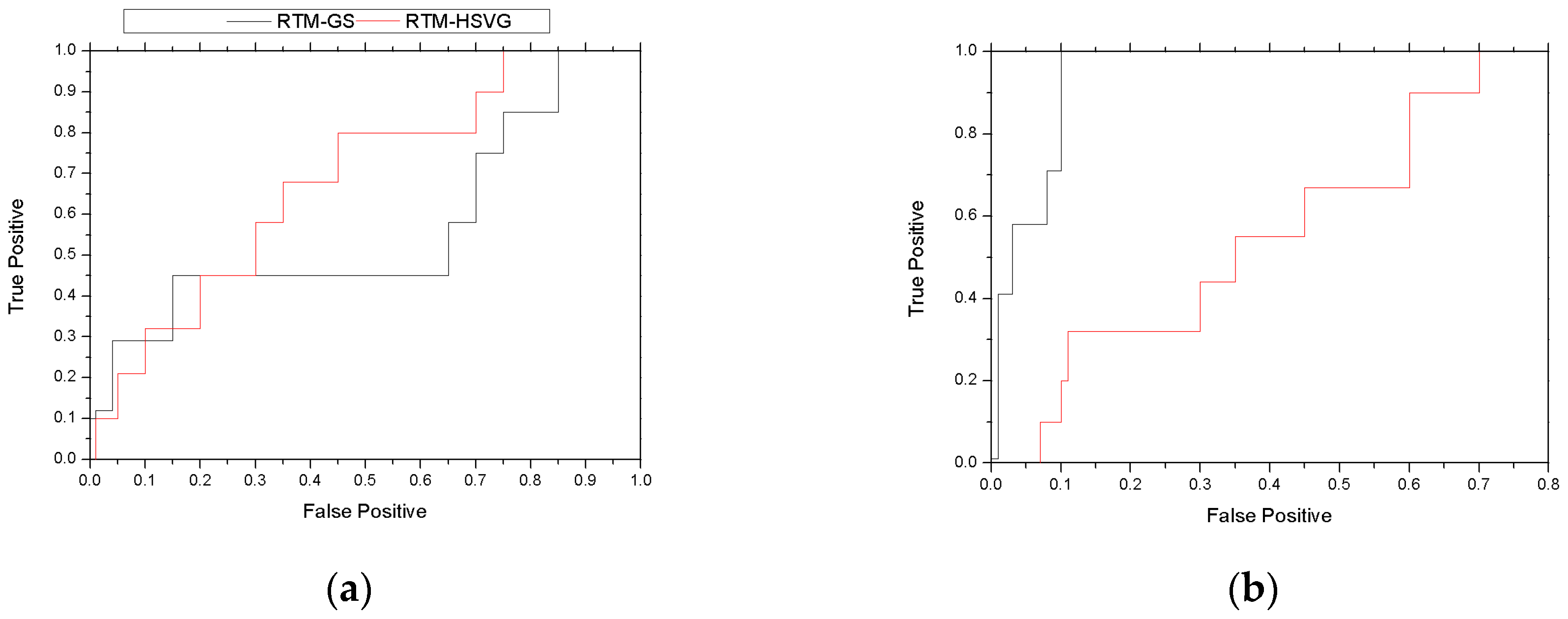
4. Results
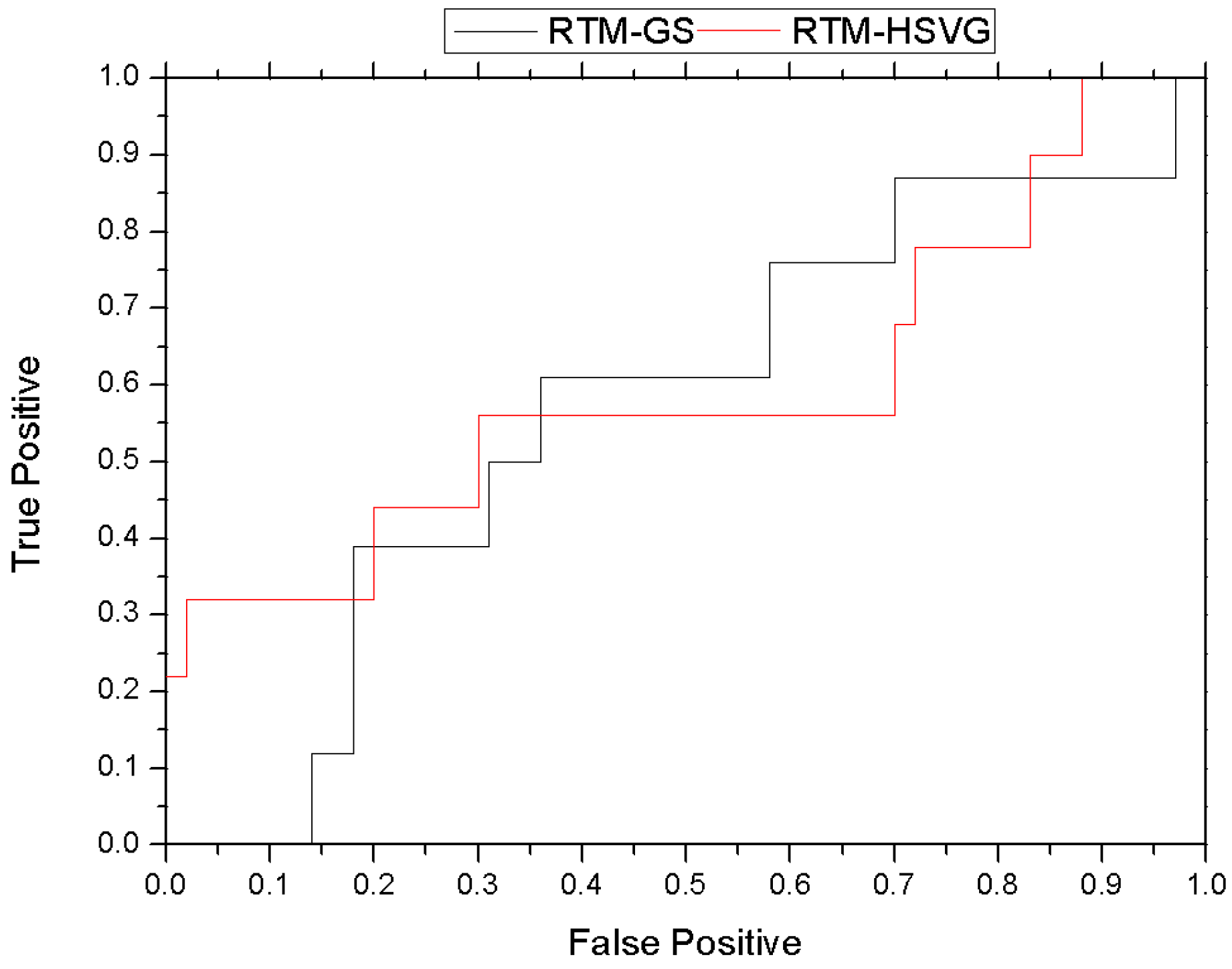
4.1. Evaluation Criterion
4.2. Datasets and Parameter Settings
4.2.1. Simulation Video Dataset
4.2.2. Real Video Dataset
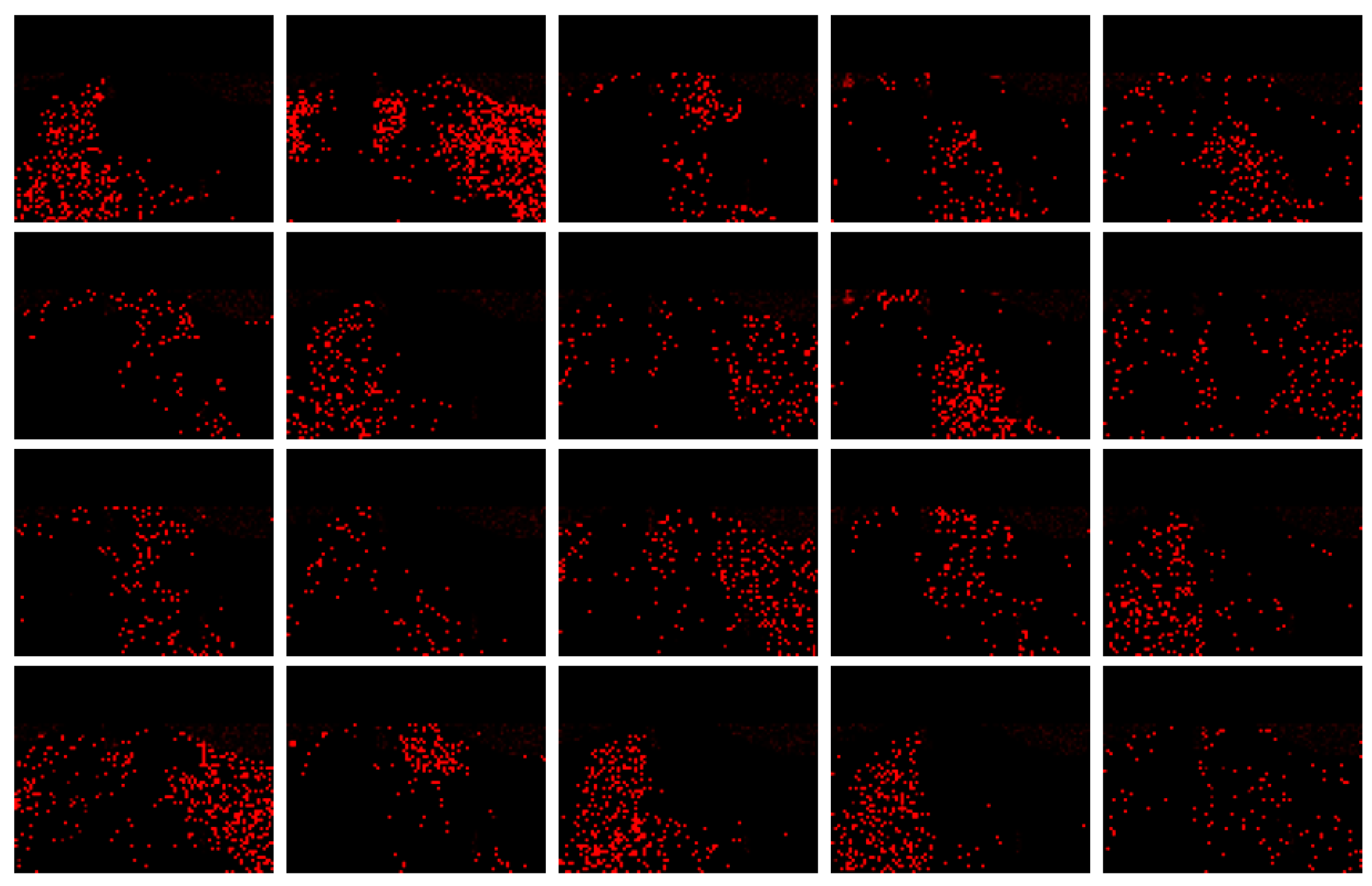
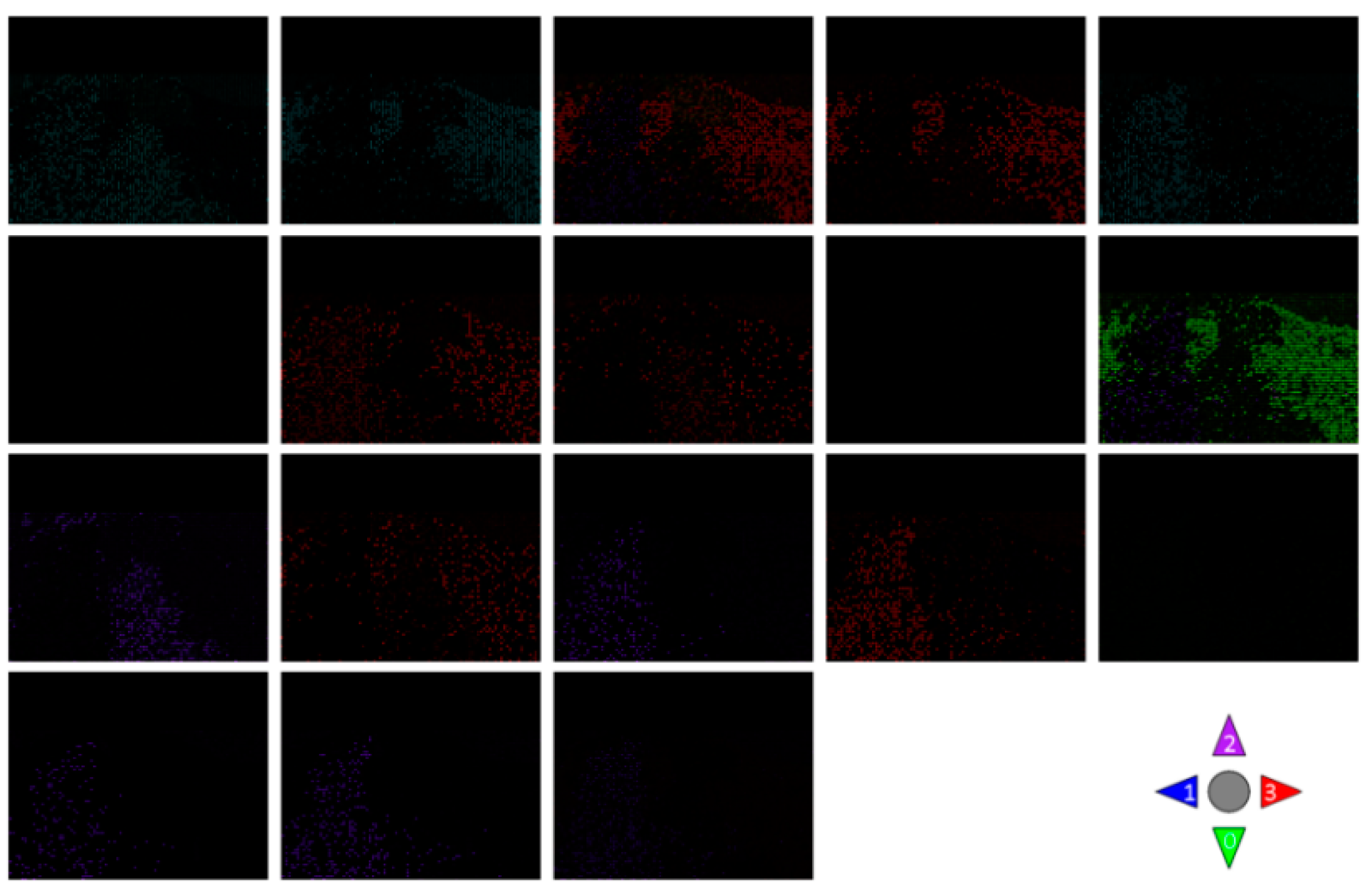
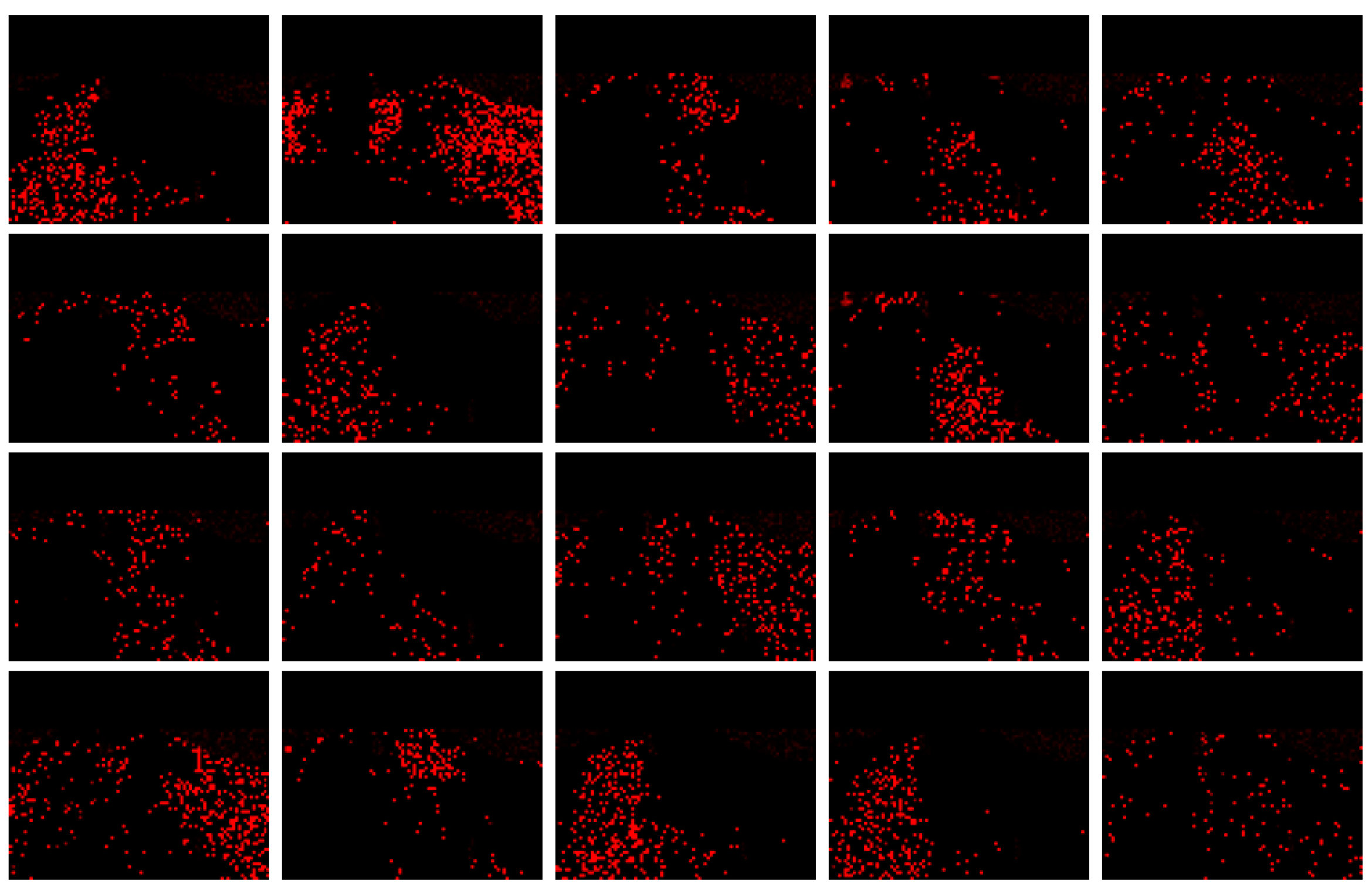
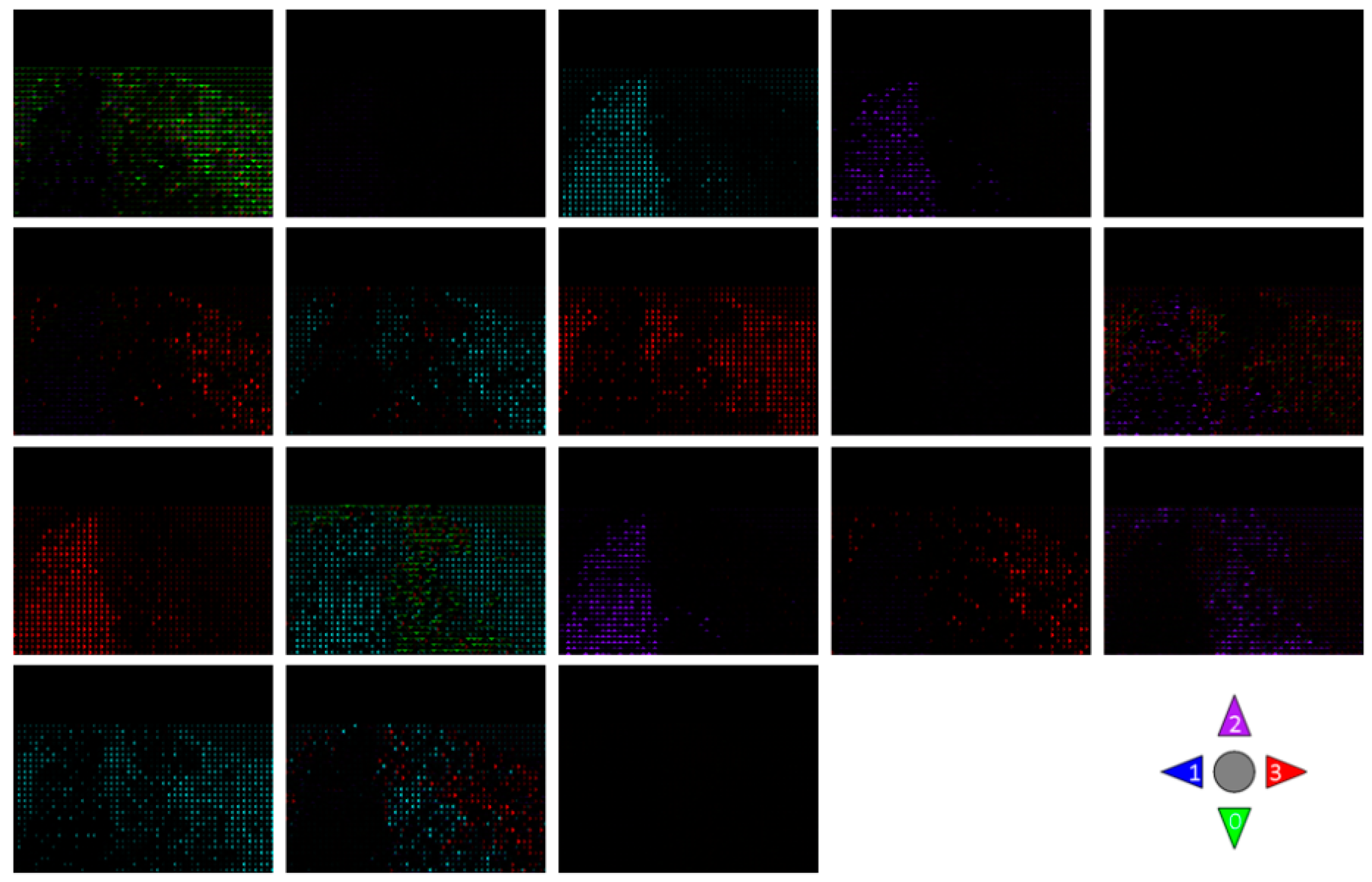
4.3. Experimental Results
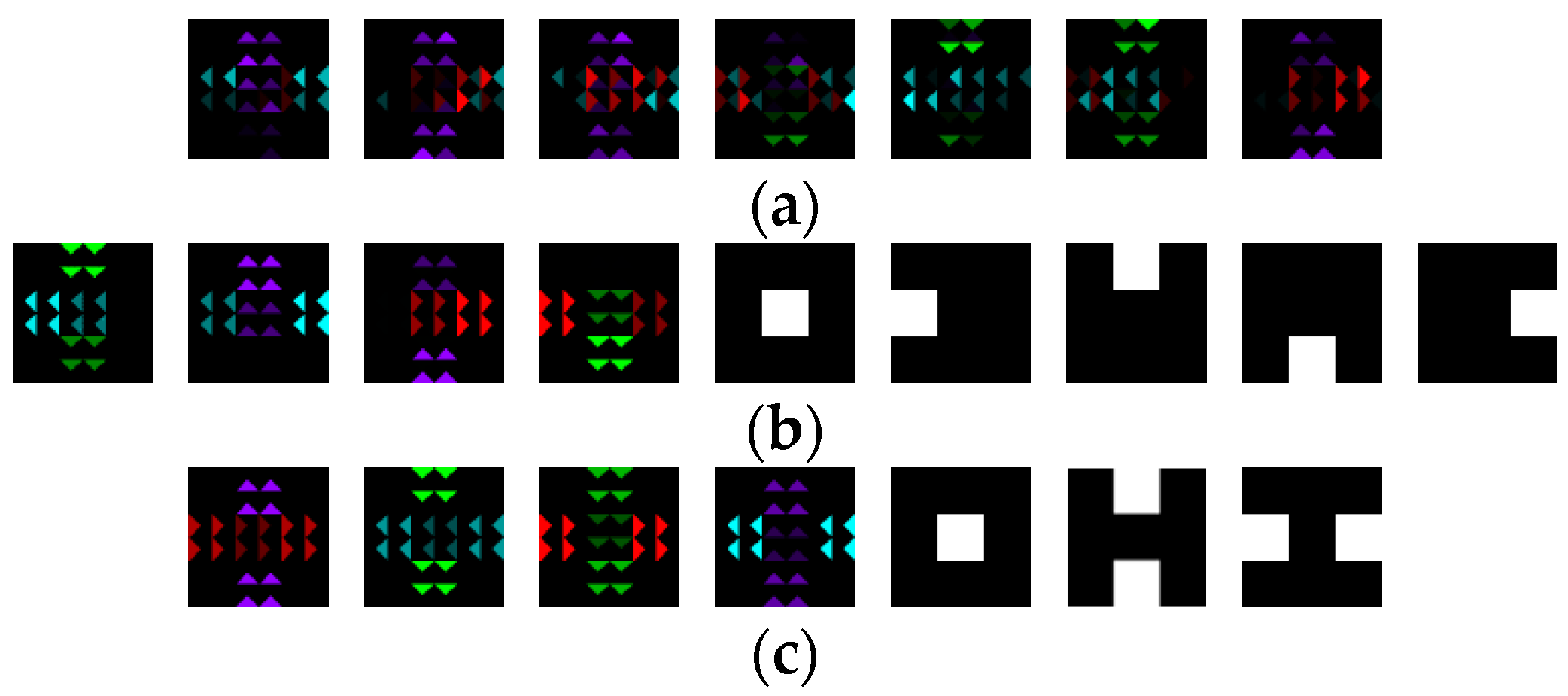
4.3.1. Simulation Experiment of Visualization Traffic Intersection
4.3.2. Real Video Experiment
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dai, K.; Zhang, J.; Li, G. Video mining: Concepts, approaches and applications. In Proceedings of the IEEE 12th International Multi-Media Modelling Conference Proceedings, Beijing, China, 4–6 January 2006. [Google Scholar]
- Chen, S.C.; Shyu, M.L.; Zhang, C.; Strickrott, J. A multimedia data mining framework: Mining information from traffic video sequences. Intell. Inf. Syst. 2002, 19, 61–77. [Google Scholar] [CrossRef]
- Blei, D.; Carin, L.; Dunson, D. Probabilistic topic models. IEEE Signal Process. Mag. 2010, 27, 55–65. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.H.; Zhao, G.G.; Sun, D.H. Modeling documents with event model. Algorithms 2015, 8, 562–572. [Google Scholar] [CrossRef]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent dirichlet allocation. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Griffiths, T.L.; Steyvers, M. Finding scientific topics. Proc. Natl. Acad. Sci. USA 2004, 101, 5228–5235. [Google Scholar] [CrossRef] [PubMed]
- Teh, Y.W.; Jordan, M.I.; Beal, M.J.; Blei, D.M. Hierarchical dirichlet processes. Am. Stat. Assoc. 2006, 101, 1566–1581. [Google Scholar] [CrossRef]
- Larlus, D.; Verbeek, J. Category Level Object Segmentation by Combining Bag-of-Words Models with Dirichlet Processes and Random Fields. Int. J. Comput. Vis. 2010, 88, 238–253. [Google Scholar] [CrossRef]
- Hofmann, T. Probabilistic latent semantic analysis. In Proceedings of the Fifteenth Conference on Uncertainty in Artificial Intelligence, Stockholm, Sweden, 30 July–1 August 1999; pp. 289–296. [Google Scholar]
- Wang, X.; Ma, X.; Grimson, W.E.L. Unsupervised Activity Perception in Crowded and Complicated Scenes Using Hierarchical Bayesian Models. IEEE Trans. Pattern Anal. 2009, 31, 539–555. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Ma, K.T.; Ng, G.W. Trajectory analysis and semantic region modeling using a nonparametric Bayesian model. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Li, J.; Gong, S.; Xiang, T. Scene segmentation for behaviour correlation. In Proceedings of the European Conference on Computer Vision, Marseille, France, 12–18 October 2008; pp. 383–395. [Google Scholar]
- Li, J. Learning behavioural context. Int. J. Comput. Vis. 2012, 97, 276–304. [Google Scholar] [CrossRef]
- Hospedales, T.M.; Li, J.; Gong, S.; Xiang, T. Identifying rare and subtle behaviors: A weakly supervised joint topic model. Int. J. Comput. Vis. 2012, 33, 2451–2464. [Google Scholar] [CrossRef] [PubMed]
- Emonet, R.; Varadarajan, J.; Odobez, J. Extracting and locating temporal motifs in video scenes using a hierarchical non parametric Bayesian model. Int. J. Comput. Vis. 2011, 32, 3233–3240. [Google Scholar]
- Fu, W.; Wang, J.; Lu, H.; Ma, S. Dynamic scene understanding by improved sparse topical coding. Pattern Recogn. 2013, 46, 1841–1850. [Google Scholar] [CrossRef]
- Yuan, J.; Zheng, Y.; Xie, X. Discovering regions of different functions in a city using human mobility and POIs. In Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; pp. 186–194. [Google Scholar]
- Farrahi, K.; Gatica-Perez, D. Discovering routines from large-scale human locations using probabilistic topic models. ACM Trans. Intell. Syst. Technol. 2011, 2. [Google Scholar] [CrossRef]
- Zhao, Z.; Xu, W.; Chen, D. EM-LDA model of user behavior detection for energy efficiency. In Proceedings of the IEEE International Conference on System Science and Engineering, Shanghai, China, 11–13 July 2014; pp. 295–300. [Google Scholar]
- Yu, R.; He, X.; Liu, Y. GLAD: Group anomaly detection in social media analysis. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 372–381. [Google Scholar]
- Kinoshita, A.; Takasu, A.; Adachi, J. Real-time traffic incident detection using a probabilistic topic model. J. Intell. Inf. Syst. 2015, 54, 169–188. [Google Scholar] [CrossRef]
- Hospedales, T. Video behaviour mining using a dynamic topic model. Int. J. Comput. Vis. 2012, 98, 303–323. [Google Scholar] [CrossRef]
- Fan, Y.; Zhou, Q.; Yue, W.; Zhu, W. A dynamic causal topic model for mining activities from complex videos. Multimed. Tools Appl. 2017, 10, 1–16. [Google Scholar] [CrossRef]
- Hu, X.; Hu, S.; Zhang, X.; Zhang, H.; Luo, L. Anomaly detection based on local nearest neighbor distance descriptor in crowded scenes. Sci. World J. 2014, 2014, 632575. [Google Scholar] [CrossRef] [PubMed]
- Pathak, D.; Sharang, A.; Mukerjee, A. Anomaly localization in topic-based analysis of surveillance videos. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 5–9 January 2015; pp. 389–395. [Google Scholar]
- Jeong, H.; Yoo, Y.; Yi, K.M.; Choi, J.Y. Two-stage online inference model for traffic pattern analysis and anomaly detection. Mach. Vis. Appl. 2014, 25, 1501–1517. [Google Scholar] [CrossRef]
- Kaviani, R.; Ahmadi, P.; Gholampour, I. Incorporating fully sparse topic models for abnormality detection in traffic videos. In Proceedings of the International Conference on Computer and Knowledge Engineering, Mashhad, Iran, 29–30 October 2014; pp. 586–591. [Google Scholar]
- Isupova, O.; Kuzin, D.; Mihaylova, L. Anomaly detection in video with Bayesian nonparametrics. arXiv, 2016arXiv:1606.08455v1.
- Zou, J.; Chen, X.; Wei, P.; Han, Z.; Jiao, J. A belief based correlated topic model for semantic region analysis in far-field video surveillance systems. In Proceedings of the Pacific-Rim Conference on Multimedia, Nanjing, China, 13–16 December 2013; pp. 779–790. [Google Scholar]
- Haines, T.S.F.; Xiang, T. Video topic modelling with behavioural segmentation. In Proceedings of the ACM International Workshop on Multimodal Pervasive Video Analysis, Firenze, Italy, 29 October 2010; pp. 53–58. [Google Scholar]
- Gasparini, M. Markov chain monte carlo in practice. Technometrics 1997, 39, 338. [Google Scholar] [CrossRef]
- Schölkopf, B.; Platt, J.; Hofmann, T. A collapsed variational bayesian inference algorithm for latent dirichlet allocation. Adv. Neural Inf. Process. Syst. 2007, 19, 1353–1360. [Google Scholar]
- Hoffman, M.D.; Blei, D.M.; Bach, F. Online learning for latent dirichlet allocation. In Proceedings of the International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 6–9 December 2010; pp. 856–864. [Google Scholar]
- Mimno, D.; Hoffman, M.; Blei, D. Sparse stochastic inference for latent dirichlet allocation. arXiv, 2012arXiv:1206.6425.
- Girolami, M.; Calderhead, B. Riemann manifold langevin and hamiltonian monte carlo methods. J. R. Stat. Soc. 2015, 73, 123–214. [Google Scholar] [CrossRef]
- Welling, M.; Teh, Y.W. Bayesian learning via stochastic gradient langevin dynamics. In Proceedings of the International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011; pp. 681–688. [Google Scholar]
- Patterson, S.; Teh, Y.W. Stochastic gradient riemannian langevin dynamics on the probability simplex. In Advances in Neural Information Processing Systems, Harrahs and Harveys, Lake Tahoe, 5–10 December 2013. 3102–3110.
- Isupova, O.; Kuzin, D.; Mihaylova, L. Learning methods for dynamic topic modeling in automated behavior analysis. IEEE Trans. Neural Netw. Learn. 2017, 99, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Rosen-Zvi, M.; Chemudugunta, C.; Griffiths, T.; Smyth, P.; Steyvers, M. Learning author-topic models from text corpora. ACM Trans. Inf. Syst. 2010, 28, 1–38. [Google Scholar] [CrossRef]
- Bao, S.; Xu, S.; Zhang, L.; Yan, R.; Su, Z.; Han, D.; Yu, Y. Mining social emotions from affective text. IEEE Trans. Knowl. Data Eng. 2012, 24, 1658–1670. [Google Scholar] [CrossRef]
- Junction Dataset. Available online: http://www.eecs.qmul.ac.uk/~sgg/QMUL_Junction_Datasets/Junction/Junction.html (accessed on 29 May 2017).




| CPU | Intel® Core(TM) 2 Duo CPU E8400 @ 3.00 GHz 3.00 GHz |
| Memory | 2.00 G |
| OS | Window7 |
| Programing platform | Python 2.7.5 |
| RTM-GS | RTM-HSVG |
|---|---|
| Burn-in time ; After Markov chain convergence, sampling at intervals of 100 times; the total number of sampling is ; ; ; The hyper parameter is ; ; | Burn-in time ; After Markov chain convergence, sampling at intervals of 10 times; the total number of sampling is ; ;; The hyper parameter is ; ; |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, L.; Liu, L.; Gan, J. A Regional Topic Model Using Hybrid Stochastic Variational Gibbs Sampling for Real-Time Video Mining. Algorithms 2018, 11, 97. https://doi.org/10.3390/a11070097
Tang L, Liu L, Gan J. A Regional Topic Model Using Hybrid Stochastic Variational Gibbs Sampling for Real-Time Video Mining. Algorithms. 2018; 11(7):97. https://doi.org/10.3390/a11070097
Chicago/Turabian StyleTang, Lin, Lin Liu, and Jianhou Gan. 2018. "A Regional Topic Model Using Hybrid Stochastic Variational Gibbs Sampling for Real-Time Video Mining" Algorithms 11, no. 7: 97. https://doi.org/10.3390/a11070097
APA StyleTang, L., Liu, L., & Gan, J. (2018). A Regional Topic Model Using Hybrid Stochastic Variational Gibbs Sampling for Real-Time Video Mining. Algorithms, 11(7), 97. https://doi.org/10.3390/a11070097




