Solutions to the Sub-Optimality and Stability Issues of Recursive Pole and Zero Distribution Algorithms for the Approximation of Fractional Order Models
Abstract
1. Introduction
- -
- -
- -
- biology for modelling complex dynamics in biological tissues [9];
- -
- mechanics with the dynamical property of viscoelastic materials and for wave propagation problems in these materials [10];
- -
- acoustics where fractional differentiation is used to model visco-thermal losses in wind instruments [11];
- -
- robotics through environmental modeling [12];
- -
- electrical distribution networks [13];
- -
- modelling of explosive materials [14].
- -
- -
- -
- -
2. The Existing Algorithms Based on Pole and Zero Recursive (Geometric) Distribution
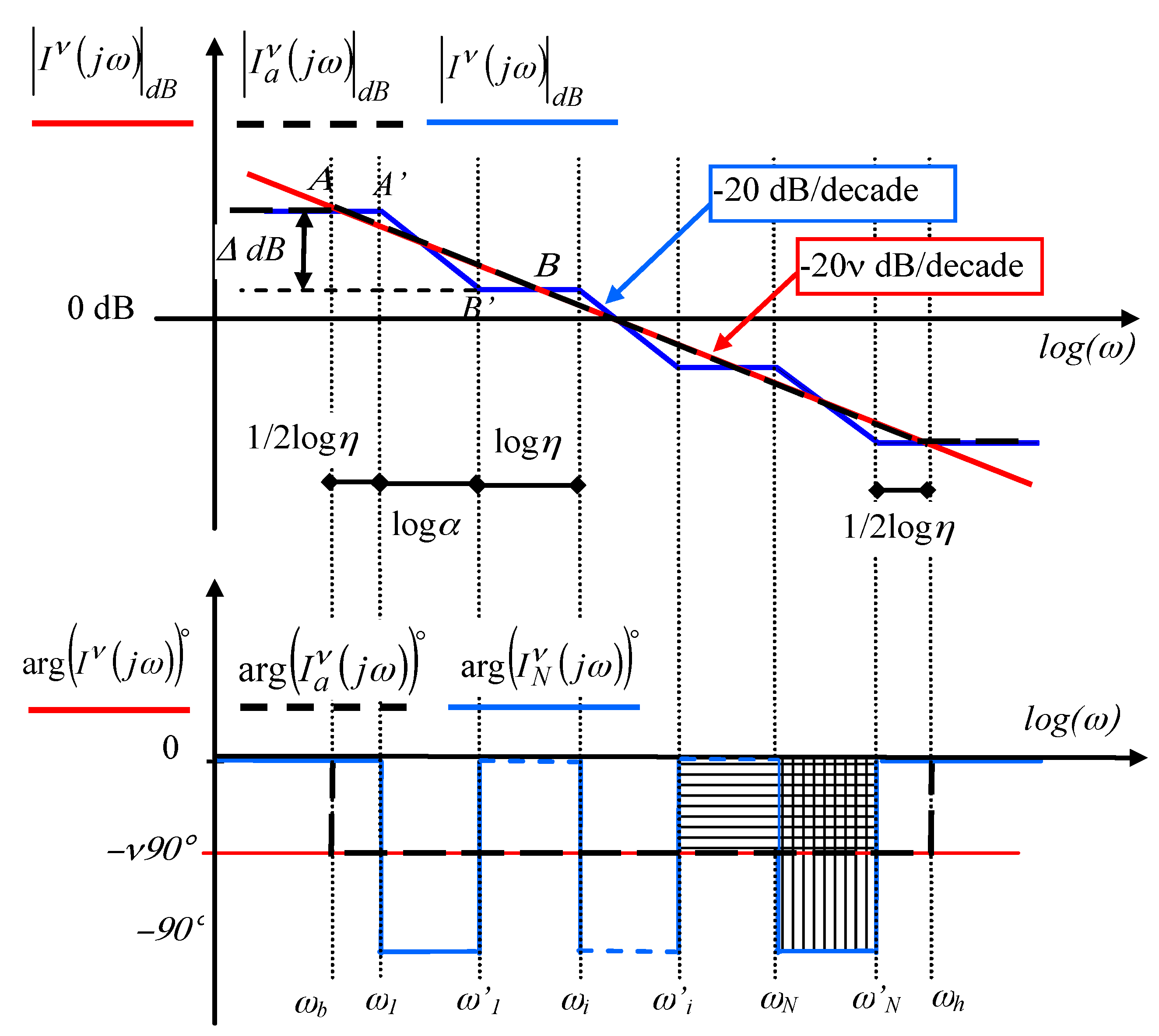
2.1. Approximation of a Fractional Integrator and Differentiator by a Recursive (Geometric) Distribution of Pole and Zeros: A Graphical Approach
- -
- a gain whose slope is a fractional multiple of −20 dB/decade,
- -
- a constant phase whose value is a fractional multiple of −90°.
| Algorithm 1. Fractional integrator approximation—first method | |
| 1. Initialize 3. Compute | |
| Algorithm 2. Fractional integrator approximation—second method | |
| 1. Initialize 3. Compute with relation (5) 4. Define the fractional integrator (1) approximation in the frequency band [ωb, ωh], by the transfer function | |
| Algorithm 3. Fractional differentiator approximation—first method | |
| 1. Initialize 3. Compute with relation (5) 4. Define the fractional differentiator (12) approximation in the frequency band [ωb, ωh], by the transfer function | |
| Algorithm 4. Fractional differentiator approximation—second method | |
| 1. Initialize 3. Compute with relation (5) 4. Define the fractional differentiator (12) approximation in the frequency band [ωb, ωh], by the transfer function | |
2.2. Approximation of a Fractional Integrator by a Recursive Distribution of Poles and Zeros: An Analytical Approach
- -
- a number N of poles that tends towards infinity,
- -
- a ratio r or Δz that tends towards 1.
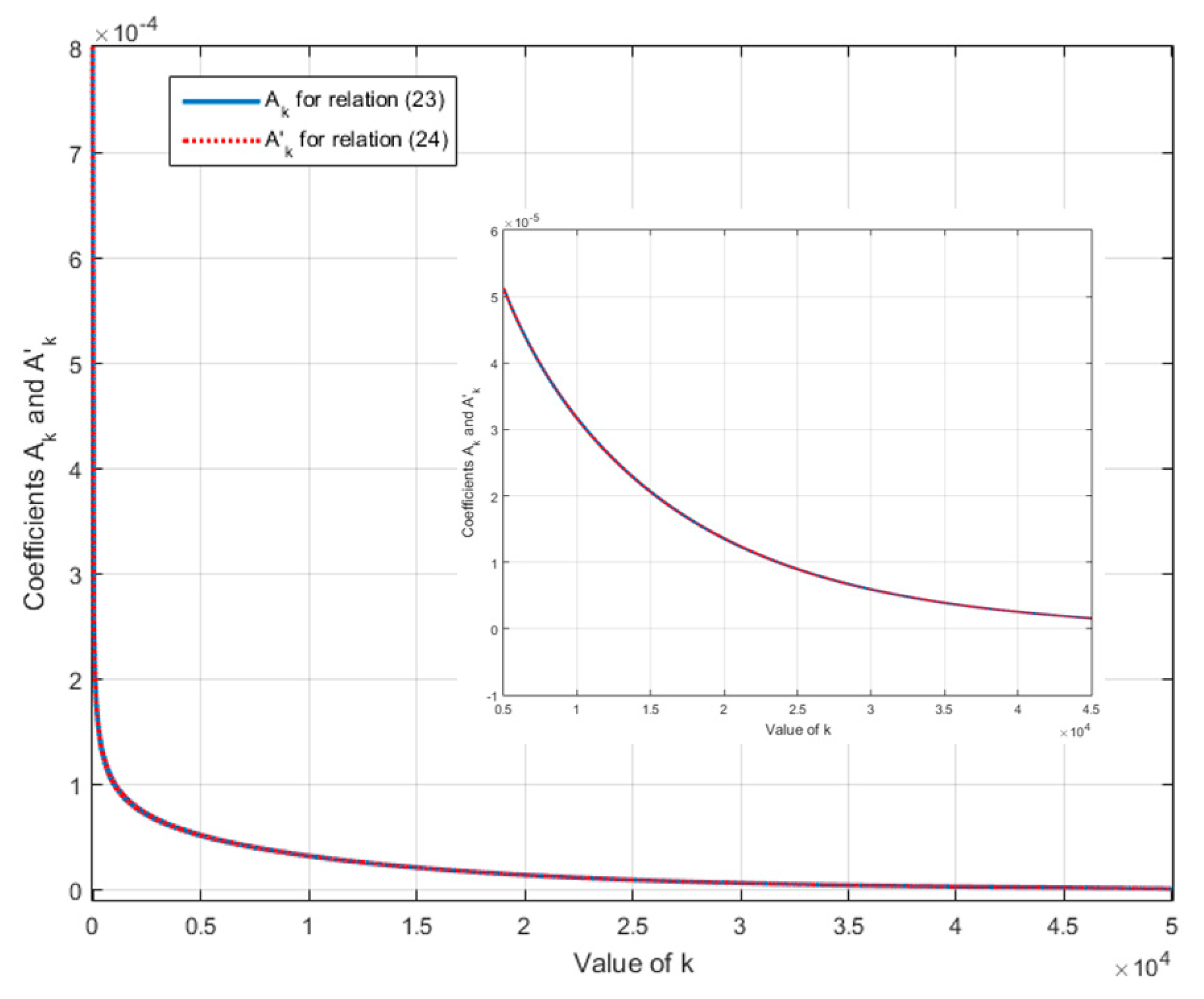
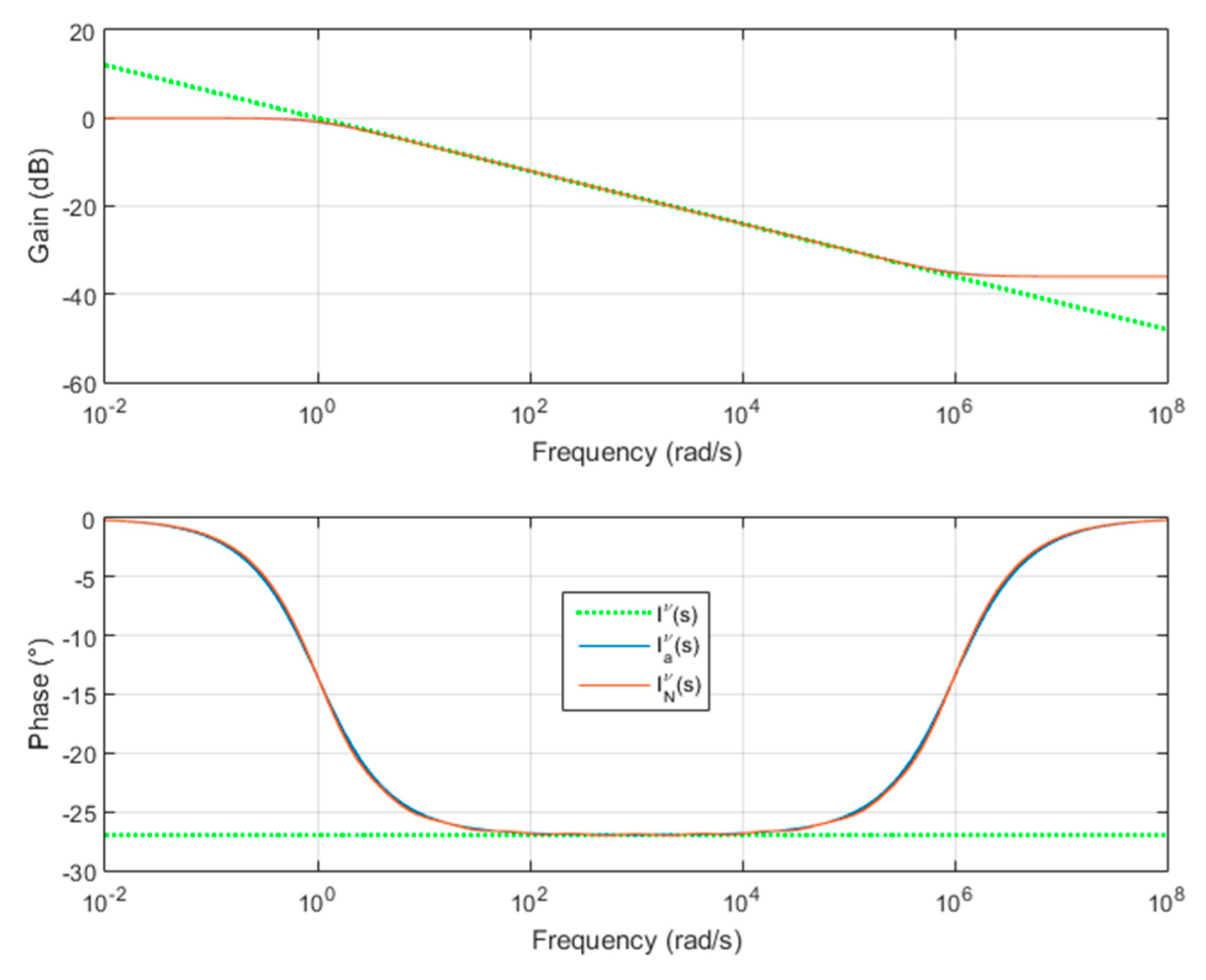
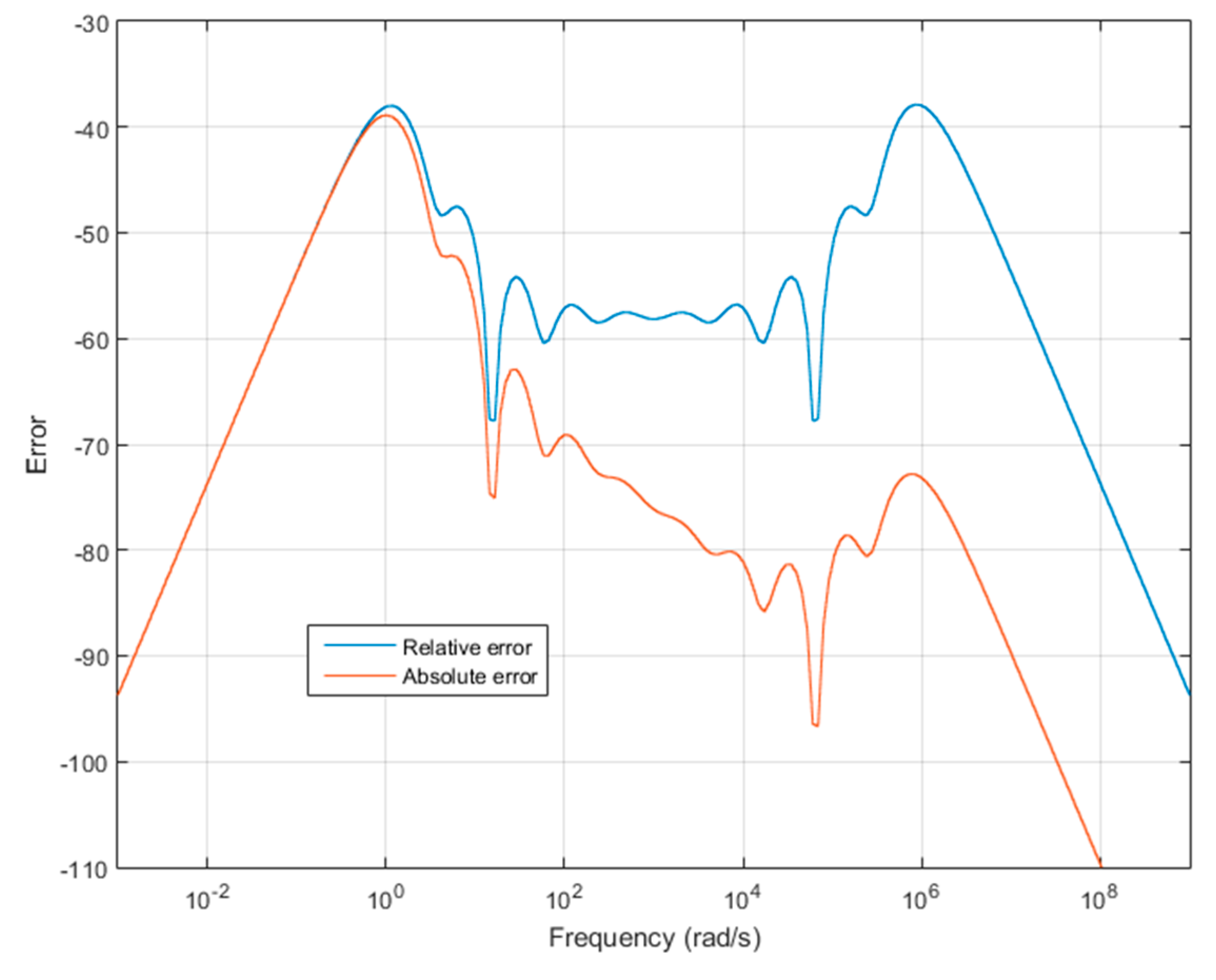
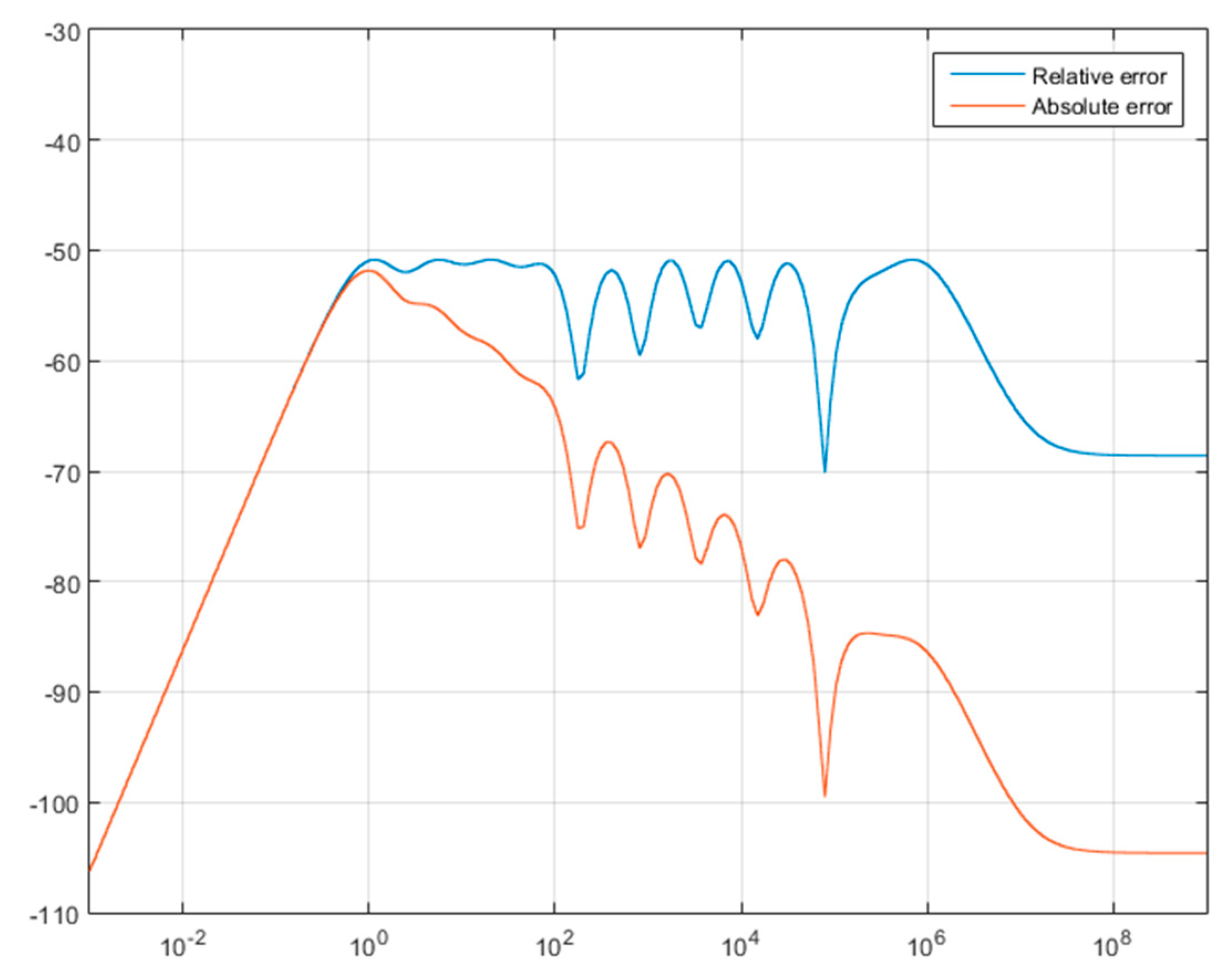
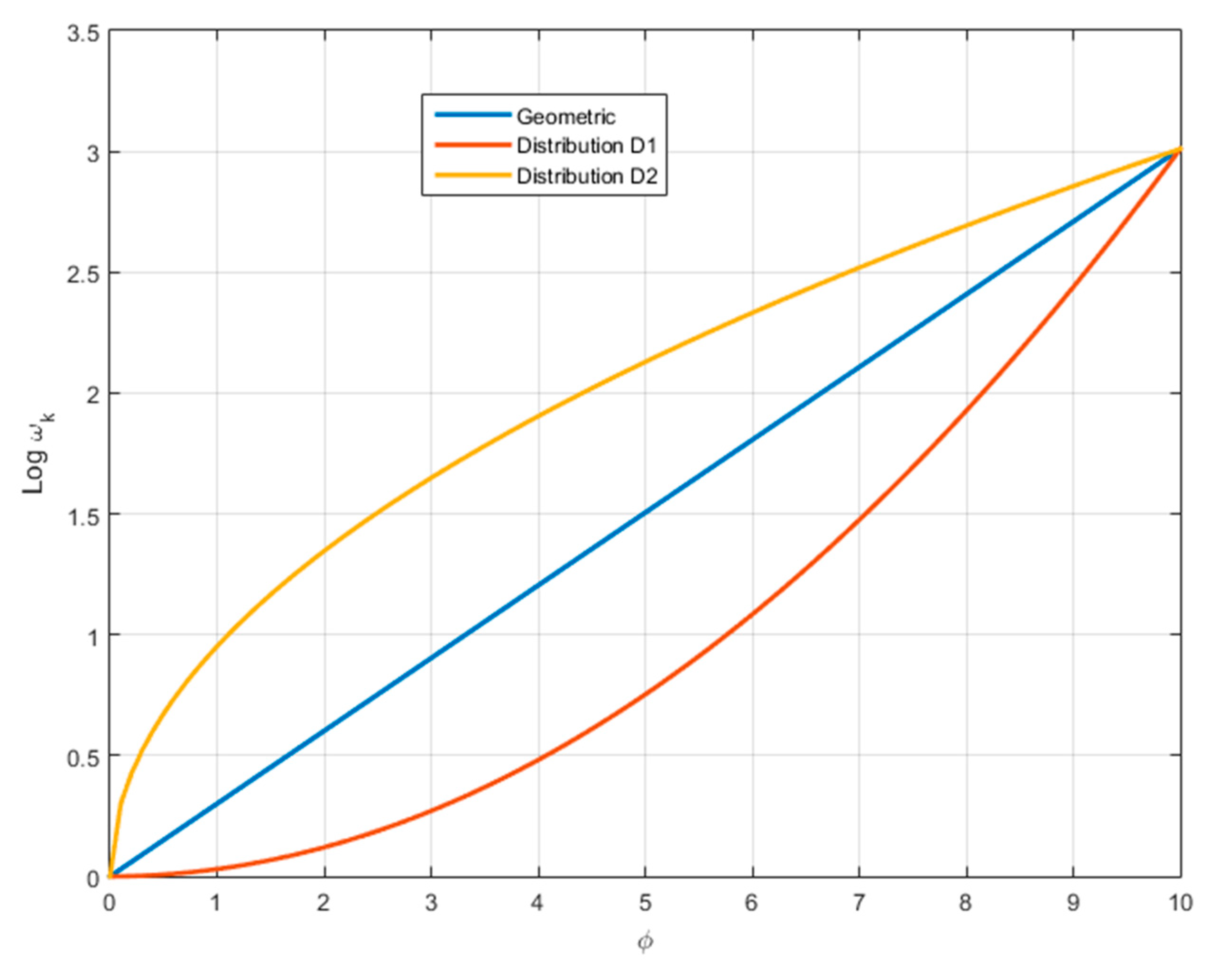
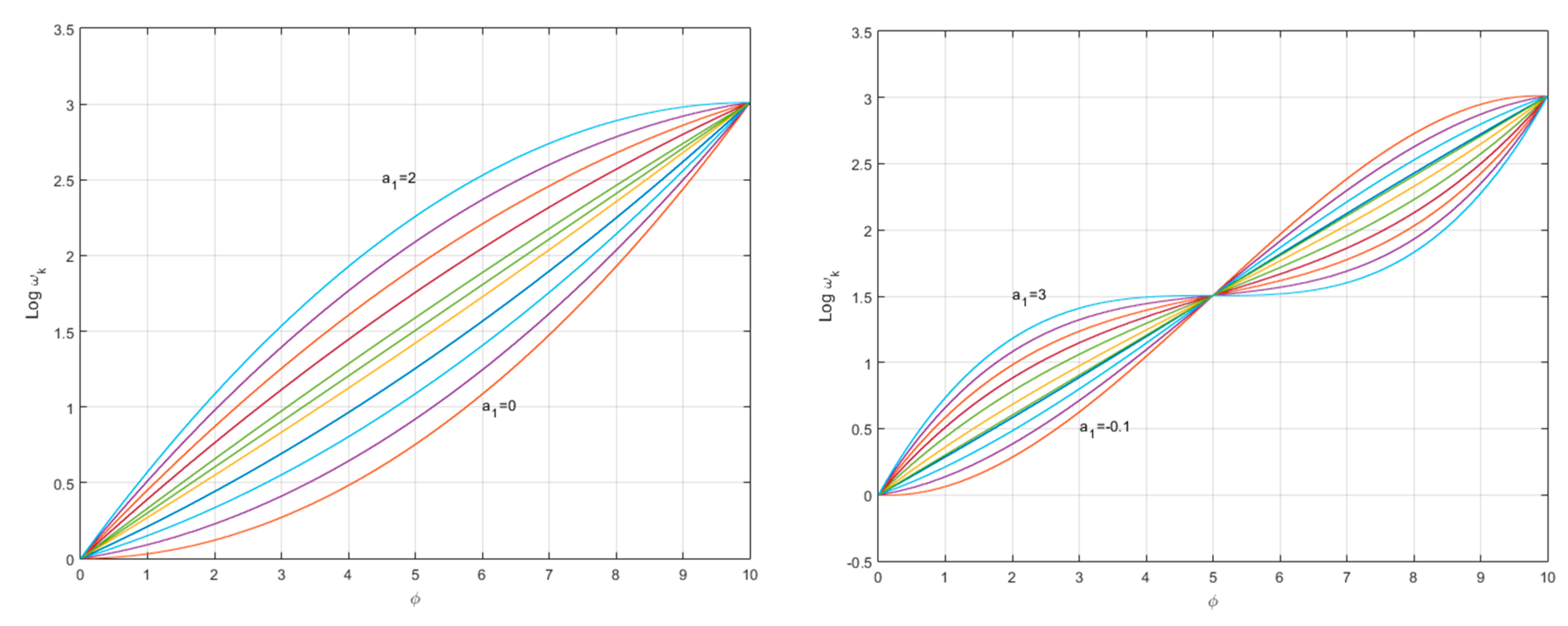
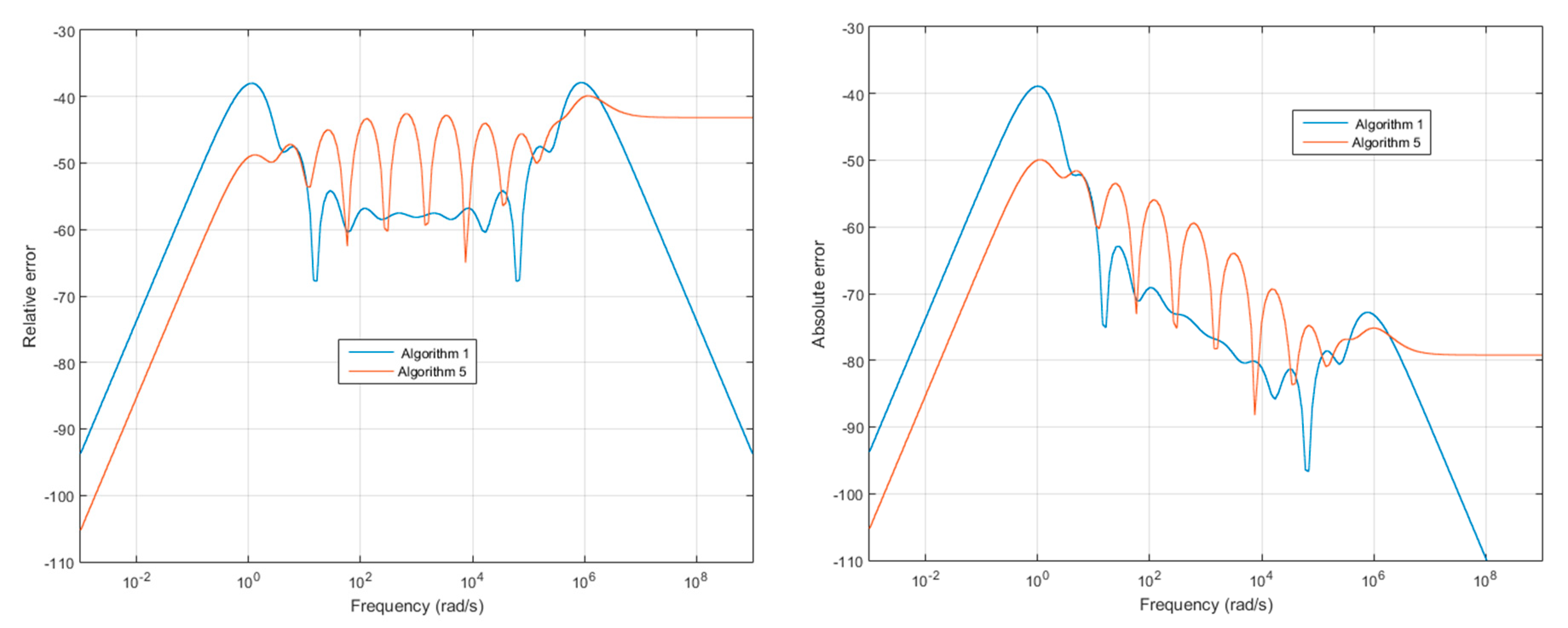
3. Sub-Optimality of Algorithms 1–4 and Beyond Geometric Distribution
| Algorithm 5. Fractional integrator approximation—improved method | |
| 1. Initialize 3. Compute with relation (5) 4. Define the fractional integrator (1) approximation in the frequency band [ωb, ωh], by the transfer function | |
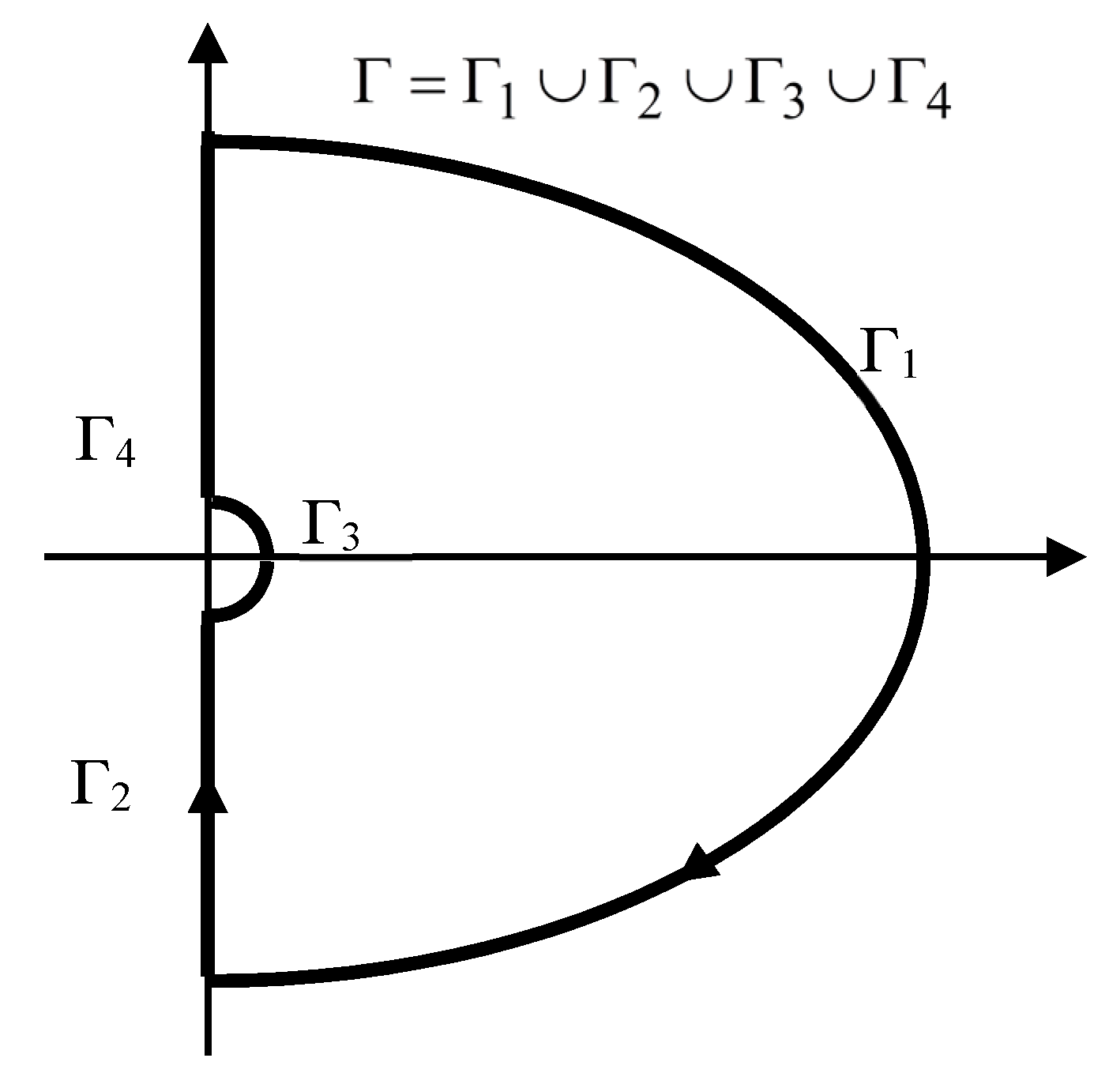
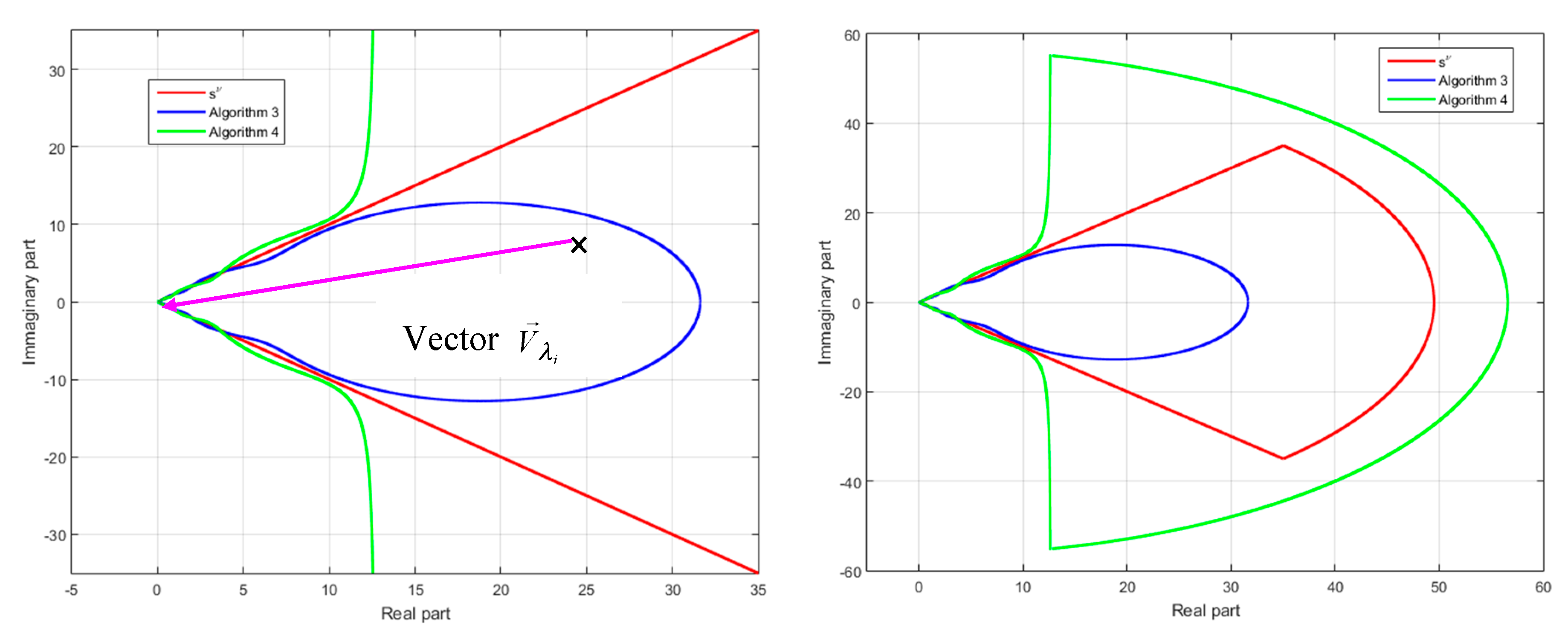
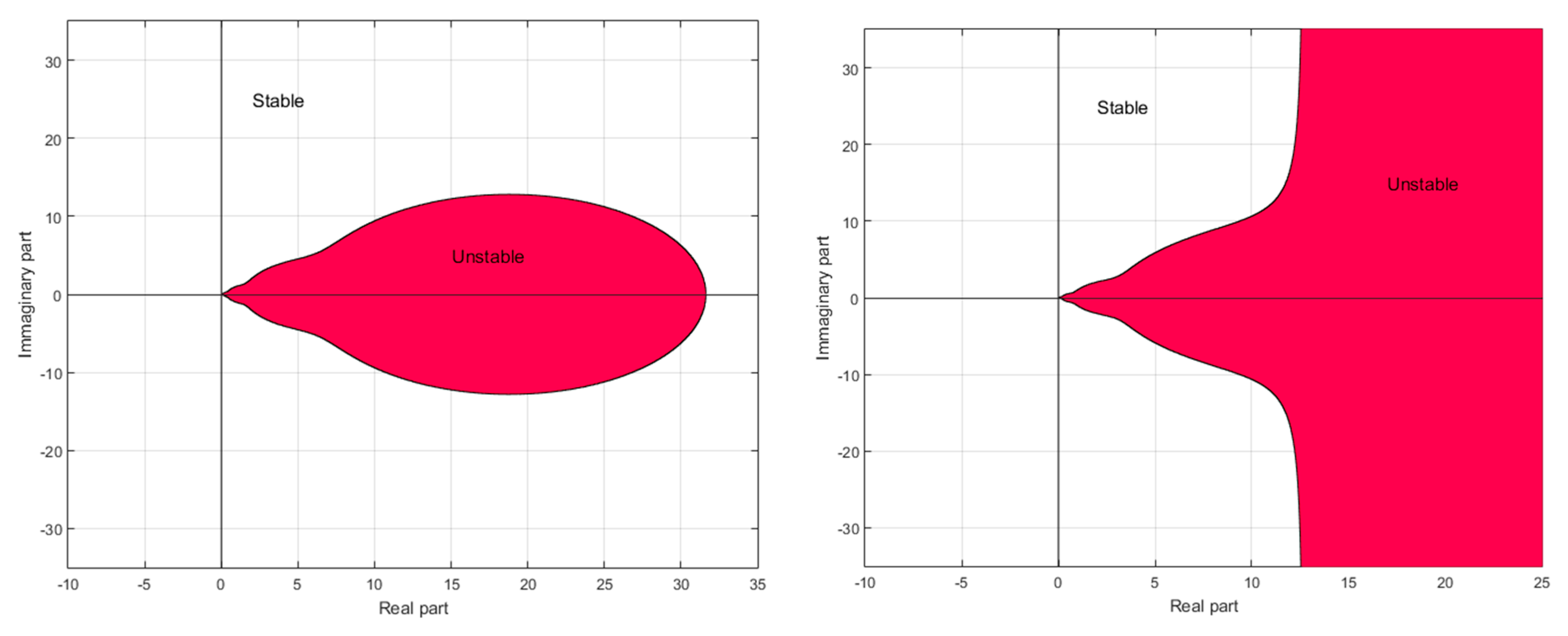
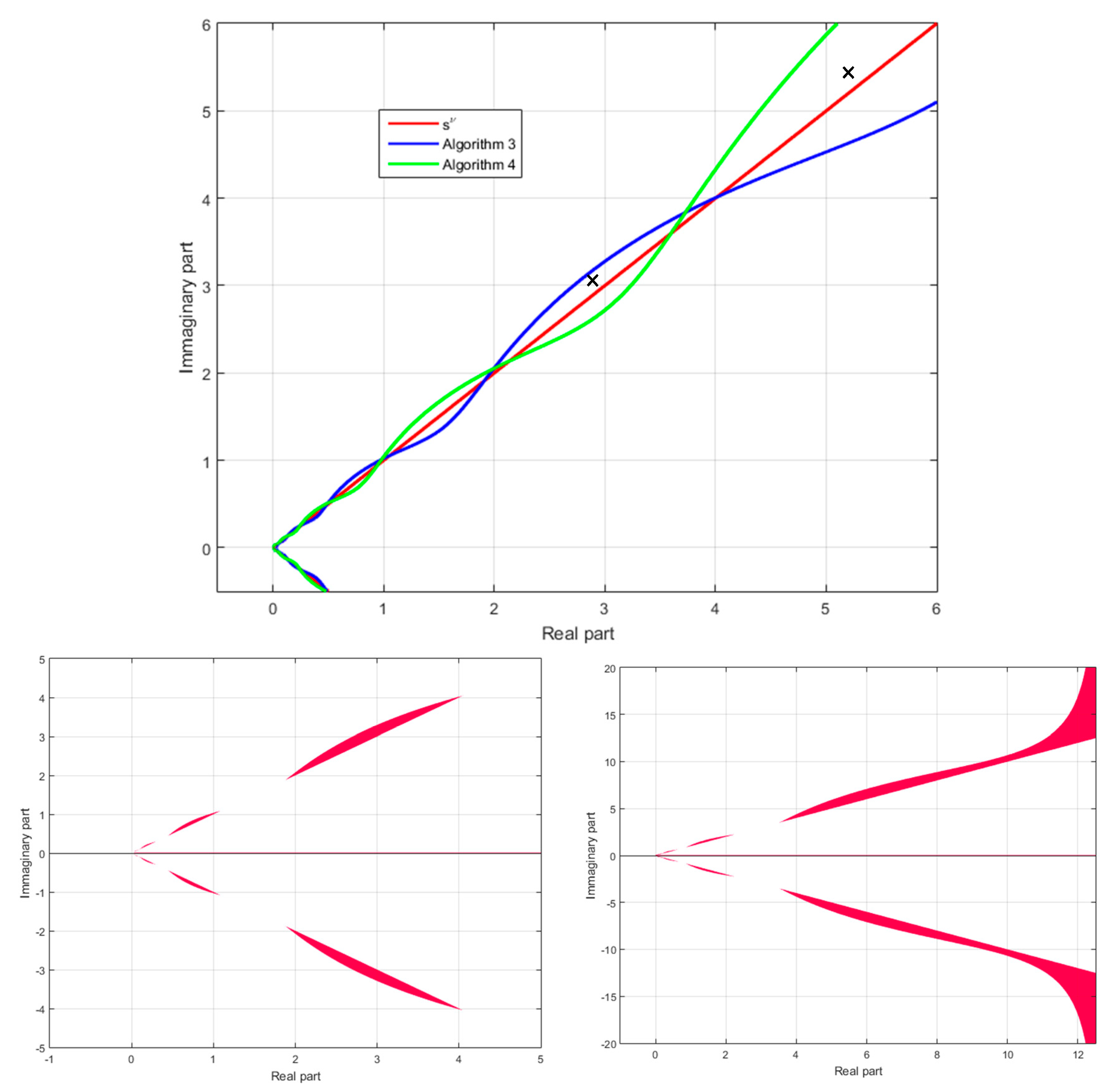
4. Fractional Model Approximation and Stability Issues
- -
- outside the domain defined by,,,for approximation (15)
- -
- outside the domain on the right of the curve,,, for approximation (18).
5. Conclusions
- -
- result in the discretization of the impulse response of a fractional model,
- -
- are sub-optimal,
- -
- are one among an infinity of other permitted distributions.
Funding
Conflicts of Interest
References
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Theory and Applications of Differentiation and Integration to Arbitrary Order (Mathematics in Science and Engineering, V); Academic Press: Cambridge, MA, USA, 1974. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional differential equations. In Mathematics in Sciences and Engineering; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Rodrigues, S.; Munichandraiah, N.; Shukla, A.K. A review of state-of-charge indication of batteries by means of a.c. impedance measurements. J. Power Sources 2000, 87, 12–20. [Google Scholar] [CrossRef]
- Jocelyn Sabatier, J.; Mohamed, A.; Oustaloup, A.; Grégoire, G.; Ragot, F.; Roy, P. Fractional system identification for lead acid battery state charge estimation. Signal Process. 2006, 86, 2645–2657. [Google Scholar] [CrossRef]
- Sabatier, J.; Merveillaut, M.; Francisco, J.; Guillemard, F. Lithium-ion batteries modelling involving fractional differentiation, Journal of power sources. J. Power Sources 2014, 262, 36–43. [Google Scholar] [CrossRef]
- Dlugosz, M.; Skruch, P. The application of fractional-order models for thermal process modelling inside buildings. J. Build. Phys. 2016, 39, 440–451. [Google Scholar] [CrossRef]
- Sabatier, J.; Farges, C.; Fadiga, L. Approximation of a fractional order model by an integer order model: A new approach taking into account approximation error as an uncertainty. J. Vib. Control 2016, 22, 2069–2082. [Google Scholar] [CrossRef]
- Magin, R. Fractional Calculus in Bioengineering; Begell House Publishers: Danbury, CT, USA, 2006. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity; Imperial College Press: London, UK, 2010. [Google Scholar]
- Matignon, D.; D’Andréa-Novel, B.; Depalle, P.; Oustaloup, A. Viscothermal losses in wind instruments: A non-integer model. Math. Res. 1994, 79, 789. [Google Scholar]
- Fonseca Ferreira, N.M.; Duarte, F.B.; Miguel, F.M.; Lima, M.F.M.; Marcos, M.G.; Tenreiro Machado, J.A. Application of fractional calculus in the dynamical analysis and control of mechanical manipulators. Fract. Calc. Appl. Anal. J. 2008, 11, 91–113. [Google Scholar]
- Enacheanu, O.; Riu, D.; Retiere, N. Half-order modelling of electrical networks Application to stability studies. IFAC Proc. Vol. 2008, 41, 14277–14282. [Google Scholar] [CrossRef]
- Gruau, C.; Picart, D.; Belmas, R.; Bouton, E.; Delmaire-Size, F.; Sabatier, J.; Trumel, H. Ignition of a confined high explosive under low velocity impact. Int. J. Impact Eng. 2009, 36, 537–550. [Google Scholar] [CrossRef]
- Sabatier, J.; Merveillaut, M.; Malti, R.; Oustaloup, A. On a Representation of Fractional Order Systems: Interests for the Initial Condition Problem. In Proceedings of the 3rd IFAC Workshop on “Fractional Differentiation and its Applications” (FDA’08), Ankara, Turkey, 5–7 November 2008. [Google Scholar]
- Sabatier, J.; Merveillaut, M.; Malti, R.; Oustaloup, A. How to Impose Physically Coherent Initial Conditions to a Fractional System? Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1318–1326. [Google Scholar] [CrossRef]
- Sabatier, J.; Farges, C.; Trigeassou, J.C. Fractional systems state space description: Some wrong ideas and proposed solutions. J. Vib. Control 2014, 20, 1076–1084. [Google Scholar] [CrossRef]
- Sabatier, J.; Farges, C. Comments on the description and initialization of fractional partial differential equations using Riemann-Liouville’s and Caputo’s definitions. J. Comput. Appl. Math. 2018, 339, 30–39. [Google Scholar] [CrossRef]
- Sabatier, J.; Farges, C.; Merveillaut, M.; Feneteau, L. On observability and pseudo state estimation of fractional order systems. Eur. J. Control 2012, 18, 1–12. [Google Scholar] [CrossRef]
- Malti, R.; Sabatier, J.; Akçay, H. Thermal modeling and identification of an aluminum rod using fractional calculus. In Proceedings of the 15th IFAC Symposium on System Identification, Saint-Malo, France, 6–8 July 2009; pp. 958–963. [Google Scholar]
- Oustaloup, A.; Levron, F.; Mathieu, B.; Nanot, F. Frequency-band complex non integer differentiator: Characterization and synthesis. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 25–39. [Google Scholar] [CrossRef]
- Poinot, T.; Trigeassou, J.-C. A method for modelling and simulation of fractional systems. Signal Process. 2003, 83, 2319–2333. [Google Scholar] [CrossRef]
- Manabe, S. The non-integer Integral and its Application to control systems. ETJ Jpn. 1961, 6, 83–87. [Google Scholar]
- Carlson, G.E.; Halijak, C.A. Simulation of the Fractional Derivative Operator and the Fractional Integral Operator. Available online: http://krex.k-state.edu/dspace/handle/2097/16007 (accessed on 30 June 2018).
- Ichise, M.; Nagayanagi, Y.; Kojima, T. An analog simulation of non-integer order transfer functions for analysis of electrode processes. J. Electroanal. Chem. Interfacial Electrochem. 1971, 33, 253–265. [Google Scholar] [CrossRef]
- Oustaloup, A. Systèmes Asservis Linéaires d’ordre Fractionnaire; Masson: Paris, France, 1983. [Google Scholar]
- Raynaud, H.F.; Zergaïnoh, A. State-space representation for fractional order controllers. Automatica 2000, 36, 1017–1021. [Google Scholar] [CrossRef]
- Charef, A. Analogue realisation of fractional-order integrator, differentiator and fractional PI/^ lambda/D/^ mu/ controller. IEE Proc. Control Theory Appl. 2006, 153, 714–720. [Google Scholar] [CrossRef]
- Oustaloup, A. Diversity and Non-integer Differentiation for System Dynamics; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sabatier, J. Solutions to the Sub-Optimality and Stability Issues of Recursive Pole and Zero Distribution Algorithms for the Approximation of Fractional Order Models. Algorithms 2018, 11, 103. https://doi.org/10.3390/a11070103
Sabatier J. Solutions to the Sub-Optimality and Stability Issues of Recursive Pole and Zero Distribution Algorithms for the Approximation of Fractional Order Models. Algorithms. 2018; 11(7):103. https://doi.org/10.3390/a11070103
Chicago/Turabian StyleSabatier, Jocelyn. 2018. "Solutions to the Sub-Optimality and Stability Issues of Recursive Pole and Zero Distribution Algorithms for the Approximation of Fractional Order Models" Algorithms 11, no. 7: 103. https://doi.org/10.3390/a11070103
APA StyleSabatier, J. (2018). Solutions to the Sub-Optimality and Stability Issues of Recursive Pole and Zero Distribution Algorithms for the Approximation of Fractional Order Models. Algorithms, 11(7), 103. https://doi.org/10.3390/a11070103



