1. Introduction
Iterative learning control (ILC) is an effective technique for improving the performance of systems that operate repetitively over a fixed time interval [
1,
2,
3,
4]. The fundamental idea in ILC is that the task to be carried out by the system is of a repetitive nature. By using such a repetitive nature, it is possible to adjust the input signal such that the output signal follows the reference signal as closely as possible. Owing to its simplicity and effectiveness, ILC is playing an important role in many areas and applications [
5,
6,
7].
Distributed parameter systems are a class of complicated infinite-dimensional systems, whose states depend on both spatial position and time [
8,
9,
10,
11]. In recent years, the application of ILC to distributed parameter systems has become a new topic [
12,
13,
14,
15]. In [
12], an open-loop P-type iterative learning controller was designed for the first order hyperbolic distributed parameter system. The P-type and D-type ILC algorithms were studied in [
13] for a class of parabolic distributed parameter systems. For a class of single-input single-output coupling nonlinear distributed parameter systems, a P-type learning controller was designed, and the convergence conditions, speed and robustness of the iterative learning algorithm were also discussed in [
14]. For uncertain nonlinear distributed parameter systems and state time-delay distributed parameter systems, the P-type ILC was investigated in [
15,
16], respectively. A D-type anticipatory ILC scheme was applied to the boundary control of a class of inhomogeneous heat equations in [
17]. In [
18], a framework in the frequency domain of ILC was designed for linear inhomogeneous distributed parameter systems. By using the Gronwall–Bellman inequality, a close-loop P-type iterative learning algorithm is proposed for linear parabolic distributed parameter systems in [
19]. In addition, based on the eigenspectrum and reduced order model, the ILC was proposed for a class of parabolic distributed parameter systems in [
20].
Note that the above existing ILC methods for distributed parameter systems only focus on the lower order ILC. That is, to update the input profile, the learning algorithms use only the information from the last cycle. As we all known, the higher order learning algorithm incorporates the information not only from the last cycle, which can lead to better performance in terms of both robustness and convergence rate [
21,
22,
23]. In [
24], for a class of parabolic linear distributed parameter systems with uncertainty coefficients, an ILC algorithm with a forgetting factor was proposed, and the conditions for the convergence of the algorithm were established.
On the other hand, in recent years, fractional order control systems have attracted increasing interest. It was found that many systems in interdisciplinary fields could be elegantly described with the help of fractional derivatives and integrals, such as viscoelastic systems, dielectric polarization, electrode-electrolyte polarization and electromagnetic waves [
25,
26,
27]. In [
28], a fractional order distributed parameter system was used to describe radial ground water flow. The existence and uniqueness of mild and classical solutions for a class of distributed order fractional differential equations had been studied in [
29]. By using the differential inequality method, some sufficient conditions for the oscillation of solutions for partial fractional differential equations were presented in [
30]. A fundamental solution of a fractional order distributed parameter system was presented in [
31]. The numerical solutions of such systems were proposed in the literature by means of finite difference methods [
32], spectral collocation methods and others [
33,
34]. However, it is worth pointing out that up to now, there is no concern about ILC for fractional order distributed parameter systems.
The purpose of this paper is to present a second order P-type ILC algorithm with initial state learning for fractional order linear distributed parameter systems. The main contributions of this paper are as follows. (1) By analyzing the control and learning processes, the second order P-type ILC design problem for fractional order linear distributed parameter systems is converted to a stability problem for a discrete system. (2) Using the generalized Gronwall inequality, the control input and the tracking errors convergence analysis are given in detail. The obtained convergence condition is less conservative than some existing ones in recent literature in the case of integral order. (3) The proposed design method can be extended to ILC for fractional order parabolic distributed parameter systems involving time-delay, locally Lipschitz, as well as bounded external disturbance.
The rest of this paper is organized as follows: In
Section 2, the problem formulation and some preliminaries are presented. The convergence analysis for the second order p-type ILC algorithm is derived in
Section 3.
Section 4 presents a numerical example that demonstrates the effectiveness of the method. Finally, some conclusions are drawn in
Section 5.
2. Preliminaries and Problem Statement
In this section, some basic definitions and properties (for more details, see [
25]) are first introduced, which will be used in the following sections.
Definition 1 ([
25]).
The definition of the Liouville fractional integral is described by:where is the well-known Gamma function, which is defined by . Definition 2 ([
25]).
The Caputo derivative is defined by:where n is the first integer, which is not less than α, i.e., In the following, for simplicity, we denote the fractional integral by and the Caputo derivative by , respectively.
Definition 3 ([
25]).
The two-parameter Mittag–Leffler function is defined by:For Especially, To proceed with the discussion of the main results, the following lemmas are given.
Lemma 1 ([
25]).
From the definition of the Caputo derivative, when , we have: Lemma 2 ([
35]).
Let be a vector of a differentiable function. Then, for any time instant , the following relationship holds:where is a constant, square, symmetric and positive definite matrix. Lemma 3 ([
25]).
The fractional order differentiation or integral of the Mittag–Leffler function is:where . Lemma 4 (Generalized Gronwall inequality [
36]).
Suppose , a(t) is a nonnegative, nondecreasing function locally integrable on (some ) and g(t) is a nonnegative, nondecreasing continuous function defined on , (constant), and suppose is nonnegative and locally integrable on with:on the interval. Then: In this paper, we consider a class of fractional order linear distributed parameter systems with repetitive operation characteristics as follows:
where subscript
k denotes the iterative number of the process;
x and
t respectively denote space and time variables,
;
is a bounded open subset with smooth boundary
;
,
are the state vector, input vector and output vector of the system, respectively. The time-varying matrices
with appropriate dimensions are assumed to be bounded and square integrable on
D is a bounded positive constant diagonal matrix, i.e.,
.
and
are known, and
is a Laplace operator on
.
Remark 1. When the fractional order the fractional order distributed parameter System (1) is reduced to an integral order one, which has been widely investigated in [11,16,17,18,19]. The corresponding initial and boundary conditions of System (
1) are:
where
is the unit outward normal derivative on
and
and
are known constant diagonal matrices, satisfying:
The design objective in this paper is to find an iterative learning control law to generate the control input such that the system output tracks the desired output trajectory as accurately as possible when k goes to infinity for all .
To this end, the updating law considered in this manuscript is a second order P-type ILC updating law given by:
where
denotes the tracking error,
are two initial inputs,
is a constant and
,
and
L are unknown parameters to be determined.
Remark 2. The identical initial condition is commonly used in ILC. As pointed out in [37], it will limit the application of ILC. Many modified strategies have been used to avoid this restriction. Borrowed from [37,38], we designed a P-type ILC updating law (7) with initial state learning where the strict identical initial condition is not required. Throughout, this paper, denotes an n-dimensional Euclidean space, and I means an identity matrix of appropriate order. For the n-dimensional vector , its two-norm for the n-dimensional vector is defined as , and the spectrum norm of the order square matrix A is where represents the maximum eigenvalue. denotes the spectral radius of matrix A. Let be the Hilbert space. If we define then
For the function
we define the norm of
as:
For the function sequence
, the norm of
is defined as:
3. Convergence Analysis for Second Order P-Type ILC
To obtain the main results, some useful lemmas are introduced.
Lemma 5 (Greens formula [
39]).
Let , then:where is the unit outward normal derivative on . For fractional order linear distribute parameter System (
1) with the P-type ILC updating law (
7), we first give the following lemmas.
Lemma 6. Let , and:where:then Proof. It follows from (
7) that:
Since
, then from (
1), it can be obtained that:
From (
9) and (
10), by some calculation, it can be obtained that:
The proof is complete. ☐
Based on Lemma 6, it is not difficult to prove the following lemma.
Lemma 7. For fractional order linear distribute parameter System (1), if:where:then for all , the second order P-type ILC updating law (7) guarantees that: Proof. According to Lemma 6, we have:
where:
Substituting (
14) into (
13) gives:
Therefore, according to the contracting mapping principle, we have:
The proof is complete. ☐
From Lemma 6, it can be see that the design problem of a second order P-type ILC updating law (
7) for fractional order linear distributed parameter System (
1) is equivalent to the stability problem of the discrete System (
8).
Lemma 8. If an appropriate constant λ is chosen such that , then: Proof. It follows the definition of
and the assumptions that:
Then, using the Green formula and the boundary condition (
2) to
, we have:
Using the H
lder inequality of
, we get:
Therefore, from (
20) to (
23), we obtain:
Integrating both sides of (
24) above
t, we can get:
where
Following from Lemma 3 and the definition of the Mittag–Leffler function that for
, we have:
As a result,
is an increasing function.
Using the generalized Gronwall inequality of Inequality (
25), it results:
Furthermore, it can be easily proven that:
Substituting it into Inequality (
26), one has:
Multiplying both sides of the above inequality by
, one has:
It follows from (
7), and we have
By substituting it into (
29), we can obtain:
On the other hand, it follows from (
9) that:
where
According to (
8), we have:
where
. As a result, we obtain from (
30) to (
32) that:
Thus, by defining
,
and selecting a sufficiently large
such that
, we can get:
By applying the
-norm and substituting the above equality into (
18), we can obtain:
Furthermore, applying the
-norm to Inequality (
35), it yields (
17), which completes the proof. ☐
In the following, based on Lemmas 6 to 8, a convergent condition for both tracking errors and control input is derived for fractional order linear distributed parameter System (
1).
Theorem 1. For fractional order linear distributed parameter System (1) and a given reference , suppose that the condition in Lemma 7 is satisfied. If:where Π
is the same as in Lemma 6, then for all , the second order P-type ILC updating law (7) guarantees that: Proof. It follows from (
8) for
that:
Noting that
by assumption, then there exists a constant
,
, and a sufficiently large
such that
and:
For the above
and
, multiplying both sides of Inequality (
39) by
and taking the
-norm, it yields:
It follows from (
17) and (
41), and we have:
where
Therefore,
Consequently, one obtains from (
44) and (
45) that:
Note that the condition in Lemma 7 is satisfied. Theretofore,
is convergent and bounded. Besides,
, it follows from (
46) that:
Thus, for all
,
we have:
The proof is complete. ☐
In particular, we have the following corollary.
Corollary 1. For fractional order linear distributed parameter System (1) and a given reference , if:and:then for all , the following P-type ILC updating law:guarantees that: Proof. Setting
, from Theorem 1, it can be concluded that if:
where:
and:
where
, then the P-type ILC updating law (
51) guarantees that
Noting that:
and:
it follows from the definition of the spectral radius that:
The proof is completed. ☐
The following corollary is obvious.
Corollary 2. For fractional order linear distributed parameter System (1) and a given reference , if:and:then for all , the close-loop P-type ILC updating law:guarantees that: From the proof of Theorem 1, it is not difficult to show the following Corollary.
Corollary 3. For fractional order linear distributed parameter System (1) and a given reference , suppose that in the learning process, the system states start from the same initial value, or more generally,if:then for all , the close-loop P-type ILC updating law:guarantees that: Remark 3. It should be pointed out that the derived result in Corollary 3 is still true for the integral order () case. Note that the convergence analysis of ILC updating law (62) for integer order linear distributed parameter System (1) has been investigated in [19], in which the convergence condition is: Since , the convergence Condition (61) is less conservative than Condition (64) (see, e.g., the example in Section 4). 4. Numerical Example
In this section, two numerical examples are presented to demonstrate the validity of the design method.
Consider a tubular flow reactor with a cooling jacket where an irreversible exothermic zeroth order reaction takes place. The reaction rate is considered to be temperature dependent, then it varies with time and the location of the reactor. The cooling jacket and feed temperatures are chosen as the manipulated variables. The thermal spatiotemporal dynamics can be derived from the energy balance inside the reactor and can be presented as the following distributed parameter systems [
40]:
where
T is the stream temperature inside the reactor,
t is time and
denotes the spatial coordinate,
L is the reactor length. The terms
and
h are used for thermal conductivity, density, heat capacity, axial velocity, heat of reaction, pre-exponential reaction constant, activation energy and the heat transfer coefficient between the reactor and cooling jacket, respectively.
presents the cooling jacket temperature.
In the vicinity of the steady-state working point, nonlinear Model (
65) can be linearized as [
41]:
where
and
vary nonlinearly with temperature during the entire heating process. Define the measured value of the thermocouple as:
In order to simplify the example, set the above distributed parameter system with fractional order
and:
where
.
Let the reference be
,
. For the above system, we apply the following P-type ILC updating law:
where
The initial state value is
, while the control input value at the beginning of learning is set to zero.
By some straightforward calculations, we can find:
That is, the convergence Condition (64) is not satisfied (Theorem 1 in [
19] is invalid). However,
From Corollary 3, it can be concluded that the tracking error is convergent.
To simulate the fractional order operator, we use the following expression: [
42]
where
h represents the sampling interval and the number of samples is denoted as
k.
is the notation of the binomial coefficients. To conserve computing resources, the length of the memory
L is set as a finite recording number [
42], usually
. To obtain the numerical solution, we use the two order explicit center difference scheme, in which the sampling periods are taken as
.
From the viewpoint of viscoelastic theory, the initial history (terminal) should be the state over a time-interval, not a state at a given time [
43,
44]. To consider the physically consistent initial conditions, a simple solution could be obtained by the procedure proposed in [
43,
45]. To simplify this discussion, the initial time of setting the integral is zero.
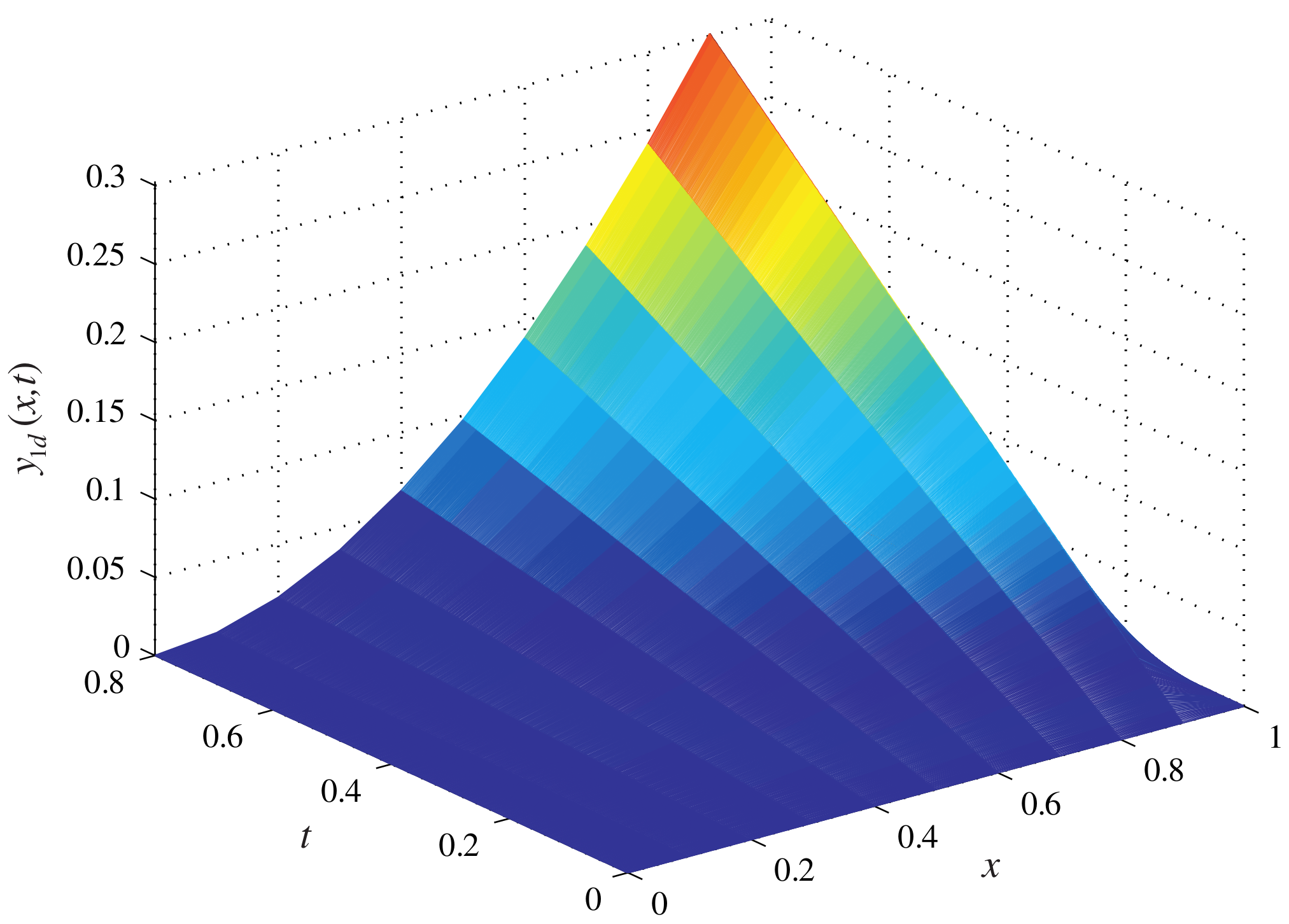
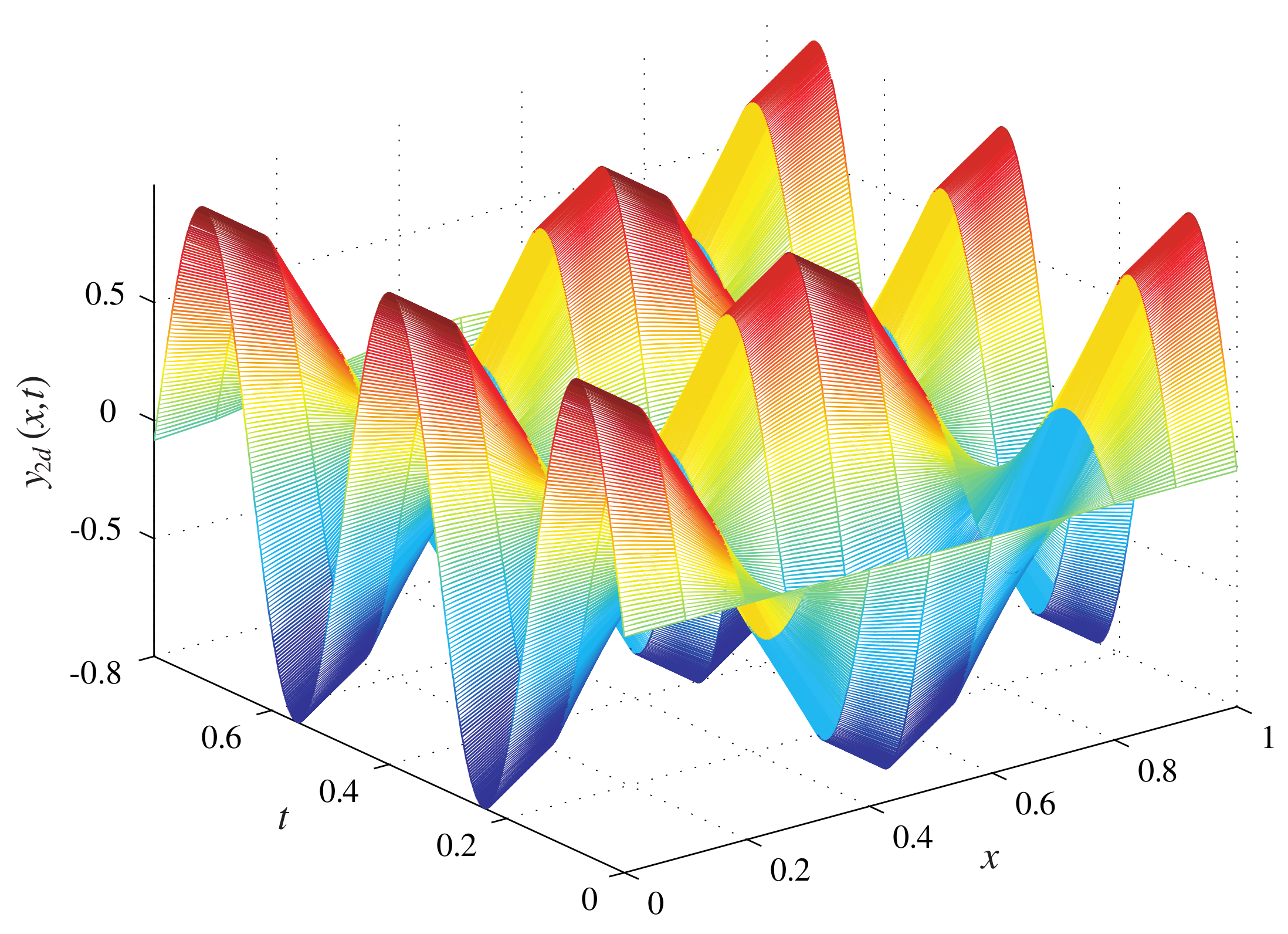
Figure 1 and
Figure 2 are the desired curved surfaces.
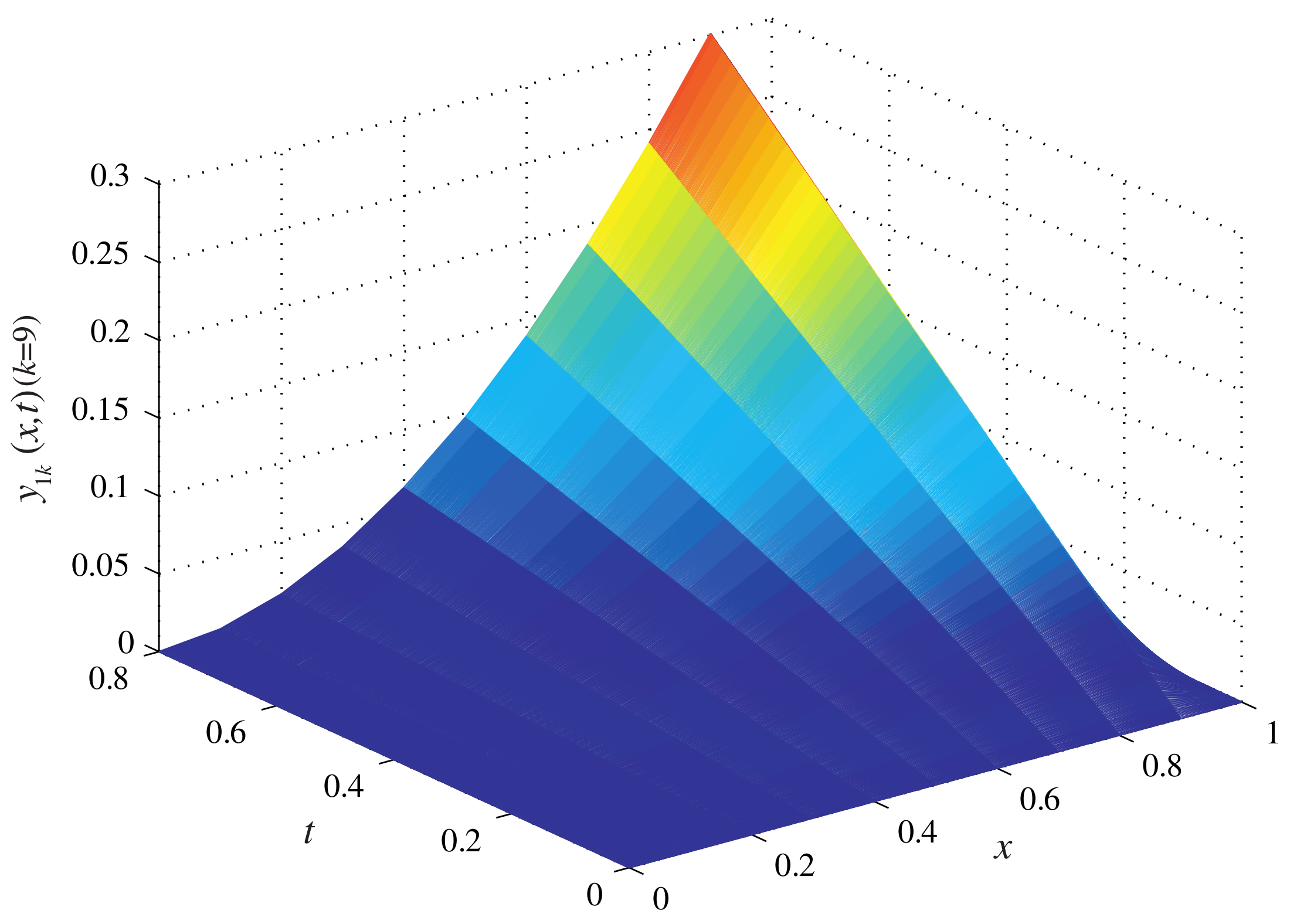
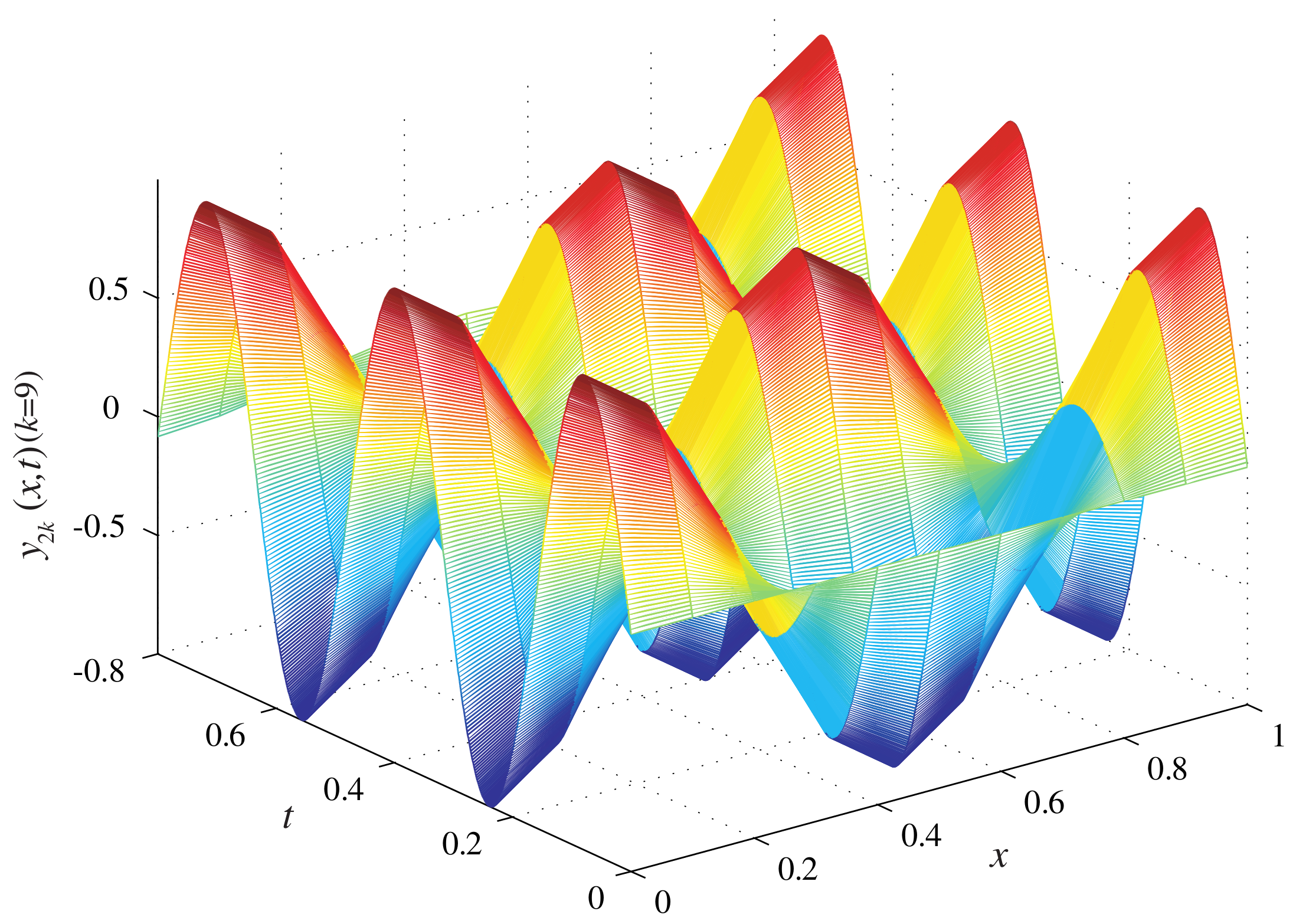
Figure 3 and
Figure 4 show the system output of the ninth iterations. It can be seen that the system output is capable of approaching the desired trajectory accurately within a few iterations.
Figure 5 and
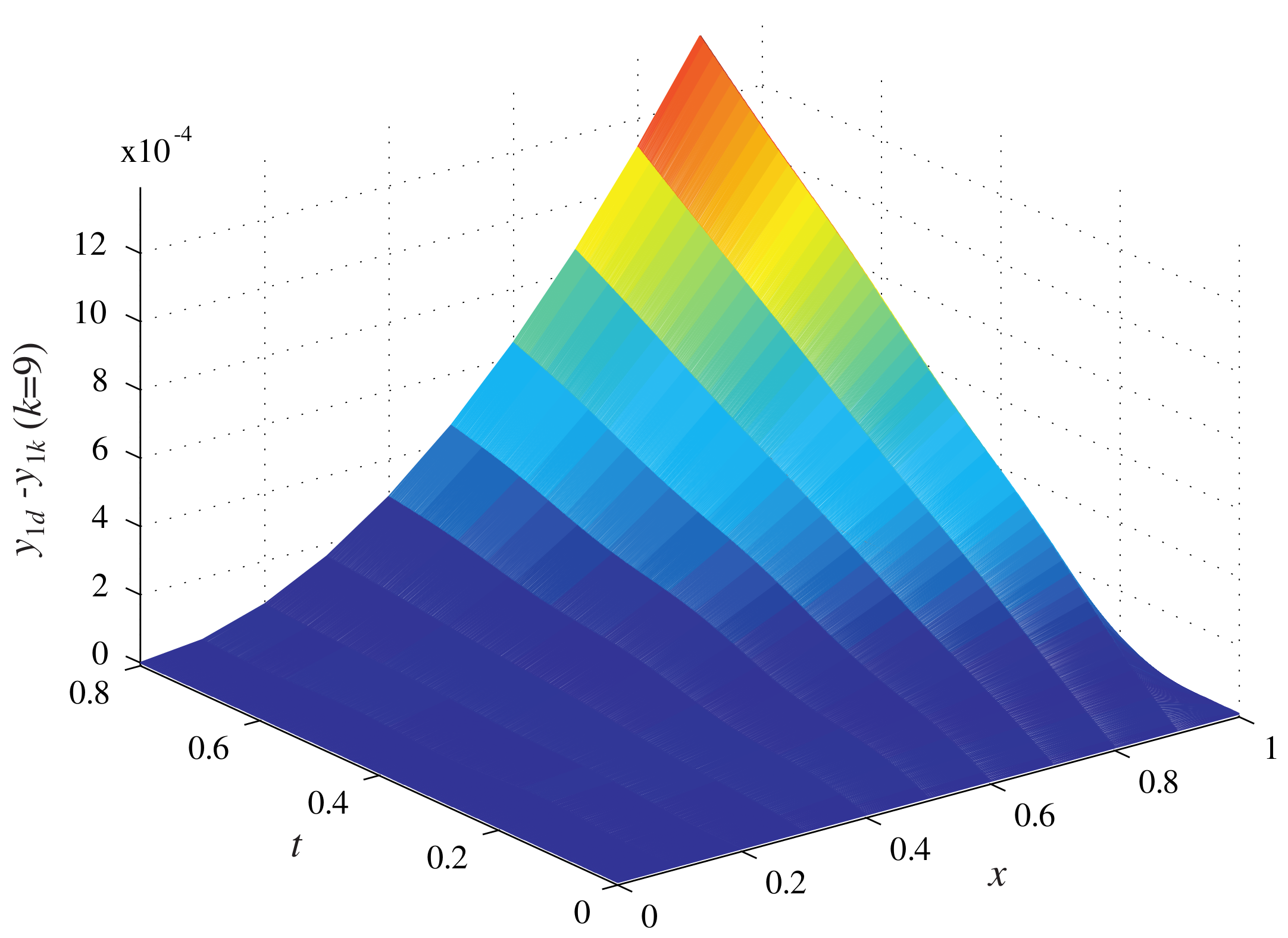
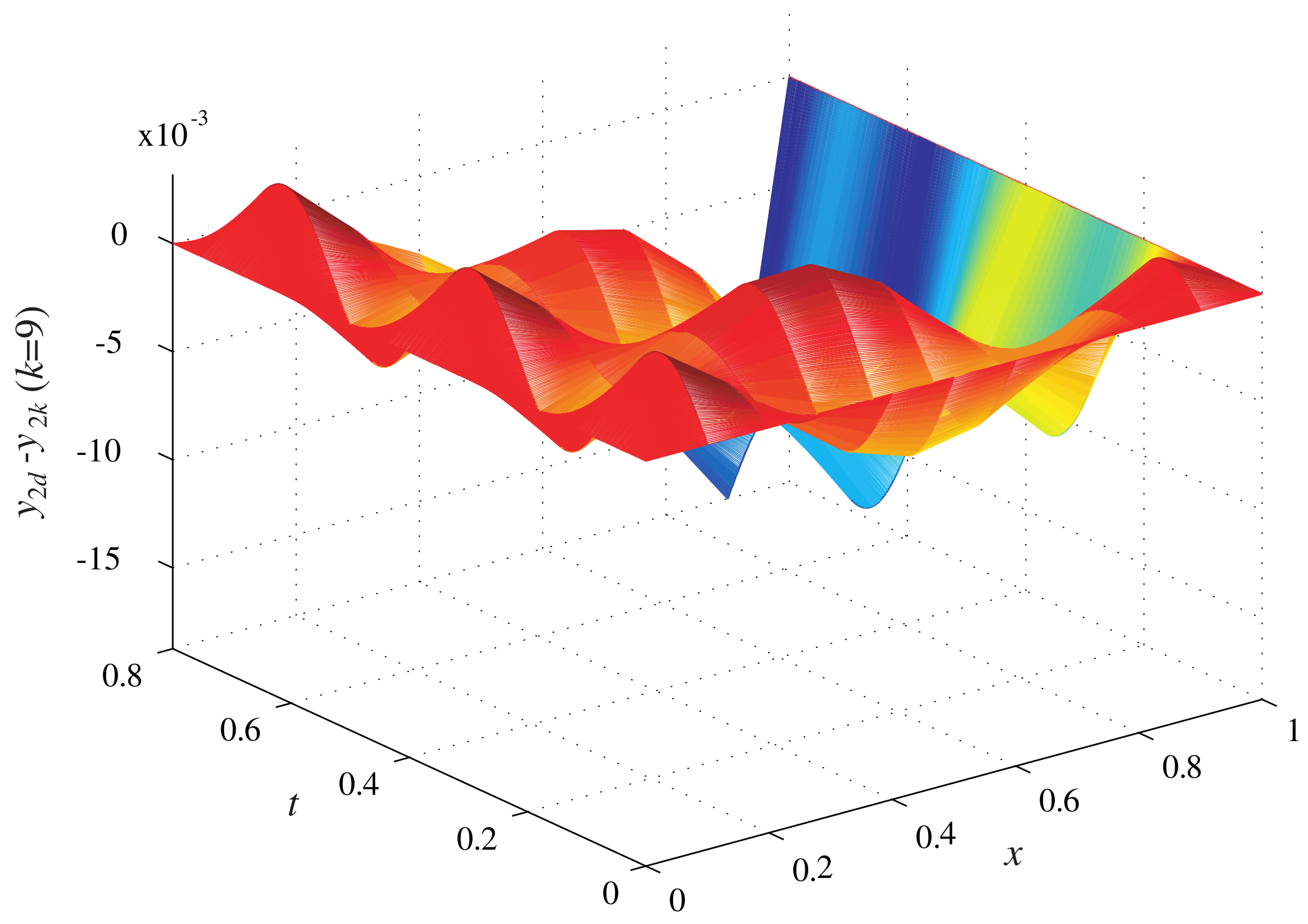
Figure 6 are the error surface when iteration number
When the number of iterations is nine, the absolute values of the maximum tracking error are
, respectively.
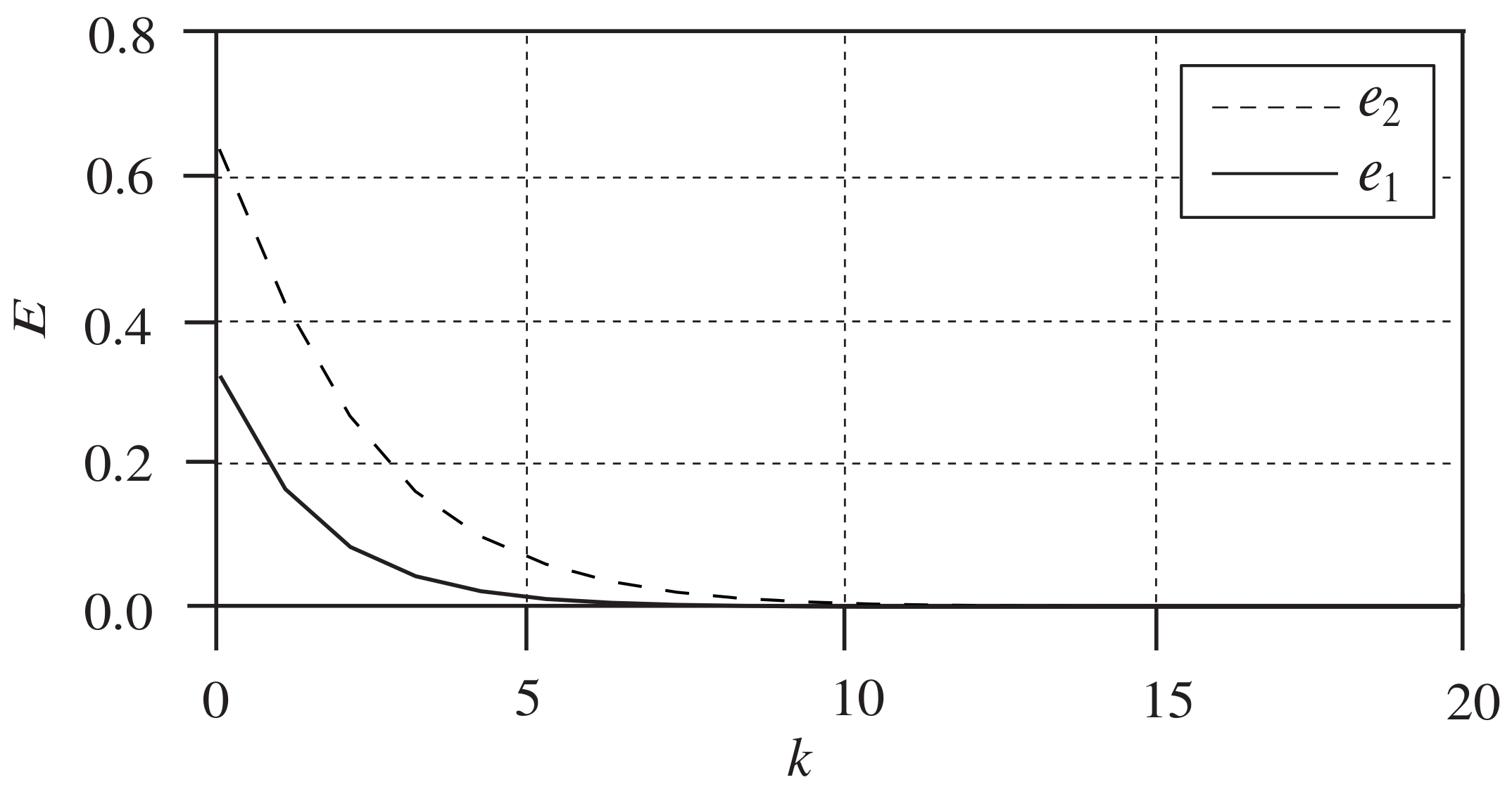
Figure 7 shows the
-norm of the tracking errors in each iteration. Thus,
Figure 1 to
Figure 7 show that the designed ILC is effective.
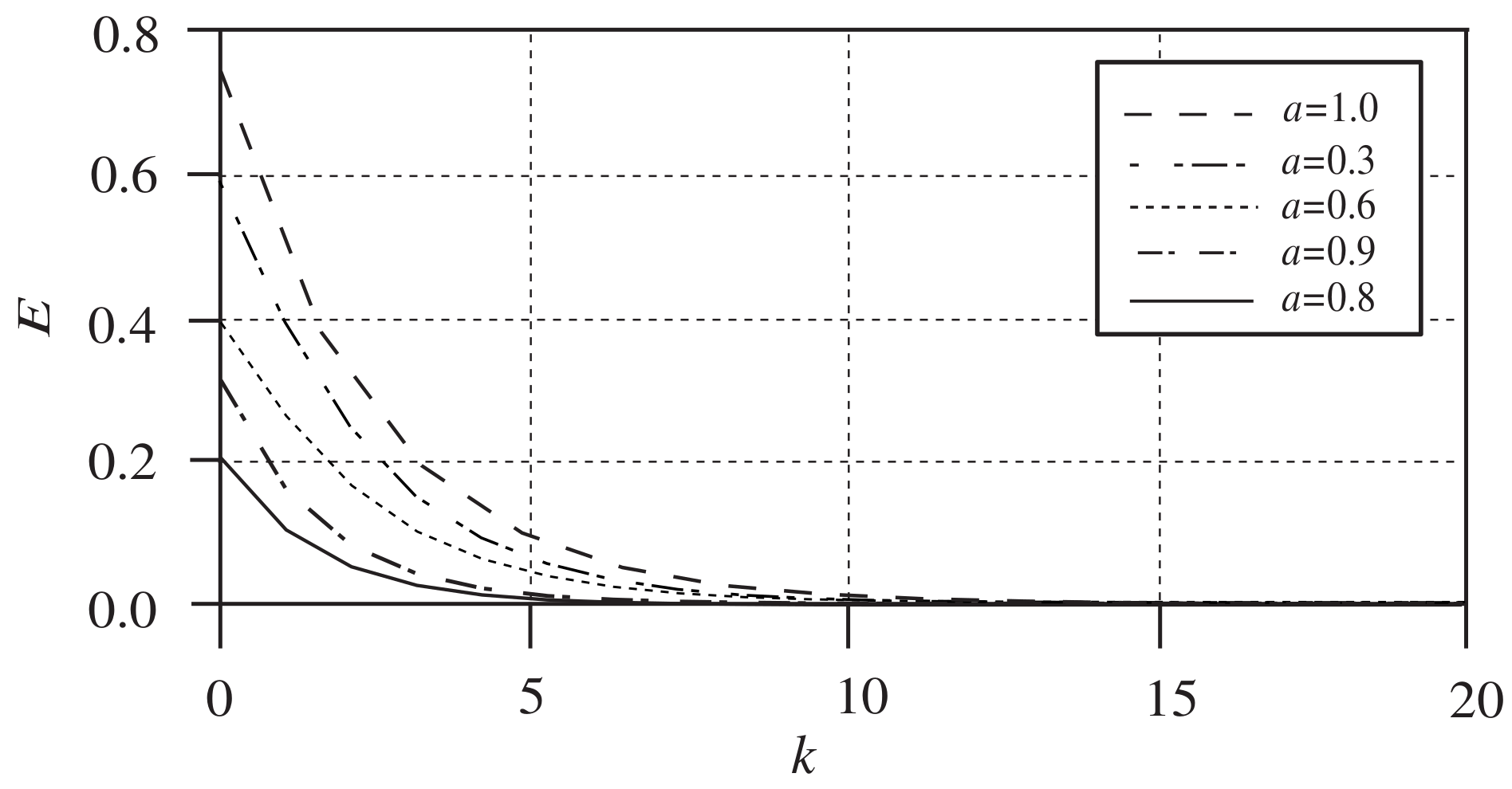
Let the reference be
and the fractional order
. The two-norm of the tracking errors in each iterations is shown in
Figure 8. It can be seen that the fastest tracking speed happens as
.
5. Conclusions
In this paper, a second order P-type ILC scheme was applied to fractional order distributed parameter systems. The convergent condition was derived using the Gronwall inequality, which has a broader range of applications and is less conservative than some existing ones. The validity of the proposed design method was demonstrated by a numerical example. Our future work includes ILC with initial state learning and D-type ILC. Moreover, the high order ILC law will also be included.