1. Introduction
To optimize is to maximize or minimize given functions in a certain domain. In real life, human beings are driven to maximize profit or minimize cost. In mathematics and computer science, these real-world problems can be mathematically modeled, and then further tackled by various optimization techniques. In general, these optimization techniques can loosely be divided into two categories: traditional optimization methods and modern intelligent optimization algorithms. For each run, the traditional optimization methods will generate the same results under the same initial conditions; while modern intelligent optimization algorithms will generate fully different results even if the same conditions are provided. Since current problems are becoming more and more complicated, traditional optimization methods do not effeciently solve them. Therefore, more and more researchers have turned to modern intelligent optimization algorithms [
1], which mainly include evolutionary computation [
2], swarm intelligence, extreme learning machines [
3], or artificial neural networks [
4]. Among the different kinds of intelligent algorithms, swarm intelligence (SI) algorithms [
5,
6,
7,
8] are one of the most representative paradigms.
In 1995, particle swarm optimization (PSO) [
9,
10,
11,
12,
13,
14,
15] was proposed based on the inspiration of bird flocking. In a sense, the development of PSO is one of the milestones in the history of swarm intelligence algorithms. Since then, many researchers have performed numerous in-depth studies on PSO, and it has been successfully used to solve various complicated engineering problems [
16]. Such problems include gesture segmentation [
17], scheduling [
18], shape design [
19], vehicle routing [
20], test-sheet composition [
21], malicious code detection [
22], economic load dispatch [
23,
24], IIR system identification [
25], prediction of pupylation sites [
26], target assessment [
27,
28], unit commitment [
29], path planning [
30,
31,
32], directing orbits of chaotic systems [
33], image processing [
34], task assignment problem [
35], floorplanning [
36,
37], clustering [
38], wind generator optimization [
39], reliability problems [
40], knapsack problem [
41,
42,
43], and fault diagnosis [
44]. Recently, immediately following PSO, many excellent SI algorithms have been put forward, including the ant colony optimization (ACO) [
45,
46,
47], harmony search (HS) [
48,
49], artificial bee colony (ABC) [
50,
51,
52,
53,
54], cuckoo search (CS) [
55,
56,
57,
58,
59,
60,
61], fireworks algorithm (FWA) [
62], bat algorithm (BA) [
63,
64,
65,
66,
67], fruit fly optimization algorithm (FOA) [
68], earthworm optimization algorithm (EWA) [
69], elephant herding optimization (EHO) [
70,
71,
72], moth search (MS) algorithm [
73,
74], biogeography-based optimization (BBO) [
75,
76,
77], firefly algorithm (FA) [
78,
79,
80], krill herd (KH) [
81,
82,
83,
84,
85,
86,
87], and monarch butterfly optimization (MBO) [
88]. These various algorithms are inspired by the swarm behavior of ants, honey bees, cuckoos, bats, grey wolves, krill, and butterflies.
Recently, after a careful study of the migration behavior of monarch butterflies, Wang et al. [
88] designed a novel promising swarm intelligence-based optimization technique, called the monarch butterfly optimization (MBO). In MBO, all the monarch butterflies are located at land 1 and land 2, which are updated through implementation of the migration operator and butterfly adjusting operator at each generation. Based on thorough in-depth comparative studies of thirty-eight benchmark problems selected from previous literature, it was found that MBO significantly outperforms five other state-of-the-art metaheuristic algorithms.
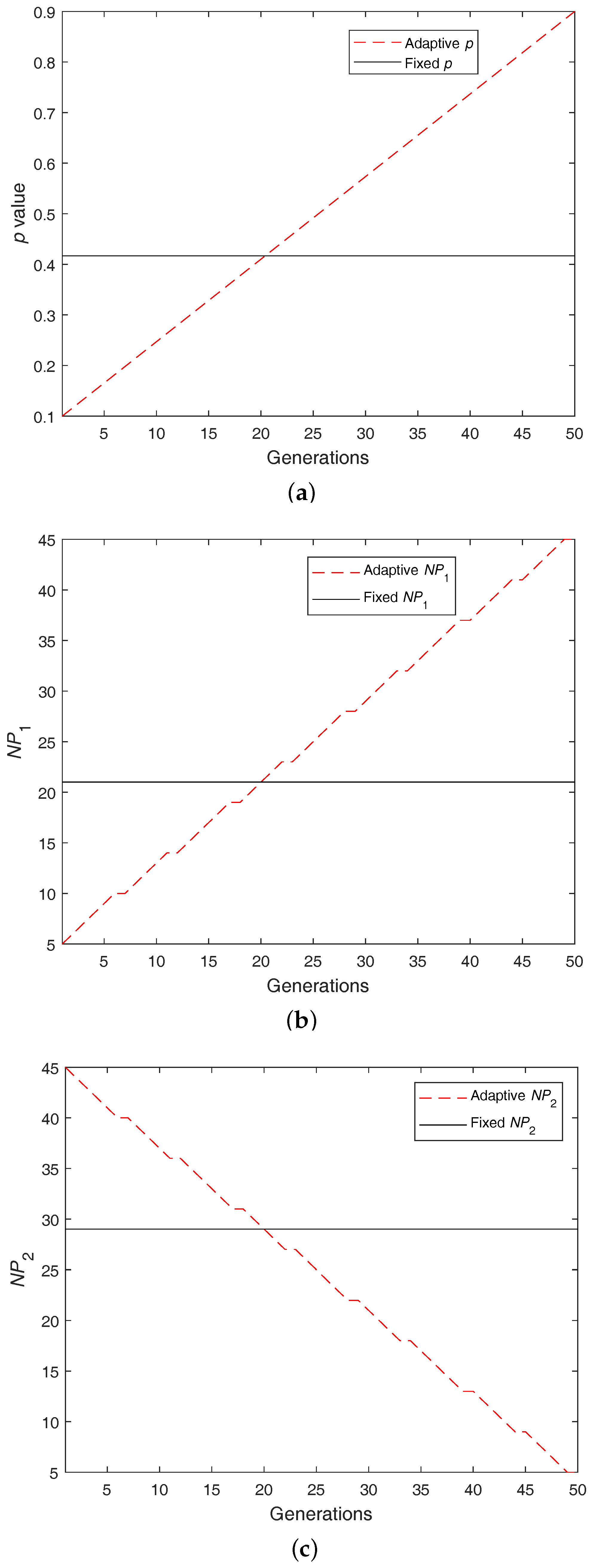
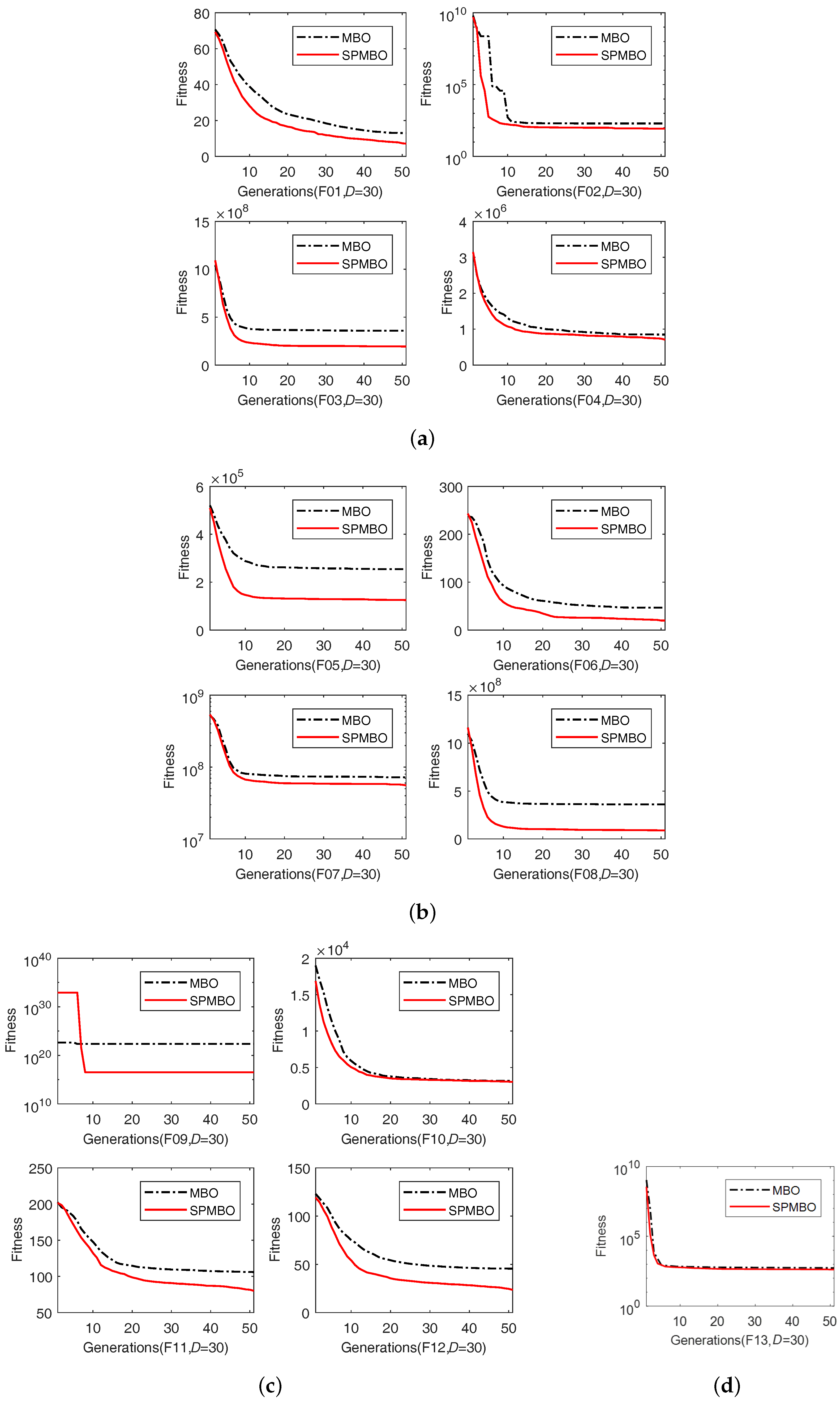
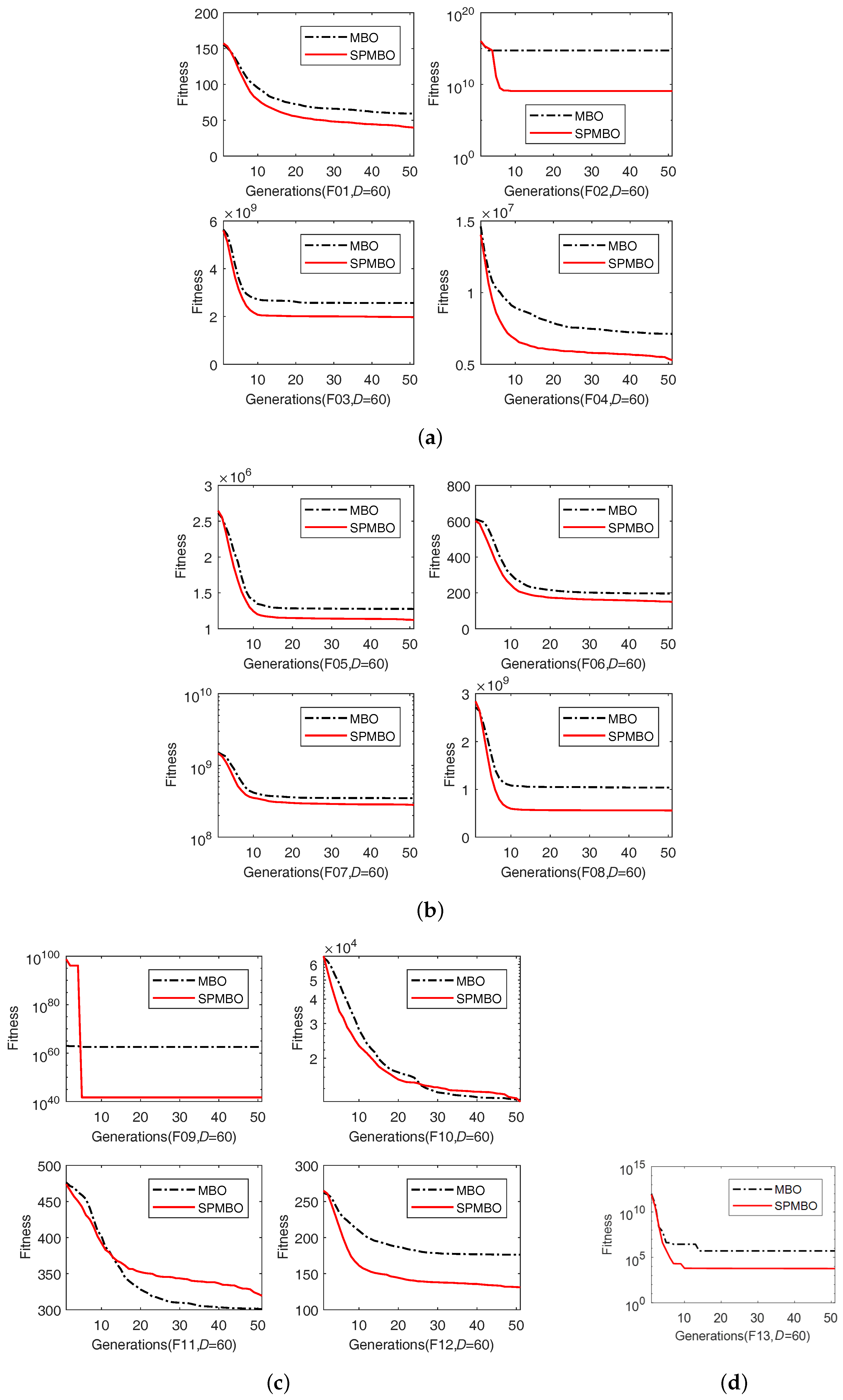
However, in the basic MBO algorithm, after implementing the migration operator, the generated monarch butterfly will be accepted as a new butterfly individual in the next generation regardless of whether it is better or worse. Also, the number of monarch butterflies in land 1 and land 2 are fixed and unchanged during the entire optimization process, which are calculated at the begin of the search according to the parameter p. In this paper, two main modifications are proposed to improve the performance of the basic MBO algorithm, which are self-adaptive and greedy strategies. A self-adaptive strategy is introduced to adjust the butterfly number in land 1 and land 2 in a linear fashion during the optimization process. Additionally, only an improved butterfly individual generated by the migration operator is accepted and considered as a new butterfly individual in the next generation. This greedy strategy can make the butterfly population move toward a better status at all times. In this way, this also guarantees that the generated population is at least not worse than before. After inserting the two modifications into the basic MBO algorithm, a new variant of MBO, called the self-adaptive population MBO (SPMBO), is proposed. Furthermore, the performance of SPMBO is fully investigated by experiments on thirteen standard test functions with dimensions of 30 and 60. The experimental results indicate that the proposed SPMBO approach has much better search ability than the basic MBO algorithm in most cases. This also implies the self-adaptive strategy is an effective way to improve the performance of the basic MBO algorithm when addressing high-dimensional global optimization problems.
The rest of this paper is structured as follows.
Section 2 provides an overview of related work on the MBO algorithm, followed by a description of the basic MBO method in
Section 3.
Section 4 discusses how the self-adaptive and greedy strategies were incorporated to improve the performance of the basic MBO. Subsequently, SPMBO was fully investigated on 30-D and 60-D benchmarks and the corresponding outcomes are described in
Section 5. The paper ends with
Section 6, after presenting some concluding remarks as well as scope for further work.
2. Related Work
Since the monarch butterfly optimization algorithm [
88] was proposed, many scholars have worked on MBO algorithm. In this section, some of the most representative work regarding MBO and other metaheuristic algorithms are summarized and reviewed.
Kaedi [
89] proposed a population-based metaheuristic algorithm, namely the fractal-based algorithm, for tackling continuous optimization problems. In this algorithm, the density of high quality and promising points in an area is considered as a heuristic which estimates the degree of promise for finding the optimal solution in that area. The promising areas of state space are then iteratively detected and partitioned into self-similar and fractal-shaped subspaces, each being searched more precisely and more extensively. Comparison with some other, metaheuristic algorithms, demonstrated that this algorithm could find high quality solutions within an appropriate time.
Shams et al. [
90] proposed a novel optimization algorithm, the ideal gas optimization (IGO) with the inspiration of the first law of thermodynamics and kinetic theory. In IGO, the searcher agents are a collection of molecules with pressure and temperature. IGO uses the interaction between gas systems and molecules to search the problem space for the solution. The IGO algorithm was benchmarked by an array of benchmarks. Comparison of the results with PSO and the genetic algorithm (GA) showed an advantage of the IGO approach.
Precup et al. [
91] suggested a synergy of fuzzy logic and nature-inspired algorithms in the context of the nature-inspired optimal tuning of the input membership functions of a class of Takagi–Sugeno–Kang (TSK) fuzzy models dedicated to anti-lock braking systems (ABSs). The TSK fuzzy model structure and initial TSK fuzzy models were obtained by the modal equivalence principle in terms of placing local state-space models in the domain of TSK fuzzy models. The optimization problems were defined to minimize objective functions expressed as the average of the square modeling errors over the time horizon. Two representative nature-inspired algorithms, simulated annealing (SA) and PSO, were implemented to solve the optimization problems and to obtain optimal TSK fuzzy models.
Baruah et al. [
92] proposed a new online evolving clustering approach for streaming data. Unlike other approaches, which consider either the data density or distance from existing cluster centers, this approach uses cluster weight and distance before generating new clusters. To capture the dynamics of the data stream, the cluster weight is defined in both data and time space in such a way that it decays exponentially with time. A distinction is made between core and noncore clusters to effectively identify the real outliers. Experimental results with developed models showed that the proposed approach obtains results at par or better than existing approaches and significantly reduces the computational overhead, which makes it suitable for real-time applications.
Yi et al. [
93] proposed a novel quantum-inspired MBO methodology, called QMBO, by incorporating quantum computation into the basic MBO algorithm. In QMBO, a certain number of the worst butterflies are updated by quantum operators. The path planning navigation problem for unmanned combat air vehicles (UCAVs) was modeled, and its optimal path was obtained by the proposed QMBO algorithm. Furthermore, B-Spline curves were utilized to refine the obtained path, making it more suitable for UCAVs. The UCAV path obtained by QMBO was studied and analyzed in comparison with the basic MBO. Experimental results showed that QMBO can find a much shorter path than MBO.
Ghetas et al. [
94] incorporated the harmony search (HS) algorithm into the basic MBO algorithm, and proposed a variant of MBO, called MBHS, to deal with the standard benchmark problems. In MBHS, the HS algorithm is considered as a mutation operator to improve the butterfly adjusting operator, with the aim of accelerating the convergence rate of MBO.
Feng et al. [
95] presented a novel binary MBO (BMBO) method used to address the 0-1 knapsack problem (0-1 KP). In BMBO, each butterfly individual is represented as a two-tuple string. Several individual allocation techniques are used to improve BMBO’s performance. In order to keep the number of infeasible solutions to a minimum, a novel repair operator was applied. The comparative study of BMBO with other optimization techniques showed the superiority of the former in solving 0-1 KP.
Wang et al. [
96,
97] put forward another variant of the MBO method, the GCMBO. In GCMBO, two modification strategies, including a self-adaptive crossover (SAC) operator and a greedy strategy, were utilized to improve its search ability.
Feng et al. [
98] combined chaos theory with the basic MBO algorithm, and proposed a novel chaotic MBO (CMBO) algorithm. The proposed CMBO algorithm enhanced the search effectiveness significantly. In CMBO, in order to tune the two main operators, the best chaotic map is selected from 12 maps. Meanwhile, some of the worst individuals are improved by using a Gaussian mutation operator to avoid premature convergence.
Ghanem and Jantan [
99] combined ABC with elements from MBO to proposed a new hybrid metaheuristic algorithm named hybrid ABC/MBO (HAM). The combined method uses an updated butterfly adjusting operator, considered to be a mutation operator, with the aim of sharing information with the employee bees in ABC.
Wang et al. [
100] proposed a discrete version of MBO (DMBO) that was applied successfully to tackle the Chinese TSP (CTSP). They also studied and analyzed the parameter butterfly adjusting rate (BAR). The chosen BAR was used to find the best solution for the CTSP.
Feng et al. [
101] proposed a type of multi-strategy MBO (MMBO) technique for the discounted 0-1 knapsack problem (DKP). In MMBO, two modifications, including neighborhood mutation and Gaussian perturbation, are utilized to retain the diversity of the population. An array of experimental results showed that the neighborhood mutation and Gaussian perturbation were quite capable of providing significant improvement in the exploration and exploitation of the MMBO approach, respectively. Accordingly, two kinds of NMBO were proposed: NCMBO and GMMBO.
Feng et al. [
102] combined MBO with seven kinds of DE mutation strategies, using the intrinsic mechanism of the search process of MBO and the character of the differential mutation operator. They presented a novel DEMBO based on MBO and an improved DE mutation strategy. In this work, the migration operator was replaced by a differential mutation operator with the aim of improving its global optimization ability. The overall performance of DEMBO was fully assessed using thirty typical discounted 0-1 knapsack problem instances. The experimental results demonstrated that DEMBO could enhance the search ability while not increasing the time complexity. Meanwhile, the approximation ratio of all the 0-1 KP instances obtained by DEMBO were close to 1.0.
Wang et al. [
103] proposed a new population initialization strategy in order to improve MBO’s performance. First, the whole search space is equally divided into
NP (population size) parts at each dimension. Subsequently, two random distributions (the
T and
F distributions) are used to mutate the equally divided population. Accordingly, five variants of MBOs are proposed with a new initialization strategy.
Feng et al. [
104] presented OMBO, a generalized opposition-based learning (OBL) [
105,
106] MBO with Gaussian perturbation. The authors used the OBL strategy on the portion of the individuals in the late stage of evolution, and used Gaussian perturbation on the individuals with poor fitness in each evolution. OBL guaranteed a higher convergence speed of OMBO, and Gaussian perturbation avoided the possibility of falling into a local optimum. For the sake of testing and verifying the effectiveness of OMBO, three categories of 15 large-scale 0-1 KP cases from 800 to 2000 dimensions were used. The experimental results indicated that OMBO could find high-quality solutions.
Chen et al. [
107] proposed a new variant of MBO by introducing a greedy strategy to solve dynamic vehicle routing problems (DVRPs). In contrast to the basic MBO algorithm, the proposed algorithm accepted only butterfly individuals that had better fitness than before implementation of the migration and butterfly adjusting operators. Also, a later perturbation procedure was introduced to make a trade-off between global and local search.
Meng et al. [
108] proposed an improved MBO (IMBO) for the sake of enhancing the optimization ability of MBO. In IMBO, the authors divided the two subpopulations in a dynamic and random fashion at each generation, instead of using the fixed strategy applied in the original MBO approach. Also, the butterfly individuals were updated in two different ways for the sake of maintaining the diversity of the population.
Faris et al. [
109] modified the position updating strategy used in the basic MBO algorithm by utilizing both the previous solutions and the butterfly individuals with the best fitness at the time. For the sake of fully exploring the search behavior of the improved MBO (IMBO), it was benchmarked by 23 functions. Furthermore, the IMBO was applied to train neural networks. The IMBO-based trainer was verified on 15 machine learning datasets from the UCI repository. Experimental results showed that the IMBO algorithm could enhance the learning ability of neural networks significantly.
Ehteram et al. [
110] used the MBO algorithm to address the utilization of a multi-reservoir system for the sake of improving production of hydroelectric energy. They studied three periods of dry (1963–1964), wet (1951–1952), and normal (1985–1986) conditions in a four reservoir system. The experiments indicated that MBO can generate more energy compared to particle swarm optimization (PSO) and the genetic algorithm (GA).
Though many scholars have made several in-depth studies of the MBO algorithm from different aspects. The number of monarch butterflies in land 1 and 2 is unchanged. In this paper, a self-adaptive strategy is introduced to update the subpopulation sizes during the optimization process. A detailed description of the proposed algorithm will be given in the following sections.
6. Conclusions
Inspired by the migration behavior of monarch butterflies, one of the most promising swarm intelligence algorithms, monarch butterfly optimization (MBO), was proposed by Wang et al. in 2015. In the basic MBO algorithm, the number of butterflies in land 1 () and land 2 () is fixed, which is calculated according to the parameter p at the begin of the search. MBO includes two main operators: a migration operator and a butterfly adjusting operator. For the migration operator, all the generated butterfly individuals are accepted and passed to the next generation. In some cases, this is an ineffective way to find the best function values. In this paper, we introduced two techniques to overcome these drawbacks: self-adaptive and greedy strategies. The parameter p is linearly adjusted in a dynamic way. Therefore, at the beginning of the search, the number of butterflies in land 1 () and land 2 () is determined by the parameter p. Additionally, only newly-generated butterfly individuals having better fitness will be accepted and passed to the next generation. This greedy strategy will surely accelerate the convergence speed. The proposed SPMBO algorithm is tested by thirteen 30-D and 60-D test functions. The experimental results indicate that the search ability of the proposed SPMBO approach outperforms significantly the basic MBO algorithm on most test functions.
Despite showing various advantages of the SPMBO approach, the following points should be highlighted in our future research. On one hand, the parameter p is changed during the entire optimization process. In fact, if the algorithm performs in a good manner, there is no need to adjust the parameter p. Therefore, developing a method to adjust the parameter p in a more intelligent way is worthy of further studies. Second, for the updated migration operator, only better butterfly individuals are accepted and passed to the next generation. The butterfly individuals having worse fitness may include better elements, which may help the search algorithm. Thus, the migration operator should accept a few butterfly individuals with worse fitness. Last, only thirteen benchmarks were used to test our proposed SPMBO approach. In the future, more benchmark problems, especially real-world applications, should be used for further verifying SPMBO, such as image processing, video coding, and wireless sensor networks.