Abstract
Supplier selection is an important decision-making link in bidding activity. When overall scores of several suppliers are similar, it is hard to obtain an accurate ranking of these suppliers. Applying the Diversity Factors Method (Diversity Factors Method, DFM) may lead to over correction of weights, which would degrade the capability of indexes to reflect the importance. A Limited Diversity Factors Method (Limited Diversity Factors Method, LDFM) based on entropy is presented in this paper in order to adjust the weights, in order to relieve the over correction in DFM and to improve the capability of identification of indexes in supplier selection. An example of salvage ship bidding demonstrates the advantages of the LDFM, in which the raking of overall scores of suppliers is more accurate.
1. Introduction
China’s coastline covers 18,000 km. The development of international business has promoted the rapid development of China’s sea transportation over the past three decades. Meanwhile, offshore accidents and risks increased fast because of the frequent economic activity. There is strong demand for the salvage departments of China to carry out the periodic replacement of new salvage equipment and extended service, with the development of technical equipment and management capability of salvage. Based on this, by taking optimal supplier selection for the purchasing of salvage ships as an example, this paper studied the special circumstances in optimal supplier selection, when the overall scores of several suppliers are similar and the optimal supplier is hard to identify.
The methods of weight determination can be mainly divided into three types: subjective methods [1,2,3,4], objective methods, and correspondence between subjectivity and objectivity methods [5,6,7]. In research, different methods of weight determination are supposed to be chosen for different objects [8,9,10,11]. In the foreign and domestic research of index weight determination of supplier, at an early stage, the method of weight determination was mainly subjective method, such as Analytic Hierarchy Process (AHP) [12,13], the MCDM-ANP (Multiple Criteria Decision Making-Analytic Network Process) method [14,15], and Fuzzy Group Decision Making Method [16], but the evaluation of weight carried out on the basis of human experience, weight determination is overly dependent on expert judgement, leading to data features underutilization. In recent years, the method of combining subjective and objective was presented [17,18,19,20,21,22]. Most of them using diversity factors of entropy and extra weights were endowed to the indexes with high discreteness as identifying highly recognizable indexes, and the identifying difficulty was relieved when the overall scores of several suppliers are similar. However, when using the Diversity Factors Method (DFM) in supplier selection, since numbers of the sample data of supplier are fewer, it may lead to over correction of weight in adjustment process, while the importance of index cannot be considered.
Therefore, this paper makes an improvement on the DFM by presenting the Limited Diversity Factors Method (LDFM) in order to relieve the over correction of weight in adjustment process by using the DFM in supplier selection. The initial weight that was calculated by AHP can be adjusted through the LDFM and the final index weight of salvage ships supplier can be obtained. By comparing the LDFM and the DFM as well as validating the effectiveness and rationality of the LDFM through quantitative analysis, finding that the shortage of the DFM can be made up.
2. Establishment of an Index System of Salvage Ship Supplier Selection
Unlike ordinary commercial ships, salvage ships are professional ships for salvage in extreme conditions, where machinery equipment is often in a critical state of operation. Hence, in the course of supplier selection, the particularity of salvage ships should be paid attention to in evaluation of various indexes of potential suppliers. Essentially, the government should be responsible for bidding and purchase of salvage ships. Unlike purchase of commercial ships, purchase of salvage ships is not for profit. Meanwhile, the government should play a role in supervising and guiding supplier during purchase of salvage ships and take account of related social goals. Hence, the government should focus on examinations of indexes, such as quality control and production capacity. According to relevant provisions in official documents “Rules for Classification and Construction of Ships (ISBN: 7-204-04309-7)” and “Shipbuilding Quality Standard (ISBN: 9787810076104)”, and score indexes in the bidding document “The Project of Construction of X Salvage Ships”, due to the excessive index will lead to the index of the redundancy of information, makes the weight of each index low, unable to give full play to the important degree of reaction index weights, so the categorized Index Layer and get Criterion Layer, using the Criterion Layer as indicators of evaluation factors, and index layer as an expert on scores of specific judgment criterion layer. Based on it, this paper established an index system, as shown in Table 1.

Table 1.
Indicator System of Salvage Ship Supplier Selection.
3. Determination of Index Weight by Analytic Hierarchy Process
3.1. Constriction of Pairwise Judgment Matrixes
AHP method compared with other methods of weight determination that were used in Supplier selection that should not need to steep themselves for long in technical training to organize their thinking and to discover what judgments they hold, and it is successful in practice of supplier selection decision [23,24,25]. So, this paper using the AHP method to obtain the initial weight.
Six related experts (three managers with experience in salvage operation, three senior engineer in ship construction.) who had served as judges in “The Project of Construction of X Salvage Ships” were invited to mark indexes in Table 1. The differences in the judgment matrix of six experts were finally agreed upon through five feedback discussions. The judgment matrixes were built, as follows:
Criterion layer X1, X2, X6, X7, and X8 with no need for construct the judgment matrix due to only one determinant in Table 1. The judgement matrixes of criterion layer X3, X4, X5, and X7 in the criteria layer are as follows:
where, scales involved in the constriction of pairwise judgment matrixes and their definitions are shown in Table 2.

Table 2.
Importance scale of factors in pair-wise comparison.
3.2. Calculation of Index Weight and Consistency Check
According to calculation of elements in judgment matrixes, it was determined that the consistency of the judgment matrixes was satisfactory.
Due to low orders of judgment matrixes in the third, fourth, and seventh criterion layer, evaluation of their consistency could be conducted through observation. However, due to the high order of the judgment matrix in the fifth layer, the verification of its consistency required mathematical calculation.
CI5, the coincidence indicator of the judgment matrix in the fifth layer, was solved through Equation (1).
where n refers to the order of the judgment matrix. As n = 15,
Consistency Ration (CR) was calculated with
where RI is the Radom Consistency Index. Since CR ≤ 0.1, the consistency ration is acceptable.
Consistency Ration of the criteria (CR′) was calculated in the same way with
Since CR′ ≤ 0.1, the consistency ration CR′ is acceptable, too.
Due to limited space of this paper, the similar calculation of index weights corresponding to each layer is ignored. Results of index weights obtained through calculation are shown in Table 3.

Table 3.
Weight Summary Table.
According to weights obtained through calculation, it can be seen that the characteristic of these indexes for salvage ship supplier selection was that the index weights of the salvage ship supplier selection mainly focused on price indexes X1 and indexes of quality control and production capacity X5. This is because salvage ship supplier selection requires demanding technical capacity of suppliers. If the scores of indexes X1 and X5 are similar, discrimination of other indexes will greatly decrease because of the high weights of indexes X1 and X5. Hence, a proper marking table for weight adjustment should be selected through comparative analysis of marking table within or without the same dimension and quantitative analysis should be carried out through diversity factors.
4. Solution for Declining Discrimination of Salvage Ship Supplier Selection
In salvage ship supplier selection, when overall scores of suppliers are similar, discrimination of the index system on suppliers decreases greatly and the system fails to distinguish the differences of comprehensive strength of suppliers. Therefore, this problem can be solved by enhancing the discrimination of other indexes with large differences properly through weight adjustment. This paper put forward the LDFM to adjust weights that were obtained through the analytic hierarchy process, covering the shortage of the DFM. In addition, a comparison of adjusted weights and weights before adjustment and related quantitative analysis were conducted. There is the flow chart of the LDFM are shown in Figure 1.
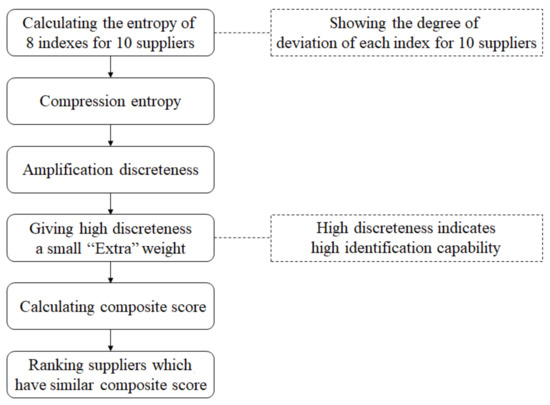
Figure 1.
The flow chart of the Limited Diversity Factors Method (LDFM).
4.1. Correction of Index Weights by Limited Diversity Factors
Weights that were obtained through entropy could objectively reflect the difference degree of each index in the system, namely the influence degree of change of each index on the final evaluation results, providing an objective mathematical methods and theoretical basis for weight determination [26].
If the diversity factors of entropy are directly applied to the adjustment of weights that were obtained through the analytic hierarchy process, it may lead to over correction because of an excessive adjustment range. Hence, the LDFM was put forward in order to carry out the fine adjustment of index weights on the basis of remaining the relative importance of index.
Steps of adjustment of weights obtained through analytic hierarchy process by diversity factors are: first, p(xij), the weight of Index xij in Index j, is figured out through Equation (2).
For example, on the basis of eight evaluation indexes in criterion layers, six experts who had served as judges in projects of supplier selection of this ship model, and three of them have experience in operating salvage ships, while three of them are senior engineers in shipbuilding field, were invited to mark indexes of 25 shipyards, which has the ability to building salvage ships, according to the data, such as technical equipment data, historical building data, numbers of senior engineering, and the collecting of historical shipbuilding scheme, which were obtained from these shipyards. If the variance of set of scores, which is made by six experts, is more than 0.6, all of the scores should be re-evaluate by using Delphi method. Finally, for each index, take the average scores of six experts as the final score of the supplier. In order to study the difficulty of distinguishing indexes when the overall scores of different suppliers are similar in the bidding process, 10 shipyards with similar overall scores have been selected out of 25 shipyards, the table of scoring, as shown in Table 4.

Table 4.
Supplier’s Rating Scale.
According to Equation (2),
By working out ej, the entropy of Index xij, Equation (3) was obtained:
where k > 0 and ej ≥ 0. If k = 1/ln(n), 0 ≤ ej ≤ 1. So k = 1/ln(n) is token in Equation (3).
Hence, the weights of indexes with similar scores should be properly reduced and transferred to indexes with significant differences. The greater the difference between indexes is, the smaller ej will be, as shown in Equation (4). Thus, the greater the difference is, the smaller δ will be.
δ can be used to characterize differences of indexes. However, application of δ to adjustment of weights may lead to over correction, where the importance of indexes is ignored. Therefore, this paper proposed ζ, the limited diversity factors, in order to cover the shortage of the DFM.
Scoring for the various indexes of suppliers and the arrays of the index scores, which represent the scores of single index for all suppliers and lie in the interval of (6.5, 10), can be obtained. Generally speaking, the supplier is not capable of satisfying the requirements of bidding when score of single index is too low. The analysis of all the possible arrays of an index scores for 10 supplies, which lie in the interval of (6.5, 10) is conducted. Among all of the arrays, the array of (6.5, 6.5, 6.5, 6.5, 6.5, 10, 10, 10, 10, 10) has the highest discreteness, and its entropy value ej is 0.9902. The array of (8, 8, 8, 8, 8, 8, 8, 8, 8, 8) has the lowest discreteness, and its entropy value ej is 1. Therefore, the entropy values of arrays always lie in the interval of (0.9902, 1), regardless of the change of scores in the array within the above mentioned interval, and the entropy values vary only on the second or third decimal place. By using data in Table 4, the entropy values of eight index scores arrays of 10 suppliers can be calculated, and they are, respectively, 0.9997, 0.9966, 0.9979, 0.9959, 0.9996, 0.9972, 0.9973, and 0.9959.
Due to the linear operation, the change interval of ζ′ was also changed at the third and fourth significant digit, as shown in Equation (5). ζ′ retained the discreteness of characterization data of entropy and it plays a similar role in correcting weights. Limited diversity factors ζ was obtained through the diversity factors of ζ′, as shown in Equation (6).
with ζ = (0.8747, 0.8751, 0.8749, 0.8752, 0.8747, 0.8750, 0.8750, and 0.8752). Its change interval was also less than tenths and transformation of entropy into the limited diversity factors was realized through linear operation, ensuring 0.87 as the significant figure of a limited diversity factors, regardless of the index value and realizing fine adjustment of index weight.
The diversity factors and the limited diversity factors were normalized with the results of (0.0145, 0.1695, 0.1041, 0.2052, 0.0206, 0.1412, 0.1367, and 0.2082) and (0.12496, 0.12501, 0.12499, 0.12502, 0.12496, 0.12500, 0.12500, and 0.12503), respectively. It can be seen that the direct application of the diversity factors to adjustment of weights may lead to over correction, which may impair the weight of index with high importance. In other words, the adjustment process cannot take the importance of the index into consideration while conducting correction.
However, the direct application of the limited diversity factors to the adjustment of weights results in a small adjustment range. In order to enhance its adjustment range, as the significant figure of a limited diversity factors, 0.87 was used to reserve the initial weight. Then, significant figures of discreteness of other characterization data were used to reallocate the rest weight, leading to adjustment.
Reserved weight is wi′ = 0.87 × wi, wi′ = (0.31600, 0.05222, 0.05612, 0.08302, 0.31104, 0.04977, 0.07967, and 0.05216). The rest weight is
The limited diversity factors were used to reallocate the rest weight and the diversity factors of each index wic = (0.015639, 0.015646, 0.015643, 0.015648, 0.015639, 0.015645, 0.015645, and 0.015648).
The final adjusted weight wif = wi′ + wic = (0.31600, 0.05222, 0.05612, 0.08302, 0.31104, 0.04977, 0.07967, and 0.05216). Results of the weight adjustment and the computation process are shown in Table 5.

Table 5.
Corrected Weights.
In order to further analyze corrected effects, the integrated computation and ranking of final results of ten suppliers were carried out with index weights before and after adjustment. Comparative analysis of their final results before and after adjustment and related ranking were conducted. The final scores are shown in Table 6.

Table 6.
Comparison of scoring before and after correction.
According to Table 4 and Table 6, a comparison of weight changes before and after correction was conducted. After weight adjustment through ζ, the overall scores of suppliers before correction were very close and many suppliers got the same score and ranking.
After adjustment through the limited diversity factors can be seen from Table 5, the revised weight of indicators index X1 and X5 is reduced due to common scores being similar, while the other which difference of scores is bigger but significant be neglected had be improved, according to a different degree, so the problem that the suppliers have the same score and rank can not identify the optimal supplier. Contrast Table 4 and Table 5 we can find the sorting before correction, ranking in the first three suppliers mainly because the X1 and X5 index of excellent performance, but as a result of each supplier in the X1 and X5 index, difference between small, other indexes with more difference degree should be focused on considering to get a more reasonable supplier sorting, so after correction, due to the rest of the indicators such as X2 more difference degree and higher score, supplier S2, S5, S9 enter into the top 3. For example, supplier S5 took a first from the sixth and its scores were (9.00, 9.40, 9.00, 6.70, 8.50, 7.50, 8.70, and 9.40). However, S4 took the fourth place from the first place after the adjustment and its scores were (9.50, 9.40, 8.60, 9.40, 7.80, 7.40, 7.20, and 6.80). Results of highly weighted Indexes X1 and X5 of these two suppliers were similar. Proper enhancement of weights of other indexes, such as “Launching pattern” X6, “Important test” X7 and “Centralized purchasing of equipment” X8, enhanced the overall score of S5, making expected weight adjustment realized. After adjustment, results became more practical.
According to analysis above, the diversity factors of entropy played a proper role in adjusting weights, which is a good solution for declining discrimination of salvage ship supplier selection.
After calculation, the purpose of reordering has been achieved by once correction. But, if there are two conditions that need to be corrected multiple times, the result of LDFM will not apply or will achieve a similar effect by the DFM method:
- (1)
- change the order of the original weight after repeated correction; and,
- (2)
- the weight correction of an index or some indexes by the LDFM with multiple times is greater than the results of DFM with once correction.
4.2. Limitation of Correction by Diversity Factors
Application of diversity factors to the adjustment of weights may lead to over correction. Equation (7) was used to correct weights that were obtained through the analytic hierarchy process.
Comparison between results that were corrected by diversity factors and limited diversity factors were carried out, where Ai0 stands for the overall score obtained through analytic hierarchy process, Ais means that the overall score that was obtained through diversity factors and Ais refers to the overall score that was obtained through limited diversity factors, as shown in Table 7.

Table 7.
Comparison of the Two Revisions.
According to Table 7, the distinction of suppliers with similar scores was realized through application of diversity factors. However, due to strong reduction of two important indexes, Price X1 and Quality control and production capacity X5, caused by diversity factors, where the weight of X1 was reduced from 0.343 to 0.0782 and that of X5 was changed from 0.338 to 0.1087, final overall scores failed to reflect comprehensive strength of suppliers correctly. It also led to ranking the difference of Ais and Aif. Through diversity factors, indexes with high scoring difference were adjusted into important indexes, so that scores of indexes with high scoring difference became important indexes evaluating comprehensive strength of suppliers, leading to ranking that did not accord with actual needs. For instance, the weight of X4 was adjusted from 0.077 to 0.2475 through diversity factors, making X4 become the most important index, so that S6 who got a high score of X4 (9.1) took the first from the seventh place, ignoring the importance of indexes.
However, the problems above can be avoided through limited diversity factors. This is because the importance of indexes could be maintained and proper enhancement of weights of indexes with a large difference could be realized through limited diversity factors. In this way, actual needs during bidding can be met.
5. Conclusions and Prospect
- Taking a bidding project of purchase of salvage ships as an example, this paper particularity analyzed salvage ships, related industry standards, and differences between government procurement and commercial procurement and established an index system of salvage ship supplier selection.
- Initial weights were determined through analytic hierarchy process. The LDFM was put forward against similar overall scores for bidding and difficulties in distinguishing the strength of different suppliers. As this method could characterize the dispersion of indexes and consider the importance of indexes, weight adjustment, and accurate ranking of suppliers were carried out by this method.
- Comparison between results corrected by diversity factors and limited diversity factors were carried out to determine the advantages of limited diversity factors and cover the shortage of diversity factors in supplier selection.
Taking supplier selection for a bidding project of salvage ships as an example, this paper carried out weight adjustment in combination with limited diversity factors of entropy and solved the problem that the failure of optimal supplier selection that was caused by similar overall scores of different suppliers.
Some other methods can also be combined in the establishments of the judgment matrices to avoid time-consuming human-triggered information exchanges. For instance, the Soft-Fusion Technique [27,28] could be adopted when categorizing the indexes into observable data. The Delphi Method could be used when categorizing the indexes into unobserved data.
In the actual situation, if the scores of all indexes are similar, the discrimination of important indexes should be enhanced through weight adjustment. Weights can be adjusted repeatedly by LDFM. However, it is hard to obtain an optimal result. The theory of variable weight is widely applied with strong ability of weight adjustment. The combination of a variable weight model and entropy may be a new solution for this problem.
Author Contributions
M.S. and Y.S. conceived and proposed the algorithm; B.W. compiled the computing programs and analyzed data; Y.C. provided the case of bid and established the index system. M.S. wrote the manuscript. All authors have read and approved the final manuscript.
Funding
This research is funded by the National Natural Science Foundation of China (71771061), the Fundamental Research Funds for the Central Universities (HEUCFW170903), the Project of Research and Development about Harbin Application Technology (Distinguished youth talents) (2017RAYXJ027), the Science Foundation for Youths of Heilongjiang Institute of Technology (2014QJ15).
Conflicts of Interest
The authors declare that there is no conflict of interests regarding the publication of article.
References
- Ren, D.; Wang, Q. Analysis of the adjustment of CPI weight of China. J. Quant. Tech. Econ. 2013, 30, 51. [Google Scholar]
- Yuan, Y.; Dou, Y.; Liu, Y.; Zhang, M.Y. Evaluation of droughts and floods based on fuzzy variable model with combined weights. Syst. Eng. Theory Pract. 2013, 33, 2583–2589. [Google Scholar]
- Zhao, Y.D.; Fang, Z.H. Particle swarm optimization algorithm with weight function’s learning factor. J. Comput. Appl. 2013, 33, 2265. [Google Scholar] [CrossRef]
- Mahapatra, A.P.; Samal, R.K.; Samal, R.N.; Roy, G.S. Evaluation of viscosity-molecular weight constant (K), short range parameter (A) and long range parameter (B) of dextran in polar solvents. Phys. Chem. Liq. 2001, 39, 343–356. [Google Scholar] [CrossRef]
- Zhou, Y.N.; Zhu, Y.A. Algorithm for adjusting weights of decision-makers in multi-attribute group decision-making based on grey system theory. Control Decis. 2012, 27, 1113–1116. [Google Scholar]
- Ren, Y.H.; You, W.H. A new selection method of spatial weight matrix. Stat. Res. 2012, 29, 99. [Google Scholar]
- Luo, Y.Q.; Xia, J.B.; Chen, T.P. Comparison of objective weight determination methods in network performance evaluation. J. Comput. Appl. 2009, 29, 2524–2526. [Google Scholar] [CrossRef]
- Kahraman, A.; Akdam, H.; Alp, A.; Huyut, M.A.; Akgullu, C.; Balaban, T.; Dinleyen, F.; Topcu, A.; Gelmez, H.; Atakan, N.; et al. Impact of Inter Dialytic Weight Gain (IDWG) on nutritional parameters, cardiovascular risk factors and quality of life in hemodialysis patients. Bantao J. 2015, 13, 25–33. [Google Scholar] [CrossRef]
- De Nijs, R.; Holm, S.; Thomsen, G.; Ziebell, M.; Svarer, C. Experimental determination of the weighting factor for the energy window subtraction-based down scatter correction for I-123 in brain SPECT studies. J. Med. Phys. 2010, 35, 215. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.X.; Xu, M.H.; Sun, C.J.; Aboul-Enein, H.Y. Weighting factor in calculation of comprehensive quality index and optimization of PVC membrane composition for ion selective electrode. Instrum. Sci. Technol. 2007, 35, 469–479. [Google Scholar] [CrossRef]
- Li, Z.; Cao, L.Z.; Wu, H.C.; Shen, W. Sensitivity analysis for the weighting factor in the least-square method for the PWR on-line power-distribution monitoring. Ann. Nucl. Energy 2017, 109, 675–683. [Google Scholar] [CrossRef]
- Saaty, T.L. A Scaling Method for Priorities in Hierarchical Structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Park, S.C.; Lee, J.H. Supplier selection and stepwise benchmarking: A new hybrid model using DEA and AHP based on cluster analysis. J. Oper. Res. Soc. 2018, 69, 449–466. [Google Scholar] [CrossRef]
- Saaty, T.L. The modern science of multicriteria decision making and its practical applications: The AHP/ANP approach. Oper. Res. 2013, 61, 1101–1118. [Google Scholar] [CrossRef]
- He, L.H.; Wang, L.Q.; Zhang, L.Y. A method for determining the experts’ weights of multi-attribute group decision-making based on clustering analysis. Oper. Res. Manag. Sci. 2014, 23, 65. [Google Scholar]
- Banaeian, N.; Mobli, H.; Fahimnia, B.; Nielsen, I.E.; Omid, M. Green supplier selection using fuzzy group decision making methods: A case study from the agri-food industry. Comput. Oper. Res. 2018, 89, 337–347. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Zhou, S.S.; Wu, D. Research on Supplier Selection of Home Appliance Industry Supply Chain Based On Entropy Weight and TOPSIS Method. Adv. Eng. Res. 2017, 130, 649–653. [Google Scholar]
- Zhang, Y.H.; Zhu, X.N.; Wang, L. Evaluation and Selection of Emergency Material Suppliers by Combining Entropy Weight Method with COPRAS Method. J. China Railw. Soc. 2017, 39, 14–18. [Google Scholar]
- Wood, D.A. Supplier selection for development of petroleum industry facilities, applying multi-criteria decision making techniques including fuzzy and intuitionistic fuzzy TOPSIS with flexible entropy weighting. J. Nat. Gas Sci. Eng. 2017, 28, 594–612. [Google Scholar] [CrossRef]
- Freeman, J.; Chen, T. Green supplier selection using an AHP-Entropy-TOPSIS framework. Supply Chain Manag. 2015, 20, 327–340. [Google Scholar] [CrossRef]
- Yang, Y.Z.; Wu, L.Y. Grey Entropy Method for Green Supplier Selection. In Proceedings of the International Conference on Wireless Communications, Networking and Mobile Computing, Shanghai, China, 21–25 September 2007; pp. 4682–4685. [Google Scholar]
- Jia, Z.Y.; He, B. Grid Material Supplier Selection Based on Entropy Weight Correction from Perspective of Low Carbon. In Proceedings of the International Conference on Advanced Nano-Technology and Biomedical Material (ANTBM), Guangzhou, China, 29–30 June 2014; pp. 603–607. [Google Scholar]
- Ozdemir, Y.S. Supplier selection by using fuzzy AHP-electre and an application in textile company. In Proceedings of the 2017 Electric Electronics, Computer Science, Biomedical Engineering’s Meeting (EBBT), Istanbul, Turkey, 20–21 April 2017. [Google Scholar]
- Secundo, G.; Magarielli, D.; Esposito, E. Supporting decision-making in service supplier selection using a hybrid fuzzy extended AHP approach A case study. Bus. Process Manag. J. 2017, 23, 196–222. [Google Scholar] [CrossRef]
- Sultana, I.; Ahmed, I.; Azeem, A. An integrated approach for multiple criteria supplier selection combining Fuzzy Delphi, Fuzzy AHP & Fuzzy TOPSIS. J. Intell. Fuzzy Syst. 2015, 29, 1273–1287. [Google Scholar]
- Wang, D.P.; Wang, X. Research on the green vendor selection index weight of iron & steel enterprises based on AHP and Entropy Method. Soft Sci. 2010, 24, 117–122. [Google Scholar]
- Aceto, G.; Ciuonzo, D.; Montieri, A.; Pescapé, A. Multi-classification approaches for classifying mobile app traffic. J. Netw. Comput. Appl. 2018, 103, 131–145. [Google Scholar] [CrossRef]
- Aceto, G.; Ciuonzo, D.; Montieri, A.; Pescapé, A. Traffic Classification of Mobile Apps through Multi-classification. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Marina Bay Sands, Singapore, 4–8 December 2017. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).