Estimating Functional Connectivity Symmetry between Oxy- and Deoxy-Haemoglobin: Implications for fNIRS Connectivity Analysis
Abstract
1. Introduction
2. Materials and Methods
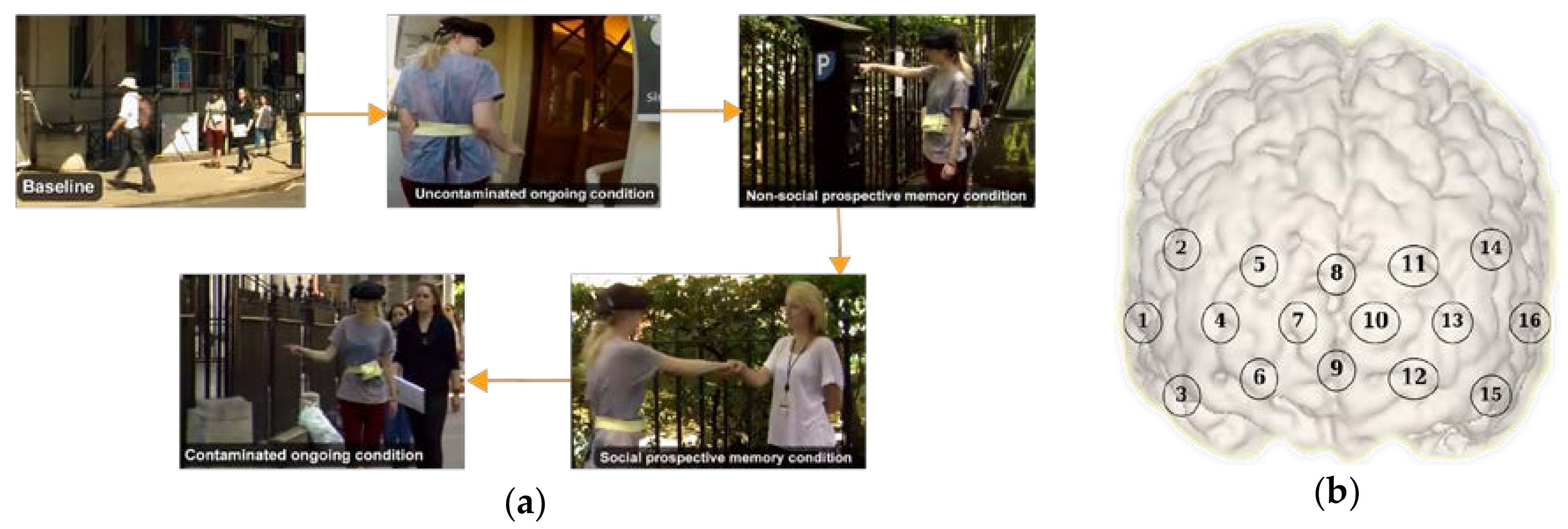
2.1. Experimental Protocol
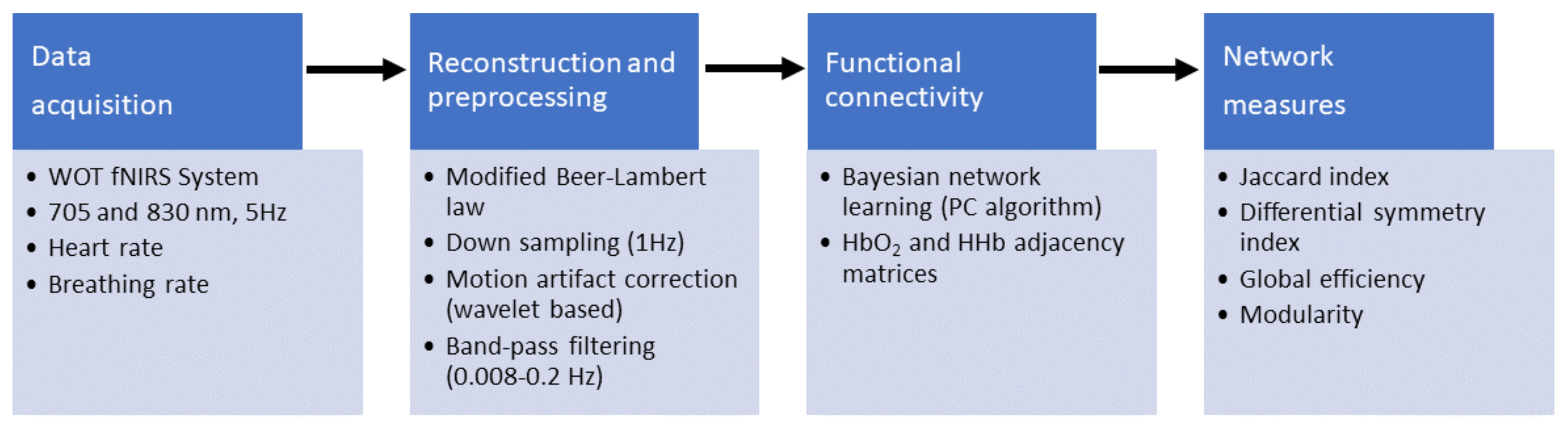
2.2. Data Acquisition and Processing
2.3. Functional Connectivity Analysis
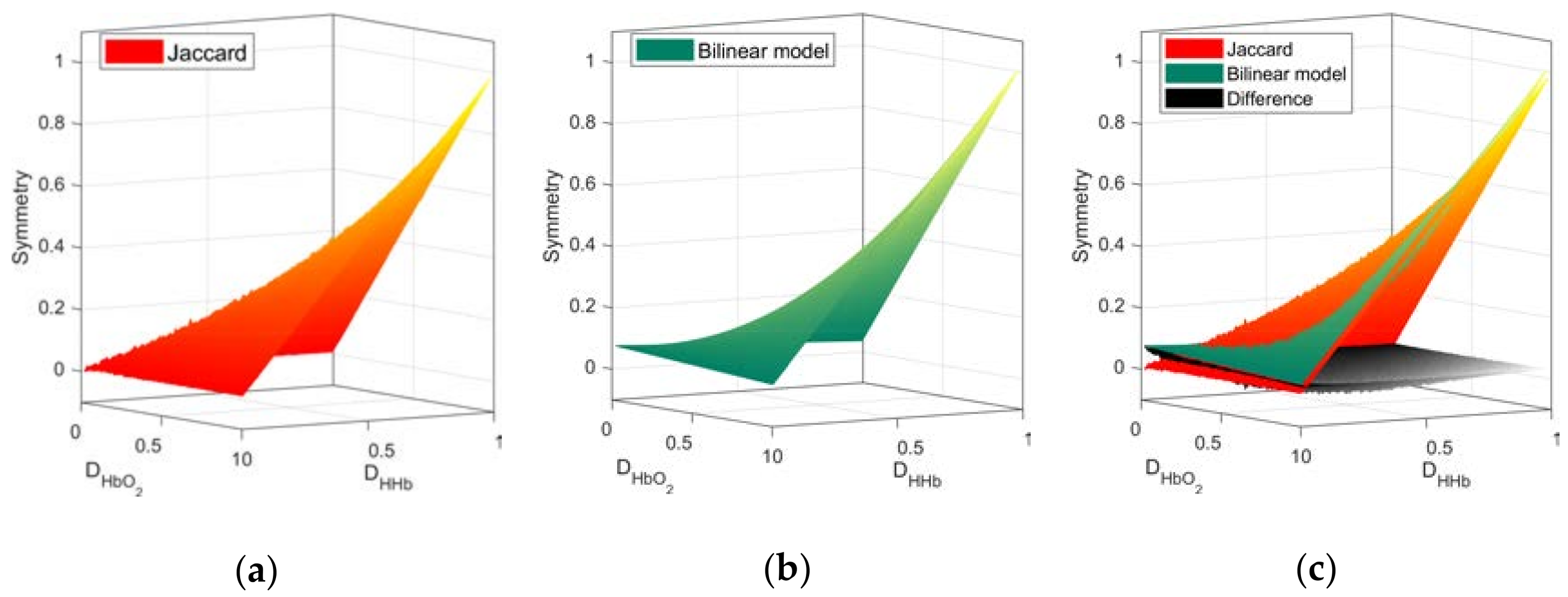
2.4. Quantification of Network Symmetry
3. Results
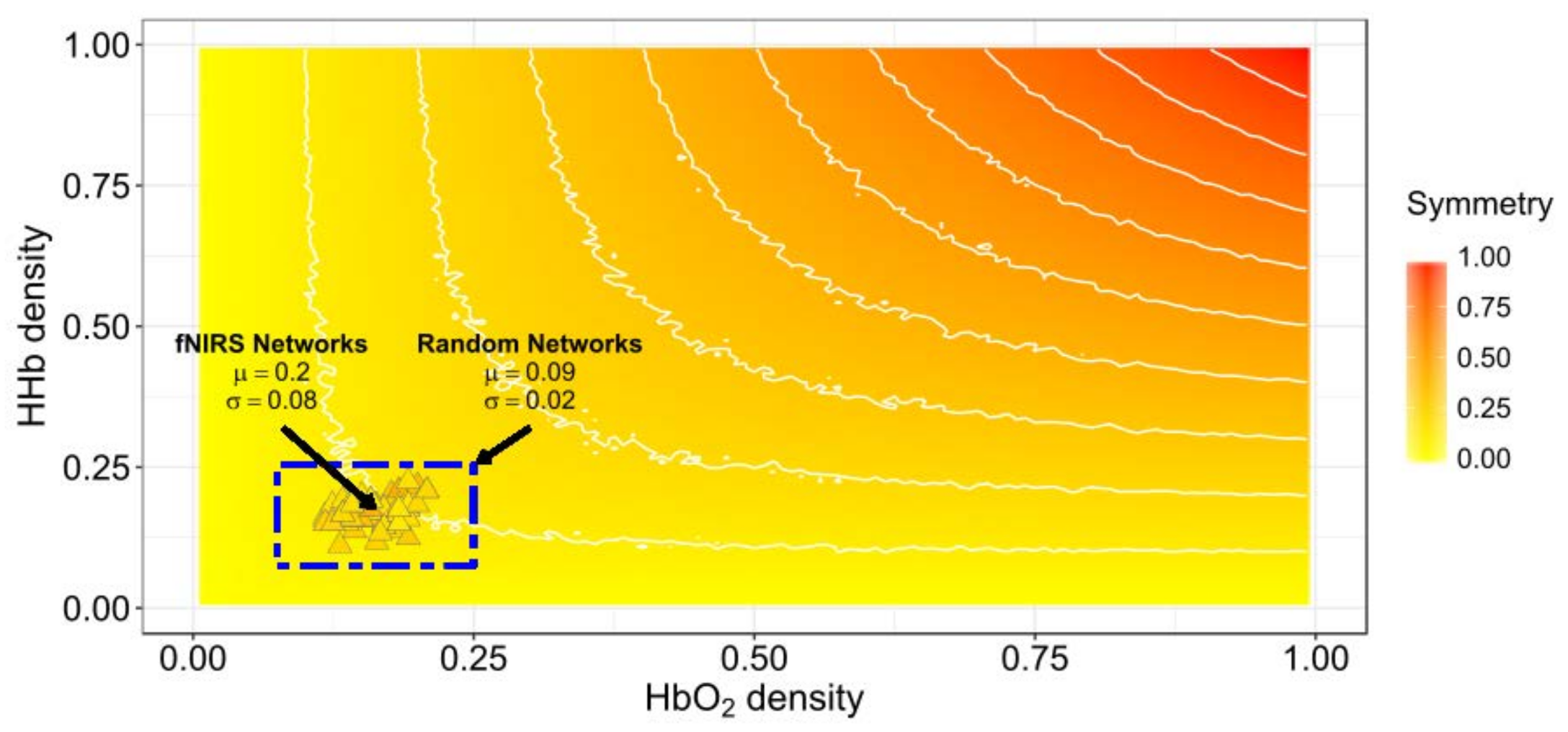
3.1. Network Symmetry Analysis
3.2. Integrational Analysis of Connectivity
4. Discussion
4.1. Symmetry between HbO2 and HHb Connectivity Networks
4.2. Inclusion of Systemic Data in fNIRS Functional Connectivity Analysis
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Villringer, A.; Chance, B. Non-invasive optical spectroscopy and imaging of human brain function. Trends Neurosci. 1997, 20, 435–442. [Google Scholar] [CrossRef]
- Yücel, M.A.; Selb, J.J.; Huppert, T.J.; Franceschini, M.A.; Boas, D.A. Functional near infrared spectroscopy: Enabling routine functional brain imaging. Curr. Opin. Biomed. Eng. 2017, 4, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J. Functional and effective connectivity in neuroimaging: A synthesis. Hum. Brain Mapp. 1994, 2, 56–78. [Google Scholar] [CrossRef]
- Friston, K.J. Functional and Effective Connectivity: A Review. Brain Connect. 2011, 1, 13–36. [Google Scholar] [CrossRef] [PubMed]
- Leff, D.R.; Orihuela-Espina, F.; Elwell, C.; Athanasiou, T.; Delpy, D.; Darzi, A.W.; Yang, G.-Z. Assessment of the Cerebral Cortex during Motor Task Behaviours in Adults: A Systematic Review of Functional Near Infrared Spectroscopy (fNIRS) Studies. Neuroimage 2011, 54, 2922–2936. [Google Scholar] [CrossRef] [PubMed]
- Villringer, A.; Dirnagl, U. Coupling of brain activity and cerebral blood flow: Basis of functional neuroimaging. Cerebrovasc. Brain Metab. Rev. 1995, 7, 240–276. [Google Scholar] [PubMed]
- Raichle, M.E.; Mintun, M.A. Brain Work and Brain Imaging. Annu. Rev. Neurosci. 2006, 29, 449–476. [Google Scholar] [CrossRef] [PubMed]
- Van Wijk, B.C.M.; Stam, C.J.; Daffertshofer, A. Comparing brain networks of different size and connectivity density using graph theory. PLoS ONE 2010, 5, e13701. [Google Scholar] [CrossRef] [PubMed]
- Toronov, V.Y.; Zhang, X.; Webb, A.G. A spatial and temporal comparison of hemodynamic signals measured using optical and functional magnetic resonance imaging during activation in the human primary visual cortex. Neuroimage 2007, 34, 1136–1148. [Google Scholar] [CrossRef] [PubMed]
- Mesquita, R.C.; Franceschini, M.A.; Boas, D.A. Resting state functional connectivity of the whole head with near-infrared spectroscopy. Biomed. Opt. Express 2010, 1, 324–336. [Google Scholar] [CrossRef] [PubMed]
- White, B.R.; Snyder, A.Z.; Cohen, A.L.; Petersen, S.E.; Raichle, M.E.; Schlaggar, B.L.; Culver, J.P. Resting-state functional connectivity in the human brain revealed with diffuse optical tomography. Neuroimage 2009, 47, 148–156. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhang, Y.J.; Lu, C.M.; Ma, S.Y.; Zang, Y.F.; Zhu, C.Z. Functional connectivity as revealed by independent component analysis of resting-state fNIRS measurements. Neuroimage 2010, 51, 1150–1161. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Duan, L.; Zhang, Y.-J.; Lu, C.-M.; Liu, H.; Zhu, C.-Z. Test–retest assessment of independent component analysis-derived resting-state functional connectivity based on functional near-infrared spectroscopy. Neuroimage 2011, 55, 607–615. [Google Scholar] [CrossRef] [PubMed]
- Lu, C.-M.; Zhang, Y.-J.; Biswal, B.B.; Zang, Y.-F.; Peng, D.-L.; Zhu, C.-Z. Use of fNIRS to assess resting state functional connectivity. J. Neurosci. Methods 2010, 186, 242–249. [Google Scholar] [CrossRef] [PubMed]
- Novi, S.L.; Rodrigues, R.B.M.L.; Mesquita, R.C. Resting state connectivity patterns with near-infrared spectroscopy data of the whole head. Biomed. Opt. Express 2016, 7, 2524–2537. [Google Scholar] [CrossRef] [PubMed]
- Tachtsidis, I.; Scholkmann, F. Publisher’s note: False positives and false negatives in functional near-infrared spectroscopy: Issues, challenges, and the way forward. Neurophotonics 2016, 3, 39801. [Google Scholar] [CrossRef] [PubMed]
- Orihuela-Espina, F.; Leff, D.R.; James, D.R.C.; Darzi, A.W.; Yang, G.-Z.Z. Quality control and assurance in functional near infrared spectroscopy (fNIRS) experimentation. Phys. Med. Biol. 2010, 55, 3701–3724. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, M.; Scholkmann, F.; Wolf, U.; Wolf, M.; Elwell, C.; Tachtsidis, I. Modelling confounding effects from extracerebral contamination and systemic factors on functional near-infrared spectroscopy. Neuroimage 2016, 143, 91–105. [Google Scholar] [CrossRef] [PubMed]
- Kirilina, E.; Jelzow, A.; Heine, A.; Niessing, M.; Wabnitz, H.; Brühl, R.; Ittermann, B.; Jacobs, A.M.; Tachtsidis, I. The physiological origin of task-evoked systemic artefacts in functional near infrared spectroscopy. Neuroimage 2012, 61, 70–81. [Google Scholar] [CrossRef] [PubMed]
- Tong, Y.; Hocke, L.M.; Fan, X.; Janes, A.C.; Frederick, B. deB Can apparent resting state connectivity arise from systemic fluctuations? Front. Hum. Neurosci. 2015, 9, 285. [Google Scholar] [CrossRef] [PubMed]
- Scholkmann, F.; Holper, L.; Wolf, U.; Wolf, M. A new methodical approach in neuroscience: Assessing inter-personal brain coupling using functional near-infrared imaging (fNIRI) hyperscanning. Front. Hum. Neurosci. 2013, 7, 813. [Google Scholar] [CrossRef] [PubMed]
- Crivelli, D.; Balconi, M. Near-Infrared Spectroscopy Applied to Complex Systems and Human Hyperscanning Networking. Appl. Sci. 2017, 7, 922. [Google Scholar] [CrossRef]
- Uludag, K.; Steinbrink, J.; Villringer, A.; Obrig, H. Separability and cross-talk: Optimizing dual wavelength combinations for near-infrared spectroscopy of the adult head. Neuroimage 2004, 22, 583–589. [Google Scholar] [CrossRef] [PubMed]
- Strangman, G.; Culver, J.P.; Thompson, J.H.; Boas, D.A. A quantitative comparison of simultaneous BOLD fMRI and NIRS recordings during functional brain activation. Neuroimage 2002, 17, 719–731. [Google Scholar] [CrossRef] [PubMed]
- Wolf, M.; Wolf, U.; Toronov, V.; Michalos, A.; Paunescu, L.A.; Choi, J.H.; Gratton, E. Different time evolution of oxyhemoglobin and deoxyhemoglobin concentration changes in the visual and motor cortices during functional stimulation: A near-infrared spectroscopy study. Neuroimage 2002, 16, 704–712. [Google Scholar] [CrossRef] [PubMed]
- Sasai, S.; Homae, F.; Watanabe, H.; Taga, G. Frequency-specific functional connectivity in the brain during resting state revealed by NIRS. Neuroimage 2011, 56, 252–257. [Google Scholar] [CrossRef] [PubMed]
- Huppert, T.J.; Diamond, S.G.; Franceschini, M.A.; Boas, D. A HomER: A review of time-series analysis methods for near-infrared spectroscopy of the brain. Appl. Opt. 2009, 48, D280–D298. [Google Scholar] [CrossRef] [PubMed]
- Craddock, R.C.; Holtzheimer, P.E.; Hu, X.P.; Mayberg, H.S. Disease state prediction from resting state functional connectivity. Magn. Reson. Med. 2009, 62, 1619–1628. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Wang, L.; Liu, Y.; Hu, D. Discriminative analysis of resting-state functional connectivity patterns of schizophrenia using low dimensional embedding of fMRI. Neuroimage 2010, 49, 3110–3121. [Google Scholar] [CrossRef] [PubMed]
- Pinti, P.; Aichelburg, C.; Lind, F.; Power, S.; Swingler, E.; Merla, A.; Hamilton, A.; Gilbert, S.; Burgess, P.; Tachtsidis, I. Using Fiberless, Wearable fNIRS to Monitor Brain Activity in Real-world Cognitive Tasks. J. Vis. Exp. 2015, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Burgess, P.W.; Scott, S.K.; Frith, C.D. The role of the rostral frontal cortex (area 10) in prospective memory: A lateral versus medial dissociation. Neuropsychologia 2003, 41, 906–918. [Google Scholar] [CrossRef]
- Atsumori, H.; Kiguchi, M.; Obata, A.; Sato, H.; Katura, T.; Funane, T.; Maki, A. Development of wearable optical topography system for mapping the prefrontal cortex activation. Rev. Sci. Instrum. 2009, 80, 43704. [Google Scholar] [CrossRef] [PubMed]
- Molavi, B.; Dumont, G.A. Wavelet-based motion artifact removal for functional near-infrared spectroscopy. Physiol. Meas. 2012, 33, 259. [Google Scholar] [CrossRef] [PubMed]
- Spirtes, P.; Glymour, C.; Scheines, R.; Burr, T. Causation, Prediction, and Search, 2nd ed.; MIT Press: Cambridge, MA, USA, 2000; Volume 45, ISBN 0262194406. [Google Scholar]
- Kalisch, M.; Machler, M.; Colombo, D.; Maathuis, M.H.; Buhlmann, P.; Mächler, M.; Colombo, D.; Maathuis, M.H. Causal Inference Using Graphical Models with the R Package pcalg. J. Stat. Softw. 2012, 47, 26. [Google Scholar] [CrossRef]
- Tong, W.; Xia, W.; Xuyun, W.; Li, Y. Group-analysis of Resting-state fMRI Based on Bayesian Network: A Comparison of Three Virtual-typical-subject Methods. Neurosci. Biomed. Eng. 2015, 2, 92–98. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.J.; Palmer, S.J.; McKeown, M.J. Dynamic Bayesian network modeling of fMRI: A comparison of group-analysis methods. Neuroimage 2008, 41, 398–407. [Google Scholar] [CrossRef] [PubMed]
- Ide, J.S.; Zhang, S.; Li, C.R. Bayesian network models in brain functional connectivity analysis. Int. J. Approx. Reason. 2014, 55, 23–35. [Google Scholar] [CrossRef] [PubMed]
- Sucar, L.E. Probabilistic Graphical Models: Principles and Applications; Advances in Computer Vision and Pattern Recognition; Springer: London, UK, 2015; ISBN 9781447166993. [Google Scholar]
- Montero-Hernandez, S.A.; Orihuela-Espina, F.; Herrera-Vega, J.; Sucar, L.E. Causal Probabilistic Graphical Models for Decoding Effective Connectivity in Functional Near InfraRed Spectroscopy. In Twenty-Ninth International Florida Artificial Intelligence Research Society Conference Causal; AAAI Press: Palo Alto, CA, USA, 2016; pp. 686–689. [Google Scholar]
- Waldorp, L.; Christoffels, I.; van de Ven, V. Effective connectivity of fMRI data using ancestral graph theory: Dealing with missing regions. Neuroimage 2011, 54, 2695–2705. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Yu, X.; Yao, L.; Li, R. Bayesian network analysis revealed the connectivity difference of the default mode network from the resting-state to task-state. Front. Comput. Neurosci. 2014, 8, 118. [Google Scholar] [CrossRef] [PubMed]
- Ramsey, J.D.; Hanson, S.J.; Hanson, C.; Halchenko, Y.O.; Poldrack, R.A.; Glymour, C. Six problems for causal inference from fMRI. Neuroimage 2010, 49, 1545–1558. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Rajapakse, J.C. Learning functional structure from fMR images. Neuroimage 2006, 31, 1601–1613. [Google Scholar] [CrossRef] [PubMed]
- Rajapakse, J.C.; Zhou, J. Learning effective brain connectivity with dynamic Bayesian networks. Neuroimage 2007, 37, 749–760. [Google Scholar] [CrossRef] [PubMed]
- Latora, V.; Marchiori, M. Efficient Behavior of Small-World Networks. Phys. Rev. Lett. 2001, 87, 198701. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. Fast algorithm for detecting community structure in networks. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2004, 69, 66133. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 69, 26113. [Google Scholar] [CrossRef] [PubMed]
- Dehmer, M.; Varmuza, K. A comparative analysis of the Tanimoto index and graph edit distance for measuring the topological similarity of trees. Appl. Math. Comput. 2015, 259, 242–250. [Google Scholar] [CrossRef]
- Landsiedel, J.; Williams, D.M.; Abbot-Smith, K. A Meta-Analysis and Critical Review of Prospective Memory in Autism Spectrum Disorder. J. Autism Dev. Disord. 2017, 47, 646–666. [Google Scholar] [CrossRef] [PubMed]
- Burgess, P.W.; Wu, H.-C. Rostral Prefrontal Cortex (Brodmann Area 10): Metacognition in the Brain. In Principles of Frontal Lobe Function; Stuss, D.T., Knight, R.T., Eds.; Oxford University Press: Oxford, UK, 2013; pp. 524–534. [Google Scholar]
- Rojkova, K.; Volle, E.; Urbanski, M.; Humbert, F.; Dell’Acqua, F.; Thiebaut de Schotten, M. Atlasing the frontal lobe connections and their variability due to age and education: A spherical deconvolution tractography study. Brain Struct. Funct. 2016, 221, 1751–1766. [Google Scholar] [CrossRef] [PubMed]
- Thiebaut de Schotten, M.; Dell’Acqua, F.; Valabregue, R. Monkey to human comparative anatomy of the frontal lobe association tracts. Cortex 2012, 48, 82–96. [Google Scholar] [CrossRef] [PubMed]
- Catani, M.; Howard, R.J.; Pajevic, S.; Jones, D.K. Virtual in Vivo interactive dissection of white matter fasciculi in the human brain. Neuroimage 2002, 17, 77–94. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, S.J.; Gonen-Yaacovi, G.; Benoit, R.G.; Volle, E.; Burgess, P.W. Distinct functional connectivity associated with lateral versus medial rostral prefrontal cortex: A meta-analysis. Neuroimage 2010, 53, 1359–1367. [Google Scholar] [CrossRef] [PubMed]
- Shallice, T.; Burgess, P. The Domain of Supervisory Processes and Temporal Organization of Behaviour. Philos. Trans. R. Soc. B Biol. Sci. 1996, 351, 1405–1412. [Google Scholar] [CrossRef] [PubMed]
- Burgess, P.W.; Alderman, N.; Forbes, C.; Costello, A.; Coates, L.M.A.; Dawson, D.R.; Anderson, N.D.; Gilbert, S.J.; Dumontheil, I.; Channon, S. The case for the development and use of “ecologically valid” measures of executive function in experimental and clinical neuropsychology. J. Int. Neuropsychol. Soc. 2006, 12, 194–209. [Google Scholar] [CrossRef] [PubMed]
- Burgess, P.W.; Gonen-Yaacovi, G.; Volle, E. Functional neuroimaging studies of prospective memory: What have we learnt so far? Neuropsychologia 2011, 49, 2246–2257. [Google Scholar] [CrossRef] [PubMed]
- Carbonell, F.; Bellec, P.; Shmuel, A. Quantification of the impact of a confounding variable on functional connectivity confirms anti-correlated networks in the resting-state. Neuroimage 2014, 86, 343–353. [Google Scholar] [CrossRef] [PubMed]
- Ramb, R.; Eichler, M.; Ing, A.; Thiel, M.; Weiller, C.; Grebogi, C.; Schwarzbauer, C.; Timmer, J.; Schelter, B. The impact of latent confounders in directed network analysis in neuroscience. Philos. Trans. A Math. Phys. Eng. Sci. 2013, 371, 20110612. [Google Scholar] [CrossRef] [PubMed]
- Obrig, H.; Neufang, M.; Wenzel, R.; Kohl, M.; Steinbrink, J.; Einhäupl, K.; Villringer, A. Spontaneous low frequency oscillations of cerebral hemodynamics and metabolism in Human Adults. Neuroimage 2000, 12, 623–639. [Google Scholar] [CrossRef] [PubMed]
- Habermehl, C.; Steinbrink, J.; Müller, K.-R.; Haufe, S. Optimizing the regularization for image reconstruction of cerebral diffuse optical tomography. J. Biomed. Opt. 2014, 19, 96006. [Google Scholar] [CrossRef] [PubMed]
- Kirlilna, E.; Yu, N.; Jelzow, A.; Wabnitz, H.; Jacobs, A.M.; Tachtsidis, I. Identifying and quantifying main components of physiological noise in functional near infrared spectroscopy on the prefrontal cortex. Front. Hum. Neurosci. 2013, 7, 864. [Google Scholar] [CrossRef] [PubMed]
- Toronov, V.; Franceschini, M.A.; Filiaci, M.; Fantini, S.; Wolf, M.; Michalos, A.; Gratton, E. Near-infrared study of fluctuations in cerebral hemodynamics during rest and motor stimulation: Temporal analysis and spatial mapping. Med. Phys. 2000, 27, 801–815. [Google Scholar] [CrossRef] [PubMed]
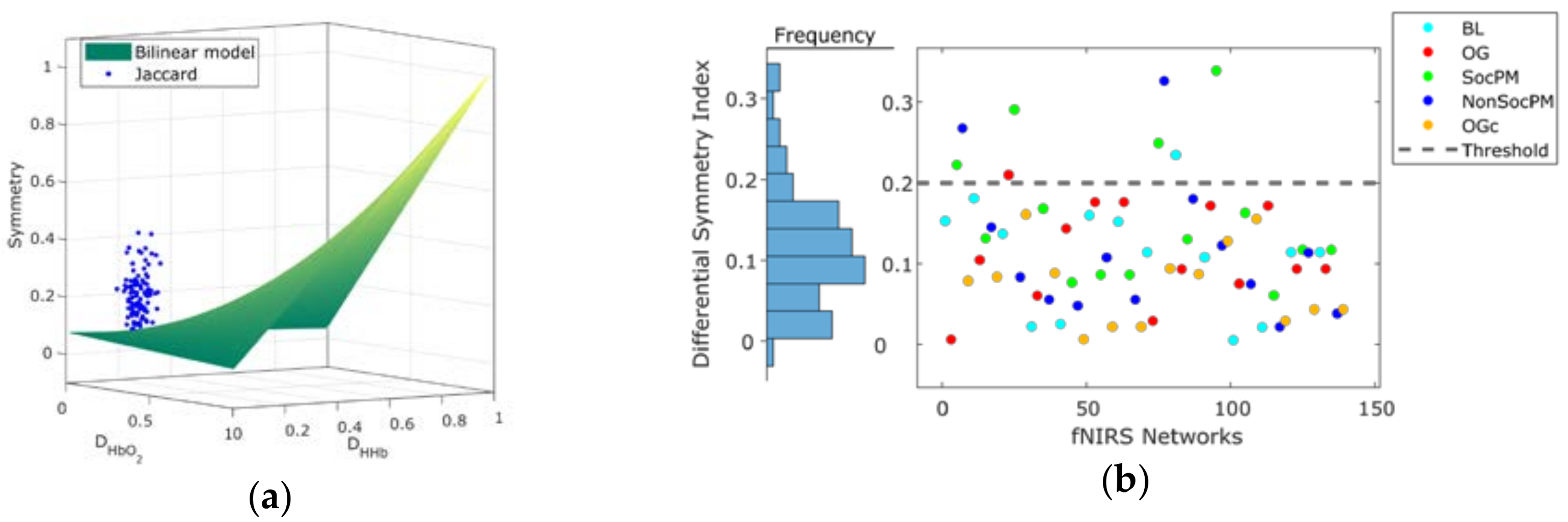
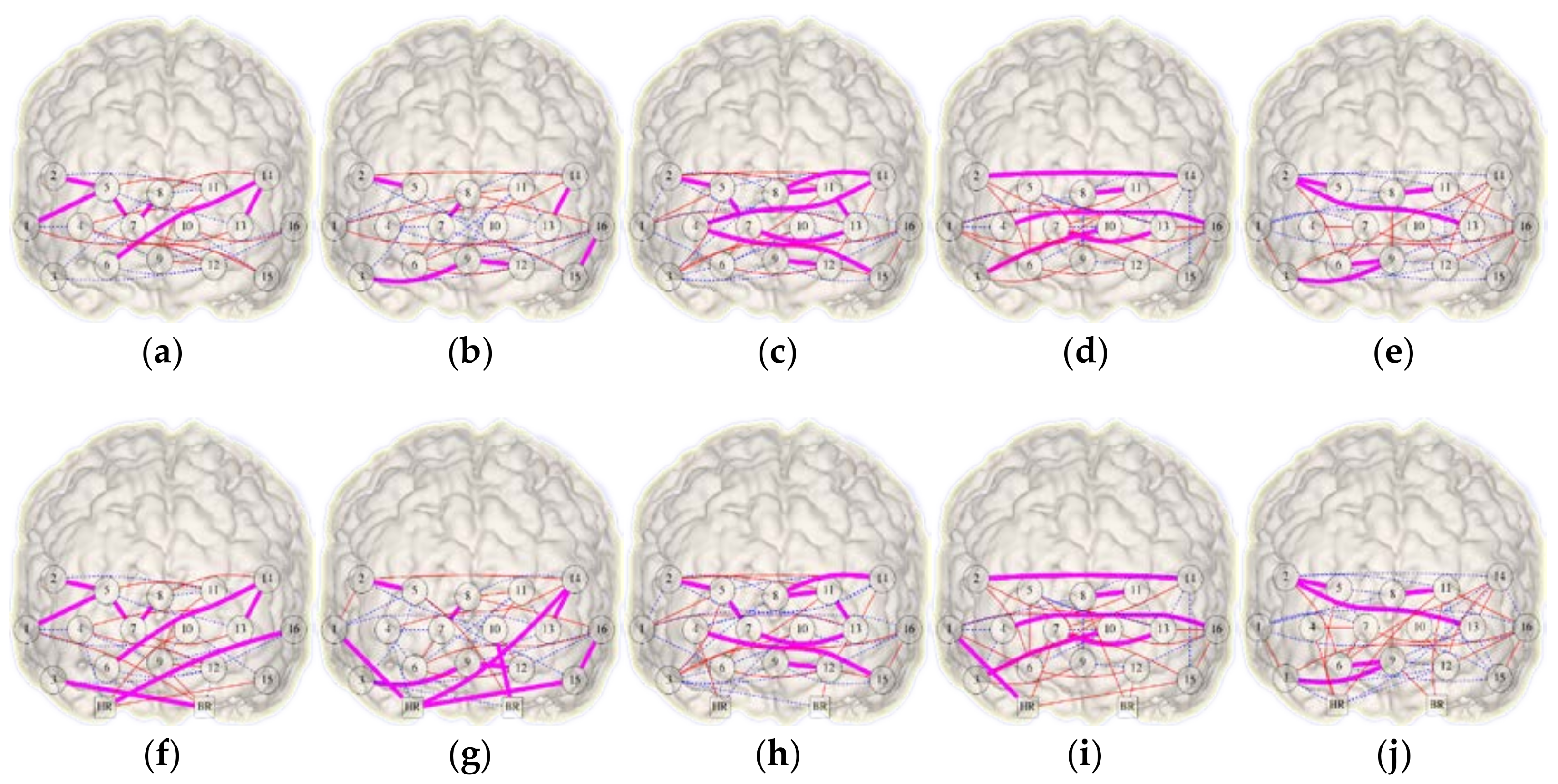
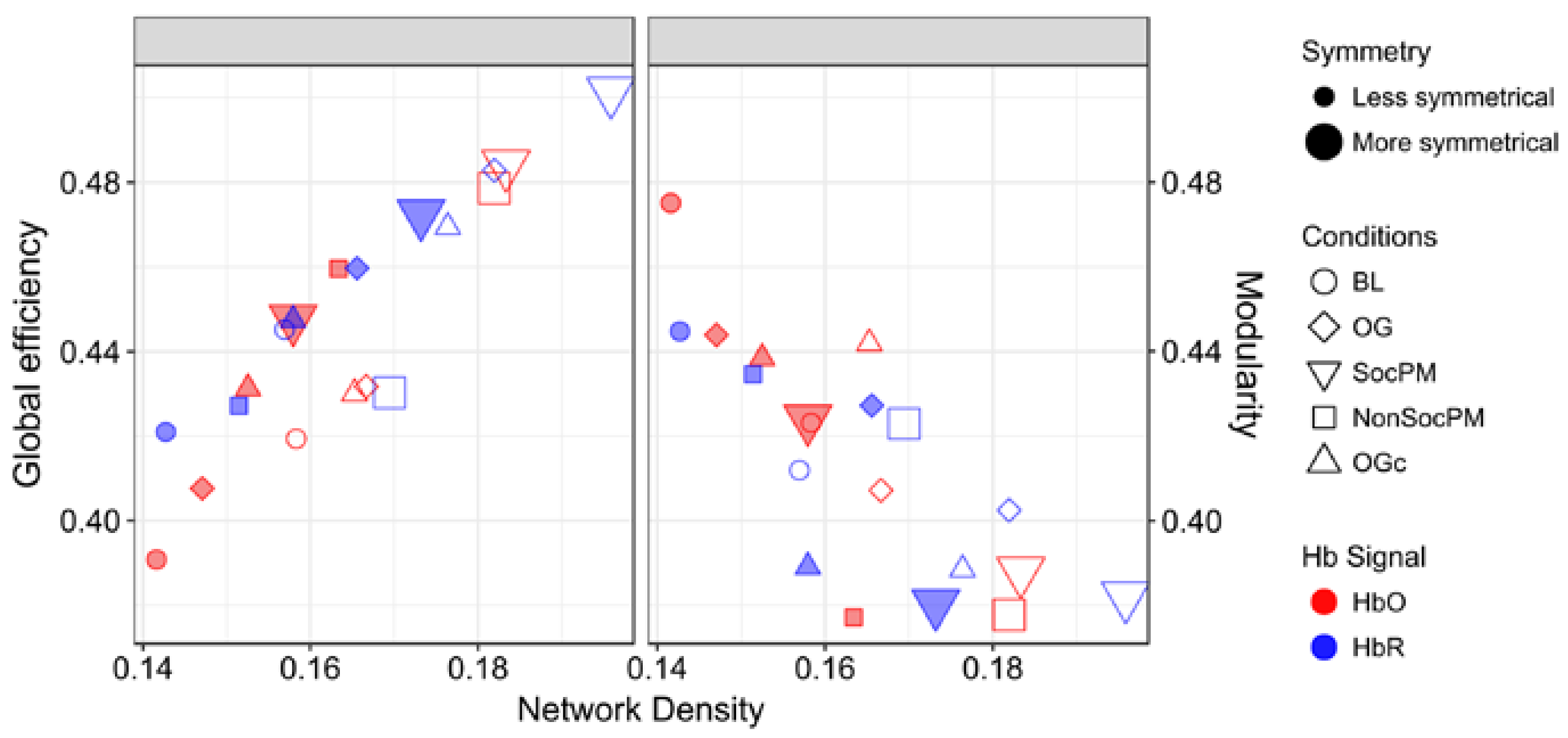
| FC Network | Density | Jaccard Symmetry | DSI Symmetry | |||
|---|---|---|---|---|---|---|
| Condition | With Systemic | Without Systemic | With Systemic | Without Systemic | With Systemic | Without Systemic |
| Baseline (BL) | 0.22 ↑ | 0.20 | 0.24 ↑ | 0.20 | 0.15 ↑ | 0.11 |
| Ongoing (OG) | 0.25 ↑ | 0.22 | 0.26 ↑ | 0.18 | 0.18 ↑ | 0.09 |
| Social PM (SocPM) | 0.29 ↑ | 0.27 | 0.18 ↓ | 0.22 | 0.09 ↓ | 0.12 |
| Non-Social PM (NonSocPM) | 0.27 ↑ | 0.25 | 0.14 ↑ | 0.13 | 0.06 ↑ | 0.04 |
| Ongoing Condition (OGc) | 0.29 ↑ | 0.24 | 0.11 ↓ | 0.14 | 0.02 ↓ | 0.04 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montero-Hernandez, S.; Orihuela-Espina, F.; Sucar, L.E.; Pinti, P.; Hamilton, A.; Burgess, P.; Tachtsidis, I. Estimating Functional Connectivity Symmetry between Oxy- and Deoxy-Haemoglobin: Implications for fNIRS Connectivity Analysis. Algorithms 2018, 11, 70. https://doi.org/10.3390/a11050070
Montero-Hernandez S, Orihuela-Espina F, Sucar LE, Pinti P, Hamilton A, Burgess P, Tachtsidis I. Estimating Functional Connectivity Symmetry between Oxy- and Deoxy-Haemoglobin: Implications for fNIRS Connectivity Analysis. Algorithms. 2018; 11(5):70. https://doi.org/10.3390/a11050070
Chicago/Turabian StyleMontero-Hernandez, Samuel, Felipe Orihuela-Espina, Luis Enrique Sucar, Paola Pinti, Antonia Hamilton, Paul Burgess, and Ilias Tachtsidis. 2018. "Estimating Functional Connectivity Symmetry between Oxy- and Deoxy-Haemoglobin: Implications for fNIRS Connectivity Analysis" Algorithms 11, no. 5: 70. https://doi.org/10.3390/a11050070
APA StyleMontero-Hernandez, S., Orihuela-Espina, F., Sucar, L. E., Pinti, P., Hamilton, A., Burgess, P., & Tachtsidis, I. (2018). Estimating Functional Connectivity Symmetry between Oxy- and Deoxy-Haemoglobin: Implications for fNIRS Connectivity Analysis. Algorithms, 11(5), 70. https://doi.org/10.3390/a11050070







