Control Strategy of Speed Servo Systems Based on Deep Reinforcement Learning
Abstract
:1. Introduction
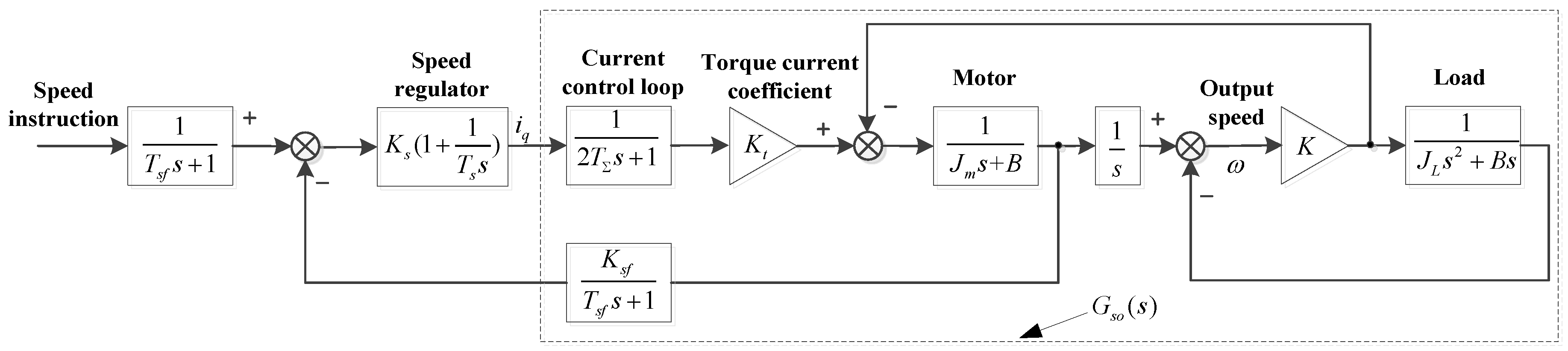
2. Model Analysis of a Speed Servo System
3. Servo System Control Strategy Based on Reinforcement Learning
3.1. Strategic Process of Reinforcement Learning
3.1.1. DQN Algorithms
3.1.2. Deterministic Policy Gradient Algorithms
3.2. PID Servo System Control Scheme Based on Reinforcement Learning
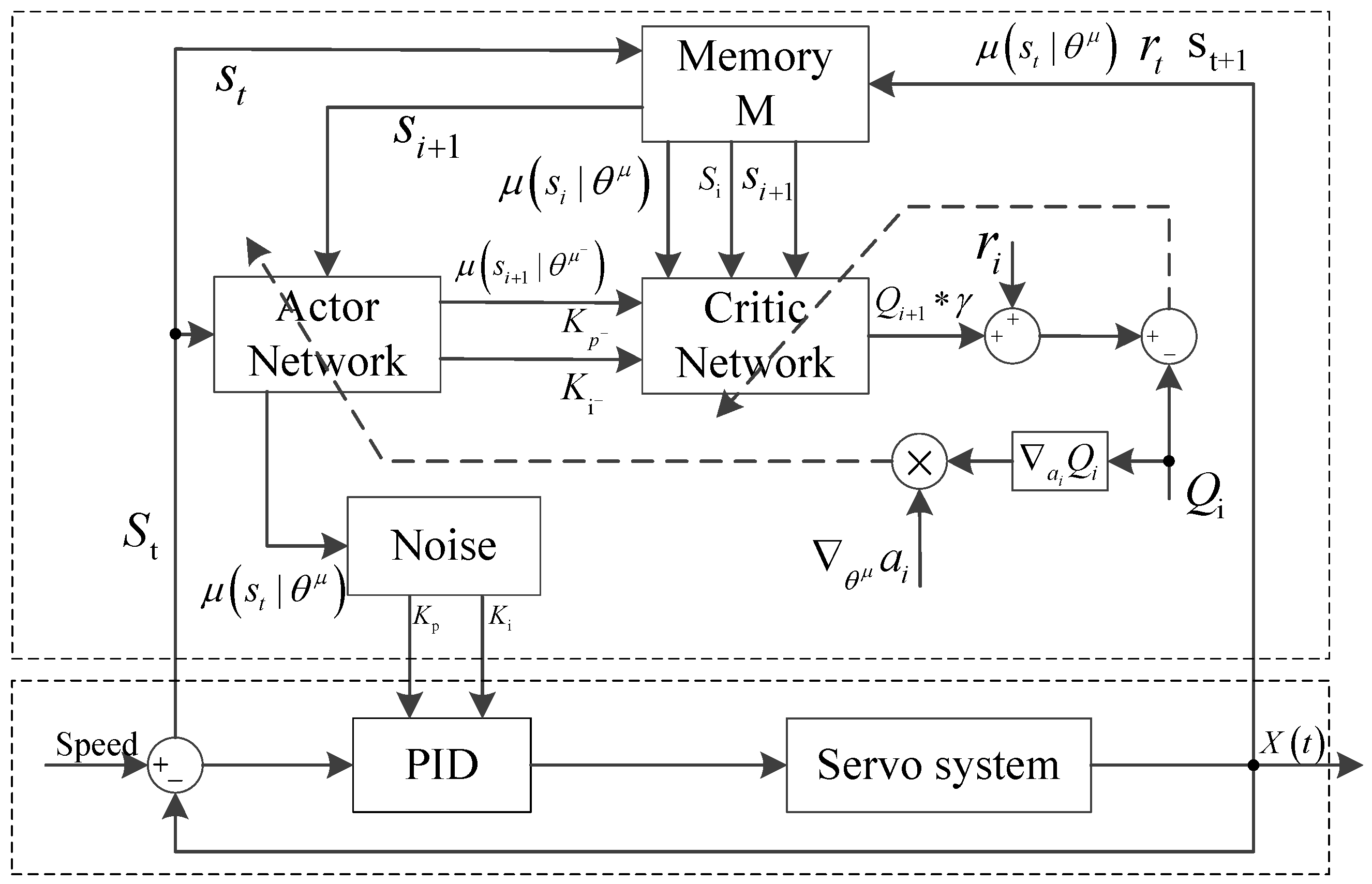
3.2.1. PID Parameter Tuning Method Based on Reinforcement Learning
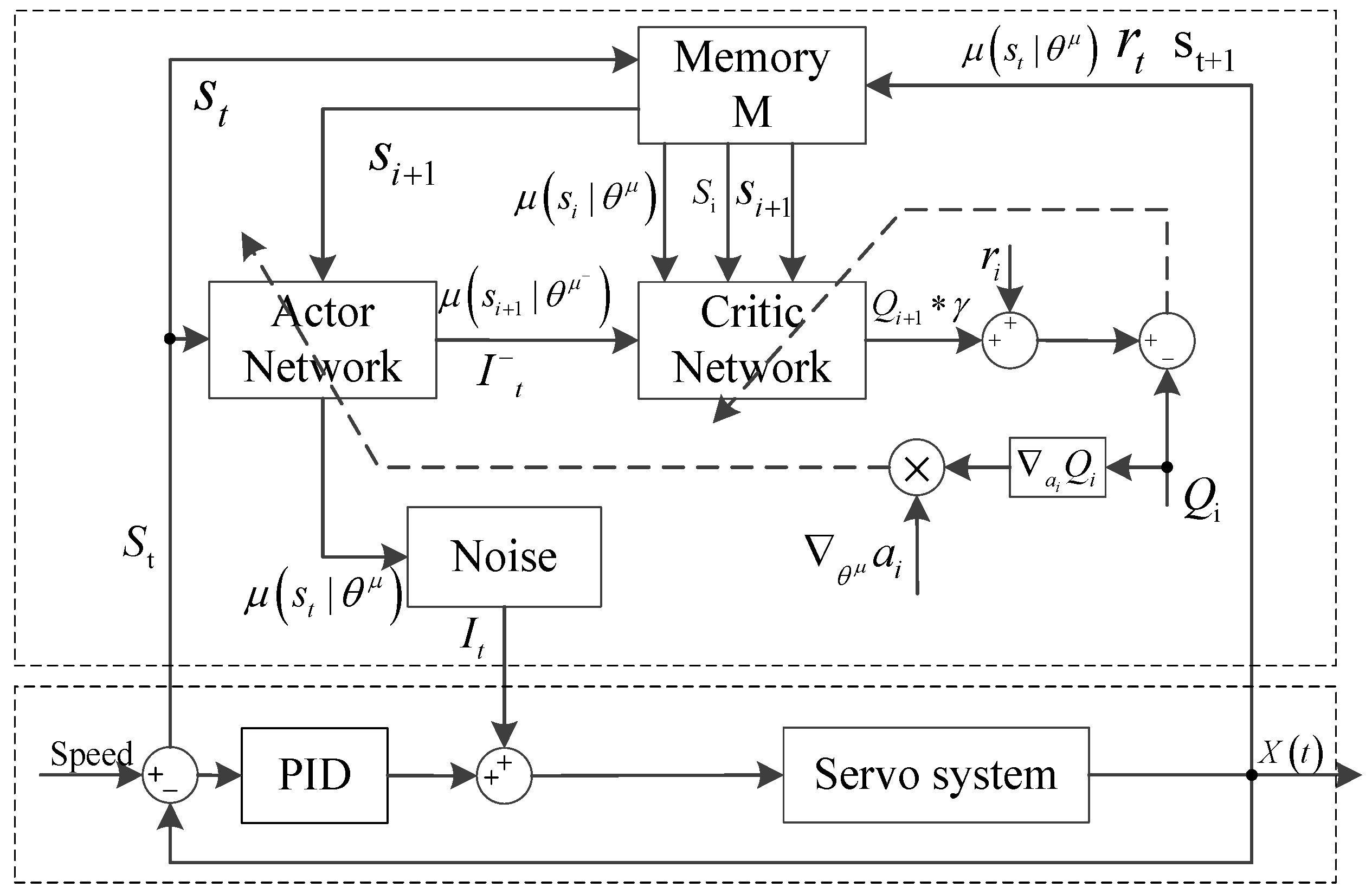
3.2.2. Adaptive PID Current Compensation Method Based on Reinforcement Learning
3.3. Design Scheme of Reinforcement Learning Agent
3.3.1. Network Design for Actor
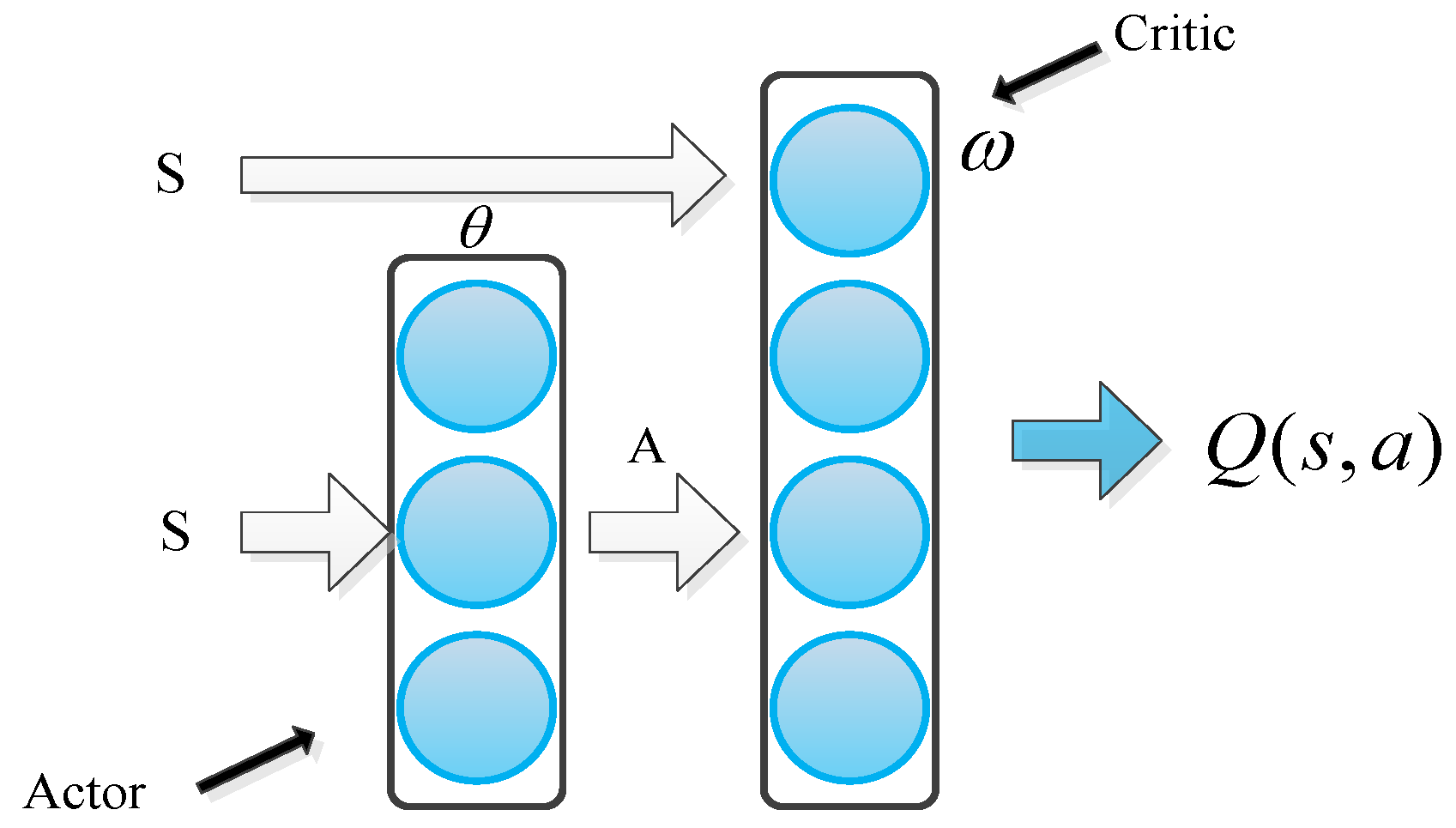
3.3.2. Network Design for Critic
3.4. Implementation Process of the Adaptive PID Algorithm Based on DDPG Algorithm
4. Result and Discussion
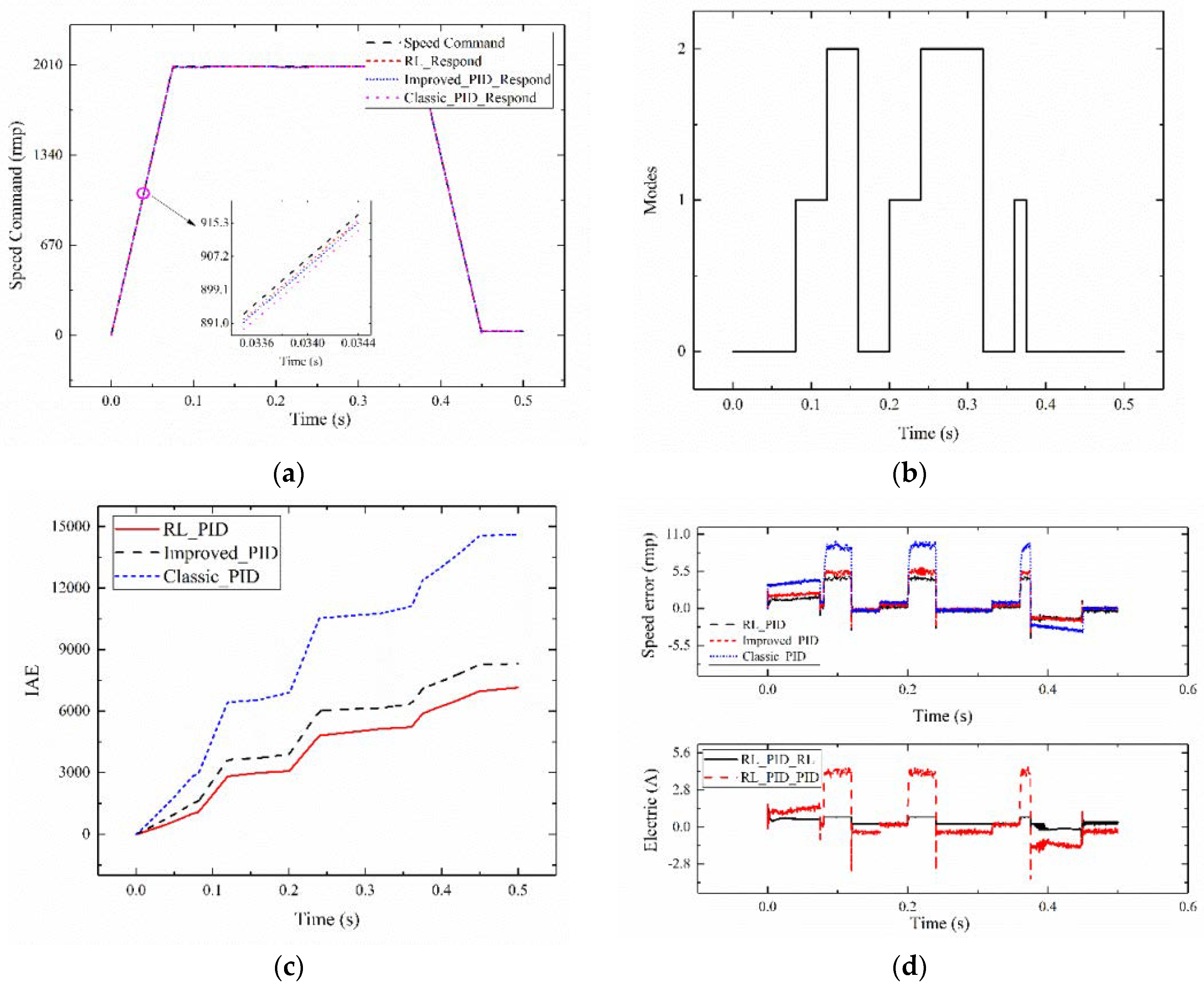
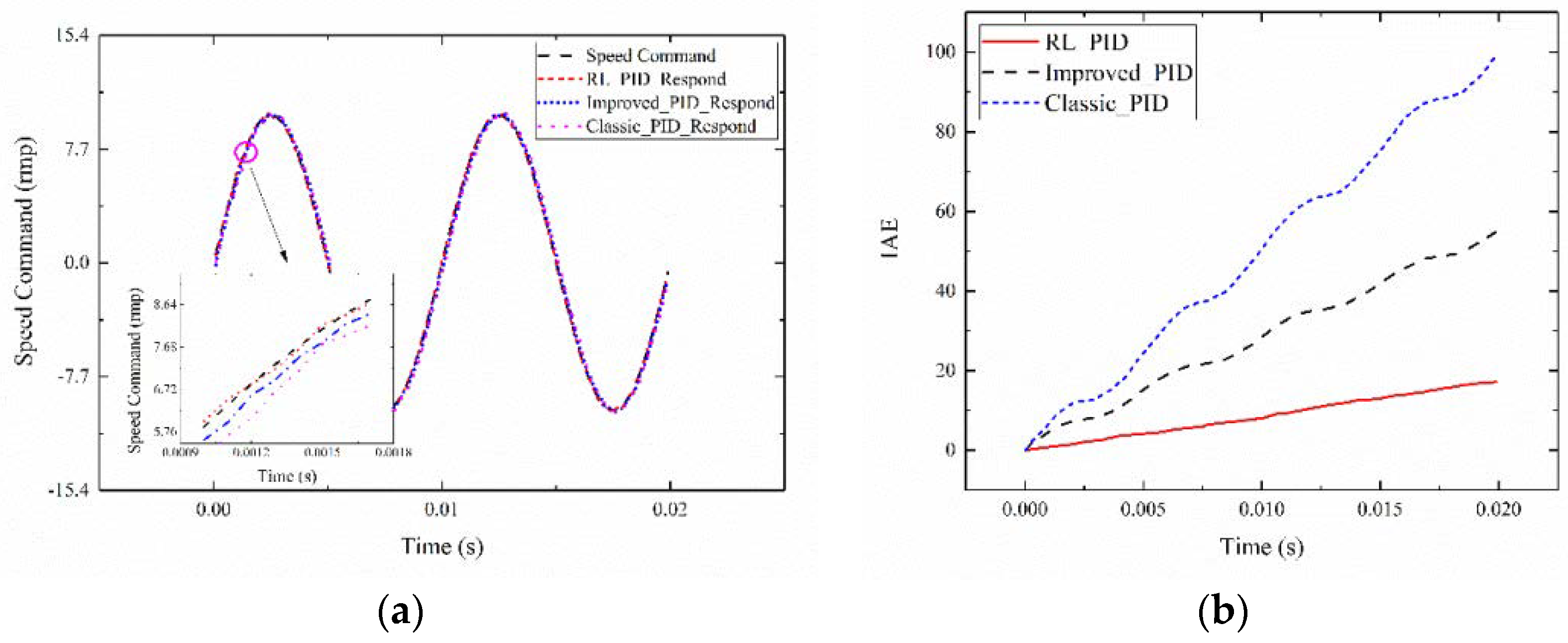
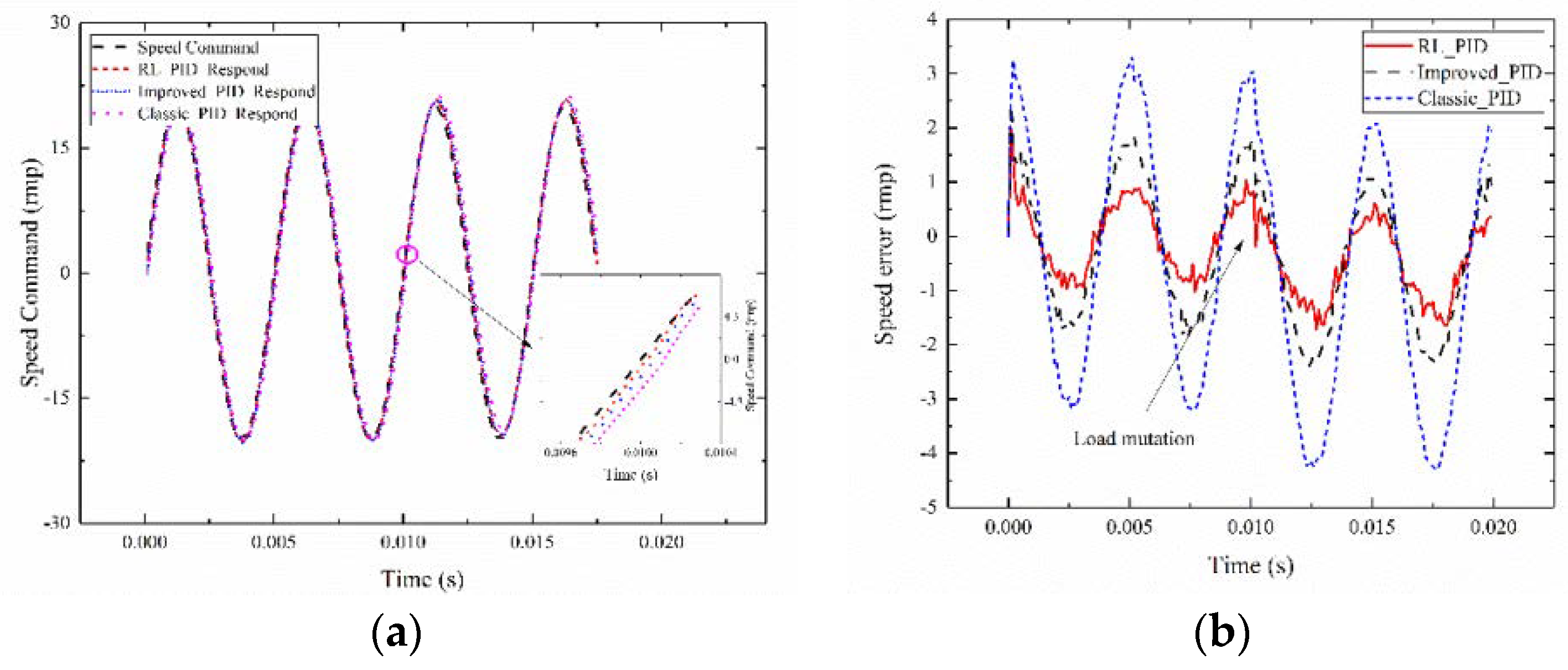
4.1. Experimental Setup
4.2. Experimental Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zheng, S.; Tang, X.; Song, B.; Ye, B. Stable adaptive PI control for permanent magnet synchronous motor drive based on improved JITL technique. ISA Trans. 2013, 52, 539–549. [Google Scholar] [CrossRef] [PubMed]
- Roy, P.; Roy, B.K. Fractional order PI control applied to level control in coupled two tank MIMO system with experimental validation. Control Eng. Pract. 2016, 48, 119–135. [Google Scholar] [CrossRef]
- Ang, K.H.; Chong, G.; Li, Y. PID control system analysis, design, and technology. IEEE Trans. Control Syst. Technol. 2005, 13, 559–576. [Google Scholar] [CrossRef]
- Sekour, M.; Hartani, K.; Draou, A.; Ahmed, A. Sensorless Fuzzy Direct Torque Control for High Performance Electric Vehicle with Four In-Wheel Motors. J. Electr. Eng. Technol. 2013, 8, 530–543. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, L.; Zhao, K.; Sun, L. Nonlinear Speed Control for PMSM System Using Sliding-Mode Control and Disturbance Compensation Techniques. IEEE Trans. Power Electron. 2012, 28, 1358–1365. [Google Scholar] [CrossRef]
- Dang, Q.D.; Vu, N.T.T.; Choi, H.H.; Jung, J.W. Neuro-Fuzzy Control of Interior Permanent Magnet Synchronous Motors. J. Electr. Eng. Technol. 2013, 8, 1439–1450. [Google Scholar] [CrossRef]
- El-Sousy, F.F.M. Adaptive hybrid control system using a recurrent RBFN-based self-evolving fuzzy-neural-network for PMSM servo drives. Appl. Soft Comput. 2014, 21, 509–532. [Google Scholar] [CrossRef]
- Jezernik, K.; Korelič, J.; Horvat, R. PMSM sliding mode FPGA-based control for torque ripple reduction. IEEE Trans. Power Electron. 2012, 28, 3549–3556. [Google Scholar] [CrossRef]
- Jung, J.W.; Leu, V.Q.; Do, T.D.; Kim, E.K.; Choi, H.H. Adaptive PID Speed Control Design for Permanent Magnet Synchronous Motor Drives. IEEE Trans. Power Electron. 2014, 30, 900–908. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. Comput. Sci. 2013. Available online: https://arxiv.org/pdf/1312.5602v1.pdf (accessed on 3 May 2018).
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. Comput. Sci. 2015, 8, A187. Available online: http://xueshu.baidu.com/s?wd=paperuri%3A%283752bdb69e8a3f4849ecba38b2b0168f%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Farxiv.org%2Fabs%2F1509.02971&ie=utf-8&sc_us=1138439324812222606 (accessed on 3 May 2018).
- Jiang, H.; Zhang, H.; Luo, Y.; Wang, J. Optimal tracking control for completely unknown nonlinear discrete-time Markov jump systems using data-based reinforcement learning method. Neurocomputing 2016, 194, 176–182. [Google Scholar] [CrossRef]
- Carlucho, I.; Paula, M.D.; Villar, S.; Acosta, G.G. Incremental Q-learning strategy for adaptive PID control of mobile robots. Expert Syst. Appl. 2017, 80, 183–199. [Google Scholar] [CrossRef]
- Yu, R.; Shi, Z.; Huang, C.; Li, T.; Ma, Q. Deep reinforcement learning based optimal trajectory tracking control of autonomous underwater vehicle. In Proceedings of the 2017 36th Chinese Control Conference (CCC), Dalian, China, 26–28 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 4958–4965. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, Y.; Zhao, M.; Sun, C.; Tan, Q. Application of Gradient Descent Continuous Actor-Critic Algorithm for Bilateral Spot Electricity Market Modeling Considering Renewable Power Penetration. Algorithms 2017, 10, 53. [Google Scholar] [CrossRef]
- Hu, Y.; Li, W.; Xu, K.; Zahid, T.; Qin, F.; Li, C. Energy Management Strategy for a Hybrid Electric Vehicle Based on Deep Reinforcement Learning. Appl. Sci. 2018, 8, 187. [Google Scholar] [CrossRef]
- Lin, C.H. Composite recurrent Laguerre orthogonal polynomials neural network dynamic control for continuously variable transmission system using altered particle swarm optimization. Nonlinear Dyn. 2015, 81, 1219–1245. [Google Scholar] [CrossRef]
- Liu, Y.J.; Tong, S. Adaptive NN tracking control of uncertain nonlinear discrete-time systems with nonaffine dead-zone input. IEEE Trans. Cybern. 2017, 45, 497–505. [Google Scholar] [CrossRef] [PubMed]
- Dos Santos Mignon, A.; da Rocha, R.L.A. An Adaptive Implementation of ε-Greedy in Reinforcement Learning. Procedia Comput. Sci. 2017, 109, 1146–1151. [Google Scholar] [CrossRef]
- Plappert, M.; Houthooft, R.; Dhariwal, P.; Sidor, S.; Chen, R.Y.; Chen, X.; Asfour, T.; Abbeel, P.; Andrychowicz, M. Parameter Space Noise for Exploration. Comput. Sci. 2017. Available online: http://xueshu.baidu.com/s?wd=paperuri%3A%28c8411e5bc5e651d776e9d4997604cc3e%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Farxiv.org%2Fabs%2F1706.01905&ie=utf-8&sc_us=8746754823928227025 (accessed on 3 May 2018).
- Nigam, K. Using maximum entropy for text classification. In Proceedings of the IJCAI-99 Workshop on Machine Learning for Information Filtering, Stockholm, Sweden, 1 August 1999; pp. 61–67. Available online: http://www.kamalnigam.com/papers/maxent-ijcaiws99.pdf (accessed on 3 May 2018).
- Ng, A.Y. Feature selection, L1 vs. L2 regularization, and rotational invariance. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 June 2004; ACM: New York, NY, USA, 2004; p. 78. Available online: http://www.yaroslavvb.com/papers/ng-feature.pdf (accessed on 3 May 2018).
- Monahan, G.E. A Survey of Partially Observable Markov Decision Processes: Theory, Models, and Algorithms. Manag. Sci. 1982, 28, 1–16. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998; Available online: http://www.umiacs.umd.edu/~hal/courses/2016F_RL/RL9.pdf (accessed on 3 May 2018).
- Silver, D.; Lever, G.; Heess, N.; Thomas, D.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the International Conference on International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 387–395. Available online: http://www0.cs.ucl.ac.uk/staff/d.silver/web/Applications_files/deterministic-policy-gradients.pdf (accessed on 3 May 2018).
- Konda, V.R.; Tsitsiklis, J.N. Actor-critic algorithms. SIAM J. Control Optim. 2002, 42, 1143–1166. Available online: http://web.mit.edu/jnt/OldFiles/www/Papers/C.-99-konda-NIPS.pdf (accessed on 3 May 2018). [CrossRef]
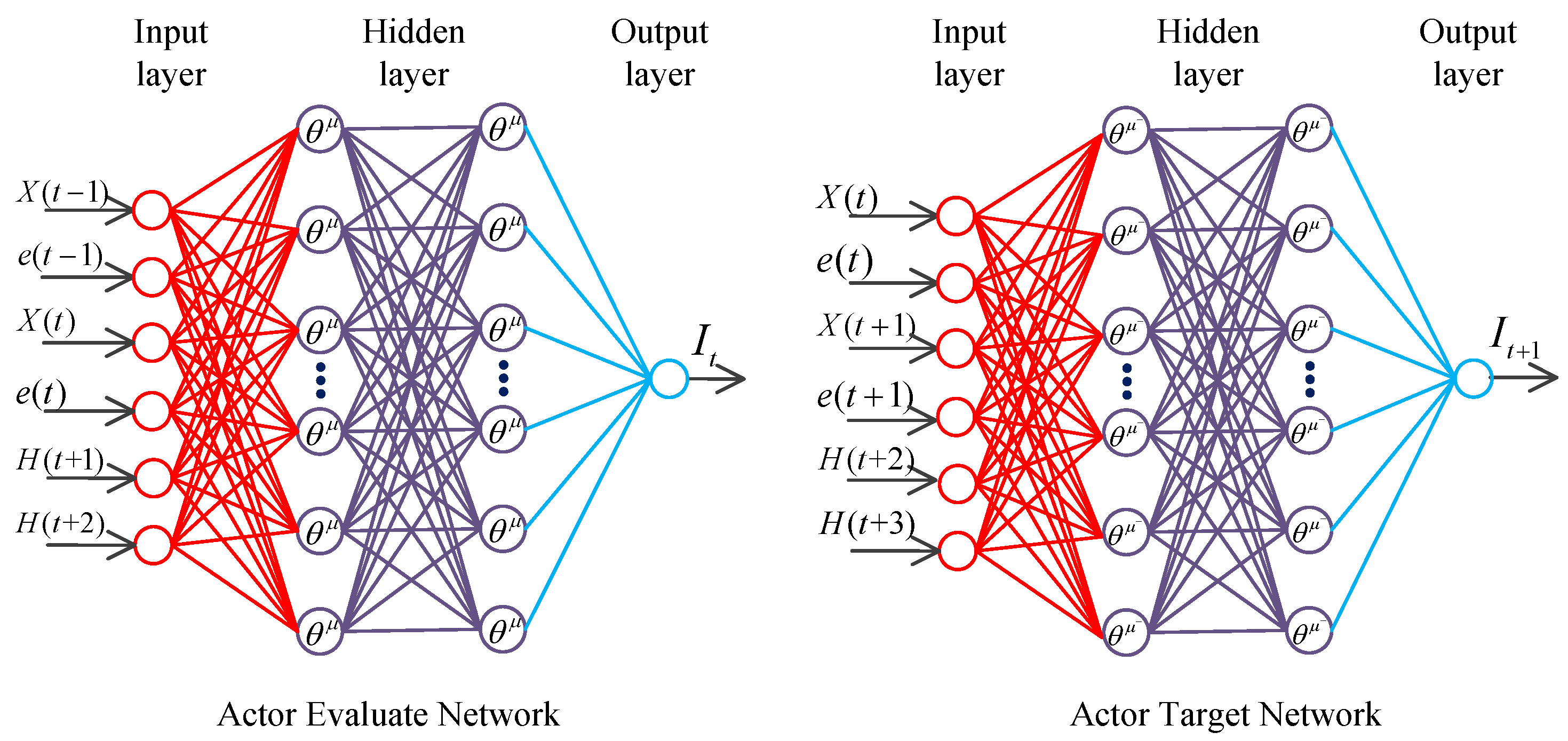
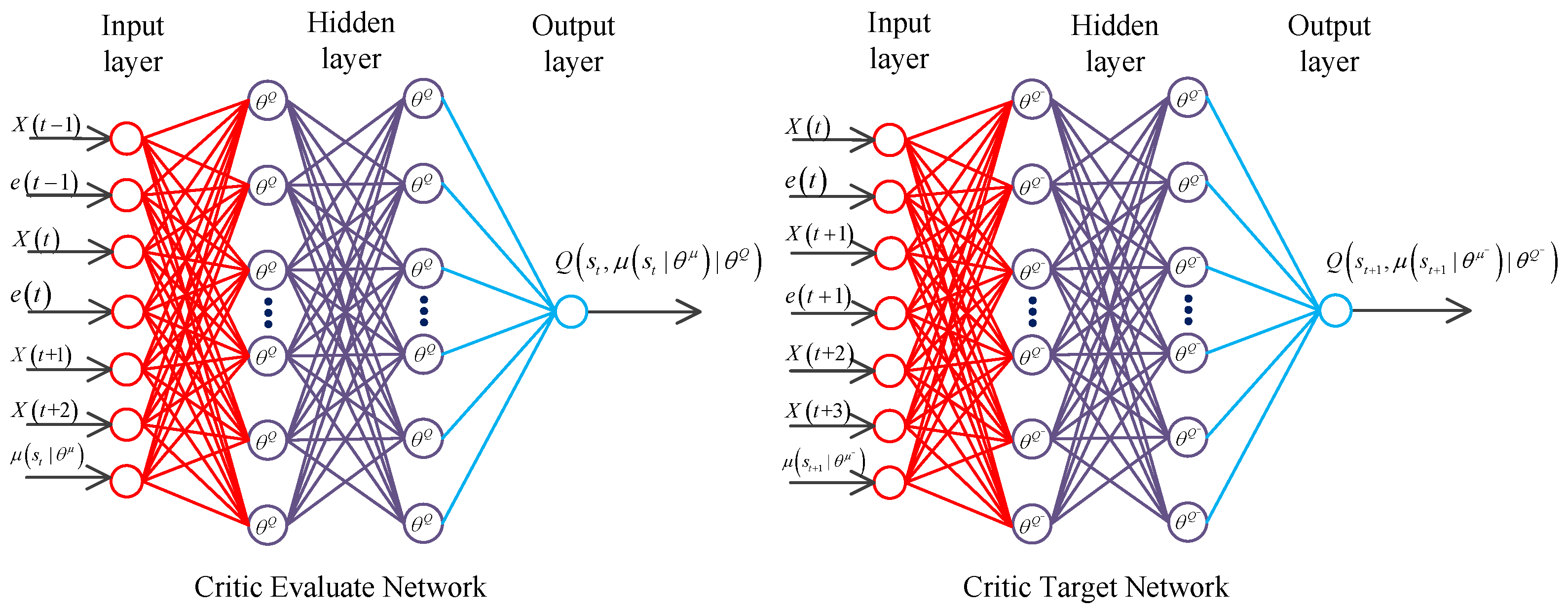
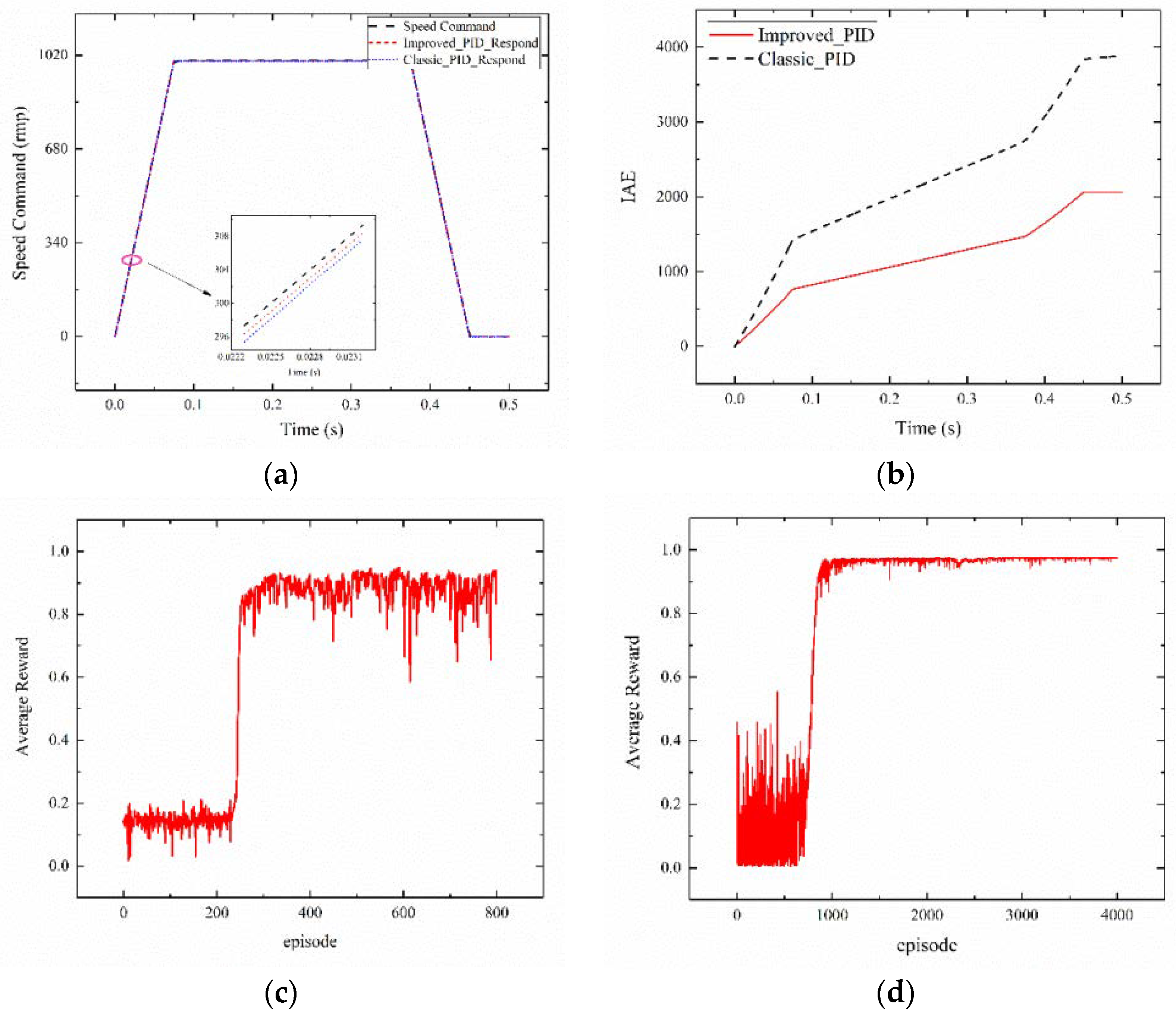
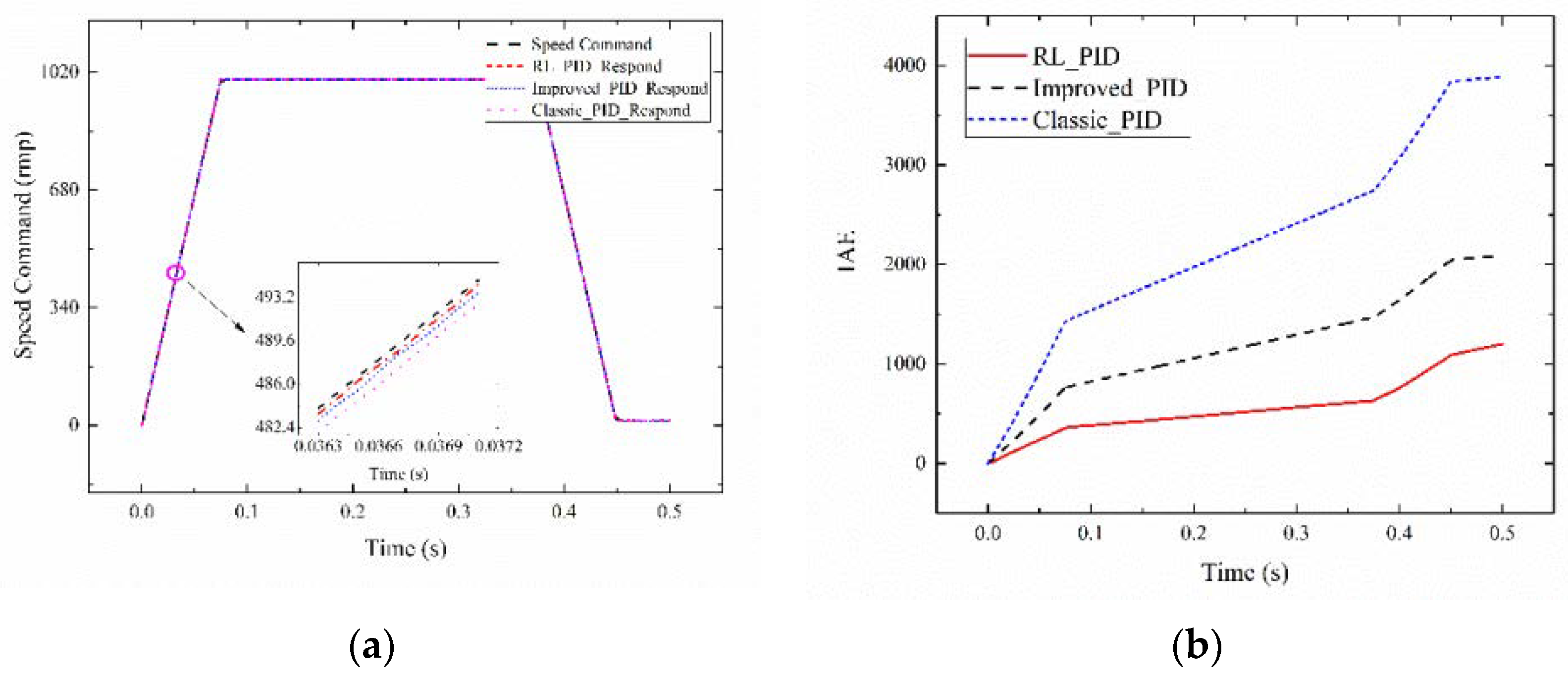
| System | Differential Equation Expression of The Mathematical Model |
|---|---|
| System 1 | |
| System 2 | |
| System 3 |
| System | RL_PID | Improved_-PID | Classic_PID |
|---|---|---|---|
| System 1 | 1199.56 | 2087.81 | 3883.61 |
| system with random mutation | 4000.01 | 5444.85 | 8017.54 |
| System | RL_PID | Improved_PID | Classic_PID |
|---|---|---|---|
| System 1 | 2937.40 | 4144.64 | 7705.06 |
| system with random mutation | 7144.29 | 8307.17 | 14,608.11 |
| System | RL_PID | Improved_PID | Classic_PID |
|---|---|---|---|
| System 1 | 17.126 | 54.412 | 99.760 |
| system with inertia mutation | 199.045 | 271.327 | 427.420 |
| system with load mutation | 60.300 | 89.819 | 166.420 |
| System | RL_PID | Improved_PID | Classic_PID |
|---|---|---|---|
| System 1 | 112.418 | 217.766 | 403.680 |
| system with inertia mutation | 827.467 | 952.202 | 1278.677 |
| system with load mutation | 129.000 | 226.029 | 417.880 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; He, Z.; Chen, C.; Xu, J. Control Strategy of Speed Servo Systems Based on Deep Reinforcement Learning. Algorithms 2018, 11, 65. https://doi.org/10.3390/a11050065
Chen P, He Z, Chen C, Xu J. Control Strategy of Speed Servo Systems Based on Deep Reinforcement Learning. Algorithms. 2018; 11(5):65. https://doi.org/10.3390/a11050065
Chicago/Turabian StyleChen, Pengzhan, Zhiqiang He, Chuanxi Chen, and Jiahong Xu. 2018. "Control Strategy of Speed Servo Systems Based on Deep Reinforcement Learning" Algorithms 11, no. 5: 65. https://doi.org/10.3390/a11050065
APA StyleChen, P., He, Z., Chen, C., & Xu, J. (2018). Control Strategy of Speed Servo Systems Based on Deep Reinforcement Learning. Algorithms, 11(5), 65. https://doi.org/10.3390/a11050065





