A Heuristic Approach to Solving the Train Traffic Re-Scheduling Problem in Real Time
Abstract
1. Introduction
2. Related Work
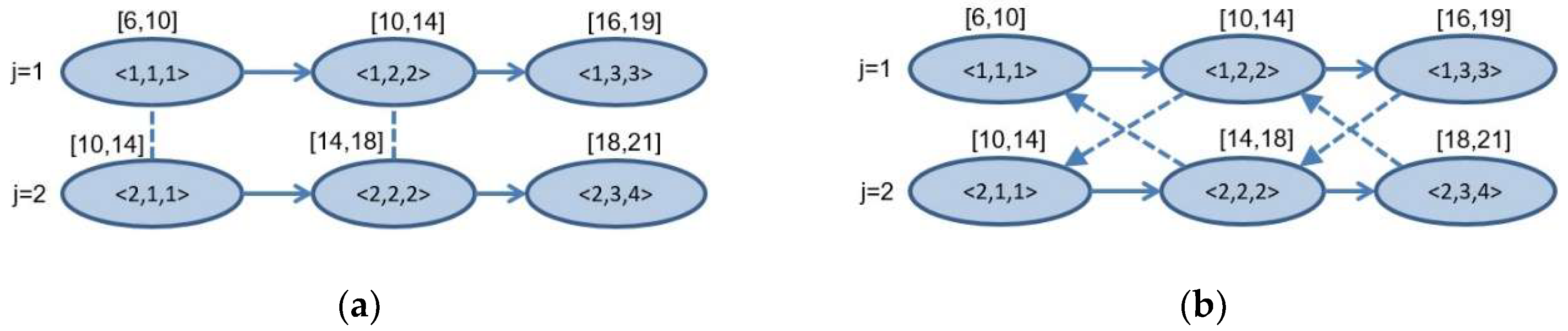
3. Modelling the Job-Shop Scheduling Problem Using a Graph
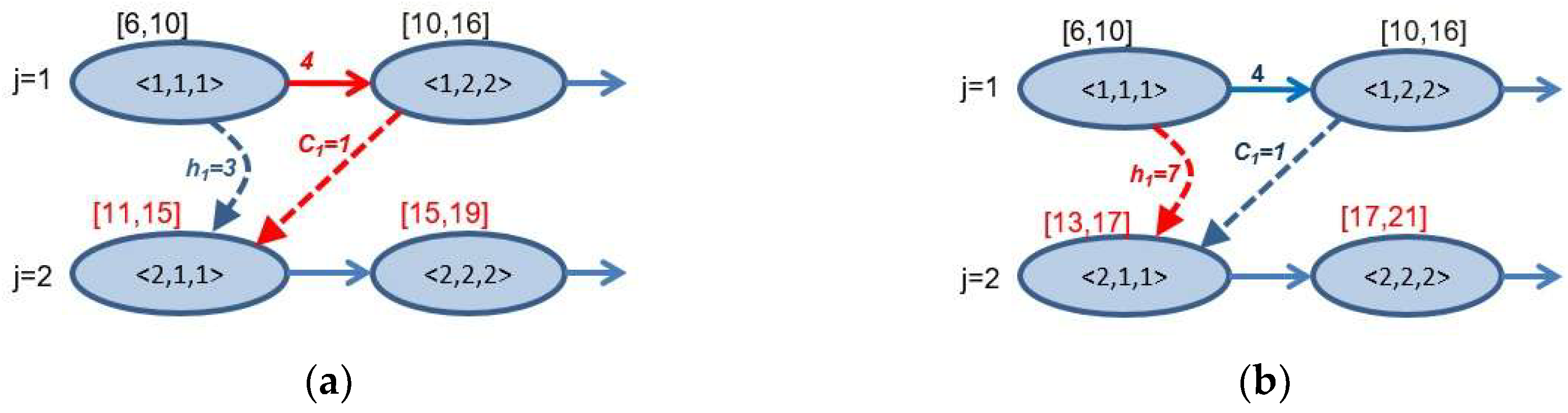
4. A Heuristic Algorithm for Conflict Resolution in the Mixed Graph
| Algorithm 1. The pseudocode for conflict resolution strategy |
| Heuristic Algorithm for Conflict Resolution in the Mixed Graph G |
| Require: The weighted mixed graph G = (O, C, D); candidList= findNeighbours(os); current = findMinimumReleaseTime(candidList); while (current ≠ od); checkList = findConflictOperations(current.machineNumber); if (conflictExist(current, checkList)) /*local re-routing*/ vt = minimumVacantTrack(current.machineNumber); modifyGraph(G, current, vt); checkList = findConflictOperations(vt); end_if for (node cl: checkList) /*conflict resolution, re-timing, re-ordering*/ a,b = findBestOrder(current, cl); if (not reachable(b, a)) addArc(a, b); updateData(G,a); else_if (not reachable(a,b)) addArc(b, a); updateData(G,b); else checkFeasibility(G); end_if end_if end_for candidList += findNeighbours(current); candidList -=current; current = findMinimumReleaseTime(candidList); end_while |
5. Experimental Application and Performance Assessment
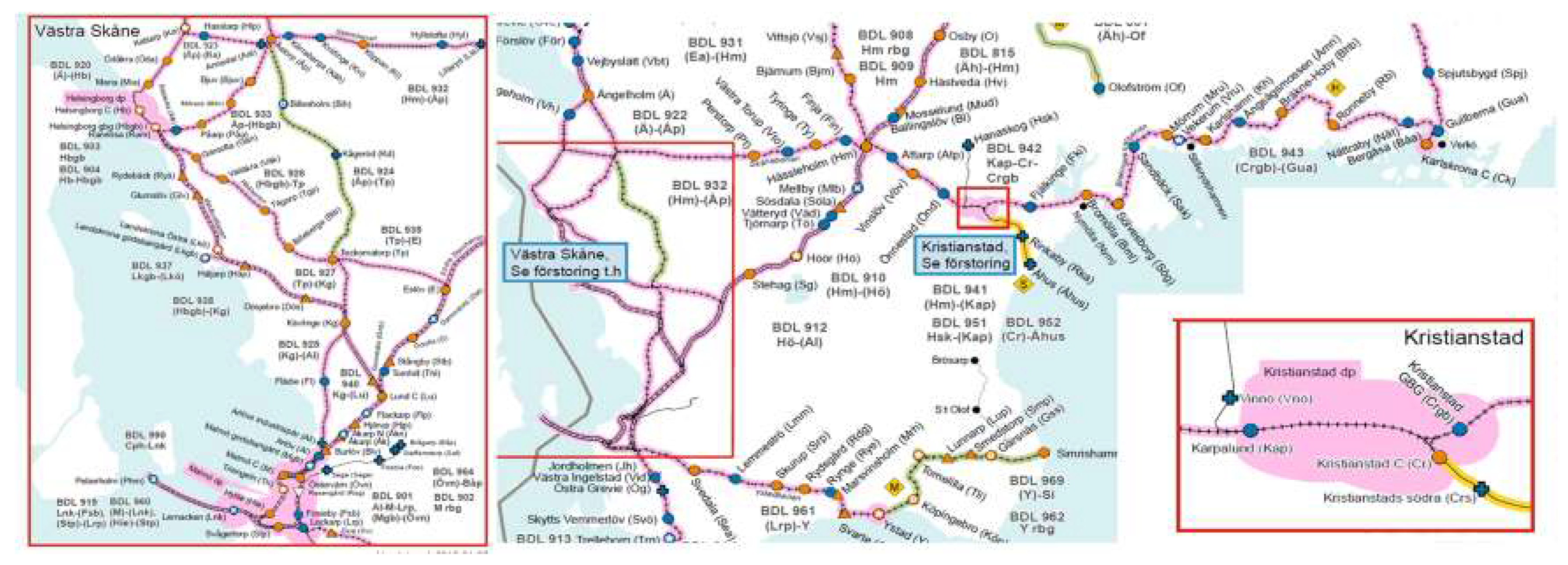
5.1. Experimental Set-Up
- Category 1 refers to a train suffering from a temporary delay at one particular section, which could occur due to, e.g., delayed train staff, or crowding at platforms resulting in increasing dwell times at stations.
- Category 2 refers to a train having a permanent malfunction, resulting in increased running times on all line sections it is planned to occupy.
- Category 3 refers to an infrastructure failure causing, e.g., a speed reduction on a particular section, which results in increased running times for all trains running through that section.
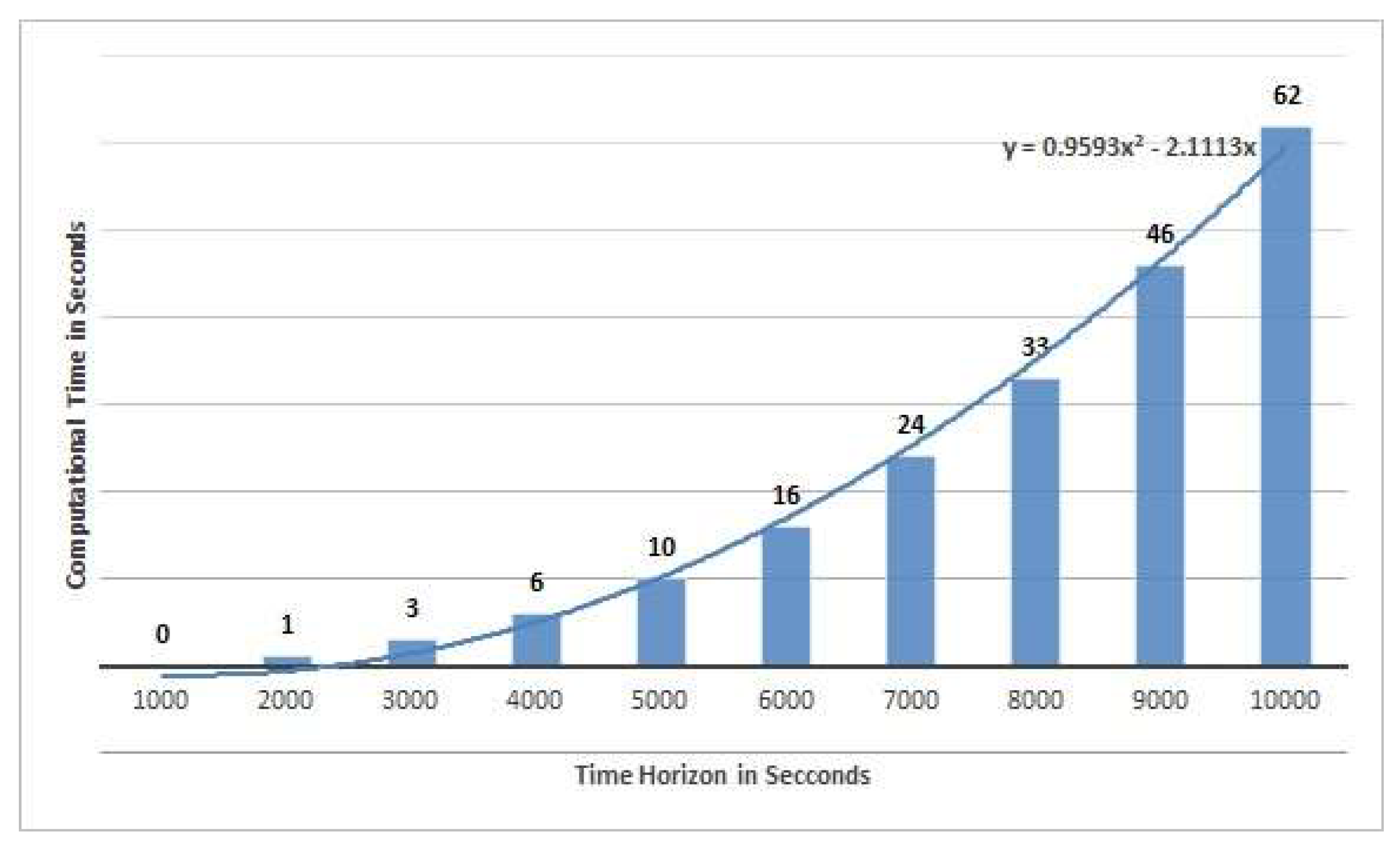
5.2. Results and Analysis
6. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Boston Consultancy Group. The 2017 European Railway Performance Index; Boston Consultancy Group: Boston, MA, USA, 18 April 2017. [Google Scholar]
- European Commission Directorate General for Mobility and Transport. Study on the Prices and Quality of Rail Passenger Services; Report Reference: MOVE/B2/2015-126; European Commission Directorate General for Mobility and Transport: Brussel, Belgium, April 2016. [Google Scholar]
- Lamorgese, L.; Mannino, C.; Pacciarelli, D.; Törnquist Krasemann, J. Train Dispatching. In Handbook of Optimization in the Railway Industry, International Series in Operations Research & Management Science; Borndörfer, R., Klug, T., Lamorgese, L., Mannino, C., Reuther, M., Schlechte, T., Eds.; Springer: Cham, Switzerland, 2018; Volume 268. [Google Scholar] [CrossRef]
- Cacchiani, V.; Huisman, D.; Kidd, M.; Kroon, L.; Toth, P.; Veelenturf, L.; Wagenaar, J. An overview of recovery models and algorithms for real-time railway rescheduling. Transp. Res. B Methodol. 2010, 63, 15–37. [Google Scholar] [CrossRef]
- Fang, W.; Yang, S.; Yao, X. A Survey on Problem Models and Solution Approaches to Rescheduling in Railway Networks. IEEE Trans. Intell. Trans. Syst. 2015, 16, 2997–3016. [Google Scholar] [CrossRef]
- Josyula, S.; Törnquist Krasemann, J. Passenger-oriented Railway Traffic Re-scheduling: A Review of Alternative Strategies utilizing Passenger Flow Data. In Proceedings of the 7th International Conference on Railway Operations Modelling and Analysis, Lille, France, 4–7 April 2017. [Google Scholar]
- Szpigel, B. Optimal train scheduling on a single track railway. Oper. Res. 1973, 72, 343–352. [Google Scholar]
- D’Ariano, A.; Pacciarelli, D.; Pranzo, M. A branch and bound algorithm for scheduling trains in a railway network. Eur. J. Oper. Res. 2017, 183, 643–657. [Google Scholar] [CrossRef]
- Khosravi, B.; Bennell, J.A.; Potts, C.N. Train Scheduling and Rescheduling in the UK with a Modified Shifting Bottleneck Procedure. In Proceedings of the 12th Workshop on Algorithmic Approaches for Transportation Modelling, Optimization, and Systems 2012, Ljubljana, Slovenia, 13 September 2012; pp. 120–131. [Google Scholar]
- Liu, S.; Kozan, E. Scheduling trains as a blocking parallel-machine job shop scheduling problem. Comput. Oper. Res. 2009, 36, 2840–2852. [Google Scholar] [CrossRef]
- Mascis, A.; Pacciarelli, D. Job-shop scheduling with blocking and no-wait constraints. Eur. J. Oper. Res. 2002, 143, 498–517. [Google Scholar] [CrossRef]
- Oliveira, E.; Smith, B.M. A Job-Shop Scheduling Model for the Single-Track Railway Scheduling Problem; Research Report Series 21; School of Computing, University of Leeds: Leeds, UK, 2000. [Google Scholar]
- Törnquist, J.; Persson, J.A. N-tracked railway traffic re-scheduling during disturbances. Transp. Res. Part B Methodol. 2007, 41, 342–362. [Google Scholar] [CrossRef]
- Pellegrini, P.; Douchet, G.; Marliere, G.; Rodriguez, J. Real-time train routing and scheduling through mixed integer linear programming: Heuristic approach. In Proceedings of the 2013 International Conference on Industrial Engineering and Systems Management (IESM), Rabat, Morocco, 28–30 October 2013. [Google Scholar]
- Xu, Y.; Jia, B.; Ghiasib, A.; Li, X. Train routing and timetabling problem for heterogeneous train traffic with switchable scheduling rules. Transp. Res. Part C Emerg. Technol. 2017, 84, 196–218. [Google Scholar] [CrossRef]
- Corman, F.; D’Ariano, A.; Pacciarelli, D.; Pranzo, M. Centralized versus distributed systems to reschedule trains in two dispatching areas. Public Trans. Plan. Oper. 2010, 2, 219–247. [Google Scholar] [CrossRef]
- Corman, F.; D’Ariano, A.; Pacciarelli, D.; Pranzo, M. Optimal inter-area coordination of train rescheduling decisions. Trans. Res. Part E 2012, 48, 71–88. [Google Scholar]
- Corman, F.; Pacciarelli, D.; D’Ariano, A.; Samá, M. Rescheduling Railway Traffic Taking into Account Minimization of Passengers’ Discomfort. In Proceedings of the International Conference on Computational Logistics, ICCL 2015, Delft, The Netherlands, 23–25 September 2015; pp. 602–616. [Google Scholar]
- Lamorgese, L.; Mannino, C. An Exact Decomposition Approach for the Real-Time Train Dispatching Problem. Oper. Res. 2015, 63, 48–64. [Google Scholar] [CrossRef]
- Meng, L.; Zhou, X. Simultaneous train rerouting and rescheduling on an N-track network: A model reformulation with network-based cumulative flow variables. Trans. Res. Part B Methodol. 2014, 67, 208–234. [Google Scholar] [CrossRef]
- Tormo, J.; Panou, K.; Tzierpoulos, P. Evaluation and Comparative Analysis of Railway Perturbation Management Methods. In Proceedings of the Conférence Mondiale sur la Recherche Dans les Transports (13th WCTR), Rio de Janeiro, Brazil, 15–18 July 2013. [Google Scholar]
- Rodriguez, J. An incremental decision algorithm for railway traffic optimisation in a complex station. Eleventh. In Proceedings of the International Conference on Computer System Design and Operation in the Railway and Other Transit Systems (COMPRAIL08), Toledo, Spain, 15–17 September 2008; pp. 495–504. [Google Scholar]
- Bettinelli, A.; Santini, A.; Vigo, D. A real-time conflict solution algorithm for the train rescheduling problem. Trans. Res. Part B Methodol. 2017, 106, 237–265. [Google Scholar] [CrossRef]
- Samà, M.; D’Ariano, A.; Corman, F.; Pacciarelli, D. A variable neighbourhood search for fast train scheduling and routing during disturbed railway traffic situations. Comput. Oper. Res. 2017, 78, 480–499. [Google Scholar] [CrossRef]
- Burdett, R.L.; Kozan, E. A sequencing approach for creating new train timetables. OR Spectr. 2010, 32, 163–193. [Google Scholar] [CrossRef]
- Tan, Y.; Jiang, Z. A Branch and Bound Algorithm and Iterative Reordering Strategies for Inserting Additional Trains in Real Time: A Case Study in Germany. Math. Probl. Eng. 2015, 2015, 289072. [Google Scholar] [CrossRef]
- Gholami, O.; Sotskov, Y.N. A fast heuristic algorithm for solving parallel-machine job-shop scheduling problems. Int. J. Adv. Manuf. Technol. 2014, 70, 531–546. [Google Scholar] [CrossRef]
- Sotskov, Y.; Gholami, O. Mixed graph model and algorithms for parallel-machine job-shop scheduling problems. Int. J. Prod. Res. 2017, 55, 1549–1564. [Google Scholar] [CrossRef]
- Krasemann, J.T. Design of an effective algorithm for fast response to the re-scheduling of railway traffic during disturbances. Transp. Res. Part C Emerg. Technol. 2012, 20, 62–78. [Google Scholar] [CrossRef]

| Sets and Indices | Description |
|---|---|
| Set of all railway sections (i.e., machines). | |
| The index used to denote a specific section in the set. | |
| The sub-set of tracks and platforms that belongs to section . (i.e., parallel machines) | |
| A track/platform/resource instance number from a set. | |
| Set of all trains (i.e., jobs). | |
| The index used to denote a specific train. | |
| Set of all train events (i.e., operations). | |
| Set of all events that belong to train . | |
| Set of all events to be scheduled on a section . | |
| Set of all events to be scheduled on track of section. | |
| The index used to denote a specific train event. | |
| The symbol used to denote the event which belongs to train. | |
| Tuple which refers to train and its event which occurs in section and scheduled for track . When the section is single line will be ignored. | |
| Prime symbol used to distinguish between two instances (i.e., job and ). | |
| Parameters | Description |
| The required minimum clear time that must pass after a train has released the assigned track of section and before another train may enter track of section. | |
| The minimum headway time distance that is required between trains (head-head and tail-tail) that run in sequence on the same track of section. | |
| The minimum running time, or dwell time, of event that belongs to train. | |
| This parameter specifies the initial starting time of event that belongs to train. | |
| This parameter specifies the initial completion time of event that belongs to train. | |
| This parameter indicates if event includes a planned stop at the associated segment. | |
| Variables | Description |
| The re-scheduled starting time of event that belongs to train. | |
| The re-scheduled completion time of event that belongs to train . | |
| The tardiness (i.e., delay for train to complete event ). | |
| Delay of even , exceeding µ time units, which is set to three minutes here. | |
| A binary variable which is 1, if the event uses track . | |
| A binary variable which is 1, if the event occurs before event. | |
| A binary variable which is 1, if the event is rescheduled to occur after event. | |
| Remaining buffer time for train to complete an event. | |
| The delay for train once it reaches its final destination, i.e., which corresponds to the delay when completing its last event. |
| Conflict Resolution Strategy | Description |
|---|---|
| 1. Minimum release time goes first | The train with the earliest initial start time ( ) goes first if no deadlock occurs. |
| 2. More delay goes first | If there is a conflict between two trains, the one with the largest tardiness (delay) goes first. The tardiness is calculated as . |
| 3. Less real buffer time goes first | The train with the smallest buffer time goes first. Buffer time is defined as a subtraction of initial ending time and real finishing time for two operations to be scheduled on the same, occupied machine. |
| 4. Less programmed buffer time goes first | The train with smallest buffer time goes first. Buffer time is defined as a subtraction of initial ending time and programmed ending time for two operations to be scheduled on the same, occupied machine. |
| 5. Less total buffer goes first | The train with smallest total buffer time goes first. Total buffer time is defined as a summation of programmed buffer times until the destination point for the trains, i.e., . |
| 6. Less total processing time | The train with smallest running time to get to the destination goes first (i.e., the minimum total processing time). The total processing time is defined as a summation of required time to pass each section, for a train, i.e., . |
| Scenario | Disturbance | Problem Size: #Events 1 | |||
|---|---|---|---|---|---|
| Category: ID | Location | Initially Disturbed Train | Initially Delay (min) | 1 h Time Window | 1.5 h Time Window |
| 1:1 | Karlshamn-Ångsågsmossen | 1058 (Eastbound) | 10 | 1753 | 2574 |
| 1:2 | Bromölla Sölvesborg | 1064 (Eastbound) | 5 | 1717 | 2441 |
| 1:3 | Kristianstad-Karpalund | 1263 (Southbound) | 8 | 1421 | 2100 |
| 1:4 | Bergåsa-Gullberna | 1097 (Westbound) | 10 | 1739 | 2482 |
| 1:5 | Bräkne Hoby-Ronneby | 1103 (Westbound) | 15 | 1393 | 2056 |
| 1:6 | Flackarp-Hjärup | 491 (Southbound) | 5 | 1467 | 2122 |
| 1:7 | Eslöv-Dammstorp | 533 (Southbound) | 10 | 1759 | 2578 |
| 1:8 | Burlöv-Åkarp | 544 (Northbound) | 7 | 1748 | 2572 |
| 1:9 | Burlöv-Åkarp | 1378 (Northbound) | 4 | 1421 | 2100 |
| 1:10 | Höör-Stehag | 1381 (Southbound) | 10 | 1687 | 2533 |
| 2:1 | Karlshamn-Ångsågsmossen | 1058 (Eastbound) | 40% | 1753 | 2574 |
| 2:2 | Bromölla Sölvesborg | 1064 (Eastbound) | 20% | 1717 | 2441 |
| 2:3 | Kristianstad-Karpalund | 1263 (Southbound) | 20% | 1421 | 2100 |
| 2:4 | Bergåsa-Gullberna | 1097 (Westbound) | 40% | 1739 | 2482 |
| 2:5 | Bräkne Hoby-Ronneby | 1103 (Westbound) | 100% | 1393 | 2056 |
| 2:6 | Flackarp-Hjärup | 491 (Southbound) | 100% | 1467 | 2122 |
| 2:7 | Eslöv-Dammstorp | 533 (Southbound) | 50% | 1759 | 2578 |
| 2:8 | Burlöv-Åkarp | 544 (Northbound) | 80% | 1748 | 2572 |
| 2:9 | Burlöv-Åkarp | 1378 (Northbound) | 40% | 1421 | 2100 |
| 2:10 | Höör-Stehag | 1381 (Southbound) | 40% | 1687 | 2533 |
| 3:1 | Karlshamn-Ångsågsmossen | All trains passing through | 4 | 1753 | 2574 |
| 3:2 | Bromölla Sölvesborg | All trains passing through | 2 | 1717 | 2441 |
| 3:3 | Kristianstad-Karpalund | All trains passing through | 3 | 1421 | 2100 |
| 3:4 | Bergåsa-Gullberna | All trains passing through | 6 | 1739 | 2482 |
| 3:5 | Bräkne Hoby-Ronneby | All trains passing through | 5 | 1393 | 2056 |
| 3:6 | Flackarp-Hjärup | All trains passing through | 3 | 1467 | 2122 |
| 3:7 | Eslöv-Dammstorp | All trains passing through | 4 | 1759 | 2578 |
| 3:8 | Burlöv-Åkarp | All trains passing through | 2 | 1748 | 2572 |
| 3:9 | Burlöv-Åkarp | All trains passing through | 2 | 1421 | 2100 |
| 3:10 | Höör-Stehag | All trains passing through | 2 | 1687 | 2533 |
| Scenario | Objective Function (hh:mm:ss) | Computational Time (hh:mm:ss) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Category: ID | Optimal Results | Dispatching Rules (DR) | MIP Model | Heuristic Algorithm | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 1:1 | 0:01:03 | 00:01:14 | 00:01:14 | 00:01:14 | 00:15:22 | 00:15:22 | 00:24:05 | 00:00:04 | 00:00:06 |
| 1:2 | 0:00:00 | 00:00:00 | 00:00:00 | 00:00:00 | 00:00:00 | 00:00:00 | 01:16:47 | 00:00:04 | 00:00:05 |
| 1:3 | 0:00:00 | 00:02:09 | 00:02:09 | 00:02:09 | 00:36:33 | 00:36:33 | 00:26:32 | 00:00:04 | 00:00:03 |
| 1:4 | 0:01:02 | 00:02:28 | 00:02:28 | 00:02:28 | 00:12:40 | 00:12:40 | 00:08:11 | 00:00:06 | 00:00:06 |
| 1:5 | 0:07:01 | 00:16:15 | 00:16:15 | 00:16:15 | 00:19:49 | 00:19:49 | 00:13:14 | 00:00:05 | 00:00:03 |
| 1:6 | 0:00:23 | 00:05:46 | 00:05:46 | 00:05:46 | 00:05:46 | 00:05:46 | 00:05:46 | 00:00:04 | 00:00:03 |
| 1:7 | 0:05:05 | 00:06:24 | 00:06:24 | 00:06:24 | 00:06:24 | 00:06:24 | 00:14:45 | 00:00:04 | 00:00:05 |
| 1:8 | 0:01:34 | 00:12:01 | 00:12:01 | 00:12:01 | 00:12:01 | 00:12:01 | 00:13:40 | 00:00:04 | 00:00:06 |
| 1:9 | 0:00:00 | 00:14:01 | 00:14:01 | 00:14:01 | 00:13:02 | 00:13:02 | 00:14:01 | 00:00:04 | 00:00:03 |
| 1:10 | 0:00:00 | 00:01:18 | 00:01:18 | 00:00:00 | 00:00:00 | 00:00:00 | 00:01:33 | 00:00:04 | 00:00:05 |
| 2:1 | 0:05:24 | 00:45:37 | 00:45:37 | 00:06:42 | 00:06:42 | 00:06:42 | 00:08:16 | 00:00:04 | 00:00:06 |
| 2:2 | 0:02:43 | 00:03:29 | 00:39:53 | 00:03:29 | 00:03:29 | 00:03:29 | 01:06:56 | 00:00:05 | 00:00:05 |
| 2:3 | 0:01:01 | 00:01:47 | 00:20:06 | 00:20:06 | 00:01:47 | 00:01:47 | 00:20:14 | 00:00:03 | 00:00:03 |
| 2:4 | 0:15:12 | 00:22:12 | 00:22:50 | 00:22:50 | 00:22:12 | 00:22:12 | 00:55:54 | 00:00:05 | 00:00:05 |
| 2:5 | 0:42:09 | 00:43:24 | 00:58:03 | 00:58:03 | 01:05:08 | 01:05:08 | 00:59:16 | 00:00:04 | 00:00:03 |
| 2:6 | 0:01:24 | 00:02:44 | 00:02:44 | 00:02:44 | 00:02:44 | 00:02:44 | 00:02:44 | 00:00:06 | 00:00:04 |
| 2:7 | 0:05:27 | 00:08:09 | 00:08:09 | 00:08:09 | 00:08:09 | 00:08:09 | 00:09:43 | 00:00:04 | 00:00:10 |
| 2:8 | 0:21:12 | 00:43:37 | 00:38:42 | 00:38:42 | 00:43:37 | 00:43:37 | 00:40:16 | 00:00:06 | 00:00:06 |
| 2:9 | 0:00:00 | 00:00:00 | 00:00:00 | 00:00:00 | 00:00:00 | 00:00:00 | 00:00:00 | 00:00:05 | 00:00:03 |
| 2:10 | 0:00:08 | 00:05:09 | 00:05:09 | 00:05:09 | 00:05:09 | 00:05:09 | 00:06:43 | 00:00:04 | 00:00:06 |
| 3:1 | 0:01:00 | 00:01:00 | 00:01:00 | 00:01:00 | 00:01:00 | 00:01:00 | 00:25:05 | 00:00:04 | 00:00:06 |
| 3:2 | 0:00:00 | 00:00:00 | 00:00:00 | 00:00:00 | 00:00:19 | 00:00:19 | 00:25:54 | 00:00:04 | 00:00:06 |
| 3:3 | 0:00:00 | 00:03:49 | 00:21:38 | 01:05:52 | 00:01:17 | 00:15:40 | 00:54:14 | 00:00:05 | 00:00:03 |
| 3:4 | 0:12:21 | 00:16:59 | 00:20:13 | 00:20:13 | 00:16:59 | 00:16:59 | 00:20:22 | 00:00:07 | 00:00:06 |
| 3:5 | 0:05:20 | 00:05:25 | 00:57:34 | 00:15:58 | 00:05:25 | 00:05:25 | 00:16:12 | 00:00:03 | 00:00:03 |
| 3:6 | 0:00:00 | 00:21:04 | 00:21:04 | 00:21:04 | 00:23:12 | 00:23:12 | 00:28:42 | 00:00:05 | 00:00:03 |
| 3:7 | 0:00:09 | 00:07:42 | 00:14:11 | 00:14:11 | 00:14:11 | 00:14:11 | 00:15:45 | 00:00:10 | 00:00:05 |
| 3:8 | 0:00:00 | 00:00:00 | 00:05:06 | 00:05:06 | 00:00:00 | 00:00:00 | 00:07:54 | 00:00:04 | 00:00:05 |
| 3:9 | 0:00:00 | 00:00:00 | 00:00:41 | 00:00:41 | 00:00:00 | 00:00:00 | 00:00:00 | 00:00:04 | 00:00:04 |
| 3:10 | 0:00:00 | 00:04:53 | 00:04:53 | 00:03:35 | 00:01:04 | 00:01:04 | 00:02:38 | 00:00:03 | 00:00:05 |
| Scenario | Objective Function | Computational Time | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Category: ID | Optimal Results | Dispatching Rules (DR) | MIP Model | Heuristic Algorithm | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 1:1 | 0:01:03 | 00:01:14 | 00:01:14 | 00:01:14 | 00:45:13 | 00:45:13 | 00:46:56 | 00:00:12 | 00:00:20 |
| 1:2 | 0:00:00 | 00:00:00 | 00:00:00 | 00:00:00 | 00:12:09 | 00:12:09 | 05:09:54 | 00:00:10 | 00:00:15 |
| 1:3 | 0:00:00 | 00:02:09 | 00:02:09 | 00:02:09 | 01:34:59 | 01:34:59 | 00:25:21 | 00:00:11 | 00:00:10 |
| 1:4 | 0:00:00 | 00:01:27 | 00:01:27 | 00:01:27 | 01:38:16 | 01:38:16 | 00:51:24 | 00:00:13 | 00:00:16 |
| 1:5 | 0:02:08 | 00:10:23 | 00:10:23 | 00:10:23 | 00:24:07 | 00:24:07 | 00:12:14 | 00:00:07 | 00:00:09 |
| 1:6 | 0:00:23 | 00:05:46 | 00:05:46 | 00:05:46 | 00:05:46 | 00:05:46 | 00:05:46 | 00:00:12 | 00:00:10 |
| 1:7 | 0:05:05 | 00:06:24 | 00:06:24 | 00:06:24 | 00:06:24 | 00:06:24 | 00:14:45 | 00:00:11 | 00:00:18 |
| 1:8 | 0:01:34 | 00:12:01 | 00:12:01 | 00:12:01 | 00:12:01 | 00:12:01 | 00:13:40 | 00:00:12 | 00:00:17 |
| 1:9 | 0:00:00 | 00:13:00 | 00:13:00 | 00:13:00 | 00:13:16 | 00:13:16 | 00:38:13 | 00:00:07 | 00:00:10 |
| 1:10 | 0:00:00 | 00:01:18 | 00:01:18 | 00:00:00 | 00:00:00 | 00:00:00 | 00:01:33 | 00:00:11 | 00:00:16 |
| 2:1 | 0:03:36 | 00:45:37 | 00:45:37 | 00:04:31 | 00:17:11 | 00:17:11 | 00:14:16 | 00:00:11 | 00:00:17 |
| 2:2 | 0:00:00 | 00:00:23 | 01:21:00 | 00:00:23 | 00:00:23 | 00:00:23 | 04:36:13 | 00:00:12 | 00:00:15 |
| 2:3 | 0:02:40 | 00:29:31 | 00:32:58 | 00:32:58 | 00:39:25 | 00:39:25 | 00:33:46 | 00:00:07 | 00:00:09 |
| 2:4 | 0:26:34 | 00:43:50 | 01:11:40 | 01:11:40 | 00:43:50 | 00:43:50 | 01:57:35 | 00:00:16 | 00:00:15 |
| 2:5 | 1:11:44 | 01:17:47 | 01:40:09 | 01:40:09 | 01:41:32 | 01:41:32 | 01:35:29 | 00:00:12 | 00:00:08 |
| 2:6 | 0:01:24 | 00:02:44 | 00:02:44 | 00:02:44 | 00:02:44 | 00:02:44 | 00:02:44 | 00:00:11 | 00:00:09 |
| 2:7 | 0:05:27 | 00:08:09 | 00:08:09 | 00:08:09 | 00:08:09 | 00:08:09 | 00:09:43 | 00:00:11 | 00:00:17 |
| 2:8 | 0:21:12 | 00:44:42 | 00:48:13 | 00:48:13 | 00:44:54 | 00:44:54 | 01:08:14 | 00:00:36 | 00:00:17 |
| 2:9 | 0:00:00 | 00:00:00 | 00:00:00 | 00:00:00 | 00:00:13 | 00:00:13 | 00:00:00 | 00:00:07 | 00:00:10 |
| 2:10 | 0:00:08 | 00:05:09 | 00:05:09 | 00:05:09 | 00:05:09 | 00:05:09 | 00:06:43 | 00:00:12 | 00:00:16 |
| 3:1 | 0:00:00 | 00:00:00 | 00:22:42 | 00:00:00 | 00:00:00 | 00:00:00 | 00:46:56 | 00:00:12 | 00:00:17 |
| 3:2 | 0:00:00 | 00:00:17 | 00:00:17 | 00:00:17 | 00:00:36 | 00:00:36 | 01:36:46 | 00:00:11 | 00:00:14 |
| 3:3 | 0:01:16 | 00:09:36 | 00:57:38 | 01:22:08 | 00:07:17 | 00:14:39 | 02:07:54 | 00:00:11 | 00:00:10 |
| 3:4 | 0:16:37 | 00:31:06 | 00:32:34 | 00:32:34 | 00:23:26 | 00:23:26 | 01:10:03 | 00:00:35 | 00:00:15 |
| 3:5 | 0:04:44 | 00:04:58 | 00:55:43 | 00:13:08 | 00:10:16 | 00:10:16 | 00:19:59 | 00:00:10 | 00:00:09 |
| 3:6 | 0:00:00 | 00:50:13 | 00:50:13 | 00:50:13 | 00:27:54 | 00:27:54 | 01:07:29 | 00:00:17 | 00:00:15 |
| 3:7 | 0:00:41 | 00:06:48 | 00:15:45 | 00:15:45 | 00:15:45 | 00:15:45 | 00:17:19 | 00:00:18 | 00:00:19 |
| 3:8 | 0:00:00 | 00:00:00 | 00:01:22 | 00:01:22 | 00:00:00 | 00:00:00 | 00:03:58 | 00:00:11 | 00:00:17 |
| 3:9 | 0:00:00 | 00:02:06 | 00:03:32 | 00:02:48 | 00:02:06 | 00:02:06 | 00:02:06 | 00:00:14 | 00:00:10 |
| 3:10 | 0:00:00 | 00:08:07 | 00:08:31 | 00:07:13 | 00:01:28 | 00:01:28 | 00:03:02 | 00:00:11 | 00:00:16 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gholami, O.; Törnquist Krasemann, J. A Heuristic Approach to Solving the Train Traffic Re-Scheduling Problem in Real Time. Algorithms 2018, 11, 55. https://doi.org/10.3390/a11040055
Gholami O, Törnquist Krasemann J. A Heuristic Approach to Solving the Train Traffic Re-Scheduling Problem in Real Time. Algorithms. 2018; 11(4):55. https://doi.org/10.3390/a11040055
Chicago/Turabian StyleGholami, Omid, and Johanna Törnquist Krasemann. 2018. "A Heuristic Approach to Solving the Train Traffic Re-Scheduling Problem in Real Time" Algorithms 11, no. 4: 55. https://doi.org/10.3390/a11040055
APA StyleGholami, O., & Törnquist Krasemann, J. (2018). A Heuristic Approach to Solving the Train Traffic Re-Scheduling Problem in Real Time. Algorithms, 11(4), 55. https://doi.org/10.3390/a11040055




