Dual Market Facility Network Design under Bounded Rationality

Abstract

A number of markets, geographically separated, with different demand characteristics for different products that share a common component, are analyzed. This common component can either be manufactured locally in each of the markets or transported between the markets to fulfill the demand. However, final assemblies are localized to the respective markets. The decision making challenge is whether to manufacture the common component centrally or locally. To formulate the underlying setting, a newsvendor modeling based approach is considered. The developed model is solved using Frank-Wolfe linearization technique along with Benders’ decomposition method. Further, the propensity of decision makers in each market to make suboptimal decisions leading to bounded rationality is considered. The results obtained for both the cases are compared.

1. Introduction

Globalization has brought about large scale integration of regional economies and culture through effective transportation and communication. International trade has been the central attention of major firms in last couple of decades. Economic globalization has led to major changes in how the companies deal with the market. Any attempt towards a competitive advantage at an international level has far reaching benefits to the company. Even supporters of globalization agree that the benefits of globalization are not without risks—such as those arising from volatile capital movements. With the recent global meltdown, capital flows reversing and international trade shrinking, getting into a non-imitable market advantage that has assumed the prime importance [1].

In this work, the focus is on firms that are present in many markets across the globe. With Asian countries like India and China gaining importance in the international market, there are issues that globalization still has to iron out before we can really see homogeneity across the globe. Low income countries are slowly gaining ground in the recent globalized world. On one hand, these countries offer huge market opportunities, with large gain in the labor cost, but it has itself associated with increased logistics cost and foreign trade barriers. Considering these paradoxical factors simultaneously, this paper works on quantifying the decision of off-shoring production facilities, modeled by taking into account the real life uncertainties and response variances. In particular, we consider the case of two economies served by a firm manufacturing two products at two localized final assemblies, using a common component which can either be produced locally or transported from a central setup which would also cause the company to incur respective transportation costs. Each of the markets has respective demand characteristics, selling price, and assembly costs. We intend to maximize the total profit of the firm, by optimally deciding where to locate the common component manufacturing setup, and also the individual transportation quantities. This situation is analyzed using the Newsvendor Model.

The notion of bounded rationality in operation management was taken from the economics literature. Initially, the “bounded rationality” term was introduced by Simon [2] to denote the decision-making behaviors where the decision maker finds the alternatives. Later, scholars constructed diverse model frameworks to cover agents’ bounded rationality by the quantal response model. To account for the limitations in the normative approach adopted by a traditional Newsvendor Model, which assumes that decision makers are perfect optimizers, the descriptive approach of bounded rationality is incorporated. The decision model of bounded rationality is basically based on classical quantal choice theory [3]. Considering all possible utility generating alternatives to be the candidates for selection, decision makers try to choose much captivating alternatives (obtaining greater utility) because their probability of selection is high. For this purpose, the analytically convenient logit choice model can be used where selection probability of alternate j is proportional to $\exp (u_j)$ [4]. The quantal choice models take into account that decision makers may commit errors. It is not necessary that one always makes the best decisions; better decisions are made frequently.

Thus, we formulate the problem with the framework of bounded rationality for the multi-market network design. The resulting formulation leads to a quadratic objective function with linear constraints. Since the constraints are not all equality constraints, it is not simple to reduce the problem into linear system of equations. The problem is solved through a novel approach of Frank-Wolfe linearization method along with Generalized Benders’ Decomposition method. The results are compared with standard gradient search method and the superior convergence is empirically proved.

The remaining part of the text is organized as follows. In Section 2, the literature is reviewed. The model and methodology are described in Section 3. Section 4 discusses the test results and comparative analysis. Some concluding remarks along with future work are given in Section 5.

2. Literature Review

A broad review has been presented by Snyder [5] on stochastic and robust facility location models, illustrating the optimization techniques that have evolved in this area. Hayes and Wheelwright [6] describe several approaches such as geographical network analysis, physical facilities analysis, functional analysis and organizational mission analysis, and product-process analysis for the formulation of multi-plant facility strategy. Skinner [7] proposes the concept of operational focus using the product-process approach, and Van Mieghem [8] models the approach of product-process focus for a multi-market scenario. Cohen and Lee [9] are the pioneers towards formulating global manufacturing strategy as a mathematical programming problem accounting factors such as local demand, sourcing constraints and taxations. Organizations may select for developing their facility with respect to product, volumes, or process. Lu et al. [1] analyze such scenarios under known demand and incorporating scale economies. Their model includes two products with distinct demand features, two geographically disjointed markets with diverse economic features, and two processes with distinct goals comprises of common component manufacturing and dedicated assembly. Multi-product firms frequently usage the commonality of foster flexibility for their process networks. In another study, the trade-offs between risk pooling and logistics cost with respect to two extreme configurations such as process and product has been investigated for commonality in a multi-plant network [10]. Melkote et al. [11] develops an optimization model for facility location and transportation network design problem.

Rationality refers to perfect optimization for the given scenario. On the contrary, the concept of bounded rationality identifies the intrinsic imperfections in human decision making. Chen et al. [12] described utility functions for the decision maker and inferred stochastic probabilities. Su [13] modeled the bounded rationality including stochastic elements in the decision process. Despite selecting the utility-maximizing alternative constantly, decision makers embrace a probabilistic opting rule such that much captivating alternatives are selected frequently. The resulting formulation led to a quadratic optimization with linear constraints.

Exact methods like Benders’ decomposition method (Benders, 1962) are frequently found in applications of operations management. Bahl et al. [14] were amongst the first to use multi-item production scheduling. Benders’ decomposition methods have also found applications in discretely constrained mathematical programs [15]. Even stochastic optimization problems have found applications of Benders’ decomposition methods. Archibald et al. [16] compared the performance of Dynamic programming versus the nested Benders’ decomposition method for optimization of hydro-electric generation problems. Velarde et al. [17] implemented a heuristic based Benders’ decomposition method for the robust international sourcing model. The methodology involved generation of cuts via Tabu search, using the dual variables from the sub-problem to obtain the neighborhoods. Benders’ decomposition method has been employed to solve the strategic and operations management problems, especially in networks based problems, which as such can be solved by linear programming methods. Ali et al. utilized it for solving multi-commodity network problems [18]. Dogan et al. [19] used Benders decomposition method for solving a mixed integer programming problem for the strategic production-distribution allocation problem for the supply chain network. Benders’ decomposition method is also utilized in project time compression problems in Critical Path Method (CPM)/Programme Evaluation Review Technique (PERT) networks, by approximating the convex or concave activity cost-duration functions to piecewise linear time cost curves [20]. The Frank-Wolfe algorithm is used to solve quadratic programming problems with linear constraints [21].

Lee et al. [22] investigated a plant allocation and inventory level decisions for serving global supply chains and revealed that the importing firm escalates its inventory level if the transportation cost increases or the exchange rate of the inventory country lessen. The result of this study has been empirically confirmed using data of Korean firms yielded from the Export-Import Bank of Korea. Jean et al. [23] studied the relationship-based product innovation in global supply chains where this research offered a context-based explanation for the contradictory and conflicting empirical indication with respect to relational capital innovation links. In another study, a single period inventory model has been proposed to encapsulate the trade-off between inventory policies and disruption risks considering the scenario of dual-sourcing supply chain [24]. Tang et al. [25] examined multiple-attribute decision making using Pythagorean 2-tuple linguistic numbers, and proposed two operators, namely, Pythagorean 2-tuple linguistic weighted Bonferroni mean (WBM) and Pythagorean 2-tuple linguistic weighted geometric Bonferroni mean (WGBM). Further, the effectiveness of this approach is verified considering the green supplier selection problem. Zhang et al. [26] developed a greedy insertion heuristic algorithm using a multi-stage filtering mechanism comprising coarse granularity and fine granularity filtering for ameliorating the energy efficiency of single machine scheduling problems. A two-product, multi-period newsvendor problem has been formulated by Zhang and Yang [27] considering fixed demand. In addition, this research used the online learning method for performing the experiment, and also proposed real and integer valued online ordering policies. Egri and Vancza [28] presented an extended version of the newsvendor model to fulfil all demands of the customer by the supplier. This model particularly minimizes the total cost comprising setup, obsolete inventory and inventory holding costs. Furthermore, the model has been developed considering the decentralized setting using asymmetric information of customer and supplier. Ren and Huang [29] summarized several methods of modeling customer bounded rationality and also surveyed implementation of approaches with respect to appropriate operations management settings. In a dyadic supply chain, Du et al. [30] examined fairness preferences especially individuals’ psychological understanding. Moreover, to formulate the fairness concerns, they used Nash bargaining solution as fairness reference. Di et al. [31] developed a systematic methodology to obtain boundedly rational user equilibria (BRUE) solutions for networks with fixed demands that assist in predicting BRUE link traffic flow patterns in a given network to guide planners for making network design decisions accordingly when travellers behave boundedly rational. Di and Liu [32] presented a comprehensive review of models as well as methodologies of bounded rationality route choice behavior. The models are mainly divided into two parts: substantive and procedural bounded rationality models. While methodologies applied on these two models are game theory and interactive congestion game for substantive bounded rationality, and random utility and non- or semi-compensatory for procedural bounded rationality.

3. Mathematical Model Formulation

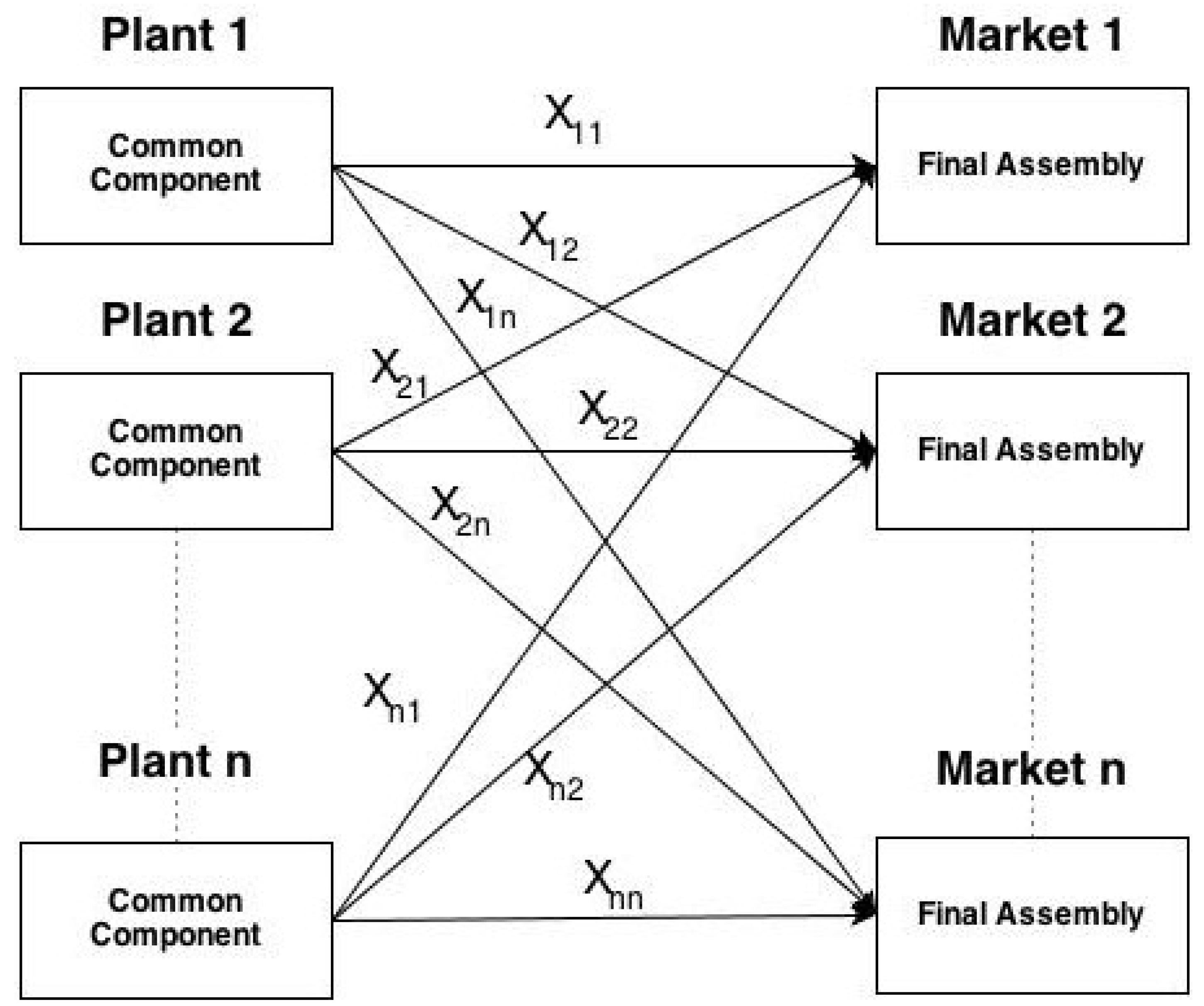
The present research investigates the operations policy of a multi-national firm which makes goods for serving geographically disjointed markets with localized final assemblies and joint parts. The joint part can be shipped from the markets with diverse financial and demand features. The cost required for transferring the joint components (intermediate goods between markets), and for foreign trade barriers like tariffs and duties provides the total transportation cost. The generalized operations strategy structure is illustrated in Figure 1 for multiple-product and multiple-market model with commonality.

This study dealt with the strategic facility location decision of engine production by taking into account the financial and demand features. The newsvendor network approach is used to evaluate the model. Firstly, we analyze the scenario under deterministic demand. The sensitivity of the trade-off between the manufacturing costs and the transportation costs are examined. Secondly, the situation under demand uncertainty is evaluated. Here, we assume uniformly distributed demand. The profit function is accordingly formulated and similar analysis is carried out. The function is solved using Frank Wolfe’s sequential linearization technique with Bender’s Decomposition method. Thirdly, the results of optimal decision scenario is compared with the scenario of bounded rationality considering uniformly distributed demand. When we consider the bounded rationality, the best option is not always picked by individuals, however, they opt for better options often. Finally, we intend to give a statistical proof of the superiority of the algorithm used over the traditional gradient search method by Rosen. Thus, a three-fold comprehensive comparison is made for the multi-market network design. The canonical setting at each market includes a newsvendor setup who has to obtain how much of the commonality to order. Every item costs c but can be sold at price p, where p > c. For a given demand, the profit is given as the product of price and minimum of demand and ordering quantity minus the procurement cost, which is cost per item multiplied by ordering quantity. Suppose we have a random demand, D having density f and cumulative distribution F. The expected profit in any of the selling points in the network under newsvendor model with demand uncertainty is given by:

$$\pi (x)=pE(\min (D,x))-cx$$

(1)

where,

• $x$: Number of items ordered
• $p$: Selling price of the item
• $c$: Cost of item, where c < p
• $D$: Demand
• $E(y)$: Expected value of y

Considering that the demand D is uniformly distributed between $[a,b]$. Then the profit function in Equation (1) can be expressed as [13]:

$$\pi (x)=A{x}^2+Bx+C$$

(2)

where,

$$A=\frac{-p}{2(b-a)}, B=\frac{pb}{b-a}-c, C=\frac{-p{a}^2}{2(b-a)}$$

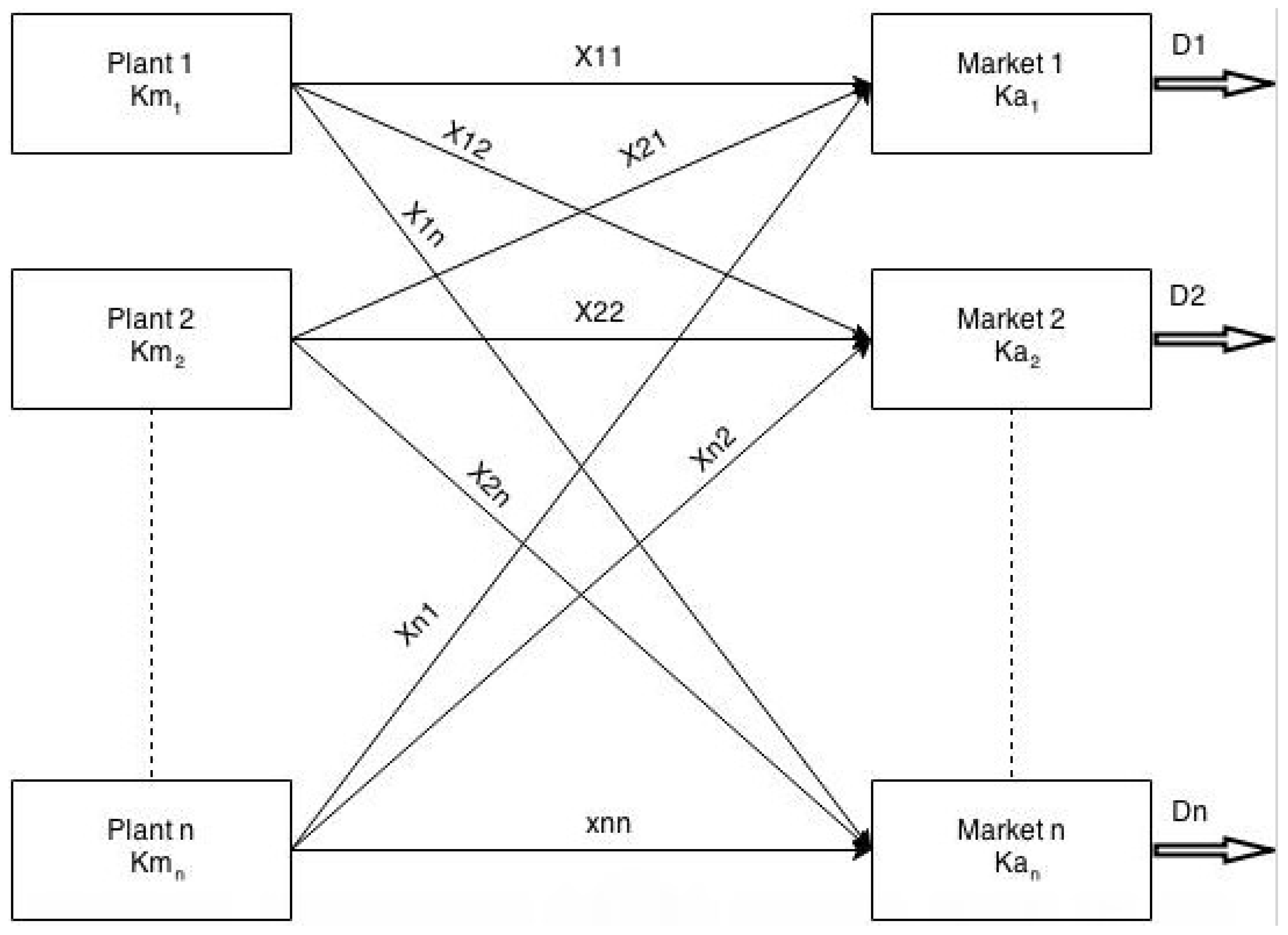
Now, we apply the above model to the multi-market scenario. Each of the markets can be considered as a newsvendor model. Consider the multi-market model as depicted in Figure 2.

With reference to Figure 2, we use the following notations:

Notations

• x_ij: Quantity of common component manufactured in plant i, and assembled at market j.
• p_j: Selling price of final assembly at market j.
• Ct_ij: Cost of transportation of common component from plant i to market j. (Ct_ii = 0)
• Cm_i: Cost of manufacturing the common component in plant i
• Km_i: Capacity limit on the common component manufacturing at plant i
• Ka_j: Capacity limit on the final assembly at market j.
• D_j: Demand at the market j, following a uniform distribution, Dj~U[aj,bj]
• a_j: Lower bound on the uniform demand distribution in market j
• b_j: Upper bound on the uniform demand distribution in market j
• Ca_j: Average cost per item incurred at market j due to various sources from which the items are transported
• v_ij: Value addition in terms of per unit profit obtained due to a common component transportation from plant i and sold at market j
• A_j: Coefficient of x² term in the Equation (2) for profit function in market j
• B_j: Coefficient of x term in the Equation (2) for profit function in market j
• C_j: Constant term in the Equation (2) for profit function in market j
• β_j: Bounded rationality parameter for market j
• π_j: Profit in market j
• n: Total number of countries in the multi-market network.
• Plant, i = 1, 2 … n
• Market j = 1, 2 … n

To apply the newsvendor’s model to each market, we need to determine the average cost per item at each market. This is taken as the weighted average of the common component manufacturing cost per item from the various source plants from which the items are transported.

$${\mathrm{Ca}}_j=\frac{{\displaystyle \sum _{j=1}^a{{\displaystyle x}}_{ij}({{\displaystyle Cm}}_i+{{\displaystyle Ct}}_{ij})}}{{\displaystyle \sum _{i=1}^a{{\displaystyle x}}_{ij}}}$$

(3)

Note here that Ct_ii = 0, as there is no transportation cost from plant i to market i. The value addition in each path in terms of per unit profit obtained due to a common component transportation from plant i and sold at market j is given by,

$$V_{ij}=p_j-C{m}_i-C{t}_{ij}$$

Thus, from Equation (2), the profit in each market j, under uniform demand distribution Dj~U[aj,bj] would be given as,

$${\pi }_j=A_j({\displaystyle \sum _{i=1}^a{x}_{ij}{)}^2}+B_j({\displaystyle \sum _{i=1}^a{x}_{ij})}+C_j$$

(4)

where,

$$A_j=\frac{-p_j}{2(b_j-a_j)},B_j=\frac{p_j{b}_j}{(b_j-a_j)}-C{a}_{j,}{C}_j=\frac{-p_j{a}_j^2}{2(b_j-a_j)}$$

Note here that Caj is not a constant term. Thus the equations is expanded and taking ${{\displaystyle BB}}_j=\frac{{{\displaystyle p}}_j{{\displaystyle b}}_j}{({{\displaystyle b}}_j-{{\displaystyle a}}_j)}$, we have the expression for the total profit π as,

$$\pi ={\displaystyle \sum _{i=1}^n{\pi }_j}={\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^n}{A}_j{x}_{ij}^2+2{\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{k=i+1}^n{A}_j}{x}_{ij}{x}_{kj}+{\displaystyle \sum _{j=1}^n}{\displaystyle \sum _{i=1}^n{x}_{ij}}(C{m}_i+C{t}_{ij}+B{B}_j)$$

(5)

Thus, we have the objective function to maximize the total profit: max π

This is subject to capacity constraints in each plant as well as each market for the final assembly,

Plant capacity constraint: ${\displaystyle \sum _{j=1}^n{x}_{ij}}\le K{m}_i\forall i=1\dots n$

Final Assembly capacity constraint: ${\displaystyle \sum _{j=1}^n{x}_{ij}}\le K{a}_j\forall j=1\dots n$

The formulation in Equation (5) is having a quadratic objective function and linear constraints. We apply Frank Wolfe’s sequential linearization method, and Bender’s Decomposition method is used for decomposing the linear problem within the Frank Wolfe’s method. Stepwise procedure for the integrated methodology is given as follows:

Consider the problem to,

Minimize π(x)
subject to x ∈ S;
where S ⊂ Rⁿ

Let, f is a continuously differentiable function.

Step 0. Choose an initial solution, x⁰$\in$S. Let k = 0. Here an arbitrary basic feasible solution is chosen, that is, an extreme point.

Step 1. Determine a search direction, p^k. In the Frank Wolfe algorithm p^k is determined through the solution of the approximation of the problem (1) that is obtained by replacing the function f with its first-order Taylor expansion around $x_k$. Therefore, solve the problem to minimize:

$$z_k\left(x\right)=\pi \left(x_k\right)+\nabla \pi {\left(x_k\right)}^T\left(x-x_k\right)$$

Subject to x $\in$ S

This is a Linear Programming (LP) problem. In large scale problems this would be computationally complex, and would require to be decomposed into smaller problems which can be solved easily. Hence we apply the Bender’s decomposition method at this point to solve the LP.

Step 2. Thus by Bender’s decomposition method x* is obtained as an optimal solution to gradient equation. The search direction is $p_k=x^{*-}-x_k,$ that is, the direction vector from the feasible point $x_k$ towards the extreme point.

Step 3. A step length is determined and represented as ${\alpha }_k$, such that $f(x_k+{\alpha }_k{p}_k)<f\left(x_k\right)$.

Step 4. New iteration point is found out using $x_{k+1}=x_k+{\alpha }_k{p}_k$.

Step 5. Check if stopping criteria is reached, else go to Step 1.

3.1. Illustration of Methodology on the Problem

The formulation in Equation (5) can be rewritten in matrix format as:

$$\begin{gathered} \mathrm{Max}{x}^{T}Qx+b^{T}x+c \\ \mathrm{s.t}Ax\le K \end{gathered}$$

where Q, b, c, A and K are appropriately defined depending on the size of the problem. With this notation on the formulation, the application of integrated Frank Wolfe’s and Bender’s decomposition method as applied to the multi-market network design problem under uniform demand uncertainty is depicted in the flowchart, in Figure 3.

3.2. Newsvendor Model under Bounded Rationality

The assumption of perfect rationality for decision makers is a typical tactic in a majority of normative analysis. In order to obtain bounded rationality, we followed the approach of [13], where multi-nomial logit choice model is applied and assumed that decision makers selects alterative j, with probability.

$${{\displaystyle \varphi }}_j=\frac{{{\displaystyle e}}^{\frac{{{\displaystyle u}}_j}{\beta }}}{{\displaystyle \sum _j{{\displaystyle e}}^{\frac{{{\displaystyle u}}_j}{\beta }}}}$$

(6)

Correspondingly, the following density function gives the logit choice probabilities over a continuous domain:

$$\varphi (y)=\frac{{{\displaystyle e}}^{\frac{u(y)}{\beta }}}{{\displaystyle {\int }_y{{\displaystyle e}}^{\frac{u(y)}{\beta }}}}$$

(7)

Thus, the selection of agents is a random variable. The superior options are selected frequently using the above logit structure. The best alternative depends on the mode of the selection distribution. The magnitude of cognitive and computational restrictions suffered by the decision makers is elucidated by β parameter. This can be observed when selection distribution approximates the uniform distribution over the options in $\beta \to \infty$ limit. In some utmost instances, decision makers randomize the options with equal probabilities when they failed to make any informed choices. In the other scenario, when $\beta \to \infty$ the choice distribution in (1) completely focused on utility maximizing options. The selection of perfect rational decision maker corresponds with this choice. Therefore, we can consider the magnitude of β as the extent of bounded rationality. The logit choice framework to the newsvendor problem is employed here. The profit function is as stated in Equation (1) is

$$\pi (x)=pE(\min (D,x))-cx$$

This is uniquely maximized at,

$$x^{*}=F^{-1}\left(1-c/p\right)$$

(8)

where, F is the cumulative distribution function of demand D. All other symbols are as used before. This solution is selected when the decision maker is perfectly rational, although the newsvendor’s ordering amount is dependent on noise and it called the behavioral solution in bounded rationality. The bounded rational newsvendor can order any amount of product within the range of minimum possible and maximum possible demand realizations in the domain S. Then, the Equation (9) gives the probability density function associated with behavioral solution:

$$\varphi (y)=\frac{{{\displaystyle e}}^{\frac{\pi (x)}{\beta }}}{{\displaystyle {\int }_s{{\displaystyle e}}^{\frac{\pi (v)}{\beta }}dv}}=\frac{{{\displaystyle e}}^{\frac{pE(\min (D,x))-cx}{\beta }}}{{\displaystyle {\int }_s{{\displaystyle e}}^{\frac{pE(\min (D,v))-cv}{\beta }}dv}}$$

(9)

Now, if the demand D is uniformly distributed in in the interval of [a, b], then the behavioral solution would follow truncated normal distribution over [a, b] with mean µ and standard deviation σ [13].

$$\mu =b-\frac{c}{p}(b-a)$$

(10)

$${\sigma }^2=\beta \frac{b-a}{p}$$

(11)

The expected value of this truncated normal distribution would be,

$$E(x)=\mu -\sigma \frac{\varphi ((b-\mu )/\sigma )-\varphi ((a-\mu )/\sigma )}{\phi ((b-\mu )/\sigma )-\phi ((a-\mu )/\sigma )}$$

(12)

where, ϕ(.) denotes cumulative normal distribution and φ(.) denotes normal density function.

As an example in the dual market scenario, each market decision maker would be subjected to bounded rationality. Thus, the expected ordering quantities in each market, with uniformly distributed demand between [a_i, b_i] (i = 1…n) and with bounded rationality parameters as ${\beta }_1$ and ${\beta }_2$ would be,

$$E(x_1+x_3)={\mu }_1-{\sigma }_1\frac{\varphi ((b_1-{\mu }_1)/{\sigma }_1)-\varphi ((a_1-{\mu }_1)/{\sigma }_1)}{\phi ((b_1-{\mu }_1)/{\sigma }_1)-\phi ((a_1-{\mu }_1)/{\sigma }_1)}$$

(13)

where,

$${\mu }_1=b_1-\frac{c_1}{p_1}(b_1-a_1){\sigma }_1^2={\beta }_1-\frac{b_1-a_1}{p_1}$$

and,

$$E(x_2+x_4)={\mu }_1-{\sigma }_1\frac{\varphi ((b_1-{\mu }_1)/{\sigma }_1)-\varphi ((a_1-{\mu }_1)/{\sigma }_1)}{\phi ((b_1-{\mu }_1)/{\sigma }_1)-\phi ((a_1-{\mu }_1)/{\sigma }_1)}$$

(14)

The concept of bounded rationality can be reconciled with original problem of multi-market network design in way that initially under uniform demand distribution, the production allocation strategy is decided by the company and then ordering decisions are made under bounded rationality, giving suboptimal. Similarly, the model can be applied to multi-market scenario with any number of plants and markets. Thus, under bounded rational conditions, we can find the expected profit as given in (3). Hence, a comprehensive comparison is made amongst the profits under various conditions in the following section.

4. Test Results and Comparative Analysis

A comprehensive analytical study was made for the different test examples of varying problem sizes. Each case depicts the results in different scenarios. We illustrate the optimal production allocation in the network design for the uniform demand distribution. Finally, we make a comparison of this with profits in the scenario of bounded rational decision maker.

All data sets used for the test examples are provided in Appendix A. These include the pricing details, the manufacturing and transportation costs and the demand distribution parameters.

X: matrix production allocation, where ${\mathit{x}}_{\mathit{i}\mathit{j}}$ represents the optimal production allocation between plant i and market j.

4.1. I. Test Case 1

Problem size n = 2.

1. Scenario of Uniform Demand Distribution

X:

The production allocation values for test case 1 are given in

Table 1. Production allocation values for test case 1.

	Market 1	Market 2
Plant 1	1636.36	0
Plant 2	0	1187.5

.

Objective function value = 108,678.

We observe that the solution indicates a market focused strategy for the company as depicted in Figure 4.

2. Scenario of Bounded Rational Decision Maker

Table 2. Ordering quantities and profits under bounded rationality for test case 1.

Cases for Bounded Rationality Conditions with Varying β Parameter
β1	β2	Ordering Quantity in Market 1	Ordering Quantity in Market 2	Total Profits	% Deviation from Achievable Profits
0	0	1409	1156	108,640	0.12
10	10	1409	1187	105,802	1.34
100	100	1491	1482	104,054	1.88
1000	1000	1499	1499	103,753	1.97
10,000	10,000	1499	1499	103,752	2.03
100,000	100,000	1500	1500	103,750	2.45
1,000,000	1,000,000	1500	1500	103,750	2.56

depicts the ordering quantities and profits under bounded rationality for test case 1

4.2. II. Test Case 2

Problem size n = 4.

1. Scenario of Uniform Demand Distribution:

Table 3. Production allocation values for test case 2.

	Market 1	Market 2	Market 3	Market 4
Plant 1	1518	0	482	0
Plant 2	0	1187.5	0	0
Plant 3	0	0	968	0
Plant 4	0	0	0	1608

illustrates the Production allocation values.

X:

Objective function value = 286,553.59.

Strategic allocation of common component is shown in Figure 5.

2. Scenario of Bounded Rational Decision Maker

The ordering quantities and profits under bounded rationality for test case 2 are reported in

Table 4. Ordering quantities and profits under bounded rationality for test case 2.

	Cases for Bounded Rationality Conditions with Varying β Parameter
β	Ordering Quantity in Market 1	Ordering Quantity in Market 2	Ordering Quantity in Market 3	Ordering Quantity in Market 4	Total Profits	% Deviation from Achievable Profits
0	1225	1263	923	1234	286,550	0.45
10	1232	1305	940	1258	262,834	1.53
100	1242	1360	1051	1264	213,850	2.24
1000	1335	1374	1066	1395	204,467	2.2
10,000	1409	1444	1066	1395	216,800	2.57
100,000	1462	1471	1066	1402	283,890	2.83
1,000,000	1500	1498	1075	1428	278,777	3.44

.

4.3. III. Test Case 3

Problem size n = 10

1. Scenario of Uniform Demand Distribution

X:

Table 5. Production allocation values for test case 3.

	Market 1	Market 2	Market 3	Market 4	Market 1	Market 2	Market 3	Market 4	Market 9	Market 10
Plant 1	1153	0	0	780	0	0	0	0	0	0
Plant 2	0	593	782	0	0	0	0	543	0	0
Plant 3	0	0	0	0	0	0	1472	0	0	0
Plant 4	1673	0	0	0	0	0	0	0	0	0
Plant 5	0	630	0	226	0	0	0	0	0	476
Plant 6	1885	0	0	0	0	0	0	0	0	0
Plant 7	0	252	378	150	0	0	0	474	0	720
Plant 8	0	0	0	0	0	1836	0	0	0	0
Plant 9	0	0	0	1566	0	0	0	0	0	0
Plant 10	1724	0	0	0	0	0	0	0	0	0

shows the production allocation values of test case 3.

Objective function value = 723,977

2. Scenario of Bounded Rational Decision Maker

The Profits under bounded rationality for test case 3 are presented in

Table 6. Profits under bounded rationality for test case 3.

Cases for Bounded Rationality Conditions with Varying β Parameter
β	Total profits	% Deviation from Achievable Profits
0	723,908	0.53
10	615,322	2.19
100	553,790	2.85
1000	498,411	2.68
10,000	448,570	2.61
100,000	723,908	3.45

.

Bounded rationality factor β = 100.

4.4. Comparative Analysis

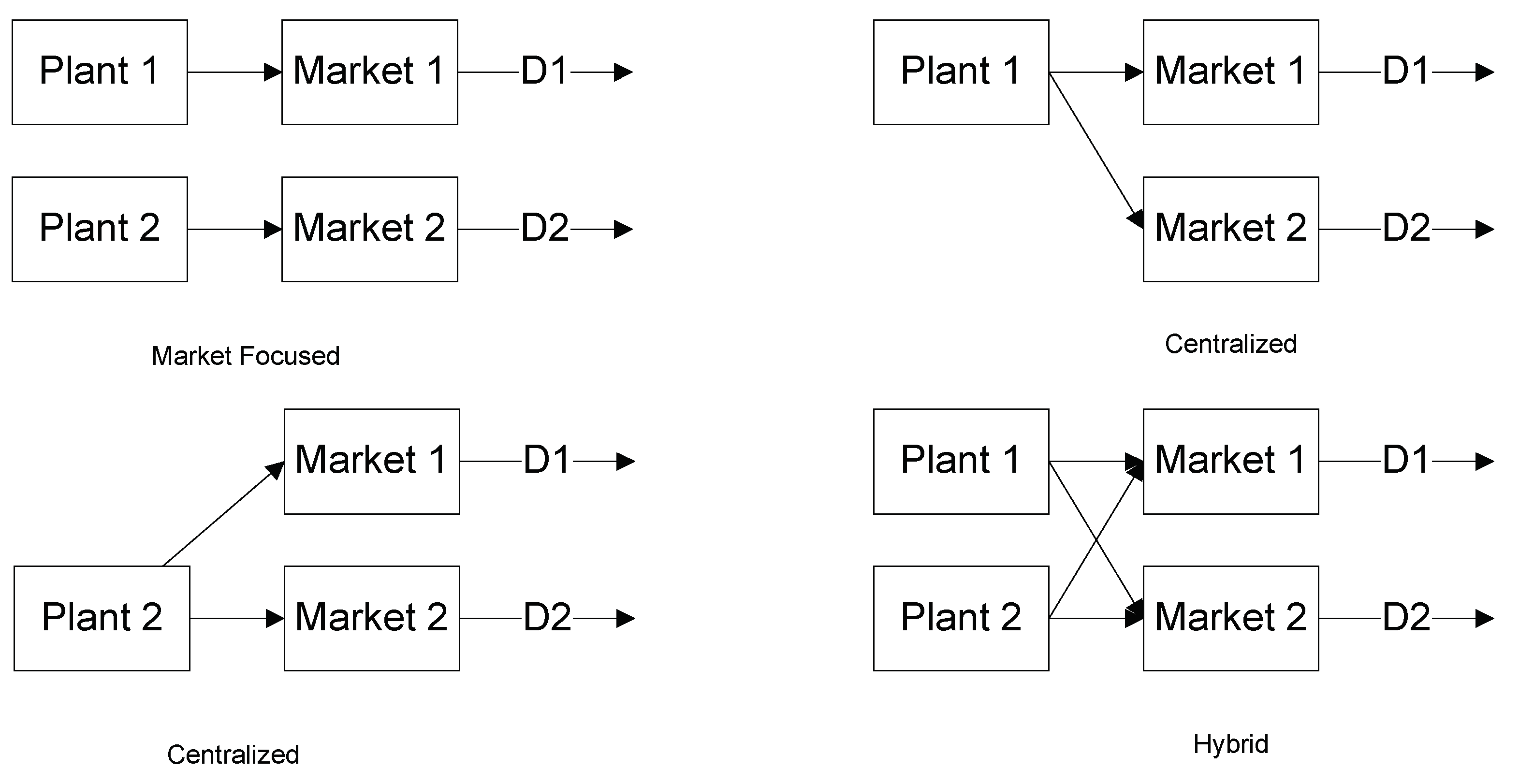
For a problem size of 2 (dual market scenario), there are various possible cases and scenarios that might arise due to the tradeoffs between the prices and the costs. In order to evaluate the financial desirability of the options processing actions for every product, the investment decisions declined. For the analysis of various possible cases in the dual market scenario, we take the value addition into consideration, which represents the per-unit profit of the company, due to the particular path taken in the production allocation. Let v1 denote the value addition due to path from plant 1 to market 1, similarly, v2 be for plant 1 to market 2, v3 for plant 2 to market 1 and v4 for plant 2 to market 2. The probable orderings of the four net values are 24 (=4!) without considering any assumption, but their definitions suggest an interdependence, v4 ≥ v1 ⇒ v2 ≥ v3, which removes 6 orderings (where, as mentioned earlier vi represents the per unit profit value addition in any path). The outstanding 18 are distributed into two clusters, one of which is a replica of the other. The following study emphasizes the 9 orderings because of symmetry in results. These result in 4 possible allocation strategies of market focused, centralized with two possible centralization and hybrid type of model as indicated in Figure 6.

Table 7. Profit results of Scenario 1.

Scenario 1		Case of Deterministic Demand		Case of Uniform Demand Distribution D $\sim$ [1000, 200]
$v_1>v_2>v_3>v_4$ $c_{t,1}>\Delta c_m$ $c_{t,2}>\Delta c_m$	$p_1=100$	$x_1=D_1$		$x_1=1565$
	$p_2=80$	$x_2=0$		$x_2=0$
	$c_{m,1}=40$	$x_3=0$		$x_3=0$
	$c_{m,2}=65$	$x_4=D_2$		$x_4=1142$
	$c_{t,1}=30$	$D=D_1=D_2$	T.P	T.P. = 105,951.9
	$c_{t,2}=25$	1000	85,000
		2000	170,000
		1500	127,500

depicts 1 of the 9 possible scenarios which is analyzed under cases of deterministic demand, uniform demand and uniform demand under bounded rationality, and the total profits (T.P) in each case is found. For the case of uniform distribution, the Frank Wolfe’s Bender decomposition method is compared with the Rosen’s gradient search method which is depicted in the Figure 7.

5. Conclusions and Future Work

The decision regarding the manufacturing of the common component has been analytically modeled and solved for a multi-market scenario. For the case of deterministic demand, the linear formulation was solved for the 3 distinct scenarios. Then, the case of uncertainty has been analyzed, where the demand is uniformly distributed. This was formulated as a quadratic problem and solved using a proposed integrated methodology exploiting the Frank-Wolfe linearization technique, along with Benders’ decomposition method. To establish the superiority of the proposed solution methodology, in terms of convergence, we compared it with Rosen’s gradient search technique. In case of uniform demand with bounded rationality, the decision maker ordering a specific number of units for selling in the respective market cannot make the optimal choice, but his choice is guided by a probabilistic logit choice model, with higher probability of making the right choice. We have demonstrated (as expected) that bounded rational decisions are less profitable than the rational decision making and get reinforced when the lack of clarity of decision makers becomes more prominent. Scope for future studies can include, but is not limited to, incorporating some other behavioral characteristics along with bounded rationality.