Abstract
Reconfiguration is concerned with relationships among solutions to a problem instance, where the reconfiguration of one solution to another is a sequence of steps such that each step produces an intermediate feasible solution. The solution space can be represented as a reconfiguration graph, where two vertices representing solutions are adjacent if one can be formed from the other in a single step. Work in the area encompasses both structural questions (Is the reconfiguration graph connected?) and algorithmic ones (How can one find the shortest sequence of steps between two solutions?) This survey discusses techniques, results, and future directions in the area.
1. Introduction
Solving puzzles, planning robot motion, and editing between strings can all be viewed as the transformation between states or configurations, where a configuration can be the arrangement of puzzle pieces, the location of a robot with respect to obstacles in space, or the ordering of symbols to form a string. When configurations are defined as feasible solutions to a problem, such as the coloring of vertices in a graph, a step in a transformation between solutions can be viewed as an adjacency relation between configurations. The area of reconfiguration considers both structural and algorithmic problems on the space of solutions, under various definitions of feasibility and adjacency.
Reconfiguration arises in countless problems that involve movement and change, including problems in computational geometry such as morphing graph drawings [1] and polygons [2], and problems relating to games and puzzles, such as the 15-puzzle (Figure 1a), a topic of research since 1879 [3]. Work on related problems was unified into a common framework in 2011 [4], leading to a widening interest in the area and the types of problems and approaches considered. Reconfiguration is distinct from other approaches to the solution space of problems, such as local search [5,6,7,8] (given a solution to an instance, find a better solution that is close to the input solution), reoptimization [9,10] (given an instance, an optimal solution, and changes to the instance, find an optimal solution to the changed instance), and incremental problems [11] (given a yes-instance, a witness that it is a yes-instance, and changes to the instance, determine if the changed instance is a yes-instance).
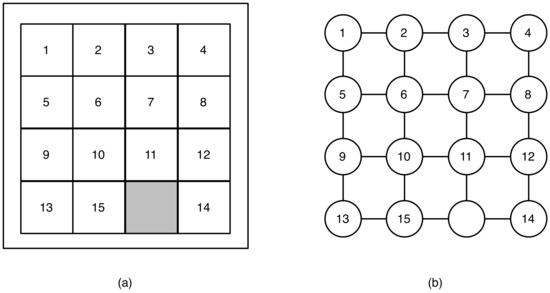
Figure 1.
(a) one arrangement of tiles of the 15-puzzle; (b) the puzzle represented as a graph.
The reconfiguration framework is defined in terms of a source problem, an instance of the source problem, a definition of a feasible solution, and a definition of adjacency of feasible solutions. Whereas in principle there are no restrictions on the definitions of feasible solutions and adjacency, for the sake of tractability, adjacency is typically polynomially testible. We can then view the solution space as a reconfiguration graph, in which vertices represent feasible solutions to the given instance of the source problem, and two vertices are joined by an edge if their corresponding feasible solutions are adjacent. In addition to being represented as a graph, the relationship among feasible solutions can be viewed as a process, where two solutions are adjacent if one can be transformed into another by a single reconfiguration step. We will use the graph view and the transformation view interchangeably. For example, a path between two solutions in the reconfiguration graph can be seen as a sequence of reconfiguration steps, or reconfiguration sequence, transforming one into the other. Although the terminology has not yet stabilized, for the sake of readability, consistent terminology is used throughout this paper and, where possible, unnecessary notation will be avoided. We will refer to the framework using the name of the source problem, such as Satisfiability Reconfiguration, with the definitions of feasible solution and/or adjacency omitted when clear from context.
So far, we have not yet specified any problems to solve in the reconfiguration framework; the specification of the problem (as discussed in more detail in Section 2) adds a fifth dimension to the dimensions of source problem, instance, definition of feasible solutions, and definition of adjacency. The multitude of dimensions leads to challenges in specifying problems as well as in organizing this survey. In order to highlight key elements of the area, each section focuses on a few dimensions at a time, often with a focus on a single source problem. In order not to overwhelm the reader, terminology is introduced gradually, and many open problems are raised when the relevant dimension is being considered.
This paper does not attempt to catalog all research results that can be categorized as reconfiguration, but instead focuses on demonstrating the main themes in the area, the scope of the approach, and promising directions for the future. In order to cover a large range of source problems, in many cases, the source problems and their complexity will be mentioned without formal definitions or lemma statements; the reader can find details in standard references on problems and algorithms [12,13]. Various complexity classes will be defined informally, with references provided for those interested in more detail. The goal is to complement, not subsume, other similar work, such as van den Heuvel’s survey [14] and the introduction to Mouawad’s thesis [15], where one can also find details on practical applications of reconfiguration, such as maintaining a firewall in a changing network, assigning frequencies in a changing mobile network, characterizing Glauber dynamics Markov chains in statistical physics, and planning motion, including 3D printing and robot movement.
We first use sliding-block puzzles to introduce problems that arise under the reconfiguration framework, such as reachability, connectivity, diameter, and shortest/bounded transformation (Section 2), as well as to introduce definitions of feasibility and adjacency. Next, we outline general approaches taken to solve the reachability problem for a variety of host problems (Section 3). Thereafter, we use specific source problems as case studies for various aspects of reconfiguration. In Section 4, we consider the dividing line between tractability and intractability of reachability of Independent Set Reconfiguration for different classes of input graphs and different definitions of adjacency. Our examination of the reachability of Independent Set Reconfiguration is continued in Section 5, where parameterized complexity is introduced and applied as well as extended to Vertex Cover Reconfiguration. The problems of connectivity and diameter are considered for k-Coloring Reconfiguration (Section 6), followed by other structural problems for Dominating Set Reconfiguration and other source problems in Section 7, and then by shortest transformation for Flip Distance and Satisfiability Reconfiguration (Section 8). Finally, we come full circle by seeing how work on sliding-block puzzles can inspire future work (Section 9), ending with a summary of other directions for research (Section 10).
2. Specifying and Analyzing Reconfiguration Graphs
Long before the term reconfiguration was used to categorize problems, sliding-block puzzles, such as the 15-puzzle (Figure 1a) were studied by mathematicians. In the reconfiguration framework, each arrangement of the tiles can be seen as a feasible solution, where a reconfiguration step consists of the movement of a single tile into an adjacent hole. Equivalently, the 15-puzzle can be viewed as a graph problem, where each feasible solution is the placement of distinctly labeled tokens on fifteen of the vertices in a grid graph (corresponding to the placement of the tiles), leaving one vertex uncovered (corresponding to the placement of the hole). For this formulation of the problem, a reconfiguration step consists of moving a token to the uncovered vertex from one of its neighbors in the graph (Figure 1b). Adding further constraints on the feasible solutions gave rise to a variety of source problems with feasible solutions that can be represented as the placement of tokens. In subsequent work, different types of reconfiguration steps were defined by other ways of moving tokens, and eventually to problems for which tokens were not used at all.
Questions that arise in the context of puzzles form the foundation of questions asked about reconfiguration today, such as determining whether one arrangement can be reached from another (reachability) or indeed if all arrangements can be reached from all others (connectivity), and if so, finding the shortest sequence of steps possible (shortest transformation), a sequence of at most a specified length (bounded transformation), or a bound on the number of steps for any pair of arrangements (or, equivalently, on the diameter of the reconfiguration graph, hence diameter). In the remainder of this section, we formalize definitions of feasibility and adjacency (Section 2.1) and definitions of problems in the reconfiguration framework (Section 2.2). We will return to sliding-block puzzles at the end of the paper (Section 9) after briefly noting that the answer to the connectivity problem for the 15-puzzle was shown to be negative more than a century ago [3].
2.1. Defining Feasible Solutions and Adjacency
For many graph problems, a feasible solution can be represented as a subset of the vertices in the instance, or equivalently as the placement of a set of tokens on a subset of the vertices. Reconfiguration steps can then be described with respect to the placement of the tokens. In token sliding (TS), a step can be seen as the sliding of a token along an edge [16]. Two solutions are adjacent under token sliding if they have the same cardinality, the size of their intersection is one less than the size of the solutions, and the two vertices not in the intersection are connected by an edge. If we remove the constraint that the vertices outside the intersection be connected, the adjacency relationship is known as token jumping (TJ) [17]. More formally, two solutions are adjacent under token jumping if they have the same cardinality and the size of the intersection is one less than the size of the solutions. Both token sliding and token jumping can be viewed as the replacement of a vertex in one solution with a vertex outside the solution.
If we instead allow a token to be either added or removed at each reconfiguration step, we are considering the adjacency relation of token addition/removal (TAR) [4]. Whereas all solutions are of the same size under TS and TJ, under TAR the sizes of solutions can differ. To avoid triviality, sizes are bounded below for maximization problems and bounded above for minimization problems under TAR.
To illustrate the need for bounds on solution sizes, we consider the example of Vertex Cover Reconfiguration under TAR, in which each feasible solution is a vertex cover (a set of vertices containing at least one endpoint of each edge) of any size, and two solutions are adjacent if they differ by a single vertex. As there is no bound on size, one of the solutions, the maximum vertex cover, consists of all the vertices in the graph. Finding a path in the graph between any two vertex covers s and t is then trivial; by adding vertices one by one, we can form a path from any vertex cover to the maximum vertex cover, and by deleting vertices one by one, we can form a path from the maximum vertex cover to any vertex cover. We can then obtain a path from s to the maximum vertex cover to t (Figure 2a). As seen in Figure 2b, placing a bound on the size of a solution may mean that there is no path between s and t.
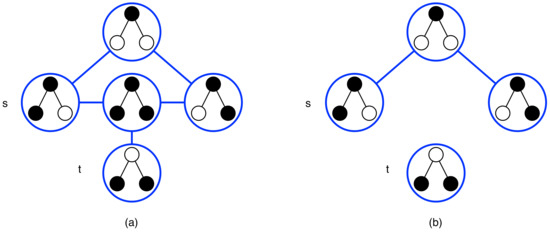
Figure 2.
(a) Vertex Cover Reconfiguration under TAR with no limit on solution size; (b) Vertex Cover Reconfiguration under TAR with solutions of size at most two.
For solutions that cannot be expressed as subsets of vertices, most definitions of reconfiguration steps entail a single change to a solution. In the source problem Shortest Path, a solution is typically given as a sequence, rather than a set, of vertices forming a shortest path, as there may be more than one shortest path in the graph induced on a subset of vertices [18]; two solutions are adjacent if they differ by a single vertex. For Satisfiability Reconfiguration, each solution is an assignment of variables to the values true and false such that the instance formula evaluates to true; the reconfiguration step is the changing of the value of a single variable. For problems related to coloring of vertices or edges, a solution is an assignment of colors to vertices or edges, and a reconfiguration step involves changing the color of a single entity.
Relatively little work has been done on reconfiguration steps that allow multiple changes at once, such as in Multiple Token Jumping (MTJ) [19] or in coloring multiple vertices at once [20]; the modification with most attention thus far is Kempe changes (Section 6.2). For many source problems with solutions that are represented as sequences, unlike for Shortest Path, solutions will typically differ by more than the replacement of a single item in the sequence. For example, for String Editing, an instance is a pair of strings s and t and each solution is a sequence of edit operations, such as addition, deletion, and changing of symbols, that transforms s into t. Although changing a single edit operation will usually result in a sequence of operations that fails to be a solution for the given instance, in some cases, the order of operations can be changed or a pair of operations can be altered [21]. Determining natural definitions of adjacency for solutions that are sequences would open up the consideration of a larger set of problems, including the reconfiguration of reconfiguration itself [21].
Little attention has been paid to the impact of the representation of solutions. In the reconfiguration of subgraphs [22,23], the complexity of problems may differ depending on whether subgraphs are represented as sets of vertices or sets of edges, whether or not specific vertices are labeled, and whether the subgraph is contained in or isomorphic to the subgraph induced on the subset of vertices. The use of labels to identify parts of solutions, while used extensively in generalizations of sliding-block puzzles, has rarely been considered, as discussed further in Section 9.
2.2. Defining Problems
Viewing reconfiguration as both a sequence of steps and as a path in a graph gives rise to interrelated algorithmic and structural questions. The main focus of algorithmic work has been to determine the existence of paths between solutions in the reconfiguration graph, such as between a starting and ending configuration of the 15-puzzle. More formally, the reachability problem determines whether or not there is a reconfiguration sequence joining two input solutions, sometimes designated as the source solution and target solution; it should be noted that since the reconfiguration graph is undirected, the designation of one input as the source and the other as the target is arbitrary. So prevalent was the focus on the reachability problem that it appears in the literature as the “reconfigurability problem” [17] or simply the “reconfiguration version” of a problem.
There is no need for an algorithm for reachability if one can determine that the reconfiguration graph is connected, and hence that all instances of the reachability problem are yes-instances. For a fixed source problem, instance, definition of feasible solutions, and definition of adjacency, the connectivity problem asks whether the reconfiguration graph is connected. Most work on connectivity focuses on determining properties of the instance that result in the reconfiguration graph being connected rather than the complexity of algorithms used to check those properties.
The shortest transformation problem is an extension of reachability, where the goal is to find a shortest reconfiguration sequence between a pair of input solutions. In the related decision problem of bounded transformation, the input includes both a pair of solutions and a positive integer bound; the problem is to determine whether the solutions are connected by a sequence of length no greater than the bound. Other terms for these problems that appear in the literature include the length-bounded version of reachability, bounded reconfiguration, and shortest path, not to be confused with the source problem Shortest Path. An upper bound on the length of the shortest transformation can be determined by finding a solution to the structural diameter problem, the problem of determining the diameter of the reconfiguration graph (or of its connected components).
Although most of the work on reconfiguration to date has focused on reachability, connectivity, shortest/bounded transformation, and diameter (and, at times, producing an actual reconfiguration sequence, when one exists, typically as a minor extension of the algorithm for the decision problem of reachability), there are also results that consider other structural properties of the reconfiguration graph. We discuss these in more detail in Section 7.
A new direction in algorithmic problems is the optimization variant [24], where the goal is to find an optimal solution reachable from a given solution. Various related problems have been considered for the problem of k-Coloring, starting with an assignment of colors to vertices that may not form a proper coloring (a coloring in which the endpoints of each edge have different colors). In one case, the graphs are directed, and the goal is to reach a particular proper coloring by giving a vertex a color different from that of its neighbors [25]. In Color-Fixing, starting with an assignment of colors to vertices, the goal is to determine the minimum number of vertex recolorings required in order to find any proper coloring [26].
The examination of the role of reconfiguration steps gives rise to further problems of interest. Reconfiguration steps are equivalent for a given source problem if an instance is solvable using one type of reconfiguration step if and only if it is solvable using another type of reconfiguration step. It has been shown that, for Independent Set Reconfiguration, TJ and TAR are equivalent [17], and, for Clique Reconfiguration, TJ, TS, and TAR are equivalent [27]. For most problems, however, such relationships are unknown.
The fact that reachability may be trivial under TAR for unbounded solution sizes leads to the question of the size needed for there to be a path between a source and a target solution. The term reconfiguration index [28] has been used to denote the minimum value of solution size required for a yes-instance; the threshold [19] expresses the same concept in terms of the difference between the largest and smallest solutions in the reconfiguration sequence. As such values are not easy to determine, many of the results have focused on approximations [29]; here, we use the terms inapproximable, approximation algorithm, and polynomial-time approximation scheme (a family of approximation algorithms) without providing details. Results include inapproximability results for Clique Reconfiguration [4], Satisfiability Reconfiguration [4], and Set Cover Reconfiguration [4], approximation algorithms for Power Supply Reconfiguration [4] and Vertex Cover Reconfiguration [28], a polynomial-time approximation scheme for Subset Sum Reconfiguration [30], and a characterization of properties of graphs that result in large thresholds for Independent Set Reconfiguration [19].
3. Tools for Proving the Complexity of Reachability
By considering reconfiguration as a framework that highlights the commonality of a large variety of source problems, often studied in isolation, it becomes possible to devise general approaches and detect patterns. In the initial results obtained on reachability, the dividing line between tractable and intractable problems followed the dividing line for the source problems. Typically an intractable source problem is NP-complete and an intractable reachability problem is PSPACE-complete, where the class PSPACE includes all problems that can be solved using polynomial space [12]. Polynomial-time reachability algorithms have been developed for tractable source problems such as 2-Coloring [31,32,33], Matching [4], Minimum Spanning Tree [4], and 2-Satisfiability [34]. Reachability has been shown to be PSPACE-complete for many NP-complete source problems, such as Clique [4], 4-Coloring [35], Independent Set [4,17], 3-Satisfiability [34], Vertex Cover [4], Dominating Set [4], List Edge-Coloring [36], List -Labeling [37], Integer Programming [4], Steiner Tree [38], and Set Cover [4].
As was conjectured early on [4], there are exceptions to the general pattern. One such exception is 3-Coloring [33], for which the source problem is NP-hard but the reachability problem is solvable in polynomial time. The problem Shortest Path is an example that breaks the pattern in the opposite direction, as the source problem is solvable in polynomial time but the reachability problem is PSPACE-complete [39]. What remains unclear is which properties of source problems result in their deviating from the general pattern of NP-hard source problems resulting in PSPACE-hard reachability problems; further work is needed on this question.
Many of the reductions used in proving PSPACE-hardness results mimic NP-hardness reductions on the source problems. The basis for these hardness results is the reconfiguration of the Nondeterministic Constraint Logic (NCL) machine, an undirected graph with integer weights on vertices and edges [16]. Reconfiguration on the NCL machine uses as solutions orientations of the edges such that the weight of each vertex is no greater than the sum of the weights of incoming edges; a reconfiguration step is the changing of the direction of a single edge. By forming substructures that behave like OR and AND gates (Figure 3), the problem was shown to be PSPACE-complete by a reduction from Quantified Boolean Formula [12]. The result on NCL Reconfiguration was then used as the basis for proving the PSPACE-completeness of sliding tokens on a graph [16], which in turn became the basis for many of the known PSPACE-completeness results for reconfiguration. In subsequent work, NCL has been generalized to include neutral, undirected edges; a new type of gadget has been used to complete the classification of reachability for List Edge-Coloring Reconfiguration to be solvable in polynomial time for at most three colors and PSPACE-complete otherwise [40].
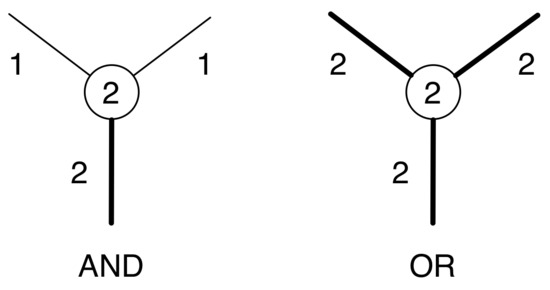
Figure 3.
OR and AND gates in an NCL machine.
As yet, there are few general algorithmic paradigms for reachability. Many algorithms in fact solve the connectivity problem as well, as they consist of identifying a canonical configuration for a particular instance and then showing that there is a reconfiguration sequence between any input solution and the canonical configuration (and hence a sequence from the source solution to the target solution that goes through the canonical configuration).
When reachability is intractable, possible approaches include an analysis using parameterized complexity (as discussed in detail in Section 5) and determining the dividing line between classes of instances for which the problem is tractable and those for which it is not (as discussed in Section 4 for the source problem Independent Set). For a specific problem, a natural starting point is to determine whether the dividing line for reachability is the same as the dividing line for the source problem. For a more general result, such as on graph problems, one might try to identify a class of graphs for which reachability is tractable for a large class of source problems. Formal definitions of graph classes and properties mentioned without accompanying citations can be found in a textbook on graph theory [41].
As many results are more easily obtained on simple graphs such as paths and trees, one approach is to try to generalize results by considering classes of graphs that contain paths and trees (Figure 4). Paths and trees are bipartite (properly colorable using two colors), planar (embeddable on the plane without any edges crossing), and chordal (containing no induced cycle on more than three vertices). Various graph classes are characterized by various width measures, such as pathwidth and treewidth (measures of how path-like or tree-like a graph is); one can generalize from paths (with pathwidth one) and trees (with treewidth one) to graphs of pathwidth k or treewidth k for a given constant k. Such graphs retain useful properties, such as the solving of various problems using dynamic programming. Other graph parameters to be discussed later include bandwidth (the minimum over all mappings f of the vertices to the set of natural numbers of the maximum of over all edges in the graph), and modular-width [42].
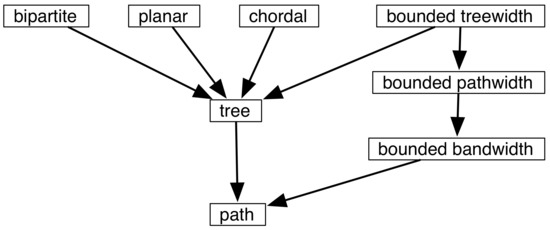
Figure 4.
Arrows depict inclusion relations among classes of graphs.
The contracted solution graph method has been proposed as a general method for developing algorithms by compacting the information in the reconfiguration graph and then applying dynamic programming, using tree decompositions. The method has been used for algorithms for Shortest Path Reconfiguration on planar graphs [43], List Coloring Reconfiguration on caterpillars [44], and k-Coloring Reconfiguration on -connected chordal graphs [45]. The technique led to a conjecture that treewidth could be exploited to obtain algorithms. Instead, a general technique was developed to show the PSPACE-hardness of reachability for instances of bounded bandwidth. Because a graph of bandwidth b has pathwidth and treewidth at most b [46], the use of treewidth in forming algorithms is limited. Bonsma noted that dynamic programming has also been effectively used in solving reachability of Independent Set Reconfiguration for cographs [42]; as these are graphs of bounded modular-width, there may be a general method possible for graphs of bounded modular-width. It remains to be seen whether general results on reachability are possible for particular classes of graphs.
The result on bandwidth was proved using H-Word Reconfiguration, where given an alphabet and a binary relation between symbols, an H-word is a word in which each pair of consecutive symbols is in the relation. Wrochna [47] proved the PSPACE-completeness of the reachability problem, where the reconfiguration step is changing a single symbol, based on the classic proof of undecidability for general Thue systems [48]. Using this result, the following reachability problems were shown to be PSPACE-complete for graphs of bounded bandwidth: Shortest Path [47], k-Coloring [47], List Coloring [47], Independent Set [47], Vertex Cover [49], Feedback Vertex Set [49], Odd Cycle Transversal [49], Induced Forest [49], Induced Bipartite Subgraph [49], and Dominating Set [50]. In investigations of the parameterized complexity (defined in Section 5) of NCL under the parameters treewidth, maximum degree, and length of the reconfiguration sequence, H-Word Reconfiguration has been used to strengthen the framework to remain PSPACE-complete for graph of bounded bandwidth [51]. Moreover, H-Word Reconfiguration has been generalized to Even/Odd Word Reconfiguration, in which even and odd positions can be treated independently; this variant has been used for proving the PSPACE-completeness of reachability for Independent Set Reconfiguration under TS for bipartite graphs [52].
4. Analysis Using Graph Classes for Independent Set
In this section, we focus on the complexity of reachability of Independent Set Reconfiguration for various choices of graph classes and reconfiguration steps. The problem was proposed as a natural extension of token-sliding puzzles with the added constraint that all tokens form an independent set (a subset of the vertices such that there is no edge between any pair of vertices in the set) [16]. Early results established the PSPACE-completeness of the problem under TS [16] and TAR [4]. Moreover, it was shown that there exists a reconfiguration sequence under TJ using k tokens if and only if there exists a sequence under TAR for bound , proving the equivalence of TJ and TAR for both reachability and shortest transformation [17].
Subsequent (and ongoing) research has focused on the question of the boundaries between tractability and intractability for the source problem based on various graph classes, both to determine whether the boundaries are the same for the source problem and for reachability, and to determine whether the boundaries for reachability are the same for both TS and TAR/TJ. Analyses of this type have also been considered for other problems for which reachability is PSPACE-complete on general graphs, including Clique Reconfiguration [53], Cluster Vertex Deletion Reconfiguration [53], Dominating Set Reconfiguration [50], and Vertex Cover Reconfiguration (discussed in more detail in Section 5).
Figure 5 and Table 1 represent the results known so far. For both TS and TAR/TJ, there exist classes of graphs (such as perfect graphs and graphs of bounded bandwidth) for which the source problem can be solved in polynomial time, but reachability is PSPACE-complete. Although this makes clear that the dividing lines are not the same for the source problem and for reachability, it remains to be determined exactly where and why the boundaries diverge. Similarly, the result on bipartite graphs shows that boundaries are not identical for TS and TAR/TJ, but still leaves open the underlying cause of the difference, as well as its extent. Restriction to even-hole-free graphs is also of interest, as the complexity is unknown for both the source problem and under TS, but polynomial-time algorithms are possible under TAR/TJ.
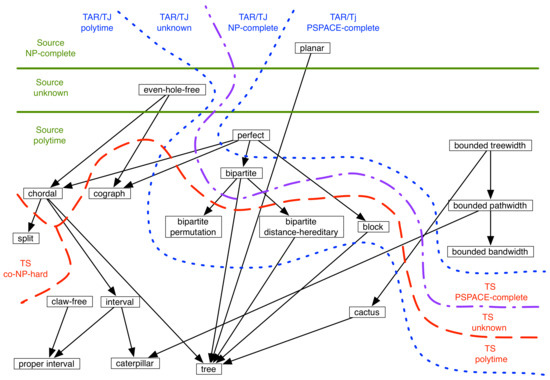
Figure 5.
Complexity of reachability for Independent Set Reconfiguration; graph classes are divided by complexity for the source problem (solid lines), TAR/TJ (dotted lines), and TS (dashed lines). The dotted-and-dashed line is a dividing line for both TAR/TJ and TS.

Table 1.
Results on reachability for Independent Set Reconfiguration; question marks indicate problems for which there are no known complexity results.
Results on Independent Set Reconfiguration have not been confined to reachability. Polynomial-time algorithms have been developed for shortest transformation under TS for proper interval graphs, trivially perfect graphs, and caterpillars [58] (though NP-hard in general for all reconfiguration steps [17]), for connectivity under TS for interval graphs [56] and under TAR for cographs [55], and for finding an actual reconfiguration sequence under TS for trees (as an extension of the reachability algorithm) [59]. It has also been shown that there is an infinite family of instances on paths for which the length of the reconfiguration sequence is at least quadratic in the number of vertices [59]; in contrast, for every yes-instance of reachability on cographs, there is a bound on the length of the reconfiguration sequence [42] as well as a bound on the diameter for claw-free graphs [57]. In other work, the idea of reconfiguration of independent sets in graphs has been extended to reconfiguration of independent sets in matroids [64].
5. Parameterized Complexity (Independent Set and Vertex Cover)
Parameterized complexity offers a way of distinguishing among intractable problems by identifying situations in which the running time is tied to one or more parameters of the problem or instance. A problem is fixed-parameter tractable (or in the class FPT) if it can be solved in time , for n the size of the input, p a parameter, and f a computable function [65]. A parameterized algorithm makes it possible to associate the non-polynomial part of the running time with a parameter. Problems that are intractable with respect to fixed-parameter complexity are -hard for some .
Choosing the size of the solutions or a property of an instance (such as its treewidth or degree) as a parameter allows us to compare the parameterized complexity of reconfiguration with the parameterized complexity of the source problem. A further motivation for considering parameterized complexity follows from the observation that, in many cases, there appears to be a correlation between the diameter of the reconfiguration graph and the complexity of reachability. When polynomial diameter is associated with polynomial-time reachability algorithms and exponential diameter with PSPACE-completeness for reachability, it is natural to wonder whether the length of the shortest reconfiguration sequence (for which the diameter is an upper bound) plays a role in the complexity. Certainly, a bound on diameter implies a bound on the length of a reconfiguration sequence, which perhaps would imply a bound on the time to determine if one exists. This suggests that parameterizing by the length of the reconfiguration sequence might result in fixed-parameter algorithms for instances even when the diameter is not guaranteed to be polynomial. Prior to its use in reconfiguration, length was used to parameterize a problem by the number of moves in a solution to a puzzle (which can, in fact, be viewed as a reconfiguration sequence) [66].
With respect to classical complexity, results for Independent Set Reconfiguration and Vertex Cover Reconfiguration are interchangeable: we simply reinterpret the placement of tokens on vertices to indicate the subset of vertices not in the solution (recall that each edge has at least one endpoint in a vertex cover, so that the remaining vertices form an independent set). More precisely, for a given instance G, the reconfiguration graphs for G for Independent Set and Vertex Cover will be isomorphic under TJ and TS, as well as under TAR when the bound on the size of solutions to one problem is k and the bound on the size of solutions to the other problem is . The difference in the size of solutions required to translate between reconfiguration graphs of the two problems, while insignificant under classical complexity, reveals a more fundamental difference between the source problems with respect to fixed-parameter complexity. With respect to reachability there is a dividing line between the parameterized version of Independent Set, which is -hard, and Vertex Cover, which is in FPT, and is so amenable to algorithmic approaches that it has earned the moniker of “Drosophila” of fixed-parameter algorithmics [67]. Consequently, it would not be surprising to find a significant difference in the complexities of reachability for the two problems.
The relationship between Independent Set and Vertex Cover can be characterized in terms of a hereditary property (a property of a graph that is also a property of any of its induced subgraphs). The subset problem for hereditary property π is the problem of finding a subset of the vertices such that the subgraph induced on has property ; thus, Independent Set is the subset problem for being the absence of edges. For any hereditary property , we can define reconfiguration in terms of either a set of vertices U of size at most k such that the subgraph induced on U has property ( Subset Reconfiguration) or a set of vertices U of size at most k such that the subgraph induced on all vertices except those in U has property ( Deletion Reconfiguration). For the absence of edges, Subset Reconfiguration is Independent Set Reconfiguration and Deletion Reconfiguration is Vertex Cover Reconfiguration.
General results have been found for hereditary properties that satisfy certain conditions, relating the complexity of Subset Reconfiguration and Deletion Reconfiguration under TAR to the complexity of the subset problem for . Determining if there is a reconfiguration sequence of length at most ℓ for Subset Reconfiguration parameterized by or for Deletion Reconfiguration parameterized by ℓ is at least as hard as the source subset problem [68]. Subsequent work focused on connected hereditary properties, considering the reconfiguring of induced trees [69]. Due to the -hardness of Independent Set, reachability is -hard for Independent Set Reconfiguration parameterized by and for Vertex Cover Reconfiguration parameterized by ℓ. Although this does not immediately imply a difference in the parameterized complexity of the two problems, further results, discussed later, do.
One of the common algorithmic paradigms for fixed-parameter algorithms, kernelization, has been adapted to form a reconfiguration kernel, used to obtain fixed-parameter reachability algorithms for Bounded Hitting Set Reconfiguration, Vertex Cover Reconfiguration, and Feedback Vertex Set Reconfiguration under TAR, all parameterized by the solution size [70]. Although every problem in FPT can be shown to have a kernel, because kernels often represent only minimal or maximal solutions to the problem, whereas a reconfiguration sequence under TAR may make use of non-optimal solutions, the translation is not immediate [70]. In fact, it has been shown that there exists a source problem (Cluster Graph Reconfiguration) which, although in FPT when parameterized by k, is -hard for reachability even when parameterized by both k and ℓ [70] (a hardness result on multiple parameters immediately implies hardness on a smaller number of parameters).
The results on Vertex Cover Reconfiguration and Independent Set Reconfiguration mentioned above indicate a difference in complexity when parameterized by the solution size, as the former is in FPT using a reconfiguration kernel and the latter is -hard using the general result on hereditary properties. Further work on Vertex Cover Reconfiguration has demonstrated that although it is -hard when parameterized by ℓ [70] (by the general result on hereditary properties), it is in FPT when parameterized by ℓ and the treewidth of the instance [49]. As Vertex Cover is fixed-parameter tractable on general graphs, one might imagine that the boundary between tractability and intractability of the source problem could predict the parameterized complexity of reachability on various graph classes, parameterized by ℓ. To the contrary, although Vertex Cover is NP-complete when restricted to planar graphs, reachability is in FPT parameterized by ℓ for planar graphs [49] and graphs of degree at most d, [54]. In contrast, despite the polynomial-time algorithm for Vertex Cover on bipartite graphs, reachability is -hard when parameterized by ℓ [54].
The parameterized complexity of Independent Set Reconfiguration has been considered under both TS and TAR/TJ; as in the case of classical complexity, TAR and TJ are equivalent. By the general result for subset problems with hereditary properties, it is -hard parameterized by for TAR, and hence parameterized by k [70]; the result carries over for TJ, and was also shown directly [71]. The problem has been shown to be in FPT when restricted to graphs of bounded degree [71] and planar graphs (or, stated more generally, graphs excluding as a subgraph, for any fixed ) [72]. The latter result was further generalized to graphs forbidding as a minor for fixed [73], and the results both on graphs of bounded degree and on planar graphs are implied by an FPT algorithm for the class of nowhere dense graphs [74]. An FPT algorithm was also developed for the incomparable class of graphs of bounded degeneracy, where the degeneracy (or coloring number) of G is the maximum over all subgraphs H of G of the minimum degree of H [74]. In addition, under TS, reachability has been shown to be not only co-NP-hard but also co-W[2]-hard on split graphs [56].
Parameterized complexity has also been used to analyze the problems Dominating Set Reconfiguration [74] and List Coloring Reconfiguration [75]; the results on nowhere dense graphs have also been applied to the more general problems of Distance-r Independent Set Reconfiguration and Distance-r Dominating Set Reconfiguration [76].
6. Connectivity and Diameter for -Coloring
Inspired by an application of coloring related to the rapid mixing of Markov chains, connectivity of the reconfiguration graph for k-Coloring has been studied extensively under the name k-Mixing [77]; each solution is an assignment of each vertex to one of k colors such that each edge has endpoints with different colors, and a reconfiguration step is the changing of a color of one vertex. We first focus on connectivity, diameter, reachability, and shortest transformation in Section 6.1, thereafter considering variants on problems and reconfiguration steps in Section 6.2.
6.1. k-Coloring Reconfiguration
To get a sense of the importance of the choice of k for connectivity and diameter, we consider both large and small values of k. When k is sufficiently large, the reconfiguration graph is connected and has diameter linear in the number of vertices: each vertex is first recolored to a distinct color not used in either the source or target solution, and then is recolored to its target color. At the other extreme, consider an even cycle and ; in this case, k is equal to , the chromatic number of G (the smallest number of colors for which it is possible to find a coloring of G); no vertex of the cycle can be recolored.
Early results in the area focused on the difference between small and large values of k, such as by showing that for , the reconfiguration graph is not connected for [31]. This left open the question of connectivity of bipartite graphs () for ; the yes-instances were characterized, and it was shown that the problem of deciding connectedness for bipartite graphs is coNP-complete, but restricted to planar bipartite graphs can be solved in polynomial time [78]. For , it was shown that the diameter is in for each connected component (and that this bound is tight, as there exist configurations at distance ), and that both reachability and shortest transformation can be solved in polynomial time [32]. In contrast, for , there are both yes-instances and no-instances for connectivity [31], and there exists a family of graphs and a such that for every graph in the family there exist components of diameter superpolynomial in [35]. Moreover, for , reachability is strongly NP-hard [79] and PSPACE-complete, even for bipartite graphs, planar graphs for , and bipartite planar graphs for [35].
We can consider the relationship between k and various properties of the instance, related to but distinct from the chromatic number. One choice is the maximum degree, , as it is known that the chromatic number of G is at most unless G is a complete graph or a cycle with an odd number of vertices [80]. Recall that the degeneracy, , is the largest minimum degree of any subgraph of G; the degeneracy of G is an upper bound on its maximum degree, and the treewidth of G, , is an upper bound on . More precisely, for any connected graph that is not regular, [81], and the chromatic number is at most one greater than the degeneracy. Yet another property of use is the Grundy number, , defined as the largest possible number of colors used by a greedy coloring of G; . It has been shown that for every graph, the reconfiguration graph is connected when [82], and in fact for [83]. Investigations into c-color-dense graphs proved that the reconfiguration graph is connected for chordal and chordal bipartite graphs [84], subsequently generalized to hold for any [85] and [85].
So far, there are no known families where the reconfiguration graph is connected and of superpolynomial diameter; in fact, Cereceda [77,78] conjectured that for , the diameter of the reconfiguration graph is in , and showed that the conjecture is true for the values and [77]. The results on connectivity also showed quadratic bounds on diameter, including a lower bound on diameter for chordal graphs, culminating in the proof of the conjecture for [85]. Subsequently, the conjecture was proved for and ; in this case, the reconfiguration graph consists of isolated vertices and one more component, with diameter [81]. It was further observed that by increasing the number of colors, it is possible to obtain linear diameter, in particular, for every [86].
For , defined to be the maximum average degree of a non-empty induced subgraph of G, [86], it has been shown that, for every integer and every , there exists such that for every G such that and every , the diameter is in [86]. As a consequence of the result on maximum average degree, since every planar graph has , the diameter is polynomial for every [86], providing support for the planar graph version of Cereceda’s conjecture, which states that, if G is planar, then for any , the diameter is polynomial [85].
Algorithmic results focus on both reachability and finding a reconfiguration sequence. For bounded-degree graphs, reachability can be solved in constant time when , linear time when and , and quadratic time when and [81]. With respect to parameterized complexity, the problem is fixed-parameter tractable when parameterized by (where ℓ is the length of the reconfiguration sequence) [79,87] but -hard when parameterized by ℓ alone [79]. The problem of finding a path for was shown to be solvable in quadratic time for any G such that and [80]; by a recent result applying to -regular graphs, the result was extended to hold for any connected graph with [88].
6.2. Variants of Coloring
We first consider an alternate choice of reconfiguration step, and then consider related problems using coloring. Instead of recoloring a single vertex at one step, a Kempe change, introduced by Kempe in his attempted proof of the Four Color Theorem [89], consists of exchanging the colors of all vertices in a connected component in the subgraph induced on vertices using a particular pair of colors. Such recolorings have been used in the proof of the Five Color Theorem, Vizing’s Edge-Coloring Theorem, in theoretical physics, and in the determination of timetables [90].
The reconfiguration graph under Kempe changes is connected for the following cases: for Eulerian triangulation of the plane [91], for planar graphs [92], generalized to for planar graphs [93] and for -minor free graphs [94], and all colorings of a perfectly contractile graph [95]. Edge-coloring has also been considered under the same reconfiguration rule [93,96,97].
When restricted to k-regular graphs, Mohar conjectured that the reconfiguration graph is connected for , except when the instance is a clique on vertices [93], and although it was shown to be false for for the triangular prism [14], further investigations have focused on finding cases in which it holds. The conjecture was proved for [98], and eventually it was shown that the triangular prism and are the only 3-regular graphs for which the reconfiguration graph for is not connected [99].
In List Coloring Reconfiguration [35], a generalization of k-Coloring Reconfiguration, each vertex v is supplied with a list of allowable colors. Early results in the area were obtained by generalizing results on k-Coloring Reconfiguration: the polynomial-time reachability algorithm for can be extended to this variant [32], and the reconfiguration graph is connected when the size of each list is at least [83]. The reachability problem for List Coloring Reconfiguration has been shown to be PSPACE-complete for graphs of bounded bandwidth [47] as well as for complete split graphs (with modular-width zero) [44], and to be -hard parameterized by size of minimum vertex cover [75]. Fixed-parameter algorithms have been found when parameterized by (where ℓ is the length of the reconfiguration sequence) [79,87], parameterized by k and modular-width of the input graph (and hence for cographs when parameterized by k) [75], and for shortest transformation, parameterized by k and the size of the minimum vertex cover (and hence for split graphs parameterized by k) [75]. Other variants for which reconfiguration has been studied include List Edge-Coloring [36,40,100], List(2,1)-Labeling [37], Circular Coloring [101,102], Acyclic Coloring [103], and Equitable Coloring [103]. The problem of k-Coloring Reconfiguration can also be seen as a special case of Homomorphism Reconfiguration [101,104] and Constraint Satisfaction Reconfiguration (Section 8).
7. Other Structural Problems
In other work, various properties of reconfiguration graphs have been investigated, both towards an understanding of connectivity or diameter (such as the characterization of isolated vertices [105], also known as frozen configurations [31]) and in their own right. Most work on such questions has focused on Dominating Set Reconfiguration and k-Coloring Reconfiguration, including variants in which j vertices can be colored in a single reconfiguration step [20] as well as one in which only canonical colorings, non-isomorphic colorings that are lexicographically least under an ordering of the vertices, are considered [106]. Results have also been obtained for Shortest Path Reconfiguration [107], Independent Set Reconfiguration [108], and Token Sliding [109], as defined in Section 9.2. Examples of properties that have been studied include chromatic number [109], Hamiltonicity [20,106,109,110,111,112], and girth [107,113], often in service of determining limits on the classes of graphs represented by reconfiguration graphs [108,113,114,115]. For a source problem in which the instance is a graph, one can also identify when the reconfiguration graph for an instance is isomorphic to the instance itself [114,115].
In the remainder of this section, we focus on Dominating Set (the problem of determining a set of vertices such that each vertex in the graph is either in the set or the neighbor of a vertex in the set); its wide applicability and amenability to variants has led to significant interest in reconfiguration graphs and their structure. Two different graphs with similar names have been based on the domination number, where is the minimum cardinality of a dominating set of G and a γ set is a dominating set of minimum cardinality. The graph [116] uses under TJ, whereas the -graph of G uses under TS [117], later considered for different variants such as the total dominating number, paired domination number, and connected dominating number [118]. Work on both the TJ model [119,120,121,122,123,124,125] and the TS model [126] has focused on characterizing which graphs are gamma graphs under the various definitions.
Haas and Seyffarth considered a reconfiguration graph in which solutions are not limited to minimum cardinality dominating sets; their k-dominating graph is a reconfiguration graph under TAR in which each solution is a dominating set of size at most k [114]. For , the upper domination number (the maximum cardinality of a minimal dominating set of G), the connectivity of the k-dominating graph has been shown for the following cases:
- [114],
- bipartite and chordal, when [114],
- and there is a matching of cardinality at least [127],
- for certain classes of well-covered graphs [128],
- for graphs that are both perfect and irredundant perfect [128].
In contrast, the k-dominating graph can be disconnected for , even for planar, bounded tree-width, or b-partite for [127]. In addition, there is an infinite family of graphs with exponential diameter for [127].
Under TAR, the reachability problem is PSPACE-complete even for graphs of bounded bandwidth, split graphs, planar graphs, and bipartite graphs [50], whereas linear-time algorithms have been developed for cographs, trees, and interval graphs [50]. Although -hard when parameterized by k, the problem is fixed-parameter tractable when parameterized by k when the input graph does not contain large bicliques (including bounded degeneracy and nowhere dense graphs) [74].
8. Shortest Transformation
Shortest transformation is a logical direction for investigation for problems once reachability has been solved, or as an outgrowth of work on reachability. We can find a lower bound on the length of a reconfiguration sequence in a simple way: we focus only on the type of reconfiguration step, and determine the number of steps required to change the source solution to the target solution, ignoring the feasibility of solutions as well as the source problem. For example, under TAR, the minimum number of steps is the number of vertices in the source solution but not the target solution (all of which need to be removed) plus the number of vertices in the target solution but not the source solution (all of which need to be added). For TS or TJ, the minimum number of steps is the number of vertices that differ in the source and target solutions. More generally, we refer to the parts of the solution that differ in the source and target solutions as the symmetric difference. Many of the algorithmic results on shortest transformation for special graphs classes result from the observation that reachability can be solved by changing only the symmetric difference. This raises the question of whether shortest transformation is possible in situations where it is necessary to change parts of the solutions outside of the symmetric difference.
The question is answered in the analysis of Satisfiability Reconfiguration, for which we consider the dividing lines between tractability and intractability of the source problem as well as for reachability and shortest transformation. Given that Satisfiability is NP-complete, it is not surprising to discover that reachability of Satisfiability Reconfiguration is PSPACE-complete [34]. To determine the dividing line between tractable and intractable classes of formulas for reachability, researchers have built on Schaefer’s dichotomy theorem [129] for the classical problem of Satisfiability. Schaefer [129] introduced a framework for expressing formulas in terms of Boolean relations, and proved the problem is in P for instances built from Schaefer relations and NP-complete for all other formulas in the framework.
In work by Gopalan et al. [34], later corrected by Schwerdtfeger [130], an analogous dichotomy theorem was obtained for the reachability problem. By defining the class of tight relations, a superset of the Schaefer relations, the authors were able to show that reachability is in P for formulas built from tight relations and PSPACE-complete for all other formulas in the framework. Moreover, they proved a dichotomy theorem for the connectivity problem, where the problem is in coNP for formulas built from tight relations and PSPACE-complete for all other formulas in the framework, and showed that the diameter of connected components is linear for tight relations but can be exponential otherwise. Subsequent work showed that reachability is co-NP-complete for some of the Schaefer relations (Horn and dual Horn) [131], that connectivity can be solved in polynomial time given a characteristic set of Horn relations [131], and that there is an exact algorithm for connectivity [132].
Mouawad, Nishimura, Pathak, and Raman [133] considered shortest transformation, and obtained a trichotomy, based on both tight relations and navigable relations, a subset of tight relations. They showed that the problem is in P for formulas built from navigable relations, NP-complete for formulas built from relations that are tight but not navigable, and PSPACE-complete otherwise. Of particular significance is the fact that the shortest transformation result holds even though more than the symmetric difference of the source and target solutions may need to be changed in the reconfiguration sequence.
Work on Satisfiability Reconfiguration was later generalized by Gharibian and Sikora to a quantum version [134] and by Wrochna to constraint satisfaction [47], where a constraint satisfaction problem consists of a set of variables and a set of constraints and a solution to the problem is an assignment of values to variables that satisfies all the constraints. Constraint satisfaction reachability was shown to be in FPT when parameterized by [79].
We have already seen how parameterized complexity has been used to handle the length of a reconfiguration sequence (Section 5). Not surprisingly, there have also been investigations into approximation algorithms that, instead of returning the length of the shortest sequence, determine a length that approximates the optimal. Such results have been found for Token Swapping (to be discussed in Section 9.2). As another example, we consider various results that involve the reconfigurations of triangulations (such as for polygons or sets of points in the plane), where the reconfiguration step is the flipping of a diagonal of a quadrilateral (Figure 6). After it was shown that the reconfiguration graph is always connected and the diameter quadratic [135], the focus has been on the shortest transformation (or Flip Distance) problem, which has been shown to be NP-complete [136] and inapproximable [137] but fixed-parameter tractable when parameterized by the length of the reconfiguration sequence [138].
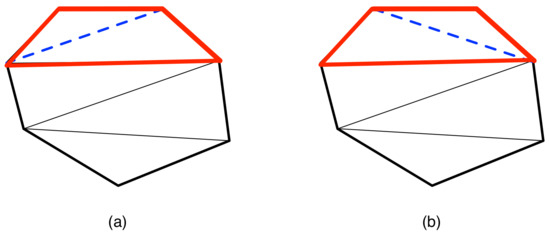
Figure 6.
(a) A triangulation, with one diagonal of a quadrilateral highlighted; (b) an adjacent triangulation, resulting from the reconfiguration step of flipping the diagonal.
9. Labels and Colors on Tokens
We return, at last, to the 15-puzzle, interpreted as a graph problem. In the years since it was first considered, curiosity about the problem has resulted in generalizing the problem, starting with problems using tiles arranged in a square and moving to arbitrary arrangements represented as graphs. The problem has since been generalized further and has been applied to various scenarios, such as sorting [139] and robot motion [140,141]. Other variants have considered different ways of defining reconfiguration steps, including the sliding of a token any distance along a path unoccupied by tokens [142], the movement of a token along a path by a sequence of swaps [143], and the sliding and rotation of squares [144], as well as the consideration of directed graphs [141].
In the remainder of our discussion, we focus on undirected graphs and the movement of a token along an edge in a single reconfiguration step. In Section 9.1, we explore in more detail various generalizations of the 15-puzzle, and, in Section 9.2, we investigate problems in which tokens are placed on all vertices. The results in this section should serve as an indication of the wealth of research directions possible when problems are generalized and when different definitions of feasible solutions are considered. Although the representation of feasible solutions as tokens on vertices has been used in the investigation of most source graph problems, most such research considers only the case of indistinguishable tokens. Labeled solutions have been considered for the reconfiguration of triangulations of point sets in the plane [145] as well as for the reconfigurations of subgraphs [22] and minors [146]. While using distinct or colored tokens does not apply to all source problems, there remains substantial scope for further investigations in this direction.
9.1. Generalizing the 15-Puzzle
The literature on generalizations to the 15-puzzle is a study in the evolution of a problem and in the use of labeled tokens; as a rare example of a problem studied in such depth, it serves as a model for investigations of other source problems. Here, we focus on developments rather than details of results, which are summarized in Table 2 and discussed in van den Heuvel’s survey [14]. Quantities for algorithmic problems indicate running times, and for diameter indicate bounds on diameter.

Table 2.
Results on the 15-puzzle and generalizations.
When the 15-puzzle was reinterpreted as a problem on graphs, investigations expanded from grids to general graphs, and instead of requiring exactly one vertex without a token (a hole), multiple holes were allowed. The column for Type in the figure indicates variants where, in addition to viewing each token as distinct (type “distinct”), tokens have been labeled as a single robot and indistinguishable obstacles (type “robot”), considered as indistinguishable (type “same”), or assigned colors such that tokens with the same color are indistinguishable (type “color”).
9.2. Placing Tokens on All Vertices
Inspired by sorting networks, further research has considered the case in which the number of tokens is equal to the number of vertices in the graph. In this case, the reconfiguration step swaps tokens on a pair of adjacent vertices with distinct labels. Research in the area considers two variants: one in which all tokens are distinct, and one in which each token has a specified color, where the number of colors can be smaller than the number of vertices.
When the tokens are all distinct, the reconfiguration graph is connected and has diameter in [155]. Determining the shortest transformation sequence, Token Swapping, is NP-complete [156], even on graphs of treewidth at most two [157], -hard with respect to the length of the reconfiguration sequence [157], and inapproximable [156]. Algorithmic results include polynomial-time solutions on paths [82], cycles [82], complete graphs [158], stars [159], complete bipartite graphs [139], and complete split graphs [160], as well as approximation algorithms for squares of paths [161], trees [139,156], and general graphs [156], fixed-parameter algorithms for nowhere dense graphs, which include planar graphs and graphs of bounded treewidth [157], and exact algorithms (with matching lower bounds) [156].
In a variant, others consider the problem of shortest transformation when all vertices have tokens, tokens can have different colors, but tokens of the same color are indistinguishable. In contrast to Token Swapping, for which no general hardness result is known, here the problem is NP-complete for at least three colors even for connected planar bipartite graphs of maximum degree four. A polynomial-time algorithm has been found for the case with two colors, and a linear-time algorithm for trees [162]. In addition, it has been shown that the reconfiguration graph is connected when there are at least three colors, G is not a cycle, and G has no -isthmus (where is the size of the largest color class), and the number of connected components has been determined for various cases [163]. In “parallel” variants, swapping is allowed on non-adjacent edges at the same time; the problem of determining the minimum number of swaps needed has been shown to be NP-complete, with a polynomial-time approximation algorithm for paths, and NP-complete for colored tokens, even with as few as two colors [164]. Various results have been shown for a “subset” variant, in which each token has a set of possible destinations [157].
10. Further Research Directions
Reconfiguration provides fertile ground for further research, both in general understanding of the framework and on specific source problems. For example, general algorithmic approaches remain elusive, with one of the current sources of algorithms being the generalization of problems known to have polynomial reachability algorithms, such as Matching Reconfiguration, which has been generalized to specifying upper and lower bounds on each vertex [23] as well as by allowing edges to be chosen more than once [165]. Although there is partial progress in determining dividing lines between tractable and intractable instances for reachability, further work is needed to determine the reasons behind differences in the dividing lines, as well as between dividing lines for different definitions of adjacency and different graph classes.
For many source problems, most of the reconfiguration problems, especially structural ones, have received little attention. In addition, only a few problems have been approached using the tools of approximation and parameterized complexity; for the latter, a greater variety of parameters can be considered, as has been done so far only for List Coloring Reconfiguration [75]. As sparse as the work in considering different definitions of adjacency may be, the work on different definitions of feasible solutions is even more meager.
Another direction for further research is the consideration of a wider range of source problems. Although much of the work has focused on graph problems, already work has considered other domains, such as matroids [4,64,166]. In many cases, the barrier to considering the reconfiguration of a problem stems from the difficulty in determining how to define feasible solutions or adjacency. When a solution represents a class of possible graphs, reconfiguration can be used to consider graph editing problems [167]. Particularly challenging are solutions that can be defined as sequences, such as in String Editing; results in the reconfiguration of sequences would permit the reconfiguration of reconfiguration sequences, and hence reconfiguration itself [21].
Acknowledgments
Research supported by the Natural Sciences and Engineering Research Council of Canada, including funds to cover the costs of publishing in open access.
Conflicts of Interest
The author declares no conflict of interest.
References
- Alamdari, S.; Angelini, P.; Barrera-Cruz, F.; Chan, T.M.; Da Lozzo, G.; Di Battista, G.; Frati, F.; Haxell, P.; Lubiw, A.; Patrignani, M.; et al. How to Morph Planar Graph Drawings. SIAM J. Comput. 2017, 46, 824–852. [Google Scholar] [CrossRef]
- Connelly, R.; Demaine, E.D.; Rote, G. Blowing Up Polygonal Linkages. Discret. Comput. Geom. 2003, 30, 205–239. [Google Scholar] [CrossRef]
- Johnson, W.W.; Story, W.E. Notes on the “15” Puzzle. Am. J. Math. 1879, 2, 397–404. [Google Scholar] [CrossRef]
- Ito, T.; Demaine, E.D.; Harvey, N.J.A.; Papadimitriou, C.H.; Sideri, M.; Uehara, R.; Uno, Y. On the complexity of reconfiguration problems. Theor. Comput. Sci. 2011, 412, 1054–1065. [Google Scholar] [CrossRef]
- Ahuja, R.K.; Ergun, O.; Orlin, J.B.; Punnen, A.P. A survey of very large-scale neighborhood search techniques. Discret. Appl. Math. 2002, 123, 75–102. [Google Scholar] [CrossRef]
- Fellows, M.R.; Fomin, F.V.; Lokshtanov, D.; Rosamond, F.; Saurabh, S.; Villanger, Y. Local Search: Is Brute-force Avoidable? J. Comput. Syst. Sci. 2012, 78, 707–719. [Google Scholar] [CrossRef]
- Gaspers, S.; Kim, E.J.; Ordyniak, S.; Saurabh, S.; Szeider, S. Don’t Be Strict in Local Search! In Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence, Toronto, ON, Canada, 22–26 July 2012; pp. 486–492. [Google Scholar]
- Gutin, G.; Punnen, A.P. (Eds.) The Traveling Salesman Problem and Its Variations; Combinatorial Optimization, Kluwer Academic: Dordrecht, UK, 2002. [Google Scholar]
- Archetti, C.; Bertazzi, L.; Speranza, M.G. Reoptimizing the traveling salesman problem. Networks 2003, 42, 154–159. [Google Scholar] [CrossRef]
- Shachnai, H.; Tamir, G.; Tamir, T. A Theory and Algorithms for Combinatorial Reoptimization. In Proceedings of the 10th Latin American Symposium on LATIN 2012: Theoretical Informatics, Arequipa, Peru, 16–20 April 2012; pp. 618–630. [Google Scholar]
- Mans, B.; Mathieson, L. Incremental Problems in the Parameterized Complexity Setting. Theory Comput. Syst. 2017, 60, 3–19. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W. H. Freeman & Co.: New York, NY, USA, 1990. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Van den Heuvel, J. The complexity of change. In Surveys in Combinatorics 2013; Cambridge University Press: Cambridge, UK, 2013; Volume 409, pp. 127–160. [Google Scholar]
- Mouawad, A.E. On Reconfiguration Problems: Structure and Tractability. Ph.D. Thesis, University of Waterloo, Waterloo, ON, Canada, 2015. [Google Scholar]
- Hearn, R.A.; Demaine, E.D. PSPACE-completeness of sliding-block puzzles and other problems through the nondeterministic constraint logic model of computation. Theor. Comput. Sci. 2005, 343, 72–96. [Google Scholar] [CrossRef]
- Kamiński, M.; Medvedev, P.; Milanič, M. Complexity of independent set reconfigurability problems. Theor. Comput. Sci. 2012, 439, 9–15. [Google Scholar] [CrossRef]
- Kamiński, M.; Medvedev, P.; Milanič, M. Shortest paths between shortest paths. Theor. Comput. Sci. 2011, 412, 5205–5210. [Google Scholar] [CrossRef]
- De Berg, M.; Jansen, B.M.P.; Mukherjee, D. Independent-Set Reconfiguration Thresholds of Hereditary Graph Classes. In Proceedings of the 36th IARCS Annual Conference on Foundations of Software Technology and Theoretical Computer Science, FSTTCS 2016, Chennai, India, 13–15 December 2016. [Google Scholar]
- McDonald, D.C. Connectedness and Hamiltonicity of graphs on vertex colorings. arXiv, 2015; arXiv:1507.05344. [Google Scholar]
- Fernau, H.; Haas, R.; Nishimura, N.; Seyffarth, K. Private Discussion, 2017.
- Hanaka, T.; Ito, T.; Mizuta, H.; Moore, B.; Nishimura, N.; Subramanya, V.; Suzuki, A.; Vaidyanathan, K. Reconfiguring spanning and induced subgraphs. arXiv, 2018; arXiv:1803.06074. [Google Scholar]
- Mühlenthaler, M. Degree-contrained Subgraph Reconfiguration is in P. In Proceedings of the 40th International Symposium on Mathematical Foundations of Computer Science, Milan, Italy, 24–28 August 2015; pp. 505–516. [Google Scholar]
- Hatanaka, T. Private Communication, 2017.
- Felsner, S.; Huemer, C.; Saumell, M. Recoloring Directed Graphs. In Proceedings of the XIII Encuentros de Geometría Computacional, Zaragoza, Spain, 29 June–1 July 2009; pp. 91–97. [Google Scholar]
- Garnero, V.; Junosza-Szaniawski, K.; Liedloff, M.; Montealegre, P.; Rzążewski, P. Fixing improper colorings of graphs. Theor. Comput. Sci. 2018, 711, 66–78. [Google Scholar] [CrossRef]
- Ito, T.; Ono, H.; Otachi, Y. Reconfiguration of Cliques in a Graph. In Proceedings of the 12th Annual Conference on Theory and Applications of Models of Computation, Singapore, 18–20 May 2015; pp. 212–223. [Google Scholar]
- Ito, T.; Nooka, H.; Zhou, X. Reconfiguration of Vertex Covers in a Graph. IEICE Trans. 2016, 99-D, 598–606. [Google Scholar] [CrossRef]
- Ausiello, G. Complexity and Approximation: Combinatorial Optimization Problems and Their Approximability Properties; Springer: Berlin, Germany, 1999. [Google Scholar]
- Ito, T.; Demaine, E.D. Approximability of the subset sum reconfiguration problem. J. Comb. Optim. 2014, 28, 639–654. [Google Scholar] [CrossRef]
- Cereceda, L.; van den Heuvel, J.; Johnson, M. Connectedness of the graph of vertex-colourings. Discret. Math. 2008, 308, 913–919. [Google Scholar] [CrossRef]
- Cereceda, L.; van den Heuvel, J.; Johnson, M. Finding paths between 3-colorings. J. Graph Theory 2011, 67, 69–82. [Google Scholar] [CrossRef]
- Johnson, M.; Kratsch, D.; Kratsch, S.; Patel, V.; Paulusma, D. Finding Shortest Paths Between Graph Colourings. In Proceedings of the 9th International Symposium on Parameterized and Exact Computation, IPEC 2014, Wroclaw, Poland, 10–12 September 2014; pp. 221–233. [Google Scholar]
- Gopalan, P.; Kolaitis, P.G.; Maneva, E.N.; Papadimitriou, C.H. The connectivity of Boolean satisfiability: Computational and structural dichotomies. SIAM J. Comput. 2009, 38, 2330–2355. [Google Scholar] [CrossRef]
- Bonsma, P.S.; Cereceda, L. Finding Paths between graph colourings: PSPACE-completeness and superpolynomial distances. Theor. Comput. Sci. 2009, 410, 5215–5226. [Google Scholar] [CrossRef]
- Ito, T.; Kamiński, M.; Demaine, E.D. Reconfiguration of list edge-colorings in a graph. Discret. Appl. Math. 2012, 160, 2199–2207. [Google Scholar] [CrossRef]
- Ito, T.; Kawamura, K.; Ono, H.; Zhou, X. Reconfiguration of list L(2,1)-labelings in a graph. Theor. Comput. Sci. 2014, 544, 84–97. [Google Scholar] [CrossRef]
- Mizuta, H.; Ito, T.; Zhou, X. Reconfiguration of Steiner Trees in an Unweighted Graph. In Proceedings of the 27th International Workshop on Combinatorial Algorithms, IWOCA 2016, Helsinki, Finland, 17–19 August 2016; pp. 163–175. [Google Scholar]
- Bonsma, P.S. The complexity of rerouting shortest paths. In Proceedings of the 37th International Symposium on Mathematical Foundations of Computer Science, Bratislava, Slovakia, 27–31 August 2012; pp. 222–233. [Google Scholar]
- Osawa, H.; Suzuki, A.; Ito, T.; Zhou, X. The complexity of (list) edge-coloring reconfiguration problem. In Proceedings of the 11th International Conference and Workshops on Algorithms and Computation, Limerick, Ireland, 16–20 January 2017. [Google Scholar]
- Diestel, R. Graph Theory; Electronic Edition; Springer: Berlin, Germany, 2005. [Google Scholar]
- Bonsma, P.S. Independent Set Reconfiguration in Cographs and their Generalizations. J. Graph Theory 2016, 83, 164–195. [Google Scholar] [CrossRef]
- Bonsma, P.S. Rerouting shortest paths in planar graphs. In Proceedings of the IARCS Annual Conference on Foundations of Software Technology and Theoretical Computer Science, FSTTCS 2012, Hyderabad, India, 15–17 December 2012; pp. 337–349. [Google Scholar]
- Hatanaka, T.; Ito, T.; Zhou, X. The List Coloring Reconfiguration Problem for Bounded Pathwidth Graphs. IEICE Trans. 2015, 98-A, 1168–1178. [Google Scholar] [CrossRef]
- Bonsma, P.S.; Paulusma, D. Using Contracted Solution Graphs for Solving Reconfiguration Problems. In Proceedings of the 41st International Symposium on Mathematical Foundations of Computer Science, MFCS 2016, Kraków, Poland, 22–26 August 2016. [Google Scholar]
- Schiex, T. A Note on CSP Graph Parameters; Technical Report 1999/03; French National Institute for Agricultural Research (INRA): Paris, France, 1999. [Google Scholar]
- Wrochna, M. Reconfiguration in bounded bandwidth and tree-depth. J. Comput. Syst. Sci. 2018, 93, 1–10. [Google Scholar] [CrossRef]
- Post, E.L. Recursive unsolvability of a problem of Thue. J. Symb. Log. 1947, 12, 1–11. [Google Scholar] [CrossRef]
- Mouawad, A.E.; Nishimura, N.; Raman, V.; Wrochna, M. Reconfiguration over Tree Decompositions. In Proceedings of the 9th International Symposium on Parameterized and Exact Computation, IPEC 2014, Wroclaw, Poland, 10–12 September 2014; pp. 246–257. [Google Scholar]
- Haddadan, A.; Ito, T.; Mouawad, A.E.; Nishimura, N.; Ono, H.; Suzuki, A.; Tebbal, Y. The complexity of dominating set reconfiguration. Theor. Comput. Sci. 2016, 651, 37–49. [Google Scholar] [CrossRef]
- Van der Zanden, T.C. Parameterized Complexity of Graph Constraint Logic. In Proceedings of the 10th International Symposium on Parameterized and Exact Computation, IPEC 2015, Patras, Greece, 16–18 September 2015; pp. 282–293. [Google Scholar]
- Lokshtanov, D.; Mouawad, A.E. The complexity of independent set reconfiguration on biparite graphs. In Proceedings of the 29th Annual ACM-SIAM Symposium on Discrete Algorithms, San Francisco, CA, USA, 20–22 January 2008. [Google Scholar]
- Tebbal, Y. On the Complexity of Reconfiguration of Clique, Cluster Vertex Deletion, and Dominating Set. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2015. [Google Scholar]
- Mouawad, A.E.; Nishimura, N.; Raman, V. Vertex Cover Reconfiguration and Beyond. In Proceedings of the 25th International Symposium on Algorithms and Computation, ISAAC 2014, Jeonju, Korea, 15–17 December 2014; pp. 452–463. [Google Scholar]
- Bonamy, M.; Bousquet, N. Reconfiguring Independent Sets in Cographs. CoRR, 2014; arXiv:1406.1433v1. [Google Scholar]
- Bonamy, M.; Bousquet, N. Token Sliding on Chordal Graphs. In Proceedings of the 43rd International Workshop on Graph-Theoretic Concepts in Computer Science (WG 2017), Eindhoven, The Netherlands, 21–23 June 2017; pp. 127–139. [Google Scholar]
- Bonsma, P.S.; Kaminski, M.; Wrochna, M. Reconfiguring Independent Sets in Claw-Free Graphs. In Proceedings of the 14th Scandinavian Symposium and Workshops on Algorithm Theory—SWAT 2014, Copenhagen, Denmark, 2–4 July 2014; pp. 86–97. [Google Scholar]
- Yamada, T.; Uehara, R. Shortest Reconfiguration of Sliding Tokens on a Caterpillar. In Proceedings of the 10th International Workshop on WALCOM: Algorithms and Computation, WALCOM 2016, Kathmandu, Nepal, 29–31 March 2016; pp. 236–248. [Google Scholar]
- Demaine, E.D.; Demaine, M.L.; Fox-Epstein, E.; Hoang, D.A.; Ito, T.; Ono, H.; Otachi, Y.; Uehara, R.; Yamada, T. Linear-time algorithm for sliding tokens on trees. Theor. Comput. Sci. 2015, 600, 132–142. [Google Scholar] [CrossRef]
- Fox-Epstein, E.; Hoang, D.A.; Otachi, Y.; Uehara, R. Sliding Token on Bipartite Permutation Graphs. In Proceedings of the 26th International Symposium on Algorithms and Computation, ISAAC 2015, Nagoya, Japan, 9–11 December 2015; pp. 237–247. [Google Scholar]
- Hoang, D.A.; Uehara, R. Polynomial-Time Algorithms for Sliding Tokens on Cactus Graphs and Block Graphs. CoRR, 2017; arXiv:1705.00429v1. [Google Scholar]
- Hoang, D.A.; Fox-Epstein, E.; Uehara, R. Sliding Tokens on Block Graphs. In Proceedings of the 11th International Conference and Workshops on WALCOM: Algorithms and Computation, WALCOM 2017, Hsinchu, Taiwan, 29–31 March 2017; pp. 460–471. [Google Scholar]
- Hoang, D.A.; Uehara, R. Sliding Tokens on a Cactus. In Proceedings of the 27th International Symposium on Algorithms and Computation, ISAAC 2016, Sydney, Australia, 12–14 December 2016. [Google Scholar]
- Mühlenthaler, M. st-Connectivity of Common Independent Sets of Partition Matroids. unpublished. 2017. [Google Scholar]
- Downey, R.G.; Fellows, M.R. Parameterized Complexity; Springer: New York, NY, USA, 1997. [Google Scholar]
- Fernau, H.; Hagerup, T.; Nishimura, N.; Ragde, P.; Reinhardt, K. On the parameterized complexity of the generalized Rush Hour puzzle. In Proceedings of the 15th Canadian Conference on Computational Geometry, Halifax, Nova Scotia, 11–13 August 2003; pp. 6–9. [Google Scholar]
- Niedermeier, R. Invitation to Fixed-Parameter Algorithms; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Mouawad, A.E.; Nishimura, N.; Raman, V.; Simjour, N.; Suzuki, A. On the parameterized complexity of reconfiguration problems. In Proceedings of the 8th International Symposium on Parameterized and Exact Computation, Sophia Antipolis, France, 4–6 September 2013. [Google Scholar]
- Wasa, K.; Yamanaka, K.; Arimura, H. The Complexity of Induced Tree Reconfiguration Problems. In Proceedings of the 10th International Conference on Language and Automata Theory and Applications, LATA 2016, Prague, Czech Republic, 14–18 March 2016; pp. 330–342. [Google Scholar]
- Mouawad, A.E.; Nishimura, N.; Raman, V.; Simjour, N.; Suzuki, A. On the Parameterized Complexity of Reconfiguration Problems. Algorithmica 2017, 78, 274–297. [Google Scholar] [CrossRef]
- Ito, T.; Kaminski, M.; Ono, H.; Suzuki, A.; Uehara, R.; Yamanaka, K. On the Parameterized Complexity for Token Jumping on Graphs. In Proceedings of the 11th Annual Conference on Theory and Applications of Models of Computation, TAMC 2014, Chennai, India, 11–13 April 2014; pp. 341–351. [Google Scholar]
- Ito, T.; Kaminski, M.J.; Ono, H. Fixed-Parameter Tractability of Token Jumping on Planar Graphs. In Proceedings of the 25th International Symposium on Algorithms and Computation, ISAAC 2014, Jeonju, Korea, 15–17 December 2014; pp. 208–219. [Google Scholar]
- Bousquet, N.; Mary, A.; Parreau, A. Token Jumping in Minor-Closed Classes. In Proceedings of the 21st International Symposium on Fundamentals in Computation Theory (FCT 2017), Bordeaux, France, 11–13 September 2017; pp. 136–149. [Google Scholar]
- Lokshtanov, D.; Mouawad, A.E.; Panolan, F.; Ramanujan, M.S.; Saurabh, S. Reconfiguration on Sparse Graphs. In Proceedings of the 14th International Symposium on Algorithms and Data Structures, WADS 2015, Victoria, BC, Canada, 5–7 August 2015; pp. 506–517. [Google Scholar]
- Hatanaka, T.; Ito, T.; Zhou, X. Parameterized Complexity of the List Coloring Reconfiguration Problem with Graph Parameters. In Proceedings of the 42nd International Symposium on Mathematical Foundations of Computer Science (MFCS 2017), Liverpool, UK, 27–31 August 2017; pp. 51:1–51:13. [Google Scholar]
- Siebertz, S. Reconfiguration on nowhere dense graphs. CoRR, 2017; arXiv:1707.06775. [Google Scholar]
- Cereceda, L. Mixing Graph Colourings. Ph.D. Thesis, London School of Economics and Political Science, London, UK, 2007. [Google Scholar]
- Cereceda, L.; van den Heuvel, J.; Johnson, M. Mixing 3-colourings in bipartite graphs. Eur. J. Comb. 2009, 30, 1593–1606. [Google Scholar] [CrossRef]
- Bonsma, P.S.; Mouawad, A.E.; Nishimura, N.; Raman, V. The Complexity of Bounded Length Graph Recoloring and CSP Reconfiguration. In Proceedings of the 9th International Symposium on Parameterized and Exact Computation, IPEC 2014, Wroclaw, Poland, 10–12 September 2014; pp. 110–121. [Google Scholar]
- Brooks, R.L. On colouring the nodes of a network. Math. Proc. Camb. Philos. Soc. 1941, 37, 194–197. [Google Scholar] [CrossRef]
- Feghali, C.; Johnson, M.; Paulusma, D. A Reconfigurations Analogue of Brooks’ Theorem and Its Consequences. J. Graph Theory 2016, 83, 340–358. [Google Scholar] [CrossRef]
- Jerrum, M. A Very Simple Algorithm for Estimating the Number of k-Colorings of a Low-Degree Graph. Random Struct. Algorithms 1995, 7, 157–166. [Google Scholar] [CrossRef]
- Dyer, M.E.; Flaxman, A.D.; Frieze, A.M.; Vigoda, E. Randomly coloring sparse random graphs with fewer colors than the maximum degree. Random Struct. Algorithms 2006, 29, 450–465. [Google Scholar] [CrossRef]
- Bonamy, M.; Johnson, M.; Lignos, I.; Patel, V.; Paulusma, D. Reconfiguration graphs for vertex colourings of chordal and chordal bipartite graphs. J. Comb. Optim. 2014, 27, 132–143. [Google Scholar] [CrossRef]
- Bonamy, M.; Bousquet, N. Recoloring bounded treewidth graphs. Electron. Notes Discret. Math. 2013, 44, 257–262. [Google Scholar] [CrossRef]
- Bousquet, N.; Perarnau, G. Fast recoloring of sparse graphs. Eur. J. Comb. 2016, 52, 1–11. [Google Scholar] [CrossRef]
- Johnson, M.; Kratsch, D.; Kratsch, S.; Patel, V.; Paulusma, D. Finding Shortest Paths Between Graph Colourings. Algorithmica 2016, 75, 295–321. [Google Scholar] [CrossRef]
- Bonamy, M.; Dabrowski, K.K.; Feghali, C.; Johnson, M.; Paulusma, D. Recognizing Graphs Close to Bipartite Graphs with an Application to Colouring Reconfiguration. CoRR, 2017; arXiv:1707.09817v1. [Google Scholar]
- Kempe, A.B. On the geographical problem of the four colours. Am. J. Math. 1879, 2, 193–200. [Google Scholar] [CrossRef]
- Mühlenthaler, M.; Wanka, R. On the Connectedness of Clash-free Timetables. CoRR, 2015; arXiv:1507.02805. [Google Scholar]
- Fisk, S. Geometric coloring theory. Adv. Math. 1977, 24, 298–340. [Google Scholar] [CrossRef]
- Meyniel, H. Les 5-colorations d’un graphe planaire forment une classe de commutation unique. J. Comb. Theory Ser. B 1978, 24, 251–257. [Google Scholar] [CrossRef]
- Mohar, B. Kempe equivalence of colorings. In Graph Theory in Paris; Trends in Mathematics; Birkhauser: Basel, Switzerland, 2007; pp. 287–297. [Google Scholar]
- Vergnas, M.L.; Meyniel, H. Kempe classes and the Hadwiger Conjecture. J. Comb. Theory Ser. B 1981, 31, 95–104. [Google Scholar] [CrossRef]
- Bertschi, M.E. Perfectly contractile graphs. J. Comb. Theory Ser. B 1990, 50, 222–230. [Google Scholar] [CrossRef]
- McDonald, J.; Mohar, B.; Scheide, D. Kempe Equivalence of Edge-Colorings in Subcubic and Subquartic Graphs. J. Graph Theory 2012, 70, 226–239. [Google Scholar] [CrossRef]
- Belcastro, S.; Haas, R. Counting edge-Kempe-equivalence classes for 3-edge-colored cubic graphs. Discret. Math. 2014, 325, 77–84. [Google Scholar] [CrossRef]
- Bonamy, M.; Bousquet, N.; Feghali, C.; Johnson, M. On a conjecture of Mohar concerning Kempe equivalence of regular graphs. CoRR, 2015; arXiv:1510.06964. [Google Scholar]
- Feghali, C.; Johnson, M.; Paulusma, D. Kempe equivalence of colourings of cubic graphs. Eur. J. Comb. 2017, 59, 1–10. [Google Scholar] [CrossRef]
- Ito, T.; Kawamura, K.; Zhou, X. An Improved Sufficient Condition for Reconfiguration of List Edge-Colorings in a Tree. IEICE Trans. 2012, 95-D, 737–745. [Google Scholar] [CrossRef]
- Brewster, R.C.; Noel, J.A. Mixing Homomorphisms, Recolorings, and Extending Circular Precolorings. J. Graph Theory 2015, 80, 173–198. [Google Scholar] [CrossRef]
- Brewster, R.C.; McGuinness, S.; Moore, B.; Noel, J.A. A dichotomy theorem for circular colouring reconfiguration. Theor. Comput. Sci. 2016, 639, 1–13. [Google Scholar] [CrossRef]
- Vaidyanathan, K. Refiguring Graph Colorings. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2017. [Google Scholar]
- Wrochna, M. Homomorphism Reconfiguration via Homotopy. In Proceedings of the 32nd International Symposium on Theoretical Aspects of Computer Science, STACS 2015, Garching, Germany, 4–7 March 2015; pp. 730–742. [Google Scholar]
- Brewster, R.C.; Lee, J.B.; Moore, B.; Noel, J.A.; Siggers, M. Graph Homomorphism Reconfiguration and Frozen H-Colourings. arXiv, 2017; arXiv:1712.00200. [Google Scholar]
- Haas, R. The canonical coloring graph of trees and cycles. Ars Math. Contemp. 2012, 5, 149–157. [Google Scholar]
- Asplund, J.; Edoh, K.; Haas, R.; Hristova, Y.; Novick, B.; Werner, B. Reconfiguration graphs of shortest paths. CoRR, 2017; arXiv:1705.09385. [Google Scholar]
- Fatehi, D.; Alikhani, S.; Khalaf, A.J.M. The k-independent graph of a graph. Adv. Appl. Discret. Math. 2017, 18, 45–56. [Google Scholar] [CrossRef]
- Monroy, R.F.; Flores-Peñaloza, D.; Huemer, C.; Hurtado, F.; Urrutia, J.; Wood, D.R. Token Graphs. Graphs Comb. 2012, 28, 365–380. [Google Scholar] [CrossRef]
- Choo, K.; MacGillivray, G. Gray code numbers for graphs. Ars Math. Contemp. 2011, 4, 125–139. [Google Scholar]
- Celaya, M.; Choo, K.; MacGillivray, G.; Seyffarth, K. Reconfiguring k-colourings of complete bipartite graphs. Kyungpook Math. J. 2016, 56, 647–655. [Google Scholar] [CrossRef]
- Bard, S. Gray Code Numbers of Complete Multipartite Graphs. Master’s Thesis, University of Victoria, Victoria, BC, Canada, 2012. [Google Scholar]
- Beier, J.; Fierson, J.; Haas, R.; Russell, H.M.; Shavo, K. Classifying coloring graphs. Discret. Math. 2016, 339, 2100–2112. [Google Scholar] [CrossRef]
- Haas, R.; Seyffarth, K. The k-Dominating Graph. Graphs Comb. 2014, 30, 609–617. [Google Scholar] [CrossRef]
- Alikhani, S.; Fatehi, D.; Klavzar, S. On the Structure of Dominating Graphs. Graphs Comb. 2017, 33, 665–672. [Google Scholar] [CrossRef]
- Subramanian, K.; Sridharan, N. γ-graph of a graph. Bull. Kerala Math. Assoc. 2008, 5, 17–34. [Google Scholar]
- Fricke, G.; Hedetniemi, S.M.; Hedetniemi, S.T.; Hutson, K.R. γ-graphs of graphs. Discuss. Math. Graph Theory 2011, 31, 517–531. [Google Scholar] [CrossRef]
- Mynhardt, C.M.; Teshima, L.E. A note on some variations of the γ-graph. CoRR, 2017; arXiv:1707.02039. [Google Scholar]
- Edwards, M. Vertex-Criticality and Bicriticality for Independent Domination and Total Domination in Graphs. Ph.D. Thesis, University of Victoria, Victoria, BC, Canada, 2015. [Google Scholar]
- Lakshmanan, S.A.; Vijayakumar, A. The gamma graph of a graph. AKCE Int. J. Graphs Comb. 2010, 7, 53–59. [Google Scholar]
- Sridharan, N.; Subramanian, K. Trees and unicyclic graphs are γ-graphs. J. Comb. Math. Comb. Comput. 2009, 69, 231–236. [Google Scholar]
- Sridharan, N.; Amutha, S.; Rao, S.B. Induced subgraphs of gamma graphs. Discret. Math. Algorithms Appl. 2013, 5. [Google Scholar] [CrossRef]
- Dyck, A.; Jedwab, J.; DeVos, M.; Simon, S. The realisability of γ-graphs. unpublished. 2017. [Google Scholar]
- Dyck, A. The Realisability of γ-Graphs. Master’s Thesis, Simon Fraser University, Burnaby, BC, Canda, 2017. [Google Scholar]
- Bień, A. Gamma graphs of some special classes of trees. Ann. Math. Sil. 2015, 29, 25–34. [Google Scholar] [CrossRef]
- Connelly, E.; Hedetniemi, S.T.; Hutson, K. A note on γ-Graphs. AKCE Int. J. Graphs Comb. 2010, 8, 23–31. [Google Scholar]
- Suzuki, A.; Mouawad, A.E.; Nishimura, N. Reconfiguration of dominating sets. J. Comb. Optim. 2016, 32, 1182–1195. [Google Scholar] [CrossRef]
- Haas, R.; Seyffarth, K. Reconfiguring dominating sets in some well-covered and other classes of graphs. Discret. Math. 2017, 340, 1802–1817. [Google Scholar] [CrossRef]
- Schaefer, T.J. The Complexity of Satisfiability Problems. In Proceedings of the 10th Annual ACM Symposium on Theory of Computing, San Diego, CA, USA, 1–3 May 1978; pp. 216–226. [Google Scholar]
- Schwerdtfeger, K.W. A Computational Trichotomy for Connectivity of Boolean Satisfiability. J. Satisf. Boolean Model. Comput. 2014, 8, 173–195. [Google Scholar]
- Makino, K.; Tamaki, S.; Yamamoto, M. On the Boolean connectivity problem for Horn relations. Discret. Appl. Math. 2010, 158, 2024–2030. [Google Scholar] [CrossRef]
- Makino, K.; Tamaki, S.; Yamamoto, M. An exact algorithm for the Boolean connectivity problem for k-CNF. Theor. Comput. Sci. 2011, 412, 4613–4618. [Google Scholar] [CrossRef]
- Mouawad, A.E.; Nishimura, N.; Pathak, V.; Raman, V. Shortest Reconfiguration Paths in the Solution Space of Boolean Formulas. In Proceedings of the 42nd International Colloquium on Automata, Languages, and Programming, ICALP 2015, Kyoto, Japan, 6–10 July 2015; Part I. pp. 985–996. [Google Scholar]
- Gharibian, S.; Sikora, J. Ground State Connectivity of Local Hamiltonians. In Proceedings of the 42nd International Colloquium on Automata, Languages, and Programming, ICALP 2015, Kyoto, Japan, 6–10 July 2015; Part I. 2015; pp. 617–628. [Google Scholar]
- Lawson, C. Software for c1 surface interpolation. In Mathematical Software III; Academic Press: Cambridge, MA, USA, 1977; pp. 161–194. [Google Scholar]
- Lubiw, A.; Pathak, V. Flip distance between two triangulations of a point set is NP-complete. Comput. Geom. 2015, 49, 17–23. [Google Scholar] [CrossRef]
- Pilz, A. Flip distance between triangulations of a planar point set is APX-hard. Comput. Geom. 2014, 47, 589–604. [Google Scholar] [CrossRef]
- Kanj, I.A.; Xia, G. Flip Distance is in FPT time O(n + k · ck). In Proceedings of the 32nd International Symposium on Theoretical Aspects of Computer Science, STACS 2015, Garching, Germany, 4–7 March 2015; pp. 500–512. [Google Scholar]
- Yamanaka, K.; Demaine, E.D.; Ito, T.; Kawahara, J.; Kiyomi, M.; Okamoto, Y.; Saitoh, T.; Suzuki, A.; Uchizawa, K.; Uno, T. Swapping labeled tokens on graphs. Theor. Comput. Sci. 2015, 586, 81–94. [Google Scholar] [CrossRef]
- Papadimitriou, C.H.; Raghavan, P.; Sudan, M.; Tamaki, H. Motion Planning on a Graph (Extended Abstract). In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 511–520. [Google Scholar]
- Wu, Z.; Grumbach, S. Feasibility of motion planning on acyclic and strongly connected directed graphs. Discret. Appl. Math. 2010, 158, 1017–1028. [Google Scholar] [CrossRef]
- Călinescu, G.; Dumitrescu, A.; Pach, J. Reconfigurations in Graphs and Grids. SIAM J. Discret. Math. 2008, 22, 124–138. [Google Scholar] [CrossRef]
- Yamanaka, K.; Demaine, E.D.; Horiyama, T.; Kawamura, A.; Nakano, S.; Okamoto, Y.; Saitoh, T.; Suzuki, A.; Uehara, R.; Uno, T. Sequentially Swapping Colored Tokens on Graphs. In Proceedings of the 11th International Conference and Workshops on WALCOM: Algorithms and Computation (WALCOM 2017), Hsinchu, Taiwan, 29–31 March 2017; pp. 435–447. [Google Scholar]
- Dumitrescu, A.; Pach, J. Pushing Squares Around. Graphs Comb. 2006, 22, 37–50. [Google Scholar] [CrossRef]
- Lubiw, A.; Masárová, Z.; Wagner, U. Proof of the Orbit Conjecture for Flipping Edge-Labelled Triangulations. In Proceedings of the 33rd International Symposium on Computational Geometry, Brisbane, Australia, 4–7 July 2017. [Google Scholar]
- Moore, B.; Nishimura, N.; Subramanya, V. Reconfiguring minors. unpublished. 2018. [Google Scholar]
- Wilson, R.M. Graph puzzles, homotopy, and the alternating group. J. Comb. Theory Ser. B 1974, 16, 86–96. [Google Scholar] [CrossRef]
- Parberry, I. Solving the (n2 - 1)-Puzzle with 8/3 n3 Expected Moves. Algorithms 2015, 8, 459–465. [Google Scholar] [CrossRef]
- Ratner, D.; Warmuth, M.K. Finding a Shortest Solution for the N × N Extension of the 15-PUZZLE Is Intractable. In Proceedings of the 5th National Conference on Artificial Intelligence, Philadelphia, PA, USA, 11–15 August 1986; Volume 1, pp. 168–172. [Google Scholar]
- Goldreich, O. Finding the Shortest Move-Sequence in the Graph-Generalized 15-Puzzle Is NP-Hard. In Studies in Complexity and Cryptography. Miscellanea on the Interplay between Randomness and Computation—In Collaboration with Lidor Avigad, Mihir Bellare, Zvika Brakerski, Shafi Goldwasser, Shai Halevi, Tali Kaufman, Leonid Levin, Noam Nisan, Dana Ron, Madhu Sudan, Luca Trevisan, Salil Vadhan, Avi Wigderson, David Zuckerman; Springer: Berlin/Heidelberg, Gernamy, 2011; pp. 1–5. [Google Scholar]
- Kornhauser, D.; Miller, G.L.; Spirakis, P.G. Coordinating Pebble Motion on Graphs, the Diameter of Permutation Groups, and Applications. In Proceedings of the 25th Annual Symposium on Foundations of Computer Science, West Palm Beach, FL, USA, 24–26 October 1984; pp. 241–250. [Google Scholar]
- Auletta, V.; Monti, A.; Parente, M.; Persiano, P. A Linear-Time Algorithm for the Feasibility of Pebble Motion on Trees. Algorithmica 1999, 23, 223–245. [Google Scholar] [CrossRef]
- Goraly, G.; Hassin, R. Multi-Color Pebble Motion on Graphs. Algorithmica 2010, 58, 610–636. [Google Scholar] [CrossRef]
- Trakultraipruk, S. Connectivity Properties of Some Transformation Graphs. Ph.D. Thesis, London School of Economics and Political Science, London, UK, 2013. [Google Scholar]
- Akers, S.B.; Krishnamurthy, B. A Group-Theoretic Model for Symmetric Interconnection Networks. IEEE Trans. Comput. 1989, 38, 555–566. [Google Scholar] [CrossRef]
- Miltzow, T.; Narins, L.; Okamoto, Y.; Rote, G.; Thomas, A.; Uno, T. Approximation and Hardness of Token Swapping. In Proceedings of the 24th Annual European Symposium on Algorithms, ESA 2016, Aarhus, Denmark, 22–24 August 2016. [Google Scholar]
- Bonnet, É.; Miltzow, T.; Rzążewski, P. Complexity of Token Swapping and its Variants. In Proceedings of the 34th Symposium on Theoretical Aspects of Computer Science, STACS 2017, Hannover, Germany, 8–11 March 2017. [Google Scholar]
- Cayley, A. LXXVII. Note on the theory of permutations. Philos. Mag. 1849, 34, 527–529. [Google Scholar] [CrossRef]
- Pak, I. Reduced decompositions of permutations in terms of star transpositions, generalized Catalan numbers and k-ARY trees. Discret. Math. 1999, 204, 329–335. [Google Scholar] [CrossRef]
- Yasui, G.; Abe, K.; Yamanaka, K.; Hirayama, T. Swapping Labeled Tokens on Complete Split Graphs. Inf. Process. Soc. Jpn. SIG Tech. Rep. 2015, 2015-AL-153, 1–4. [Google Scholar]
- Heath, L.S.; Vergara, J.P.C. Sorting by Short Swaps. J. Comput. Biol. 2003, 10, 775–789. [Google Scholar] [CrossRef] [PubMed]
- Yamanaka, K.; Horiyama, T.; Kirkpatrick, D.G.; Otachi, Y.; Saitoh, T.; Uehara, R.; Uno, Y. Swapping Colored Tokens on Graphs. In Proceedings of the 14th International Symposium on Algorithms and Data Structures, WADS 2015, Victoria, BC, Canada, 5–7 August 2015; pp. 619–628. [Google Scholar]
- Fujita, S.; Nakamigawa, T.; Sakuma, T. Colored pebble motion on graphs. Eur. J. Comb. 2012, 33, 884–892. [Google Scholar] [CrossRef]
- Kawahara, J.; Saitoh, T.; Yoshinaka, R. The Time Complexity of the Token Swapping Problem and Its Parallel Variants. In Proceedings of the 11th International Conference and Workshops on WALCOM: Algorithms and Computation (WALCOM 2017), Hsinchu, Taiwan, 29–31 March 2017; pp. 448–459. [Google Scholar]
- Ito, T.; Kakimura, N.; Kamiyama, N.; Kobayashi, Y.; Okamoto, Y. Reconfiguration of Maximum-Weight b-Matchings in a Graph. In Proceedings of the 23rd International Conference on Computing and Combinatorics, COCOON 2017, Hong Kong, China, 3–5 August 2017; pp. 287–296. [Google Scholar]
- Lubiw, A.; Pathak, V. Reconfiguring Ordered Bases of a Matroid. CoRR, 2016; arXiv:1612.00958. [Google Scholar]
- Nishimura, N.; Subramanya, V. Graph Editing to a Given Neighbourhood Degree List is Fixed-Parameter Tractable. In Proceedings of the 11th Annual International Conference on International Conference on Combinatorial Optimization and Applications (COCOA 2017), Shanghai, China, 16–18 December 2017. [Google Scholar]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).