Abstract
Let R denote a connected region inside a simple polygon, P. By building barriers (typically straight-line segments) in , we want to separate from R part(s) of P of maximum area. All edges of the boundary of P are assumed to be already constructed or natural barriers. In this paper we introduce two versions of this problem. In the budget fence version the region R is static, and there is an upper bound on the total length of barriers we may build. In the basic geometric firefighter version we assume that R represents a fire that is spreading over P at constant speed (varying speed can also be handled). Building a barrier takes time proportional to its length, and each barrier must be completed before the fire arrives. In this paper we are assuming that barriers are chosen from a given set B that satisfies certain conditions. Even for simple cases (e.g., P is a convex polygon and B the set of all diagonals), both problems are shown to be NP-hard. Our main result is an efficient ≈11.65 approximation algorithm for the firefighter problem, where the set B of allowed barriers is any set of straight-line segments with all endpoints on the boundary of P and pairwise disjoint interiors. Since this algorithm solves a much more general problem—a hybrid of scheduling and maximum coverage—it may find wider applications. We also provide a polynomial-time approximation scheme for the budget fence problem, for the case where barriers chosen from a set of straight-line cuts of the polygon must not cross.
1. Introduction
The firefighter problem in graphs has recently received significant attention [1,2,3,4]. It models a situation where a fire, infection, computer virus, etc., spreads through a network, and the goal is to save as many network nodes as possible by a suitable placement of firefighters.
At the beginning a fire breaks out at the source vertex of the input graph. At each subsequent time step a bounded number of firefighters (just one in the standard version) may be placed at vertices that are not already on fire, to defend them. Once defended, a vertex will never catch fire. After the firefighters have been placed, the fire spreads from each burning vertex to all its undefended neighbors. The process ends when the fire can no longer spread. All vertices which are not on fire are considered to be saved. The objective is to determine a placement of firefighters that maximizes the number of vertices saved.
This graph firefighter problem is NP-hard already for trees [3,5], and hard to approximate within , for any , in polynomial-time in the general case [2]. Only trees are known to admit polynomial-time constant-factor () approximation algorithms [2].
Real firefighting takes place in environments different from graphs. The importance of the problem poses a big challenge to research: how should fire brigades best deploy their forces in order to efficiently quench or contain a raging fire?
In this paper we focus on geometric aspects of the problem, leaving aside, for now, additional constraints imposed by climate, geology, area utilization and other factors. We propose a natural geometric firefighter problem. Instead of a graph, we consider a polygonal region P with a distinguished point R where a fire starts spreading through P at a given constant speed. Instead of placing firefighters, we can build one-dimensional barriers (i.e., straight-line segments or curves) also at a given constant speed in the area still free of fire, one at a time. Thus, building a barrier takes time proportional to its length. A barrier must be built continuously and each barrier point must be completed before the fire reaches any point on the yet not completed fragments of this barrier. The goal is to maximize the area of P that is separated from the fire by the barriers. All edges of the boundary of P are assumed to be already constructed or natural barriers. (Our results can be modified to apply to other variants of the problem. For example, the fire can spread at various speeds, and the time it takes to build various barriers can also vary.)
We also consider a simpler version termed the budget fence problem. For a polygonal region P, a contaminated subregion and a fence budget we want to separate a maximum area of P from R by drawing barriers within of total length not exceeding In this static case no time constraints need to be observed.
Both problems have several variants depending on the type of polygonal region and the set B of barriers allowed.
1.1. Our Contributions
In general, our contributions are pioneering in the crucial geometric aspects of firefighting.
In Theorem 2, we show the NP-hardness of the geometric firefighter problem for convex polygons, even if the set of allowed barriersis restricted to a set of pairwise disjoint diagonals. Theorem 3 states that the problem is also NP-hard for star-shaped polygons and unrestricted sets of barriers. These hardness results carry over to the budget fence problem.
Our main result is a constant (≈11.65) approximation greedy algorithm for the firefighter problem in simple polygons, where the set B of allowed barriers is any set of straight-line segments with all endpoints on the boundary of P and pairwise disjoint interiors. (In the preliminary conference version [6], we have not taken into accountthe possibility of delaying fire propagation by previously inserted not straight-line or intersecting barriers to not yet saved areas. For this reason, we have erroneously allowed B to be less restricted.) The approximation algorithm runs in time polynomial in the size of B; see Theorems 4 and 8. This algorithm solves, in fact, a more general problem which is a hybrid of scheduling and maximum coverage. We are given a finite set of non-splittable jobs with release, duration, and completion time demands. Each job covers some part of a universe. The objective is to feasibly schedule a subset of jobs so that the profit from the total part of universe covered is maximized. Since this hybrid problem is a generalization of the maximum coverage problem, it cannot be approximated within a factor smaller than in polynomial time unless [7].
In Theorem 9, we address the budget fence problem in a simple polygon. Here, the set B consists of any set of straight-line segments within the polygon and outside the contaminated subregion, having all endpoints on the polygon boundary. We additionally require that those fence segments the algorithm selects from the given set B must have pairwise disjoint interiors. We present a polynomial-time approximation scheme (PTAS) based on dynamic programming. It also yields a low-constant approximation for the geometric firefighter problem with disjoint selected barriers in simple polygons, provided the geodesic distances of the given straight-line barriers from the fire source do not differ too much; see Corollary 10.
1.2. Related Results
Several different generalizations and variants of the graph firefighter problem have been studied in the literature [1,2,3,4]. Recently, this problem has also been studied in the context of random geometric graphs, whose nodes correspond to random points according to a random distribution; in this setting, two points are connected by an edge if the distance between them is shorter than a specified constant [8].
There are other papers beside Khuller et al. [9] which study generalizations of the maximum coverage problem, e.g., Cohen and Katzir [10]. Some of them are also partly related to scheduling, since they consider picking one element or set at a time, e.g., in Bansal et al. [11]. However, these generalizations are still very different from our hybrid problem, and therefore none of the techniques used in those papers seem applicable to our problem. Other papers relating set cover to scheduling also deal with very different problems. See, for example, Bansal and Pruhs [12], Hassin and Levin [13] and Ghaderi et al. [14]. Following the general approach for submodular function maximization, as described in Chekuri et al. [15], it may be possible to design an algorithm for our hybrid problem, although perhaps with a much worse approximation ratio.
Recently, Klein et al. [16] have studied another variation of the geometric firefighter problem, where the fire is expanding in an open field without any boundaries, and a single (curved) barrier which surrounds the fire is being built in order to contain it. Very recently, Zambon et al. [17] has reported on experimental efforts to solve a variant of the geometric firefighter problem for instances of up to 300 polygon vertices.
To the best of our knowledge, the budget fence problem has not been studied except for very special cases, e.g., for rectilinear strips [18]. A related problem which has been studied is to select, among a given set of curves, a minimum number of curves which separates two sets of points [19] .
2. Barriers
By a barrier in a polygonal region we mean a curve of constant algebraic degree that does not intersect itself and has both endpoints on the polygon’s boundary (in other words, a cut). The barriers constructed must be disjoint (no intersections allowed), except that their endpoints are allowed to coincide. Barriers must be built (drawn) from one endpoint to the other at constant speed, a single barrier at a time, but there is no travel cost between different barrier locations. In the firefighter problem, no point b on a barrier can be built after the expanding fire has reached b.
As part of the problem definition, a set B of allowed barriers is specified.
3. NP-Hardness
A natural approach to show NP-hardness of the geometric firefighter problem is a reduction from the graph firefighter problem, which is known to be NP-hard even for trees of maximum degree three [3]. This approach yields the following theorem.
Theorem 1.
The geometric firefighter problem is -hard for simple polygons, when the barriers can be chosen from a given set of pairwise disjoint diagonals of identical length.
Proof.
Let T be a rooted tree with maximum degree three which is a part of an instance of the aforementioned firefighter problem on trees. The fire is supposed to break at the root of
First, we draw T in the plane in such a way that each drawn edge has the same length Next, we replace each vertex with a small square of the same size s that is polynomially smaller than the edge length. The fire is supposed to break at the top of the root square. The edge from the parent (if any) is supposed to touch the top of the square while the at most three edges to the children are supposed to touch the bottom of the square. Then, we split each drawn edge into two parallel edges forming an “edge pipe” of thickness that is polynomially smaller than the square size The thickness is also so small that the area of such an edge pipe is polynomially smaller than that of a vertex square.
In this way, we obtain a simple polygon Furthermore, we set the propagation speed of the fire and the speed of drawing a barrier so that in a time unit, the fire can propagate within the radius of in an open area and a barrier of length can be drawn. Observe that the fire while reaching vertices may be delayed by the time taken by a traversal of polynomially small fraction of the edge length d since in general the distance to traverse in a vertex square may slightly exceed This however does not affect the main arguments. Finally, we define the set of allowed barriers to be the diagonals of length “closing” the pipes at their ends further away from the root square.
Now the crucial observation is that drawing such an allowed diagonal e saves roughly the area of k vertex squares, i.e., , in where k is the number of vertices without firefighter saved by placing a firefighter at the root of the subtree of T corresponding to the subpolygon of cut off by
In this way we can efficiently reduce an instance (of the decision version) of the aforementioned known NP-hard firefighter problem on the tree T to an instance (of the decision version) of the geometric firefighter problem on the polygon . ☐
If we allow for a large range of the lengths of barriers, then we obtain NP-hardness for the geometric firefighter problem with diagonal barriers even for convex polygons.
Theorem 2.
The geometric firefighter problem is -hard even for convex polygons, even if the set of allowed barriers is restricted to a set of pairwise disjoint diagonals.
Proof.
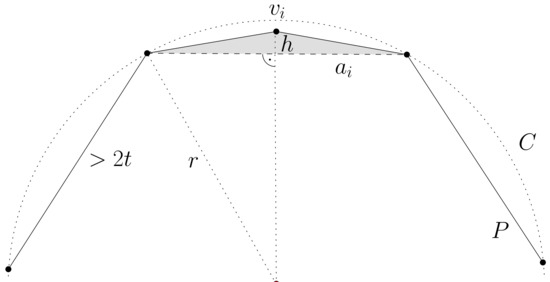
We reduce from the subset-sum problem [20]. Let be the set of positive integers, s := , and let t be the desired target sum in the subset-sum problem we want to solve by using the firefighter algorithm for convex polygons.
The convex polygon P is constructed as follows. It has vertices. Of these vertices, lie on a circle C of radius r (to be determined later) centred at the fire source. Every third vertex of the convex polygon lies in the interior of this circle C.
Vertex can be cut off by a diagonal of length ; see Figure 1. The resulting triangle is of height h, independent of index i, so that its area equals . Two consecutive vertices of polygon P situated on C are at distance greater than . ( The precise location of the vertex is not essential, as long as it lies on or inside the circle C.)

Figure 1.
Constructing firefighter instances to show NP-hardness.
The set B of possible barriers in this proof is the set of all k diagonals , for .
Let us assume that barriers can be built at speed one. Defining the fire’s speed, v, by ensures that the firefighter can build barriers of total length at most before the fire reaches the circle and the whole process terminates. Hence, no diagonal of length >2t can be built. On the other hand, if we make radius r large enough to satisfy
Then holds, meaning that the fire has not reached the ith triangle at time t (the shaded region in Figure 1).
Therefore, finding the optimal solution for the firefighting problem is equivalent to finding the subset of integers from the subset-sum problem whose sum is as close to t as possible, without exceeding t.
We observe that an additive error less than in the lengths of the diagonals would be tolerable in this construction. Thus, vertices can be described by rationals of length polynomial in the bit length of the input. ☐
The proof of Theorem 2 would not work if the firefighter were allowed to build barriers freely anywhere in the polygon. But it turns out that the complexity of the problem does not decrease in this more liberal setting.
Theorem 3.
The geometric firefighter problem and the budget fence problem are NP-hard for star-shaped polygons even if there is no restriction as to where the barriers can be built, and curved barriers are allowed.
Proof.
First, we shall show that the geometric firefighter problem for a simple polygon is -hard even if the endpoints of the barriers are not required to be vertices of the polygon. This holds both in the case where the barriers have to be straight-line segments, and in the case where they are allowed to be arbitrary curves.
We modify the construction used in the proof for the convex polygons, where of the points lie on the circle C and k points lie inside C. The modification is as follows. We will use unnecessarily huge values to simplify the arguments.
Firstly, we become more specific concerning the edges connecting consecutive vertices lying on the circle C. This means that the circle C may have to be much larger than it had to be in the previous proof. We require that each one of these longer edges has length at least , where s is the sum of all the integers in the instance of the subset-sum problem. (It is still acceptable if some of these diagonals are much larger, but their length has to be bounded by a polynomial in s.) We will assume without loss of generality that , that each integer is smaller than t and that (otherwise the problem is easy to solve).
Secondly, we adjust the relative speed of the firefighter with respect to the fire. As before, the firefighter has enough time to build barriers of total length precisely t, until the fire reaches anyone of the small diagonals of length , which are the candidate barriers and cut the corresponding triangles. But, in addition, we require that the speed of the fire is times larger than the speed of the firefighter.
Thirdly, we replace each small triangle cut by one of the small diagonals by a square of area (In this way, its side has length smaller than , which suffices in order to make all these squares fit around the circle C with no overlaps.). Recall that is the length of . The square is placed in such a way that the diagonal cuts off this square from the rest of the polygon, and is in the middle of one of the sides of the square.
This finishes the construction. It remains to show that any optimal solution saves an area of size at least if and only if the answer to the subset-sum problem is “yes”, i.e., there is a subset of integers whose total sum is t. Clearly, if there is such a subset of integers whose total sum is t it follows that barriers can be constructed along the corresponding diagonals before the fire comes, and so an area of size can be saved.
What happens if the answer to the subset-sum problem is “no”? Then the area saved by cutting off squares along diagonals is no more than , which leaves an area of size at least to be saved in some other way (other than by building barriers along diagonals), if we should be able to achieve the goal of .
Is there some way to save area of size in some other way, for example by using curved barriers? Recall that the total length of barriers which the firefighter can build until the fire comes to the first square is t. From that moment, the fire has to advance a geodesic distance no longer than before the whole process is over. Since the speed of the fire is times larger than the speed of the firefighter, it follows that: from the moment the fire reaches the first square until the whole process is over the firefighter can build barrier(s) of (total) length no more than , and hence . So, the total length of the barrier which the firefighter can build during the whole process is not larger than . With such a possible length, the maximum area one can save is , if one does not utilize “valves” like the small diagonals which cut off the squares. A generous, straightforward estimate, to simplify the argument, would be that no more than area can be saved, which is still far off the value which we would have to achieve.
In the following second part of the proof, we shall show that the polygon constructed in the first part can be modified to be star-shaped.
The modification is that instead of attaching a small square to each one of the diagonals , we attach a rectangle whose one side is , and whose area is the same as the area of the corresponding square in the previous proof, i.e., . Thus, the height of each one of the rectangles is . We observe that the whole polygon is now visible from the fire-centre, and hence it is star-shaped.
Furthermore in order to ensure that the fire can move across any such rectangle sufficiently fast, we now require that the speed of the fire is larger than the speed of building barriers. Hence, we adjust the size of the circle C, and enlarge it so that the distance from the fire source (circle center) to the closest diagonal should be . In this way, as in the previous proof, the firefighter has precisely the time needed to build barriers of total length t before the fire reaches the first diagonal , but still the total length of barriers which can be built before the whole process is over is not larger than .
Otherwise, the argument goes as for the previously constructed polygon in this proof, but instead of valves we consider barriers cutting off (pieces of) rectangles. ☐
The proof of Theorem 3 applies equally well to the budget fence problem.
4. An Approximation Algorithm for the Geometric Firefighter Problem
In this section we present an efficient greedy algorithm for solving the geometric firefighter problem for a finite barrier set B, that achieves a constant approximation factor, where B consists of disjoint straight-line segments with both endpoints on the boundary of P.
Our algorithm works in a more general setting, related to job scheduling and maximum coverage. Each barrier of the firefighter problem can be considered a job. It has a duration (the time needed to build it) and a completion time (the last point in time where the fire permits the construction of b to be completed). Each job is assumed to cover a subset of some finite universe U. The elements of U carry profits, and a job’s profit equals the sum of profits of all elements it covers.
The goal is to compute a feasible job schedule whose total profit (i.e., the sum of all profits of jobs scheduled) is maximized. Since this problem generalizes the max-coverage problem, it inherits its inapproximability results. Thus, no approximation factor smaller than ≈1.5819 can be guaranteed by any polynomial time algorithm, unless [7]. (However, this inapproximability result does not necessarily apply to our original firefighter problem).
We will now present an approximation algorithm GlobalGreedy that runs in low polynomial time in the size of B and guarantees an approximation factor of ≈11.65. After proving this result, we comment more precisely on how this can be applied to the geometric firefighter problem.
GlobalGreedy maintains a feasible time schedule L of jobs, with precise start and completion times for each of the jobs in L. (We may think of the schedule as a list of jobs, sorted according to their scheduled start time, although a more advanced data structure can be employed in order to perform searches and changes of the list more efficiently). The algorithm starts with the empty schedule L. It considers each input job J exactly once for possible insertion into the schedule L. If J is rejected, it will never be considered again for inclusion. If J is scheduled and inserted into the schedule L, its scheduled starting time will never change. However, it may still happen that J is later deleted from L, in order to make it possible for some other job to be scheduled (partly) during the scheduled time for J. Once J is deleted, it will never again be considered for insertion into the schedule.
Since GlobalGreedy inspects each job only once for possible insertion, the order in which the jobs are considered is crucial. To define this order, and for easier reference in the subsequent proof, we assign colours to all elements of universe U. These colours may change during the process. In the beginning, all elements are coloured red. Each time GlobalGreedy inserts a job J into the schedule L the following happens: all red elements covered by J are irrevocably associated to J, and change colour to green. We will call these elements the property elements of J, and denote by the property profit of J the total profits of all the property elements of J.
Finally, if some job J is later deleted from the schedule L, in order to make place in the schedule for some other job, then the property elements of J change colour from green to grey during the deletion of J.
GlobalGreedy starts with the empty schedule L, and colours all elements of the universe red. Then it runs the following while-loop, one iteration for every input job J, possibly altering the schedule L, until there are no more jobs left unconsidered. Finally it outputs the schedule L. The order in which the jobs are considered is defined inside the while loop. A parameter specifies when jobs will be deleted from the schedule L in order to accommodate job J currently under consideration.
while there is still any unconsidered job do
Consider an unconsidered job J which maximizes the ratio of the total profit of the red elements it covers, divided by its duration. Insert J into schedule L if and only if this can be done respecting the deadline for J and without any re-scheduling of other jobs, except for possibly deleting consecutive jobs in L whose property profits are altogether not greater than times the total profit of all red elements covered by J. (In case there are several options for when to schedule J satisfying this condition, choose one of them arbitrarily.) If J is inserted, change to green the colour of all red elements covered by J. For each job deleted from schedule L, change from green to grey the property elements of .
end-while
Theorem 4.
The above algorithm GlobalGreedy runs in polynomial time and achieves an approximation factor of ≈11.65 if parameter μ is set to .
Proof.
We will need the following lemma. For ease of reference, let us denote by the total profit of all green elements in U, at a given time, and similarly for the other colours.
Lemma 5.
At each time, we have
Proof.
By induction on the number of job insertions with deletions. Before the first job is deleted from the schedule L, there are no grey elements, and the lemma holds. Suppose that, upon inserting job J, jobs with a total green profit of z are deleted from L. All this green profit turns grey. But, by definition of GlobalGreedy, job J wins at least new green profit, so that
☐
Let us run algorithm GlobalGreedy. All jobs in the final schedule are called green, and those jobs that were inserted into L and later removed, grey.
Now let us define OPT to be any specific schedule achieving maximum profit. We change to blue the colour of all elements still red that are covered by OPT (noting that no green or grey elements become blue). Such a blue element is assigned, as a blue property element, to the first job J in OPT that covers it. Job J cannot be green or grey, because then it would no longer cover red elements. Consequently, if we name such a job J blue, the three colour classes are pairwise disjoint.
In order to prove Theorem 4 we are using a paying scheme, where each green or grey job J pays money to any blue job performed at least partially during the same time as J (note that every job ever inserted into L is assigned a unique execution time that will never be altered by GlobalGreedy). The paying scheme is specified as follows.
The Paying Scheme.
Case 1: The execution time of is totally included within the execution time of J. In this case, J gives to money equal to the property profit of J, times the ratio of the duration of divided by the duration of J.
Case 2: In all other cases where the execution intervals of J and overlap, J gives to money equal to times the property profit of J.
Lemma 6.
A green or grey job J pays at most 1 + 2 times its property profit to blue jobs.
Proof.
J pays times its property profit to at most two blue job whose execution intervals include the start or end time of J. In addition, J pays money to blue jobs whose scheduled times are totally included within the execution interval of J, in linear proportion to their respective duration; together, these payments do not exceed the property profit of J. ☐
The following lemma shows that each blue job is well-paid by this scheme.
Lemma 7.
By the above paying scheme, each blue job receives an amount of money not smaller than its property profit.
Proof.
We define the efficiency ratio of any coloured job J to be the ratio of its property profit divided by the duration of J.
Let be any blue job. Let us study the iteration of the while-loop when GlobalGreedy considered for possible inclusion into the schedule L. Let be the jobs in schedule L during that step, whose execution times (partially) overlap with the execution time of . Since became a blue job, it was rejected by GlobalGreedy. Thus, the total property profits of must have been be at least times the red property profit of , which is no less than times its current blue property profit because all blue property profits of were red during that iteration.
Moreover, by the order according to which GlobalGreedy considers jobs for possible insertion into L, it follows that the efficiency ratio of each one of the jobs must be at least as large as the efficiency ratio of .
Let us first handle the case where . If the execution time of is totally included within the execution time of , job receives from
According to Case 1 of the paying scheme. In all other configurations, gives to the amount of
By Case 2, and we are done. If , then the same arguments apply to . ☐
By Lemmas 6 and 7,
Now Lemma 5 allows us to bound all profits by green profits, and we obtain for the profits of OPT and GlobalGreedy
The factor is minimized for to the value . This completes the proof of Theorem 4. ☐
The same proof works if the jobs to be scheduled have release times, in addition to duration and completion times. Also, their durations might depend on their actual start times, as long as there are only a polynomial number of changes. We summarize our main result as follows, observing that is the inverse of .
Theorem 8.
Let U be a set of elements, each associated with a real profit, and let be a set of jobs, where each job J in covers a given subset of universe U, and is given a release time, a completion deadline and a duration. Algorithm GlobalGreedy runs in polynomial time and constructs a feasible schedule whose total profit is at least times the maximum possible profit.
In the geometric firefighter problem, universe U can be defined as follows. The set B of allowed barriers consists of a number of straight-line barriers with pairwise disjoint interiors and all endpoints on the boundary of P. We take the arrangement of all barriers of B inside polygon P, pick a representative point from each cell c, and let the profit of be the area of c; observe that all points in c share their fates with , with respect to the fire. Universe U equals the set of the points , and each barrier b covers those points whose cells are separated by b from the fire’s starting point. We observe that U is of size linear in the size of B since each barrier is placed on the border of at most two cells. Also, each cell that can be saved from the fire at all by barriers in can be saved by a single barrier in Thus, the above theorem yields an approximation to the geometric firefighter problem (on a Real RAM that can compute square roots in constant time), where the set B of allowed barriers consists of a number of straight-line barriers with pairwise disjoint interiors.
5. A PTAS for the Budget Fence Problem and a Special Case of the Firefighter Problem
Recall that an instance of the budget fence problem consists of a simple polygon P of n edges, a “contaminated” connected region R contained within P (it can be degenerated to a point), the available total fence length and an allowed set B of barriers, none of them intersecting the interior of The objective is to fence off from R the largest possible area of polygon P by barriers from B of total length not exceeding While B may contain candidates that cross each other, an algorithm may use only barriers whose interiors are pairwise disjoint.
In the absence of time constraints, this problem seems of a more combinatorial nature than the firefighter problem. First, let us assume that B consists of diagonals of P. Then the following standard dynamic programming and discretization approach yields a close approximation.
For each pair of vertices of and a number parameter we consider the problem of finding a shortest simple path saving at least an area of size s, from a to b in clockwise direction; the path can contain diagonals from B and edges of P between a and b, but only the total length of diagonals counts.
Let be the maximum area that can be saved by a single diagonal. Clearly, no path can save more area than We may assume the parameter s belongs to , where is an appropriate polynomial. Then, we can solve by considering solutions to all pairs and , where c is a vertex between a and b in clockwise direction on the perimeter of P, and We pick the pair that minimizes the length of the path from a to b through c and compare it with the direct diagonal connection between a and b if this diagonal exists in B. We obtain an approximate solution of the budget fence problem for P by picking the largest such that the minimum length path solving for some vertex a of P has length less than or equal to
Any feasible solution includes at most diagonals. By the definitions of S and our dynamic programming scheme, the area saved by each of them can be underestimated by at most Hence, since the optimal solution saves at least , the approximation factor of our dynamic programming method is It follows that it is sufficient to set to , for a sufficiently large constant c, in order to obtain a approximation.
Note that this method can be immediately adapted to work for any finite set B of straight-line barriers within with all endpoints on the polygon boundary (extending the set of vertices). Hence, we have the following theorem.
Theorem 9.
There is a PTAS for the budget fence problem for a simple polygon P and a contaminated region R, where the set B of allowed barriers is any finite set of straight-line segments within having all endpoints on the boundary of P and the selected barriers have pairwise disjoint interiors.
Remarkably, a good approximation to the budget fence problem can also yield a good approximation to the firefighter problem, under the assumptions from above (barriers are straight-line segments within P and all barriers chosen must have pairwise disjoint interiors). In fact, we obtain the following corollary from Theorem 9.
Corollary 10.
Let P be the input polygon and let the set B of allowed barriers in P be a finite set of straight-line segments within P having all endpoints on the boundary of P. Next, let and be, respectively, the minimum and maximum geodesic distance of a barrier in B from the fire source. For any the firefighter problem in P can be approximated within in polynomial time, under the assumption that the chosen barriers have pairwise disjoint interiors.
Proof.
For , divide B into classes such that the geodesic distance between the barriers in and the fire source falls in the interval There exists such that the barriers in save at least of the area saved by an optimal solution to the geometric firefighter instance. Therefore, it is sufficient to approximate within an optimal solution to the instance constrained to barriers in for i = , and then choose the best solution in order to obtain the corollary.
Fix . First, find a set of at most k barriers in that jointly save the largest area. This can be easily done in polynomial time. If contains at most k barriers which jointly save at least area saved by then we are done. To handle the opposite case, we proceed as follows.
Let t be the time it takes for the fire to reach the geodesic distance from the source. Note that contains at most one barrier that is finished after the time t elapsed. For proof’s sake, remove such a barrier (if any) and all the barriers that need at least time to be build. Let be the resulting set of barriers. Since at most k barriers have been removed, the barriers in save at least half the area saved by . Sort the barriers in by their ratio between the saved area and barrier length in non-decreasing order. Consider the maximum prefix of the sorted sequence of barriers that can be build within the time By the definition of the sorted sequence, the area saved by the barriers in the prefix is at least of the area saved by the barriers in We can pick k sufficiently large so the area saved by the barriers in the prefix is at least of that saved by the barriers in We can obtain at least approximation of the area saved by the barriers in the prefix by running our PTAS for the budget fence problem on the polygon P with the set of allowed barriers and the length constraint equal to the time multiplied by the speed of building a barrier. Consequently, we obtain an approximation of ☐
6. Generalizations and Refinements
In this paper we have introduced a geometric version of the firefighter problem, and the closely related budget fence problem. There is a number of generalizations and interesting questions deserving further research.
For example, Algorithm GlobalGreedy could as well be applied to a situation where some parts of the polygonal domain P are more important than others. Moreover, by adjusting the deadlines of the jobs, we can handle the cases when the speed of the fire and/or of building the barriers may vary.
The proof of a constant approximation ratio for GlobalGreedy would still work even if the barrier considered in the next iteration of the while-loop has only approximately largest efficiency ratio. The approximation constant would increase somewhat, but it would still be a constant. This observation may enable faster computation of the next candidate barrier to be considered, and improve the overall time performance of the algorithm.
Acknowledgments
The authors are very grateful to anonymous reviewers of the preliminary conference version of this paper as well as anonymous reviewers for this journal for their valuable comments. This work has been supported in part by the grant Kl 655/19 (DACH project) and the grant 2017-03750 of Swedish Research Council.
Author Contributions
Rolf Klein, Christos Levcopoulos and Andrzej Lingas equally contributed to research discussions and writing down their outcomes.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Anshelevich, E.; Chakrabarty, D.; Hate, A.; Swamy, C. Approximability of the Firefighter Problem: Computing Cuts over Time. Algorithmica 2012, 62, 520–536. [Google Scholar] [CrossRef]
- Cai, L.; Verbin, E.; Yang, L. Firefighting on Trees: (1-1/e)-Approximation, Fixed Parameter Tractability and a Subexponential Algorithm. In Proceedings of the 19th International Symposium ISAAC 2008, LNCS 5369, Gold Coast, Australia, 15–17 December 2008; pp. 258–269. [Google Scholar]
- Finbow, S.; King, A.; MacGillivray, G.; Rizzi, R. The firefighter problem for graphs of maximum degree three. Discret. Math. 2007, 307, 2094–2105. [Google Scholar] [CrossRef]
- Floderus, P.; Lingas, A.; Persson, M. Towards more efficient infection and fire fighting. In Proceedings of the Computing: The Australasian Theory Symposium (CATS 2011), CRPIT 119, Perth, Australia, 17–20 January 2011; pp. 69–74. [Google Scholar]
- Finbow, S.; MacGillivray, G. The Firefighter Problem: A survey of results, directions and questions. Australas. J. Comb. 2009, 43, 57–78. [Google Scholar]
- Klein, R.; Levcopoulos, C.; Lingas, A. Approximation algorithms for the geometric firefighter and budget fence problems. In Lecture Notes in Computer Science, Proceedings of the 11th Latin American Symposium in Theoretical Informatics (LATIN 2014), Montevideo, Uruguay, 31 March–4 April 2014; Springer: Berlin/Heidelberg, Germnay, 2014; Volume 8392, pp. 261–272. [Google Scholar]
- Feige, U. A threshold of ln n for approximating set cover. J. ACM 1998, 45, 634–652. [Google Scholar] [CrossRef]
- Barghi, A.; Winkler, P. Firefighting on a random geometric graph. Random Struct. Algorithms 2013, 46, 466–477. [Google Scholar] [CrossRef]
- Khuller, S.; Moss, A.; Naor, J.S. The budgeted maximum coverage problem. Inf. Process. Lett. 1999, 70, 39–45. [Google Scholar] [CrossRef]
- Cohen, R.; Katzir, L. The Generalized Maximum Coverage Problem. Inf. Process. Lett. 2008, 108, 15–22. [Google Scholar] [CrossRef]
- Bansal, N.; Gupta, A.; Krishnaswamy, R. A Constant Factor Approximation Algorithm for Generalized Min-Sum Set Cover. In Proceedings of the Twenty-First Annual ACM–SIAM Symposium on Discrete Algorithms (SODA), Austin, TX, USA, 17–19 January 2010; pp. 1539–1545. [Google Scholar]
- Bansal, N.; Pruhs, K. The Geometry of Scheduling. In Proceedings of the 51th Annual IEEE Symposium on Foundations of Computer Science (FOCS), Las Vegas, NV, USA, 23–26 October 2010; pp. 407–414. [Google Scholar]
- Hassin, R.; Levin, A. An Approximation Algorithm for the Minimum Latency Set Cover Problem. In Proceedings of the 13th Annual European Symposium on Algorithms (ESA), Mallorca, Spain, 3–6 October 2005; pp. 726–733. [Google Scholar]
- Ghaderi, R.; Esnaashari, M.; Meybodi, M.R. An Adaptive Scheduling Algorithm for Set Cover Problem in Wireless Sensor Networks: A Cellular Learning Automata Approach. Int. J. Mach. Learn. Comput. 2012, 2, 626–632. [Google Scholar] [CrossRef]
- Chekuri, C.; Vondrák, R.; Zenklusen, R. Submodular Function Maximization via the Multilinear Relaxation and Contention Resolution Schemes. In Proceedings of the STOC’11 43rd ACM Symposium on Theory of Computing, San Jose, CA, USA, 6–8 June 2011; pp. 783–792. Available online: http://arxiv.org/pdf/1105.4593v3.pdf (accessed on 30 July 2012).
- Klein, R.; Langetepe, E.; Levcopoulos, C.; Lingas, A.; Schwarzwald, B. On a Fire Fighter’s Problem. In Proceedings of the 31st International Symposium on Computational Geometry (SoCG 2015), Eindhoven, The Netherlands, 22–25 June 2015; pp. 768–780. [Google Scholar]
- Zambon, M.J.O.; de Rezende, P.J.; de Souza, C.C. Exact Solutions for the Geometric Firefighter Problem. In Proceedings of the 28th Canadian Conference on Computational Geometry (CCCG), Vancouver, BC, Canada, 3–5 August 2016; pp. 221–229. [Google Scholar]
- Altshuler, Y.; Bruckstein, A.M. On Short Cuts or Fencing in Rectangular Strips. arXiv, 2010; arXiv:1911.5920v1. [Google Scholar]
- Cabello, S.; Giannopoulos, P. The Complexity of Separating Points in the Plane. In Proceedings of the 29th ACM Symposium on Computational Geometry, Rio de Janeiro, Brazil, 17–20 June 2013; pp. 379–386. [Google Scholar]
- Garey, M.R.; Johnson, D.S. Computers and Intractability. A Guide to the Theory of NP-Completeness; W.H. Freeman and Company: New York, NY, USA, 1979. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).