1. Introduction
One definition of a k-colouring of a graph G is as a function such that whenever . Under this definition, k-colourings and are different whenever there exists a vertex x such that . Each k-colouring f is equivalent to a k-tuple in which the set of non-empty components is a partition of into independent sets.
A k-colouring is canonical with respect to an ordering of the vertices of G if, whenever , every colour less than c has been assigned to some vertex that precedes in . Thus is necessarily assigned colour 1, and colour 3 can only be assigned to some vertex after colour 2 has been assigned to a vertex that appears earlier in the sequence . Note that canonical colourings may be very different than the colourings arising from applying the usual greedy colouring algorithm to G using the vertex ordering .
Define an equivalence relation ∼ on the set of k-colourings of G by if and only if and determine the same partition of into independent sets. The set of canonical k-colourings of G with respect to is then the set of representatives of the equivalence classes of ∼ that are lexicographically least with respect to . Thus, canonical k-colourings exist for every and every proper colouring is equivalent to a canonical colouring.
For an ordering
of the vertices of a graph
G, the
canonical k-colouring graph of G, denoted
, has vertex set equal to the set of canonical
k-colourings of
G with respect to
, with two of these being adjacent when they differ in the colour assigned to exactly one vertex. While every ordering gives a set of representatives of the possible
k-colourings, different orderings can lead to different canonical
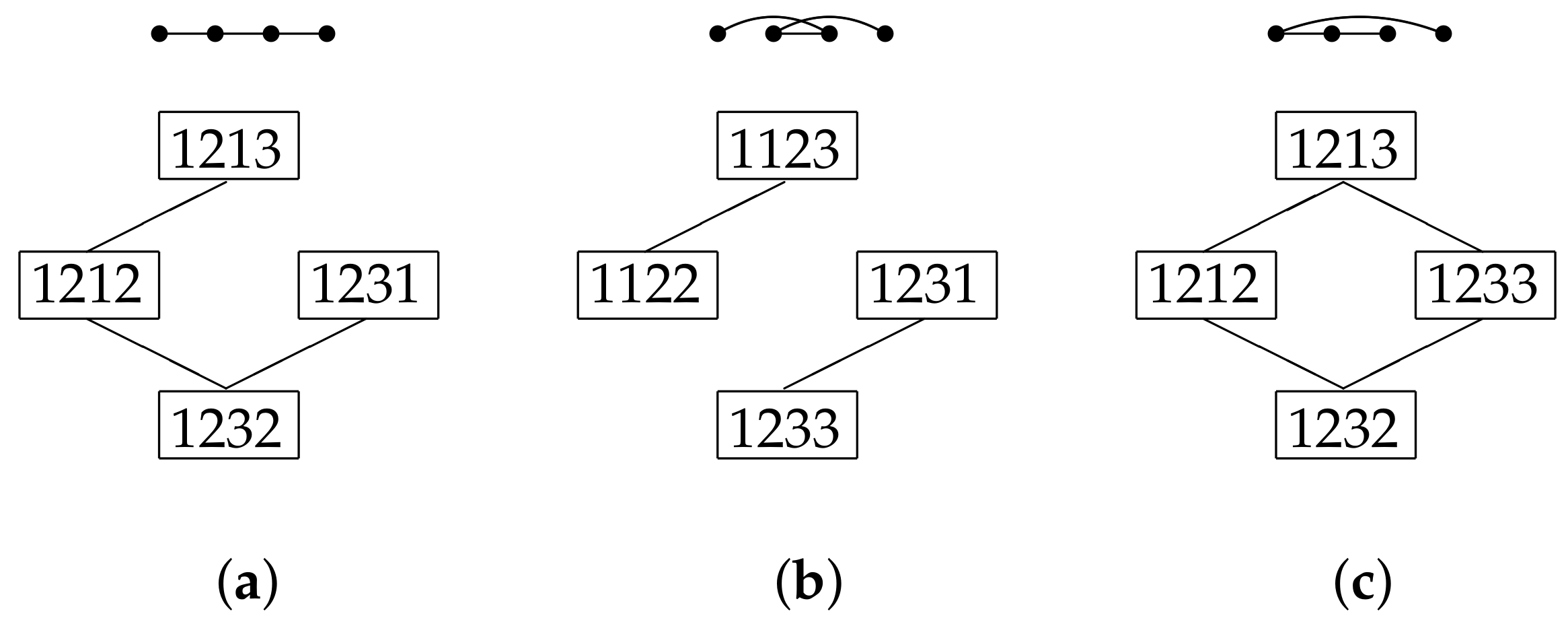
k-colourings graphs. Examples of the canonical 3-colouring graph of the path on 4 vertices are given in
Figure 1 for three different orderings of the vertices of the path. When a canonical colour graph is connected, any given canonical
k-colouring can be reconfigured into any other via a sequence of recolourings which each change the colour of exactly one vertex. When it is Hamiltonian, there is a cyclic list that contains all of the
k-colourings of
G and consecutive elements of the list differ in the colour of exactly one vertex, that is, there is a cyclic Gray code of the
k-colourings of
G.
This paper is organized as follows. Relevant definitions and background information are reviewed in
Section 2. A generalization of a lemma of [
1] concerning vertex orderings such that
is disconnected for all
is proved. Connectivity and Hamiltonicity of canonical colouring graphs of unions and joins of graphs are considered in
Section 3. The main focus is on the situation where one of the graphs involved is a complete graph or a complement of a complete graph. For
and any vertex ordering
, canonical
k-colourings of
correspond exactly to partitions of
with at most
k cells. Our results give a Gray code listing of these partitions similar to that of Kaye [
2]. Since the complete multipartite graph
is the join of
, our results show that there are vertex orderings
for which
is connected whenever
. In
Section 4, we first show that there exists a vertex ordering
such that the canonical
k-colouring graph of a bipartite graph is connected whenever
, and then give an example showing that this bound is the best possible. We then prove a negative result which implies that complete multipartite graphs with at least two nontrivial parts can not have Hamiltonian canonical colouring graphs, and there cannot be a Hamilton path if there are at least three parts of size that have at least two. This leaves open the possibility that canonical colouring graphs of complete bipartite graphs may have a Hamilton path. We show that there exists an ordering
such that
has a Hamilton path for all
. In the final section of the paper, we study the canonical
k-colouring graph of the complete multipartite graph in which each part has exactly two vertices. We show that, for any vertex ordering
and any integer
k at least as large as the number of parts, the canonical
k-colouring graph is either disconnected, or isomorphic to a particular tree.
Throughout the paper, proofs of existence results are constructive and lead to algorithms which generate the desired sequences.
2. Background, and a Preliminary Result
For basic definitions in graph theory, we refer to the text of Bondy and Murty [
3].
Before briefly surveying some previous research on colour graphs we recall the definition of , the colouring number of G. Let be an ordering of the vertices of G. Let be the subgraph of G induced by , for . Define . Then . Equivalently, , where the maximum is taken over all subgraphs of G. The quantity is an upper bound on the number of colours needed if the greedy colouring algorithm is applied to G and vertices are coloured in the order . Hence .
For
, let
be the set of
k-colourings of a graph
G. The
k-colouring graph of G, denoted
, has vertex set
, with two
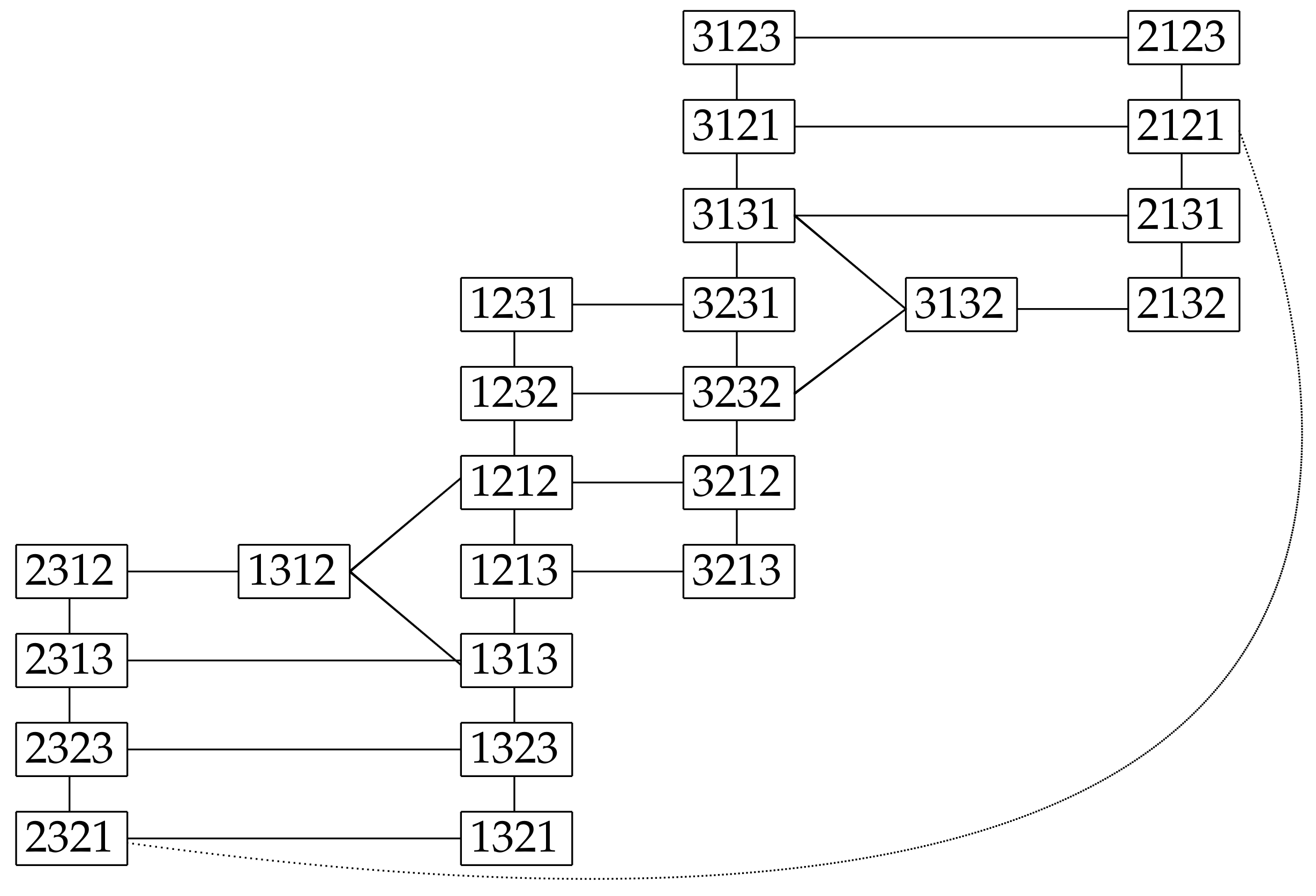
k-colourings being adjacent if and only if they differ in the colour of exactly one vertex. For example, the 3-colouring graph of a path on four vertices is given in
Figure 2. This is an example of a reconfiguration graph in which vertices represent feasible solutions to a problem and there is an edge between two solutions if one can be transformed to the other by some allowable reconfiguration rule. There is a vast literature on the complexity of reconfiguration problems, for example see [
4,
5]. The graph
is the most studied of the various colour graphs (that is, among the different allowable sets of colourings, and different reconfiguration rules). Connectivity of
arises in random sampling of
k-colourings, and approximating the number of
k-colourings, for example see [
6,
7,
8]. Dyer, Flaxman, Frieze and Vigoda proved that there is a least integer
such that
k-colouring graph of
G is connected for all
[
6] (also see [
9]). It is NP-complete to decide if the 3-colouring graph of a bipartite graph is connected [
10], but polynomial-time to decide if two 3-colourings of a bipartite graph belong to the same component of
[
11]. Hamiltonicity of the
k-colouring graph was first considered in [
12], wherein it was proved that there is always a least integer
such that the
k-colouring graph of the graph
G is Hamiltonian for all
. The number
is known for complete graphs, trees and cycles [
12], 2-trees [
13], complete bipartite graphs [
14], and some complete multipartite graphs [
15]. For other results on
, see [
16], and for related results concerning the graph of
-labellings (colourings with additional conditions), see [
17].
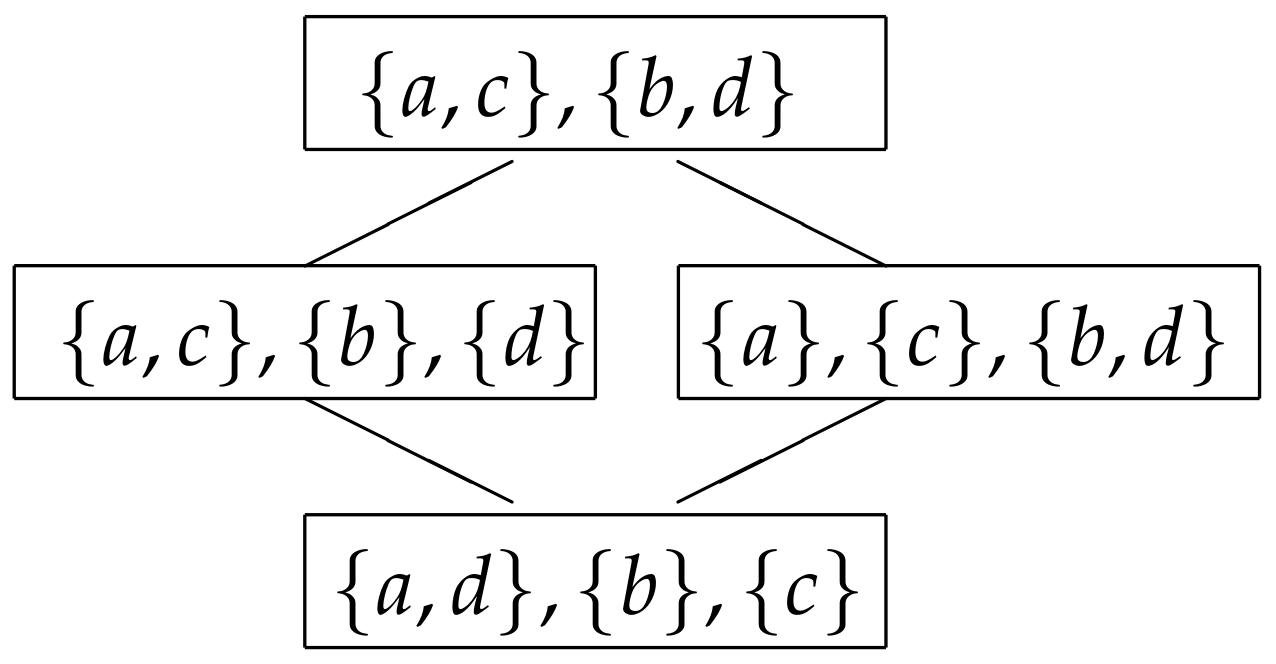
The
Bell k-colouring graph of G, denoted
, has as vertices the partitions of
into at most
k independent sets, with two of these being adjacent when there is a vertex
x such that these partitions are equal when restricted to
. The Bell
colouring graph of the path on four vertices is given in
Figure 3. Bell
k-colouring graphs are staudied in [
18], as is the
Stirling ℓ-colouring graph of G, the subgraph of
induced by the partitions with exactly
ℓ cells. It is proved that
is Hamiltonian for every graph
G except
and
, and the quantity
is the best possible. It is also proved that the Bell
k-colouring graph of a tree with at least four vertices is Hamiltonian for all
, and the Stirling
ℓ-colouring graph of a tree on at least
vertices is Hamiltonian for all
.
The graph is a spanning subgraph of ; the restriction to canonical colourings eliminates some edges of . Thus results asserting connectivity or Hamiltonicity of imply connectivity or Hamiltonicity of , respectively. Since at most n colours can be assigned to the vertices of an n-vertex graph G, it follows that and for all .
Canonical
k-colouring graphs were first considered in [
1]. For every tree
T there exists an ordering
of the vertices such that the canonical
k-colouring graph of
T with respect to
is Hamiltonian for all
. The canonical 3-colouring graph of the cycle
is disconnected for all vertex orderings
, while for each
there exists an ordering
for which
is connected. It is an open problem to find general conditions on
k and
such that
is connected. Most results are negative assertions about certain vertex orders
. In [
1] it was proved that if
G is connected, but not complete then there is always a vertex ordering
such that
is disconnected for all
. In particular, the graph
is disconnected whenever the first three vertices
of the vertex ordering
are such that
but
. Our first proposition generalizes that statement.
Proposition 1. Let be a vertex ordering of G. If there exists such that is adjacent to each of , and the subgraph of G induced by is not complete, then is disconnected for all .
Proof. Let be the subgraph of G induced by . Since is not complete, .
Let be a canonical -colouring of G with respect to . Then }. Furthermore, if is an adjacent colouring in then it differs on only one vertex. The colour of cannot change (because we are only considering canonical colourings) so must differ on a vertex other than . It follows that the vertex is assigned the same colour in any canonical colouring that is joined to by a path.
Suppose first that assigns the same colour to two of , say for some . Then, there is a (non-canonical) colouring of G in which is coloured with colour , and all other vertices, for are assigned the same colour as in . Let be the equivalent canonical colouring to this with respect to (defines the same partition of ). Then . Hence, there is no path in joining and .
Now assume assigns distinct colours to each of . Since is not complete, it has a pair of non-adjacent vertices. There is a colouring of G in which these two vertices are assigned the same colour, and all other vertices are assigned the same colour as in . Let be the canonical version of this colouring. Then . Hence, there is no path in joining and .
In both cases, is disconnected. This completes the proof. ☐
3. Unions and Joins
In this section we explore connectivity and Hamiltonian properties of graphs constructed by the operations of disjoint union and join. Our main focus is the situation where one of the graphs involved is complete, or has no edges.
Recall that the disjoint union of disjoint graphs and is the graph with vertex set and edge set . The join of disjoint graphs and is the graph with vertex set and edge set . We shall consider unions first, and joins second.
Observe that the canonical
k-colouring graph of
is the graph of partitions of an
n-set into at most
k parts. Hence the number of vertices is the sum of Stirling numbers of the second kind,
. A Hamilton cycle in this graph corresponds to a cyclic Gray code for set partitions. Many different Gray codes, cyclic and otherwise, for set partitions are known to exist [
19]; our method gives a different point of view and leads to a recursive algorithm similar to that of Kaye [
2]. A related method that gives Hamilton paths rather than Hamilton cycles is given in Theorem 4.
Theorem 1. Let π be a vertex ordering such that is Hamiltonian. Then, for the vertex ordering of obtained by placing the vertex of at the end of π, the graph is Hamiltonian.
Proof. Since has at least three vertices, we have .
Suppose . Then, G is bipartite and has at least three components. Let be the component of G containing the first vertex of . Then is isomorphic to the cube of dimension equal to the number of components of , and is isomorphic to the cube of one higher dimension. Since the t-cube is Hamiltonian for all , the statement follows.
Now suppose . If c is a canonical k-colouring of with respect to , then the restriction of c to G is a canonical k-colouring of G. We will say that the colouring c on is an extension of the colouring on G. Furthermore, each canonical k-colouring of G has at least two extensions to a canonical k-colouring of , and there are exactly two extensions if and only if and only one colour is used on the vertices of G. Notice that the set of canonical k-colourings of which agree on their restriction to induces a complete subgraph of .
By hypothesis, has a Hamilton cycle . Thus , and there exists i such that and both use at least two colours. Without loss of generality, . Thus, the canonical k-colourings and each have at least three extensions to canonical k-colouring of . For , let denote the extension of to a canonical k-colouring of in which the vertex of is assigned colour ℓ. Observe that and are adjacent to and , respectively, and and are adjacent to and , respectively.
A Hamilton cycle in can be constructed as follows. The first vertex is . Then, for , list all extensions of such that is first and is last if i is even, and is first and is last if i is odd. Observe that any pair of consecutive vertices in the list are adjacent. Let be the last vertex listed according to this procedure. The Hamilton cycle is completed by listing , then all other extensions of in such a way that is listed last and, finally, and all extensions of in such a way that is listed last (recall that was the first vertex listed).
This completes the proof. ☐
Corollary 1. Let π be a vertex ordering such that is Hamiltonian. Then, for the vertex ordering of obtained by placing the vertices of at the end of π, the graph is Hamiltonian.
The Gray code for set partitions implied by the following is similar to the one found by Kaye [
2].
Corollary 2. For all and , and any vertex ordering π, the graph is Hamiltonian.
We now turn our attention to connectivity of the canonical k-colouring graph of the disjoint union of graphs and . Since it is an open problem to determine general conditions under which the canonical k-colouring graph of a (connected) graph G is connected, in the results that follow we assume the canonical k-colouring graph of is connected and give conditions under which a canonical colouring graph of is connected, no matter how the vertices of are ordered following the vertex ordering of .
Theorem 2. Let and be disjoint graphs such that . Suppose there exists an integer k, and an ordering ϕ of the vertices of , such that is connected. Then, for any ordering π of the vertices of obtained by putting an ordering of the vertices of after , the graph is connected.
Proof. Let c be some particular canonical colouring of with colours such that colours appear on the vertices of (as they must), and colours appear on the vertices of . Let be the restriction of c to .
We complete the proof by showing that any canonical k-colouring of can be transformed into c by a finite number of steps corresponding to edges in . Suppose a canonical k-colouring d of is given. Let M be the largest colour which d assigns to a vertex of . Let be the subgraph of induced by the set of vertices on which colours appear.
Since
, the (ordinary)
M-colouring graph of
is connected [
6,
9]. Hence there is a sequence of steps corresponding to edges in
that transforms
d to a canonical colouring
which agrees with
on
. The following step can then be repeated until
is transformed into a canonical colouring that agrees with
on
. If the current colouring does not agree with
on
, then let
x be the last vertex of
which is not coloured
, and recolour
x with
(Note that any the colour of any such
x is greater than
M). The resulting colouring is proper because of the recolouring of
done earlier, and canonical by the maximality of the position of
x.
Finally, since is connected and , the subgraph of induced by the set of (canonical) colourings for which the restriction to is is isomorphic to , and is therefore connected. Hence there is a sequence of steps corresponding to edges in that transforms a canonical colouring which agrees with on into c. This completes the proof. ☐
The hypothesis of the above theorem can be relaxed slightly to
, where
is the least integer such that
k-colouring graph of
G is connected for all
. By the result of [
6],
.
Corollary 3. Let and G be a graph with at least one edge. If there exists a vertex ordering π such that is connected, then there exists an order for which is connected.
Proof. The colouring number of equals 1. Apply Theorem 2 inductively. ☐
We conclude this section by considering the join operation. Observe that in any colouring of , the set of colours that appear on the vertices of is disjoint from the set of colours that appear on the vertices of . With this observation, the proof of the first proposition below is straightforward, and hence is omitted.
Proposition 2. Let π be a vertex ordering of the graph G. If is the vertex ordering obtained by inserting the vertices of the at the beginning of π, then .
Corollary 4. If is connected (resp. has a Hamilton path, has a Hamilton cycle) then there exists an order such that is connected (resp. has a Hamilton path, has a Hamilton cycle).
In contrast, by Proposition 1, in almost any ordering of the vertices that does not begin with all the vertices of the corresponding will be disconnected.
Corollary 5. Let T be a tree with at least three vertices, and . For any integer , there exists a vertex ordering such that is Hamiltonian.
Proof. For any such
k, there is a vertex ordering
such that
is Hamiltonian [
1]. ☐
The next corollary implies, among other things, that the canonical c-colouring graph of a wheel on n spokes is connected for all .
Corollary 6. Let , and . There exists a vertex ordering such that is connected.
Proof. For any such
k, there is a vertex ordering
such that
is connected [
1]. ☐
Proposition 3. Let . Suppose there exists a vertex ordering π such that is connected. Then there exists an order for which is connected for all .
Proof. Let be the order obtained from by inserting one vertex of at the beginning of the ordering and all the others at the end. Note that the subgraph of induced by the set of canonical colourings in which every vertex of is coloured 1 is isomorphic to . Since, for any canonical colouring c, there is a path in to a canonical colouring in which every vertex of is coloured 1 and the colour of every vertex of G is the same as in c, the result follows. ☐
We note that connected cannot be replaced by Hamiltonian in the above proposition. It follows from Proposition 4 that, for example, there is no vertex ordering such that has a Hamilton cycle for any , and no ordering such that has a Hamilton path for any .
Corollary 7. Let H be a complete multipartite graph with p parts. For any , there exists a vertex ordering π such that is connected.
Proof. Suppose one of the maximal independents sets has size s. Take in Proposition 3, and apply the proposition inductively to construct H and . ☐
4. Bipartite Graphs
We now show that, once k is sufficiently large, there is always a vertex ordering such that the canonical k-colouring graph of a bipartite graph is connected. We then show that the bound given is the best possible.
Theorem 3. Let G be a bipartite graph on n vertices, then there exists an ordering π of the vertices such that is connected for .
Proof. Suppose G has bipartition , where . Choose , such that . Define to be . That is vertex a is coloured first, b is coloured second, the rest of B are the third through st vertices to be coloured, the rest of A are the nd through nth vertices to receive colours. Label the vertices according to this order.
The standard two colouring is if or , and otherwise. The method will be to show that any colouring can be obtained from the standard 2-colouring s in a finite number of steps.
First, suppose colour 1 is only used on vertices of A. In this case the colouring c can be transformed into s as follows. Recolour (if necessary) each vertex of A to colour 1 by recolouring from vertex down to , and then recolour each vertex of B to colour 2 by recolouring from vertex down to . It is clear that at every stage there is a proper colouring.
If colour 1 is used on vertices in both parts then the number of colours used on B is at most . Suppose exactly colours (including colour 1) are used on vertices in B, and let be the number of the first vertex to receive colour i, . That is and for all , . Clearly , and since c is a canonical colouring . Set .
We will use the to define an intermediate colouring by , for . This is a proper colouring because no colour is used on vertices in both parts B and A. It uses colours in total. The colours are used in numerical order, so it is canonical.
The proof is completed by showing that the standard colouring s can be transformed to colouring and colouring can be transformed to colouring c. Since colouring does not use any colour on both parts, the standard colouring s can be transformed to by changing the colours on to in order, if needed. That is change the colour on vertex from to the colour for .
Next transform
to
c. Do this by passing through the vertices from
to
r times, once for each of the
r colours used in
c. On the
kth pass change vertices to colour
k if they are colour
k in
c. That is, in pass
k, step
m we will change the colour of vertex
, only if
. We need to show that this gives a proper canonical colouring at every step. Let
be the colouring obtained after the
mth step in the
kth pass. Then
To see that each is proper, we must show that, , the set of vertices coloured i, is independent for all colours and all . For , the set of vertices coloured i in equals the set of vertices coloured i in c. Thus is an independent set for . For , the set of vertices coloured i in is a subset of the set of vertices coloured i in thus is an independent set for . It remains to consider . The vertices coloured k under are .
When then since and , we get , for all m so this is an independent set. At the other end, when all vertices coloured k by either colouring c or will be in part A. So is independent for all m.
If then only assigns colour k to vertices in part B. No vertex in part A is coloured k until the only vertices coloured k on part B are those coloured k under c. There are two cases.
If then all vertices coloured k in are in B so the set is independent.
If , this means that the only vertices in B that are still coloured k are coloured k under c, that is: . No vertices in A are coloured k under so if and , then and . Thus which is independent.
Finally we show the colourings are canonical. By construction, for all colours, i, , and no vertex before is coloured or higher in any of the colourings. Thus each of is a canonical proper colouring. ☐
Consider the graph , where F is a perfect matching. In the n-colouring of where the opposite ends of edges in F are assigned the same colour, every vertex has a neighbour of any different colour. Thus, if c is the canonical version of this colouring with respect to a vertex ordering , then c is an isolated vertex in . Since has vertices, it follows that the lower bound in the above theorem is the best possible.
By Corollary 7, there is always a vertex ordering
such that
is connected. We now show that there is no Hamilton cycle, and frequently no Hamilton path, in the canonical
k-colouring graph of a complete multipartite graph. By Corollary 4 it suffices to consider the case where
for all
i. The specific example of
will be considered in detail in
Section 5.
Proposition 4. Let , where , for all i. Then, for all vertex orderings π and ,
- 1.
has a cut vertex and hence has no Hamilton cycle;
- 2.
if then has no Hamilton path.
Proof. We first prove statement 1. The colouring c where every vertex in the ith part gets colour i is a cut vertex. Note that no colour can be used on vertices in more than one part. Any colouring where a vertex in part i gets colour cannot change to a colouring where a vertex in part j gets coloured without first changing the colour of . If the colour is removed from part i then no higher colour can be used without violating canonicity. So if there is a path from to , it must pass through c.
We now prove statement 2. If does not start with a maximum clique, then is disconnected by Proposition 1. Hence assume the first r vertices of induce a maximum clique. The argument above shows that the cut vertex c actually partitions the colourings into r cells, corresponding to using the colour in each of the r independent sets. Thus there can be no Hamilton path if there are at least three independent sets with at least two vertices each. ☐
By Proposition 4, for
and
, the graph
has a cut vertex, and hence no Hamilton cycle. On the other hand, for
, the graph
has a Hamilton cycle for all
[
1]. The possibility remains that the canonical
k-colouring graphs of complete bipartite graphs which are not stars have a Hamilton path. We show next that
in fact has a Hamilton path for all admissible values of
. To do so, we first give a Gray code (not cyclic) for
which has certain properties. The proof is recursive and similar to, but more elaborate than, that of Theorem 1.
Theorem 4. For all and , and any vertex ordering π, the graph has a Hamilton path such that:
- (i)
the colouring , and the colouring uses all k colours.
- (ii)
For each , the set of colours used by is identical to the set used by either , .
Proof. The sequences 11 and clearly work for and respectively. We induct first on n and then on k. Note that because colourings are canonical we only consider .
Let be a Hamilton path in with properties (i) and (ii). For , let denote the extension of to a canonical k-colouring of in which the last vertex is assigned colour ℓ. Observe that is adjacent to whenever both of these are canonical colourings.
First the special case . For a Hamilton path in is constructed from the one for as follows: .
For , a Hamilton path in can be constructed from the one for as follows. The first vertices are . Starting with , and then repeating for the next unused prefix , suppose is a maximal sequence such that each uses exactly the same set of colours, and suppose the maximum allowable colour that can be added to each of them is . We construct a Hamilton path on the subgraph induced by . These will be pieced together to get the Hamilton path for . This path must start with and end with .
Suppose j is odd. Take everything from each prefix before proceeding to the next prefix. In particular take the Hamilton path starting at and ending with for and in the reverse order and ending with for .
Suppose j is even. Recall that for , the subgraph induced by is complete, and by assumption . First use any Hamilton path through the subgraph induced by which starts at , and ends at and satisfies property (ii). Next, proceed as in the odd case alternating the direction of the Hamilton path, so that again the path through ends at .
In either case, the set of colours used on is identical for all except possibly when , and the set of colours used on is identical to the set of colours used on and these colourings are adjacent in the path. That the last colouring in the path uses all k colours follows from the induction hypothesis.
The Hamilton path for is obtained from the one of by appending to the last vertex in , which will be of the form . ☐
The properties for the Hamilton paths required in the above proof are similar to those studied by various authors in the context of Gray codes for set partitions. In [
19] the authors give Gray codes for the set of restricted growth functions, which is the set of non-negative integer sequences
. While these Gray codes start with
and end with
, they do not have the property that at least two sequences in a row use the same set of integers (see for example Figure 5 in [
19]). The set of bounded restricted growth functions is
. Ruskey and Savage also considered Gray codes on
, but restrict their attention to strict and weak Gray codes which have the further property that successive elements can differ by only 1 (if strict) or 2 (weak) in the one position in which they differ. They show that such codes cannot exist. In the Gray codes considered here, successive sequences can differ in only one position, but the elements can differ by any amount. In other words, Theorem 4 says there is a (non strict, non weak) Gray Code for the set of bounded restricted growth functions,
, that satisfies properties (i) and (ii).
Theorem 5. There exists a vertex ordering π such that has a Hamilton path for , .
Proof. Let have bipartition , where , . Let the vertex ordering .
By Theorem 4 there is a Hamilton path, , with properties (i) and (ii), in the canonical k-colouring graph of the subgraph induced by the restriction of to its first vertices, (since is an independent set, and will always be assigned the same colour in any canonical colouring). For each such colouring , let be the subgraph of consisting of the canonical colourings which are extensions of . Note that each subgraph is isomorphic to a graph , corresponding to the colourings of the vertices in the colours not used on (starting with 2 which was the colour used on ), and also that .
The Hamilton path in will be constructed by piecing together Hamilton paths from the in the order . In order to be able to piece these paths together, the first colouring in the Hamilton path of must be identical to the last colouring in the Hamilton path of . Note that if and use different colours then the only colouring that and will have in common is . For each there is a Hamilton path that satisfies the conditions of Theorem 4, in this case one end is and the other uses all the colours of .
Suppose that is a maximal sequence which use the same set of colours, and further that neither nor . The Hamilton path from that is used must start with and the one from must end with . If j is odd, this is accomplished by taking the Hamilton path starting at for , for , and ending with for for . If j is even, then first use a Hamilton path through the subgraph induced by which starts with and ends in a colouring that uses all the colours. Then proceed as in the even case alternating the direction of the Hamilton path, so that the Hamilton path through can end with .
We finish the argument by reiterating the conditions that must hold for the construction to succeed. The Hamilton path in the subgraph induced by the canonical k-colourings of the first vertices of needs the property that for each , the set of colours used for is identical to the set used on either , or . In addition, for each , there should be a Hamilton path in that starts with . These are precisely the conditions guaranteed by our choice of the Hamilton path . ☐
5.
For , let be the complete n-partite graph on vertices in which each independent set is size two. Then , , , and so on.
The purpose of this section is to study the canonical k-colouring graphs of . The results proved in this section are summarized in Theorem 6 below. In the cases where the canonical colour graph is connected, we describe it completely.
Theorem 6. Let . Then
- 1.
for any vertex ordering π.
- 2.
If , then for any vertex ordering π.
- 3.
If and the subgraph of induced by the first n vertices in the vertex ordering π is not complete, then is disconnected.
- 4.
If and the subgraph of induced by the first n vertices in the vertex ordering π is complete, then is a tree. Further, if and are both trees, then .
- 5.
never has a Hamilton cycle and has a Hamilton path only when , .
Statements 1 and 2 are clear. Statement 3 is immediate by Proposition 1. The proof of statement 4 is partitioned into a sequence of propositions. First, we consider the graphs , for vertex orderings that start with a maximal clique. The graphs , with , will be considered later. According to statement 2 we need not consider the situations in which .
Proposition 5. Let . If the subgraph of induced by the first n vertices in the sequence π is complete, then is a tree on vertices. Further, if the subgraph of induced by the first n vertices in the sequence ϕ is complete, then .
Proof. In any colouring of , a pair of independent vertices either has the same colour, or different colours. In the latter case, each vertex in the pair is the only vertex to be assigned that colour. Suppose that the last n vertices of are . A canonical -colouring with respect to can be encoded as a binary sequence of length n in which the i-th element is 0 if vertex is assigned the same colour as its unique non-neighbour (which is one of the first n vertices of ), and 1 if it is assigned the first colour not used on a vertex earlier in the sequence. Thus, has precisely vertices.
We claim that an element of the binary sequence can change (from 0 to 1, or 1 to 0) if and only if for all . Suppose that is the only vertex of its colour, that is, it has a different colour than its unique non-neighbour, w, and . If there exists such that also has a different colour than its unique non-neighbour, then the colouring arising from assigning the colour of w to is not canonical (because the colour of , which is smaller than the colour of , would not be used on any vertex). Similarly, if has the same colour as its unique non-neighbour, then it can only be assigned a different colour if there is no such that has a different colour than its unique non-neighbour. This proves the claim.
We now show that, for any such sequence
, the graph
is a tree. According to the discussion above, the vertices of
can be taken to be the binary sequences of length
n, with two sequences being adjacent if and only if they differ in exactly one position, and all entries to the right of that position are zero. Since any binary sequence can be reached from
by introducing 1s from left to right, the graph
is connected. The proof is complete once we show that the sum of the vertex degrees equals
. The degree of
is
n. Any other binary sequence contains at least one 1. If the rightmost 1 is in position
i then the degree of
is
and the number of such sequences is
. Hence, the sum of the vertex degrees is
Since the description of uses no properties of other than that the subgraph of induced by the first n vertices of is complete, it is clear that any two trees arising from such sequences are isomorphic. This can also be proved by induction on n by using the observation that the subtree induced by the set of sequences in which the first entry is 0 is isomorphic to , as is the subtree induced by the set of sequences in which the first entry is 1. ☐
The argument above shows that, for , the leaves of correspond to precisely the binary sequences in which . Thus, has exactly leaves, and hence never has a Hamilton cycle. There is a Hamilton path only when (recall that , and ).
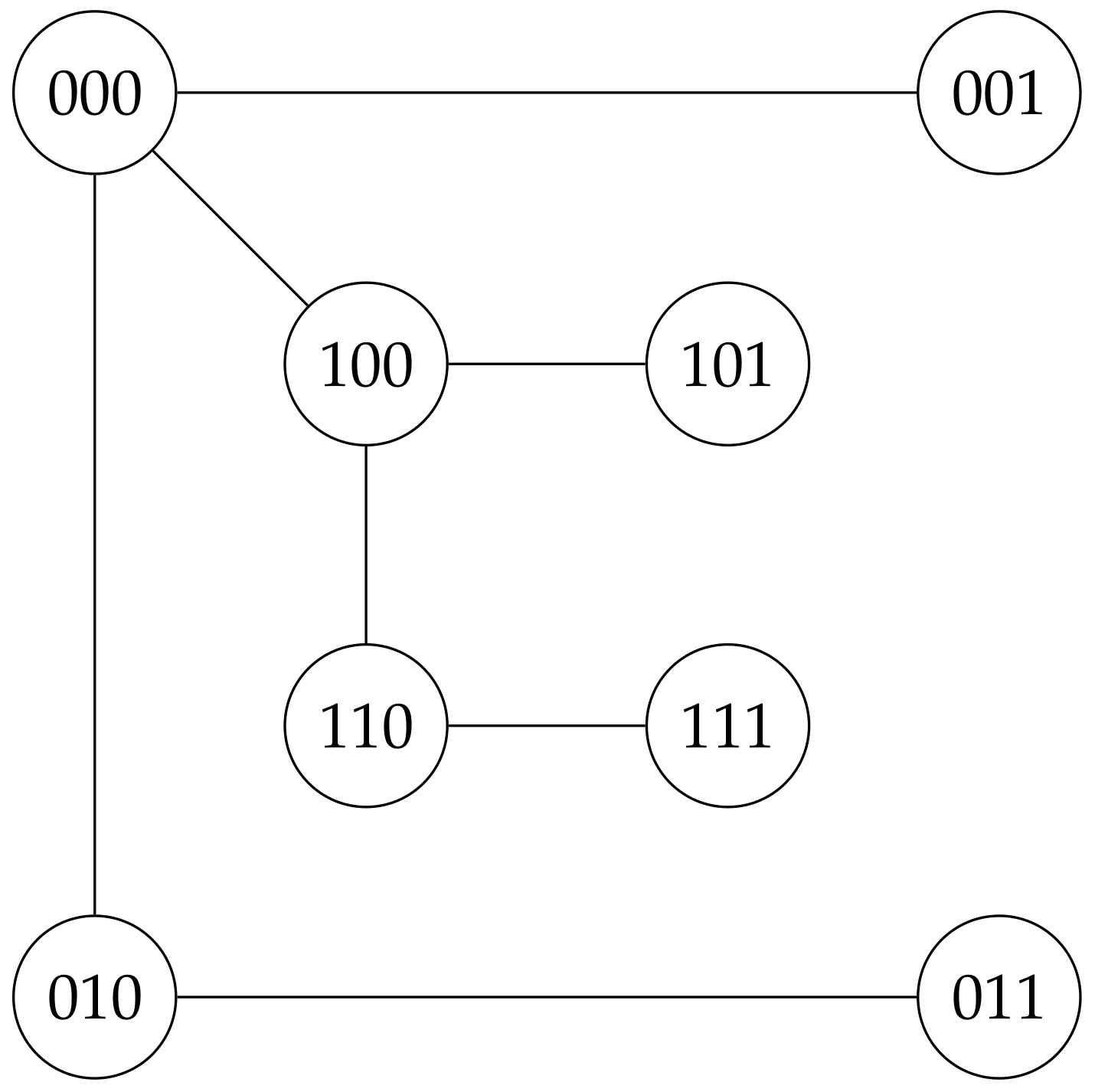
For an ordering
such that the subgraph induced by the first
n vertices is complete, the tree
is shown in
Figure 4. For any such ordering, the tree
is constructed from two copies of this tree, one arising from concatenating a 1 on the left of each sequence and the other arising from concatenating a 0 on the left of each sequence, and then joining the vertices 0000 and 1000.
It remains to consider the graphs for and sequences for which the first n vertices is complete.
Proposition 6. Let and . If the subgraph of induced by the first n vertices in the sequence π is complete, then is a tree on vertices. Further, if the subgraph of induced by the first n vertices in the sequence ϕ is complete, then .
Proof. Observe that is the subgraph of induced by the sequences with at most ones. There are such sequences. Hence has exactly vertices.
As before, since any binary sequence with at most t ones can be reached from by introducing ones from left to right, the graph is connected, and therefore is a tree. In addition, as before, the description of uses no properties of other than that of the subgraph of induced by the first n vertices of is complete. Thus, once again it is clear that any two trees arising from such sequences are isomorphic. ☐
For and , the leaves of the tree are the binary sequences with exactly k ones and a zero in the last position, or with at most k ones and a one in the last position. Hence there cannot be a Hamilton cycle, and there is a Hamilton path only when and .
The proof of Theorem 6 is now complete.