A Gradient-Based Cuckoo Search Algorithm for a Reservoir-Generation Scheduling Problem
Abstract
:1. Introduction
2. Reservoir-Scheduling Problem
2.1. Long-Term Hydropower-Generation Scheduling (LHGS) Model
2.2. Constraints
3. Cuckoo Search Algorithm
3.1. Basic Cuckoo Search Algorithm
- Each cuckoo lays one egg at a time, and dumps its egg in randomly chosen nest;
- The best nests with a high quality of eggs will carry over to the next generation;
- The number of available host nests is fixed, and the egg laid by a cuckoo is discovered by the host bird with a probability pa. Discovering operates on some set of the worst nests, and discovered solutions are dumped from further calculations.
| Algorithm 1. Cuckoo search via Lévy flights |
| Objective function Generate initial population of n host nests While (t < MaxIteration) or (stop criterion) Get a cuckoo i randomly by Lévy flights and evaluate its fitness Choose a nest j among n randomly If Replace by the new solution End if If Init the worst nest End if If Replace by End if End while |
3.2. Improvement for Cuckoo Search Algorithm
3.2.1. Dynamic Parameter Adjustment Strategy
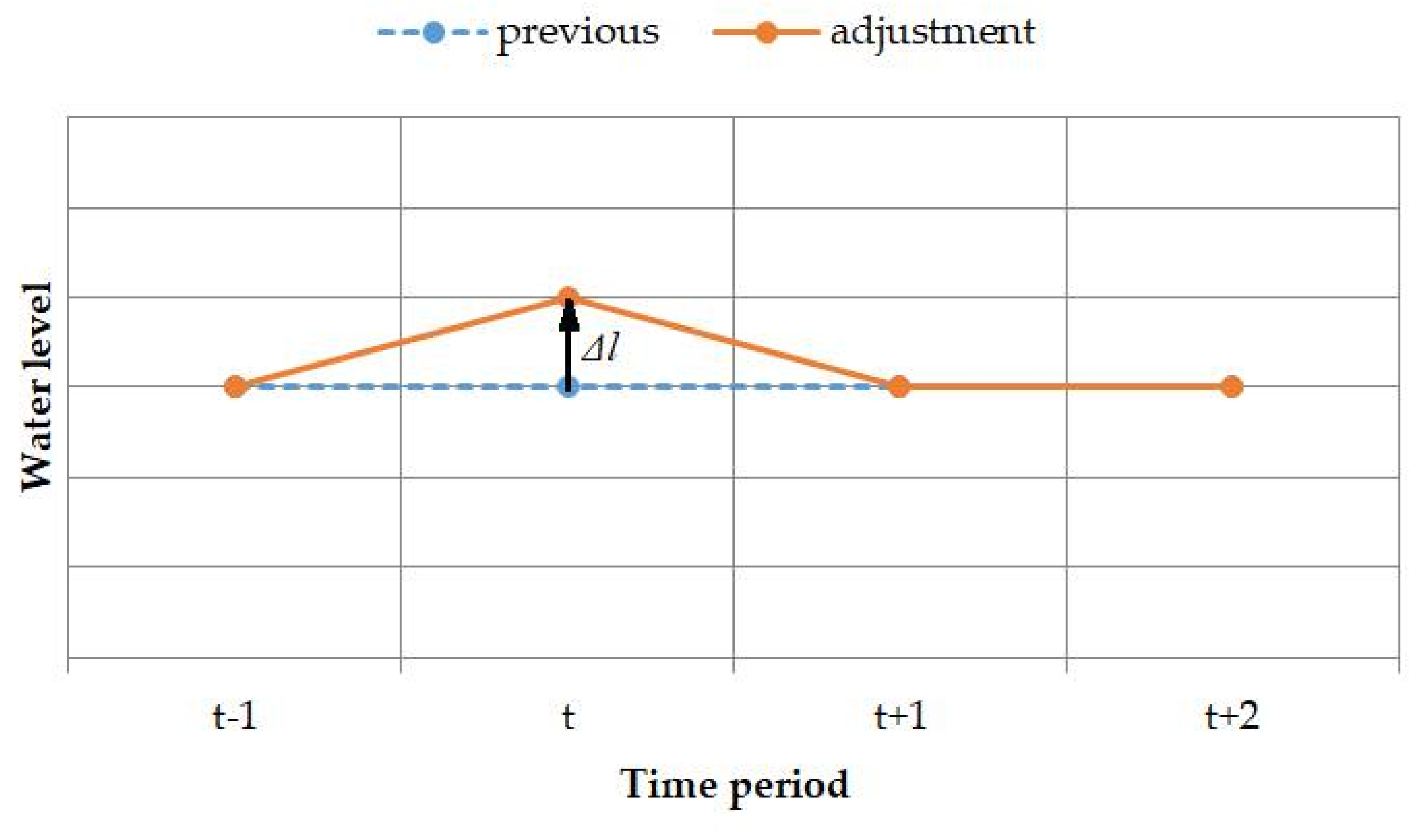
3.2.2. A Boundary Value Perturbation Strategy
3.2.3. Differential Strategy for Lévy Flight
3.2.4. Solution Updates Strategy Changes
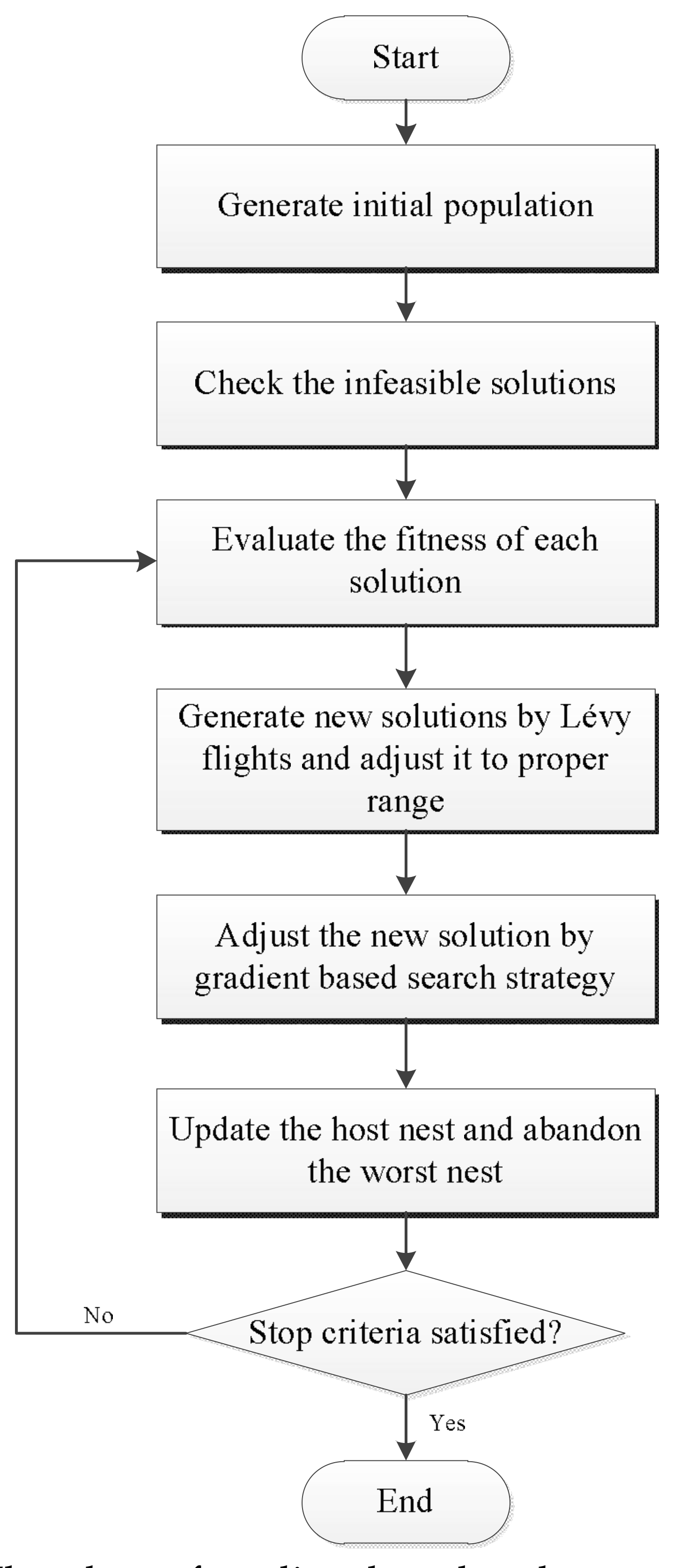
3.3. Implementation of Improved Cuckoo Search (ICS)
| Algorithm 2. Improved cuckoo search |
| Objective function Initialize default parameters Generate initial population of n host nests While (t < MaxEvaluation) or (stop criterion) Select two solution from host nests randomly For d=1,...,D do End for If Replace by the new solution End if If Init the worst nest End if End while |
4. Gradient Cuckoo Search for Reservoir Scheduling
4.1. Constraints Handling
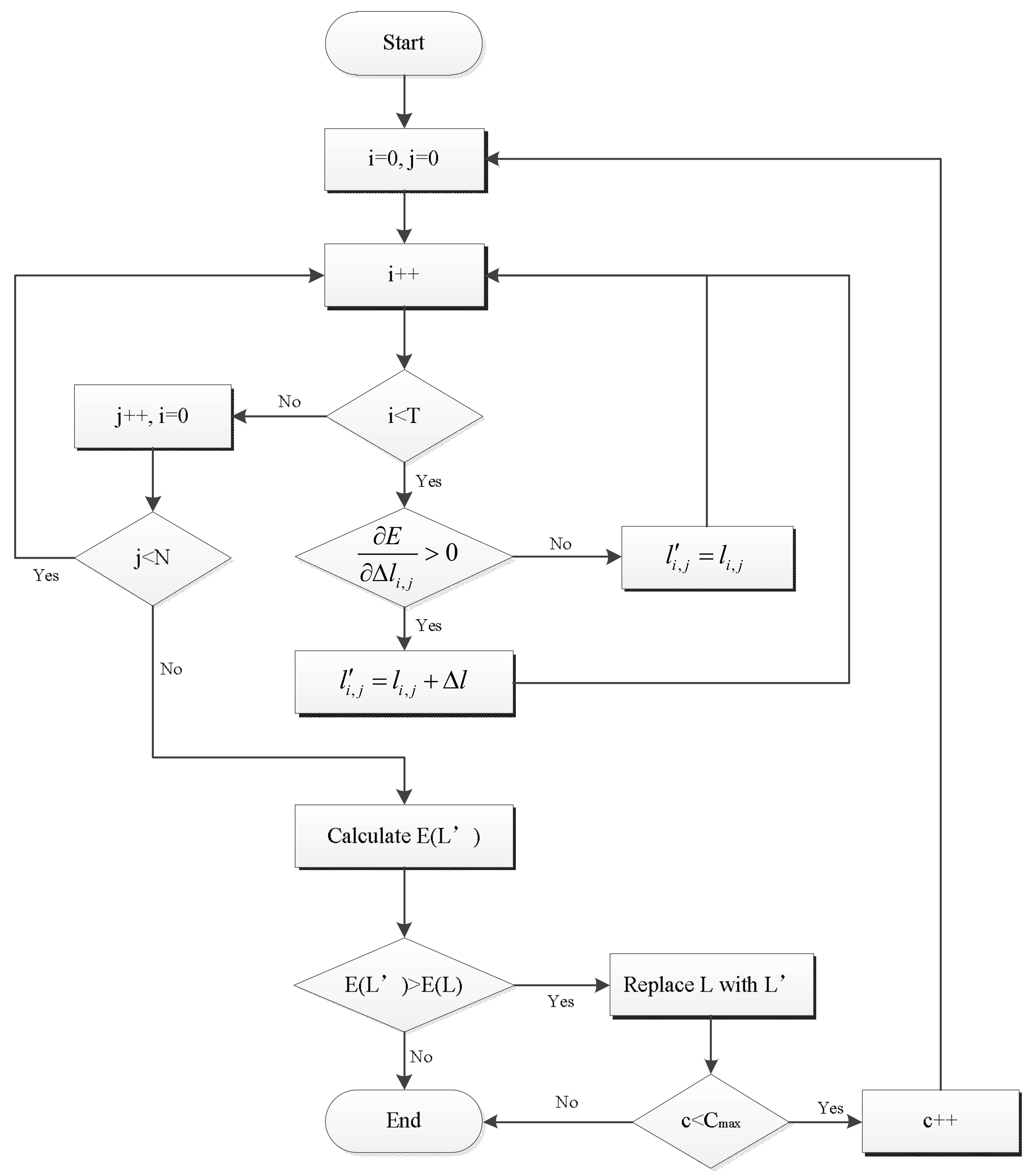
4.2. Gradient-Based Search Strategy
4.3. Implementation of Gradient-Based Cuckoo Search (GCS) for Long-Term Hydropower Generation Scheduling (LHGS)
- Step 1:
- Randomly generate feasible initial solutions.
- Step 2:
- Evaluate fitness of the solutions.
- Step 3:
- Generate new solutions by Lévy flights.
- Step 4:
- If the new solution is infeasible, adjust it by two-way solution correction strategy.
- Step 5:
- Adjust the new solution by gradient-based search strategy.
- Step 6:
- Update the host nest.
- Step 7:
- Abandon the worst nest.
- Step 8:
- Repeat Steps 3 to 7 until the stop criteria is reached.
5. Case Study
5.1. Study Area
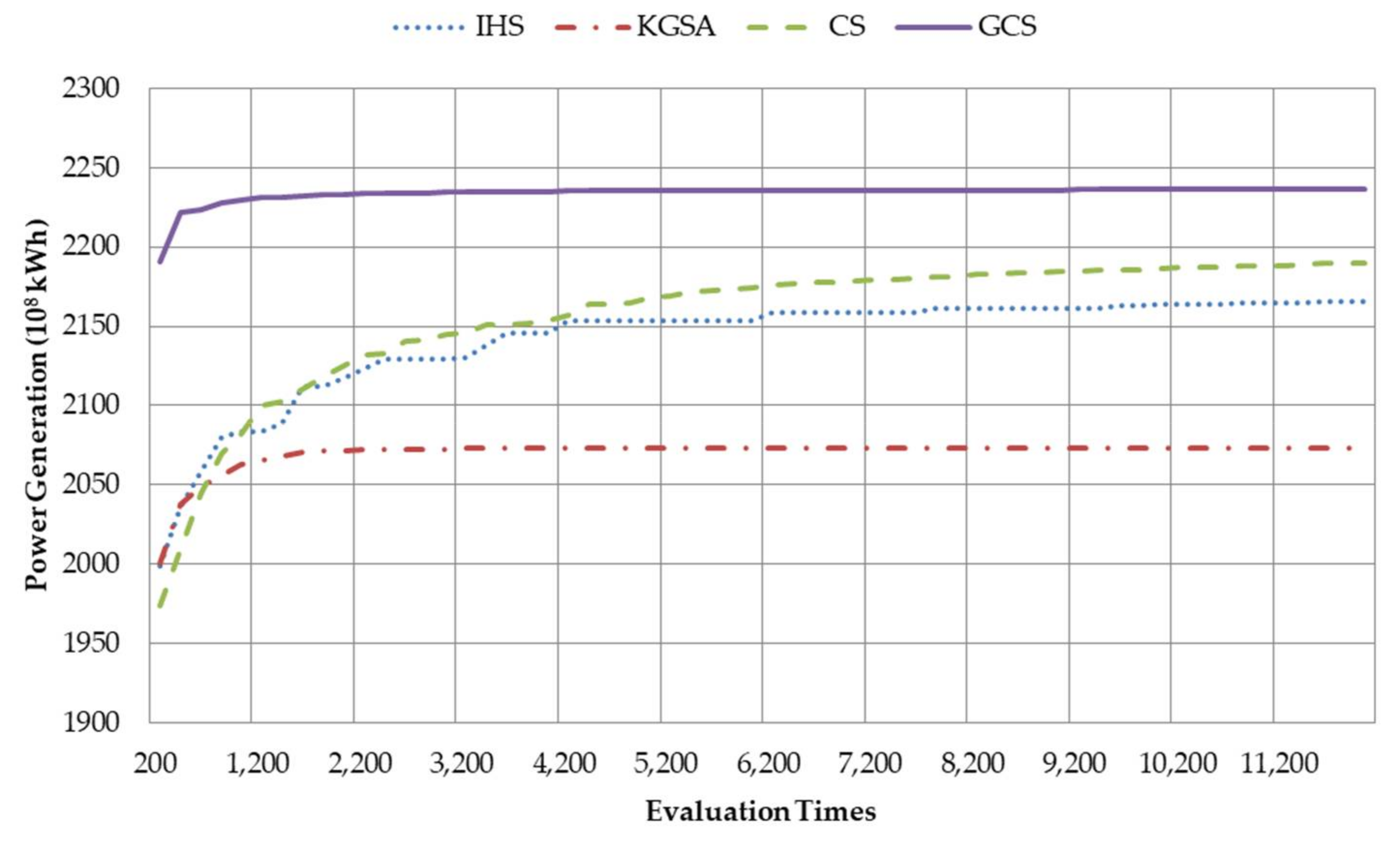
5.2. Benchmark Function Tests
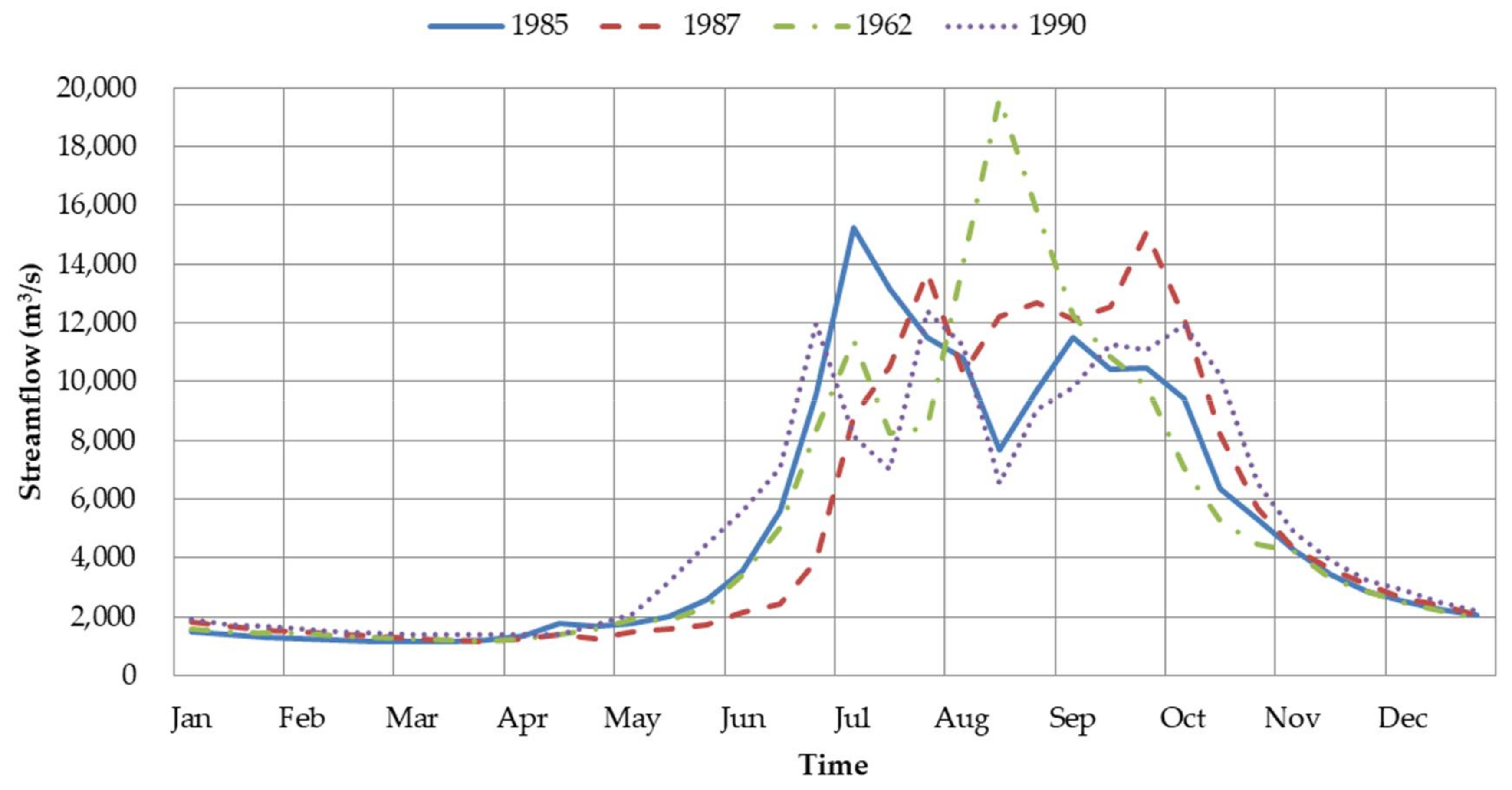
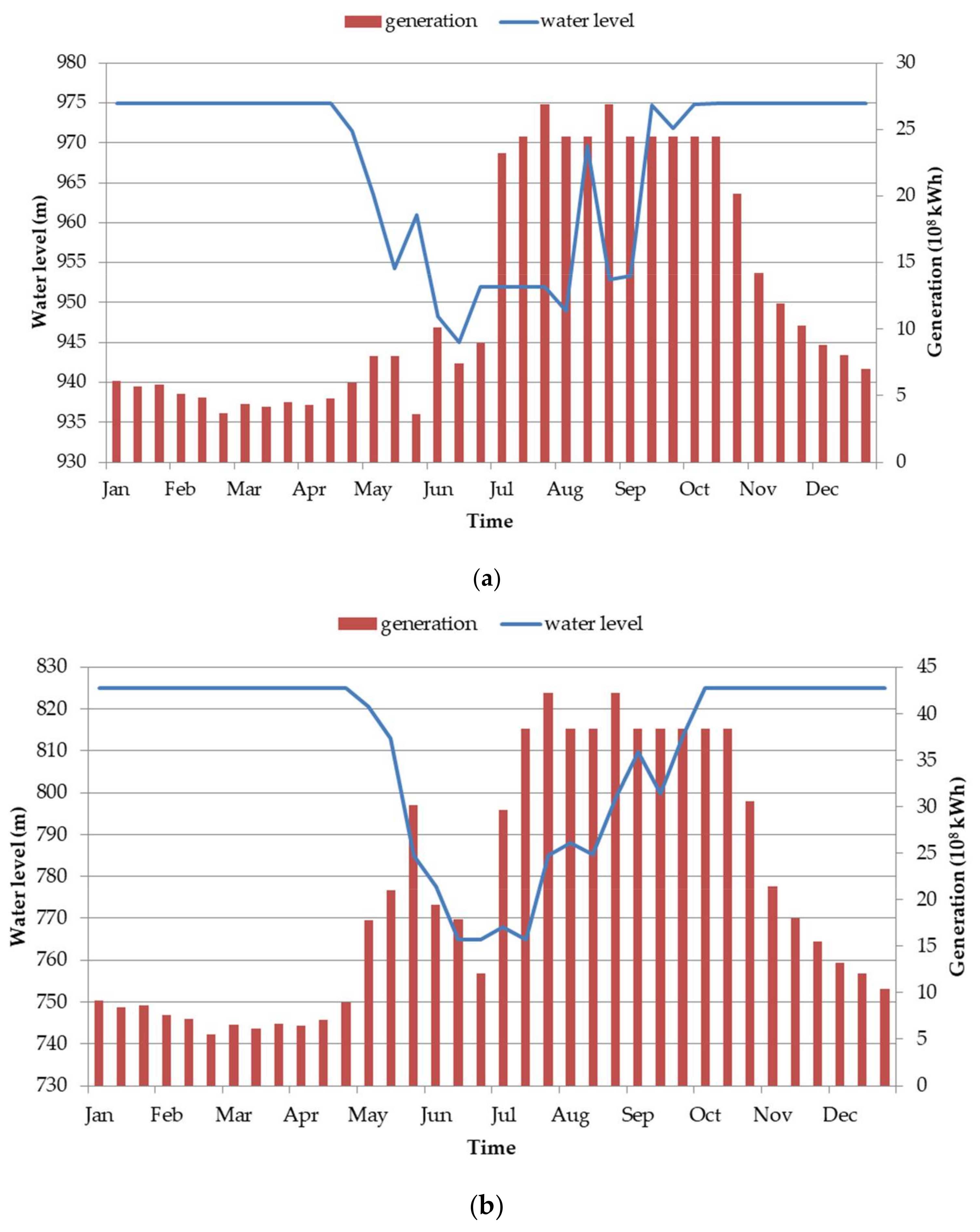
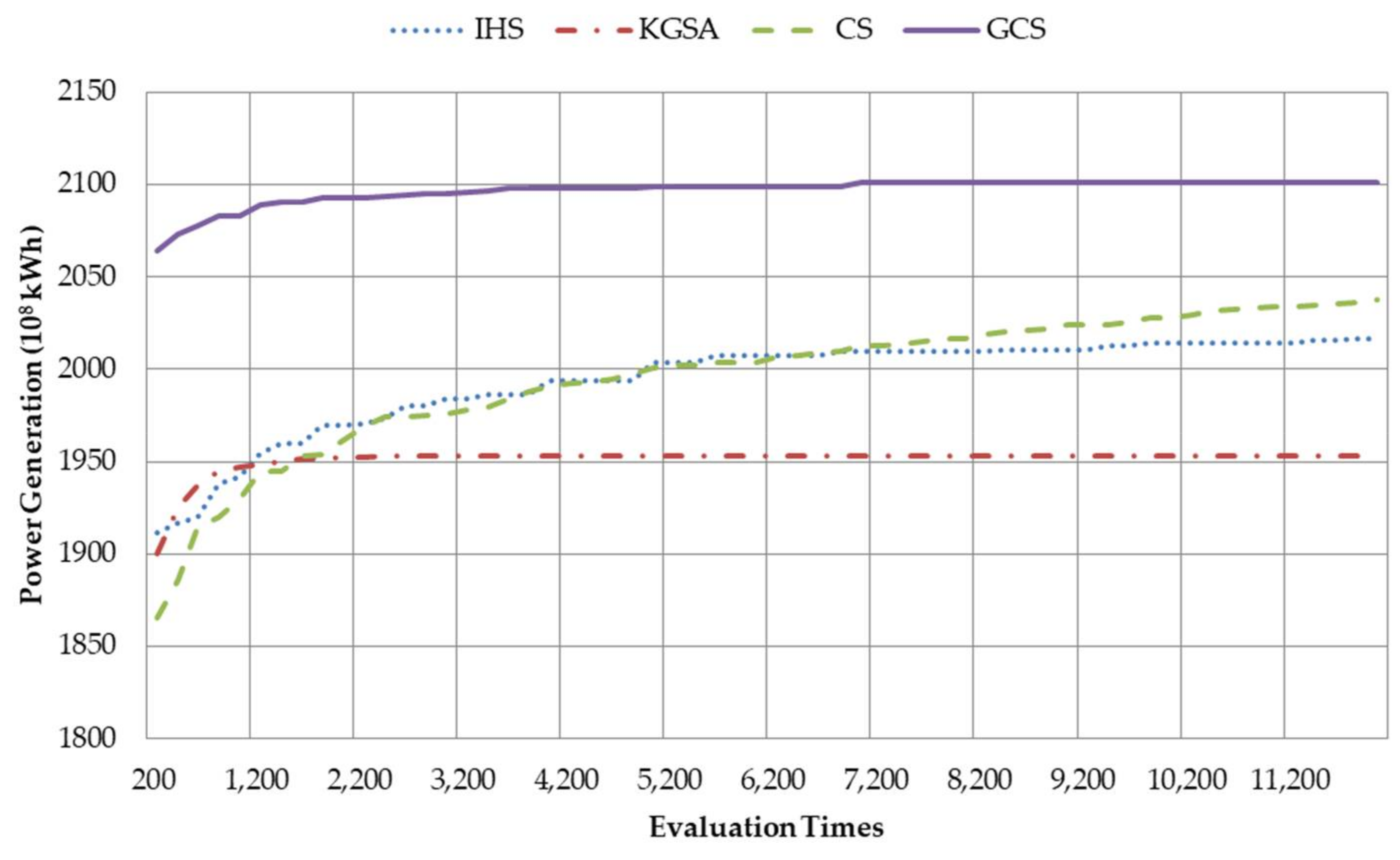
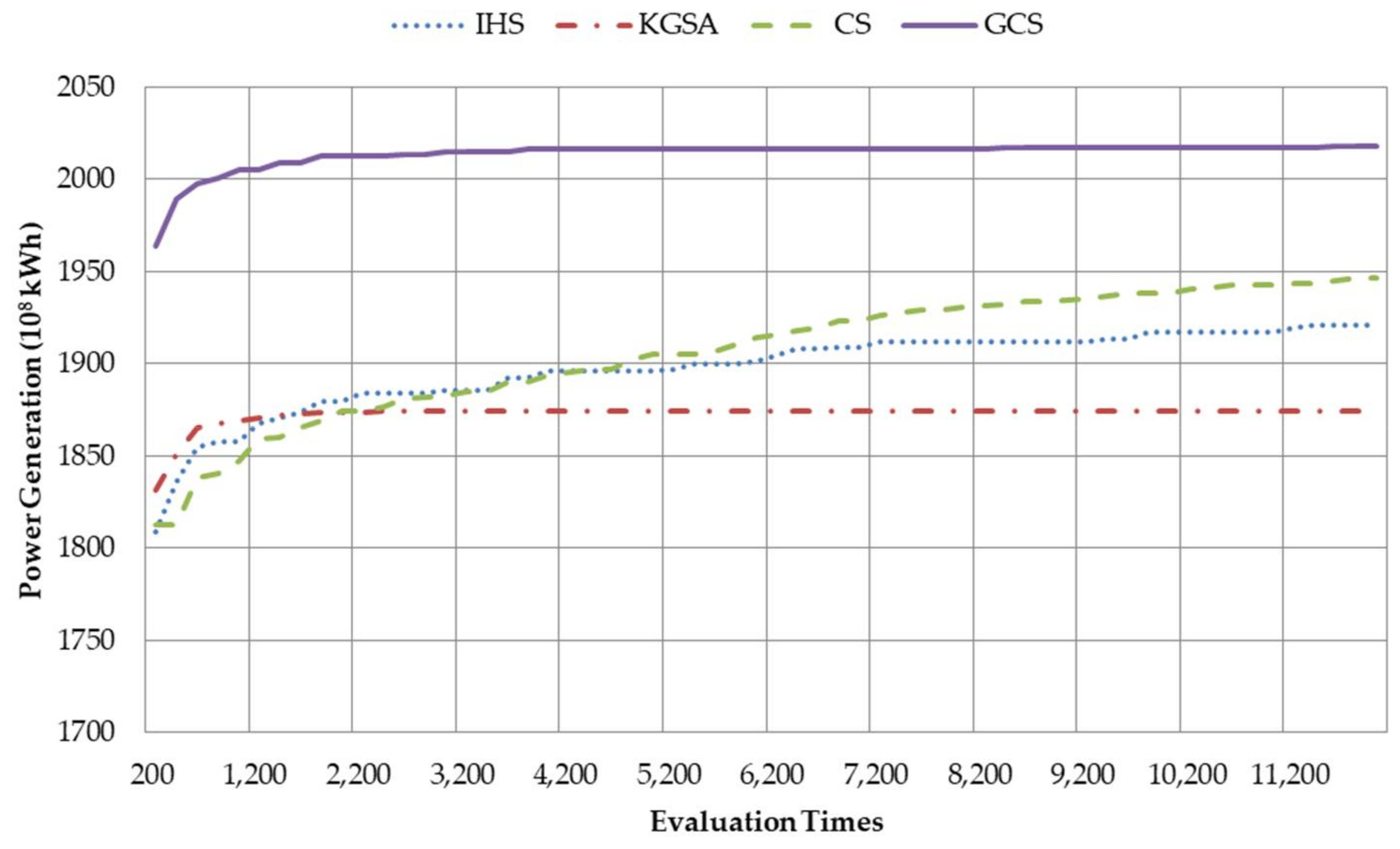
5.3. Reservoir Scheduling in Wet Years
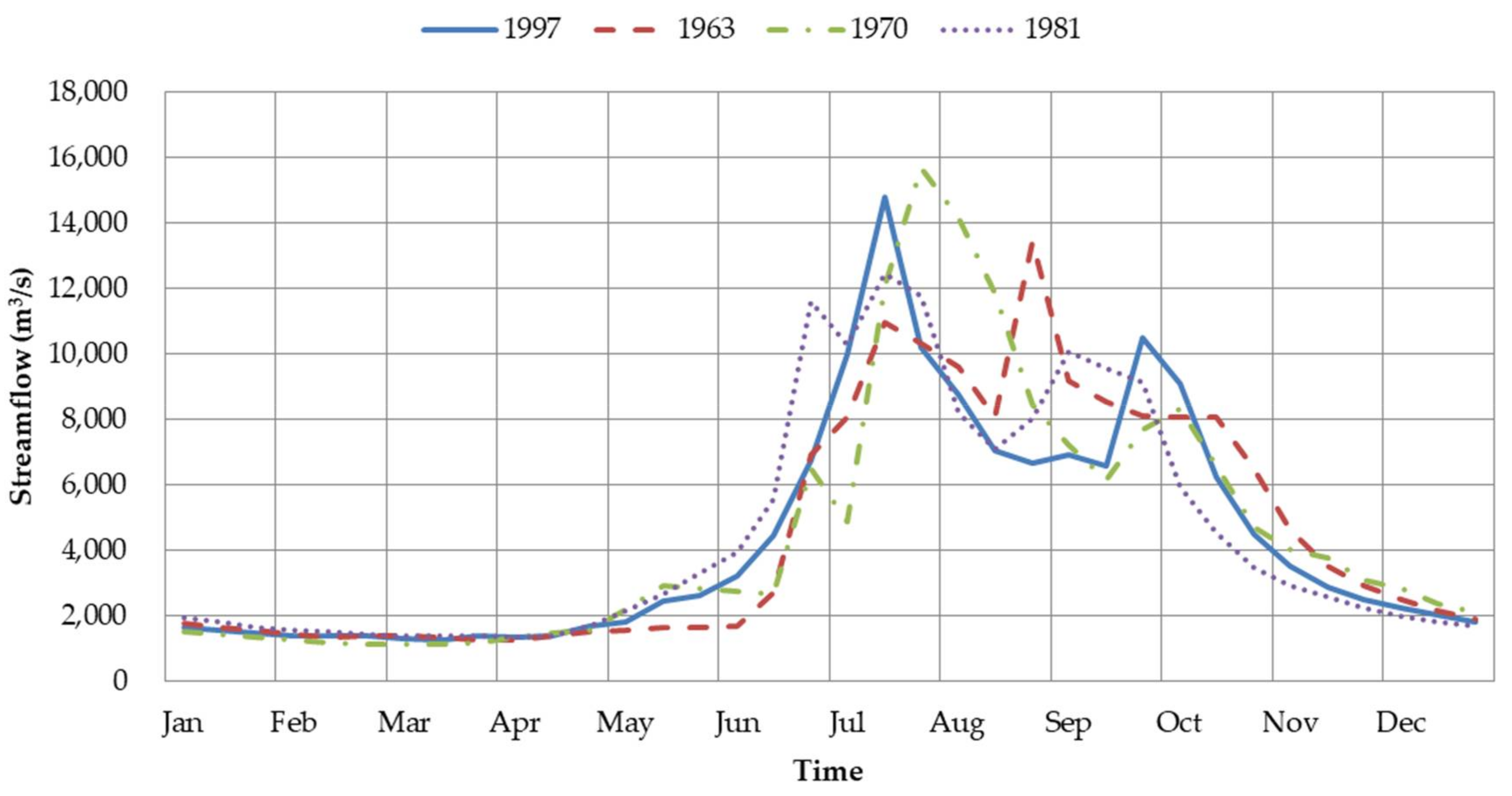
5.4. Reservoir Scheduling in Normal Years
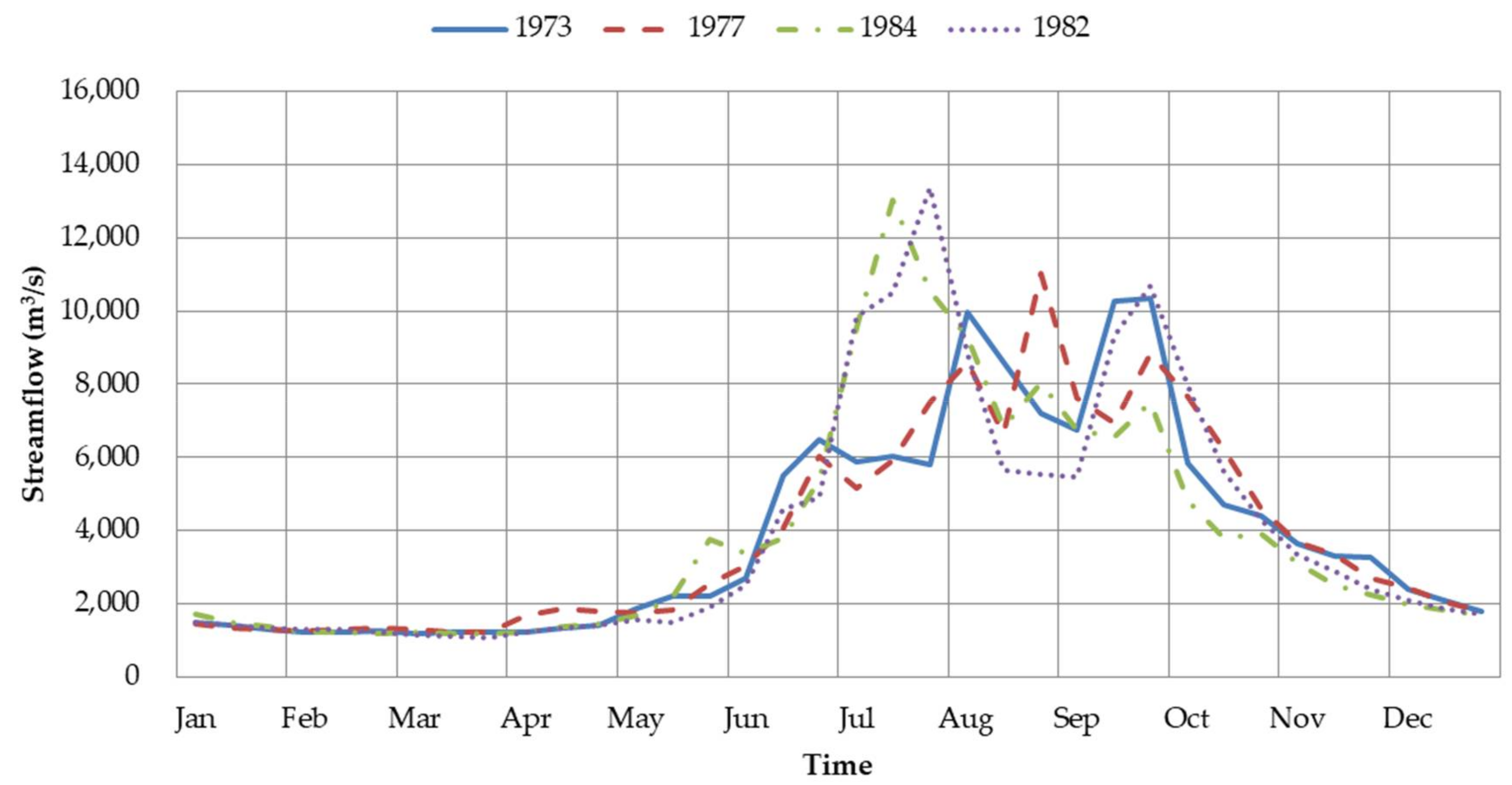
5.5. Reservoir Scheduling in Dry Years
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Reddy, S.S.; Momoh, J.A. Realistic and transparent optimum scheduling strategy for hybrid power system. IEEE Trans. Smart Grid 2015, 6, 3114–3125. [Google Scholar] [CrossRef]
- Reddy, S.S.; Abhyankar, A.R.; Bijwe, P.R. Market clearing for a wind-thermal power system incorporating wind generation and load forecast uncertainties. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Reddy, S.S.; Panigrahi, B.K.; Kundu, R.; Mukherjee, R.; Debchoudhury, S. Energy and spinning reserve scheduling for a wind-thermal power system using cma-es with mean learning technique. Int. J. Electr. Power Energy Syst. 2013, 53, 113–122. [Google Scholar] [CrossRef]
- Reddy, S.S.; Bijwe, P.R.; Abhyankar, A.R. Real-time economic dispatch considering renewable power generation variability and uncertainty over scheduling period. IEEE Syst. J. 2015, 9, 1440–1451. [Google Scholar] [CrossRef]
- Liao, X.; Zhou, J.; Ouyang, S.; Zhang, R.; Zhang, Y. An adaptive chaotic artificial bee colony algorithm for short-term hydrothermal generation scheduling. Int. J. Electr. Power Energy Syst. 2013, 53, 34–42. [Google Scholar] [CrossRef]
- Tian, H.; Yuan, X.; Ji, B.; Chen, Z. Multi-objective optimization of short-term hydrothermal scheduling using non-dominated sorting gravitational search algorithm with chaotic mutation. Energy Convers. Manag. 2014, 81, 504–519. [Google Scholar] [CrossRef]
- Wang, K.W.; Chang, L.C.; Chang, F.J. Multi-tier interactive genetic algorithms for the optimization of long-term reservoir operation. Adv. Water Resour. 2011, 34, 1343–1351. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, J.; Fang, N.; Zhang, R.; Zhang, Y. An efficient multi-objective adaptive differential evolution with chaotic neuron network and its application on long-term hydropower operation with considering ecological environment problem. Int. J. Electr. Power Energy Syst. 2013, 45, 60–70. [Google Scholar] [CrossRef]
- Liao, X.; Zhou, J.; Zhang, R.; Zhang, Y. An adaptive artificial bee colony algorithm for long-term economic dispatch in cascaded hydropower systems. Int. J. Electr. Power Energy Syst. 2012, 43, 1340–1345. [Google Scholar] [CrossRef]
- Soares, S.; Ohishi, T.; Cicogna, M.; Arce, A. Dynamic Dispatch of Hydro Generating Units. In Proceedings of the 2003 IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003; Volume 2, p. 6. [Google Scholar]
- Cheng, C.T.; Liao, S.L.; Tang, Z.T.; Zhao, M.Y. Comparison of particle swarm optimization and dynamic programming for large scale hydro unit load dispatch. Energy Convers. Manag. 2009, 50, 3007–3014. [Google Scholar] [CrossRef]
- Tu, M.-Y.; Hsu, N.-S.; Yeh, W.W.-G. Optimization of reservoir management and operation with hedging rules. J. Water Resour. Plan. Manag. 2003, 129, 86–97. [Google Scholar] [CrossRef]
- Juhwan, Y. Maximization of hydropower generation through the application of a linear programming model. J. Hydrol. 2009, 376, 182–187. [Google Scholar]
- Nanda, J.; Bijwe, P.R. Optimal hydrothermal scheduling with cascaded plants using progressive optimality algorithm. IEEE Trans. Power Appar. Syst. 1981, PAS-100, 2093–2099. [Google Scholar] [CrossRef]
- Cheng, C.; Shen, J.; Wu, X. Short-term scheduling for large-scale cascaded hydropower systems with multivibration zones of high head. J. Water Resour. Plan. Manag. 2011, 138, 257–267. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Tauxe, G.W. Computer time and memory requirements for DP and DDDP in water resource systems analysis. Water Resour. Res. 1975, 11, 621–628. [Google Scholar] [CrossRef]
- Cheng, C.; Wang, S.; Chau, K.W.; Wu, X. Parallel discrete differential dynamic programming for multireservoir operation. Environ. Model. Softw. 2014, 57, 152–164. [Google Scholar] [CrossRef]
- Wang, C.; Zhou, J.; Peng, L.; Liu, Y. Long-term scheduling of large cascade hydropower stations in Jinsha River, China. Energy Convers. Manag. 2015, 90, 476–487. [Google Scholar] [CrossRef]
- Beck, A.T.; Gomes, W.J.D.S. A comparison of deterministic, reliability-based and risk-based structural optimization under uncertainty. Probab. Eng. Mech. 2012, 28, 18–29. [Google Scholar] [CrossRef]
- Yoo, D.G. Improved mine blast algorithm for optimal cost design of water distribution systems. Eng. Optim. 2014, 47, 1602–1618. [Google Scholar]
- Almasi, M.H.; Sadollah, A.; Mounes, S.M.; Karim, M.R. Optimization of a transit services model with a feeder bus and rail system using metaheuristic algorithms. J. Comput. Civ. Eng. 2015, 29, 04014090. [Google Scholar] [CrossRef]
- Moeini, R.; Soltani-Nezhad, M.; Daei, M. Constrained gravitational search algorithm for large scale reservoir operation optimization problem. Eng. Appl. Artif. Intell. 2017, 62, 222–233. [Google Scholar] [CrossRef]
- Bianchi, L.; Dorigo, M.; Gambardella, L.M.; Gutjahr, W.J. A survey on metaheuristics for stochastic combinatorial optimization. Nat. Comput. 2009, 8, 239–287. [Google Scholar] [CrossRef]
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. 2003, 35, 268–308. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo search via levy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Ouyang, P.; Pano, V. Comparative study of de, pso and ga for position domain pid controller tuning. Algorithms 2015, 8, 697–711. [Google Scholar] [CrossRef]
- Rabanal, P.; Rodríguez, I.; Rubio, F. Parallelizing particle swarm optimization in a functional programming environment. Algorithms 2014, 7, 554–581. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Vo, D.N. Modified cuckoo search algorithm for multiobjective short-term hydrothermal scheduling. Swarm Evol. Comput. 2017, 37, 73–89. [Google Scholar] [CrossRef]
- Din, M.; Pal, S.K.; Muttoo, S.K.; Jain, A. Applying cuckoo search for analysis of lfsr based cryptosystem. Perspect. Sci. 2016, 8, 435–439. [Google Scholar] [CrossRef]
- Bhateja, A.K.; Bhateja, A.; Chaudhury, S.; Saxena, P.K. Cryptanalysis of vigenere cipher using cuckoo search. Appl. Soft Comput. 2015, 26, 315–324. [Google Scholar] [CrossRef]
- Naik, M.K.; Panda, R. A novel adaptive cuckoo search algorithm for intrinsic discriminant analysis based face recognition. Appl. Soft Comput. 2016, 38, 661–675. [Google Scholar] [CrossRef]
- Walton, S.; Hassan, O.; Morgan, K.; Brown, M.R. Modified cuckoo search: A new gradient free optimisation algorithm. Chaos Solitons Fractals 2011, 44, 710–718. [Google Scholar] [CrossRef]
- Mlakar, U.; Fister, I., Jr.; Fister, I. Hybrid self-adaptive cuckoo search for global optimization. Swarm Evol. Comput. 2016, 29, 47–72. [Google Scholar] [CrossRef]
- Du, X.; Wang, J.; Jegatheesan, V.; Shi, G. Parameter estimation of activated sludge process based on an improved cuckoo search algorithm. Bioresour. Technol. 2017, 249, 447–456. [Google Scholar] [CrossRef] [PubMed]
- Mahdavi, M.; Fesanghary, M.; Damangir, E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. Gsa: A gravitational search algorithm. Inform. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
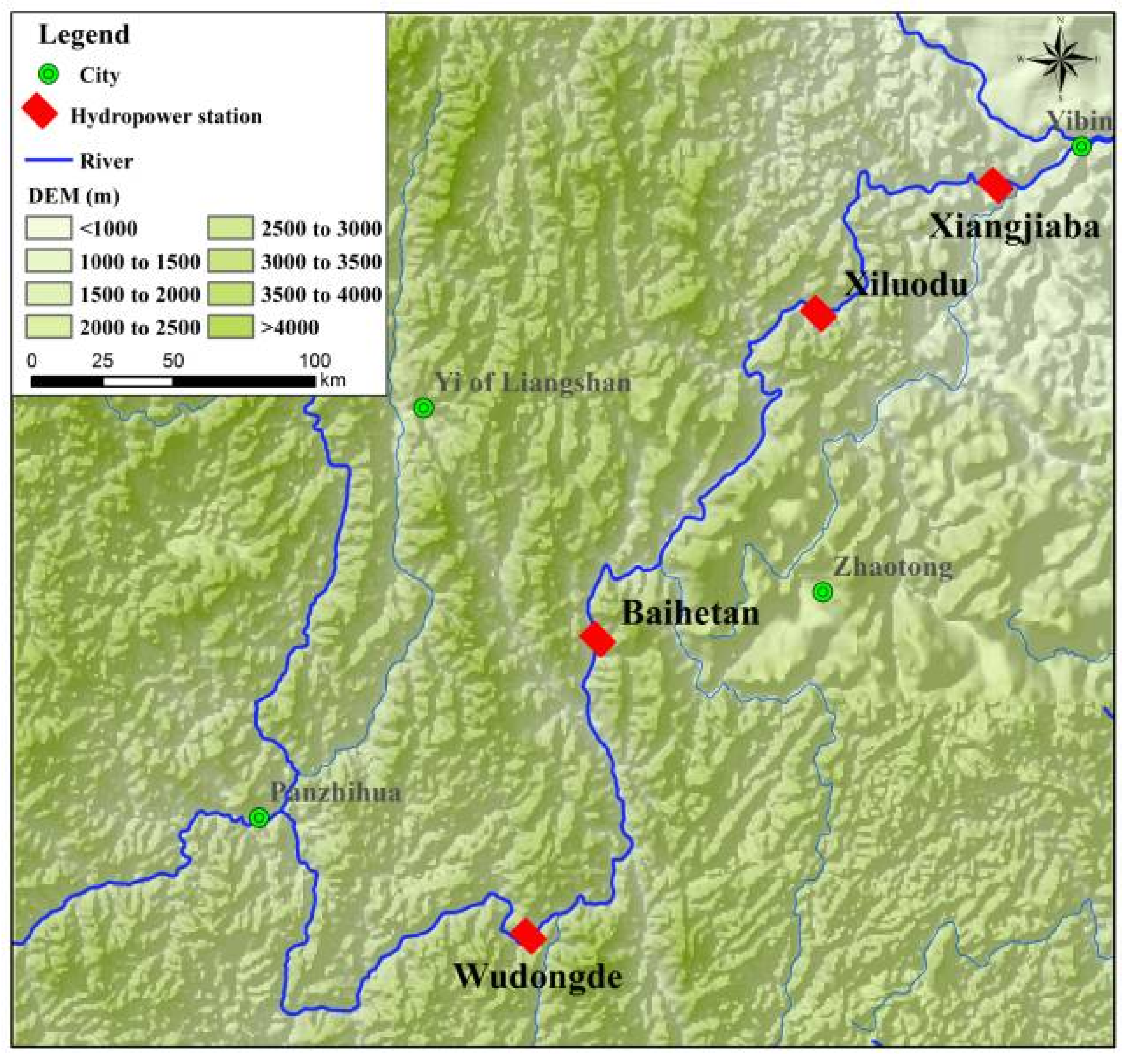
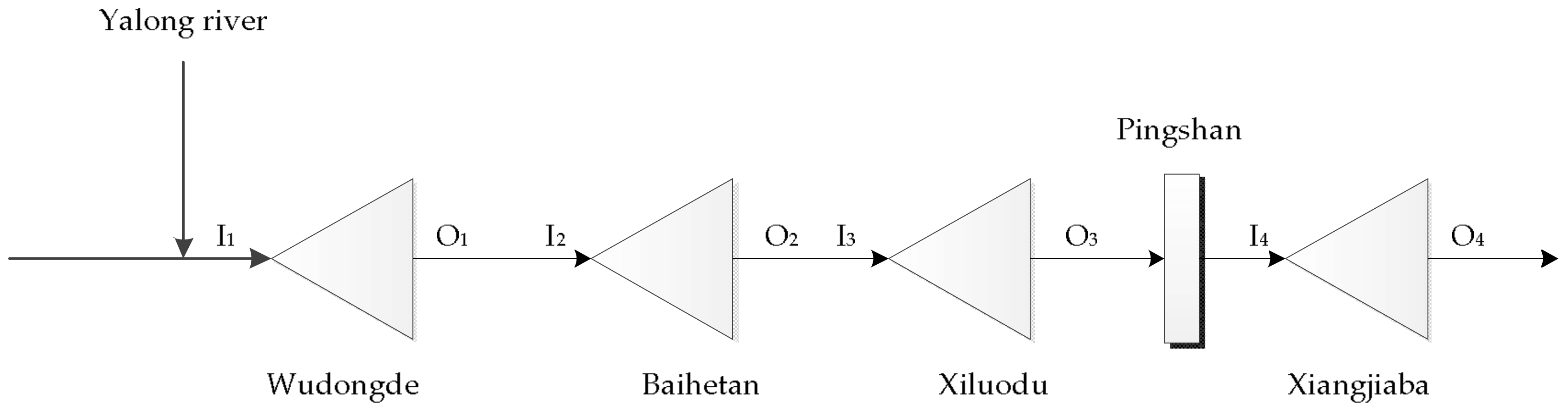
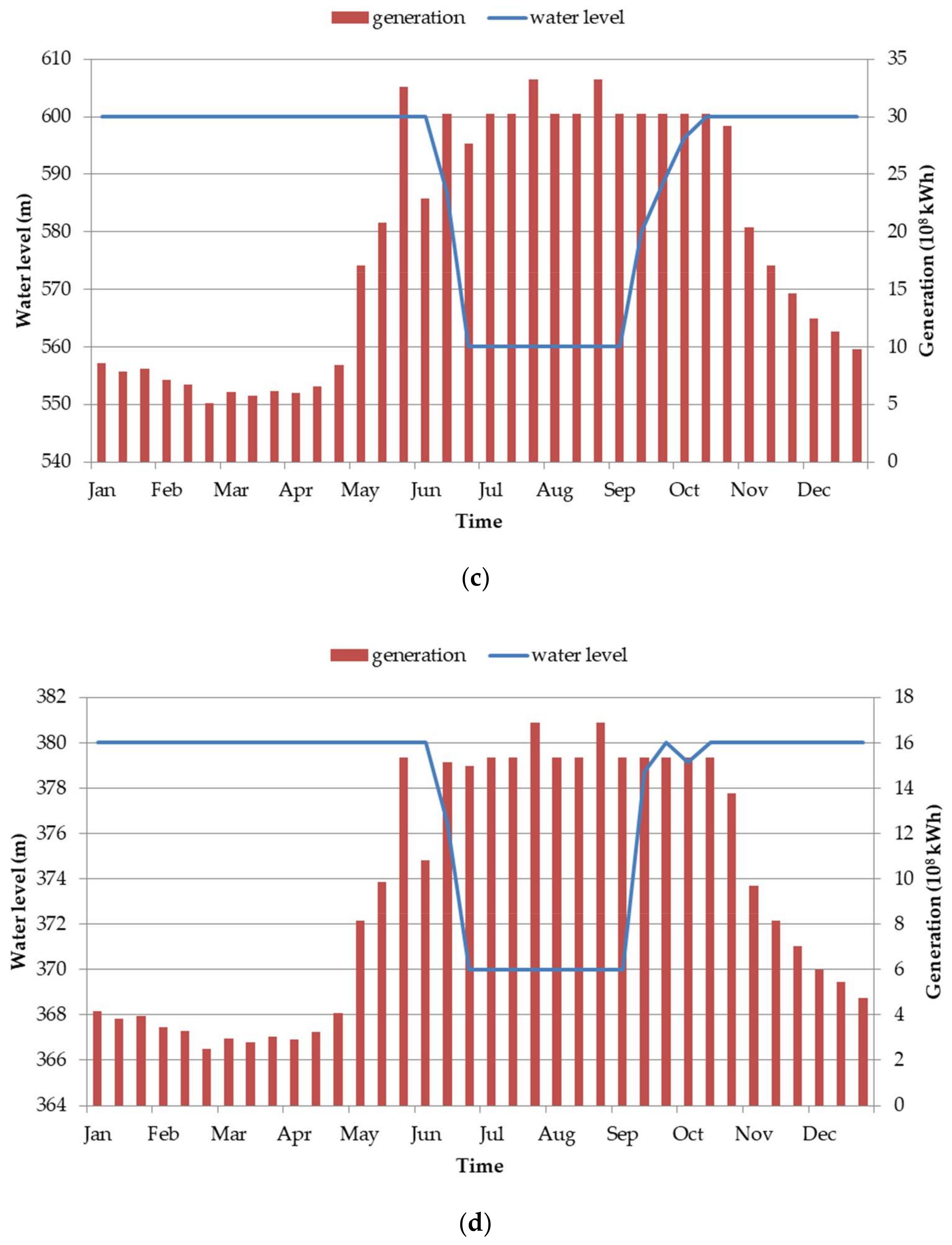
| Parameters | Wudongde | Baihetan | Xiluodu | Xiangjiaba |
|---|---|---|---|---|
| Dead water level (m) | 945 | 765 | 540 | 370 |
| Normal water level (m) | 977 | 825 | 600 | 380 |
| Flood limit water level (m) | 952 | 785 | 560 | 370 |
| Installed capacity (104 kw) | 1020 | 1600 | 1260 | 600 |
| Total capacity (108 m3) | 74.08 | 206.27 | 126.7 | 51.63 |
| Minimum outflow (m3/s) | 906 | 905 | 1500 | 1500 |
| Function | Formula | Search Domain | Optimum |
|---|---|---|---|
| Ackley | [−32.768, 32.768] | ||
| Griewank | [−600, 600] | ||
| Rastrigin | [−5.12, 5.12] | ||
| Rosenbrock | [−5, 10] | ||
| Sphere | [−100, 100] | ||
| Bent Cigar | [−100, 100] | ||
| Discus | [−100, 100] | ||
| Happy Cat | [−100, 100] | ||
| Schwefel 2.22 | [−10, 10] |
| Function | IHS | KGSA | CS | ICS | |
|---|---|---|---|---|---|
| Shifted Ackley | Mean | 4.17 × 10−03 | 6.41 × 10−15 * | 1.16 × 10−02 | 7.53 × 10−15 |
| Stdv | 1.28 × 10−03 | 5.54 × 10−15 | 1.16 × 10−01 | 7.13 × 10−15 | |
| Shifted Griewank | Mean | 2.34 × 10−02 | 1.50 × 10−02 | 1.44 × 10−01 | 4.04 × 10−05 |
| Stdv | 3.36 × 10−02 | 2.01 × 10−02 | 1.32 × 10−01 | 1.85 × 10−04 | |
| Shifted Rastrigin | Mean | 4.88 × 10−05 | 5.89 | 4.41 | 1.00 × 10−06 |
| Stdv | 3.03 × 10−05 | 3.51 | 2.46 | 9.84 × 10−06 | |
| Shifted Rosenbrock | Mean | 2.17 | 9.88 × 10−01 | 2.85 | 5.68 |
| Stdv | 1.76 | 1.75 × 10−01 | 2.14 | 1.70 | |
| Shifted Sphere | Mean | 2.27 × 10−07 | 6.88 × 10−32 | 2.71 × 10−26 | 0.00 |
| Stdv | 1.41 × 10−07 | 5.78 × 10−31 | 9.62 × 10−26 | 0.00 | |
| Shifted Bent Cigar | Mean | 3.48 × 10+01 | 5.76 × 10+02 | 6.54 × 10−15 | 0.00 |
| Stdv | 2.50 × 10+01 | 8.49 × 10+02 | 7.40 × 10−15 | 0.00 | |
| Shifted Discus | Mean | 1.70 × 10−02 | 9.08 × 10+03 | 7.25 × 10−15 | 0.00 |
| Stdv | 2.74 × 10−02 | 3.27 × 10+03 | 7.14 × 10−15 | 0.00 | |
| Shifted Happy Cat | Mean | 1.73 × 10−01 | 3.61 × 10−02 | 3.14 × 10−01 | 1.58 × 10−01 |
| Stdv | 4.17 × 10−02 | 1.63 × 10−02 | 1.67 × 10−01 | 3.67 × 10−02 | |
| Shifted Schwefel 2.22 | Mean | 2.03 × 10−03 | 4.51 × 10−13 | 5.48 × 10−13 | 1.11 × 10−14 |
| Stdv | 5.72 × 10−04 | 2.35 × 10−12 | 2.97 × 10−12 | 5.92 × 10−15 | |
| Rotated and Shifted Sphere | Mean | 2.25 × 10−07 | 1.63 × 10−01 | 8.81 × 10−15 | 0.00 |
| Stdv | 1.59 × 10−07 | 9.49 × 10−01 | 6.93 × 10−15 | 0.00 | |
| Rotated and Shifted Ackley | Mean | 7.33 × 10−01 | 6.66 × 10−15 | 2.53 | 4.22 × 10−12 |
| Stdv | 1.03 | 6.89 × 10−15 | 1.08 | 4.21 × 10−11 |
| Algorithm | 1985 | 1987 | 1962 | 1990 | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| IHS | 2216 | 27.94 | 2158 | 34.23 | 2171 | 39.95 | 2382 | 40.66 |
| KGSA | 2135 | 12.48 | 2067 | 12.45 | 2076 | 9.70 | 2292 | 12.54 |
| CS | 2250 | 10.77 | 2189 | 3.82 | 2214 | 5.33 | 2421 | 10.34 |
| GCS | 2322 | 0.52 | 2237 | 0.02 | 2263 | 0.17 | 2484 | 0.52 |
| Algorithm | 1997 | 1963 | 1970 | 1981 | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| IHS | 1966 | 284.55 | 2107 | 29.49 | 2037 | 208.99 | 2065 | 35.92 |
| KGSA | 1953 | 8.57 | 2021 | 204.31 | 1984 | 10.67 | 2007 | 10.42 |
| CS | 2039 | 5.24 | 2140 | 11.24 | 2096 | 12.60 | 2098 | 6.48 |
| GCS | 2105 | 0.38 | 2228 | 0.44 | 2181 | 0.13 | 2159 | 0.37 |
| Algorithm | 1973 | 1977 | 1984 | 1982 | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std. | Mean | Std. | Mean | Std. | Mean | Std. | |
| IHS | 1893 | 37.97 | 1913 | 33.33 | 1862 | 31.05 | 1886 | 38.38 |
| KGSA | 1851 | 6.98 | 1867 | 6.63 | 1809 | 6.63 | 1838 | 6.74 |
| CS | 1928 | 6.09 | 1946 | 7.73 | 1894 | 4.48 | 1919 | 4.49 |
| GCS | 1992 | 0.21 | 2019 | 0.07 | 1944 | 0.16 | 1977 | 0.17 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Zhou, J.; Mo, L.; Wang, C.; Yuan, Z.; Wu, J. A Gradient-Based Cuckoo Search Algorithm for a Reservoir-Generation Scheduling Problem. Algorithms 2018, 11, 36. https://doi.org/10.3390/a11040036
Feng Y, Zhou J, Mo L, Wang C, Yuan Z, Wu J. A Gradient-Based Cuckoo Search Algorithm for a Reservoir-Generation Scheduling Problem. Algorithms. 2018; 11(4):36. https://doi.org/10.3390/a11040036
Chicago/Turabian StyleFeng, Yu, Jianzhong Zhou, Li Mo, Chao Wang, Zhe Yuan, and Jiang Wu. 2018. "A Gradient-Based Cuckoo Search Algorithm for a Reservoir-Generation Scheduling Problem" Algorithms 11, no. 4: 36. https://doi.org/10.3390/a11040036
APA StyleFeng, Y., Zhou, J., Mo, L., Wang, C., Yuan, Z., & Wu, J. (2018). A Gradient-Based Cuckoo Search Algorithm for a Reservoir-Generation Scheduling Problem. Algorithms, 11(4), 36. https://doi.org/10.3390/a11040036




