Failure Mode and Effects Analysis Considering Consensus and Preferences Interdependence
Abstract
1. Introduction
2. Literature Review
2.1. Aggregation Experts’Preferences
2.2. Failure Mode Ranking
3. IVPFGBM and IVPFWGBM Operators
3.1. Basic Concepts of IVPFS
- (1)
- ;
- (2)
- ;
- (3)
- ; and
- (4)
- .
- (1)
- If , then is superior to , ;
- (2)
- If , then
- If , then is superior to , ;
- If , then is equivalent to , .
3.2. Some Interval-Valued Pythagorean Fuzzy GBM Operators
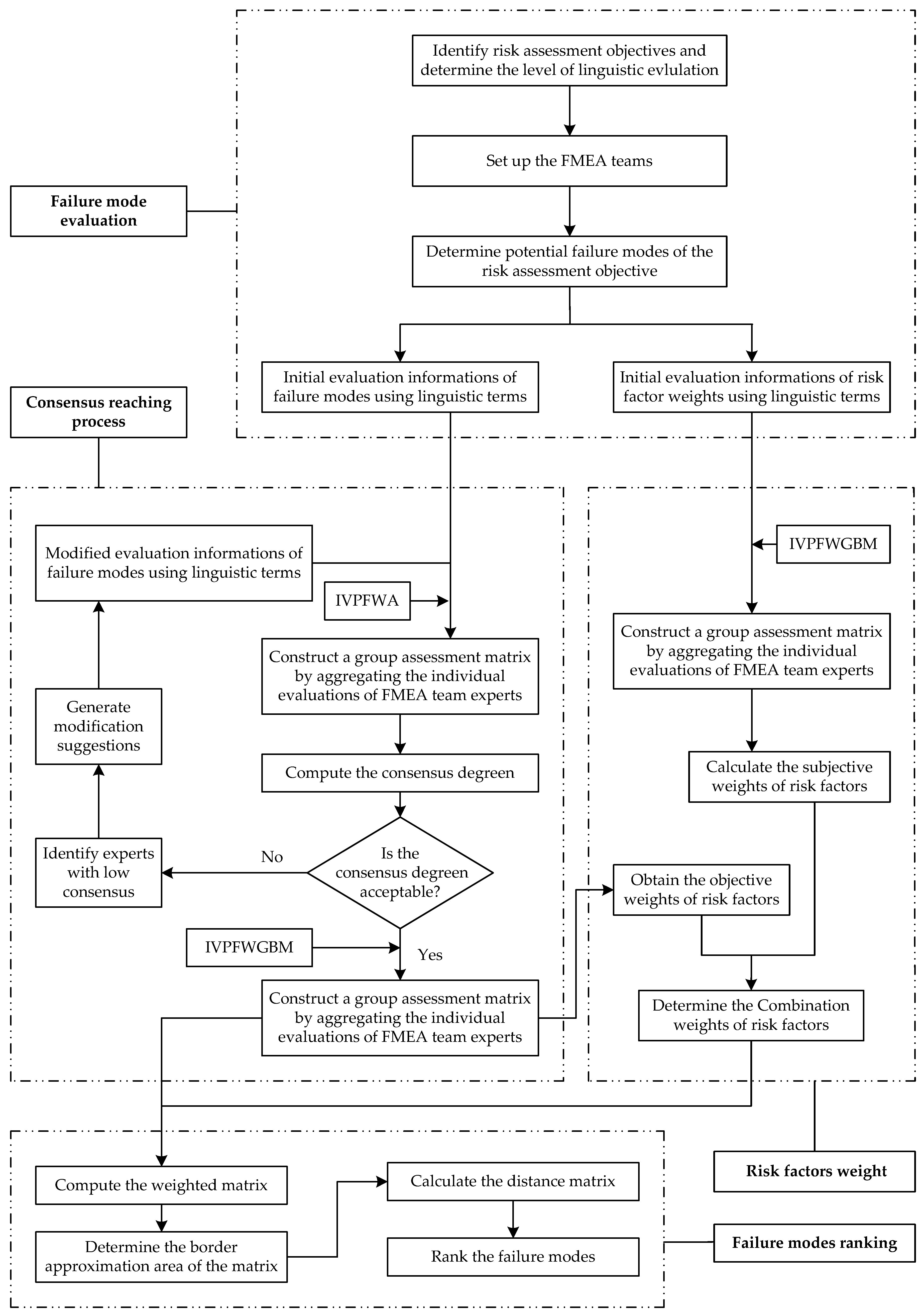
4. The Proposed Method
4.1. Failure Modes Evaluation
4.2. Consensus-ReachingProcess
- (1)
- Identify the experts for which the consensus degree is lower than threshold value :
- (2)
- For the determined experts, the failure modes with lower than are identified:
- (3)
- Finally, the elements of failure modes that need to be modified are:
4.3. Risk Factors Weight
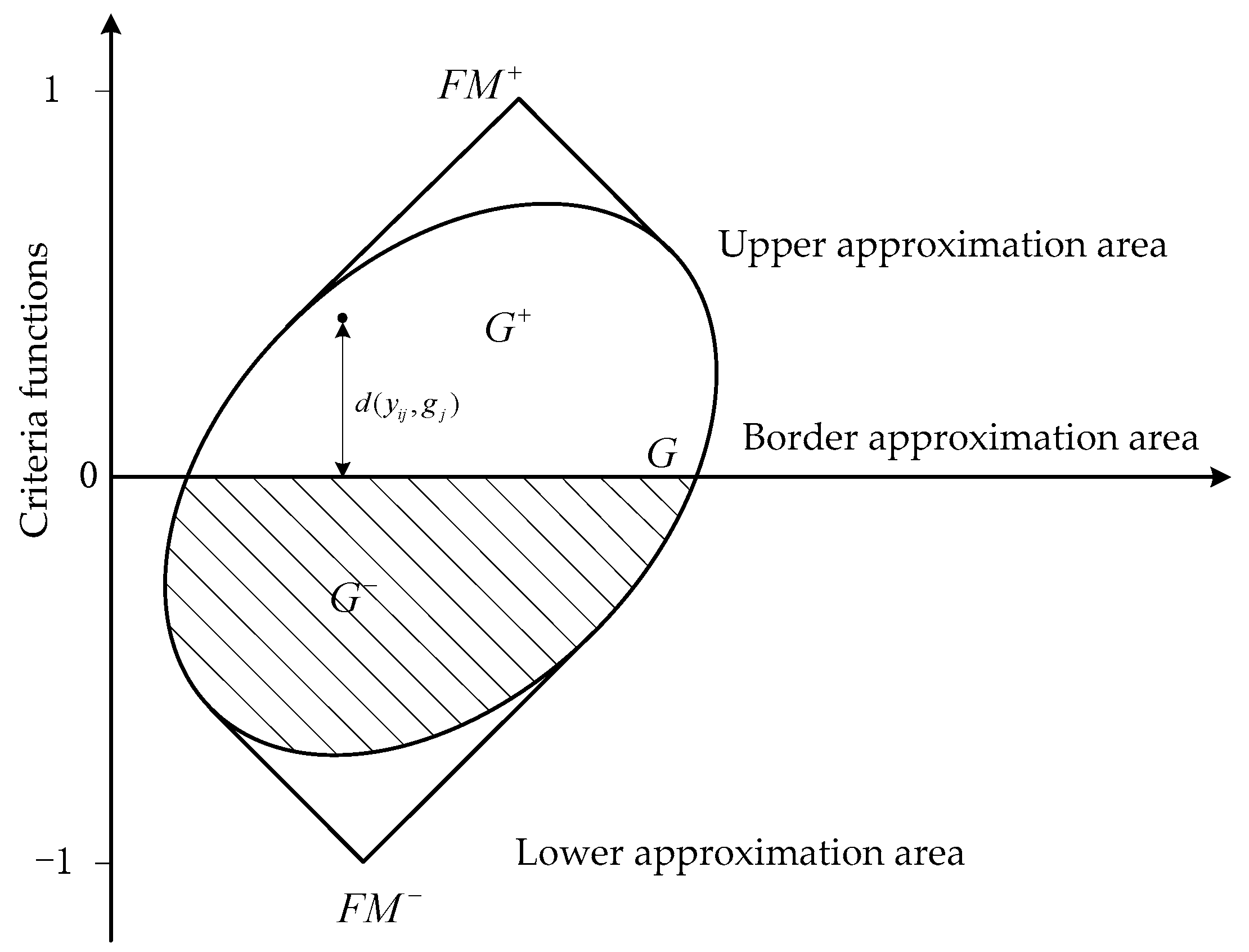
4.4. Failure Modes Ranking
5. Case Study
5.1. Implement the Proposed Method
5.2. Sensitivity Analysis
5.3. Comparisons and Discussion
- (1)
- The IVPFWGBM operator was used to aggregate the experts’ preferences into group assessments, which sufficiently reflect the interdependent relationships between the experts’ preferences.
- (2)
- Compared with the other improved FMEA approach, the ranking results obtained by the proposed method are more acceptable because the level of agreement between decision-maker and group is considered through introducing a consensus-reaching process into the risk assessment process of FMEA.
- (3)
- The ranking results of failure modes obtained by the proposed approach are more reasonable when compared with the other improved FMEA methods; the reason is that the improved MABAC method adopted the IVPFGBM operator to construct the border approximation area matrix, which considers the direct and indirect relationships among failure modes.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix B
References
- Stamatis, D.H. Failure Mode and Effect Analysis: Fmea from Theory to Execution; ASQ Quality Press: Milwaukee, WI, USA, 2003; p. 80. [Google Scholar]
- Liu, H.-C.; Liu, L.; Liu, N. Risk evaluation approaches in failure mode and effects analysis: A literature review. Expert Syst. Appl. 2013, 40, 828–838. [Google Scholar] [CrossRef]
- Du, Y.; Mo, H.; Deng, X.; Sadiq, R.; Deng, Y. A new method in failure mode and effects analysis based on evidential reasoning. Int. J. Syst. Assur. Eng. Manag. 2014, 5, 1–10. [Google Scholar] [CrossRef]
- Bowles, J.B.; Pelaez, C.E. Fuzzy logic prioritization of failures in a system failure mode, effects and criticality analysis. Reliab. Eng. Syst. Saf. 1995, 50, 203–213. [Google Scholar] [CrossRef]
- Jiang, W.; Xie, C.; Wei, B.; Zhou, D. A modified method for risk evaluation in failure modes and effects analysis of aircraft turbine rotor blades. Adv. Mech. Eng. 2016, 8. [Google Scholar] [CrossRef]
- Tazi, N.; Châtelet, E.; Bouzidi, Y. Using a hybrid cost-FMEA analysis for wind turbine reliability analysis. Energies 2017, 10, 276. [Google Scholar] [CrossRef]
- Liu, H.; Deng, X.; Jiang, W. Risk evaluation in failure mode and effects analysis using fuzzy measure and fuzzy integral. Symmetry 2017, 9, 162. [Google Scholar] [CrossRef]
- Nguyen, T.L.; Shu, M.H.; Hsu, B.M. Extended FMEA for sustainable manufacturing: An empirical study in the non-woven fabrics industry. Sustainability 2016, 8, 939. [Google Scholar] [CrossRef]
- Xia, M.; Xu, Z.; Zhu, B. Geometric Bonferroni means with their application in multi-criteria decision making. Knowl. Based Syst. 2013, 40, 88–100. [Google Scholar] [CrossRef]
- Guo, J. A risk assessment approach for failure mode and effects analysis based on intuitionistic fuzzy sets and evidence theory. J. Intell. Fuzzy Syst. 2016, 30, 869–881. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Viedma, E.; Verdegay, J.L. A model of consensus in group decision making under linguistic assessments. Fuzzy Sets Syst. 1996, 78, 73–87. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Herrera, F.; Chiclana, F. A consensus model for multiperson decision making with different preference structures. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2002, 32, 394–402. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Shen, G. An improved FMECA for feed system of CNC machining center based on ICR and DEMATEL method. Int. J. Adv. Manuf. Technol. 2016, 83, 43–54. [Google Scholar] [CrossRef]
- Song, W.; Ming, X.; Wu, Z.; Zhu, B. Failure modes and effects analysis using integrated weight-based fuzzy TOPSIS. Int. J. Comput. Integr. Manuf. 2013, 26, 1172–1186. [Google Scholar] [CrossRef]
- Bozdag, E.; Asan, U.; Soyer, A.; Serdarasan, S. Risk prioritization in failure mode and effects analysis using interval type-2 fuzzy sets. Expert Syst. Appl. 2015, 42, 4000–4015. [Google Scholar] [CrossRef]
- Mohsen, O.; Fereshteh, N. An extended VIKOR method based on entropy measure for the failure modes risk assessment—A case study of the geothermal power plant (GPP). Saf. Sci. 2017, 92, 160–172. [Google Scholar] [CrossRef]
- Zhang, Z.; Chu, X. Risk prioritization in failure mode and effects analysis under uncertainty. Expert Syst. Appl. 2011, 38, 206–214. [Google Scholar] [CrossRef]
- Kutlu, A.C.; Ekmekçioğlu, M. Fuzzy failure modes and effects analysis by using fuzzy TOPSIS-based fuzzy ahp. Expert Syst. Appl. 2012, 39, 61–67. [Google Scholar] [CrossRef]
- Chai, K.C.; Jong, C.H.; Tay, K.M.; Lim, C.P. A perceptual computing-based method to prioritize failure modes in failure mode and effect analysis and its application to edible bird nest farming. Appl. Soft Comput. 2016, 49, 734–747. [Google Scholar] [CrossRef]
- Zhao, H.; You, J.-X.; Liu, H.-C. Failure mode and effect analysis using MULTIMOORA method with continuous weighted entropy under interval-valued intuitionistic fuzzy environment. Soft Comput. 2016, 21, 5355–5367. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Liu, H.-C. New approach for failure mode and effect analysis using linguistic distribution assessments and TODIM method. Reliab. Eng. Syst. Saf. 2017, 167, 302–309. [Google Scholar] [CrossRef]
- Wang, L.-E.; Liu, H.-C.; Quan, M.-Y. Evaluating the risk of failure modes with a hybrid MCDM model under interval-valued intuitionistic fuzzy environments. Comput. Ind. Eng. 2016, 102, 175–185. [Google Scholar] [CrossRef]
- Xu, Z.S.; Da, Q.L. An overview of operators for aggregating information. Int. J. Intell. Syst. 2003, 18, 953–969. [Google Scholar] [CrossRef]
- Liu, H.-C.; You, J.-X.; Chen, S.; Chen, Y.-Z. An integrated failure mode and effect analysis approach for accurate risk assessment under uncertainty. IIE Trans. 2016, 48, 1027–1042. [Google Scholar] [CrossRef]
- Gong, Y.; Hu, N.; Zhang, J.; Liu, G.; Deng, J. Multi-attribute group decision making method based on geometric Bonferroni mean operator of trapezoidal interval type-2 fuzzy numbers. Comput. Ind. Eng. 2015, 81, 167–176. [Google Scholar] [CrossRef]
- Wei, G. Picture 2-tuple linguistic bonferroni mean operators and their application to multiple attribute decision making. Int.J. Fuzzy Syst. 2016, 19, 1–14. [Google Scholar] [CrossRef]
- Wang, Q. Research on the assessment of psycholinguistic teaching effect with triangular fuzzy information. J. Intell. Fuzzy Syst. 2016, 32, 1–8. [Google Scholar] [CrossRef]
- Liu, P.; Li, H. Multiple attribute decision-making method based on some normal neutrosophic Bonferroni mean operators. Neural Comput. Appl. 2015, 28, 1–16. [Google Scholar] [CrossRef]
- Liang, D.; Xu, Z.; Darko, A.P. Projection model for fusing the information of Pythagorean fuzzy multicriteria group decision making based on geometric Bonferroni mean. Int. J. Intell. Syst. 2017, 32, 966–987. [Google Scholar] [CrossRef]
- Zhang, Z. Geometric Bonferroni means of interval-valued intuitionistic fuzzy numbers and their application to multiple attribute group decision making. Neural Comput. Appl. 2016, 1–16. [Google Scholar] [CrossRef]
- Tang, X.; Huang, Y.; Wei, G. Approaches to multiple-attribute decision-making based on Pythagorean 2-tuple linguistic Bonferroni mean operators. Algorithms 2018, 11, 5. [Google Scholar] [CrossRef]
- Fan, C.; Ye, J.; Hu, K.; Fan, E. Bonferroni mean operators of linguistic neutrosophic numbers and their multiple attribute group decision-making methods. Information 2017, 8, 107. [Google Scholar] [CrossRef]
- Lolli, F.; Ishizaka, A.; Gamberini, R.; Rimini, B.; Messori, M. FlowSort-GDSS—A novel group multi-criteria decision support system for sorting problems with application to FMEA. Exp. Syst. Appl. 2015, 42, 6342–6349. [Google Scholar] [CrossRef]
- Franceschini, F.; Galetto, M. A new approach for evaluation of risk priorities of failure modes in FMEA. Int. J. Prod. Res. 2001, 39, 2991–3002. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; Ding, X.F.; Su, Q. Improving risk evaluation in FMEA with a hybrid multiple criteria decision making method. Int. J. Qual. Reliab. Manag. 2015, 32, 763–782. [Google Scholar] [CrossRef]
- Liu, H.-C.; You, J.-X.; You, X.-Y.; Shan, M.-M. A novel approach for failure mode and effects analysis using combination weighting and fuzzy VIKOR method. Appl. Soft Comput. 2015, 28, 579–588. [Google Scholar] [CrossRef]
- Safari, H.; Faraji, Z.; Majidian, S. Identifying and evaluating enterprise architecture risks using FMEA and fuzzy VIKOR. J. Intell. Manuf. 2016, 27, 475–486. [Google Scholar] [CrossRef]
- Liu, H.-C.; Fan, X.-J.; Li, P.; Chen, Y.-Z. Evaluating the risk of failure modes with extended MULTIMOORA method under fuzzy environment. Eng. Appl. Artif. Intell. 2014, 34, 168–177. [Google Scholar] [CrossRef]
- Xu, K.; Tang, L.C.; Xie, M.; Ho, S.L.; Zhu, M.L. Fuzzy assessment of FMEA for engine systems. Reliab. Eng. Syst. Saf. 2002, 75, 17–29. [Google Scholar] [CrossRef]
- Seyed-Hosseini, S.M.; Safaei, N.; Asgharpour, M.J. Reprioritization of failures in a system failure mode and effects analysis by decision making trial and evaluation laboratory technique. Reliab. Eng. Syst. Saf. 2006, 91, 872–881. [Google Scholar] [CrossRef]
- Chang, K.-H.; Chang, Y.-C.; Lee, Y.-T. Integrating TOPSIS and DEMATEL methods to rank the risk of failure of fmea. Int. J. Inf. Technol. Decis. Mak. 2014, 13, 1229–1257. [Google Scholar] [CrossRef]
- Liu, H.-C.; You, J.-X.; Lin, Q.-L.; Li, H. Risk assessment in system FMEA combining fuzzy weighted average with fuzzy decision-making trial and evaluation laboratory. Int. J. Comput. Integr. Manuf. 2015, 28, 701–714. [Google Scholar] [CrossRef]
- Pamučar, D.; Ćirović, G. The selection of transport and handling resources in logistics centers using multi-attributive border approximation area comparison (MABAC). Expert Syst. Appl. 2015, 42, 3016–3028. [Google Scholar] [CrossRef]
- Sun, R.; Hu, J.; Zhou, J.; Chen, X. A hesitant fuzzy linguistic projection-based MABAC method for patients’ prioritization. Int. J. Fuzzy Syst. 2017, 1–17. [Google Scholar] [CrossRef]
- Xue, Y.X.; You, J.X.; Lai, X.D.; Liu, H.C. An interval-valued intuitionistic fuzzy MABAC approach for material selection with incomplete weight information. Appl. Soft Comput. 2016, 38, 703–713. [Google Scholar] [CrossRef]
- Gigović, L.; Pamučar, D.; Božanić, D.; Ljubojević, S. Application of the GIS-DANP-MABAC multi-criteria model for selecting the location of wind farms: A case study of vojvodina, Serbia. Renew. Energy 2017, 103, 501–521. [Google Scholar] [CrossRef]
- Debnath, A.; Roy, J.; Kar, S.; Zavadskas, E.; Antucheviciene, J. A hybrid mcdm approach for strategic project portfolio selection of agro by-products. Sustainability 2017, 9, 1302. [Google Scholar] [CrossRef]
- Zhang, X. Multicriteria Pythagorean fuzzy decision analysis: A hierarchical QUALIFLEX approach with the closeness index-based ranking methods. Inf. Sci. 2016, 330, 104–124. [Google Scholar] [CrossRef]
- Peng, X.; Yang, Y. Fundamental properties of interval-valued Pythagorean fuzzy aggregation operators. Int. J. Intell. Syst. 2016, 31, 444–487. [Google Scholar] [CrossRef]
- Liu, H.-C.; Li, P.; You, J.-X.; Chen, Y.-Z. A novel approach for fmea: Combination of interval 2-tuple linguistic variables and gray relational analysis. Qual. Reliab. Eng. Int. 2015, 31, 761–772. [Google Scholar] [CrossRef]
- Deng, J.L. Introduction to grey system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Shannon; Claude, E. The Mathematical Theory of Communication; University of Illinois Press: Champaign, IL, USA, 1964; pp. 623–656. [Google Scholar]
- Wei, C.P.; Wang, P.; Zhang, Y.Z. Entropy, similarity measure of interval-valued intuitionistic fuzzy sets and their applications. Inf. Sci. 2011, 181, 4273–4286. [Google Scholar] [CrossRef]
- Liu, H.-C.; Liu, L.; Li, P. Failure mode and effects analysis using intuitionistic fuzzy hybrid weighted euclidean distance operator. Int. J. Syst. Sci. 2014, 45, 2012–2030. [Google Scholar] [CrossRef]
| Linguistic Variables | Abbreviation | IVPFNs |
|---|---|---|
| Very high | VH | ([0.8000,0.9000],[0.1000,0.2000]) |
| High | H | ([0.7000,0.8000],[0.2000,0.3000]) |
| Medium | M | ([0.5000,0.6000],[0.4000,0.5000]) |
| Low | L | ([0.3000,0.4000],[0.6000,0.7000]) |
| Very low | VL | ([0.1000,0.2000],[0.8000,0.9000]) |
| LinguisticVariables | Abbreviation | IVPFNs |
|---|---|---|
| Extremely high | EH | ([0.9000,1.0000],[0.0000,0.1000]) |
| Very high | VH | ([0.8000,0.9000],[0.1000,0.2000]) |
| High | H | ([0.7000,0.8000],[0.2000,0.3000]) |
| Medium high | MH | ([0.6000,0.7000],[0.3000,0.4000]) |
| Medium | M | ([0.5000,0.6000],[0.4000,0.5000]) |
| Medium low | ML | ([0.4000,0.5000],[0.5000,0.6000]) |
| Low | L | ([0.3000,0.4000],[0.6000,0.7000]) |
| Very low | VL | ([0.2000,0.3000],[0.7000,0.8000]) |
| Extremely low | EL | ([0.1000,0.2000],[0.8000,0.9000]) |
| Failure Modes | Severity(S) | Occurrence(O) | Detection(D) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E1 | E2 | E3 | E4 | E5 | E1 | E2 | E3 | E4 | E5 | E1 | E2 | E3 | E4 | E5 | |
| FM1 | ML | MH | ML | M | M | M | M | M | MH | M | M | L | ML | ML | ML |
| FM2 | MH | MH | H | M | H | M | MH | H | MH | MH | MH | MH | ML | MH | M |
| FM3 | MH | M | H | MH | M | ML | ML | L | M | M | H | H | H | MH | MH |
| FM4 | M | MH | ML | M | M | L | M | L | M | M | VL | ML | VL | L | VL |
| FM5 | M | H | MH | MH | M | M | ML | M | M | M | L | ML | VL | L | VL |
| FM6 | H | H | MH | MH | H | H | MH | M | MH | M | L | M | L | EL | L |
| FM7 | MH | MH | H | MH | MH | VH | MH | VH | MH | H | MH | M | MH | M | M |
| FM8 | EH | H | EH | H | VH | ML | M | L | ML | ML | ML | ML | L | L | L |
| FM9 | ML | M | ML | ML | M | M | M | ML | M | M | M | M | M | ML | ML |
| Factor weight | H | VH | H | VH | H | H | M | H | M | M | VL | L | L | M | L |
| Failure Modes | Severity(S) | Occurrence(O) | Detection(D) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E1 | E2 | E3 | E4 | E5 | E1 | E2 | E3 | E4 | E5 | E1 | E2 | E3 | E4 | E5 | |
| FM1 | ML | M | ML | M | M | M | M | M | MH | M | M | ML | ML | ML | ML |
| FM2 | MH | MH | H | M | H | M | MH | MH | MH | MH | MH | MH | M | MH | M |
| FM3 | MH | M | MH | MH | M | ML | ML | ML | M | M | H | H | H | MH | MH |
| FM4 | M | M | M | M | M | L | ML | ML | M | M | VL | L | L | L | VL |
| FM5 | M | MH | MH | MH | M | M | M | M | M | M | L | L | VL | L | VL |
| FM6 | H | H | H | MH | H | H | MH | MH | MH | M | L | ML | L | EL | L |
| FM7 | MH | MH | MH | MH | MH | VH | H | H | MH | H | MH | M | M | M | M |
| FM8 | EH | VH | EH | H | VH | ML | ML | ML | ML | ML | ML | L | L | L | L |
| FM9 | ML | M | M | ML | M | M | M | M | M | M | M | M | M | ML | ML |
| Failure Modes | ||||||||
|---|---|---|---|---|---|---|---|---|
| Scores | Ranking | Scores | Ranking | Scores | Ranking | Scores | Ranking | |
| FM1 | −0.0604 | 6 | −0.0801 | 7 | −0.0723 | 7 | −0.0544 | 6 |
| FM2 | 0.1437 | 2 | 0.1415 | 2 | 0.1276 | 2 | −0.1181 | 2 |
| FM3 | 0.0782 | 3 | 0.0742 | 3 | 0.0744 | 4 | 0.0622 | 3 |
| FM4 | −0.2074 | 9 | −0.2014 | 9 | −0.1944 | 9 | −0.1995 | 9 |
| FM5 | −0.1129 | 8 | −0.1266 | 8 | −0.1304 | 8 | −0.0853 | 7 |
| FM6 | 0.0106 | 5 | 0.0293 | 5 | 0.0422 | 5 | 0.0375 | 5 |
| FM7 | 0.2140 | 1 | 0.1821 | 1 | 0.1781 | 1 | 0.1900 | 1 |
| FM8 | 0.0563 | 4 | 0.0657 | 4 | 0.0856 | 3 | 0.0618 | 4 |
| FM9 | −0.0800 | 7 | −0.0573 | 6 | −0.0570 | 6 | −0.0989 | 8 |
| n(E) | 0 | 2 | 4 | 5 | ||||
| n(FM) | 0 | 13 | 27 | 38 | ||||
| Failure Modes | RPN Method | Proposed Method | [14] | [36] | [20] | [54] | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| S | O | D | RPN | Ranking | Round 1 | Round 2 | |||||
| FM1 | 6 | 6 | 5 | 180 | 7 | 6 | 7 | 6 | 7 | 7 | 7 |
| FM2 | 8 | 7 | 6 | 336 | 1 | 2 | 2 | 3 | 2 | 3 | 2 |
| FM3 | 7 | 5 | 8 | 280 | 3 | 3 | 3 | 4 | 5 | 4 | 5 |
| FM4 | 6 | 5 | 4 | 120 | 9 | 9 | 9 | 9 | 8 | 9 | 9 |
| FM5 | 7 | 6 | 4 | 168 | 8 | 8 | 8 | 7 | 6 | 6 | 6 |
| FM6 | 8 | 7 | 4 | 224 | 4 | 5 | 5 | 5 | 3 | 5 | 4 |
| FM7 | 7 | 8 | 6 | 336 | 1 | 1 | 1 | 2 | 1 | 2 | 1 |
| FM8 | 10 | 5 | 4 | 200 | 6 | 4 | 4 | 1 | 4 | 1 | 3 |
| FM9 | 6 | 6 | 6 | 216 | 5 | 7 | 6 | 8 | 9 | 8 | 8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Wang, R.; Li, Y. Failure Mode and Effects Analysis Considering Consensus and Preferences Interdependence. Algorithms 2018, 11, 34. https://doi.org/10.3390/a11040034
Zhu J, Wang R, Li Y. Failure Mode and Effects Analysis Considering Consensus and Preferences Interdependence. Algorithms. 2018; 11(4):34. https://doi.org/10.3390/a11040034
Chicago/Turabian StyleZhu, Jianghong, Rui Wang, and Yanlai Li. 2018. "Failure Mode and Effects Analysis Considering Consensus and Preferences Interdependence" Algorithms 11, no. 4: 34. https://doi.org/10.3390/a11040034
APA StyleZhu, J., Wang, R., & Li, Y. (2018). Failure Mode and Effects Analysis Considering Consensus and Preferences Interdependence. Algorithms, 11(4), 34. https://doi.org/10.3390/a11040034




