Abstract
Rough set theory and neutrosophic set theory are mathematical models to deal with incomplete and vague information. These two theories can be combined into a framework for modeling and processing incomplete information in information systems. Thus, the neutrosophic rough set hybrid model gives more precision, flexibility and compatibility to the system as compared to the classic and fuzzy models. In this research study, we develop neutrosophic rough digraphs based on the neutrosophic rough hybrid model. Moreover, we discuss regular neutrosophic rough digraphs, and we solve decision-making problems by using our proposed hybrid model. Finally, we give a comparison analysis of two hybrid models, namely, neutrosophic rough digraphs and rough neutrosophic digraphs.
1. Introduction
The concept of a neutrosophic set, which generalizes fuzzy sets [1] and intuitionistic fuzzy sets [2], was proposed by Smarandache [3] in 1998, and it is defined as a set about the degree of truth, indeterminacy, and falsity. A neutrosophic set A in a universal set X is characterized independently by a truth-membership function (), an indeterminacy-membership function (), and a falsity-membership function (). To apply neutrosophic sets in real-life problems more conveniently, Smarandache [3] and Wang et al., [4] defined single-valued neutrosophic sets which take the value from the subset of [0, 1].
Rough set theory was proposed by Pawlak [5] in 1982. Rough set theory is useful to study the intelligence systems containing incomplete, uncertain or inexact information. The lower and upper approximation operators of rough sets are used for managing hidden information in a system. Therefore, many hybrid models have been built such as soft rough sets, rough fuzzy sets, fuzzy rough sets, soft fuzzy rough sets, neutrosophic rough sets and rough neutrosophic sets for handling uncertainty and incomplete information effectively. Dubois and Prade [6] introduced the notions of rough fuzzy sets and fuzzy rough sets. Liu and Chen [7] have studied different decision-making methods. Mordeson and Peng [8] presented operations on fuzzy graphs. Akram et al., [9,10,11,12] considered several new concepts of neutrosophic graphs with applications. Rough fuzzy digraphs with applications are presented in [13,14]. To get the extended notion of neutrosophic sets and rough sets, many attempts have been made. Broumi et al., [15] introduced the concept of rough neutrosophic sets. Yang et al., [16] proposed single valued neutrosophic rough sets by combining single valued neutrosophic sets and rough sets, and established an algorithm for the decision-making problem based on single valued neutrosophic rough sets on two universes. Nabeela et al., [17] and Sayed et al., [18] introduced rough neutrosophic digraphs, in which they have approximated neutrosophic set under the influence of a crisp equivalence relation. In this research article, we apply another hybrid set model, neutrosophic rough, to graph theory. We deal with regular neutrosophic rough digraphs and then solve the decision-making problem by using our proposed hybrid model.
Our paper is organized as follows: Firstly, we develop the notion of neutrosophic rough digraphs and present some numerical examples. Secondly, we explore basic properties of neutrosophic rough digraphs. In particular, we investigate the regularity of neutrosophic rough digraphs. We describe novel applications of our proposed hybrid decision-making method. To compare the two notions, rough neutrosophic digraphs and neutrosophic rough digraphs, we give a comparison analysis. Finally, we end the paper by concluding remarks.
2. Neutrosophic Rough Information
Definition 1.
[4] Let Z be a nonempty universe. A neutrosophic set N on Z is defined as follows:
where the functions :Z→ represent the degree of membership, the degree of indeterminacy and the degree of falsity.
Definition 2.
[5] Let Z be a nonempty universe and R an equivalence relation on Z. A pair is called an approximation space. Let be a subset of Z and the lower and upper approximations of in the approximation space denoted by and are defined as follows:
where denotes the equivalence class of R containing x. A pair is called a rough set.
For other notations and applications, readers are referred to [19,20,21,22,23,24,25,26,27,28,29,30,31,32].
Definition 3.
[16] Let be a nonempty universe and R a neutrosophic relation on . Let X be a neutrosophic set on , defined as
Then the lower and upper approximations of X represented by and , respectively, are characterized as neutrosophic sets in such that,
where
and
A pair ia called a neutrosophic rough set.
Definition 4.
Let be a nonempty set and R a neutrosophic tolerance relation on . Let X be a neutrosophic set on defined as:
Then the lower and upper approximations of X represented by and , respectively, are characterized as neutrosophic sets in such that,
where
and
Let and S a neutrosophic tolerance relation on such that
Let Y be a neutrosophic set on defined as:
such that
Then the lower and the upper approximations of Y represented by and , are defined as follows:
where
and
A pair is called neutrosophic rough relation.
Definition 5.
A neutrosophic rough digraph on a nonempty set is a 4-ordered tuple such that
- (a)
- R is a neutrosophic tolerance relation on ,
- (b)
- S is a neutrosophic tolerance relation on ,
- (c)
- is a neutrosophic rough set on ,
- (d)
- is a neutrosophic rough relation on ,
- (e)
- is a neutrosophic rough digraph where and are lower and upper approximate neutrosophic digraphs of G such that
Example 1.
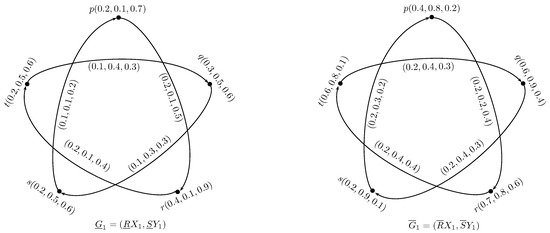
Let be a nonempty set and R a neutrosophic tolerance relation on is given as:
| R | p | q | r | s | t |
| p | (1,1,0) | (0.5,0.2,0.3) | (0.1,0.9,0.4) | (0.6,0.5,0.2) | (0.2,0.1,0.8) |
| q | (0.5,0.2,0.3) | (1,1,0) | (0.3,0.7,0.5) | (0.1,0.9,0.6) | (0.6,0.5,0.1) |
| r | (0.1,0.9,0.4) | (0.3,0.7,0.5) | (1,1,0) | (0.2,0.8,0.7) | (0.1,0.9,0.6) |
| s | (0.6,0.5,0.2) | (0.1,0.9,0.6) | (0.2,0.8,0.7) | (1,1,0) | (0.2,0.3,0.1) |
| t | (0.2,0.1,0.8) | (0.6,0.5,0.1) | (0.1,0.9,0.6) | (0.2,0.3,0.1) | (1,1,0) |
Let be a neutrosophic set on . The lower and upper approximations of are given as:
Let and S a neutrosophic tolerance relation which is given as:
| S | |||||
| (1,1,0) | (0.2,0.2,0.7) | (0.1,0.9,0.6) | (0.1,0.5,0.4) | (0.2,0.1,0.8) | |
| (0.2,0.2,0.7) | (1,1,0) | (0.2,0.3,0.5) | (0.1,0.5,0.6) | (0.1,0.5,0.6) | |
| (0.1,0.9,0.6) | (0.2,0.3,0.5) | (1,1,0) | (0.2,0.1,0.8) | (0.1,0.5,0.6) | |
| (0.1,0.5,0.4) | (0.1,0.5,0.6) | (0.2,0.1,0.8) | (1,1,0) | (0.2,0.2,0.3) | |
| (0.2,0.1,0.8) | (0.1,0.5,0.6) | (0.1,0.5,0.6) | (0.2,0.2,0.3) | (1,1,0) |
Let be a neutrosophic set on . The lower and upper approximations of are given as:
Thus, and are neutrosophic digraphs as shown in Figure 1.

Figure 1.
Neutrosophic rough digraph .
Example 2.
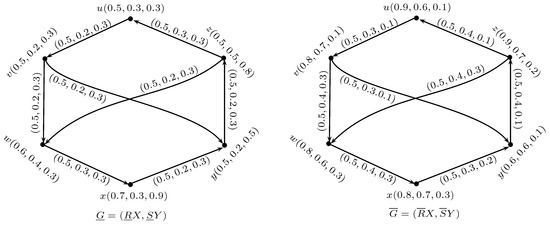
Let be a crisp set and R a neutrosophic tolerance relation on given by
| R | u | v | w | x | y | z |
| u | (1,1,0) | (0.2,0.3,0.5) | (0.5,0.6,0.9) | (0.3,0.8,0.3) | (0.3,0.2,0.1) | (0.1,0.1,0.5) |
| v | (0.2,0.3,0.5) | (1,1,0) | (0.9,0.5,0.6) | (0.1,0.5,0.7) | (0.8,0.9,0.1) | (0.8,0.9,0.1) |
| w | (0.5,0.6,0.9) | (0.9,0.5,0.6) | (1,1,0) | (0.3,0.6,0.8) | (0.2,0.3,0.6) | (0.7,0.6,0.6) |
| x | (0.3,0.8,0.3) | (0.1,0.5,0.7) | (0.3,0.6,0.8) | (1,1,0) | (0.5,0.1,0.9) | (0.8,0.7,0.2) |
| y | (0.3,0.2,0.1) | (0.8,0.9,0.1) | (0.2,0.3,0.6) | (0.5,0.1,0.9) | (1,1,0) | (0.6,0.5,0.9) |
| z | (0.1,0.1,0.5) | (0.8,0.9,0.1) | (0.7,0.6,0.6) | (0.8,0.7,0.2) | (0.6,0.5,0.9) | (1,1,0) |
Let be a neutrosophic set on . Then the lower and upper approximations of X are given as follows:
Let and S a neutrosophic tolerance relation on given as
| S | ||||||||
| (1,1,0) | (0.2,0.3,0.6) | (0.1,0.5,0.9) | (0.3,0.8,0.3) | (0.3,0.2,0.1) | (0.1,0.1,0.5) | (0.1,0.1,0.6) | (o.2,0.3,0.5) | |
| (0.2,0.3,0.6) | (1,1,0) | (0.3,0.5,0.8) | (0.1,0.3,0.7) | (0.7,0.6,0.6) | (0.5,0.6,0.9) | (0.8,0.9,0.1) | (0.2,0.3,0.6) | |
| (0.1,0.5,0.9) | (0.3,0.5,0.8) | (1,1,0) | (0.3,0.1,0.9) | (0.2,0.3,0.6) | (0.3,0.6,0.6) | (0.3,0.6,0.8) | (0.5,0.1,0.9) | |
| (0.3,0.8,0.3) | (0.1,0.3,0.7) | (0.3,0.1,0.9) | (1,1,0) | (0.5,0.1,0.9) | (0.3,0.2,0.2) | (0.2,0.3,0.6) | (0.1,0.5,0.7) | |
| (0.3,0.2,0.1) | (0.7,0.6,0.6) | (0.2,0.3,0.6) | (0.5,0.1,0.9) | (1,1,0) | (0.1,0.1,0.9) | (0.6,0.5,0.9) | (0.6,0.5,0.9) | |
| (0.1,0.1,0.5) | (0.5,0.6,0.9) | (0.3,0.6,0.6) | (0.3,0.2,0.2) | (0.1,0.1,0.9) | (1,1,0) | (0.5,0.6,0.9) | (0.3,0.3,0.1) | |
| (0.1,0.1,0.6) | (0.8,0.9,0.1) | (0.3,0.6,0.8) | (0.2,0.3,0.6) | (0,6,0.5,0.9) | (0.5,0.6,0.9) | (1,1,0) | (0.2,0.3,0.6) | |
| (0.2,0.3,0.5) | (0.2,0.3,0.6) | (0.5,0.1,0.9) | (0.1,0.5,0.7) | (0.6,0.5,0.9) | (0.3,0.2,0.1) | (0.2,0.3,0.6) | (1,1,0) |
Let Y be a neutrosophic set on defined as . Then the lower and upper approximations of Y are given as
Thus, and are the neutrosophic digraphs as shown in Figure 2.

Figure 2.
Neutrosophic rough digraph .
Now we discuss regular neutrosophic rough digraphs.
Definition 6.
Let be a neutrosophic rough digraph on a nonempty set . The indegree of a vertex is the sum of membership degree, indeterminacy and falsity of all edges towards x from other vertices in and , respectively, represented by and defined by
where
The outdegree of a vertex is the sum of membership degree, indeterminacy and falsity of all edges outward from x to other vertices in and , respectively, represented by and defined by
where
is called degree of vertex x.
Definition 7.
A neutrosophic rough digraph is called a regular neutrosophic rough digraph of degree if
Example 3.
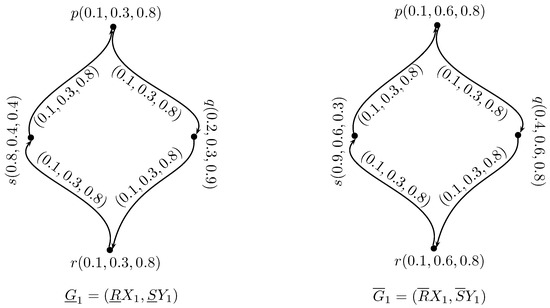
Let be a nonempty set and R a neutrosophic tolerance relation on is given as:
| R | p | q | r | s |
| p | (1,1,0) | (0.1,0.9,0.8) | (0.7,0.5,0.8) | (0.1,0.9,0.8) |
| q | (0.9,0.8,0.1) | (1,1,0) | (0.1,0.9,0.8) | (0.4,0.3,0.9) |
| r | (0.7,0.5,0.8) | (0.1,0.9,0.8) | (1,1,0) | (0.1,0.9,0.8) |
| s | (0.1,0.9,0.8) | (0.4,0.3,0.9) | (0.1,0.9,0.8) | (1,1,0) |
Let be a neutrosophic set on . The lower and upper approximations of are given as:
Let and S a neutrosophic tolerance relation on which is given as:
| S | ||||
| (1,1,0) | (0.1,0.9,0.8) | (0.4,0.3,0.9) | (0.1,0.9,0.8) | |
| (0.1,0.9,0.8) | (1,1,0) | (0.1,0.9,0.8) | (0.4,0.3,0.9) | |
| (0.4,0.3,0.9) | (0.1,0.9,0.8) | (1,1,0) | (0.1,0.9,0.8) | |
| (0.1,0.9,0.8) | (0.4,0.3,0.9) | (0.1,0.9,0.8) | (1,1,0) |
Let be a neutrosophic set on . The lower and upper approximations of are given as:
Thus, is a regular neutrosophic rough digraph as shown in Figure 3.

Figure 3.
Regular neutrosophic rough digraph .
Definition 8.
Let and be two neutrosophic rough digraphs. Then the direct sum of and is a neutrosophic rough digraph , where and are neutrosophic digraphs.
- (1)
- (2)
Example 4.
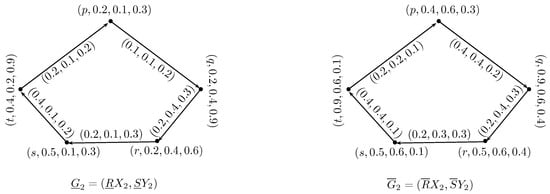
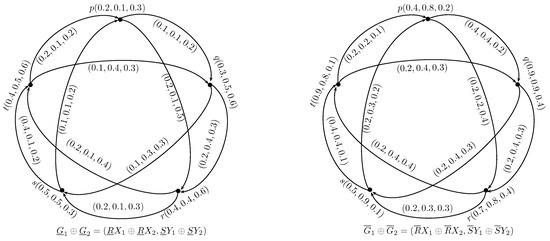
Let be a set. Let and be two neutrosophic rough digraphs on as shown in Figure 1 and Figure 4. The direct sum of and is , where and are neutrosophic digraphs as shown in Figure 5.

Figure 4.
Neutrosophic rough digraph .

Figure 5.
Neutrosophic rough digraph .
Remark 1.
The direct sum of two regular neutrosophic rough digraphs may not be regular neutrosophic rough digraph, as shown in the following example.
Example 5.
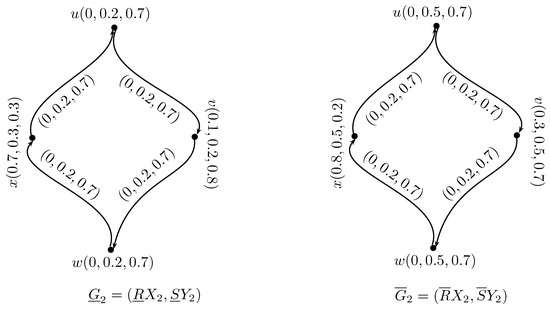
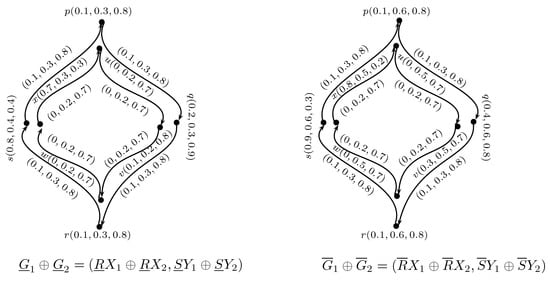
Consider the two regular neutrosophic rough digraphs and as shown in Figure 3 and Figure 6, respectively, then the direct sum of and as shown in Figure 7 is not a regular neutrosophic rough digraph.

Figure 6.
Regular neutrosophic rough digraph .

Figure 7.
Neutrosophic rough digraph .
Remark 2.
If and are two regular neutrosophic rough digraphs with degree and on , , respectively, and then is a regular neutrosophic rough digraph if and only if .
Definition 9.
Let and be two neutrosophic rough digraphs on crisp sets and respectively. The residue product of and is a neutrosophic rough digraph , where and are neutrosophic digraphs, respectively, such that
(1)
(2)
Example 6.
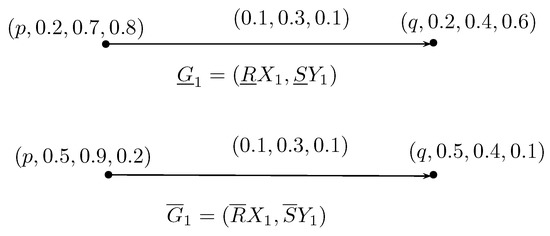
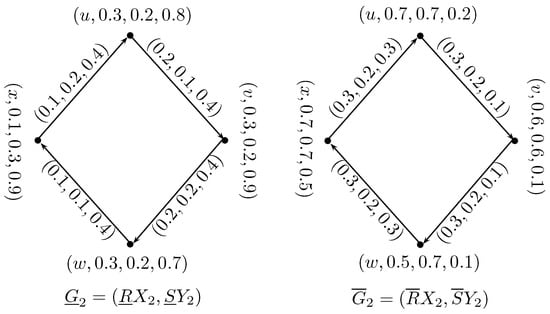
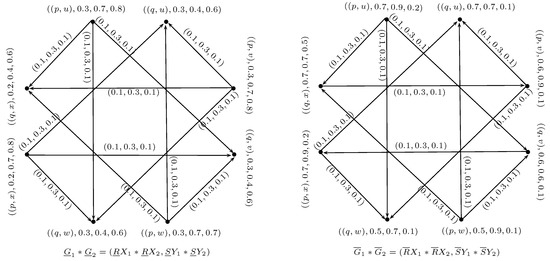
Let and be two neutrosophic rough digraphs on the two crisp sets and as shown in Figure 8 and Figure 9. Then the residue product of and is a neutrosophic rough digraph where and and the respective figures are shown in Figure 10.
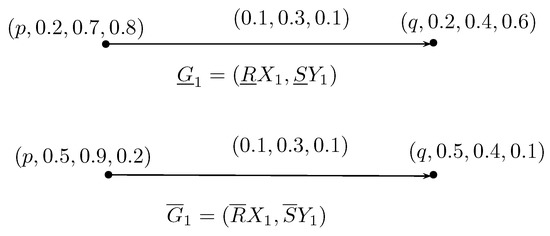
Figure 8.
Neutrosophic rough digraph .

Figure 9.
Neutrosophic rough digraph .

Figure 10.
Neutrosophic rough digraph .
Theorem 1.
If and are two neutrosophic rough digraph such that , then their residue product is regular if and only if is regular.
Proof.
Let be a regular neutrosophic rough digraph.
Then, for any two vertices and in ,
This is true for all vertices in . Hence is a regular neutrosophic rough digraph.
Conversely, suppose that is a -regular neutrosophic rough digraph and is any neutrosophic rough digraph with . If , then . This is a constant ordered-triplet for all vertices in . Hence is a regular neutrosophic rough digraph. ☐
3. Applications to Decision-Making
In this section, we present some real life applications of neutrosophic rough digraphs in decision making. In decision-making, the selection is facilitated by evaluating each choice on the set of criteria. The criteria must be measurable and their outcomes must be measured for every decision alternative.
3.1. Online Reviews and Ratings
Customer reviews are increasingly available online for a wide range of products and services. As customers search online for product information and to evaluate product alternatives, they often have access to dozens or hundreds of product reviews from other customers. These reviews are very helpful in product selection. However, only considering the good reviews about a product is not very helpful in decision-making. The customer should keep in mind bad and neutral reviews as well. We use percentages of good reviews, bad reviews and neutral reviews of a product as truth membership, false membership and indeterminacy respectively.
Mrs. Sadia wants to purchase a refrigerator. For this purpose she visits web sites of different refrigerator companies. The refrigerator companies and their ratings by other customers are shown in Table 1.

Table 1.
Companies and their ratings.
Here Pel(P),Dawlance(D),Haier(H),Waves(W),Orient(O)} and the neutrosophic set on according to the reviews will be The neutrosophic tolerance relation on is given below
| R | P | D | H | W | O |
| P | (1,1,0) | (0.5,0.6,0.9) | (0.2,0.3,0.6) | (0.1,0.2,0.3) | (0.4,0.6,0.8) |
| D | (0.5,0.6,0.9) | (1,1,0) | (0.1,0.6,0.9) | (0.4,0.5,0.9) | (0.9,0.8,0.2) |
| H | (0.2,0.3,0.6) | (0.1,0.6,0.9) | (1,1,0) | (0.2,0.9,0.6) | (0.1,0.9,0.7) |
| W | (0.1,0.2,0.3) | (0.4,0.5,0.9) | (0.2,0.9,0.6) | (1,1,0) | (0.2,0.5,0.9) |
| O | (0.4,0.6,0.8) | (0.9,0.8,0.2) | (0.1,0.9,0.7) | (0.2,0.5,0.9) | (1,1,0) |
The lower and upper approximations of X are as follows:
Let be the subset of and the tolerance relation S on is given as follows:
| S | (P,D) | (P,H) | (D,H) | (D,W) | (H,W) |
| (P,D) | (1,1,0) | (0.1,0.6,0.9) | (0.1,0.6,0.9) | (0.4,0.5,0.9) | (0.2,0.3,0.9) |
| (P,H) | (0.1,0.6,0.9) | (1,1,0) | (0.5,0.6,0.9) | (0.2,0.6,0.9) | (0.2,0.3,0.6) |
| (D,H) | (0.1,0.6,0.9) | (0.5,0.6,0.9) | (1,1,0) | (0.2,0.9,0.6) | (0.1,0.6,0.9) |
| (D,W) | (0.4,.5,.9) | (0.2,0.6,0.9) | (0.2,0.6,0.9) | (1,1,0) | (0.1,0.6,0.9) |
| (H,W) | (0.2,0.3,0.9) | (0.2,0.3,0.6) | (0.1,0.6,0.9) | (0.1,0.6,.9) | (1,1,0) |
| (H,O) | (0.2,0.3,0.6) | (0.1,0.3,0.7) | (0.1,0.6,0.9) | (0.1,0.5,0.9) | (0.2,0.5,0.9) |
| (W,P) | (0.1,0.2,0.9) | (0.1,0.2,0.6) | (0.2,0.3,0.9) | (0.1,0.2,0.9) | (0.1,0.2,0.6) |
| (W,O) | (0.1,0.2,0.3) | (0.1,0.2,0.7) | (0.1,0.5,0.9) | (0.2,0.5,0.9) | (0.2,0.5,0.9) |
| (O,P) | (0.4,0.6,0.9) | (0.2,0.3,0.8) | (0.2,0.3,0.6) | (0.1,0.2,0.3) | (0.1,0.2,0.7) |
| (O,D) | (0.4,0.6,0.8) | (0.1,0.6,0.9) | (0.1,0.6,0.9) | (0.4,0.5,0.9) | (0.1,0.5,0.9) |
| S | (H,O) | (W,P) | (W,O) | (O,P) | (O,D) |
| (P,D) | (0.2,0.3,0.6) | (0.1,0.2,0.9) | (0.1,0.2,0.3) | (0.4,0.6,0.9) | (0.4,0.6,0.8) |
| (P,H) | (0.1,0.3,0.7) | (0.1,0.2,0.6) | (0.1,0.2,0.7) | (0.2,0.3,0.8) | (0.1,0.6,0.9) |
| (D,H) | (0.2,0.3,0.9) | (0.1,0.5,0.9) | (0.2,0.3,0.6) | (0.1,0.6,0.9) | (0.1,0.6,0.9) |
| (D,W) | (0.1,0.2,0.9) | (0.2,0.5,0.9) | (0.1,0.2,0.3) | (0.4,0.5,0.9) | (0.1,0.5,0.9) |
| (H,W) | (0.1,0.2,0.6) | (0.2,0.5,0.9) | (0.1,0.2,0.7) | (0.1,0.5,0.9) | (0.2,0.5,0.9) |
| (H,O) | (1,1,0) | (0.2,0.6,0.8) | (0.2,0.9,0.6) | (0.1,0.6,0.8) | (0.1,0.8,0.7) |
| (W,P) | (0.2,0.6,0.8) | (1,1,0) | (0.4,0.6,0.8) | (0.2,0.5,0.9) | (0.2,0.5,0.9) |
| (W,O) | (0.2,0.9,0.6) | (0.4,0.6,0.8) | (1,1,0) | (0.2,0.5,0.9) | (0.2,0.5,0.9) |
| (O,P) | (0.1,0.6,0.8) | (0.2,0.5,0.9) | (0.2,0.5,0.9) | (1,1,0) | (0.5,0.6,0.9) |
| (O,D) | (0.1,0.8,0.7) | (0.2,0.5,0.9) | (0.2,0.5,0.9) | (0.5,0.6,0.9) | (1,1,0) |
Thus, the lower and upper approximations of Y are calculated as follows:
Thus, and are the neutrosophic digraphs as shown in Figure 11. To find the best company, we use the following formula:
where
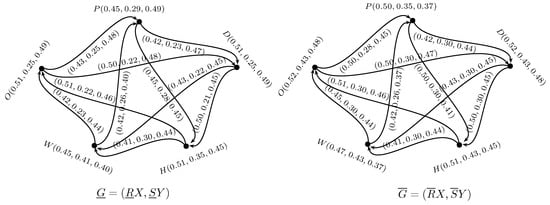
Figure 11.
.
By direct calculations we have
From the above calculations it is clear that Waves is the best company for refrigerator.
3.2. Context of Recruitment
Choosing the right candidate for the position available is not something that should be left to chance or guesswork.
How to choose the right candidate?
In any recruitment process the ability of the candidate is weighed against the suitability of the candidate. Pakistan Telecommunication Company Limited (PTCL) wants to recruit a person for the post of administrator. To keep the procedure simple, the company wants to appoint their employee on the basis of education (Edu) and experience (Exp). Let be the set of candidates who applied for the post and their corresponding attributes. Let R be a neutrosophic tolerance on given as follows:
| R | (C1,Edu) | (C1,Exp) | (C2,Edu) | (C2,Exp) | (C3,Edu) | (C3,Exp) |
| (C1,Edu) | (1,1,0) | (0.3,0.6,0.1) | (0.6,0.7,0.2) | (0.6,0.5,0.8) | (0.3,0.2,0.1) | (0.9,0.1,0.1) |
| (C1,Exp) | (0.3,0.6,0.1) | (1,1,0) | (0.9,0.9,0.3) | (0.8,0.7,0.6) | (0.4,0.5,0.9) | (0.3,0.1,0.1) |
| (C2,Edu) | (0.6,0.7,0.2) | (0.9,0.9,0.3) | (1,1,0) | (0.6,0.5,0.1) | (0.3,0.2,0.1) | (0.4,0.8,0.7) |
| (C2,Exp) | (0.6,0.5,0.8) | (0.8,0.7,0.6) | (0.6,0.5,0.1) | (1,1,0) | (0.1,0.1,0.2) | (0.5,0.6,0.7) |
| (C3,Edu) | (0.3,0.2,0.1) | (0.4,0.5,0.9) | (0.3,0.2,0.1) | (0.1,0.1,0.2) | (1,1,0) | (0.2,0.1,0.2) |
| (C3,Exp) | (0.9,0.1,0.1) | (0.3,0.1,0.1) | (0.4,0.8,0.7) | (0.5,0.6,0.7) | (0.2,0.1,0.2) | (1,1,0) |
Let be a neutrosophic set define on . Then the lower and upper approximations of X are given as:
Let and S be a neutrosophic tolerance relation on given as follows:
| S | (C1,Edu)(C1,Exp) | (C1,Exp)(C2,Edu) | (C1,Edu)(C3,Exp) | (C3,Exp)(C1,Exp) | (C1,Exp)(C2,Exp) |
| (C1,Edu)(C1,Exp) | (1,1,0) | (0.3,0.6,0.3) | (0.3,0.1,0.1) | (0.9,0.1,0.1) | (0.3,0.6,0.6) |
| (C1,Exp)(C2,Edu) | (0.3,0.6,0.3) | (1,1,0) | (0.3,0.6,0.7) | (0.3,0.1,0.3) | (0.6,0.5,0.1) |
| (C1,Edu)(C3,Exp) | (0.3,0.1,0.1) | (0.3,0.6,0.7) | (1,1,0) | (0.3,0.1,0.1) | (0.3,0.6,0.7) |
| (C3,Exp)(C1,Exp) | (0.9,0.1,0.1) | (0.3,0.1,0.3) | (0.3,0.1,0.1) | (1,1,0) | (0.3,0.1,0.6) |
| (C1,Exp)(C2,Exp) | (0.3,0.6,0.6) | (0.6,0.5,0.1) | (0.3,0.6,0.7) | (0.3,0.1,0.6) | (1,1,0) |
| (C2,Exp)(C2,Edu) | (0.6,0.5,0.8) | (0.8,0.7,0.6) | (0.4,0.5,0.8) | (0.5,0.6,0.7) | (0.6,0.5,0.6) |
| (C3,Exp)(C2,Exp) | (0.8,0.1,0.6) | (0.3,0.1,0.1) | (0.5,0.1,.7) | (0.8,0.7,0.6) | (0.3,0.1,0.1) |
| (C3,Exp)(C3,Edu) | (0.4,0.1,0.9) | (0.3,0.1,0.1) | (0.2,0.1,.2) | (0.4,0.5,0.9) | (0.1,0.1,0.2) |
| (C3,Edu)(C2,Exp) | (0.3,0.2,0.6) | (0.4,0.5,0.9) | (0.3,.2,.7) | (0.2,0.1,0.6) | (0.4,0.5,0.9) |
| S | (C2,Exp)(C2,Edu) | (C3,Exp)(C2,Exp) | (C3,Exp)(C3,Edu) | (C3,Edu)(C2,Exp) |
| (C1,Edu)(C1,Exp) | (0.6,0.5,0.8) | (0.8,0.1,0.6) | (0.4,0.1,0.9) | (0.3,0.2,0.6) |
| (C1,Exp)(C2,Edu) | (0.8,0.7,0.6) | (0.3,0.1,0.1) | (0.3,0.1,0.1) | (0.4,0.5,0.9) |
| (C1,Edu)(C3,Exp) | (0.4,0.5,0.8) | (0.5,0.1,0.7) | (0.2,0.1,0.2) | (0.3,0.2,0.7) |
| (C3,Exp)(C1,Exp) | (0.5,0.6,0.7) | (0.8,0.7,0.6) | (0.4,0.5,0.9) | (0.2,0.1,0.6) |
| (C1,Exp)(C2,Exp) | (0.6,0.5,0.6) | (0.3,0.1,0.1) | (0.1,0.1,0.2) | (0.4,0.5,0.9) |
| (C2,Exp)(C2,Edu) | ( 1,1,0) | (0.5,0.5,0.7) | (0.3,0.2,0.7) | (0.1,0.1,0.2) |
| (C3,Exp)(C2,Exp) | (0.5,0.5,0.7) | (1,1,0) | (0.1,0.1,0.2) | (0.2,0.1,0.2) |
| (C3,Exp)(C3,Edu) | (0.3,0.2,0.7) | (0.1,0.1,0.2) | ( 1,1,0) | (0.1,0.1,0.2) |
| (C3,Edu)(C2,Exp) | (0.1,0.1,0.2) | (0.2,0.1,0.2) | (0.1,0.1,0.2) | (1,1,0) |
Let be neutrosophic rough set on . Then the lower and upper approximations of Y are given as follows:
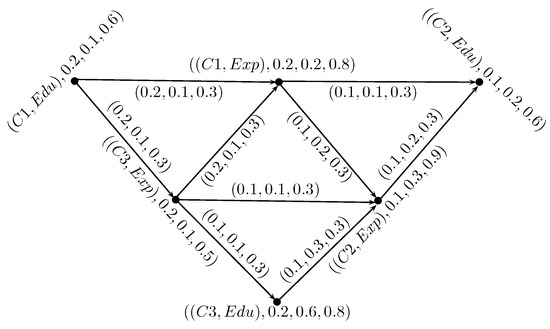
Figure 12.
Neutrosophic Digraph
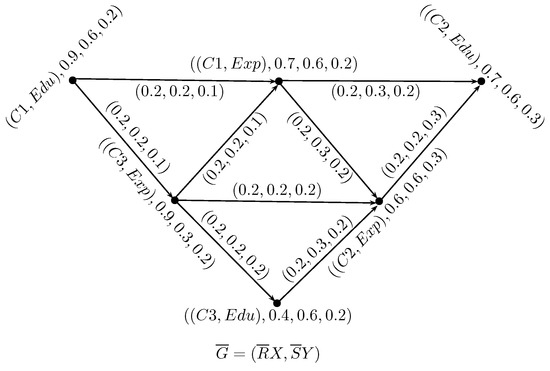
Figure 13.
Neutrosophic Digraph
To find the best employee using the following calculations, we have
Thus, is the best employee for the post under consideration. So, PTCL can hire for the post of administrator.
4. Comparative Analysis of Rough Neutrosophic Digraphs and Neutrosophic Rough Digraphs
Rough neutrosophic digraphs and neutrosophic rough digraphs are two different notions on the basis of their construction and approach. In rough neutrosophic digraphs, the relation defined on the universe of discourse is a crisp equivalence relation that only classifies the elements which are related. On the other hand, in neutrosophic rough digraphs the relation defined on the set is neutrosophic tolerance relation. The neutrosophic tolerance relation not only classifies the elements of the set which are related but also expresses their relation in terms of three components, namely truth membership (T), Indeterminacy (I) and falsity (F). This approach leaves room for indeterminacy and incompleteness. Below, we apply the method of rough neutrosophic digraphs to the above presented application (online reviews and ratings).
Here and the neutrosophic set on according to the reviews will be . The equivalence relation on is given below
| R | P | D | H | W | O |
| P | 1 | 0 | 1 | 0 | 1 |
| D | 0 | 1 | 0 | 0 | 0 |
| H | 1 | 0 | 1 | 0 | 1 |
| W | 0 | 0 | 0 | 1 | 0 |
| O | 1 | 0 | 1 | 0 | 1 |
The lower and upper approximations of X are as follows:
Let be the subset of and the equivalence relation S on is given as follows:
| S | (P,D) | (P,H) | (D,H) | (D,W) | (H,W) | (H,O) | (W,P) | (W,O) | (O,P) | (O,D) |
| (P,D) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| (P,H) | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| (D,H) | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| (D,W) | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| (H,W) | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| (H,O) | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| (W,P) | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| (W,O) | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| (O,P) | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| (O,D) | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
Thus, the lower and upper approximations of Y are calculated as follows:
To find the best company ratings, we use the following formula:
where
By direct calculations, we have
From the above calculations, we have Waves as the best choice and Dawlance as the least choice for refrigerator. This is because the relation applied in this method is crisp equivalence relation which does not consider the uncertainty between the companies of the same equivalence class. Whereas in our proposed method, least choice for refrigerator is different. So, the results may vary when we apply the method of rough neutrosophic digraphs and neutrosophic rough digraphs on the same application. This means that rough neutrosophic digraphs and neutrosophic rough digraphs have a different approach.
5. Conclusions
Neutrosophic set and rough set are two different theories to deal with uncertainty and imprecise and incomplete information. Due to the limitation of human knowledge to understand the complex problems, it is very difficult to apply only a single type of uncertainty method to deal with such problems. Therefore, it is necessary to develop hybrid models by incorporating the advantages of many other different mathematical models dealing with uncertainty. Thus, by combining these two mathematical tools, we have presented a new hybrid model, namely, neutrosophic rough digraphs. We have escribed regular neutrosophic rough digraphs and we have presented novel applications of our proposed hybrid in decision-making. We have given a comparison of both models, rough neutrosophic digraphs and neutrosophic rough digraphs. We plan to extend our research work to (1) Neutrosophic rough hypergraphs; (2) Bipolar neutrosophic rough hypergraphs; (3) Soft rough neutrosophic graphs; (4) Decision support systems based on neutrosophic rough information.
Author Contributions
M.A., N.I. and S.S. conceived and designed the experiments; F.S. analyzed the data; N.I. and S.S. wrote the paper.
Acknowledgments
The authors are very thankful to the Editor and referees for their valuable comments and suggestions for improving the paper.
Conflicts of Interest
The authors declare that they have no conflict of interest regarding the publication of the research article.
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy: Neutrosophic Probability, Set, and Logic; American Research Press: Santa Fe, NM, USA, 1998. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.; Sunderraman, R. Single-valued neutrosophic sets. Multispace Multistructure 2010, 4, 410–413. [Google Scholar]
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Rough fuzzy sets and fuzzy rough sets. Int. J. Gen. Syst. 1990, 17, 191–209. [Google Scholar] [CrossRef]
- Liu, P.; Chen, S.M. Group decision-making based on Heronian aggregation operators of intuitionistic fuzzy numbers. IEEE Trans. Cybern. 2017, 47, 2514–2530. [Google Scholar] [CrossRef] [PubMed]
- Mordeson, J.N.; Peng, C.S. Operations on fuzzy graphs. Inf. Sci. 1994, 79, 159–170. [Google Scholar] [CrossRef]
- Akram, M.; Shahzadi, S. Neutrosophic soft graphs with applicatin. J. Intell. Fuzzy Syst. 2017, 32, 841–858. [Google Scholar] [CrossRef]
- Akram, M.; Sarwar, M. Novel multiple criteria decision-making methods based on bipolar neutrosophic sets and bipolar neutrosophic graphs. Ital. J. Pure Appl. Math. 2017, 38, 368–389. [Google Scholar]
- Akram, M.; Siddique, S. Neutrosophic competition graphs with applications. J. Intell. Fuzzy Syst. 2017, 33, 921–935. [Google Scholar] [CrossRef]
- Akram, M.; Sitara, M. Interval-valued neutrosophic graph structures. Punjab Univ. J. Math. 2018, 50, 113–137. [Google Scholar]
- Akram, M.; Zafar, F. Rough fuzzy digraphs with application. J. Appl. Math. Comput. 2018. [Google Scholar] [CrossRef]
- Zafer, F.; Akram, M. A novel decision-making method based on rough fuzzy information. Int. J. Fuzzy Syst. 2018, 20, 1000–1014. [Google Scholar] [CrossRef]
- Broumi, S.; Smarandache, F.; Dhar, M. Rough neutrosophic sets. Neutrosophic Sets Syst. 2014, 3, 62–67. [Google Scholar]
- Yang, H.L.; Zhang, C.L.; Guo, Z.L.; Liu, Y.; Liao, X. A hybrid model of single valued neutrosophic sets and rough sets: Single valued neutrosophic rough set model. Soft Comput. 2016. [Google Scholar] [CrossRef]
- Nabeela, I.; Sayed, S.; Akram, M.; Smarandache, F. Notions of Rough Neutrosophic Digraphs. Mathematics 2018, 6, 18. [Google Scholar]
- Sidra, S.; Ishfaq, N.; Akram, M.; Smarandache, F. Rough Neutrosophic Digraphs with Application. Axioms 2018, 7, 5. [Google Scholar]
- Akram, M.; Shum, K.P. Bipolar neutrosophic planar graphs. J. Math. Res. Appl. 2017, 36, 631–648. [Google Scholar]
- Peng, H.G.; Zhang, H.Y.; Wang, J.Q. Probability multi-valued neutrosophic sets and its application in multi-criteria group decision-making problems. Neural Comput. Appl. 2016. [Google Scholar] [CrossRef]
- Ye, J. Multicriteria decision-making method using the correlation coefficient under single-valued neutrosophic environment. Int. J. General Syst. 2013, 42, 386–394. [Google Scholar] [CrossRef]
- Ye, J. Improved correlation coefficients of single valued neutrosophic sets and interval neutrosophic sets for multiple attribute decision-making. J. Intell. Fuzzy Syst. 2014, 27, 2453–2462. [Google Scholar]
- Smarandache, F. A Unifying Field in Logic. In Neutrosophy; American Research Press: Santa Fe, NM, USA, 1999. [Google Scholar]
- Akram, M.; Malik, H.M.; Shahzadi, S.; Smarandache, F. Neutrosophic Soft Rough Graphs with Application. Axioms 2018, 7, 14. [Google Scholar] [CrossRef]
- Banerjee, M.; Pal, S.K. Roughness of a fuzzy set. Inf. Sci. 1996, 93, 235–246. [Google Scholar] [CrossRef]
- Liu, P.; Chen, S.M.; Junlin, L. Some intuitionistic fuzzy interaction partitioned Bonferroni mean operators and their application to multi-attribute group decision-making. Inf. Sci. 2017, 41, 98–121. [Google Scholar] [CrossRef]
- Liu, P. Multiple attribute group decision-making method based on interval-valued intuitionistic fuzzy power Heronian aggregation operators. Comput. Ind. Eng. 2017, 18, 199–212. [Google Scholar] [CrossRef]
- Liang, R.X.; Wang, J.Q.; Zhang, H.Y. A multi-criteria decision-making method based on single-valued trapezoidal neutrosophic preference relations with complete weight information. Neural Comput. Appl. 2017. [Google Scholar] [CrossRef]
- Nie, R.X.; Wang, J.Q.; Zhang, H.Y. Solving solar-wind power station location problem using an extended weighted aggregated sum product assessment (WASPAS) technique with interval neutrosophic sets. Symmetry 2017, 9, 106. [Google Scholar] [CrossRef]
- Luo, S.Z.; Cheng, P.F.; Wang, J.Q.; Huang, Y.J. Selecting project delivery systems based on simplified neutrosophic linguistic preference relations. Symmetry 2017, 9, 151. [Google Scholar] [CrossRef]
- Zhang, X.; Dai, J.; Yu, Y. On the union and intersection operations of rough sets based on various approximation spaces. Inf. Sci. 2015, 292, 214–229. [Google Scholar] [CrossRef]
- Bao, Y.L.; Yang, H.L. On single valued neutrosophic refined rough set model and its application. J. Intell. Fuzzy Syst. 2017, 33, 1235–1248. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).