Abstract
In cognitive radio networks (CRNs), improving system utility and ensuring system fairness are two important issues. In this paper, we propose a spectrum allocation model to construct CRNs based on graph coloring theory, which contains three classes of matrices: available matrix, utility matrix, and interference matrix. Based on the model, we formulate a system objective function by jointly considering two features: system utility and system fairness. Based on the proposed model and the objective problem, we develop an improved gravitational search algorithm (IGSA) from two aspects: first, we introduce the pattern search algorithm (PSA) to improve the global optimization ability of the original gravitational search algorithm (GSA); second, we design the Chebyshev chaotic sequences to enhance the convergence speed and precision of the algorithm. Simulation results demonstrate that the proposed algorithm achieves better performance than traditional methods in spectrum allocation.
1. Introduction
With the massive growth of wireless devices, the conventional method of resource allocation aggravates the spectrum-scarcity situation, which significantly degrades the utilization of spectrum. However, the spatial and temporal variations in the licensed spectrum utilization range from to , according to a report by Federal Communications Commission [1]. In this condition, cognitive radio (CR) techniques are studied and developed [2]. CR is a promising technology for improving the traditional spectrum allocation methods, which enables access to the underutilized licensed spectrum to mitigate the spectrum-scarcity problem in the unlicensed band. Furthermore, cognitive radio networks (CRNs) [3] are vital wireless communication systems to utilize the spectrum resource efficiently. In these networks, the cognitive users, namely secondary users (SUs) can use licensed spectrum without interfering with the licensed users or primary users (PUs) [4]. Based on this feature, CRNs implement four main objectives of dynamic spectrum management [5]: spectrum sensing, spectrum assignment, spectrum mobility, and spectrum sharing.
Spectrum sensing [6] is mainly to achieve the detection and analysis of the spectrum hole characteristics which are time distribution, required bandwidth, noise, transmission power, and so on. Spectrum assignment [7] refers to the selection of suitable operating bands for data transmission according to the requirements of the quality of service (QoS) and determines the carrier frequency, communication system, communication parameters, and emission level. Spectrum mobility means that once the PU is found to return to this channel, the SU who using the band would move immediately and establish a new communication connection for data transmission. The purpose of spectrum sharing is to solve the problem of how to choose the spectrum between multiple SUs and ensure the maximization of spectrum utilization. Spectrum assignment is a key issue for maximizing the spectrum utilization. The scholars have done a lot of work in spectrum allocation.
One of the major topics of research for spectrum assignment is studying the mathematical model. Based on different application requirements and network structures, different system frameworks are proposed. In [8], Zhu et al. abstract a cognitive radio network into a topological map, in which each PU owns its channel and the SU cannot use it while PU is active. Furthermore, the two SUs who overlap in the communication range cannot occupy the same channel. In [9] Lu et al. focus on using bipartite graphs to solve the resource allocation problem, in which SUs and PUs are treated as two partite sets and an allocation scheme can be seen as a matching of the corresponding bipartite graph. In [10], Borhan et al. investigate the optimal scheduling of CRNs links under interference temperature theory, in which interference temperature is identical to the noise that users will create while they join the system. The authors design a cross-layered model to activate as many simultaneous primary/secondary links while the noise interference constraints are satisfied. In [11], Mohammad et al. use evolutionary game theory to model potential PU-SU dynamics; the authors focus on the emergence of bio-socially inspired foraging, socializing behaviors, and the potential impacts of these behaviors on the overall performance of the system. In [12], a modified multi-auctioneer progressive spectrum auction mechanism is introduced to optimize the utility of system. However, the graph theory not only takes into account the interference among users but develops mathematical expression to quantify the performance of algorithms, which attracts researchers to use it to formulate the channel allocation problem. Based on this, we build a graph-based mathematical model to demonstrate the spectrum allocation problem in this paper.
The other major research topic for spectrum assignment is studying the spectrum allocation algorithm. The problem of spectrum allocation is an NP-hard one. Whereas the meta-heuristic approach is one of the best ways to find a near-optimization solution for NP-hard issues. In [13], Salehinejad et al. introduce ant colony optimization (ACO) algorithm to solve the opportunistic spectrum access, but it only works in distributed strategies. He et al. propose ACO in [14] to maximize the throughput of the system. In [15], an optimized genetic algorithm (GA) based on underlay color-sensitive graph coloring framework is proposed, in which GA could avoid the remaining local optima by randomly adding the individual. GA is also proposed in [16] to solve the routing and spectrum allocation problem with multicast flows; the authors design novel selection and crossover strategies to enhance the algorithm performance. In [17], particle swarm optimization (PSO) and the modified GA algorithms are employed to find a near-optimal solution according to the specified requirements of SUs, the specified requirements can be the minimum data rate or the maximum subscription fee that they are willing to pay. Javier Del Ser et al. propose harmony search (HS) algorithm in [18] for spectrum allocation based on both centralized and distributed architecture; the proposed algorithm dramatically decreases the transmission rate required for exchanging control traffic among nodes and achieves near-optimum spectral channel assignment.
Although channel assignment based on metaheuristic algorithms has been studied for a long time, the study still faces challenges, such as algorithms easily falling into local optima and slow convergence speed. Gravitational search algorithm (GSA) [19] is a novel metaheuristic algorithm, which has been confirmed to be able to achieve higher performance in solving various non-linear problems compared with some well-known swarm algorithms [20]. In this paper, we use graph coloring theory to formulate the spectrum assignment problem, and we also design a new version of GSA (IGSA) to maximize the spectrum utilization. In IGSA, first, Chebyshev map [21] is adopted to initialize the population of IGSA to reduce the risk of trapping to the local maximum. Second, pattern search algorithm (PSA) [22] is introduced to ameliorate the inefficiency fine searchability of GSA. Besides, we investigate interference cancellation according to the interference-free principle. Based on the IGSA, we allocate the available licensed channel to SUs without interference to PUs while maximizing system utility.
2. System Model
2.1. Graph Coloring Model Based on CRN
A topological structure of the CRNs can be abstracted into a simple undirected graph that is represented as , where V is a finite set of vertices, representing SUs; E is a set of edges that are subject to interference matrix; L is a collection of available colors which represent the idle spectrum. Allocating available licensed spectrum resources to SUs is equivalent to vertex coloring in the graph coloring problem.
Assuming that there is N SUs who compete with each other to access M channels. Each SU occupies an available channel at a certain time.
Definition 1.
Channel Availability Matrix is a binary matrix, expressing availability of these licensed channels for SUs. If , channel m is available for the n-th SU; otherwise, .
Definition 2.
Channel Utility Matrix indicates the benefits that each SU can obtain from different channels. is the benefits obtained by the n-th SU when it uses the channel m.
Definition 3.
Interference Matrix is a binary matrix of , expressing the interference among SUs of each channel. means that the n-th SU and the k-th SU cannot access into channel m simultaneously, because that would cause transmission interference.
Definition 4.
Interference-Free Allocation Matrix is a binary matrix, it indicates a feasible channel allocation scheme. denotes that channel m is allocated to the n-th SU. On the contrary, .
2.2. Problem Formulation
Based on the aforementioned graph coloring model for spectrum allocation, we formulate the optimization problem. First, we introduce a commonly used objective, which is maximizing spectrum utilization and it can be expressed as
Besides, we introduce another objective to improve the fairness of the SU accessing the system, which is achieved by minimizing the standard deviation estimation of SU. It can be expressed as
Moreover, a channel assignment result should satisfy the collision-free constraint, i.e. if channel m is being accessed by the n-th SU, then the k-th SU cannot access this channel simultaneously, that is
where is the set of interfering to the n-th SU on channel m according to interference constraints and it comes from
Combine the (1)–(3) to formulate the problem. In order to reduce the complexity of the problem, we transform the above multiobjective optimization problem into a single objective problem. Let denote the optimization problem which can be expressed as
where A is a valid spectrum assignment allocation, is the set of all valid spectrum assignments given a set of N SUs and M spectrum bands.
3. Technologies
Spectrum allocation is essentially a binary multiobjective optimization problem with constraints, which is NP-hard. Heuristic algorithms, in accordance with intuitive or empirical, are extensively used in combinatorial optimization problems and express outstanding performance. GSA is a novel heuristic algorithm, which has been successfully applied to various real optimization problems, e.g., neural network training, mechanical engineering, image processing, and telecommunication. Then, we try to employ GSA to solve the spectrum assignment issue in CRNs. However, similar to other swarm intelligence algorithms, GSA has such problems as being prone to falling into local optimum and having low precision of solving. Consequently, PSA, a derivative-free evolutionary algorithm with strong fine search capability, is adopted to this paper to enhance the accuracy of GSA.
3.1. Critical Technologies
3.1.1. Encoding and Decoding
The encoding maps the position of a particle to a solution, which is an important concept in IGSA. Interference-free allocation matrix A is subject to the availability matrix L which contains many zero elements. Therefore, considering the computational complexity of spectrum allocation, this paper encodes only nonzero elements in matrix L. Following the column-priority principle, these nonzero elements are encoded into a binary row vector. After encoding, we can obtain a row vector P with length D. P represents the position of a particle in the proposed algorithm.
Decoding is the reverse process of encoding. The reverse process remaps the row vector P to an allocation scheme A. Figure 1 illustrates the process of encoding and decoding.
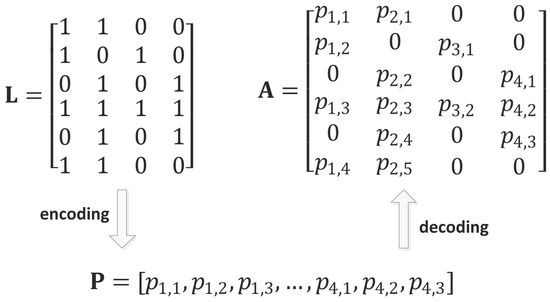
Figure 1.
The mapping process.
3.1.2. Population Initialization
In order to increase the randomness and spreadability of the particle position, Chebyshev chaotic sequences are employed to initialize the particle position in an ergodic, uniform, and randomn manner. It is expressed as follows:
where k is the degree of Chebyshev map and usually is a positive integer bigger than 1, , and . Because the spectrum allocation matrix A is in binary representation, then a threshold method is introduced to control the particle position, as shown below:
In IGSA, the first particle position is randomly generated, and the size of which is the encoding length D. Then the rest of the particle position is initialized with the Chebyshev chaotic mapping rule. The initial position of the particle i is described as follows:
3.1.3. Position Modification
The resource allocation scheme A is interference-free. However, in the process of the particle evolution or pattern move, the particle position or mesh point (spectrum allocation schemes) may not satisfy the interference constraints anymore, hence it needs to be corrected. The rule of modification is: for any spectrum m, if , then check the n and k rows in m column of allocation scheme matrix A, if they are all 1, it is necessary to set one of these two elements ( or ) to zero equal-probably. Then the spectrum allocation scheme A would be interference free.
3.2. Algorithms
3.2.1. Basic Thoughts
Some studies have shown that GSA could outperform other metaheuristic algorithms [20], especially in global search. Still, similar to other swarm intelligence algorithm, GSA can easily fall into local optimum and lack fine searchability. Based on the above, GSA and PSA are respectively chosen as coarse search and fine search of the spectrum allocation mechanism. Therefore, the position of the particle with the heaviest mass in the GSA iterations represents a close-to-optimal solution for spectrum assignment, which is used as the initial value of PSA for further local search.
3.2.2. GSA in IGSA
The GSA, one of the high-efficient heuristic search algorithm, was first proposed by Esmat Rashedi, et al. in 2009 [19]. GSA is inspired by the Newtonian law and follows the motion law. In GSA, a particle is an agent of spectrum allocation solution, the process of finding the global optimal solution for objective functions that are transformed into movement in which all agents move towards the agents with heavier mass.Therefore, the position of an agent which is heaviest will be the close-to-optimal global allocation solution.
Assuming a GSA system with N agents, position and velocity of the i-th agent can be defined as:
where , are respectively the position and velocity of the i-th agent in d-th dimension of t-th generation. The velocity of an agent in the next iteration is considered as a fraction of its current velocity added to its acceleration. Therefore, its position and its velocity could be calculated as follows:
Moreover, resource allocation is actually a binary issue, nevertheless, the original GSA is a continuous algorithm for solving a continuous problem. Hence, the sigmoid function is adapted to design a binary gravitational search algorithm for settling the binary issue. Then a new update model for position and velocity is proposed:
where is a uniformly distributed random number in the interval ; is the acceleration of i-th agent in dth dimension at t time:
is the force exerted by the remaining population upon agent i at t time:
where is the set of first k agents with the best fitness value. denotes the euclidian distance between agent i and j. is a constant. is the gravitational constant. t and T are the current iteration times and maximum iteration times. A heavier agent has a stronger attraction to others; the mass of each agent is obtained by calculating the fitness value of the agents. The mass of i-th agent is updated as
where represent the fitness value and mass of agent i at t time. Futhermore, and are the worst and the best fitness value in all agents at t time, respectively:
3.2.3. PSA in IGSA
PSA is an optimized method without any gradient information for any objective function, which is suitable to solve a variety of optimization problems. It computes a sequence of points that may or may not approach the optimal point. PSA starts with base points (or initial points) which are provided by the GSA. Around the base point, a set of points called mesh would be established. The mesh is created by adding the current point to a scalar multiple of a set of vectors called a pattern. The algorithm adaptively adjusts its mesh size and base points by fitness value comparison of the base point and mesh points. If a point in mesh has a better objective fitness value, it becomes the current point at the next iteration. The features of PSA ensure its superior exploitation ability which compensates the insufficiency of GSA.
The PSA process in IGSA is as follows:
- Building pattern. The PSA pattern is obtained by constructing a group of vectors. The group consists of a list of new points around the base point, which is used for the fine search of a base point. The vector of i-th base point is built in this way:where I is an identity matrix, D is the encoded length of spectrum allocation, is a vector group built for the base point .
- Forming mesh. The PSA establishes a series of points centered around the base point, which is called mesh. The following formula is used to generate mesh:where {} represents the new alternative point set of the base point , is the mesh size.
- Polling. In the search process of PSA, the optimum point among and original base point is selected to be the new base point of the next iteration, the new point is denoted as . Polling has two kinds of results: polling success and failure. Polling success means that an alternative point in mesh is better than the base point, otherwise polling failure.
- Adjusting mesh size. If polling success, the new alternative point replaces the base point and then use Equation (26) to enlarge mesh size (or step size) of searching, otherwise, the original base point is retained and then use Equation (27) to shrink the mesh size.where and denote the enlarge factor and shrink factor, respectively.
4. Spectrum Allocation Based on IGSA
In order to balance the exploration and exploitation ability, we design an improved algorithm which employs GSA for global optimizing and PSA for local search. In this section, we illustrate the process of IGSA-based spectrum allocation and present the algorithm in Algorithm 1. The process of IGSA-based spectrum allocation is described as below:
- Step 1:
- Initialization. Generate the system environment; initialize the parameters and constants of IGSA; define the objective function; set the maximum iteration time of GSA and PSA , , respectively.
- Step 2:
- Population initialization. Build chaotic population for IGSA using the Chebyshev chaotic map (in Section 3.2.1).
- Step 3:
- Exploration. Employ GSA to explore the search space and obtain the close-to-optimal solution.
- Step 4:
- Exploitation. Initialize PSA with the optimal solution obtained from GSA, use PSA to exploit the local area.
| Algorithm 1: An Improved Gravitational Search Algorithm. |
 |
5. Simulation Experiment
To evaluate and compare the performance of the dynamic channel allocation approaches in cognitive radio networks, we perform simulation experiments in this section. First, we introduce the evaluation criteria for algorithm performance. Second, we construct the environment for experiments and initialize parameters for algorithms (IGSA, GSA [19], PSO [23] and color sensitive graph coloring(CSGC) [24]). Third, we conduct experiments and analyze the experimental results.
5.1. Evaluation Criteria
To evaluate the performance of algorithms for assigning spectrum to SUs in CRNs from different aspects, we introduce several criteria in this paper.
- System utility: the total system utility of a spectrum allocation scheme, which is used to validate the total revenue of the system, that is
- System fairness: the standard deviation estimation of SU, which is used to validate the fairness of SUs access into spectrum, that is
- System overall performance: the total capacity of the system, which is used to validate the overall system performance, that is
5.2. Experimental Environment and Parameter
Simulations are operated in Matlab R2014a platform. We use the topology structure of cognitive radio system as suggested in [25], it is assumed that there is a wireless network covering square area. The number of PU is fixed to 10, with protection radius . The number of SUs is N, with interference radius . The number of available spectrum is M, which are completely orthogonal. The matrix B, L and C are generated according to the reference.
The parameters of the algorithms are set as shown in Table 1. Especially, the parameter setting of IGSA references the configuration of the original GSA to guarantee the comparability with GSA. The default parameter configuration cannot be the optimal setting for various problems. Thus we cannot assure they are optimal for IGSA in solving spectrum assignment. Parameter configuration could be a limitation of our current work, and we will try to find an effective parameter setting method in our further work. Additionally, the maximum iteration times of GSA and PSA in IGSA should be properly chosen so as to ensure the satisfactory performance of the algorithm with minimum computational efforts. A series of experiments were conducted to properly choose the run times in IGSA. The convergence experiments show that the original GSA usually reaches the convergence state after 100 iterations. To enhance the exploitation ability of the proposed algorithm while assuring the exploration capability, the iteration of GSA and PSA are set at 50 and 150, respectively. The population size is the same for all the algorithms in each experiment. Each individual performs one fitness evaluation after an iteration, then the best fitness value of each algorithm is selected to validate the performance of the algorithm.

Table 1.
Parameter setting for algorithms.
In addition, we use the CSGC which is commonly used to solve the spectrum allocation problem as the benchmark algorithm to compare with others, for more information on CSGC, please refer to [24]. All algorithms use the same topology, and the number of repetitions in convergence experiments is 500, others are 50, and the average is finally taken.
5.3. Simulations and Analyzation
Experiment 1.
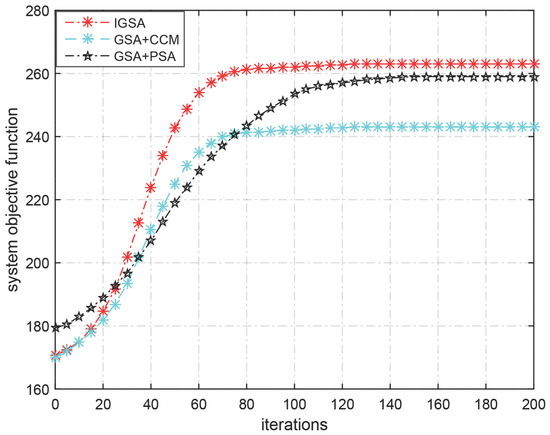
In order to validate the performance of the improved algorithms which optimizes the original GSA at different iteration stages, we conduct this experiment firstly. In Figure 2, GSA + CCM indicates an optimized method that initializes the population of GSA with Chebyshev chaotic map, and GSA + PSA is an optimized approach that enhances the local searchability of GSA using PSA. As we can see in Figure 2, in the first 50 iterations, the performance curve of GSA + CCM is close to IGSA but still lower than IGSA. Due to IGSA adopting the encoding and decoding rules to reduce the computing dimension and data redundancy, the convergence rate increases. Whereas GSA + CCM still performs better than GSA + PSA in convergence because initializing population with the chaotic map effectively avoids premature convergence. However, the insufficiency in local search leads to its inferior exploitation ability in the last stage of iteration. Different from GSA + CCM, GSA + PSA vanquishes the deficiency of GSA in fine search and achieves good performance. However, it suffers from the premature convergence which causes the convergence speed to be lower than the other algorithms. Compared with the other GSA-based improved algorithms, IGSA not only avoids premature convergence but has sufficient capability in local search.

Figure 2.
Performance of the GSA-based improved algorithm.
Experiment 2.
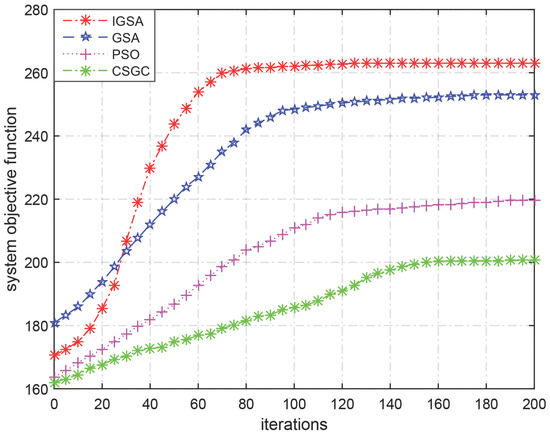
In this experiment, we evaluate the performance of the IGSA and GSA, PSO, CSGC in terms of overall system performance. From Figure 3, we can see that the overall performance grows with the iteration times, where the number of available channels is , the number of SUs is .

Figure 3.
Convergence speed.
As shown in Figure 3, the performance of CSGC is far inferior to PSO, GSA and IGSA, and it starts converging until 150 iterations. The PSO is better than CSGC but still lower than GSA and IGSA. Before 35 iterations, the performance of GSA exceeds IGSA in terms of overall system performance. However, due to GSA easily falling into local extremum and prematurely converging, GSA reaches the convergence state with the maximum overall benefits 248 until 90 iterations. Using the chaotic map initializes population causing the convergence speed of IGSA to be lower than GSA at the beginning of the iteration, but it effectively prevents IGSA from trapping in the local optimum. Besides, owing to the PSA process being introduced to IGSA, the fine searchability of IGSA is enhanced in an efficient way. IGSA gets into convergence state when it iterates 75 times with benefit 260. As is shown in Figure 3, IGSA performs better in overall system performance than other algorithms.
Experiment 3.
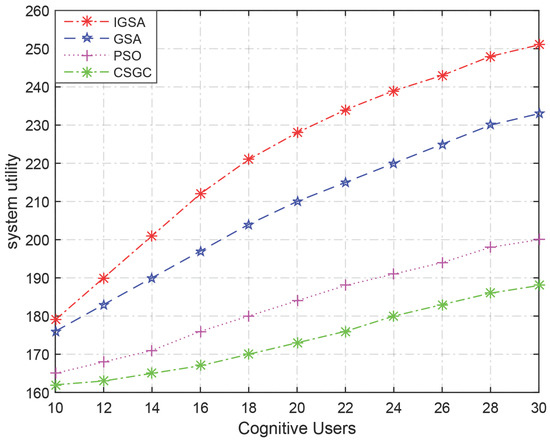
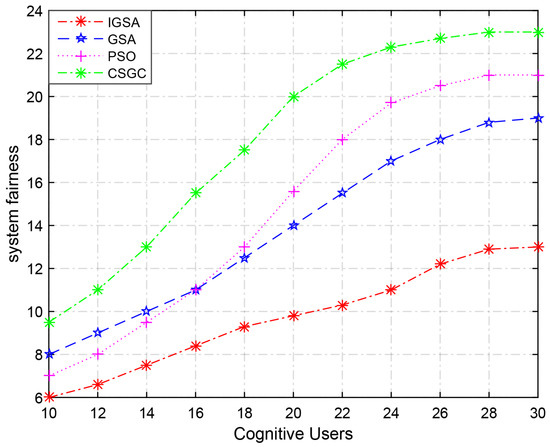
Figure 4 and Figure 5 show the performance of the four algorithms in terms of the system utility and the system fairness under the condition of fixed spectrum number and increasing SU number, respectively, where the available channel number is fixed on , the number of SUs distributes in .

Figure 4.
The system utility trend when .

Figure 5.
The system fairness trend when .
Figure 4 shows the trend of the system utility, which is growing with the increasing of SU. From the figure, we can see that the system utility grows with the increasing of SU numbers even though the the number of available channels is fixed. The growth speed of PSO and CSGC are inferior to GSA and IGSA. The curve of IGSA is always higher than others, which means that IGSA not only can escape the local extremum in a timely manner but it can also obtain the close-to-optimal solution quickly.
Figure 5 shows the trend of the system fairness, which is growing with the increasing of SU. As we can see, the fairness of SUs access to spectrum declines with the increasing of SU numbers while the available channel number is fixed. Because more SUs will cause more conflicts. Nevertheless, the descent rate of the IGSA is the slowest, and the CSGC has the worst performance in fairness.
Experiment 4.
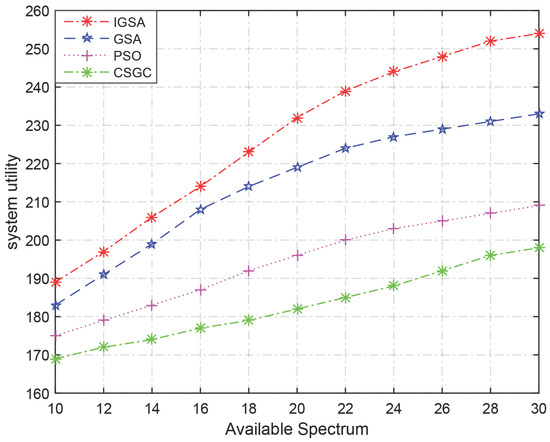
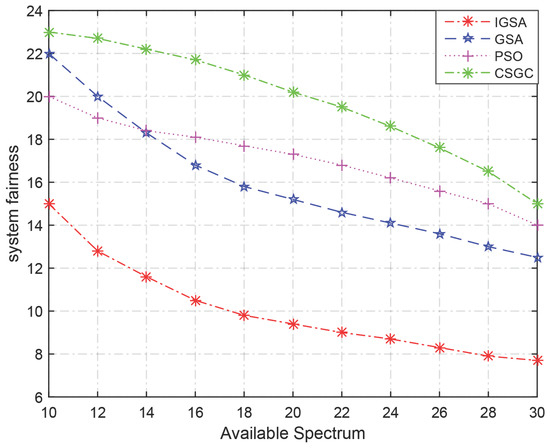
As shown in Figure 6 and Figure 7, they demonstrate the capability of the four algorithms in terms of the system utility and the system fairness under the condition of increasing spectrum number and fixed SU number, respectively, where the available channel number distributes in and the number of SUs is fixed at .

Figure 6.
The system utility trend when .

Figure 7.
The system fairness trend when .
Figure 6 shows the trend of the system utility with the increasing of the available channel while the number of SUs is fixed. From the figure, we can see that all algorithm curves augment with the increase of available spectrum. Because more available channels will allow more SU access to the system to create higher utility. In Figure 6, IGSA always performs better than other algorithms; PSO and CSGC are slightly lower.
Figure 7 shows the trend of the fairness among SUs with the increasing of the available channel under the condition of fixed SU. As we can see, the fairness curves decline with the increase of available spectrum, because more available channels offer more channel access opportunities for SUs, which reduces collision probability. IGSA always outperforms GSA, PSO or CSGC.
6. Conclusions
In CRNs, an effective spectrum allocation scheme is the key to solving the low utilization of spectrum resource. In this paper, an improved spectrum allocation approach based on gravitational search algorithm is proposed. In order to augment the randomness and spreadability of the population and reduce the risk of algorithm trapping into local optimum, the Chebyshev chaotic map is used in this paper. Besides, the PSA is introduced to refine the fine searchability of IGSA, which helps IGSA to locate the global optimal solution quickly. The simulation results show that the spectrum allocation method based on IGSA outperforms existing methods in terms of overall performance.
Acknowledgments
This work is supported by the Research Fund for Research of Method and Mechanism on Resisting Hole Attack for Wireless Sensor Network of China (Grant No. 61379110 ). This work is supported by the Fundamental Research Funds for the Central Universities of the Central South University(Grant No. 2017zzts733).
Author Contributions
L.L. and N.W. conceived and designed the experiments; N.W. performed the experiments; L.G. analyzed the data; Z.C. contributed reagents/materials/analysis tools; N.W. wrote the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Niyato, D.; Hossain, E. Cognitive radio for next-generation wireless networks: an approach to opportunistic channel selection in ieee 802.11-based wireless mesh. IEEE Wirel. Commun. 2009, 16, 46–54. [Google Scholar] [CrossRef]
- Alfa, A.S.; Maharaj, B.T.; Lall, S.; Pal, S. Mixed-integer programming based techniques for resource allocation in underlay cognitive radio networks: A survey. J. Commun. Netw. 2016, 18, 744–761. [Google Scholar]
- Tamilarasan, S.; Kumar, P. Dynamic resource allocation using priority queue scheduling in multi-hop cognitive radio networks. In Proceedings of the 2016 IEEE International Conference on Computational Intelligence and Computing Research (ICCIC), Chennai, India, 15–17 December 2016; pp. 1–5. [Google Scholar]
- Rungsawang, P.; Khawne, A. The implementation of spectrum sensing and spectrum allocation on cognitive radio. In Proceedings of the International Conference on Advanced Communication Technology, Bongpyeong, Korea, 19–22 February 2017; pp. 817–821. [Google Scholar]
- Li, J.; Liu, Y.; Li, Q.; Wang, L. Spectrum Allocation in Cognitive Radio—Quantum Immune Clonal Based Approach. In Proceedings of the 2014 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery, Shanghai, China, 13–15 October 2014; pp. 441–447. [Google Scholar]
- Tanab, M.E.; Hamouda, W. Resource Allocation for Underlay Cognitive Radio Networks: A Survey. IEEE Commun. Surv. Tutor. 2017, 19, 1249–1276. [Google Scholar] [CrossRef]
- Tragos, E.Z.; Zeadally, S.; Fragkiadakis, A.G.; Siris, V.A. Spectrum Assignment in Cognitive Radio Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2013, 15, 1108–1135. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, J.; Zhang, S. Spectrum Allocation Algorithm Based on Improved Ant Colony in Cognitive Radio Networks. In Proceedings of the 2016 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Chengdu, China, 15–18 December 2016; pp. 376–379. [Google Scholar]
- Lu, L.; He, D.; Li, G.Y.; Yu, X. Graph-Based Robust Resource Allocation for Cognitive Radio Networks. IEEE Trans. Signal Process. 2015, 63, 3825–3836. [Google Scholar] [CrossRef]
- Jalaeian, B.; Zhu, R.; Samani, H.; Motani, M. An Optimal Cross-Layer Framework for Cognitive Radio Network Under Interference Temperature Model. IEEE Syst. J. 2016, 10, 293–301. [Google Scholar] [CrossRef]
- Shattal, M.A.; Wisniewska, A.; Al-Fuqaha, A.; Khan, B.; Dombrowski, K. Evolutionary Game Theory Perspective on Dynamic Spectrum Access Etiquette. IEEE Access 2017. [Google Scholar] [CrossRef]
- Li, A.; Liao, X.; Zhang, D. A spectrum allocation algorithm for device-to-device underlaying networks based on auction theory. In Proceedings of the 2014 Sixth International Conference on Wireless Communications and Signal Processing (WCSP), Hefei, China, 23–25 October 2014; pp. 1–6. [Google Scholar]
- Salehinejad, H.; Talebi, S.; Pouladi, F. A metaheuristic approach to spectrum assignment for opportunistic spectrum access. In Proceedings of the 2010 17th International Conference on Telecommunications, Doha, Qatar, 4–7 April 2010; pp. 234–238. [Google Scholar]
- He, Q.; Zhang, P. Dynamic Channel Assignment Using Ant Colony Optimization for Cognitive Radio Networks. In Proceedings of the 2012 IEEE Vehicular Technology Conference (VTC Fall), Quebec City, QC, Canada, 3–6 September 2012; pp. 1–5. [Google Scholar]
- Huang, R.; Chang, J.; Ren, Y.; He, F.; Guan, C. Spectrum allocation of cognitive radio network based on optimized genetic algorithm in underlay network. In Proceedings of the 2016 8th IEEE International Conference on Communication Software and Networks (ICCSN), Beijing, China, 4–6 June 2016; pp. 418–422. [Google Scholar]
- Lechowicz, P.; Walkowiak, K. Genetic Algorithm for Routing and Spectrum Allocation in Elastic Optical Networks. In Proceedings of the 2016 Third European Network Intelligence Conference (ENIC), Wroclaw, Poland, 5–7 September 2016; pp. 273–280. [Google Scholar]
- Hasan, N.U.; Ejaz, W.; Ejaz, N.; Kim, H.S.; Anpalagan, A.; Jo, M. Network Selection and Channel Allocation for Spectrum Sharing in 5G Heterogeneous Networks. IEEE Access 2016, 4, 980–992. [Google Scholar] [CrossRef]
- Ser, J.D.; Matinmikko, M.; Gil-López, S.; Mustonen, M. Centralized and distributed spectrum channel assignment in cognitive wireless networks: A Harmony Search approach. Appl. Soft Comput. 2012, 12, 921–930. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-Pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Intell. Inf. Manag. 2009, 4, 390–395. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J. Parameters identification of hydraulic turbine governing system using improved gravitational search algorithm. Energy Convers. Manag. 2011, 52, 374–381. [Google Scholar] [CrossRef]
- Zhen, Y.; Hongyan, Z. Research on Uniformity Based on the Chebyshev Chaotic Map. In Proceedings of the 2015 IEEE International Conference on Computational Intelligence Communication Technology, Ghaziabad, India, 13–14 February 2015; pp. 177–179. [Google Scholar]
- Bentouati, B.; Chaib, L.; Chettih, S. A hybrid whale algorithm and pattern search technique for optimal power flow problem. In Proceedings of the 2016 8th International Conference on Modelling, Identification and Control (ICMIC), Algiers, Algeria, 15–17 November 2016; pp. 1048–1053. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. A discrete binary version of the particle swarm algorithm. IEEE Int. Conf. Syst. Man Cybern. Comput. Cybern. Simul. 2002, 5, 4104–4108. [Google Scholar]
- Peng, C.; Zheng, H.; Zhao, B.Y. Utilization and Fairness in Spectrum Assignment for Opportunistic Spectrum Access; Springer-Verlag: New York, NY, USA, 2006. [Google Scholar]
- Ghasemi, A.; Masnadi-Shirazi, M.A.; Biguesh, M.; Qassemi, F. Channel assignment based on bee algorithms in multi-hop cognitive radio networks. Commun. IET 2014, 8, 2356–2365. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).