A Novel Evolutionary Algorithm for Designing Robust Analog Filters

Abstract

Designing robust circuits that withstand environmental perturbation and device degradation is critical for many applications. Traditional robust circuit design is mainly done by tuning parameters to improve system robustness. However, the topological structure of a system may set a limit on the robustness achievable through parameter tuning. This paper proposes a new evolutionary algorithm for robust design that exploits the open-ended topological search capability of genetic programming (GP) coupled with bond graph modeling. We applied our GP-based robust design (GPRD) algorithm to evolve robust lowpass and highpass analog filters. Compared with a traditional robust design approach based on a state-of-the-art real-parameter genetic algorithm (GA), our GPRD algorithm with a fitness criterion rewarding robustness, with respect to parameter perturbations, can evolve more robust filters than what was achieved through parameter tuning alone. We also find that inappropriate GA tuning may mislead the search process and that multiple-simulation and perturbed fitness evaluation methods for evolving robustness have complementary behaviors with no absolute advantage of one over the other.

1. Introduction

Topologically open-ended computational design by genetic programming (GP) has been used for engineering design innovation, with many success stories in a variety of domains including analog circuits, digital circuits, molecular design, and mechatronic systems [1,2]. This approach uses genetic programming as an open-ended search method for functional design innovation—achieving a specified behavior without pre-specifying the design topology—and has achieved considerable success. However, in practical engineering design, there is another criterion in addition to functional specifications that should be considered during the design process. Robustness, as the ability of a system to maintain function even with changes in internal structure (including variations in parameters from nominal values) or external environment [3], is also critical to engineering design decisions. Engineering design, in reality, does not normally take into account every uncertainty or variation to which the engineered artifacts are subject to, such as manufacturing variation, degradation or non-uniformity of material properties, environmental changes, and changing operating conditions. We are interested in the following two kinds of system robustness: One is the system robustness with respect to perturbation in the parameters of the system, which has been well studied in the traditional robust design community [4] and also in evolutionary robust design [5]. The other kind is the system robustness with respect to topological perturbation—for example, accidental removal or failure of components. Reliable systems, having the least sensitivity of performance to variations or failures in the system components or environmental conditions, are highly desirable. However, there are relatively few studies that explore how a GP-based open-ended topology search may contribute to the design of robust systems such that they can withstand internal or external perturbations.

In this paper, we are interested in exploring GP algorithms for the design of robust systems such as analog filters. Specifically, we proposed a GP-based algorithm to facilitate the design of more robust systems with respect to parameter variations or uncertainty of the design variables. A set of systematic experiments are conducted to verify the following hypotheses about robust design using genetic programming: (1) that dynamic systems with high functional performance evolved by GP without considering a robustness criterion during the evolutionary process may have unacceptably low robustness with respect to parameter perturbation, (2) that the robustness of a system is strongly constrained by its topological/functional structure, and that the amount of robustness improvement available through parameter tuning is limited, and (3) that topologically open-ended synthesis by GP allows for the evolution of more robust solutions than traditional robust design approaches with parameter tuning.

Evolving robustness has a unique role in GP-based automated design. As most of such computational synthesis approaches depend on software simulators to evaluate the performance of candidate solutions, the quality of the final implementation of the evolved solutions strongly depends on how well the simulator approximates the physical behavior of the physical systems. A related issue arises when the objective function is replaced by a surrogate function (approximation) to speed up simulation [6]. One strategy to ensure effective transfer from evolved solutions to reality is to improve the robustness of the solutions by introducing noise or environmental variation during simulation or fitness evaluation, as proposed by Jakobi [7] in evolutionary robotics, for example. If the evolved solution is robust to such variations, the performance of the model evolved may sufficiently resemble (such that the model is useful) that of its physical implementation.

In natural evolution, the evolution of the functional structures of living organisms contributes significantly to their robustness with respect to the noisy environment. Functional characteristics such as modularity, redundancy, and negative feedback control are all typical features of living systems in response to survival requirements for robustness. Our hypothesis here is that control factors (design variables) as used in the robust design framework in [8] should not be limited to changing the dimensions (or sizing) and other parameters of the system, and that the system’s robustness should be considered when designing or evolving the functional or topological structure of the system. As any given function of a dynamic system can be implemented in various ways, we believe that the topological or functional design in the conceptual design phase may have a significant role in determining the ultimate robustness of the design solutions achievable through applications of traditional robust design procedures. There is already a body of research on how the structure of a system affects its functional robustness. Ferrer et al. [9] analyzed topological patterns in electric circuits and their relationship with the properties of the system behavior. Balling and Sobieszczanski-Sobieski [10,11], among others, discussed how the coupling structure of the system may affect robust parameter design. Robust design for truss topology has also been studied in [12]. However, a systematic methodology and investigation of robust design of dynamic systems based on a topologically open-ended search by genetic programming is still not available.

To examine the role of topology search in designing robust systems, design problems of two analog filters, i.e., a lowpass filter and a highpass filter, are synthesized using genetic programming. For each synthesis problem, three experiments are conducted: (a) evolutionary synthesis using GP without considering robustness criteria, (b) improvement in robustness of these evolved filters by tuning their parameters using a genetic algorithm (GA), and (c) evolution of robust filters (topological structure and parameters) using GP with a robustness criterion in the fitness function. These filter design problems are selected as they are perhaps the most popular problems in evolutionary synthesis research by either GA or GP [13,14,15].

The rest of the paper is organized as follows. Section 2 presents a short survey of applications of evolutionary algorithms in robust design. Section 3 introduces our GPRD (GP-based robust design) methodology, which exploits GP and bond graphs for automated synthesis of robust systems. Section 4 compares the experimental results of these approaches. Finally, conclusions and future research are highlighted in Section 5.

2. Related Work

Robust design [16] has been widely investigated in the engineering design community since the 1980s and remains an important topic [17]. In traditional robust design, one seeks to determine the parameter settings that produce desirable values of the mean (nominal) system performance, while at the same time minimizing the variance of the performance [16]. Many aspects of robust engineering design have been studied, such as the determination of the most robust operating points by system-wide parameter design [11], performance sensitivity distribution, and robust parameter design techniques [17]. Weng et al. [18] studied how simulation can be used to design photonic circuits that are robust to fabrication process variations. Sun et al. [19] proposed the use of norm metrics to quantify the robustness of both design parameters and performance uncertainty and then used a surrogating procedure to achieve robustness in a design space and to reduce uncertainty in performance space. Methods of representing and incorporating uncertainty in engineering design and optimization are reviewed in [4]. However, most of these approaches start from a design solution and only aim to determine its robust operating parameters with respect to different variations. The relationship between the topological or functional structure of a system and its robustness is often not treated. Especially, how robustness criteria should be incorporated into the conceptual functional design stage is not addressed. This is because the prevailing approach for engineering designs is a top-down procedure starting from the functional design to the detailed design and the robustness criterion is hard to evaluate without detailed design parameters, which are only available after the detailed design stage.

Evolutionary algorithms may provide a potential approach to address the limitations of traditional robust design. In the pioneering studies of evolutionary robotics, the Sussex group [7,20,21,22] developed a systematic methodology to evolve robust neural network controllers for robots. Husbands and Harvey [20] suggested an evolutionary approach to evolve neural network control systems for robots that are equipped with low-resolution sensors to work in uncertain environments. An incremental GA was used to evolve both the topology and connection weights of the controller. The discrepancy of simulation with reality was addressed by incorporating noise into the simulation process. They also argued that adaptive noise-tolerant networks are better building blocks than programs evolved by genetic programming for controller synthesis. Jakobi et al. [7] later showed that adding noise to simulations needs to be managed carefully. In their experiments, the correspondence between the robot behavior in simulation and that in the real world was demonstrated to be strongly correlated with the correspondence of the noise levels in the two cases. A more systematic approach to remove the gaps in transfer from simulation to reality is proposed in [23]. To ensure that the evolved robots do not exploit specifics of the simulation environments, Jakobi suggested making all implementation aspects unreliable by perturbing them randomly and in an irregular way [23]. That work suggested that it is better to resort to the evolutionary process to exploit intricate interactions and system dynamics if functional robustness is to be achieved.

Application of evolutionary algorithms to traditional parametric robust design has been attracting increasing attention in the past decade [24,25,26]. Tsutsui et al. [24] proposed a GA-based robust solution-searching scheme $(R{S}^3)$ to evolve robust solutions. This approach works by adding perturbation noise to the design variables before fitness evaluation. It thus does not rely on multiple re-sampling to evaluate the expected fitness, as was used by Wiesmann et al. [25]. In Wiesmann et al.’s approach, each individual is simulated t times to estimate its expected loss function (fitness) defined as $\frac{1}{t}·{\displaystyle \sum _{i=1}^t}(\tau -\tilde{f}(\overrightarrow{x},{\overrightarrow{\delta }}_i){)}^2$, where ${\overrightarrow{\delta }}_i,i=1,\dots ,t$ are normally distributed noise with zero mean and standard deviation $\sigma$; $\tau$ is the ideal target value. Their experiments showed that multilayer optical coating designs found by the evolutionary algorithm were substantially more robust to parameter variations than the reference design, but usually at the cost of reduced performance in undisturbed situations. This observation motivated the later work of using an evolutionary multi-objective approach to figure out the trade-off map between robustness and optimal functional performance [26,27,28]. Forouraghi [26] introduced an interval computation method to avoid artificial insertion of Gaussian noise to parameter variables in order to build tolerance against internal or external perturbations. In this approach, each design variable is represented as an interval. The robustness of a candidate solution is defined as the signal-to-noise ratio S/N, which considers both target performance and variations in face of perturbations. As a minimization criterion, they used

$$S/N={\eta }_s=-10log(\frac{{\displaystyle \sum _{i=1}^n}{y}_i^2}{n})$$

and for maximization criterion,

$$S/N={\eta }_l=-10log(\frac{{\displaystyle \sum _{i=1}^n}1/y_i^2}{n})$$

where n is the number of simulations, and $y_i$ is the performance of the i-th simulation. This robustness measure ensures that either improvement in the mean result or a reduction in variability will lead to greater S/N values. They then used a multi-objective GA to evolve a solution with multiple robustness criteria using a design-of-experiments (DOE) method with orthogonal arrays to evaluate the fitness. In a more explicit way of addressing the balance of performance and robustness, Ray [27] expressed the robust design problem as a three-criterion multi-objective problem, simultaneously optimizing an individual’s performance without perturbation, the mean performance of its neighbors resulting from perturbations, and the standard deviation of its neighbors’ performances. The perturbations in their experiments are simply modeled by deviations of $\pm 1\%$ beyond the variable values. They also observed a degradation in performance of the evolved robust solutions. In the most existing evolutionary robust design, multiple simulations are needed to evaluate the robustness of a single individual, which severely increases the computational burden. To address this problem, Jin et al. [28] used two methods for estimating the robustness measures of an individual—by exploiting its neighbor individuals in the current population as first proposed by Branke [29] and by using all evaluated individuals. They then evolved robust solutions with both performance and robustness as criteria in a two-criterion optimization as suggested by Das [30]. Jin’s robustness estimation approach can greatly reduce the number of function evaluations, when it is applicable. However, it is difficult to apply this method for evolving robust designs with variable structures as in topologically open-ended automated synthesis using GP. In these cases, it is difficult to define a neighborhood for a given individual, since most other individuals have different numbers and types of components.

A related research area to robust design focuses on evolving robustness in a noisy environment [31,32,33]. In these problems, the variation in the environment leads to uncertainty in the fitness function evaluation and the true fitness of a candidate solution needs to be evaluated based on sampling in multiple environments. In the evolutionary robotics area, Lee et al. [34] and Jakobi [23] evolved robust mobile robot controllers by training them in multiple trials of simulation, using genetic programming and a genetic algorithm, respectively. The active area of evolving robust systems is evolvable hardware [35,36,37]. Most of these approaches employ genetic algorithms or evolution strategies as the search procedures. Very recent work is the evolution of robust digital circuits [38,39]. In this work, Miller, Hartmann, and their collaborators examine the feasibility of evolving robust digital circuits using a type of “messy gate”. Hartmann et al. [40] investigated how evolution may exploit non-perfect digital gates to achieve fault tolerance, including tolerance to output noise and gate failure. However, the noise introduced to improve robustness is not applied to parametric values of the components, but to the analog outputs of the messy gates, and an evolution strategy (ES) is used as the open-ended topology search tool. This method is thus not as instructive as might be desired in exploring effects of alternative topologies.

In addition to robust design and optimization in noisy environments, evolutionary algorithms have also been successfully applied to other optimization problems with uncertainty such as time-varying optimization problems. For a complete overview on the general topic of evolutionary optimization under uncertainty including the major techniques and issues, readers are referred to an excellent survey of Jin and Branke [28].

In this paper, we chose analog filter design as our test problems. The pioneering work of Koza in automated analog circuit synthesis, including lowpass, highpass, and asymmetric bandpass filters, is described in [13,41]. However, they did not specifically work on evolving robust circuits. Lohn and Colombano [15] proposed a linear representation approach to evolve analog circuits in which several lowpass filters were used as test problems. In another work, by Goh and Li [42], a genetic algorithm with a linear direct encoding approach is used to evolve lowpass and bandpass analog filters. What is special in their work is that they constrained the component values to be chosen among the manufacturer’s preferred component values. Finally, we have applied GPBG approach to a few benchmark and real-world problems including the lowpass filter design problem [43] and pump design problem [2].

Much work has been done in both evolutionary robust design and analog circuit synthesis. However, few studies specifically address how GP-based topologically open-ended synthesis may provide a new method of open-ended robust design. This may enable us to move robust design forward to the conceptual/functional design stage, i.e., at the very beginning, which will augment the current practice of designing for robustness in the parametric design stage.

3. Methods: A Robust Analog Filter Design Using Evolutionary Algorithms

3.1. Analog Filter Design using Bond Graphs and GP

In this work, we used bond graph modeling [44] as the representation scheme for analaog filter design. A bond graph is a graphical representation of a physical dynamic system, which allows the conversion of the system into a state-space representation. This capability of seamlessly incorporating multiple domains makes our results widely applicable in the evolution/design of physical systems. Here, we briefly introduce the bond graph and show how GP can be used to evolve analog filters based on bond graph representation with details explained in our previous work [2,45,46].

3.1.1. Bond Graphs

The bond graph is a multi-domain modeling tool for the analysis and design of dynamic systems, especially hybrid multi-domain systems including mechanical, electrical, pneumatic, and hydraulic components [44]. One advantage of using bond graphs for open-ended design exploration is that the complex loops typical in electric circuit schematics can be transformed into tree-like structures by the bond graph’s 1-junction (serial connection) and 0-junction (parallel connection) concepts, which tend to be easier to evolve in general. Another advantage is that the multi-domain nature of bond graph modeling facilitates the evolution of mechatronic systems. Many researchers have explored the bond graph as a tool for system design [47]. Details of notation and methods of system analysis related to the bond graph representation can be found in [44]. Figure 1 illustrates a small bond graph that represents the accompanying electrical system. Figure 2 shows the complex bond graph model of a lowpass filter. A typical simple bond graph model is composed of inductors (I), resistors (R), capacitors (C), transformers (TF), gyrators (GY), 0-Junctions (J0), 1-junctions (J1), sources of effort (SE), and sources of flow (SF). In this paper, we are only concerned with linear dynamic systems, or more specifically, analog filters as a case study, represented as bond graphs, which are composed of I/R/C/SE(as input signals)/SF(as output signal access points). Due to the limitation of our bond graph simulation, we did not include transistors into our model so the system will have difficulty evolving active analog filters. They can be evolved using SPICE simulation and modeling software, which is beyond the scope of this paper.

3.1.2. Evolving Analog Filters Using Bond Graphs and GP: The GPBG Framework

The problem of automated synthesis of bond graphs involves two basic searches: the search for a good topology and the search for good parameters for each topology, in order to be able to evaluate its performance. Building upon Koza’s work on automated synthesis of electronic circuits [41], we created a developmental GP system for open-ended synthesis of mechatronic systems represented as bond graphs [2]. It includes the following major components: (1) an embryo bond graph with modifiable sites at which further topological operations can be applied to grow the embryo into a functional system, (2) a GP function set, composed of a set of topology manipulation and other primitive instructions which will be assembled into a GP tree by the evolutionary process (the execution of this GP program leads to topological and parametric manipulation of the developing embryo bond graph), and (3) a fitness function to evaluate the performance of candidate solutions.

Choosing a good function set for bond graph synthesis is not easy. In our earliest work [43], a basic GP function set was used for evolutionary synthesis of analog filters. In that approach, the GP functions for topological operation included {Insert_J0/J1, Add_C/I/R, and Replace_C/I/R}, which allowed evolution of a large variety of bond graph topologies. The shortcoming of this approach is that it tended to evolve redundant and sometimes causally ill-posed bond graphs [48]. Later, we used a causally well-posed modular GP function set to evolve more concise bond graphs with much less redundancy [45]. However, that encoding had a strong bias toward a chain-type topology and thus may have limited the scope of topology search [46]. In this paper, we used the following hybrid function set approach to reduce redundancy while enjoying the flexibility of topological exploration.

F = {Insert_J0E, Insert_J1E, Add_C/I/R, EndNode, EndBond, ERC}.

Details of this GP function set for bond-graph-based analog filter synthesis are available in [46,49]. Figure 3 shows a GP tree that develops an embryo bond graph into a complete bond graph solution. Our comparison experiments [46] showed that this function set is more effective on both an eigenvalue and an analog filter test problem, so the new set was used in this paper.

In this study, two types of analog filters including lowpass and highpass filters were synthesized. In such GPBG-based filter design problems [43], a bond-graph-represented analog filter composed of capacitors, resistors, and inductors is evolved such that the magnitude of its frequency response approximates a specified filter frequency response specification. An embryo bond graph and its equivalent circuit are illustrated in Figure 1 and are used in all experiments. Note that the 0-junction is the initial modifiable site, where further topological developments can proceed as instructed by a GP program tree. The voltage at this 0-junction is the output signal.

Instead of using the sophisticated SPICE simulation program as used in the existing analog filter synthesis [13,50], the frequency response of a bond graph can be simulated in a more convenient way: first, a state equation of a bond graph is derived automatically from the model, which generates the A, B, C, and D matrices [44]. These state space models can then be simulated on Linux PCs using C++ simulation code generated from Matlab Compiler 3.0.

The detailed specifications of the three analog filter synthesis problems are as follows:

• The lowpass filter synthesis problem is extracted from [13], in which the frequency response performance of a candidate filter is defined as the weighted sum of deviations from an ideal frequency response magnitude over 101 points:

  $$F_{koza}(t)={\displaystyle \sum _{i=0}^{100}}[W(d(f_i),f_i)\times d(f_i)]$$

  (1)

  where $f_i$ is the sampling frequency, $d(x)$ is the absolute deviation of candidate frequency response from target response at frequency x, and W(x,y) is the weight function specifying the penalty level for a given frequency response at a specified frequency range. The sampling points range from 1 Hz to 100 KHz, evenly distributed on a logarithmic scale. If the deviation from the ideal magnitude is less than 0.03 V, the weight W is 1. If the deviation is more than 0.03 V, the weight W is 10. The pass band is [1, 1K] Hz, and the stop band is [2K, 10K] Hz. A “don’t care” band between 1 and 2 KHz neglects any deviation from the target response there.
• The highpass filter synthesis problem has a similar configuration to the lowpass filter except for the complementary definitions of the pass and stop bands. The pass band is now defined as [2K, 10K] Hz, while the stop band is [1, 1K] Hz.

To evolve an analog filter without considering robustness, the fitness function is defined as follows. First, we calculate the raw fitness defined as the average absolute deviation between the frequency response magnitude of the candidate solution and the target frequency response over all 101 sampling frequencies:

$$f_{raw}=\frac{1}{101}·F_{koza}(t)=\frac{1}{101}·{\displaystyle \sum _{i=0}^{100}}[W(d(f_i),f_i)\times d(f_i)].$$

(2)

Note that this $f_{raw}$ definition differs from Koza’s raw fitness definition in Equation (1) by a multiplier equal to the number of sampling frequencies. We use the average deviation rather than sum of deviations to remove the influence of the number of sampling points.

The raw fitness of a candidate solution is then normalized as follows:

$$f_{norm}=\frac{NORM}{NORM+f_{raw}}.$$

(3)

where NORM is a normalization term aiming to adjust the $f_{norm}$ into the range of [0, 1]. This transformation also serves to convert the minimization of deviation from the target frequency response into the maximizing of fitness process used by our GP system. Since tournament selection is used as the selection operator, the normalization term can be arbitrary positive numbers. Here, the tournament selection operator is used due to its capability of achieving a good balance between exploiting and exploration and is widely used in GP [51]. For the lowpass and highpass filter problems here, NORM is set to 10, which gives a fitness range of [0, 1].

In this paper, a standard strongly-typed multi-population generational GP enhanced with the above features is used to evolve analog filters represented as bond graphs. The running parameters are specified in Section 4.

3.2. Evolving Robust Analog Filters With Respect to Parameter Variation: The Unified Approach

In this paper, we examine how to evolve robust analog filters with respect to parameter variations. There are many ways to achieve this by combining GP for an open-ended topological search and GA or differential evolution (DE) for fine-tuning the evolved solutions from GP. In this section, first the common characteristics of the various methods for evolving robustness are presented, followed by details of each individual approach.

The typical approach for evolving robust designs [32] is to use multiple Monte Carlo samplings with different environmental or system configurations (e.g., perturbation of parameter values of the system) to calculate a worst-case or an average fitness for a given candidate solution, as shown in Equation (3). This robust-by-multiple-simulation (RMS) method is used in [25]. Another method is to simply add a perturbation to the design variable before evaluation. This perturbation, however, is not incorporated into the genome, making it different from a “normal” parameter mutation operator or Larmarckian-style evolution algorithms. This robust-by-perturbed-evaluation (RPE) method is used in [24] and is suggested to be more efficient by Jin et al. [28]. Both methods are tested in this work. For the RPE method, no special fitness function is needed. One only needs to perturb the parameters before normal fitness evaluation. For the RMS multi-simulation method, the raw fitness for a design solution with robustness criterion is defined as the sum of a number SPI of 101-point deviations from the target frequency response curve:

$$f_{robustraw}={\displaystyle \sum _{k=1}^{SPI}}{f}_{raw}^k$$

(4)

where SPI is the number of Monte Carlo sampling evaluations for each individual, and $f_{raw}^k$ is the raw fitness of the k-th sampled evaluation with a different Monte Carlo perturbation of the parameters as defined in Equation (2). With this raw robustness fitness, we then calculate the final fitness according to Equation (3).

In the experiments reported below, the perturbation of the component values during evolution is implemented by adding to each component parameter Gaussian noise $N(\mu ,\sigma )$ with a mean $\mu$ of 0 and the standard deviation $\sigma$ set to 20% of the parameter value. This perturbation model has been widely used by previous researchers [24,25]; while it may not be appropriate for all manufacturing processes, it is sufficient for our purposes as an approximation to the real component value degradation model in some situations. When more sophisticated models are used in the future to capture all parameter variations due to process, temperature, and voltage changes and simulate them in our system design evolution, the evolved systems can be more robust to these variations in reality. We also need to consider the parasitic effects existing in the evolved circuits. One difficulty with this definition is that if the original parameter value is zero, then no perturbation will be generated. Although this is rare in evolutionary experiments, we have incorporated a special step to check whether the component value is zero. If that is the case, we set the standard deviation for the perturbation to 1.

3.3. Genetic Algorithms for Robust Analog Filter Design: The Traditional Robust Design

In this section, we follow the practice of traditional robust design methodology to improve system robustness by tuning its parameters. We first use the improved GPBG approach as described in Section 3.1.2 to evolve a high-performance analog filter, without incorporating any robustness criterion in the fitness function. We shall then apply to the evolved filter a state-of-the-art real parameter genetic algorithm—the G3PCX-GA proposed by Deb [52]—to tune its parameters so as to improve its robustness with respect to parameter perturbation, while its functional structure remains unchanged. Since parameter search for dynamic systems is a complex highly multi-modal search problem, we choose G3PCX-GA to approximate the highest robustness achievable through parameter tuning within a given budget of functional evaluations. When the multi-simulation method (RMS) to evolve robustness is used, we call this hybrid GP/GA method the GPGARMS method. When the robust-by-perturbed-evaluation (RPE) method is used to evolve robustness, we call the hybrid GP/GA method the GPGARPE method, which, however, is not evaluated in this study.

In the minimization by G3PCX-GA, we used the robust raw fitness defined in Equation (4) as the final fitness of an individual. We believe this fitness measure is better than the average of normalized final fitness of each sampling evaluation for its lower distortion of the optimization objective values.

3.4. GPRD: Robust Analog Filter Design Using GP

In natural evolution, many structural patterns, such as modularity, emerge naturally as responses to a robustness requirement for survival. In a similar way, open-ended evolutionary synthesis by GP also provides such a capability for the evolution of robust systems. Unlike traditional engineering design, in this framework, topology search and parameter tuning are conducted simultaneously, so there is no distinct boundary between the conceptual design stage and the detailed design stage.

Two GP-based approaches for synthesizing robust designs are tested in this paper. The first is the GP with robustness-by-multi-simulation (GPRMS), which uses multiple simulation to estimate the robustness fitness of a candidate solution. The second is GP with robustness-by-perturbed-evaluation (GPRPE), which temporarily adds perturbation noise to the design variables before evaluating its fitness.

To be consistent with the experiments in Section 3.1.2, we use the generational GP, which is also employed by the experiments of Section 3.1.2. The final fitness of an individual, calculated from the sampling fitnesses, is the same as that defined in Equation (2), where $f_i^k$ is defined as $Fitnes{s}_{norm}$ in Equation (3).

3.5. Evaluation Criteria

For all evolved filters, we used the following criteria to evaluate their robustness and functional performance. For each candidate filter, we run SPI = 10,000 simulations, each with different perturbations of its component parameters. This SPI number is chosen so that the statistical values from a set of simulations remain stable. The perturbation is modeled as Gaussian noise $N(\mu ,\sigma )$ with the mean $\mu$ set to 0 and the standard deviation $\sigma$ set to 10–50% of parameter values, in steps of 10%.

There are two ways to calculate the robustness of a candidate design. One approach is the definition of robustness fitness as used by Forouraghi [26] and defined in Equation (4). This Type-I robustness $f_{robustI}$ definition uses the average (or sum) of the total 101-point deviation from the target frequency response curve for SPI simulations as the final robustness. The benefit of this robustness definition is that it incorporates requirements on both performance and its variation: increasing mean performance and reducing performance variation both lead to increased robustness. This measure is especially good for evolving robustness during which the absolute performance is also important in addition to the stability of functions. The disadvantage of this definition is that it cannot distinguish the robustness if a specified level of performance is satisfied by all solutions being compared. For such a case, it is more desirable to use the standard deviation of the 101-point deviations from the target frequency response curve for all 10,000 simulations as the robustness criterion. We call this robustness definition Type-II robustness. Note that this is not the other form of robustness (to component failure) but rather another definition of robustness to parameter variation. The ideal case is to use a multi-objective method to separate performance and its variation completely, as suggested by Das [30] and Jin et al. [28]. We defined this Type-II robustness criterion as in Equation (5). In this paper, both criteria will be evaluated.

$$f_{robustII}=\sqrt{\frac{{\displaystyle \sum _{k=1}^{SPI}}{(f_{raw}^k-{\overline{f}}_{raw})}^2}{SPI}}$$

(5)

where ${\overline{f}}_{raw}$ is the average 101-point-deviation from the target frequency response curve; $f_{raw}$ is the 101-point-deviation of a single simulation from target frequency response curve; SPI is the number of simulations used to evaluate the fitness of an individual.

4. Experiments and Results

In this section, the following four different methods for evolving robust or non-robust lowpass and highpass filters are presented:

• standard genetic programming (GP) without considering robustness requirements;
• genetic programming with robustness-by-multi-simulation (GPRMS);
• genetic programming with robustness-by-perturbed-evaluation (GPRPE);
• hybrid GP/GA robust design method (GPGARMS).

For all these methods, a fixed number of function evaluations is allocated to ensure fairness of comparison. Here, one function evaluation means one simulation of a design for measuring its performance, which is different from one fitness evaluation for an individual. In the multi-simulation robust design method GPRMS, multiple simulations (SPI = 10) are used to evaluate the fitness of a single design. For the lowpass and highpass filter design problem, the computation budget is 1,000,000 function evaluations. Note that, for methods that use multiple simulations to estimate the robustness fitness, each simulation is counted as one function evaluation. In addition, for the hybrid GPGARMS method, we allocate 500,000 function evaluations for GP evolution and the remaining 500,000 for GA evolution for robustness.

We used only one parameter perturbation model in the evolutionary synthesis experiments—Gaussian noise $N(\mu ,\sigma )$ with a mean $\mu$ of 0 and the standard deviation $\sigma$ set to 20% of the parameter value. However, the evaluation of the evolved filters are subject to multiple perturbation magnitudes with extensive simulation.

To assess the statistical significance of the performance discrepancy between these methods, for each target filter type and each synthesis method, 15 runs were conducted. The size of these experiments was determined by the computing resources available. However, since we found that the results are quite stable across multiple runs, the level of replication appears to be sufficient for the purposes of this paper.

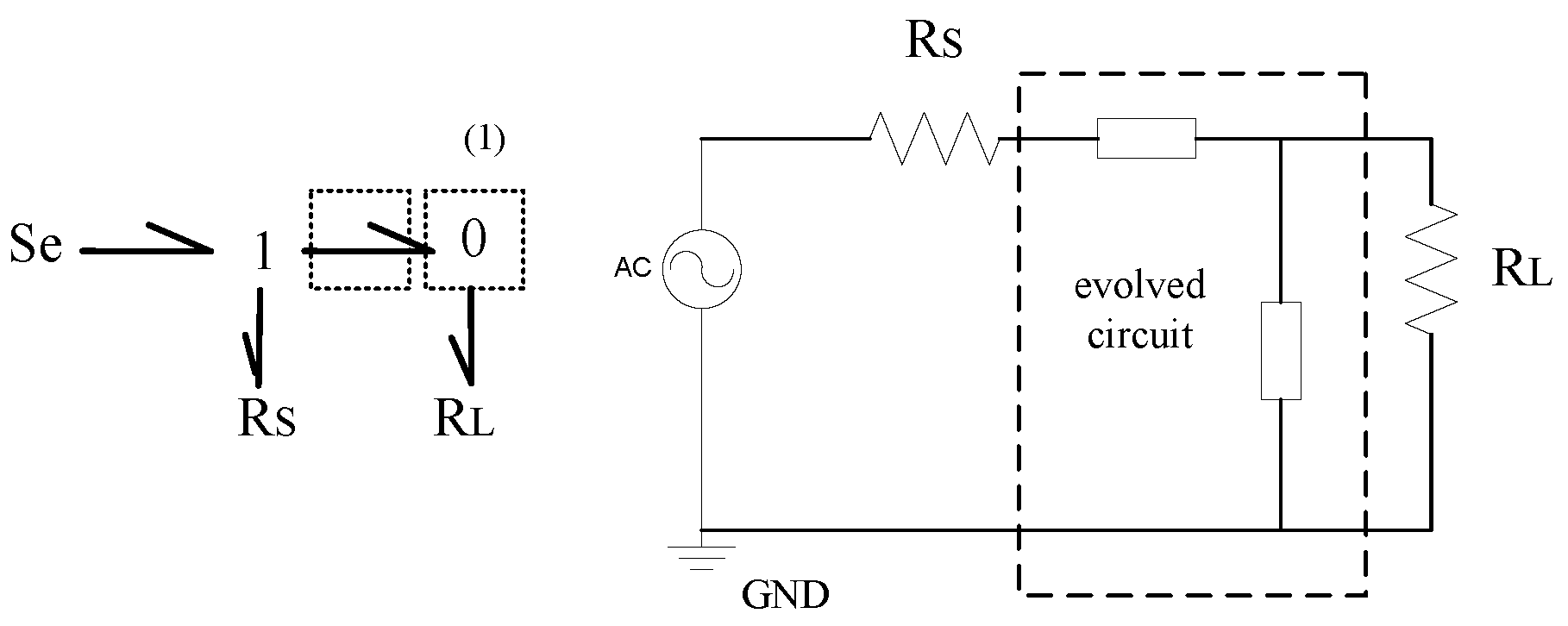
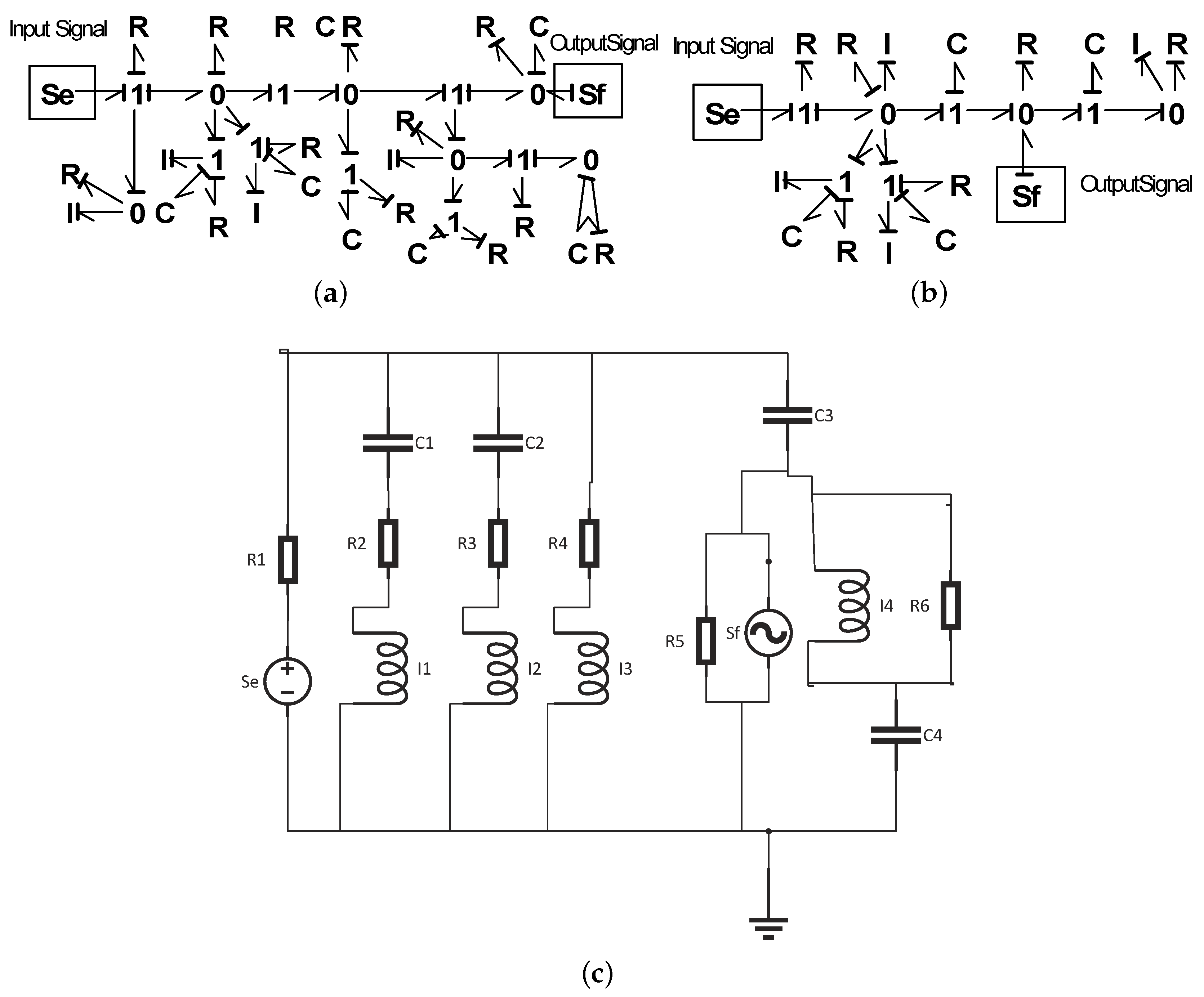
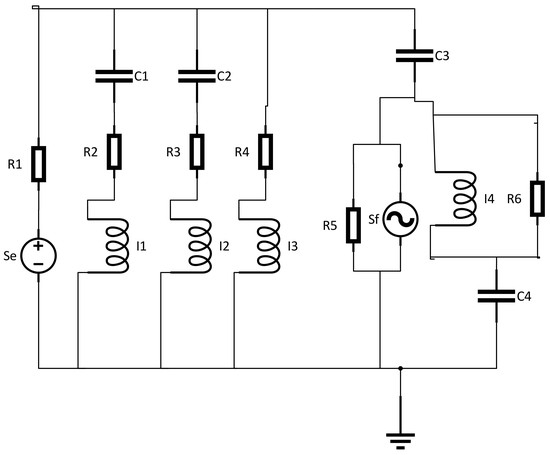
All experiments described below used the same embryo bond graph shown in Figure 1. The component values of source resistor $R_s$ and load resistor $R_{load}$ are both 1 $\Omega$ for lowpass and highpass filter synthesis.

In the following sections, we first describe separately the experimental configuration of each method, the best evolved bond graph models of each filter type, and the frequency response of the best solutions from each method. These results provide some general ideas regarding how robustness is evolved with respect to the parameter perturbations. Then, in Section 4.4, a statistical comparison of the performances of five algorithms for evolving robust filters are presented. These analyses will be used to support the hypothesis outlined in the introduction section.

4.1. Evolving Analog Filters Using GP without Considering Robustness in the Fitness Function

In this experiment, 15 analog lowpass and highpass filters are evolved using standard GP without incorporating a robustness criterion in the fitness function Equation (3). The following common running parameters (

Table 1. Experimental parameters for analog filter synthesis without robustness criterion.

Total Population Size: 2000 (400/400/400/400/400)	Number of Subpopulations: 5
Migration interval: 5 generations	Migration size: 30 individuals
Max tree depth: 8	Crossover probability: 0.7
InitTreeDepth: 3–5	Standard mutation probability: 0.1
Flag bit mutation rate: 0.1	Swapping-tree mutation rate: 0.1
Tournament size: 7	Parametric mutation probability: 0.5
Max evaluations: 1,000,000	Flag mutation probability: 0.3
Pool size of elite individuals: 20	Elite pool update frequency: 5 generations

) are used throughout all GP experiments in this paper:

Note that the maximum tree size here is 8 rather than 17, used in many other works. This parameter was selected by considering the reduced tree sizes due to our simplified parameter representation method and available computational resources. The maximum tree depth of 8 allows for the synthesis of analog filters with up to 100 components, which is sufficient for our purpose.

We select the evolved filter with the highest performance to test its noise tolerance over the degradation or variation in the component parameters with different perturbation magnitudes. As described above, the evaluation of robustness with respect to parameter perturbation is conducted by running 10,000 simulations of the configurations of the Gaussian parameter perturbations.

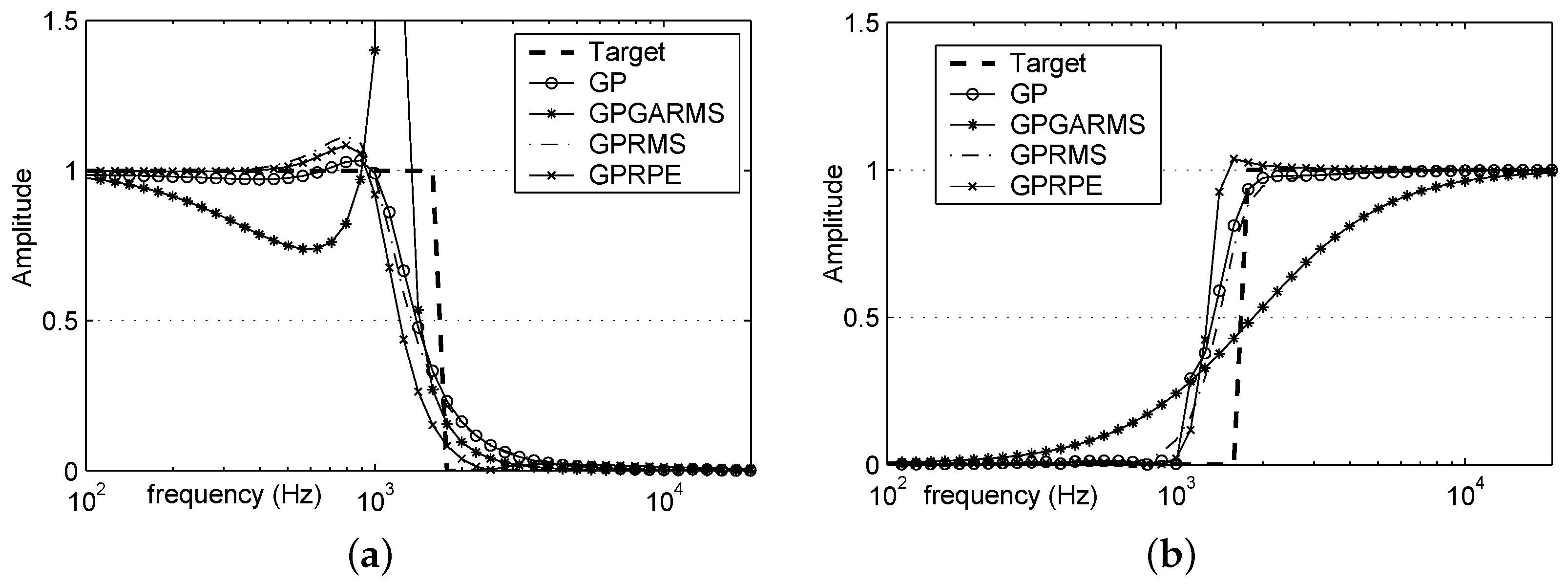
Figure 2 and Figure 4 show the topology of the evolved lowpass and highpass filters with the highest performance out of 15 runs. The frequency responses of these filters are summarized in Figure 5 along with the results of evolved robust filters. The evolved best lowpass and highpass filters have 39 and 27 components, respectively. The lowpass and highpass filters approximate the ideal frequency response closely, with the sum of deviations over 101 points being only 6.43 and 0.32, respectively.

Figure 5a,b show the frequency responses of the four best lowpass and four highpass filters evolved using GP, GPGARMS, GPRMS, and GPRPE. The performances of the evolved filters in an ideal condition without parametric perturbation were compared. Here, the “best” means the highest fitness of each approach out of 15 runs. Only standard GP has no consideration of robustness. The other three methods considered robustness in their fitness function definition.

From Figure 5, first, one can see that the frequency responses of the filters evolved by GP, GPRMS, and GPRPE are very similar. That means introducing robustness requirements does not necessarily decrease performance with nominal parameters significantly. The only exception is GPGARMS, which distinguishes itself from the others with much worse nominal performance (larger deviations). After checking the standard deviation of the sum of deviations of 10,000 runs with 20%-level parametric perturbation, it appears that the nominal performance is sacrified by the GA for better robustness. One can also observe that the filters with highest performance for both filter types are evolved using GPRPE. This can be explained by the actual number of genetic topological and parametric operations. Here, standard GP only ran 500,000 fitness/function evaluations during which genetic operations were conducted (we did not run 1,000,000 function evaluations for GP because standard GP always converges to local optima long before running out of 500,000 evaluations). GPRMS actually only ran 100,000 fitness evaluations (with 1,000,000 function evaluations) during which genetic operations were conducted, because 10 simulations were used for each individual during fitness evaluation, while genetic information was kept unchanged. The GPRPE, however, ran 1,000,000 fitness (function) evaluations during which genetic operations were conducted.

4.2. Evolving Robust Analog Filters Using Genetic Algorithms: The Classical Robust Design

In this experiment, the G3PCX-GA [52] is used to improve the robustness of the best filters evolved using standard GP through parameter tuning while keeping functional structure unchanged. As we can see from Figure 2 and Figure 4, these two evolved filters are very complex, with 39 and 27 parameters to search. As the objective function of this optimization is highly multi-modal, this is hard optimization even for G3PCX-GA, as the experiment demonstrates. The running parameters for this experiment are summarized in

Table 2. Experimental parameters for robust design by G3PCX-GA.

Total Population Size: 200	Max Evaluations: 500,000
Number of parents in crossover: 3	Family size: 2
${\sigma }_{\zeta }$: 0.1	${\sigma }_{\eta }$: 0.1
SPI: 10	Perturbation noise percentage: 20%

.

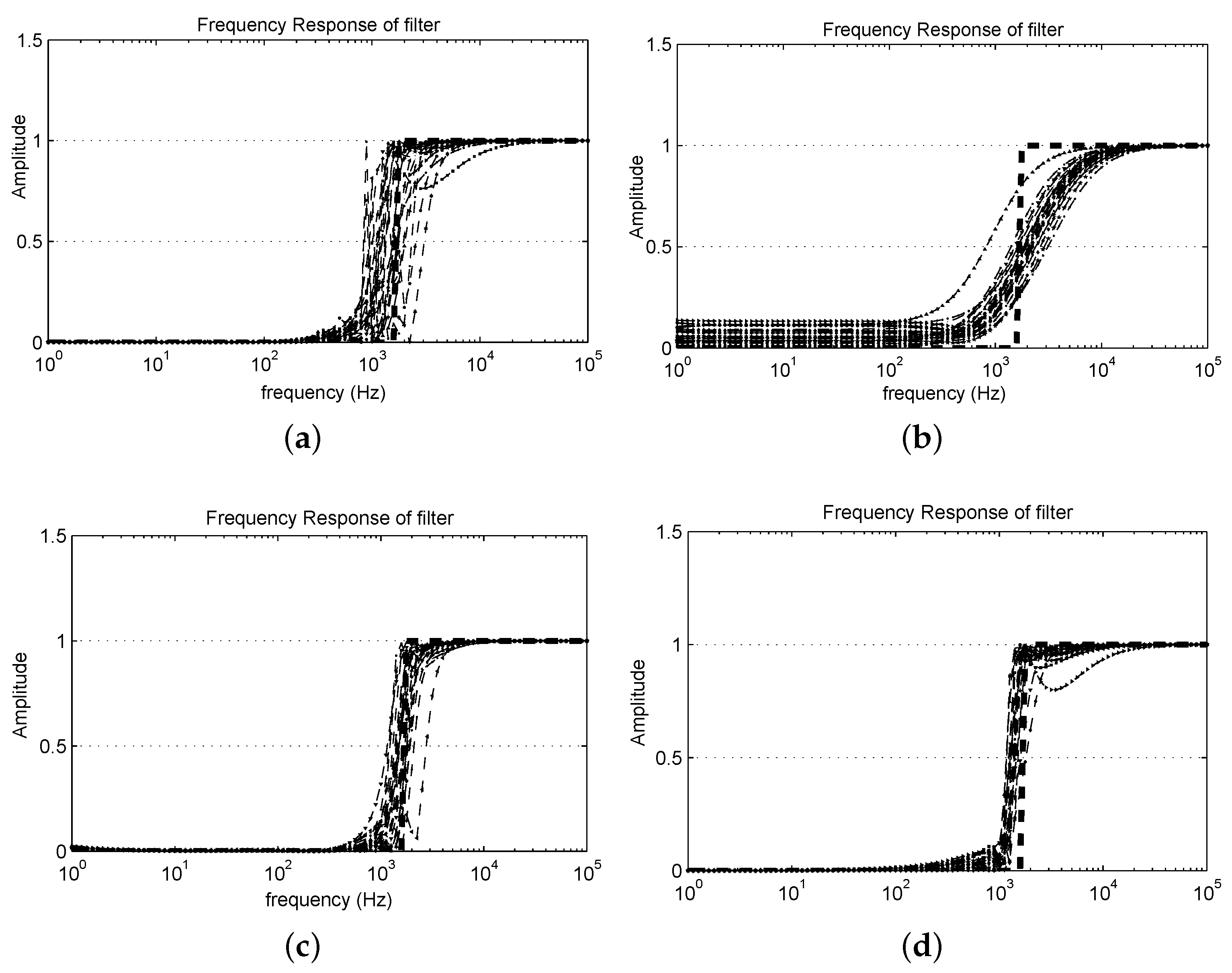
Figure 6a,b show the frequency response distributions of the filters and their perturbed variations evolved by standard GP and fine-tuned by G3PCX-GA. These perturbed filters are obtained by adding to the component values of the original solution a Gaussian parameter perturbation with a magnitude subject to Gaussian distribution $N(0,0.2)$ times the original component values. The GA-based fine tuning of the filter improves its performance, which is indicated by its robustness fitness, as defined in Equation (5): the filter originally evolved by GP has a $f_{robustII}$ of 7.21, while the filter then improved by GA has a $f_{robustII}$ of only 1.15. More systematic comparison of their performance and robustness is described in Section 4.4.

An interesting observation about G3PCX-GA’s result is that the increase in Type II robustness is accompanied by a decrease in Type I robustness, which is impacted by both performance and function stability. This phenomenon can be easily seen in Figure 7. One explanation of this severe degradation of function is that GP, where robustness is not considered, has evolved a high-fitness filter that is, however, highly sensitive to parameter perturbations. In this case, parameter tuning by G3PCX-GA can easily disrupt the highly coupled parameter relationship of these components’ values and thus decrease the functional performance and improve robustness. Another possible factor is that this parameter optimization problem with 65 variables is too difficult for G3PCX-GA to optimize well within the allocated computational effort. We also found that the best fitness of the population stagnates after about 200,000 evaluations, which may be because the best fitness has approximated or reached the limit of the best possible fitness with the given topological structure. The population may also stagnate due to premature convergence.

4.3. Evolving Robust Analog Filters Using Genetic Programming: Open-Ended Topology Innovation for Robust Design

In the following experiment, we try to evolve robust analog filters that have a higher tolerance of the variation in component values and have graceful performance degradation. Two GP algorithms for evolving robust solutions are used: GPRMS and GPRPE. The configurations for this experiment are the same as those used in Section 4.1.

Figure 8 shows the best lowpass and highpass filters evolved using GPRMS with robustness requirements. Compared with the filters evolved using standard GP in Figure 2 and Figure 4, these two filters use fewer components, while the functional performance remains similar. The robustness of these two filters is compared to that of filters evolved using GP and GPGARMS in Figure 6 for the highpass filter problem. As can be seen, both GP methods with robustness requirements (GPRMS and GPRPE) evolved filters with higher robustness, as shown by their much less dispersed frequency response distributions. Statistical evidence is presented in Section 4.4. Compared to GPGARMS, one distinguishing characteristic of GPRMS and GPRPE is that they evolved more robust filters without significant degradation of functional performance. 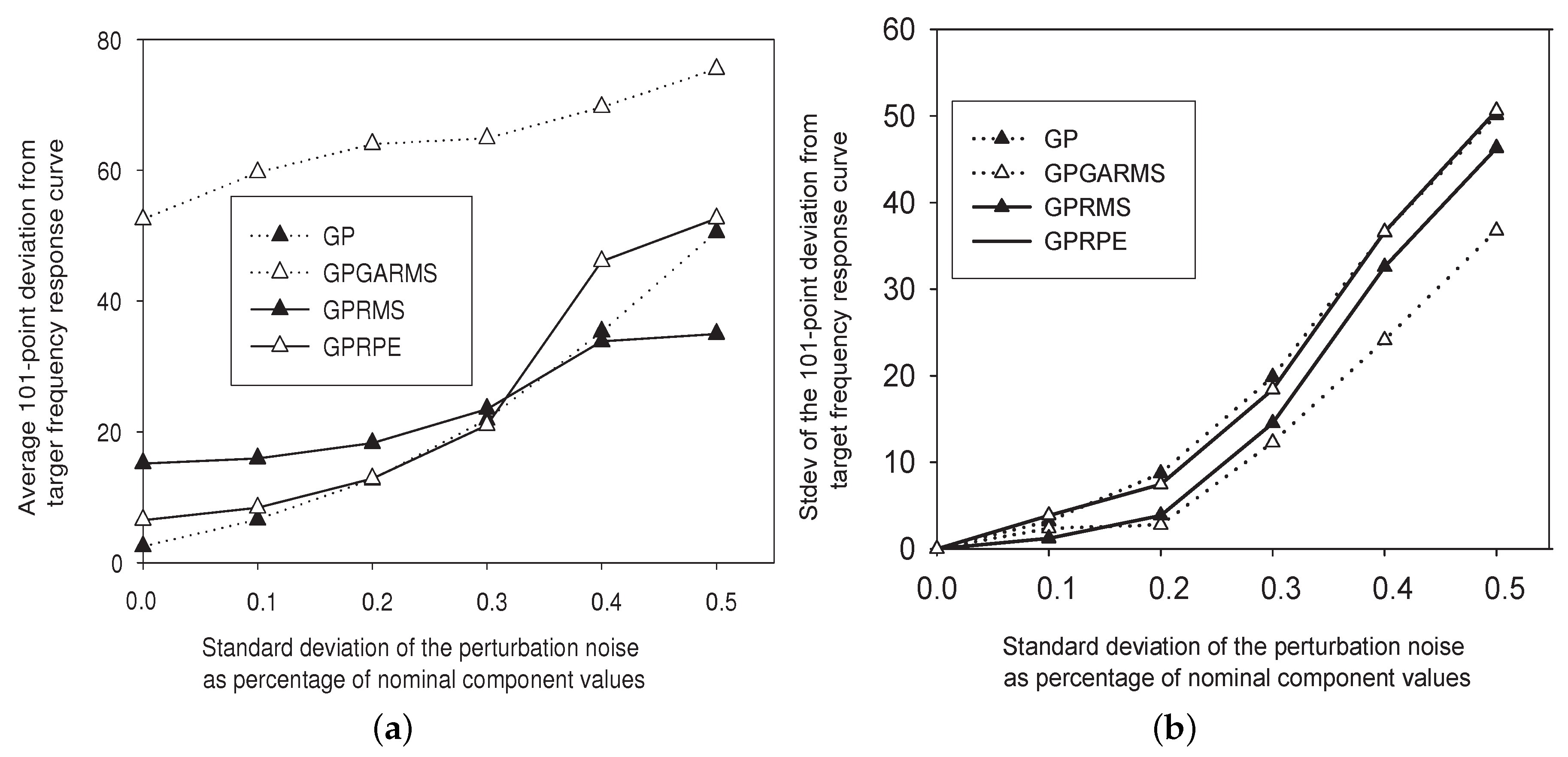This observation can also be made in Figure 7, which shows that GPGARMS has the lowest performance variation (standard deviation) across all perturbation levels but also has the highest average-101-point deviation from the target frequency response curve.

From Figure 7a, however, we find that filters evolved by both GPRMS and GPRPE, in a trade-off for higher robustness, have an average 101-point deviation higher than that evolved by standard GP for all perturbation levels less than 0.3. However, when the perturbation level is greater than 0.3, GPRMS achieves an average-101-point deviation that is lower than that achieved by GP, and GPRPE’s performance remains worse. This means that GP with the multiple-simulation method, compared with the perturbed fitness evaluation method, evolved designs with a higher tolerance to parametric perturbation. From Figure 7b, we find that GPGARMS shows a clear advantage in terms of $f_{robustII}$, which is, however, achieved by sacrificing functional performance. In other words, the performance is more stable with regard to its average frequency response. Nevertheless, the total deviation from the target response becomes larger.

To further compare the characteristics of the evaluated algorithms, we did an extensive analysis of the performances of all filters evolved by the five algorithms, and this analysis is summarized in

Table 3. The performance and robustness of evolved lowpass filters using GP, GPGARMS, GPRMS, and GPRPE.

Perturbation Magnitude		0.1		0.2		0.3		0.4		0.5
		Mean	Stderr	Mean	Stderr	Mean	Stderr	Mean	Stderr	Mean	Stderr
$f_{robustI}$	GP	36.57	5.55	40.04	5.00	45.33	4.56	54.68	4.25	61.91	4.06
	GPGARMS	65.16	6.60	50.08	6.05	64.33	3.66	73.85	3.84	79.81	5.28
	GPRMS	48.83	3.99	51.36	3.67	56.09	3.46	63.91	3.52	72.71	3.72
	GPRPE	14.08	2.65	19.64	2.22	27.25	1.82	37.51	1.81	48.98	2.21
$f_{robustII}$	GP	2.44	0.40	5.59	0.79	14.37	1.61	30.20	2.83	42.78	3.76
	GPGARMS	5.42	1.85	10.81	1.72	18.18	2.12	33.57	1.85	54.05	4.45
	GPRMS	1.35	0.34	4.58	0.54	13.58	1.05	28.46	1.95	40.88	2.64
	GPRPE	3.92	0.46	8.13	0.78	20.85	3.75	30.89	2.36	43.11	2.92

. For each algorithm, 15 runs were performed to evolve 15 lowpass filters. Each filter was then subjected to 10,000 simulations with random perturbations of their component parameters. We calculated the average 101-point deviation ($f_{robustI}$) and its standard deviation ($f_{robustII}$) from the target frequency response, for each filter. The upper half of the table shows the average of $f_{robustI}$ and its standard error over 15 runs for each algorithm under different perturbation environment. The lower half shows the average of $f_{robustII}$ and its standard error over 15 runs for each algorithm under different perturbation environments. The perturbation magnitudes are represented by the magnitudes of the Gaussian perturbation as a percentage of component parameter values.

In the top half of the table, we can see that the GPRPE method evolved filters with the highest average performance or $f_{robustI}$. These filters are not only best at a perturbation level of 0.2, which is applied during the evolution process, but also best across all other perturbation levels tested in the “evaluation” phase. This implies that ideal analog filters have continuous performance landscapes with satisfactory degradation properties. What is surprising here is that not only are the $f_{robustI}$ values of the filters evolved by GPRPE the best but also their standard error values are lowest at all perturbation levels. This means that the GPRPE has the maximum number of fitness evaluations; thus, the genetic operations algorithm evolves high-performance filters with the most reliability.

Interestingly, there is a complementary relationship between the performances of GPRPE and GPRMS. Examining the lower half of Table 3, the GPRMS turns out to be the best algorithm to evolve robust filters with the highest robustness in terms of evaluation criterion $f_{robustII}$, with minimum variation in the frequency response, and this advantage holds true for all perturbation levels. Comparing GPRPE and GPRMS, it appears that GPRMS with its multi-simulation method can evolve more stable solutions due to its superior estimation of the true robustness property of a candidate solution. GPRPE, instead, suffers from its robustness estimation error but enjoys a higher amount of genetic operations. These results show that there is no simple conclusion about which method (of GPRPE and GPRMS) is better than the other. The choice depends on the design objectives.

Another interesting observation is the performance of GPGARMS. For highpass filters, we showed that GPGARMS evolved filters with the highest type II robustness $f_{robustII}$. However, it is not the case for the lowpass filter problem. The GPGARMS shows the worst results in terms of both Type I and Type II robustness measures. How could GA produce worse results than standard GP? We have two possible explanations. First, the fitness function for GPGARMS only uses 10 simulations to estimate the robustness. This may result in large estimation error, thus misleading the evolution. Since the robustness scores in Table 3 are calculated by 10,000 perturbed simulations, results produced by a misled GPGARMS could be even worse than its starting solutions. Another projection is that the parameters of lowpass filters are located in a much more rugged landscape, so a misled GPGARMS tends to drift away quickly from the highly coupled parameters of the starting solution evolved by GP. These explanations are under investigation and will be reported elsewhere.

From these analyses, we find that, compared to evolutionary design where robustness is not considered, allowing topological variation during the evolution of robust systems can yield more robustness and a superior structure with respect to perturbations of the component parameters of the filters, through topological innovation. To further consolidate our observations, in the following section, we report a series of statistical tests run to verify the significance of the differences seen between these algorithms.

4.4. Statistical Results of the Three Methods for Evolving Robust Filters

4.4.1. GA-RMS Improves the Robustness of Standard GP Results

For the highpass filter problem, we did a t-test to compare the robustness of the evolved solutions by GPGARMS and standard GP in terms of variation (Equation (5)) at the 0.2 perturbation level. A significance level of $p\le 0.001$ is achieved, strongly indicating that GPGARMS improved the robustness of the filters evolved by standard GP. However, as shown in Figure 7, this improvement is at the cost of degraded performance. It is impressive that, in this highpass problem, GPGARMS achieves the highest robustness in terms of standard deviation for all 5 perturbation levels. However, as shown in Table 3, the GA could also potentially generate statistically significantly worse solutions or ruin the results evolved by standard GP. For the lowpass filter problem, we found that there is no significant difference in Type-I robustness between GPGARMS and GP. GA also decreased the Type-II robustness in this problem.

4.4.2. Topological Innovation Using GP-Evolved Filters with Higher Robustness than Parametric Robust Design Using GA

For the highpass problem, we applied the t-test to compare GPGARMS and GPRMS. The 95-percent confidence interval for differences in the means of Type-I robustness $f_{robustI}$ ranges from $-51.617$ to $-39.841$, showing that GPGARMS degraded Type-I robustness. The difference in the mean values of the two groups is greater than would be expected by chance ($p\le 0.001$). For GPGARMS and GPRPE, the difference is even more significant. The 95-percent confidence interval for difference of means ranges from $-57.482$ to $-44.846$ with $p\le 0.001$. In terms of $f_{robustII}$, the 95-percent confidence interval for difference of means between GPRMS and GPGARMS ranges from $-9.920$ to $-2.538$, while there is no significant difference between GPRPE and GPGARMS.

For the lowpass problem, the 95-percent confidence interval for the difference in the means of Type-I robustness $f_{robustI}$ between GPRPE and GPGARMS ranges from $-51.617$ to $-39.841$ with $p\le 0.001$. There is no significant difference between GPRMS and GPGARMS in terms of $f_{robustI}$. In terms of $f_{robustII}$, the 95 percent confidence interval for the difference in the means between GPRMS and GPGARMS ranges from $-9.920$ to $-2.538$, while there is no significant difference between GPRPE and GPGARMS.

4.4.3. GP with Robustness Requirements Constrains Bloating

One critical issue in GP-based evolutionary synthesis is the bloating problem, or the growing sizes of the solutions produced during the evolution process. To evaluate how a robustness requirement influences this phenomenon, we compared the number of components of the filters evolved by methods discussed in the beginning of this section. To date, we have only made 10 runs for each algorithm. The results are shown in

Table 4. The sizes of filters evolved using four algorithms with different numbers of fitness evaluations. Each algorithm was run 10 times. * A total of 1,000,000 function evaluations are required to do 100,000 actual fitness evaluations.

Algorithm (Fitness Evaluations)	1	2	3	4	5	6	7	8	9	10	Mean	Stdev
GP (100,000)	34	26	35	24	14	20	24	25	26	46	27	8.9100
GP (500,000)	46	47	37	47	57	40	40	45	48	79	51.7500	15.3200
GPRMS (100,000) *	28	15	36	21	28	14	43	26	31	20	26.2000	9.1100
GPRPE (1,000,000)	67	36	46	36	37	57	29	63	27	36	43.4000	14

. The standard GP runs with 100,000 and 500,000 function evaluations with no robustness requirements are compared with those of two GP methods with robustness requirements. Note that, for the GPRMS method, as each fitness evaluation of an individual costs 10 function evaluations, the actual number of genetic operations is only one-tenth of the number of such operations performed in the 1,000,000 function evaluations of GPRPE.

First, we found that the average sizes of the design solutions evolved by GP (in 100,000 function evaluations) and GPRSM (in 1,000,000) are similar. As both methods used the same number of genetic operations, it seems that the sizes of the evolved filters are determined more by the actual number of genetic operations rather than the number of fitness evaluations. Since the number of evolved solutions by GP and GPRSM are too small to satisfy the normality condition, a Mann–Whitney rank sum test was used to show that any difference in these two groups of sizes is not statistically significant, at the level of p = 0.880. Second, we compared the solution sizes of GP (100,000) with GP (500,000) using the same Mann–Whitney rank sum test. A statistically significant difference exists at the level of $p<0.001$. This demonstrates that the solution sizes indeed grow with an increasing number of fitness evaluations. A third Mann–Whitney rank sum test was applied to show the size difference between the solutions evolved using GP (500,000) and GPRPE (1,000,000). There was no statistically significant evidence that shows that these two size groups are different (p = 0.127). This means that the robustness requirement in the GPRPE method may have constrained the bloating process such that even doubling the number of fitness evaluations does not lead to larger filter sizes. For highpass filter problems, we reached similar conclusions. Of course, a larger number of replicates may later show these differences to be statistically significant.

4.4.4. Comparison with Other Approaches for Robust Filter Design

There are several previous works focusing on evolving (robust) passive analog filters. Ando and Iba [50] suggested a simple linear genome method to evolve lowpass and bandpass filters with a small number (<50) of components. Particularly related to this work, they used 5%, 10%, and 20% disturbances to the component values to evaluate the robustness of the evolved circuits. Although they did not evolve robust circuits in their work, they suggested that a consideration of manufacturing errors (tolerances) of component values is needed and that in evolvable hardware, the component errors intrinsic in physical components can be absorbed during the evolutionary process. Dib and El-Asir [53] proposed using a symbiotic organisms search (SOS) algorithm to determine the values of the passive components (resistors and capacitors) used in active filters. They compared SOS performance with those obtained using other optimization methods, such as particle swarm optimization, seeker optimization algorithms, and differential evolution, and found that SOS works best. However, they used a fixed topology of the active filters and did not consider the robustness of the evolved filters. In another, similar work [54], analytical characterization of a 2nd order Gm-C Sallen-Key LP filter was considered, as was the corresponding symbolic expressions for their sensitivity to component value variations. When the sensitivity is used as a goal minimization function in the optimization process, parasitic capacitances are canceled and robust designs are obtained. Recently, Lovay [55] proposed using multi-objective optimization, by minimizing the sensitivity to variations in the parameters and the design errors, to determine the values of the passive components (resistors and capacitors) of robust active filters. In summary, these related works all focused on parameter search instead of open-ended topological exploration to evolve robust analog filters.

5. Conclusions

We proposed a GPRD, a novel algorithm for designing robust dynamic systems based on genetic programming and bond graph modeling, and applied it to the synthesis of analog filters. Comparative studies of evolving robustness by GAs (parameter tuning) and by GP (simultaneous topology and parameter search) showed that traditional parameter-tuning-based robust design puts severe limits on the possible robustness achievable through parameter-tuning. We also found that our GPRD robust design algorithm enabled us to find analog filters with much higher robustness (Type-I, Type-II, or both) with respect to the variations in its parameters compared to the parameter-tuning-type evolutionary algorithms (G3PCX-GA) for robust design of fixed functional structures.

There are several issues related to GP-based robust design. One is the computational complexity, since GP is notorious for its high computational demand. Unfortunately, the multiple samplings used to evaluate the robustness of candidate solutions add additional computational load to the evolutionary robust design process. Improved Monte Carlo sampling strategies are needed. The second issue is the need to develop algorithms that evolve robust systems with respect to topology perturbation or component failures. Another related question is how the perturbation pattern affects structures. For example, how does the evolution system respond differentially to component removal as an absolute number or as a percentage of components. Trade-offs between improving robustness by parameter search and by topological innovation will be studied and methods to control it will also be developed. We also observed that, while the proposed methodology is effective for the case study on analog filter design, it may require more refinement; for example, topology constraints may need to be added to the evolved topology to achieve a practical, realistic design.