Modeling the Trend of Credit Card Usage Behavior for Different Age Groups Based on Singular Spectrum Analysis
Abstract
:1. Introduction
2. Literature Review
2.1. On Analysis Based on SCPC Data
2.2. On Developments and Applications of Singular Spectrum Analysis
2.3. On Trend Studies of Credit Card Usage
3. Singular Spectrum Analysis
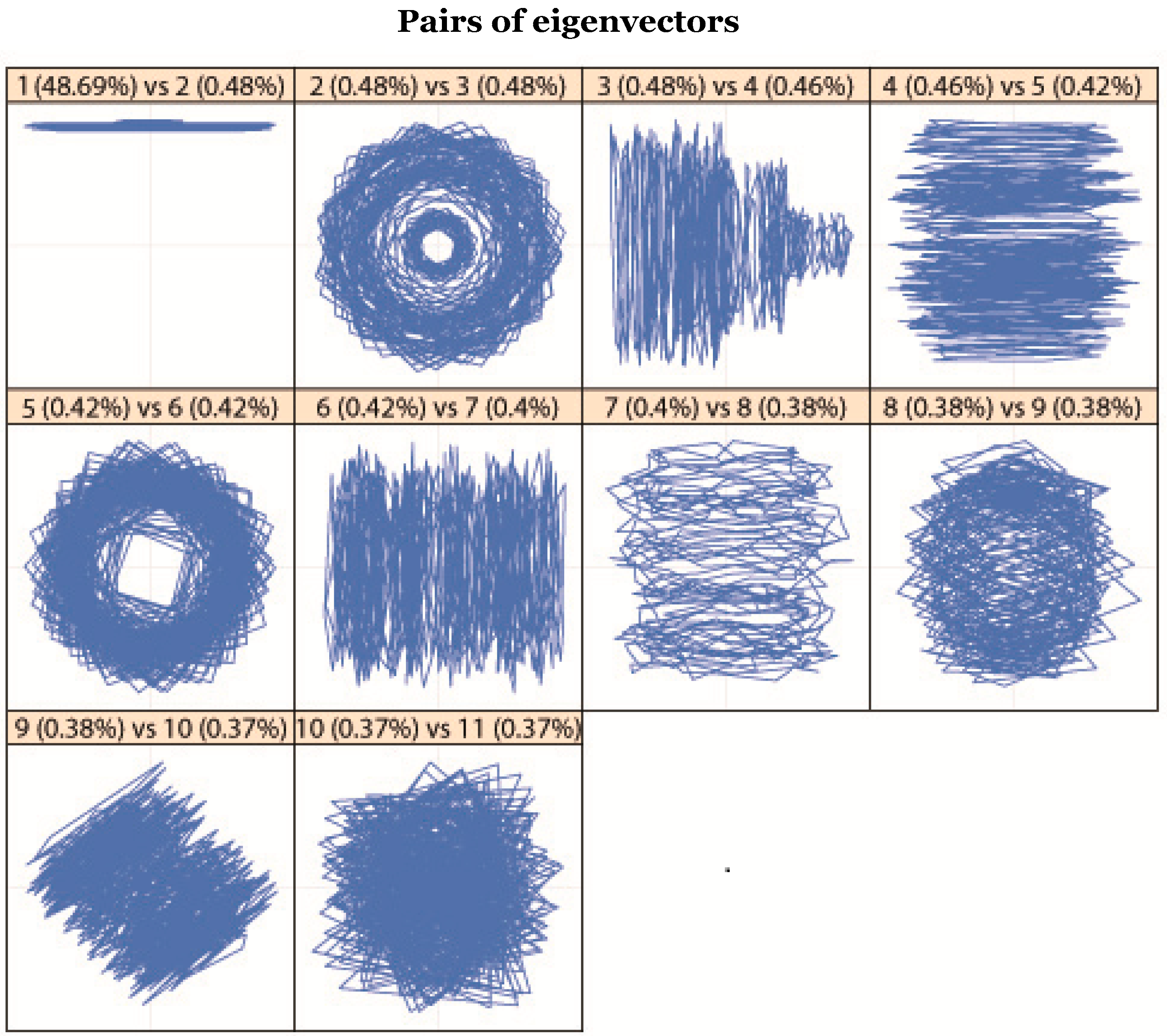
3.1. Decomposition
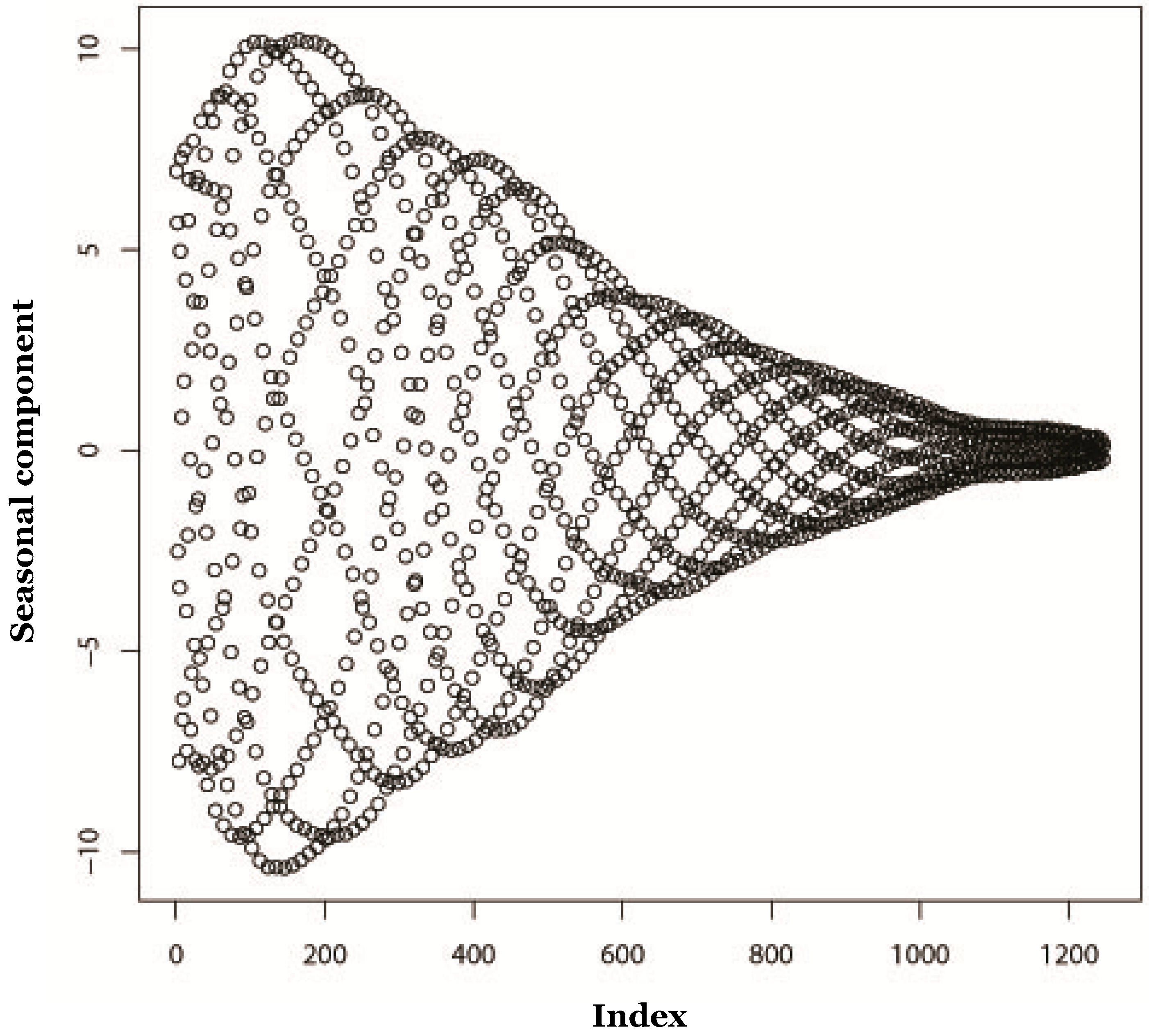
3.2. Reconstruction
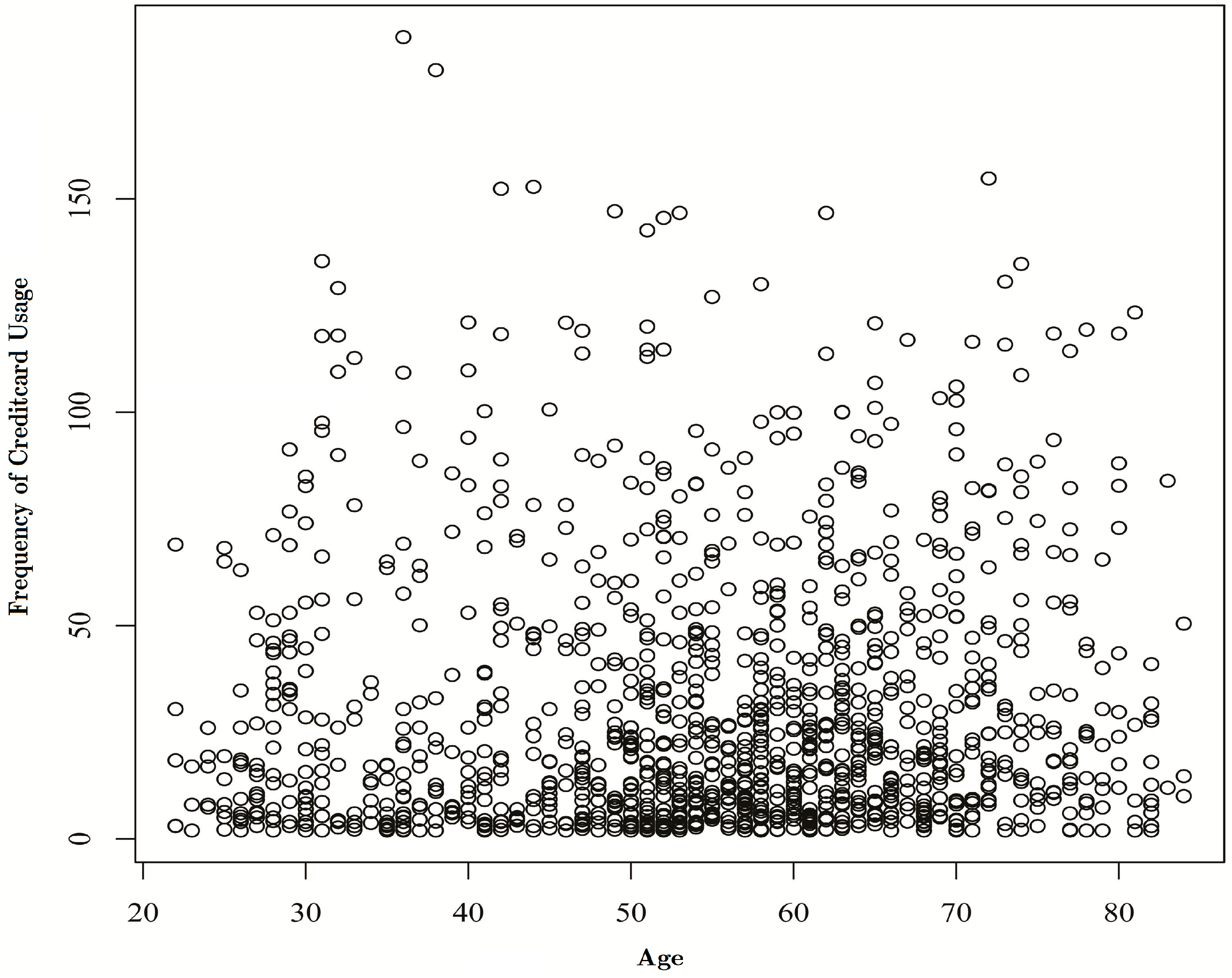
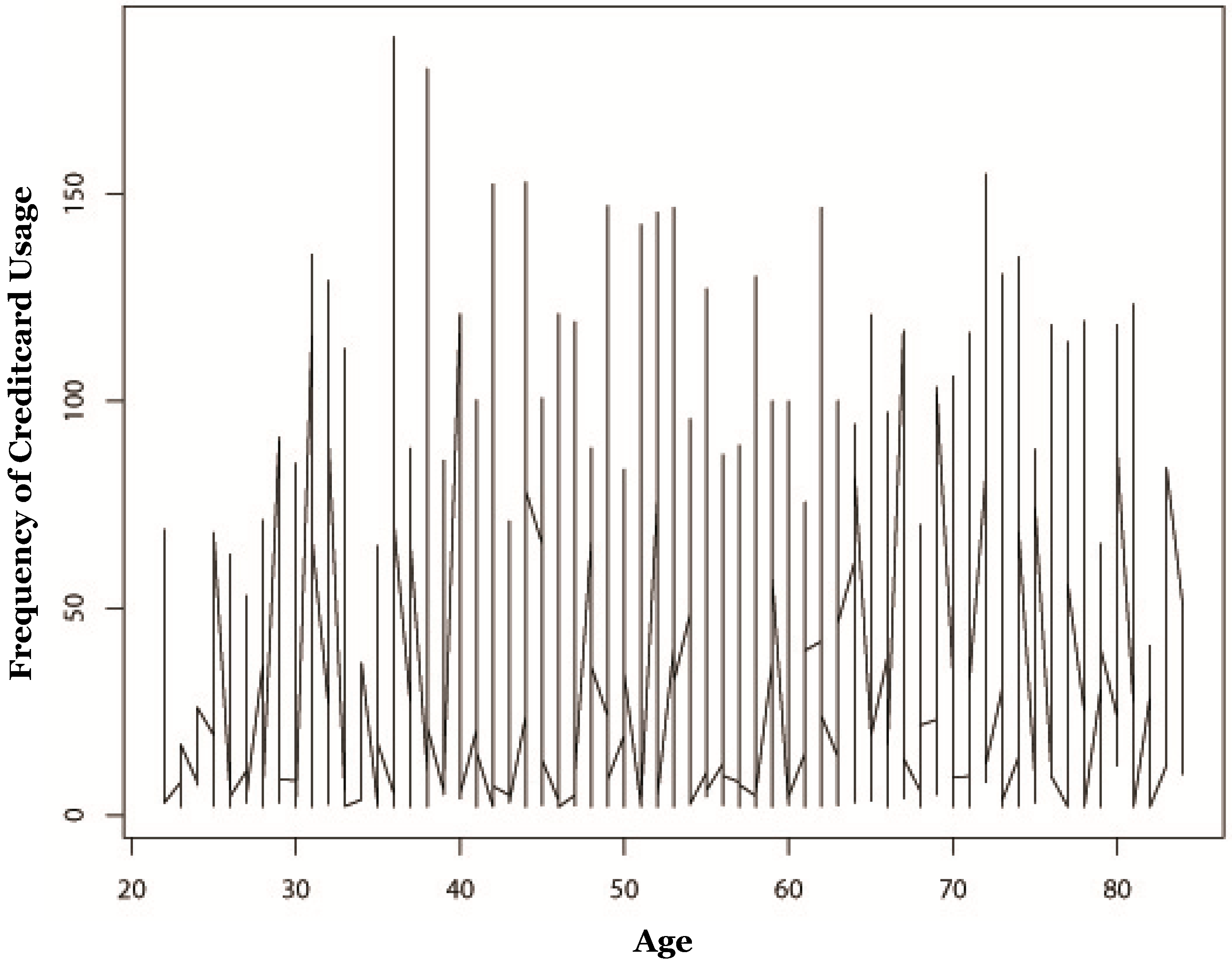
4. Data Description
4.1. The Survey of Consumer Payment Choice
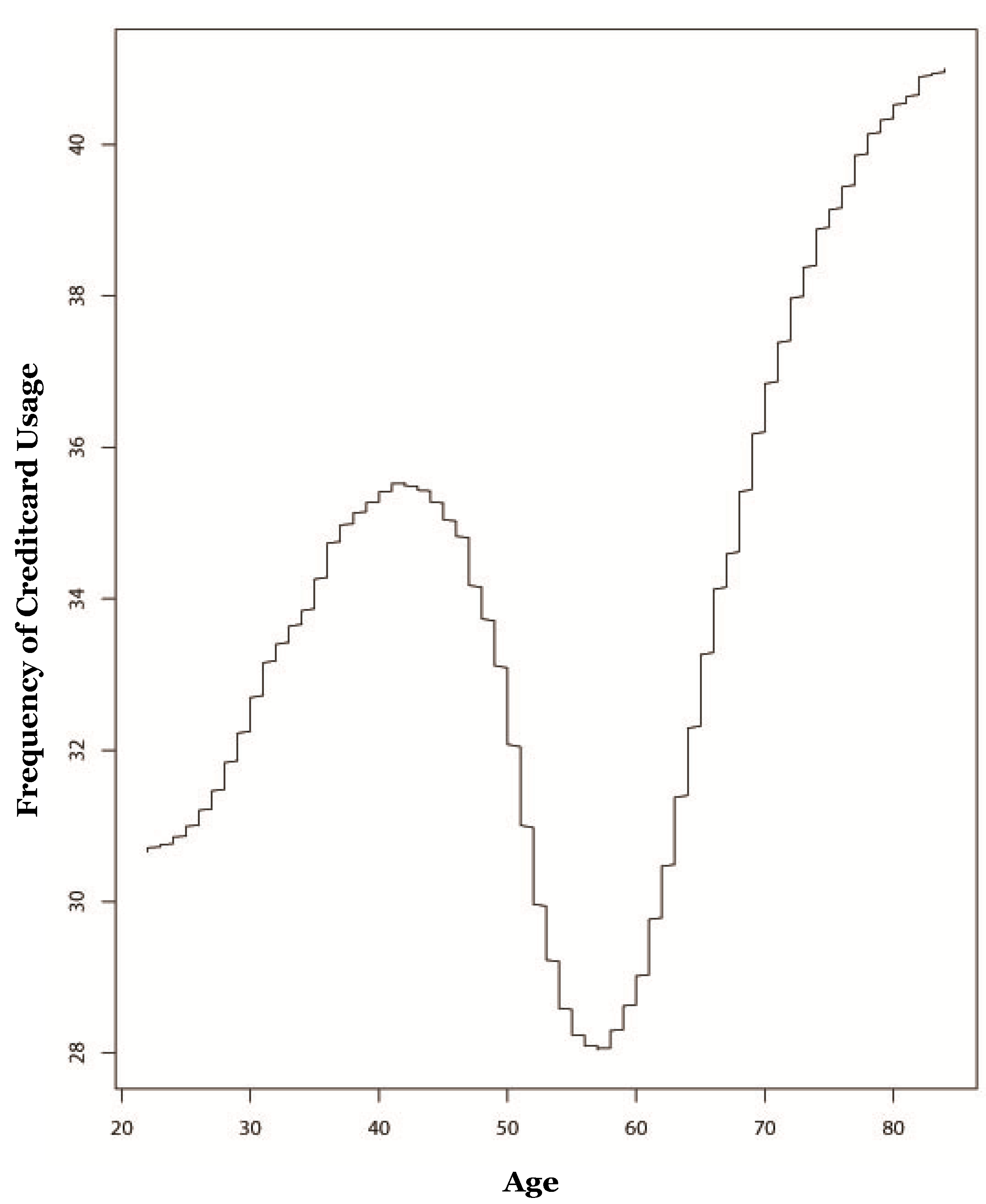
4.2. Credit Card Usage
5. Model Results
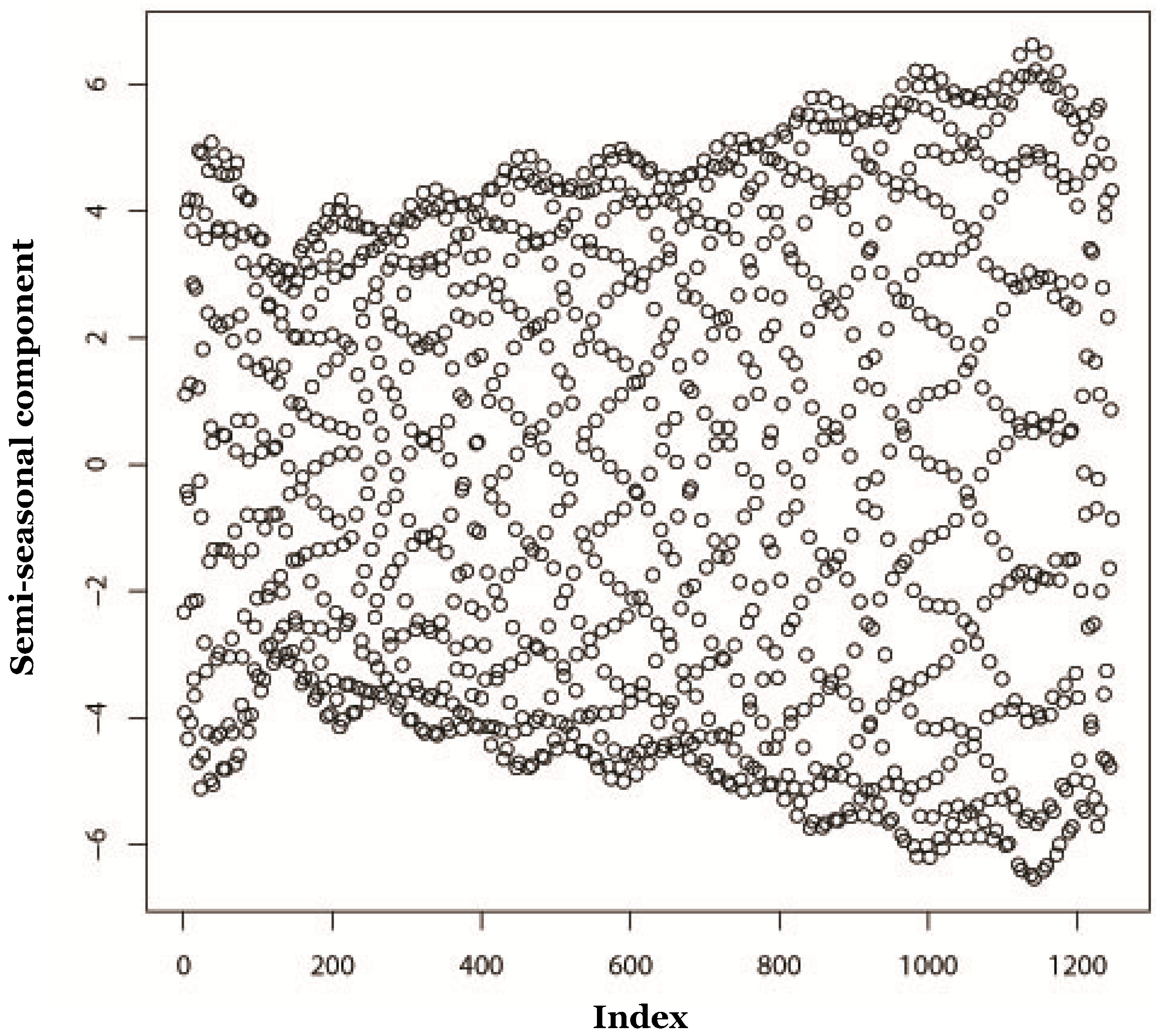
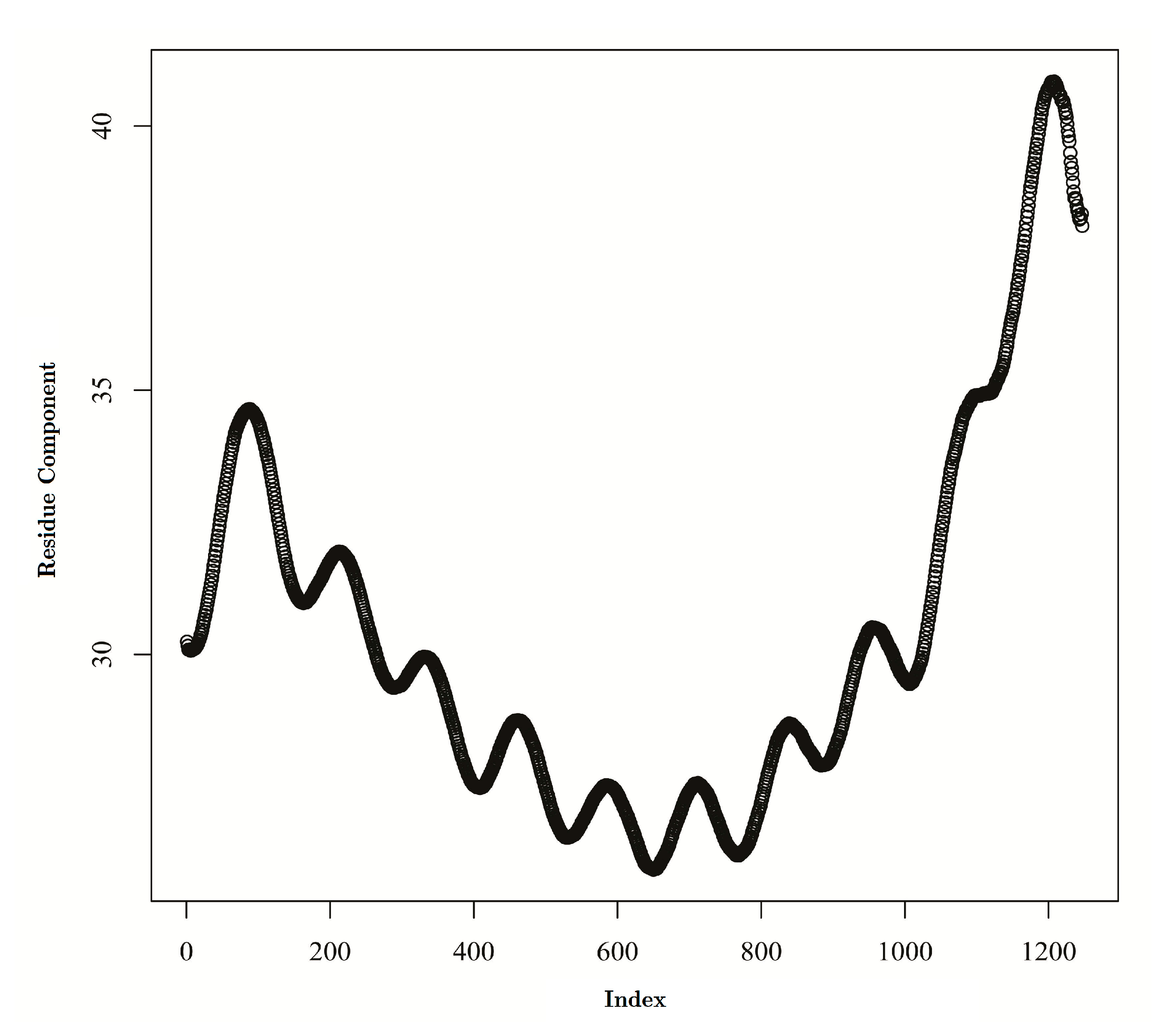
5.1. Decomposition
5.2. Reconstruction
6. Summary, Conclusions, and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- G.19 Report. 2012. Available online: http://www.federalreserve.gov/releases/g19/Current (accessed on 9 December 2014).
- Credit Stats. Available online: http://ficoforums.myfico.com/t5/Credit (accessed on 9 December 2014).
- Trai, C.Y.; Wang, J.C.; Chen, C.J. Mining usage behavior change for credit card users. WSEAS Trans. Inf. Sci. Appl. 2007, 4, 529–536. [Google Scholar]
- Awanis, S.; Cui, C.C. Consumer susceptibility to credit card misuse and indebtedness. Asia Pac. J. Mark. Logist. 2014, 26, 408–429. [Google Scholar] [CrossRef]
- Foster, K.; Meijer, D.; Schuh, S.; Zabek, M.A. The 2008 Survey of Consumer Payment Choice; FRB of Boston Public Policy Discussion Paper No. 09-10; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar] [CrossRef]
- Stavins, J.; Shy, O. Merchant steering of consumer payment choice: Evidence from a 2012 diary survey. J. Behav. Exp. Econ. 2015, 155, 1–9. [Google Scholar] [CrossRef]
- Koulayev, S.; Rysman, M.; Schuh, S.; Stavins, J. Explaining adoption and use of payment instruments by US consumers. RAND J. Econ. 2016, 47, 293–325. [Google Scholar] [CrossRef]
- Broomhead, D.S.; King, G.P. Extracting qualitative dynamics from experimental data. Phys. D Nonlinear Phenom. 1986, 20, 217–236. [Google Scholar] [CrossRef]
- Sarkar, S. Nonlinear Phenomena and Chaos; Hilger: Bristol, UK, 1986; pp. 113–144. ISBN 0852744943. [Google Scholar]
- Vautard, R.; Ghil, M. Singular spectrum analysis in nonlinear dynamics, with applications to paleoclimatic time series. Phys. D Nonlinear Phenom. 1989, 35, 395–424. [Google Scholar] [CrossRef]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-spectrum analysis: A toolkit for short, noisy chaotic signals. Phys. D Nonlinear Phenom. 1992, 52, 95–126. [Google Scholar] [CrossRef]
- Ghil, M.; Vautard, R. Interdecadal oscillations and the warming trend in global temperature time series. Nature 1991, 350, 324–327. [Google Scholar] [CrossRef]
- Ghil, M.; Allen, R.M.; Dettinger, M.D.; Ide, K.; Dondrashov, D.; Mann, M.E.; Robertson, A.W.; Saunders, A.; Tian, Y.; Varadi, F.; et al. Advanced spectral methods for climatic time series. Rev. Geophys. 2002, 40, 1003. [Google Scholar] [CrossRef]
- Golyandina, N.; Osipov, E. The caterpillar-SSA method for analysis of time series with missing values. J. Stat. Plan. Inference 2007, 137, 2642–2653. [Google Scholar] [CrossRef]
- Hassani, H.; Thomakos, D. A review on singular spectrum analysis for economic and financial time series. Stat. Its Interface 2010, 3, 377–397. [Google Scholar] [CrossRef]
- Hassani, H.; Soofi, A.; Zhigljavsky, A. Predicting daily exchange rate with singular spectrum analysis. Nonlinear Anal. Real World Appl. 2011, 11, 2023–2034. [Google Scholar] [CrossRef]
- Hassani, H.; Heravi, S.; Zhigljavsky, A. Forecasting UK industrial production with multivariate singular spectrum analysis. J. Forecast. 2013, 32, 395–408. [Google Scholar] [CrossRef]
- Safari, N.; Chung, C.Y.; Price, G.C.D. Novel multi-step short-term wind power prediction framework based on Chaotic Time Series Analysis and Singular Spectrum Analysis. IEEE Trans. Power Syst. 2018, 33, 590–601. [Google Scholar] [CrossRef]
- Credit Card Horrors for Senior Citizens. Available online: http://www.bankruptcylawnetwork.com/2010/12/29/credit-card-horrors-for-senior-citizens (accessed on 9 December 2014).
- Adams, T.; Moore, M. High-risk health and credit behavior among 18-to-25-year-old college students. J. Am. Coll. Health 2007, 56, 101–108. [Google Scholar] [CrossRef] [PubMed]
- Manning, R.D. Credit card nation: The consequences of America’s addiction to credit. Contemp. Sociol. 2003, 32, 464–465. [Google Scholar]
- Personal Bankruptcies Rose 8 Percent in 2010. Available online: http://www.creditcards.com/credit-card-news/bankruptcy-statistics-2010-q4.php (accessed on 9 December 2014).
- Total Bankruptcy Fillings Up 11% through First Nine Months of 2010 While Business Filling Decrease. Available online: http://www.abiworld.org/AM/Tenplate.cfm?Section-Home&TEMPLATE=/CM/contentDisplay.cfm&CONTENTID=62410 (accessed on 9 December 2014).
- Seeja, K.R.; Zareapoor, M. FraudMiner: A novel credit card fraud detection model based on frequent itemset mining. Sci. World J. 2014, 2014, 252797. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Xiao, J.J. Buying behavior, social support and credit card indebtedness of college students. Int. J. Consum. Stud. 2009, 33, 2–10. [Google Scholar] [CrossRef]
- Yang, B.; Spinella, M.; Lester, D. Credit card use and prefrontal cortex dysfunction: A study in NeuroEconomics. Psychol. Rep. 2004, 94, 1267–1268. [Google Scholar] [CrossRef] [PubMed]
- Mansfield, P.M.; Pinto, M.B.; Robb, C.A. Consumers and credit cards: A review of the empirical literature. J. Manag. Mark. Res. 2013, 12, 1–26. [Google Scholar]
- Myung, N.K. Singular Spectrum Analysis. Master’s Thesis, University of California, Los Angeles, CA, USA, 2009. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nai, W.; Liu, L.; Wang, S.; Dong, D. Modeling the Trend of Credit Card Usage Behavior for Different Age Groups Based on Singular Spectrum Analysis. Algorithms 2018, 11, 15. https://doi.org/10.3390/a11020015
Nai W, Liu L, Wang S, Dong D. Modeling the Trend of Credit Card Usage Behavior for Different Age Groups Based on Singular Spectrum Analysis. Algorithms. 2018; 11(2):15. https://doi.org/10.3390/a11020015
Chicago/Turabian StyleNai, Wei, Lu Liu, Shaoyin Wang, and Decun Dong. 2018. "Modeling the Trend of Credit Card Usage Behavior for Different Age Groups Based on Singular Spectrum Analysis" Algorithms 11, no. 2: 15. https://doi.org/10.3390/a11020015
APA StyleNai, W., Liu, L., Wang, S., & Dong, D. (2018). Modeling the Trend of Credit Card Usage Behavior for Different Age Groups Based on Singular Spectrum Analysis. Algorithms, 11(2), 15. https://doi.org/10.3390/a11020015




