Differential-Evolution-Based Coevolution Ant Colony Optimization Algorithm for Bayesian Network Structure Learning
Abstract
:1. Introduction
2. Preliminaries
2.1. Problem of BN Structure Learning
2.2. ACO
| Algorithm 1: ACO algorithm. | |
| /*Initialization */ | |
| 1 | Set the iteration counter g = 0; |
| 2 | Generate Mant ants, and initialize the pheromone matrix; |
| /* Iterative search */ | |
| 3 | while termination criteria are not satisfied do |
| 4 | iteration counter g = g + 1 |
| 5 | for i = 1: Mant do |
| /* Build a possible solution */ | |
| 6 | while the solution is not completed do |
| 7 | Randomly select a state/node according to the probabilistic transition rule; |
| 8 | Update the pheromone according to the local updating rule; |
| 9 | end while |
| 10 | end for |
| /* Pheromone updating */ | |
| 11 | Select the best solution and perform the global updating process; |
| 12 | end while |
| 13 | Return the best solution S+. |
2.3. ACO Applied to BNs
| Algorithm 2: Basic ACO based BN learning. | |
| /* Initialization */ | |
| 1 | Set the iteration counter t = 0; |
| 2 | Generate Mant ants; |
| 3 | Initialize the pheromone matrix τ(0): for all arcs aij, set τij(0) = τ0; |
| 4 | Set G+ be an empty graph; |
| /* Iterative search */ | |
| 5 | while termination criteria are not satisfied do |
| 6 | iteration counter t = t + 1 |
| 7 | for k = 1:Mant do |
| 8 | Generate an empty network Gk: for i = 1 to n, do πi = ϕ; |
| 9 | Calculate the heuristic information: for i, j = 1 to n (I ≠ j) do ηij = fBIC(Xi, Xj) − fBIC(Xi, ϕ); |
| 10 | while ηij > 0 do |
| /* Add an arc */ | |
| 11 | Select an arc aij from the feasible domain allowed according to (9) and (10); |
| 12 | if ηij > 0 then πi = πi∪{Xj} and construct the network Gk = Gk∪aji; |
| 13 | Set ηij = −∞; |
| /* Avoiding directed cycles */ | |
| 14 | for u, v = 1 to n do |
| 15 | if Gk∪auv includes a directed cycle, then ηuv = −∞; |
| 16 | end for |
| /* Calculation the heuristic information */ | |
| 17 | for u = 1 to n do |
| 18 | if ηiu > −∞ then ηiu = fBIC(Xi, πi∪{Xu}) − fBIC(Xi, πi); |
| 19 | end for |
| /* Local updating */ | |
| 20 | Update the pheromone: τij = (1 − ψ)·τij + ψ·τ0; |
| /* Local updating */ | |
| 21 | Update the pheromone: τij = (1 − ψ)·τij + ψ·τ0; |
| 22 | end while |
| 23 | end for |
| 24 | /* Pheromone update */ |
| 26 | Select Gt = arg max fBIC(Gk, D) |
| 27 | if fBIC(Gt, D) ≥ fBIC(G+, D), then G+ = Gt |
| 28 | Update the pheromone matrix according to (8) and (12) using fBIC(G+, D) |
| 29 | end while |
| 30 | Return the best BN structure G+. |
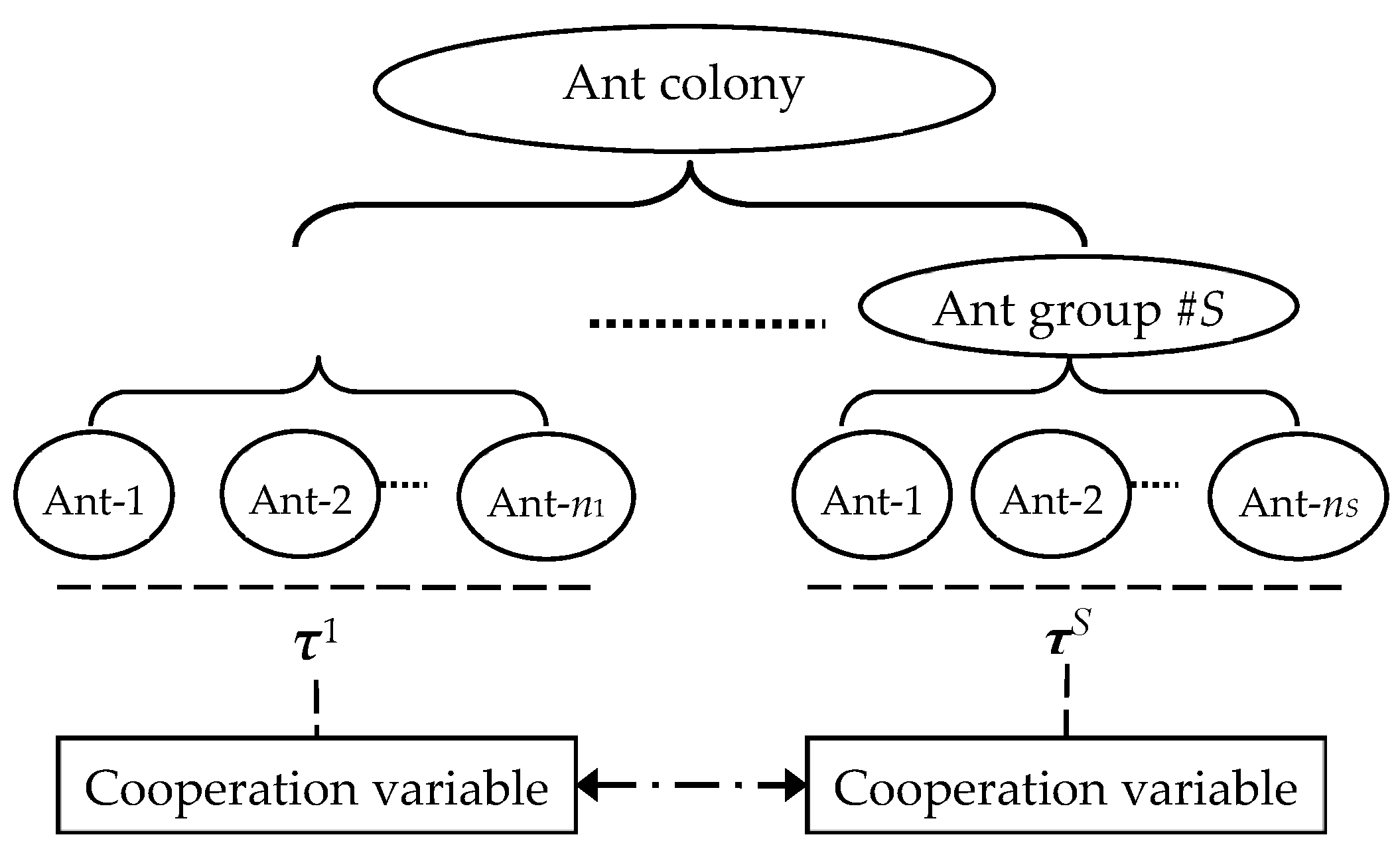
3. Method
- Step 1.
- Initialization of parameters: the maximum number of iteration as Tmax, the initial iteration counter t = 0, the number of ants Mant, the number of ant groups S, and other parameters α, β, ρ, F, cr, q0.
- Step 2.
- Initialization of ants: divide the whole ant colony into different ant groups; record the number of ants in each groups as n1, n2, … and nS; set the initial pheromone matrix τijs(0) = τ0, s = 1,2, …, nS for all arcs aij; set G+ to be an empty graph.
- Step 3.
- t = t + 1; s = 1.
- Step 4.
- Perform the mutation and crossover operations to the initial pheromone matrix τs(t) of each ant group using Equations (13) and (14), and generate the trial pheromone matrix vs(t).
- Step 5.
- s = s + 1; if s ≤ S, return to Step 4.
- Step 6.
- s = 1, k = 1.
- Step 7.
- The k-th ant constructs the BN Gk(τs) using the pheromone matrix τs according to the codes from Line 8 to Line 12 in Algorithm 2.
- Step 8.
- The k-th ant constructs the BN Gk(vs) using the pheromone matrix vs according to the codes from Line 8 to Line 12 in Algorithm 2.
- Step 9.
- k = k + 1; if k ≤ ns, return to Step 7.
- Step 10.
- Compute the BIC score for Gk(τs), k = 1, 2, …, ns, choose the best BN with the maximum score and set the maximum score as the fitness f(τs(t)) for τs.
- Step 11.
- Compute the BIC score for Gk(vs), k = 1, 2, …, ns, choose the best BN with the maximum score and set the maximum score as the fitness f(vs(t)) for vs.
- Step 12.
- Compare f(τs(t)) and f(vs(t)), select the better pheromone matrix according to (15), and select the corresponding BN for the ant group.
- Step 13.
- s = s + 1; if s ≤ S, k = k + 1 and return to Step 7.
- Step 14.
- Select the BN with maximum score from all ant groups, which is recorded as Gt.
- Step 15.
- If Gt has the larger BIC score than G+, then G+ = Gt.
- Step 16.
- Update the pheromone matrix τs, s = 1, 2, …, S, for each ant group according to (8) and (12) based on G+.
- Step 17.
- Return to Step 3 until t > Tmax.
- Step 18.
- Terminate and output the best BN structure, namely G+.
| Algorithm 3: coACO algorithm to learn BN. | |
| /* Initialization */ | |
| 1 | Set the iteration counter t = 0; |
| 2 | Generate Mant ants and divide them to nS groups; |
| 3 | Initialize the pheromone matrix τs(0), s = 1,2, …, nS: for all arcs aij, set τij(0) = τ0; |
| 4 | Set G+ be an empty graph; |
| /* Iterative search */ | |
| 5 | while termination criteria are not satisfied do |
| 6 | iteration counter t = t + 1 |
| 7 | for s = 1:S do |
| /* Mutation */ | |
| 8 | Choose r1, r2, r3 from [1, 2, …, S] s.t. r1 ≠ r2 ≠ r3 ≠ s, and generate the donor pheromone matrix us via (13). |
| /* Crossover */ | |
| 9 | for i, j = 1:n do |
| 10 | Generate the trial vector vs = {vsij} according to (14) |
| 11 | end for |
| 12 | end for |
| 13 | for s = 1:S do |
| /* Evaluation the fitness of pheromone matrixes */ | |
| 14 | for each ant k in the s-th group do |
| 15 | Construct a BN structure Gk(vs) using the pheromone matrix vs according to the codes from Line 8 to Line 12 in Algorithm 1; |
| 16 | Construct a BN structure Gk(τs) using the pheromone matrix τs according to the codes from Line 8 to Line 12 in Algorithm 1; |
| 17 | end for |
| 18 | Calculate the BIC score for each BN structure Gk(vs), choose the best structure and assign the maximum score to f(vs); |
| 19 | Calculate the BIC score for each BN structure Gk(τs), choose the best structure and assign the maximum score to f(τs); |
| /* Selection */ | |
| 20 | Compare f(τs) and f(vs), select the better one to be the new pheromone matrix according to (14); |
| 21 | end for |
| /* Pheromone update */ | |
| 22 | Select the best structure Gt obtained by all ants in various groups; |
| 23 | if fBIC(Gt, D) ≥ fBIC(G+, D), then G+ = Gt |
| 24 | Update each pheromone matrix τs according to (8) and (12) using fBIC(G+, D) |
| 25 | end while |
| 26 | Return the best BN structure G+. |
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pinto, P.C.; Nägele, A.; Dejori, M.; Runkler, T.A.; Sousa, J.M.C. Using a local discovery ant algorithm for Bayesian network structure learning. IEEE Trans. Evol. Comput. 2009, 13, 767–779. [Google Scholar] [CrossRef]
- Campos, L.M.; Fernández-Luna, J.M.; Gámez, J.A.; Puerta, J.M. Ant colony optimization for learning Bayesian networks. Int. J. Approx. Reason. 2002, 31, 291–311. [Google Scholar] [CrossRef]
- Larrañaga, P.; Karshenas, H.; Bielza, C.; Santana, R. A review on evolutionary algorithms in Bayesian network learning and inference tasks. Inf. Sci. 2013, 233, 109–125. [Google Scholar] [CrossRef]
- Gheisari, S.; Meybodi, M.R.; Dehghan, M.; Ebadzadeh, M.M. Bayesian network structure training based on a game of learning automata. Int. J. Mach. Learn. Cybern. 2017, 8, 1093–1105. [Google Scholar] [CrossRef]
- Martínez-Rodríguez, A.M.; May, J.H.; Vargas, L.G. An optimization-based approach for the design of Bayesian networks. Math. Comput. Model. 2008, 48, 1265–1278. [Google Scholar] [CrossRef]
- Cano, A.; Masegosa, A.R.; Moral, S.A. A method for integrating expert knowledge when learning Bayesian networks from data. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2011, 41, 1382–1394. [Google Scholar] [CrossRef] [PubMed]
- Campos, L.M.; Castellano, J.G. Bayesian network learning algorithms using structural restrictions. Int. J. Approx. Reason. 2007, 45, 233–254. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Jia, S.M.; Li, X.Z.; Guo, G. Learning the Bayesian networks structure based on ant colony optimization and differential evolution. In Proceedings of the 2018 4th International Conference on Control, Automation and Robotics (ICCAR), Auckland, New Zealand, 20–23 April 2018; pp. 354–358. [Google Scholar]
- Arefi, M.; Taheri, S.M. Possibilistic Bayesian inference based on fuzzy data. Int. J. Mach. Learn. Cybern. 2016, 7, 753–763. [Google Scholar] [CrossRef]
- Yan, L.J.; Cercone, N. Bayesian network modeling for evolutionary genetic structures. Comput. Math. Appl. 2010, 59, 2541–2551. [Google Scholar] [CrossRef]
- Khanteymoori, A.R.; Olyaee, M.-H.; Abbaszadeh, O.; Valian, M. A novel method for Bayesian networks structure learning based on Breeding Swarm algorithm. Soft Comput. 2017, 21, 6713–6738. [Google Scholar] [CrossRef]
- Wong, M.L.; Leung, K.S. An efficient data mining method for learning Bayesian networks using an evolutionary algorithm-based hybrid approach. IEEE Trans. Evol. Comput. 2004, 8, 378–404. [Google Scholar] [CrossRef]
- Wang, T.; Yang, J. A heuristic method for learning Bayesian networks using discrete particle swarm optimization. Knowl. Inf. Syst. 2010, 24, 269–281. [Google Scholar] [CrossRef]
- Ji, J.Z.; Zhang, H.X.; Hu, R.B. A Bayesian network learning algorithm based on independence test and ant colony optimization. Acta Autom. Sin. 2009, 35, 281–288. [Google Scholar] [CrossRef]
- Ji, J.Z.; Zhang, H.X.; Hu, R.B. A hybrid method for learning Bayesian networks based on ant colony optimization. Appl. Soft Comput. 2011, 11, 3373–3384. [Google Scholar] [CrossRef]
- Yang, J.; Li, L.; Wang, A.G. A partial correlation-based Bayesian network structure learning algorithm under linear SEM. Knowl. Based Syst. 2011, 24, 963–976. [Google Scholar] [CrossRef]
- Baumgartner, K.; Ferrari, S.; Palermo, G. Constructing Bayesian networks for criminal profiling from limited data. Knowl. Based Syst. 2008, 21, 563–572. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; WH Freeman Publishers: New York, NY, USA, 1979. [Google Scholar]
- Colorni, A.; Dorigo, M.; Maniezzo, V. Distributed optimization by ant colonies. In Proceedings of the First European Conference on Artificial Life, Paris, France, 11–13 December 1991; pp. 134–142. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. The ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Storn, R.; Price, K. Differential evolution: A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Das, S.; Suganthan, P.N. Differential evolution: A survey of the state-of-the-art. IEEE Trans. Evol. Comput. 2011, 9, 4–31. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Duan, H.B.; Yu, Y.X.; Zhang, X.Y. Three-dimension path planning for UCAV using hybrid meta-heuristic ACO-DE algorithm. Simul. Model. Pract. Theory 2010, 18, 1104–1115. [Google Scholar] [CrossRef]
- Serani, A.; Leotardi, C.; Iemma, U.; Campana, E.F.; Fasano, G.; Diez, M. Parameter selection in synchronous and asynchronous deterministic particle swarm optimization for ship hydrodynamics problems. Appl. Soft Comput. 2016, 49, 313–334. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.Y.; Duan, H.B.; Yu, Y.X. Receding horizon control for multi-UAVs close formation control based on differential evolution. Sci. China Inf. Sci. 2010, 53, 223–235. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Duan, H.B. An improved constrained differential evolution algorithm for unmanned aerial vehicle global route planning. Appl. Soft Comput. 2015, 26, 270–284. [Google Scholar] [CrossRef]
- Murphy, K. The Bayes Net Toolbox for Matlab. Comput. Sci. Stat. 2001, 33, 1024–1034. [Google Scholar]


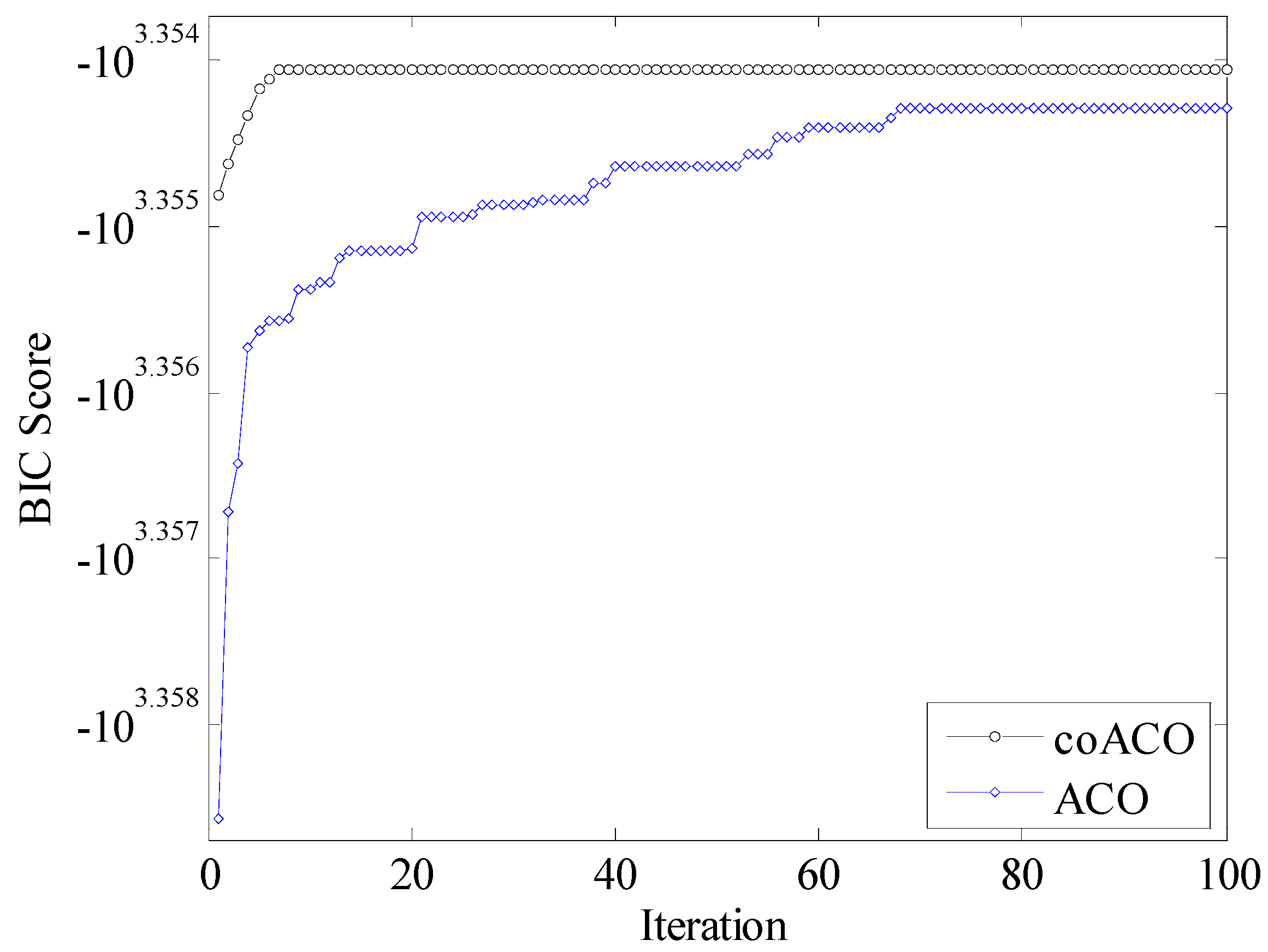
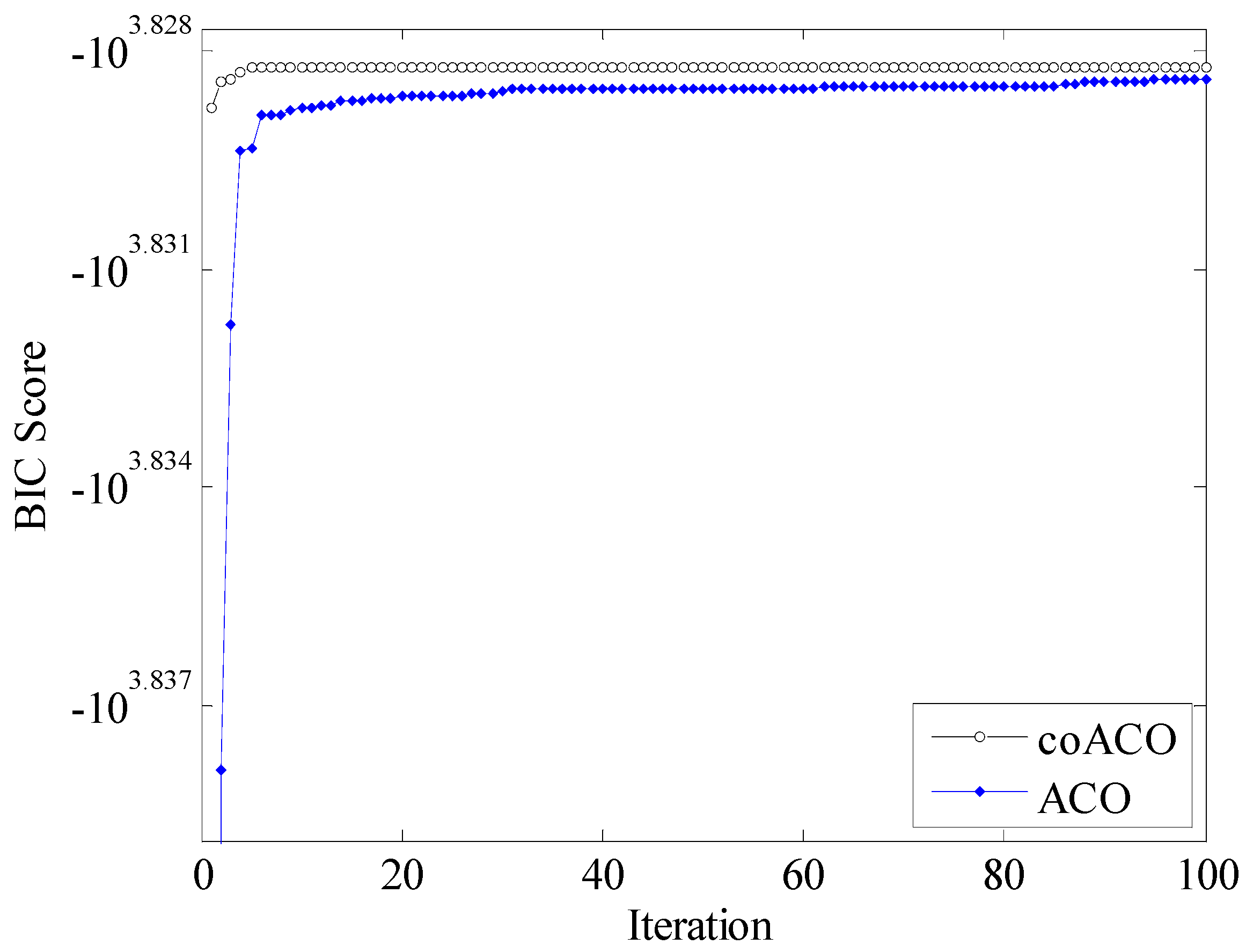

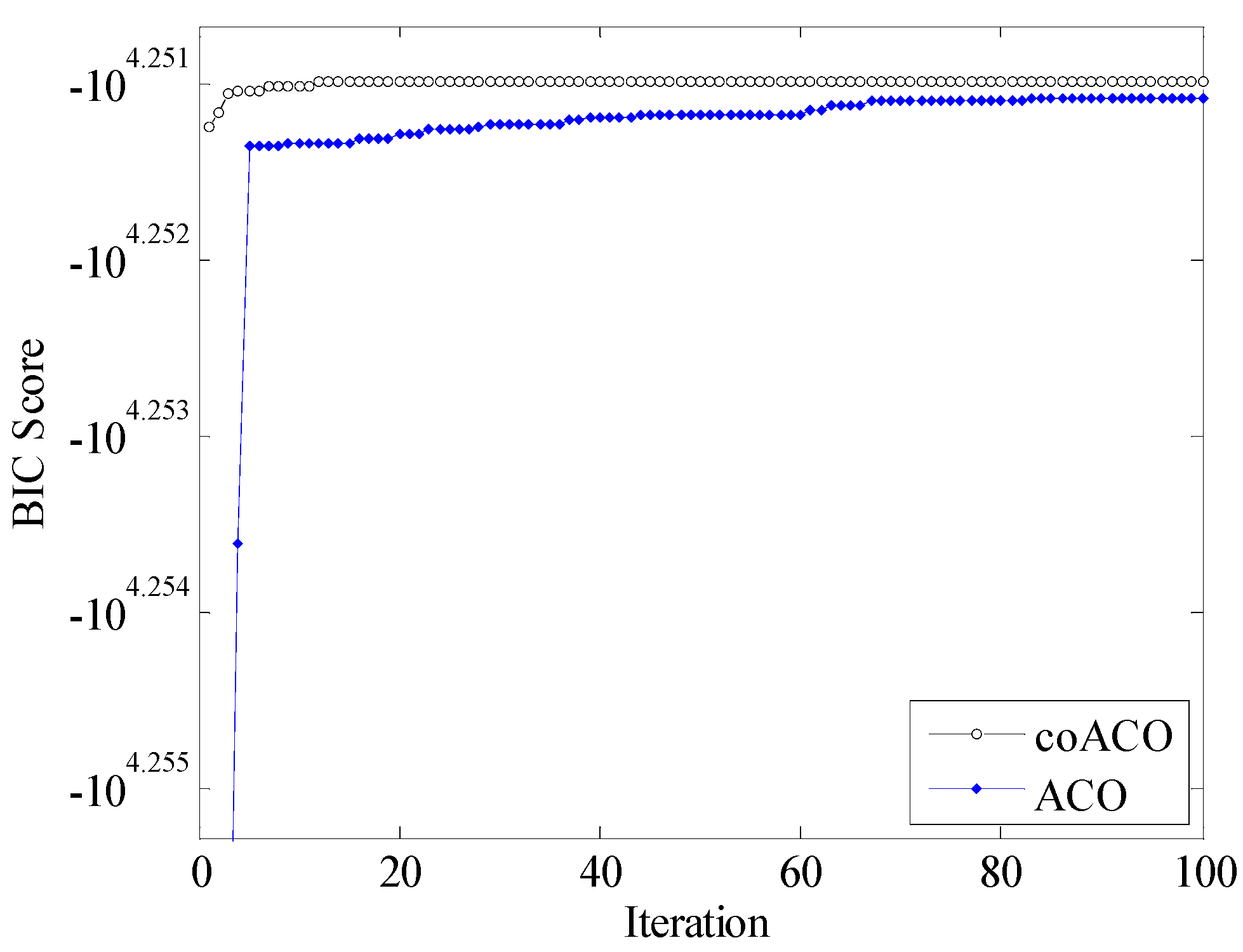
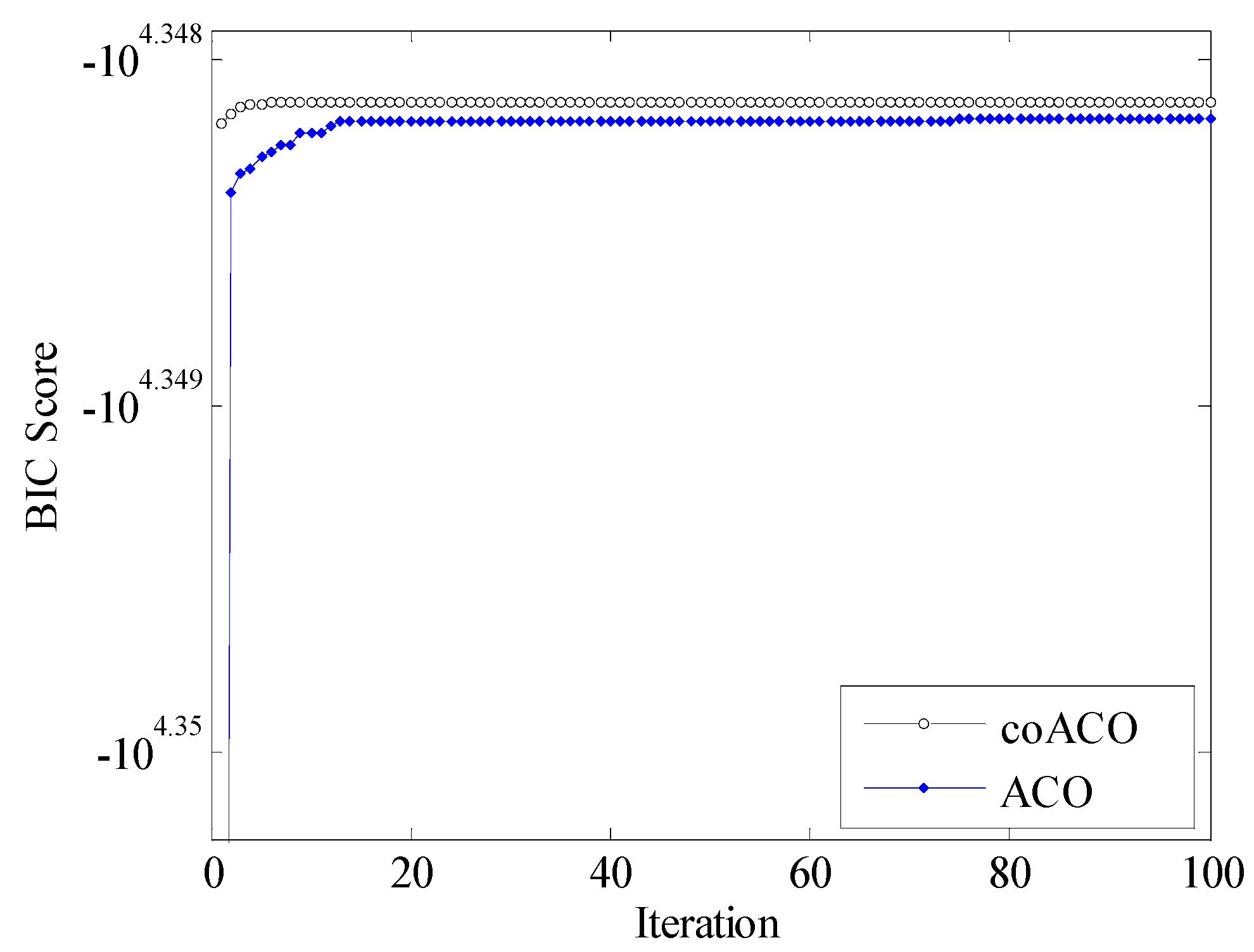
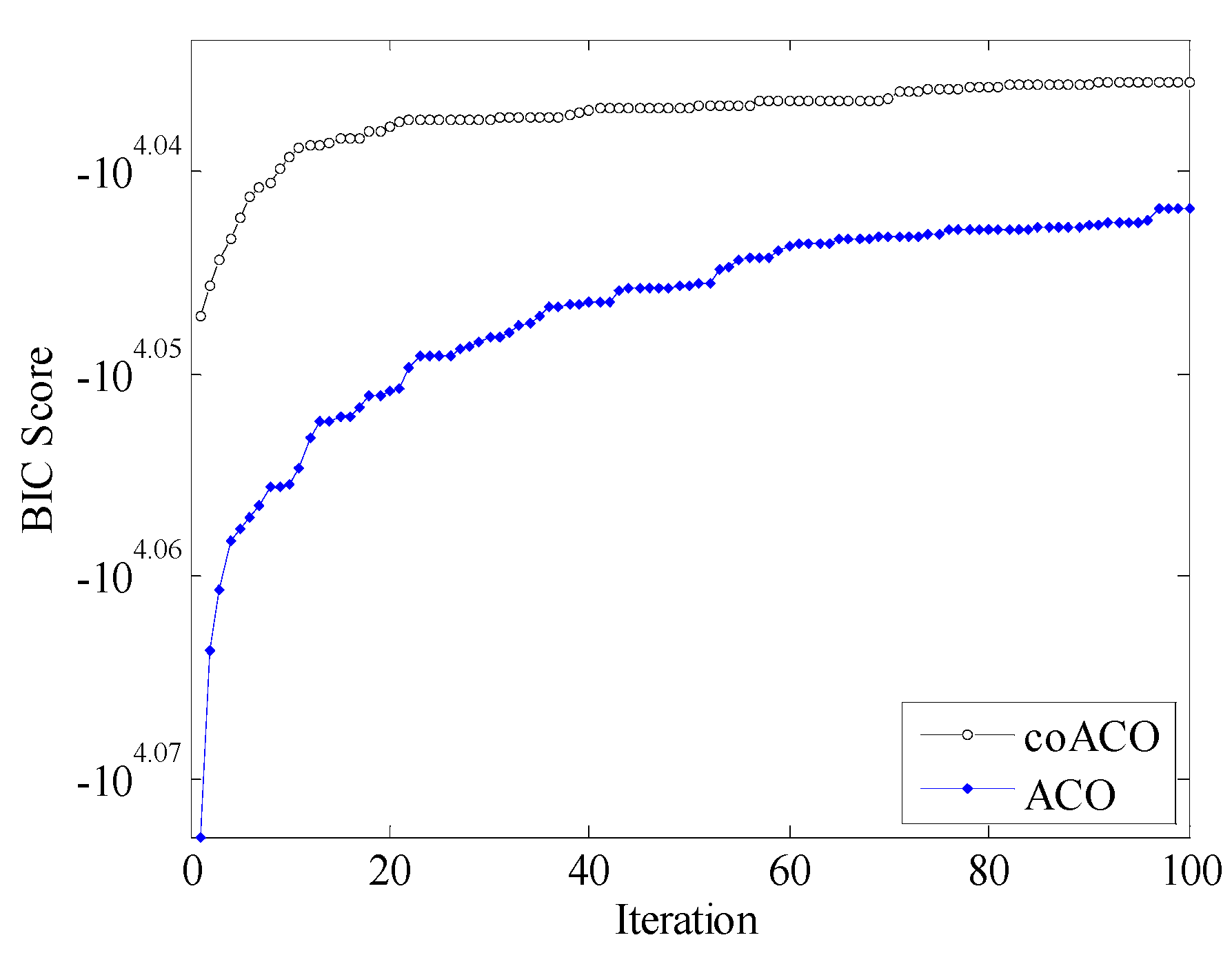
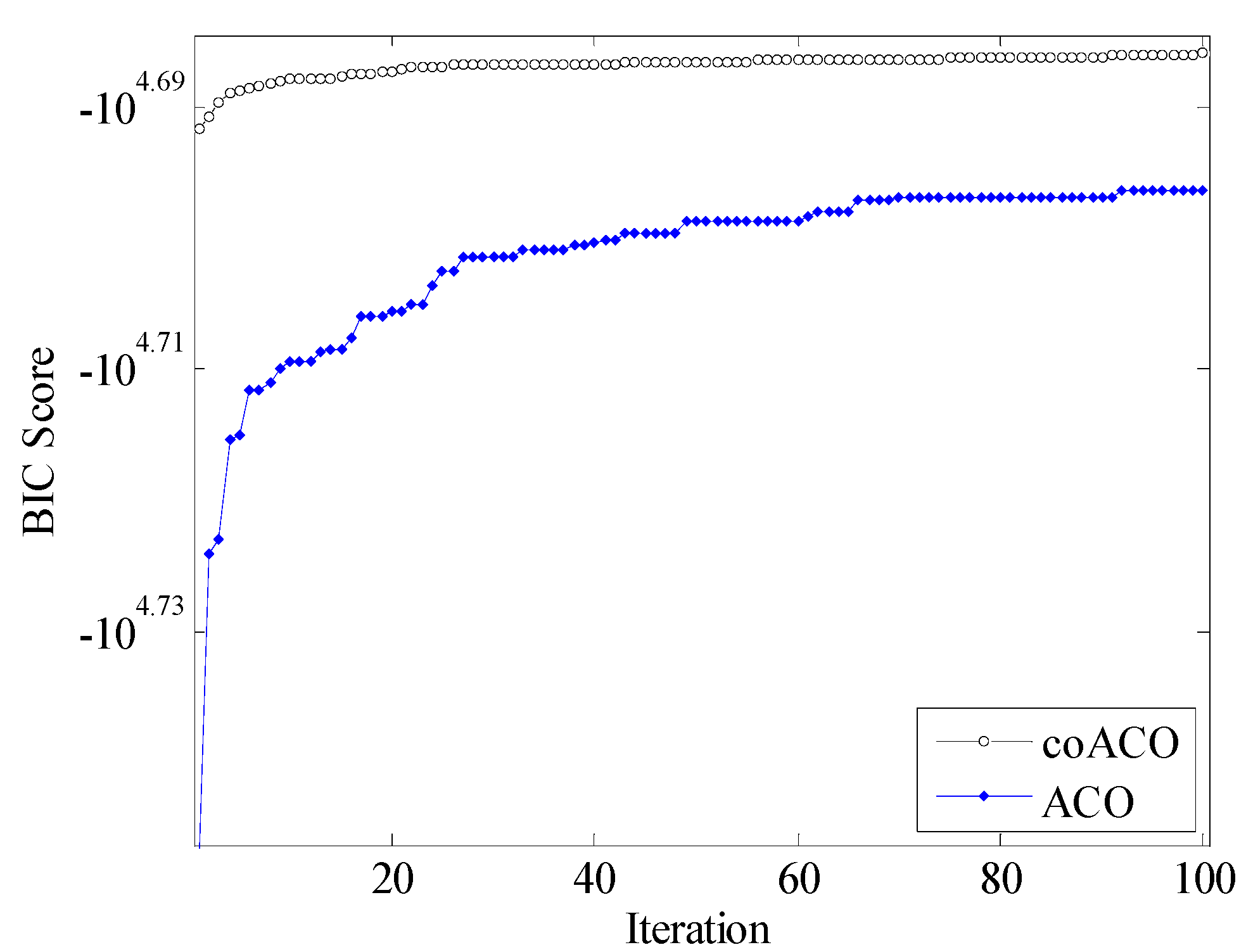
| Network | Number of Cases | Nodes | Arcs | BIC Score |
|---|---|---|---|---|
| ASIA | 1000 | 8 | 8 | −2261.37 |
| 3000 | 8 | 8 | −6733.48 | |
| 5000 | 8 | 8 | −11,194.67 | |
| 8000 | 8 | 8 | −17,823.01 | |
| 10,000 | 8 | 8 | −22,290.78 | |
| ALARM | 1000 | 37 | 46 | −11,156.05 |
| 5000 | 37 | 46 | −48,593.10 |
| Network | N | Method | Best | Median | Mean | Worst | Std. | SR (%) | CPU Time (s) |
|---|---|---|---|---|---|---|---|---|---|
| ASIA | 1000 | coACO | −2259.70 | −2259.70 | −2259.70 | −2259.70 | 0 | 100 | 116.826 |
| ACO | −2259.73 | −2259.73 | −2260.94 | −2262.76 | 1.564 | 60 | 74.335 | ||
| K2 | −2267.64 | −2275.90 | −2276.53 | −2288.06 | 8.376 | 0 | 0.118 | ||
| B | −2304.07 | - | - | - | - | 0 | 0.213 | ||
| 3000 | coACO | −6733.48 | −6733.48 | −6733.48 | −6733.48 | 0 | 100 | 173.060 | |
| ACO | −6733.48 | −6733.47 | −6736.14 | −6744.19 | 4.376 | 60 | 103.114 | ||
| K2 | −6739.60 | −6755.06 | −6755.95 | −6797.71 | 16.688 | 0 | 0.142 | ||
| B | −6873.20 | - | - | - | - | 0 | 0.276 | ||
| 5000 | coACO | −11,193.42 | −11,193.42 | −11,193.42 | −11,193.42 | 1.92 × 10−12 | 100 | 163.858 | |
| ACO | −11,193.42 | −11,197.08 | −11,197.23 | −11,205.13 | 4.512 | 40 | 100.373 | ||
| K2 | −11,197.08 | −11,218.39 | −11,224.51 | −11,300.65 | 28.867 | 0 | 0.174 | ||
| B | −11,450.81 | - | - | - | - | 0 | 0.288 | ||
| 8000 | coACO | −17,823.01 | −17,823.01 | −17,823.01 | −17,823.01 | 0 | 100 | 203.835 | |
| ACO | −17,823.01 | −17,823.01 | −17,826.72 | −17,837.12 | 5.774 | 60 | 127.463 | ||
| K2 | −17,834.80 | −17,844.42 | −17,863.88 | −17,951.13 | 38.805 | 0 | 0.187 | ||
| B | −18,100.86 | - | - | - | - | 0 | 0.345 | ||
| 10,000 | coACO | −22,290.78 | −22,290.78 | −22,290.78 | −22,290.78 | 3.83 × 10−12 | 100 | 246.144 | |
| ACO | −22,290.78 | −22,294.73 | −22,293.15 | −22,294.73 | 2.043 | 40 | 153.925 | ||
| K2 | −22,303.21 | −22,324.18 | −22,342.28 | −22,442.17 | 42.487 | 0 | 0.226s | ||
| B | −22,572.73 | - | - | - | - | 0 | 0.459 | ||
| ALARM | 1000 | coACO | −10,818.45 | −10,852.26 | −10,852.26 | −10,950.47 | 41.256 | 100 | 6481.540 |
| ACO | −10,957.50 | −11,002.89 | −11,012.03 | −11,138.50 | 52.234 | 100 | 3687.500 | ||
| K2 | −11,443.44 | −11,694.90 | −11699.26 | −11,993.50 | 189.450 | 0 | 3.285 | ||
| B | −3,425,441.5 | - | - | - | - | 0 | 7.913 | ||
| 5000 | coACO | −48,501.03 | −48,517.21 | −48,525.78 | −48579.64 | 28.656 | 100 | 10,800.721 | |
| ACO | −49,341.99 | −49,661.63 | −49,701.69 | −50,329.43 | 279.589 | 0 | 6921.368 | ||
| K2 | −50,968.63 | −51,949.21 | −51,858.65 | −52,867.42 | 595.86 | 0 | 4.867 | ||
| B | −5,425,441.5 | - | - | - | - | 0 | 25.681 |
| Network | n | Method | It. | A. | D. | I. |
|---|---|---|---|---|---|---|
| ASIA | 1000 | coACO | 6.4 ± 4.76 (1) | 0 ± 0 (0) | 1 ± 0 (1) | 1 ± 0 (1) |
| ACO | 43.8 ± 26.17 (4) | 0 ± 0 (0) | 1 ± 0 (1) | 1.9 ± 2.33 (0) | ||
| K2 | - | 0 ± 0 (0) | 2.5 ± 0.85 (1) | 4.40 ± 1.90 (2) | ||
| B | - | 0 | 1 | 3 | ||
| 3000 | coACO | 2.7 ± 1.83 (1) | 0 ± 0 (0) | 0 ± 0 (0) | 1 ± 0 (1) | |
| ACO | 47.9 ± 39.02 (2) | 0 ± 0 (0) | 0 ± 0 (0) | 3.3 ± 2.95 (1) | ||
| K2 | - | 0 ± 0 (0) | 1.3 ± 0.68 (0) | 4.6 ± 0.84 (3) | ||
| B | - | 0 | 0 | 7 | ||
| 5000 | coACO | 4.9 ± 3.87 (1) | 0 ± 0 (0) | 1 ± 0 (1) | 0 ± 0 (0) | |
| ACO | 42.2 ± 22.58 (11) | 0 ± 0 (0) | 1 ± 0 (1) | 2.9 ± 2.88 (0) | ||
| K2 | - | 0 ± 0 (0) | 2.2 ± 0.79 (1) | 4.8 ± 1.48 (3) | ||
| B | - | 0 | 1 | 3 | ||
| 8000 | coACO | 6.2 ± 4.00 (2) | 0 ± 0 (0) | 0 ± 0 (0) | 1 ± 0 (1) | |
| ACO | 52.1 ± 31.88 (5) | 0 ± 0 (0) | 0 ± 0 (0) | 3.5 ± 3.27 (1) | ||
| K2 | - | 0 ± 0 (0) | 0.9 ± 0.57 (0) | 5.3 ± 2.11 (2) | ||
| B | - | 0 | 0 | 4 | ||
| 10,000 | coACO | 4.6 ± 3.60 (1) | 0 ± 0 (0) | 0 ± 0 (0) | 0 ± 0 (0) | |
| ACO | 20.5 ± 21.74 (1) | 0 ± 0 (0) | 0 ± 0 (0) | 3.2 ± 2.15 (0) | ||
| K2 | - | 0 ± 0 (0) | 0.9 ± 0.57 (0) | 5.5 ± 2.64 (2) | ||
| B | - | 0 | 0 | 8 | ||
| ALARM | 1000 | coACO | 64.7 ± 13.12 (17) | 0 ± 0 (0) | 5.2 ±1.62 (4) | 12.7 ± 3.53 (9) |
| ACO | 81.8 ± 25.02 (57) | 0 ± 0 (0) | 9.2 ±1.69 (6) | 20.8 ± 5.03 (14) | ||
| K2 | - | 0 ± 0 (0) | 15.6 ± 2.55 (13) | 22.6 ± 4.25 (17) | ||
| B | - | 0 | 6 | 42 | ||
| 5000 | coACO | 81.1 ± 15.82 (46) | 0 ± 0 (0) | 1.2 ± 0.42 (1) | 14.6 ± 2.99 (10) | |
| ACO | 58.5 ± 22.27 (20) | 0 ± 0 (0) | 5.4 ± 1.429 (3) | 58.5 ± 22.27 (20) | ||
| K2 | - | 0 ± 0 (0) | 10.1 ± 1.969 (7) | 33.4 ± 3.84 (26) | ||
| B | - | 0 | 1 | 97 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Xue, Y.; Lu, X.; Jia, S. Differential-Evolution-Based Coevolution Ant Colony Optimization Algorithm for Bayesian Network Structure Learning. Algorithms 2018, 11, 188. https://doi.org/10.3390/a11110188
Zhang X, Xue Y, Lu X, Jia S. Differential-Evolution-Based Coevolution Ant Colony Optimization Algorithm for Bayesian Network Structure Learning. Algorithms. 2018; 11(11):188. https://doi.org/10.3390/a11110188
Chicago/Turabian StyleZhang, Xiangyin, Yuying Xue, Xingyang Lu, and Songmin Jia. 2018. "Differential-Evolution-Based Coevolution Ant Colony Optimization Algorithm for Bayesian Network Structure Learning" Algorithms 11, no. 11: 188. https://doi.org/10.3390/a11110188
APA StyleZhang, X., Xue, Y., Lu, X., & Jia, S. (2018). Differential-Evolution-Based Coevolution Ant Colony Optimization Algorithm for Bayesian Network Structure Learning. Algorithms, 11(11), 188. https://doi.org/10.3390/a11110188





