A Hierarchical Multi-Label Classification Algorithm for Gene Function Prediction
Abstract
1. Introduction
2. The Proposed Algorithm
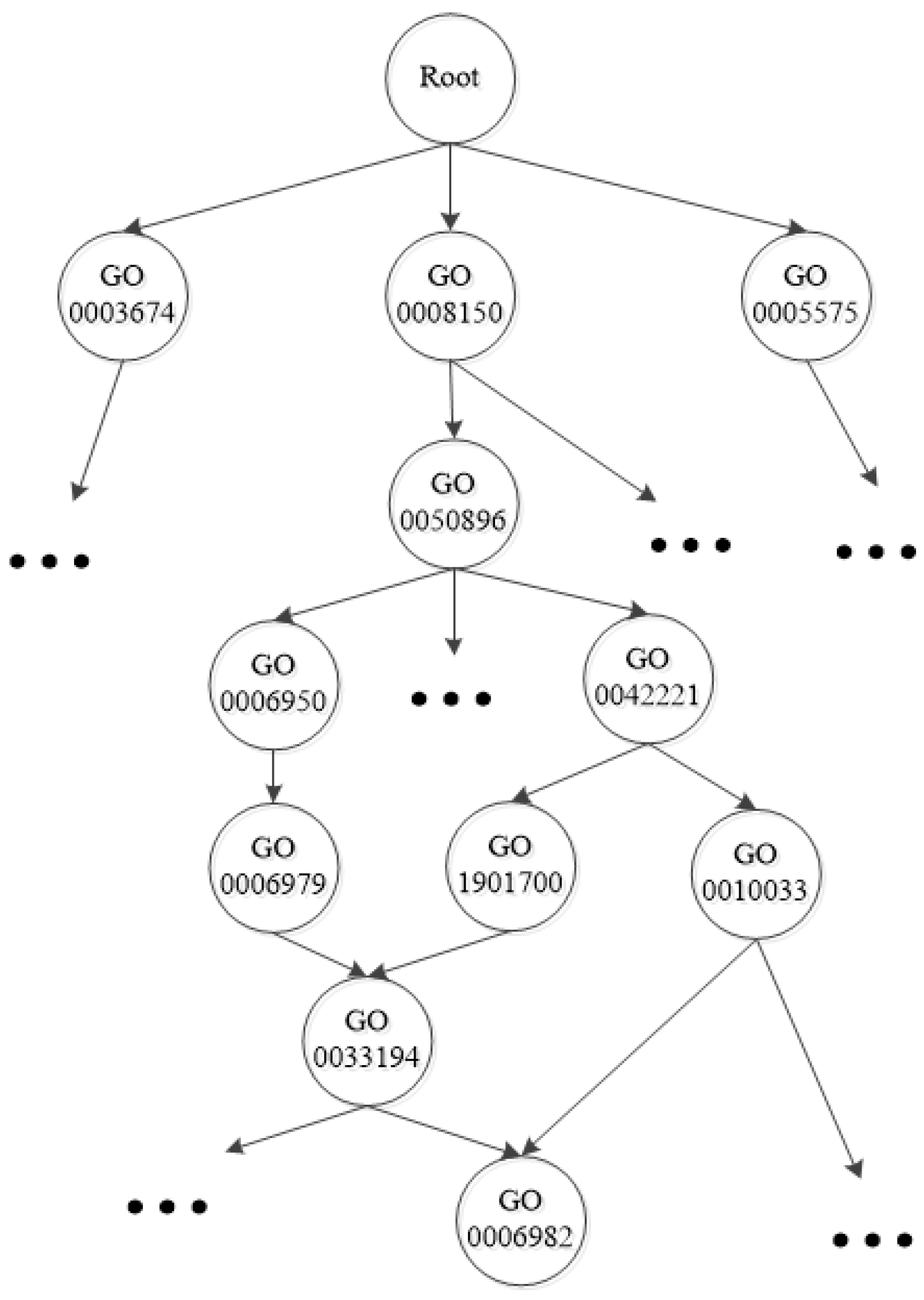
2.1. Notation and Basic Definitions
2.2. The Main Steps of the Proposed Method
2.3. Step 1: Training Data Set Preparation
2.4. Step 2: Data Set Rebalancing
2.5. Step 3: Base Classifier Training
2.6. Step 4: Prediction
3. Experiment
3.1. Data Sets and Experimental Setup
3.2. Evaluation Metrics
3.3. Experiment Results and Analysis
3.3.1. Experiments for Specific Classes
3.3.2. Experiments on Eight Data Sets
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| HMC | Hierarchical Multi-label Classification |
| DAG | Directed Acyclic Graph |
| TPR | True Path Rule |
| GO | Gene Ontology |
| SVM | Support Vector Machine |
| SMOTE | Synthetic Minority Over-sampling Technique |
References
- Madjarov, G.; Dimitrovski, I.; Gjorgjevikj, D.; Džeroski, S. Evaluation of Different Data-Derived Label Hierarchies in Multi-Label Classification; Springer: Cham, Switzerland, 2014; pp. 19–37. [Google Scholar]
- Cerri, R.; Pappa, G.L.; Carvalho, A.C.P.L.F.; Freitas, A.A. An Extensive Evaluation of Decision Tree—Based Hierarchical Multilabel Classification Methods and Performance Measures. Comput. Intell. 2013, 31, 1–46. [Google Scholar] [CrossRef]
- Romão, L.M.; Nievola, J.C. Hierarchical Multi-label Classification Problems: An LCS Approach. In Proceedings of the 12th International Conference on Distributed Computing and Artificial Intelligence, Salamanca, Spain, 3–5 June 2015; Springer: Cham, Switzerland, 2015; pp. 97–104. [Google Scholar]
- Blockeel, H.; Schietgat, L.; Struyf, J.; Džeroski, S.; Clare, A. Decision trees for hierarchical multilabel classification: A case study in functional genomics. In Proceedings of the 10th European Conference on Principle and Practice of Knowledge Discovery in Databases, Berlin, Germany, 18–22 September 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 18–29. [Google Scholar]
- Bi, W.; Kwok, J.T. Bayes-Optimal Hierarchical Multilabel Classification. IEEE Trans. Knowl. Data Eng. 2015, 27, 2907–2918. [Google Scholar] [CrossRef]
- Merschmann, L.H.D.C.; Freitas, A.A. An Extended Local Hierarchical Classifier for Prediction of Protein and Gene Functions; Springer: Berlin/Heidelberg, Germany, 2013; pp. 159–171. [Google Scholar]
- Ashburner, M.; Ball, C.A.; Blake, J.A.; Botstein, D.; Butler, H.; Cherry, J.; Davis, A.; Dolinski, K.; Dwight, S.; Eppig, J.; et al. Gene ontology: Tool for the unification of biology. The Gene Ontology Consortium. Nat. Genet. 2015, 25, 25–29. [Google Scholar] [CrossRef] [PubMed]
- Alves, R.T.; Delgado, M.R.; Freitas, A.A. Multi-Label Hierarchical Classification of Protein Functions with Artificial Immune Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–12. [Google Scholar]
- Santos, A.; Canuto, A. Applying semi-supervised learning in hierarchical multi-label classification. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 872–879. [Google Scholar]
- Cerri, R.; Barros, R.C.; de Carvalho, A. Hierarchical Multi-Label Classification for Protein Function Prediction: A Local Approach based on Neural Networks. In Proceedings of the 11th International Conference on Intelligent Systems Design and Applications (ISDA), Cordoba, Spain, 22–24 November 2011; pp. 337–343. [Google Scholar]
- Ramírez-Corona, M.; Sucar, L.E.; Morales, E.F. Multi-Label Classification for Tree and Directed Acyclic Graphs Hierarchies; Springer: Cham, Switzerland, 2014; pp. 409–425. [Google Scholar]
- Alves, R.T.; Delgado, M.R.; Freitas, A.A. Knowledge discovery with Artificial Immune Systems for hierarchical multi-label classification of protein functions. In Proceedings of the 2010 IEEE International Conference on Fuzzy Systems (FUZZ), Barcelona, Spain, 18–23 July 2010; pp. 1–8. [Google Scholar]
- Vens, C.; Struyf, J.; Schietgat, L.; Džeroski, S.; Blockeel, H. Decision trees for hierarchical multi-label classification. Mach. Learn. 2008, 73, 185–214. [Google Scholar] [CrossRef]
- Borges, H.B.; Nievola, J.C. Multi-Label Hierarchical Classification using a Competitive Neural Network for protein function prediction. In Proceedings of the International Joint Conference on Neural Networks, Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Chen, B.; Duan, L.; Hu, J. Composite kernel based SVM for hierarchical multi-label gene function classification. In Proceedings of the International Joint Conference on Neural Networks, Brisbane, Australia, 10–15 June 2012; pp. 1–6. [Google Scholar]
- Barutcuoglu, Z.; Schapire, R.; Troyanskaya, O. Hierarchical multi-label prediction of gene function. Bioinformatics 2006, 22, 830–836. [Google Scholar] [CrossRef] [PubMed]
- Valentini, G. True Path Rule Hierarchical Ensembles for Genome-Wide Gene Function Prediction. IEEE/ACM Trans. Comput. Biol. Bioinform. 2011, 8, 832–847. [Google Scholar] [CrossRef] [PubMed]
- Robinson, P.N.; Frasca, M.; Köhler, S.; Notaro, M.; Re, M.; Valentini, G. A Hierarchical Ensemble Method for DAG-Structured Taxonomies. In Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; Volume 9132, pp. 15–26. [Google Scholar]
- Otero, F.E.B.; Freitas, A.A.; Johnson, C.G. A hierarchical multi-label classification ant colony algorithm for protein function prediction. Memet. Comput. 2010, 2, 165–181. [Google Scholar] [CrossRef]
- Stojanova, D.; Ceci, M.; Malerba, D.; Dzeroski, S. Using PPI network autocorrelation in hierarchical multi-label classification trees for gene function prediction. BMC Bioinform. 2013, 14, 3955–3957. [Google Scholar] [CrossRef] [PubMed]
- Parikesit, A.A.; Steiner, L.; Stadler, P.F.; Prohaska, S.J. Pitfalls of Ascertainment Biases in Genome Annotations—Computing Comparable Protein Domain Distributions in Eukarya. Malays. J. Fundam. Appl. Sci. 2014, 10, 64–73. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2011, 16, 321–357. [Google Scholar]
- Silla, C.N.; Freitas, A.A. A survey of hierarchical classification across different application domains. In Data Mining & Knowledge Discovery; Springer: New York, NY, USA, 2011; Volume 22, pp. 31–72. [Google Scholar]
- Ramírez-Corona, M.; Sucar, L.E.; Morales, E.F. Hierarchical multilabel classification based on path evaluation. Int. J. Approx. Reason. 2016, 68, 179–193. [Google Scholar] [CrossRef]
- Dendamrongvit, S.; Vateekul, P.; Kubat, M. Irrelevant attributes and imbalanced classes in multi-label text-categorization domains. Intell. Data Anal. 2011, 15, 843–859. [Google Scholar]
- Sun, A.; Lim, E.P.; Liu, Y. On strategies for imbalanced text classification using SVM: A comparative study. Decis. Support Syst. 2009, 48, 191–201. [Google Scholar] [CrossRef]
- Lin, H.T.; Lin, C.J.; Weng, R.C. A note on Platt’s probabilistic outputs for support vector machines. Mach. Learn. 2007, 68, 267–276. [Google Scholar] [CrossRef]
- Valentini, G. Hierarchical ensemble methods for protein function prediction. Int. Sch. Res. Not. 2014, 2014, 1–34. [Google Scholar] [CrossRef] [PubMed]
- Troyanskaya, O.G.; Dolinski, K.; Owen, A.B.; Altman, R.B.; Botstein, D. A Bayesian framework for combining heterogeneous data sources for gene function prediction (in Saccharomyces cerevisiae). Proc. Natl. Acad. Sci. USA 2003, 100, 8348–8353. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Liu, C.; Bürge, L.; Ko, K.D.; Southerland, W. Predicting protein-protein interactions using full Bayesian network. In Proceedings of the IEEE International Conference on Bioinformatics and Biomedicine Workshops, Philadelphia, PA, USA, 4–7 October 2012; pp. 544–550. [Google Scholar]
- Clare, A.; King, R.D. Predicting gene function in Saccharomyces cerevisiae. Bioinformatics 2003, 19 (Suppl. S2), ii42–ii49. [Google Scholar] [CrossRef] [PubMed]
- Bi, W.; Kwok, J.T. MultiLabel Classification on Tree- and DAG-Structured Hierarchies. In Proceedings of the 28th International Conference on International Conference on Machine Learning, Bellevue, WA, USA, 28 June–2 July 2011; pp. 17–24. [Google Scholar]
- Liangxi, C.; Hongfei, L.; Yuncui, H.; Jian, W.; Zhihao, Y. Gene function prediction based on the Gene Ontology hierarchical structure. PLoS ONE 2013, 9, 896–906. [Google Scholar]
- Radivojac, P.; Clark, W.T.; Oron, T.R.; Schnoes, A.M.; Wittkop, T.; Sokolov, A.; Graim, K.; Funk, C.; Verspoor, K.; Ben-Hur, A. A large-scale evaluation of computational protein function prediction. Nat. Methods 2013, 10, 221–227. [Google Scholar] [CrossRef] [PubMed]
- Aleksovski, D.; Kocev, D.; Dzeroski, S. Evaluation of distance measures for hierarchical multilabel classification in functional genomics. In Proceedings of the 1st Workshop on Learning from Mulit-Label Data (MLD), Bled, Slovenia, 7 September 2009; pp. 5–16. [Google Scholar]
- Chen, Y.; Li, Z.; Hu, X.; Liu, J. Hierarchical Classification with Dynamic-Threshold SVM Ensemble for Gene Function Prediction. In Proceedings of the 6th International Conference on Advanced Data Mining and Applications (ADMA), Chongqing, China, 19–21 November 2010; pp. 336–347. [Google Scholar]
- Vateekul, P.; Kubat, M.; Sarinnapakorn, K. Hierarchical multi-label classification with SVMs: A case study in gene function prediction. Intell. Data Anal. 2014, 18, 717–738. [Google Scholar]
- Alaydie, N.; Reddy, C.K.; Fotouhi, F. Exploiting Label Dependency for Hierarchical Multi-label Classification. In Proceedings of the 16th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining, Kuala Lumpur, Malaysia, 29 May–1 June 2012; pp. 294–305. [Google Scholar]
| Data Set | Attributes | Training Instances | Testing Instances |
|---|---|---|---|
| D1 Cellcycle | 77 | 2290 | 1202 |
| D2 eisen | 79 | 2252 | 1182 |
| D3 derisi | 63 | 1537 | 817 |
| D4 gasch1 | 173 | 2294 | 1205 |
| D5 gasch2 | 52 | 1301 | 1212 |
| D6 church | 27 | 2289 | 1202 |
| D7 spo | 80 | 2354 | 1183 |
| D8 seq | 478 | 2321 | 1225 |
| GO ID | Original | Original | Original | Improved | Improved | Improved |
|---|---|---|---|---|---|---|
| GO:0065007 | NaN | 0 | NaN | 0.408 | 0.454 | 0.430 |
| GO:0016043 | NaN | 0 | NaN | 0.486 | 0.539 | 0.511 |
| GO:0044710 | 0.577 | 0.121 | 0.206 | 0.478 | 0.433 | 0.455 |
| GO:0006996 | NaN | 0 | NaN | 0.358 | 0.775 | 0.490 |
| GO:0044249 | 0.552 | 0.181 | 0.272 | 0.440 | 0.630 | 0.518 |
| GO:0046483 | NaN | 0 | NaN | 0.437 | 0.699 | 0.538 |
| GO:1901360 | 0.750 | 0.013 | 0.025 | 0.448 | 0.734 | 0.557 |
| GO:1901564 | 0.591 | 0.050 | 0.092 | 0.373 | 0.431 | 0.400 |
| GO:0009059 | 0.472 | 0.045 | 0.082 | 0.384 | 0.451 | 0.415 |
| GO:0019538 | 0.520 | 0.040 | 0.073 | 0.352 | 0.489 | 0.410 |
| GO:0044271 | 0.500 | 0.011 | 0.021 | 0.344 | 0.603 | 0.438 |
| GO:0034645 | 0.472 | 0.045 | 0.082 | 0.364 | 0.596 | 0.452 |
| Dataset | Method | |||
|---|---|---|---|---|
| D1 | TPR | 0.348 | 0.518 | 0.416 |
| D1 | CLUS-HMC | 0.449 | 0.306 | 0.364 |
| D1 | Proposed | 0.333 | 0.627 | 0.435 |
| D2 | TPR | 0.360 | 0.397 | 0.377 |
| D2 | CLUS-HMC | 0.402 | 0.335 | 0.365 |
| D2 | Proposed | 0.331 | 0.533 | 0.408 |
| D3 | TPR | 0.434 | 0.515 | 0.471 |
| D3 | CLUS-HMC | 0.476 | 0.387 | 0.427 |
| D3 | Proposed | 0.396 | 0.663 | 0.496 |
| D4 | TPR | 0.385 | 0.477 | 0.426 |
| D4 | CLUS-HMC | 0.453 | 0.355 | 0.398 |
| D4 | Proposed | 0.358 | 0.585 | 0.444 |
| D5 | TPR | 0.359 | 0.519 | 0.425 |
| D5 | CLUS-HMC | 0.442 | 0.322 | 0.373 |
| D5 | Proposed | 0.333 | 0.623 | 0.434 |
| D6 | TPR | 0.331 | 0.483 | 0.393 |
| D6 | CLUS-HMC | 0.487 | 0.270 | 0.348 |
| D6 | Proposed | 0.314 | 0.606 | 0.413 |
| D7 | TPR | 0.366 | 0.423 | 0.393 |
| D7 | CLUS-HMC | 0.418 | 0.331 | 0.369 |
| D7 | Proposed | 0.339 | 0.541 | 0.417 |
| D8 | TPR | 0.388 | 0.509 | 0.441 |
| D8 | CLUS-HMC | 0.444 | 0.390 | 0.415 |
| D8 | Proposed | 0.372 | 0.577 | 0.454 |
| Dataset | Method | |||
|---|---|---|---|---|
| D1 | TPR | 0.366 | 0.548 | 0.380 |
| D1 | CLUS-HMC | 0.514 | 0.362 | 0.352 |
| D1 | Proposed | 0.347 | 0.633 | 0.405 |
| D2 | TPR | 0.385 | 0.441 | 0.346 |
| D2 | CLUS-HMC | 0.468 | 0.392 | 0.347 |
| D2 | Proposed | 0.347 | 0.598 | 0.385 |
| D3 | TPR | 0.445 | 0.544 | 0.432 |
| D3 | CLUS-HMC | 0.525 | 0.423 | 0.396 |
| D3 | Proposed | 0.419 | 0.643 | 0.457 |
| D4 | TPR | 0.406 | 0.514 | 0.389 |
| D4 | CLUS-HMC | 0.518 | 0.408 | 0.379 |
| D4 | Proposed | 0.368 | 0.625 | 0.413 |
| D5 | TPR | 0.370 | 0.544 | 0.381 |
| D5 | CLUS-HMC | 0.505 | 0.379 | 0.360 |
| D5 | Proposed | 0.344 | 0.665 | 0.403 |
| D6 | TPR | 0.360 | 0.521 | 0.365 |
| D6 | CLUS-HMC | 0.554 | 0.335 | 0.350 |
| D6 | Proposed | 0.324 | 0.674 | 0.390 |
| D7 | TPR | 0.373 | 0.491 | 0.371 |
| D7 | CLUS-HMC | 0.481 | 0.379 | 0.344 |
| D7 | Proposed | 0.344 | 0.629 | 0.397 |
| D8 | TPR | 0.393 | 0.536 | 0.400 |
| D8 | CLUS-HMC | 0.501 | 0.438 | 0.395 |
| D8 | Proposed | 0.371 | 0.626 | 0.418 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, S.; Fu, P.; Zheng, W. A Hierarchical Multi-Label Classification Algorithm for Gene Function Prediction. Algorithms 2017, 10, 138. https://doi.org/10.3390/a10040138
Feng S, Fu P, Zheng W. A Hierarchical Multi-Label Classification Algorithm for Gene Function Prediction. Algorithms. 2017; 10(4):138. https://doi.org/10.3390/a10040138
Chicago/Turabian StyleFeng, Shou, Ping Fu, and Wenbin Zheng. 2017. "A Hierarchical Multi-Label Classification Algorithm for Gene Function Prediction" Algorithms 10, no. 4: 138. https://doi.org/10.3390/a10040138
APA StyleFeng, S., Fu, P., & Zheng, W. (2017). A Hierarchical Multi-Label Classification Algorithm for Gene Function Prediction. Algorithms, 10(4), 138. https://doi.org/10.3390/a10040138




