Abstract
The ever-increasing air traffic demand in China has brought huge pressure on the planning and management of, and investment in, air terminals as well as airline companies. In this context, accurate and adequate short-term air traffic forecasting is essential for the operations of those entities. In consideration of such a problem, a hybrid air traffic forecasting model based on empirical mode decomposition (EMD) and seasonal auto regressive integrated moving average (SARIMA) has been proposed in this paper. The model proposed decomposes the original time series into components at first, and models each component with the SARIMA forecasting model, then integrates all the models together to form the final combined forecast result. By using the monthly air cargo and passenger flow data from the years 2006 to 2014 available at the official website of the Civil Aviation Administration of China (CAAC), the effectiveness in forecasting of the model proposed has been demonstrated, and by a horizontal performance comparison between several other widely used forecasting models, the advantage of the proposed model has also been proved.
1. Introduction
1.1. Background
The rapid economic growth in China nowadays has already brought faster travel growth in its civil aviation market, and the airline industry in China has also been experiencing an annual growth rate of about 6% in passenger as well as cargo load during the past ten years or so [1]. It is of no doubt that air traffic forecasting plays an important role in not only the planning and the management of an airline, but in related service and hardware investment issues as well [2,3,4], as enormous pressure to provide better services has been strengthened from the ever-increasing amount of cargo and number of passengers, and most of the air terminals have already been operating at a high proportion: above 80% of their capacity [1]. Accurate short-term air traffic forecasting would help air terminals and airline companies to achieve better service quality by helping to optimize the allocation of limited resources [5]; however, giving such accurate forecasting is not as easy as might be thought, for air traffic data is a set of large-scale, multi-dimensional, nonlinear, and non-normal distribution time series data, and it not only has its own time-dependent changing tendencies, but also has some seasonal periodicity [2]. Therefore, traditional forecasting models based on a single mathematical theory based on statistics or artificial intelligence cannot realize the accuracy and adequacy of air traffic forecasting, so a novel forecasting model is strongly required for such a thorny issue [6].
Until now, modeling works for the object of forecasting in various industries, including air traffic, have already experienced remarkable progress in development. Single statistical theory-based time series modeling happened to be the earliest approach for forecasting issues [7]; then came the single artificial intelligence (AI) algorithm based on modeling reports [8,9]; later on, attempts had been made to apply hybrid theory-based models in various areas that require forecasting [10]. As far as the specific models built for air traffic forecasting are concerned, reports can be found either in an impact factors analysis or in the theory research on forecasting itself [11,12]. Hybrid theory-based models have already been applied in air passenger flow forecasting a little bit, and they have already been proved to have better performance when comparing them with those models supported by only a single mathematical theory [6]; however, reports on finding out the most suitable modeling approach for air traffic forecasting still can hardly be found. It is of no doubt that a proper demonstration of all the possible models as well as the discovery of the optimal one which applies to air traffic forecasting requires further study and discussion.
1.2. Objective of Paper
Considering that there is still much study that is required to be done in air traffic forecasting, and that the hybrid theory-based model may have better performance in prediction issues according to those modeling approaches which have already been done, in this paper, the first effort to forecast the air traffic of China’s civil aviation is attempted with the aid of empirical mode decomposition (EMD) and seasonal autoregressive integrated moving average (SARIMA). To be specific, EMD has its advantage in data analysis, and is highly adaptive, efficient, capable of dealing with nonlinear, non-stationary processes, and preserving the physical meanings of the original data [13], for the basis function in EMD can be directly derived from the data input; while autoregressive integrated moving average (ARIMA) is an integrated version of autoregressive moving average (ARMA), has a more accurate performance in short-term forecasting within time series models [14], and SARIMA can even capture the periodicity that is typical for the air passenger flow data process. Therefore, the hybrid modeling approach based on EMD–SARIMA proposed in this paper is supposed to solve the specific problems which might appear in air traffic forecasting. Moreover, a horizontal performance comparison of several hybrid theory-based forecasting models has also been made in this paper by referencing the cargo and passenger flow data from the years 2006 to 2014 available at the official website of the Civil Aviation Administration of China (CAAC). Thus, the problem of the most suitable modeling approach for short-term air traffic forecasting has been solved on one hand, and the advantage of the EMD–SARIMA-based model has been demonstrated on the other hand.
1.3. Paper Organization
The remainder of this paper is organized as follows: a comprehensive literature review will be done from three perspectives in Part 2: single mathematical theory-based forecasting models, hybrid theory-based forecasting models, and the models specific to air traffic forecasting. Then, the methodology based on EMD–SARIMA that has been employed in this paper will be presented in Part 3, which is also threefold: at first, the original time series data is decomposed into components called intrinsic mode functions (IMFs); then, each component is modeled with the SARIMA forecasting model; finally, all of the results are integrated together so as to form a combined forecasting result. After that, the air cargo and passenger flow data which is used in this paper to do forecasting from the official website of the CAAC is described in detail in Part 4, as well as how the components have been decomposed from the original time series data in the experimental setup. Later, in Part 5, the case studies made based on the China civil aviation data between the years 2006 and 2014 are discussed, including how the hybrid EMD–SARIMA theory is applied in air passenger flow forecasting, and how its performance compares with other forecasting models. Last but not least, the summary, conclusions, and comments upon future work are made in Part 6.
2. Literature Review
As has been discussed above, the forecasting models have already made remarkable progress, from statistical models to AI-based models, and from single mathematical theory-based models to hybrid theory-based ones. Moreover, forecasting models have already been employed in various areas of industry. In this part, the pros and cons of all of these forecasting models will be reviewed in a comprehensive way first, then the models which are applied specifically in the air passenger flow forecast process in the available literature will also be reviewed, and the problems in a related research area will be pointed out.
2.1. On Single Theory-Based Forecasting Models
Single theory-based forecasting models have experienced a development process from a statistics-based model stage to an AI-based model stage. The traditional time series models are statistics based models, and the famous work done by Box and Jenkins [7] has built the fundamental basis of almost all related works in this area; later on, the relatively sophisticated Holt–Winters forecasting procedure has been proposed by Chatfield [15]. For those forecasting models which have been put into the transportation industry in an early stage, the ARIMA-based time series model is the most representative one to predict the traffic volume, and the performance analysis has shown that the use of a subset of the ARIMA model can help to enhance the accuracy of short-term forecast results [16]; based on ARIMA, a Kohonen self-organized map-aided ARIMA, with the name KARIMA, was then proposed by Van Der Voort et al. [17]. It has broken the ARIMA model into two stages, by firstly clustering the time series samples and aggregating them using the Kohonen map, and then building the ARIMA model upon those clusters. The KARIMA model has shown improvement over the ARIMA based model; moreover, Kamarianakis and Prastacos [18,19] have proposed two different models, which have been called vector ARMA (VARMA) and space-time ARIMA (STARIMA). Both of these two models have been applied in traffic flow forecasting. VARMA has employed parameter matrices to model dependence relations among different time series so as to capture a linear relationship between time series, whereas STARIMA has been proved to be more suitable for dealing with the situation where only fewer parameters are available in large-scale short-term traffic flow forecasting when compared with the ARIMA and VARMA models. The SARIMA model has been proposed by Williams et al. [20] to try to capture the periodical features of the traffic flow on urban freeways.
The AI-based models have mostly been proposed during the past 20 years. Smith and Dougherty [9] happened to be a group of researchers who applied an artificial neural network (ANN) in a short-term traffic flow forecast at the earliest stage of related research. With the development of various types of AI, the applicability of an ANN for short-term forecasting has then been questioned by Watson et al. [21], who have pointed out that a neural network in a forecasting process can be seen as a “black box” with a hidden structure that cannot be approached easily and deeply by model builders. Apart from an ANN, many other AI-based theories have also been employed in short-term forecast model building. Su et al. [22] have proposed a support vector machine (SVM)-based short-term traffic flow prediction model, whereas Castro-Neto et al. [23] have developed an online short-term traffic flow prediction tool based on an SVM and have investigated its performance in both typical and atypical traffic conditions. Fuzzy logic has also been employed in short-term forecast modeling by Zhang and Ye [24], and so has the Kalman filter theory, which has been employed in estimating real-time freeway traffic conditions by Okutani and Stephanedes [8].
2.2. On Hybrid Theory-Based Forecasting Models
Even if the single theory-based forecasting models can achieve great closeness to the actual short-term situation, many flaws still exist in those models. Reliable prediction results can only be assured under specific circumstances for statistics-based models, which means that they have poor adaptabilities in dealing with nonlinear or irregular time series data; and for the AI-based models, most of them are a bit too sensitive in parameter selection and are not capable of properly dealingwith the problem of data dimensionality. In this context, hybrid theory-based models have been proposed based on the combination of different basic theories in not only short-term traffic flow forecasts, but forecasts in other industries as well. During recent years, Vlahogianni et al. [10] have proposed an approach based on the genetic algorithm (GA), which has been coupled with ANN for short-term traffic flow prediction; Zhu and Zhang [25] have proposed a hybrid layered system, which has been made up of KARIMA with several neural networks; and Monjoly et al. [26] have also proposed a global solar radiation prediction method based on multiscale decomposition methods. Considering the advantages of EMD which have been already discussed in Section 1.2, many hybrid approaches have been proposed with EMD as an irreplaceable choice, and have achieved relatively high accuracy in the forecast results. Liu et al. [27] have employed an EMD–ANN approach in forecasting wind speed, whereas Wei and Chen [28] have also used such a fusion model of EMD and ANN to make predictions on metro passenger flow. EMD–ARIMA is also a popular hybrid theory-based model, which has been used by Okolobah and Ismail [29] as well as Liu et al. [13] to forecast the peak load in a power supply system and traffic speed on a certain road section, respectively. Bao et al. [30] have even made an improvement on EMD and proposed an ensemble EMD (EEMD) data analysis approach, and have employed EEMD–SVM to a short-term air passenger flow forecast issue.
2.3. On Specific Models for Air Traffic Forecasting
When it comes to the very issue of short-term air traffic forecasting, passenger flow has been covered most in the literature as the passenger service may reflect the service quality of air terminals or airline companies in a more direct way. To be specific, research on an impact factors analysis has come up first; then likewise, the single theory-based forecasting model has been widely used in air traffic forecasting; later on, a comprehensive analysis has been made on all of the possible forecasting models; and finally, the hybrid theory-based forecasting model has also been proposed to address such an issue during recent years. The present available literature on air traffic forecasting can be summarizedas in Figure 1.
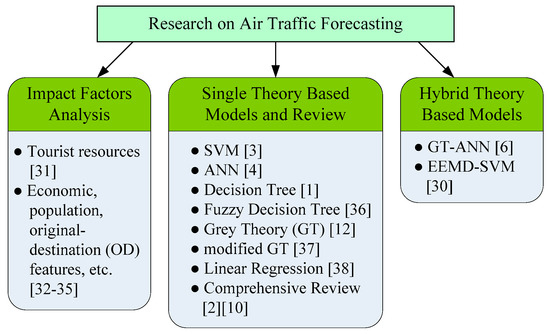
Figure 1.
Summary of research on air traffic forecasting. SVM: support vector machine; ANN: artificial neural network; EEMD: ensemble empirical mode decomposition.
To be specific, Ashford [31] is among the earliest researchers who have pointed out the basic impact factors on air passenger flow, which are economical, technical, and operational ones; later on, Bhadra [32] has analyzed the local original-destination (OD) features and found their impact on air passenger flow; Hsiao and Hansen [33] have added the competition between airlines into consideration; while Bhadra et al. [34] have utilized the impact from those various factors to estimate the flight schedules; and, when it comes to the area which has many tourist places of interest, Fang [35] have made a deep analysis in those impact factors which may just affect the tourist passenger flow.
Apart from the impact factor analysis, forecasting models have also been built based on different single mathematical theories. Yan [3] has employed an SVM, Tseytlina [4] has used an ANN, Laik et al. [1] have applied a decision tree approach, while Hsu and Wen [12] have tried to use Grey theory (GT) to predict short-term air passenger flow.Based on some of the modeling studies above, Cheng et al. [36] have introduced fuzzy theory into the decision tree approach and have proposed a fuzzy decision tree so as to build a more accurate model for forecasting; Benitez et al. [37] have made some modifications to the GT model and have helped the modified GT model to realize an accurate forecast where fewer data areavailable. Chang [38] has not only employed linear regression in a short-term air passenger flow forecast, but has compared its performance with another model called the classification and regression tree as well. As many models have been built, Fildes et al. [2] and Vlahogianni et al. [10] have made a comprehensive review of most single theory-based air passenger flow forecasting models.
Hybrid theory-based forecasting models have only attracted the attention of researchers in air traffic forecasting during recent years, and not so much related work has yet been reported. Zhang and Zhang [6] happen to be the first group of researchers to employ a hybrid model of ANN and GT for air traffic passenger volume forecasting; while as mentioned above, Bao et al. [30] have tried to use a hybrid EEMD–SVM forecasting model, and have proved that it can outperform the model only based on an SVM. It should be pointed out that even if the hybrid models have already been proved to be better than single theory-based ones, a horizontal performance comparison of the available hybrid theory-based short-term air passenger flow forecasting models has not been reported by researchers at present.
3. The Hybrid EMD–SARIMA Forecasting Framework
A hybrid method of EMD–SARIMA for air traffic forecasting is proposed here. As discussed in Section 1, in this methodology, the EMD method is used first to decompose the original air cargo and passenger series into independent components called IMFs. The main purpose of decomposition is to differentiate the modes based on different characters and improve the prediction accuracy. Utilizing the EMD method, the original air cargo and passenger series that is nonlinear and non-stationary are decomposed into a finite number of IMFs. After the decomposition step, each IMF is modeled by a SARIMA model and can be forecasted more accurately. Finally, the predictions from the SARIMA model are aggregated togenerate a forecasting result from the hybrid EMD–SARIMA model. A detailed procedure of the EMD–SARIMA modeling framework is shown in Figure 2.
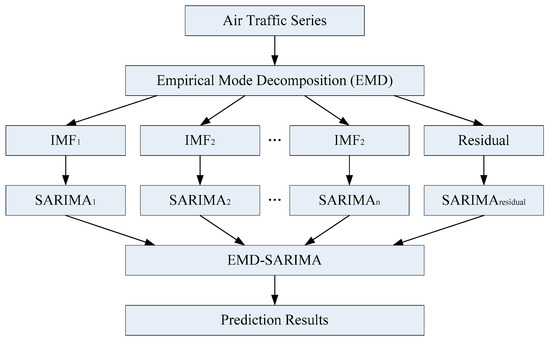
Figure 2.
The hybrid EMD–SARIMA modeling framework. IMF: intrinsic mode function; SARIMA: seasonal autoregressive integrated moving average.
3.1. Stage 1: EMD Modeling
The EMD model was first proposed by Huang et al. [39] in 1998. As a novel method of decomposing a signalinto intrinsic mode functions (IMFs), it is extremely useful for analyzing non-stationary and non-linear time series, and has aroused a lot of attention from both industry and academia. An IMF is an independent componentthat has variable amplitude and frequency, and it is acquired from a sifting process of the original time series. The sifting process is an iterative one, and is utilized to extract the different IMF components. The procedures of the sifting process can be summarized as follows:
- (I)
- Identify all the local extrema (i.e., local maxima and minima) in the original time series x(t).
- (II)
- Interpolate all the local maxima (minima) by a cubic spline from the upper envelope emax(t) and lower envelope emin(t).
- (III)
- Calculate the mean of the envelope m(t) from the upper and lower envelope.
- (IV)
- Extract the mean of the envelope from the original signal to obtain a new signal h(t).
- (V)
- Check whether h(t) is an IMF: (1) If h(t) is an IMF then set d(t) = h(t) and replace x(t) with the residual r(t) = x(t) − d(t); (2) if h(t) is not an IMF, replace x(t) with z(t) then repeat the steps from II to IV until the following stopping criterion is met in the iterative process. As has been suggested by Huang et al. in literature [39], a typical value of δ is between 0.2 and 0.3.
After this sifting process, the original time series can be written as Equation (4) shows, from where r(t) is the residual after the IMFs are derived, and di(t) is the IMF obtained from EMD:
The IMF is defined as a component that satisfies the following conditions: (1) the number of extrema and the number of zero-crossings must either be equal or differ at most by one; (2) at any point, the mean value of the envelope determined by the local maxima and the envelope determined by the local minima is zero.
3.2. Stage 2: SARIMA Modeling
The SARIMA model has been used successfully in modeling and forecasting time series with seasonality [40]. If there is seasonality in the time series, the time series can be modeled as
where Yt is a stationary process. The seasonal component is st = st−h where h is the length of the series and
If the series is differenced at lag h, the seasonal effect can be removed by
which gives
where is the lag operator. Based on this fact, the SARIMA model can be written as
where
and
The seasonal difference is defined as the difference between a value and a value with lag that is a multiple of h. For monthly data, the seasonal difference is
To generalize, there are four steps for identifying a SARIMA model:
- (I)
- Test the stationarity of the time series through a unit root test and examine its power spectrum for trend and seasonality.
- (II)
- Do necessary differencing. If there is seasonality and no trend, take a difference of lag h; if there is both a trend and seasonality, do a seasonal difference to the time series and evaluate the trend. If a trend still exists, take the first difference.
- (III)
- Examine the autocorrelation function (ACF) and partial autocorrelation function (PACF) of the differenced time series.
- (IV)
- Estimate the model and examine the residuals, and compare the Akaike information criterion (AIC) and Bayesian information criterion (BIC) to identify a best model if multiple models are tried.
4. Experimental Setup
4.1. Data Description
The data used in this paper is gathered from the official website of the Civil Aviation Administration of China (CAAC), with monthly cargo and passenger flow data, both domestic and international, ranging from January 2006 to July 2014, 103 months in total. The original time series data is plotted in Figure 3.
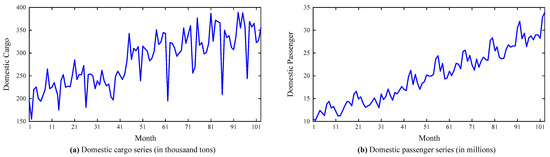
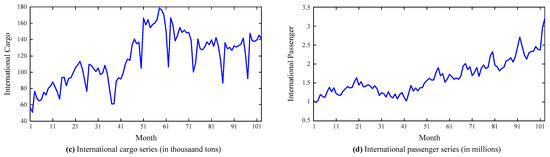
Figure 3.
Original time series.
4.2. EMD–SARIMA Modeling
Following the steps described in Section 3.1, the original time series are decomposed into components (IMF) and a residual. The four IMFs and one residual of an original domestic cargo series are plotted below in Figure 4. The short-period (or high-frequency) components are extracted in IMF 1 and IMF 2, and the long-period (or low-frequency) components are given in IMF3 and IMF 4. The last component is the residue which shows the trend of the original time series.
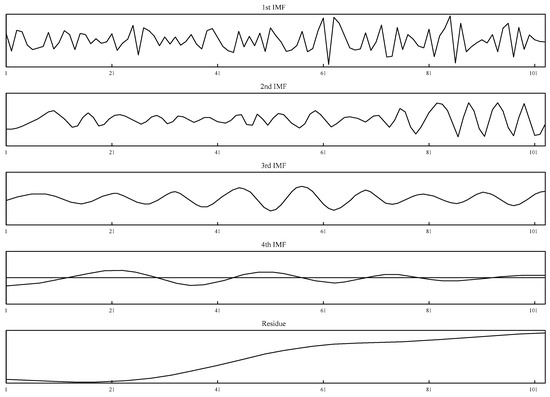
Figure 4.
IMFs and residual of original domestic cargo series.
Also, following the steps described in Section 3.2, the IMFs and residual are each modeled with the SARIMA model. The EMD–SARIMA forecasting results are compared with the SARIMA model, the Holt–Winters model, and a naive model. The Holt–Winters model is another widely used time series forecasting model as is discussed in the literature review, and for the naive model, xt+1 = xt is set to serve as a basic benchmarking model to evaluate the overall performance of different models.
After the forecasting results of each model are obtained, two different measures have been taken to compare the performance of the models: the Mean Absolute Error (MAE) and the Mean Absolute Percentage Error (MAPE), which are calculated as follows:
5. Result Analysis
5.1. Domestic Cargo
The forecasting results and comparisons with other models for domestic cargo flow are presented in Table 1 and Figure 5. From the results, it can be concluded that:

Table 1.
Comparison of different model performances on six- and twelve-month horizons for domestic cargo.
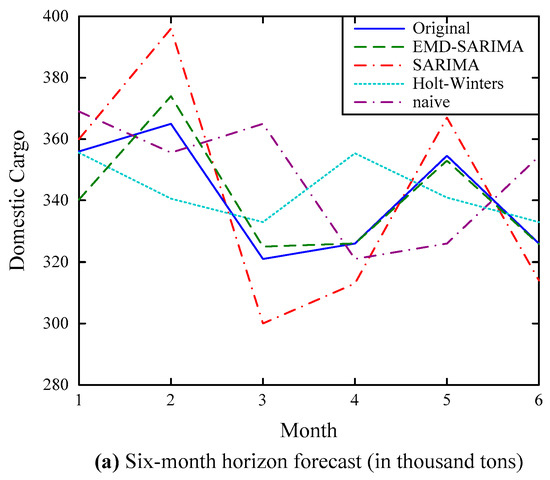
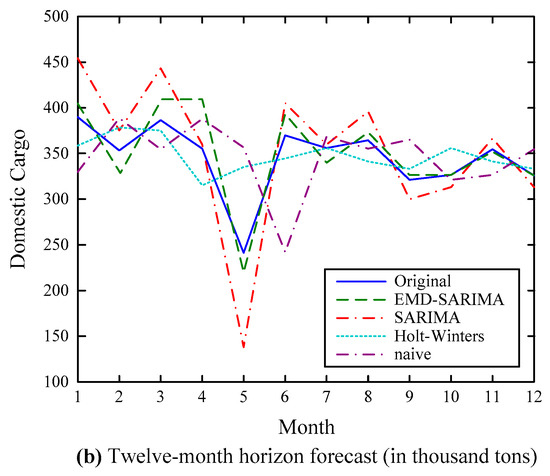
Figure 5.
Forecasting results of the domestic cargo series.
- (1)
- The performance of the EMD–SARIMA model is superiorto that of the SARIMA model, the Holt–Winters model, and the naive model, especially for the local maximum and minimum values;
- (2)
- The performance of the Holt–Winters model is the second best, and the performance is close to the SARIMA model; this is consistent with previous research, which claimed that the Holt–Winters model and the SARIMA model are comparable based on situations [41];
- (3)
- The hybrid model improves the forecasting accuracy of the traditional SARIMA model; the MAPEs of the EMD–SARIMA model for the six-month and twelve-month forecasting horizons are 1.42% and 4.64%, respectively, compared with the MAPEs of the SARIMA model for the six-month and twelve-month forecasting horizons, which are 4.62% and 9.94%, respectively;
- (4)
- By comparing with other models, the EMD–SARIMA model forecasts with better accuracy consistently regardless of whether it is single- or multi-step forecasting.
5.2. Domestic Passenger
The forecasting results and comparisons with other models for domestic passenger flow are presented in Table 2 and Figure 6. From the results, it can be concluded that:

Table 2.
Comparison of different model performances on six- and twelve-month horizons for domestic passengers.
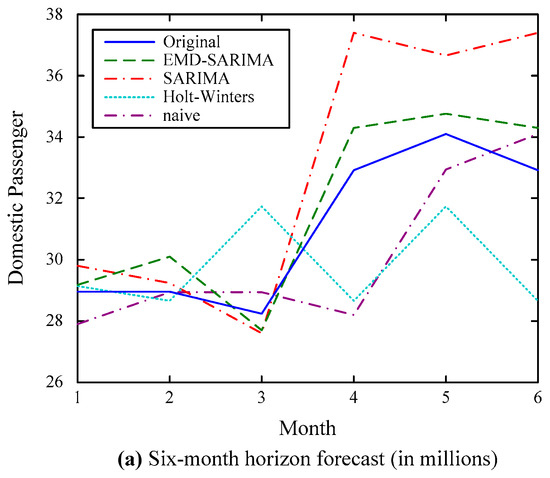
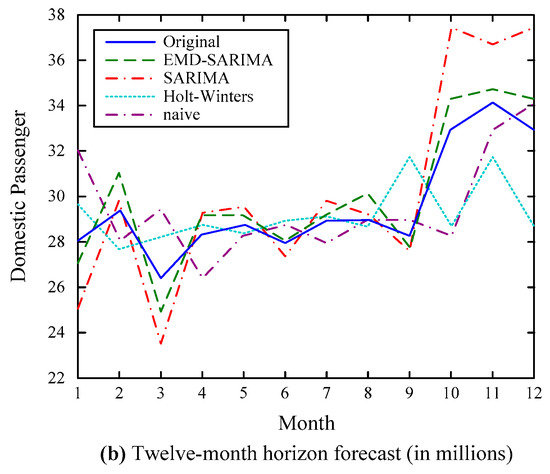
Figure 6.
Forecasting results of the domestic passenger series.
- (1)
- The EMD–SARIMA model forecasts with the best accuracy, followed by the SARIMA model, the Holt–Winters model, and the naive model, especially for the local maximum and minimum values;
- (2)
- Due to greater seasonality of the domestic passenger data, the performance of the SARIMA model is the second best, superior to the Holt–Winters model. This is again consistent with previous research claiming that the Holt–Winters model and the SARIMA model are comparable based on different time series [41];
- (3)
- Again, the EMD–SARIMA model forecasts with better accuracy consistently regardless of whether it is single- or multi-step forecasting.
5.3. International Cargo
The forecasting results and comparisons with other models for international cargo flow are presented in Table 3 and Figure 7. From the results, it can be concluded that:

Table 3.
Comparison of different model performances on six and twelve-month horizon for international cargo.
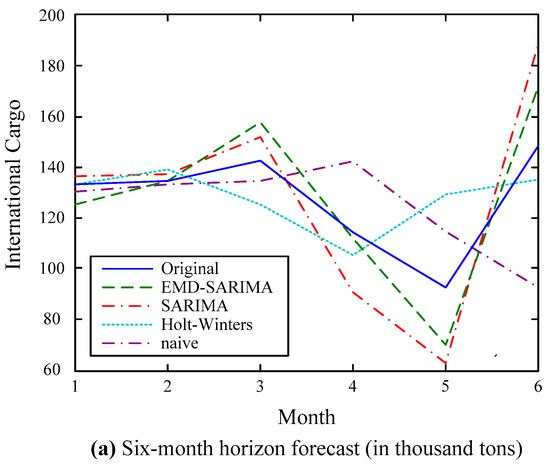
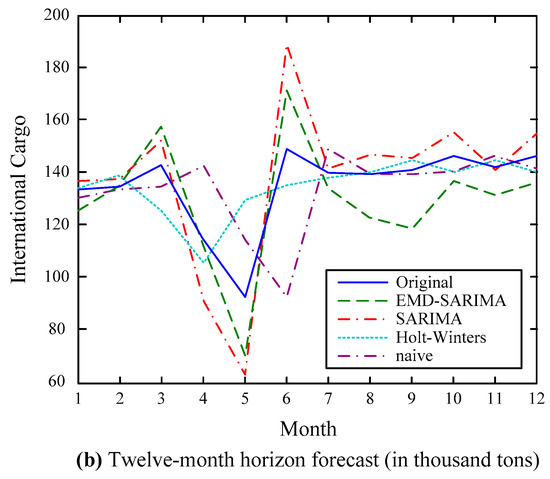
Figure 7.
Forecasting results of the international cargo series.
- (1)
- Consistent with the domestic cargo cases, the EMD–SARIMA model forecasts with the best accuracy, followed by the Holt–Winters model, the SARIMA model, and the naive model, especially for the local maximum and minimum values;
- (2)
- Due to greater variability of the international cargo data, the performances of the forecasting models generate larger prediction errors compared with the domestic cargo series;
- (3)
- Again, the EMD–SARIMA model forecasts with better accuracy consistently regardless of whether it is single- or multi-step forecasting.
5.4. International Passenger
The forecasting results and comparisons with other models for international passenger flow are presented in Table 4 and Figure 8. From the results, it can be concluded that:

Table 4.
Comparison of different model performances on six- and twelve-month horizons for international passengers.
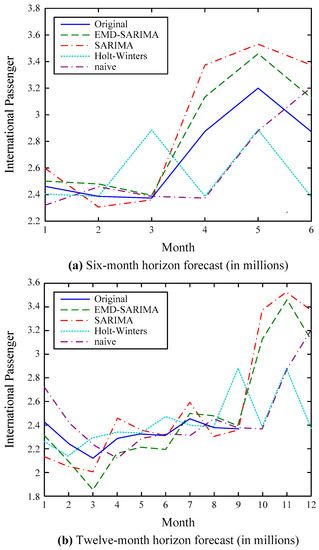
Figure 8.
Forecasting results of the international passenger series.
- (1)
- Consistent with the domestic passenger cases, the EMD–SARIMA model forecasts with the best accuracy, followed by the SARIMA model, the Holt–Winters model, and the naive model, especially for the local maximum and minimum values;
- (2)
- Due to greater variability of the international passenger data, the performances of the forecasting models generate larger prediction errors compared with the domestic passenger series;
- (3)
- Again, the EMD–SARIMA model forecasts with better accuracy consistently regardless of whether it is single- or multi-step forecasting.
Authors should discuss the results and how they can be interpreted in perspective of previous studies and of the working hypotheses. The findings and their implications should be discussed in the broadest context possible. Future research directions may also be highlighted.
6. Conclusions and Future Work
A novel hybrid forecasting framework of Empirical Mode Decomposition and Seasonal Autoregressive Integrated Moving Average (EMD–SARIMA) has been proposed in this paper. The forecasting framework is tested using the data from the year 2006 to 2014 from the official website of the Civil Aviation Administration of China (CAAC) and is compared with other widely used forecasting models (SARIMA, Holt–Winters, and a naive model) in four different cases: domestic cargo, domestic passenger, international cargo, and international passenger, and the results show that the EMD–SARIMA framework can improve the forecasting accuracy to a great level and that the forecasting result is consistent in the four different cases as well as for different forecasting steps.
In the future, the robustness of the EMD–SARIMA framework will be discussed by testing it with data where there is more seasonality (or less seasonality); also, the data sensitivity of the framework will also be discussed by testing it with more data (or less data); last but not least, the comparison of this framework to AI-based models will also be done so as to examine the performance of forecasting.
Acknowledgments
This work is supported by National Key Research and Development Program of the 13th Five-year Plan in China under Grant No. 2016YFB1200401, Fund of Shanghai Cooperative Center for Maglev and Rail Transit, and Fund of Shanghai Fei Tu You Science and Technology Company Limited under Grant No. 0217013.
Author Contributions
W. Nai and L. Liu proposed the idea of employing hybrid EMD-SARIMA algorithm into the air traffic flow forecasting; W. Nai conceived and designed the experiments; L. Liu collected the data, and set up as well as performed the experiments, S. Wang and D. Dong analyzed the data; Wei Nai and Lu Liu wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Laik, M.N.; Choy, M.; Sen, P. Predicting airline passenger load: A case study. In Proceedings of the 16th IEEE Conference on Business Informatics, Geneva, Switzerland, 14–17 July 2014; IEEE: New York, NY, USA, 2014. [Google Scholar]
- Fildes, R.; Wei, Y.; Ismail, S. Evaluating the forecasting performance of econometric models of air passenger traffic flows using multiple error measures. Int. J. Forecast. 2011, 27, 902–922. [Google Scholar] [CrossRef]
- Yan, K. Study on the forecast of air passenger flow based on SVM regression algorithm. In Proceedings of the 1st International Workshop on Database Technology and Applications, Wuhan, China, 25–26 April 2009; IEEE: New York, NY, USA, 2009. [Google Scholar]
- Tseytlina, T.O. Analysis of possibility of using neural network to forecast passenger traffic flows in Russia. Aviation 2007, 11, 28–35. [Google Scholar] [CrossRef]
- Smith, D.A.; Sherry, L. Decision support tool for predicting aircraft arrival rates from weather forecasts. In Proceedings of the Integrated Communications, Navigation and Surveillance Conference, Bethesda, MD, USA, 5–7 May 2008; IEEE: New York, NY, USA, 2008. [Google Scholar]
- Zhang, Y.; Zhang, J. A hybrid model of neural network and grey theory for air traffic passenger volume forecasting. Key Eng. Mater. 2010, 439–440, 818–822. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control, 4th ed.; John Wiley and Sons: Indianapolis, IN, USA, 2008; pp. 1–96. ISBN 9780470272848. [Google Scholar]
- Okutani, I.; Stephanedes, Y.J. Dynamic prediction of traffic volume through Kalman filtering theory. Transp. Res. Part B Methodol. 1984, 18, 1–11. [Google Scholar] [CrossRef]
- Smith, B.L.; Demetsky, M.J. Short-term traffic flow prediction: Neural network approach. Transp. Res. Rec. 1994, 1453, 98–104. [Google Scholar]
- Vlahogianni, E.I.; Karlaftis, M.G.; Golias, J.C. Optimized and meta-optimized neural networks for short-term traffic flow prediction: A genetic approach. Transp. Res. Part C Emerg. Technol. 2005, 13, 211–234. [Google Scholar] [CrossRef]
- Odoni, A.R. The importance of probability theory in the airport and air traffic control sectors. Int. J. Contin. Eng. Educ. Life-Long Learn. 1994, 4, 105–113. [Google Scholar] [CrossRef]
- Hsu, C.I.; Wen, Y.H. Improved grey prediction models for the trans-Pacific air passenger market. Transp. Plan. Technol. 1998, 22, 87–107. [Google Scholar] [CrossRef]
- Liu, L.; Wang, H.; Qian, Z.; Wei, H. EMD-ARIMA: A hybrid short-term traffic speed forecasting model. In Proceedings of the Transportation Research Board 93rd Annual Meeting, Washington, DC, USA, 12–16 January 2014; TRB: Washington, DC, USA, 2014. [Google Scholar]
- Lippi, M.; Bertini, M.; Frasconi, P. Short-term traffic flow forecasting: An experimental comparison of time-series analysis and supervised learning. IEEE Trans. Intell. Transp. Syst. 2013, 14, 871–882. [Google Scholar] [CrossRef]
- Chatfield, C. The Holt-Winters forecasting procedure. Appl. Stat. 1978, 27, 264–279. [Google Scholar] [CrossRef]
- Lee, S.; Fambro, D.B. Application of subset autoregressive integrated moving average model for short-term freeway traffic volume forecasting. Transp. Res. Rec. 1999, 1678, 179–188. [Google Scholar] [CrossRef]
- Van Der Voort, M.; Dougherty, M.; Watson, S. Combining Kohonen maps with ARIMA time series models to forecast traffic flow. Transp. Res. Part C Emerg. Technol. 1996, 4, 307–318. [Google Scholar] [CrossRef]
- Kamarianakis, Y.; Prastacos, P. Forecasting traffic flow conditions in an urban network: Comparison of multivariate and univariate approaches. Trans. Res. Rec. 2003, 1857, 74–84. [Google Scholar] [CrossRef]
- Kamarianakis, Y.; Prastacos, P. Space-time modeling of traffic flow. Comput. Geosci. 2005, 31, 119–133. [Google Scholar] [CrossRef]
- Williams, B.M.; Durvasula, P.K.; Donald, E.B. Urban freeway traffic flow prediction: Application of seasonal autoregressive integrated moving average and exponential smoothing models. Trans. Res. Rec. 1998, 1644, 131–144. [Google Scholar] [CrossRef]
- Watson, S.M.; Kirby, H.R.; Dougherty, M.S. Should we use neural networks or statistical models for short-term motorway traffic forecasting? Int. J. Forecast. 1997, 13, 43–50. [Google Scholar] [CrossRef]
- Su, H.; Zhang, L.; Yu, S. Short-term traffic flow prediction based on incremental support vector regression. In Proceedings of the International Conference on Natural Computation, Haikou, China, 24–27 August 2007; IEEE: New York, NY, USA, 2007. [Google Scholar]
- Castro-Neto, M.; Jeong, Y.S.; Jeong, M.K.; Han, L.D. Online-SVR for short-term traffic flow prediction under typical and atypical traffic conditions. Expert Syst. Appl. 2009, 36, 6164–6173. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, Z. Short-term traffic flow forecasting using fuzzy logic system methods. J. Intell. Transp. Syst. 2008, 12, 102–112. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, T. A layered neural network competitive algorithm for short-term traffic forecasting. In Proceedings of the International Conference on Computational Intelligence and Software Engineering, Wuhan, China, 11–13 December 2009; IEEE: New York, NY, USA, 2009. [Google Scholar]
- Monjoly, S.; Andre, M.; Calif, R.; Soubdhan, T. Hourly forecasting of global solar radiation based on multiscale decomposition methods: A hybrid approach. Energy 2016, 119, 288–298. [Google Scholar] [CrossRef]
- Liu, H.; Chen, C.; Tian, H.; Li, Y. A hybrid model for wind speed prediction using empirical mode decomposition and artificial neural networks. Renew. Energy 2012, 48, 545–556. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, M.C. Forecasting the short-term metro passenger flow with empirical mode decomposition and neural networks. Transp. Res. Part C Emerg. Technol. 2012, 21, 148–162. [Google Scholar] [CrossRef]
- Okolobah, V.; Ismail, A. Forecasting peak load demand by ARIMA and EMD method. Arch. Des. Sci. 2013, 66, 2–15. [Google Scholar]
- Bao, Y.; Xiong, T.; Hu, Z. Forecasting air passenger traffic by support vector machines with ensemble empirical mode decomposition and slop-based method. Discret. Dyn. Nat. Soc. 2012, 2012. [Google Scholar] [CrossRef]
- Ashford, N. Problems with long term air transport forecasting. J. Adv. Transp. 1985, 19, 101–114. [Google Scholar] [CrossRef]
- Bhadra, D. Demand for air travel in the United States: Bottom-up econometric estimation and implications for forecasts by origin-destination pairs. In Proceedings of the AIAA’S Aircraft Technology, Integration, and Operations, Los Angeles, CA, USA, 1–3 October 2002; AIAA: Reston, VA, USA, 2002. [Google Scholar]
- Hsiao, C.Y.; Hansen, M. Air transportation network flows: Equilibrium model. Transp. Res. Rec. 2005, 1915, 12–19. [Google Scholar] [CrossRef]
- Bhadra, D.; Gentry, J.; Hogan, B.; Wells, M. Future air traffic timetable estimator. J. Aircr. 2005, 42, 320–328. [Google Scholar] [CrossRef]
- Fang, G. Forecasting tourist aviation passenger flows in Sichuan province. In Proceedings of the International Conference on Transportation Engineering, Chengdu, China, 22–24 July 2007; ASCE: Reston, VA, USA, 2007. [Google Scholar]
- Cheng, S.; Mu, Q.; Zhang, H.; Zhang, Y. A fuzzy decision tree model for airport terminal departure passenger traffic forecasting. In Proceedings of the 14th COTA International Conference of Transportation Professionals, Changsha, China, 4–7 July 2014; ASCE: Reston, VA, USA, 2014. [Google Scholar]
- Benitez, C.; Bernardo, R.; Paredes, C.; Bernardo, R.; Lodewijks, G.; Nabais, J.L. Damp trend Grey Model forecasting method for airline industry. Expert Syst. Appl. 2013, 40, 4915–4921. [Google Scholar] [CrossRef]
- Chang, L.Y.; Lin, D.J. Analysis of international air passenger flows between two countries in the APEC region using non-parametric regression tree models. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, China, 17–19 March 2010; International Association of Engineers: Hong Kong, China, 2010. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Asteriou, D.; Hall, S.G. Applied Econometrics, 2nd ed.; Palgrave MacMillan: London, UK, 2011; pp. 1–434. ISBN 9780230271821. [Google Scholar]
- Gamberini, R.; Lolli, F.; Rimini, B.; Sgarbossa, F. Forecasting of sporadic demand patterns with seasonality and trend components: An empirical comparison between Holt-Winters and (S)ARIMA methods. Math. Probl. Eng. 2010, 2010. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).