Simulation Optimization of Search and Rescue in Disaster Relief Based on Distributed Auction Mechanism
Abstract
:1. Introduction
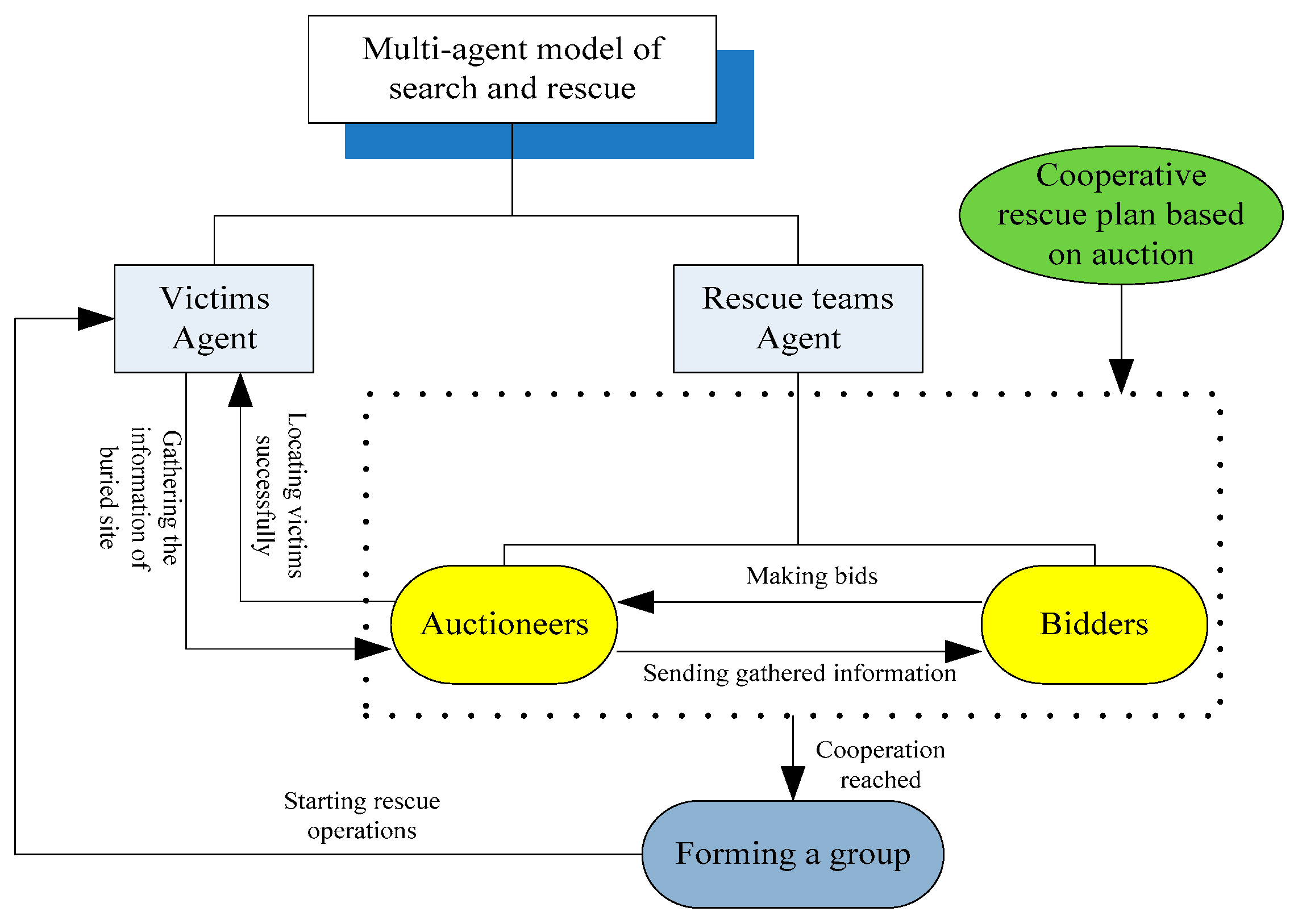
2. Description of Multi-Agent Model
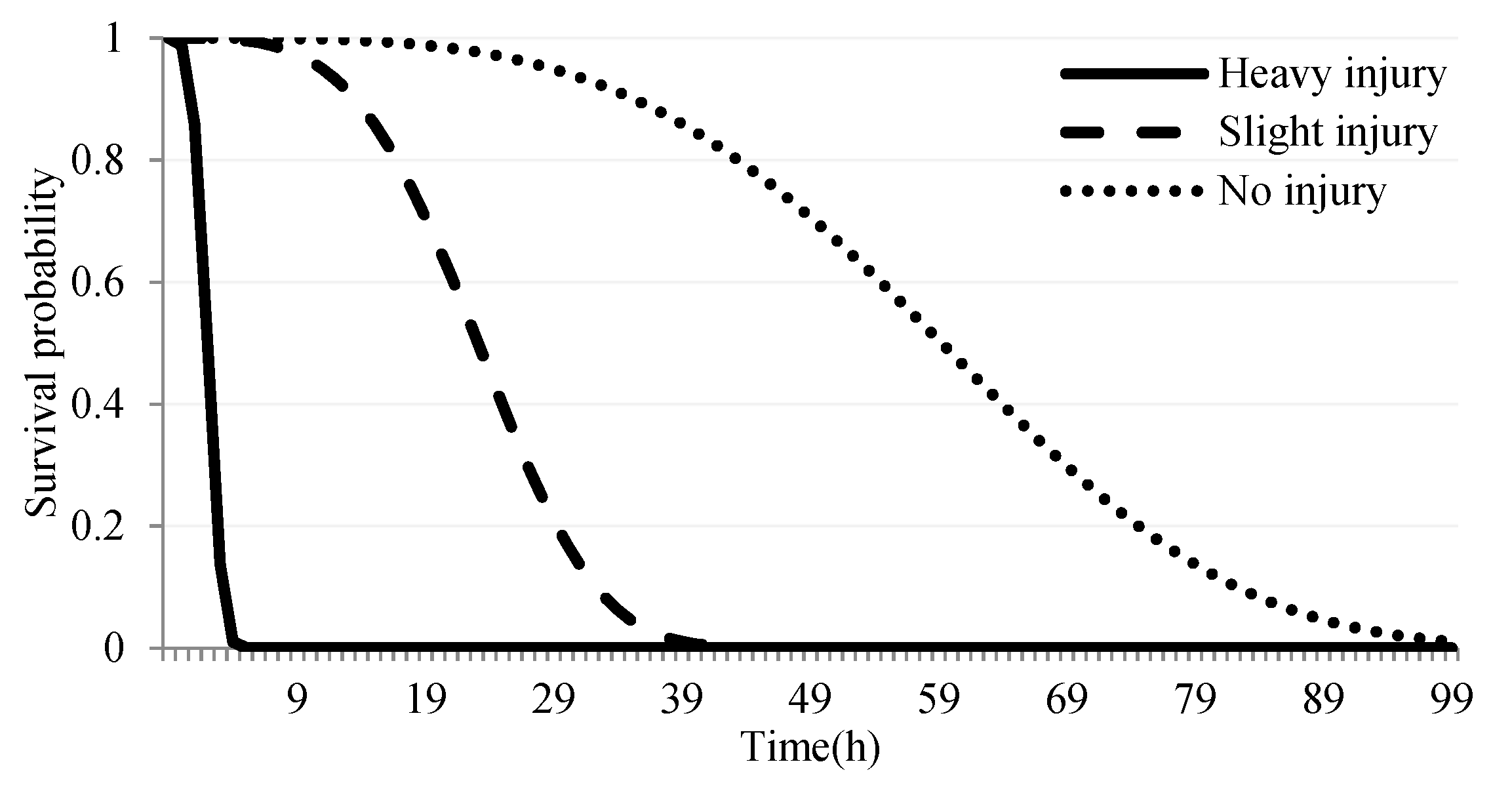
2.1. Victims
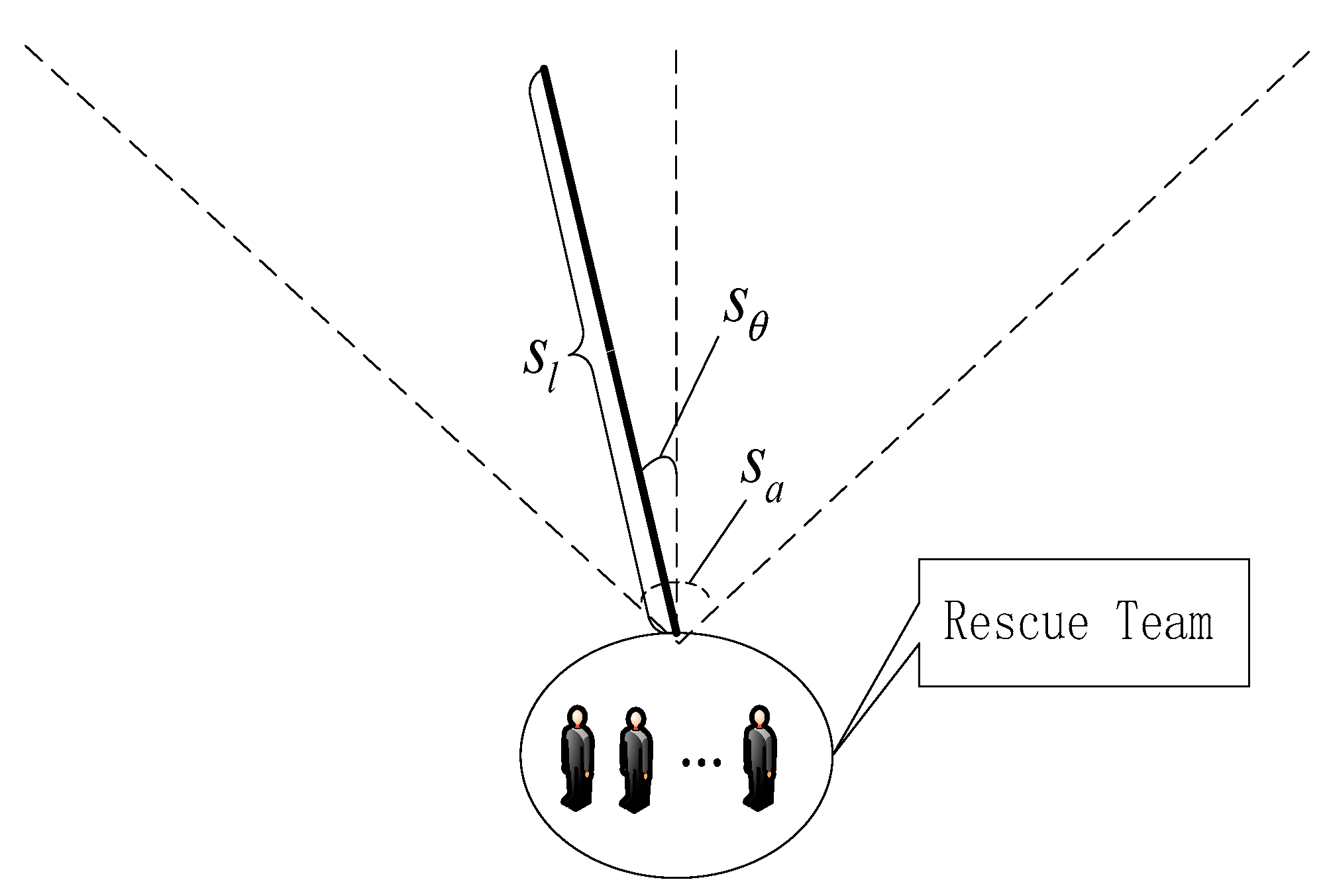
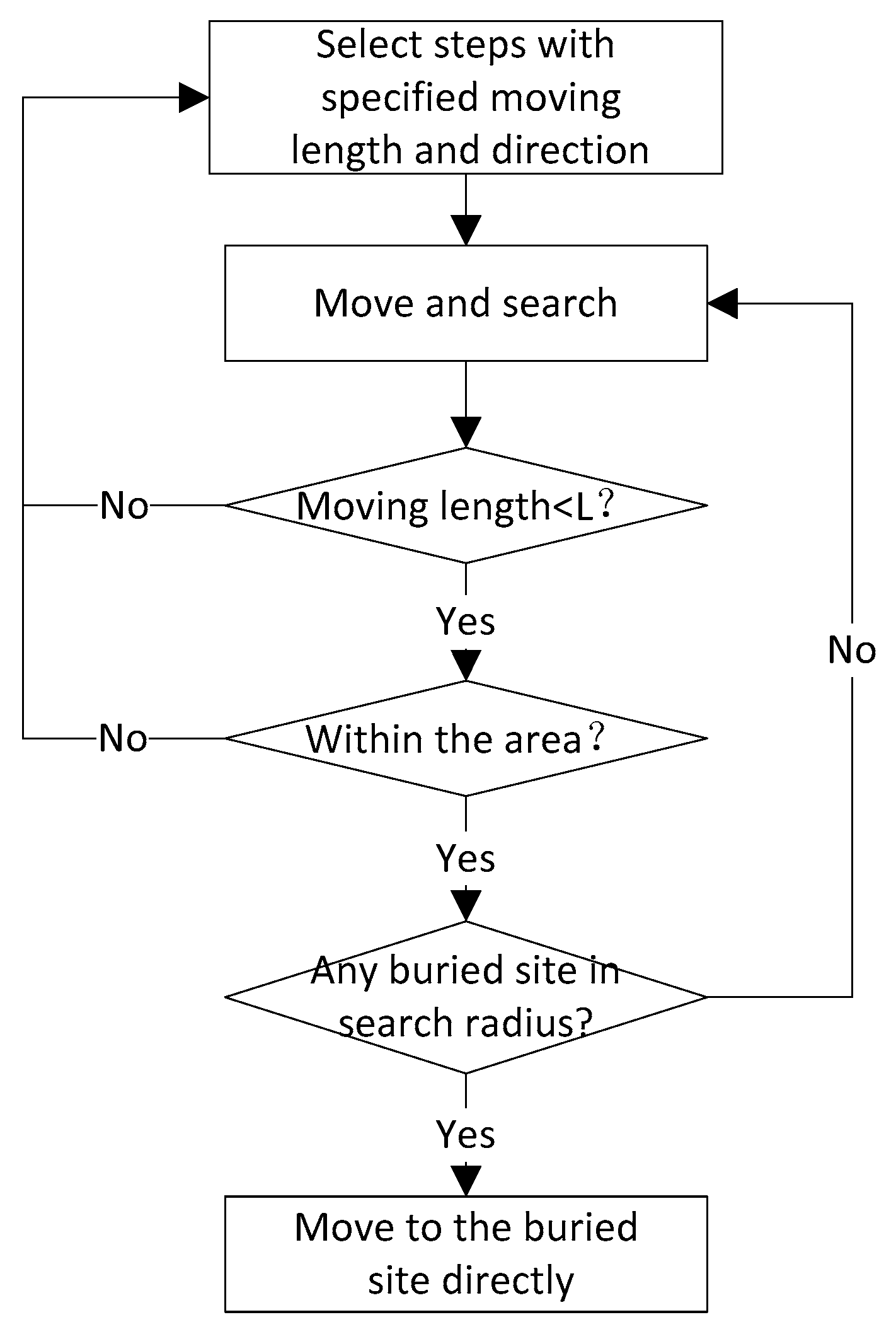
2.2. Rescue Teams
3. Auction-Based Cooperative Rescue Plan
3.1. Auctioneers
3.2. Bidders
3.2.1. The Utility Function of Bidders
3.2.2. The Cost of Bidders
3.2.3. The Bidding Strategy of Bidders
3.3. The Adjustment in Task Allocation
4. Simulation Results
4.1. Experimental Settings
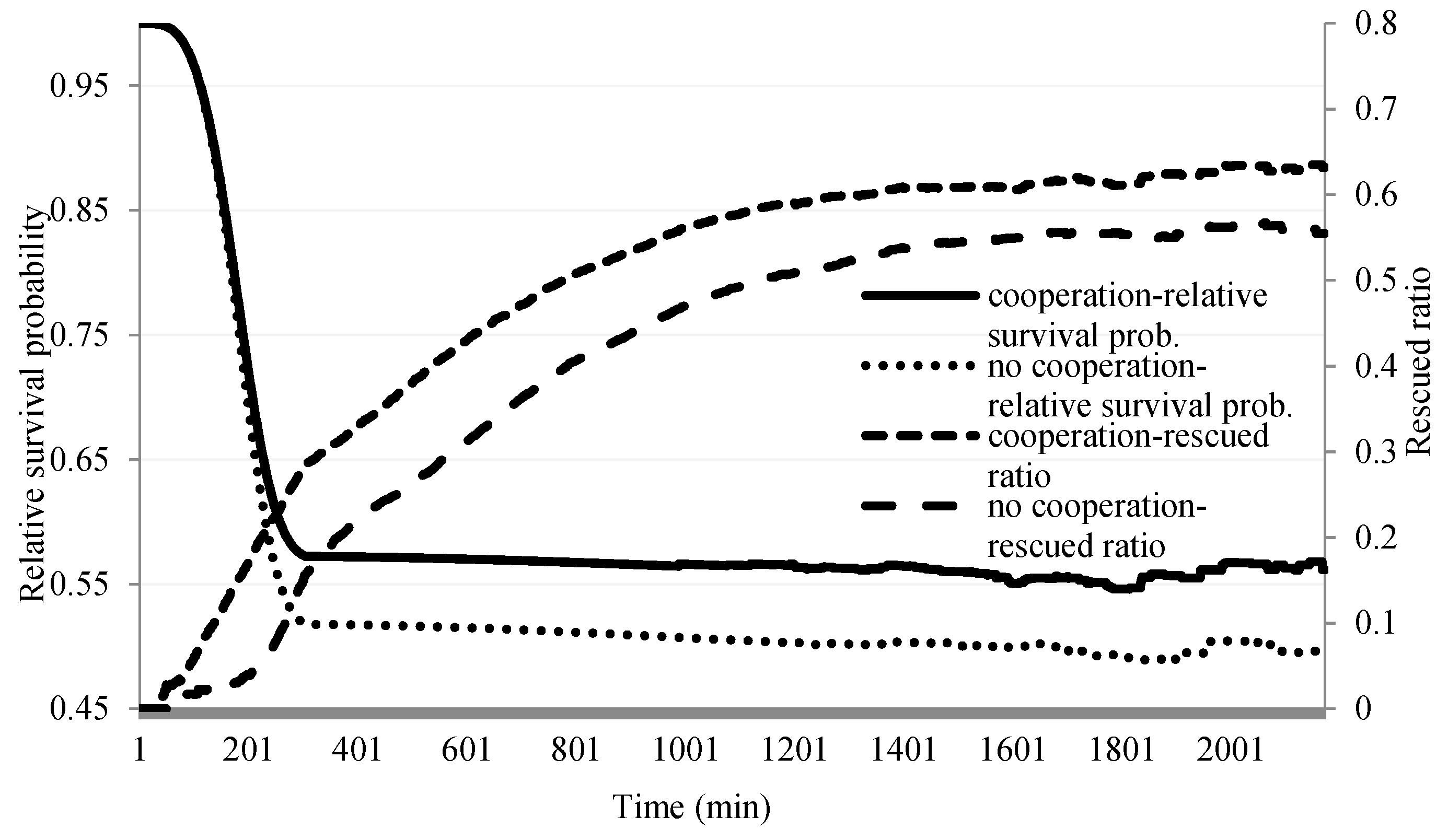
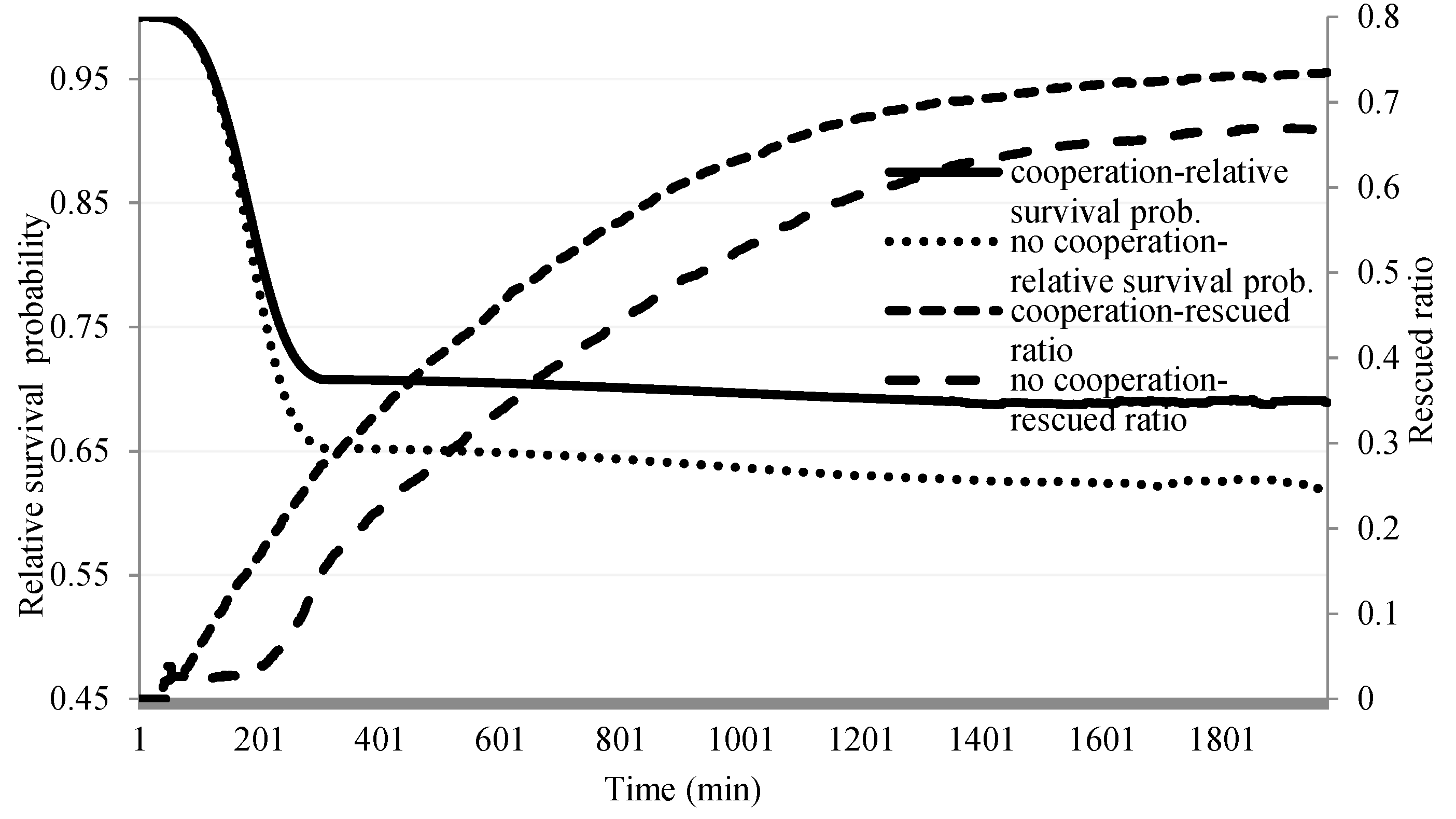
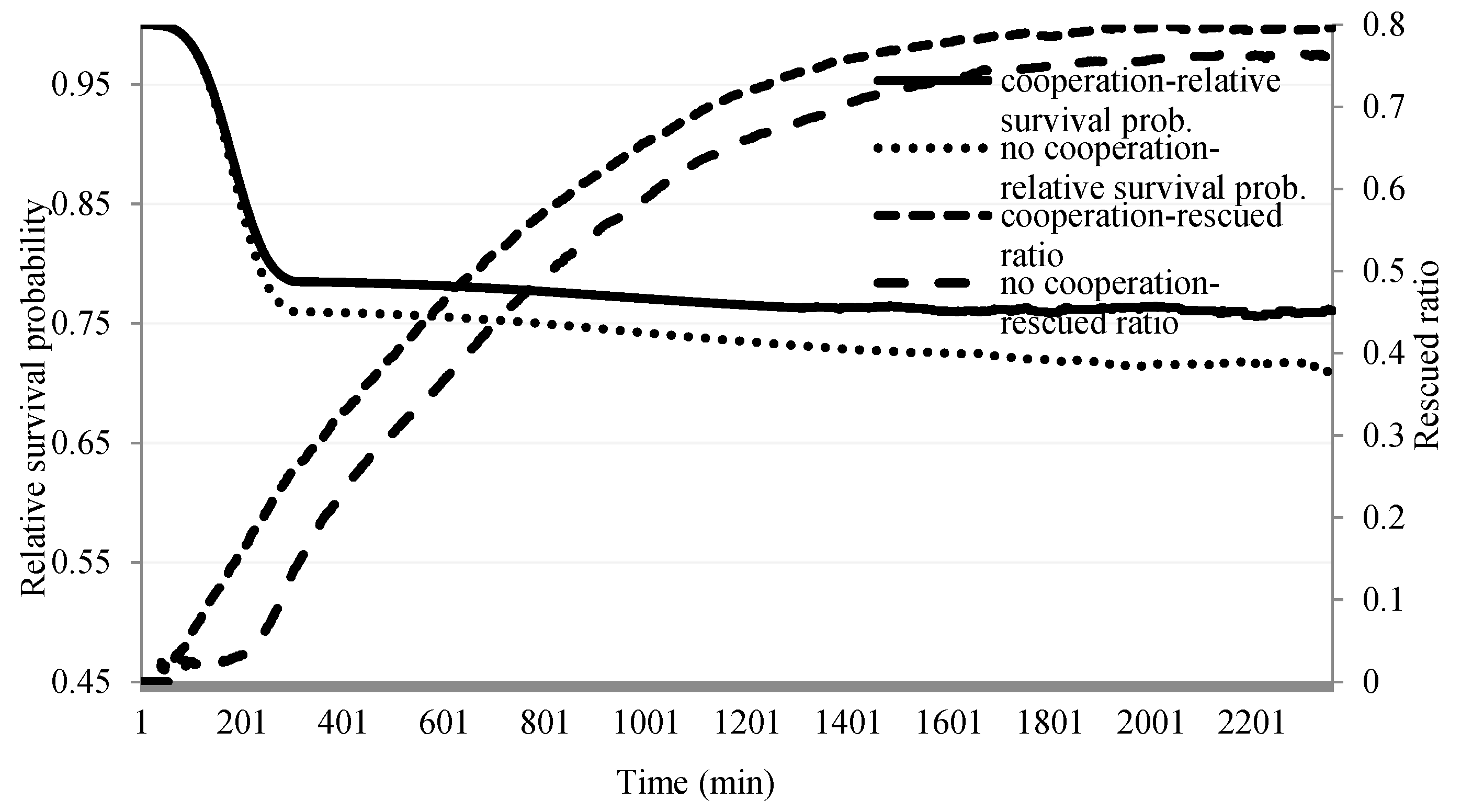
4.2. Results
4.3. Verification and Validation
5. Analytical Evaluation
5.1. Robustness Analysis
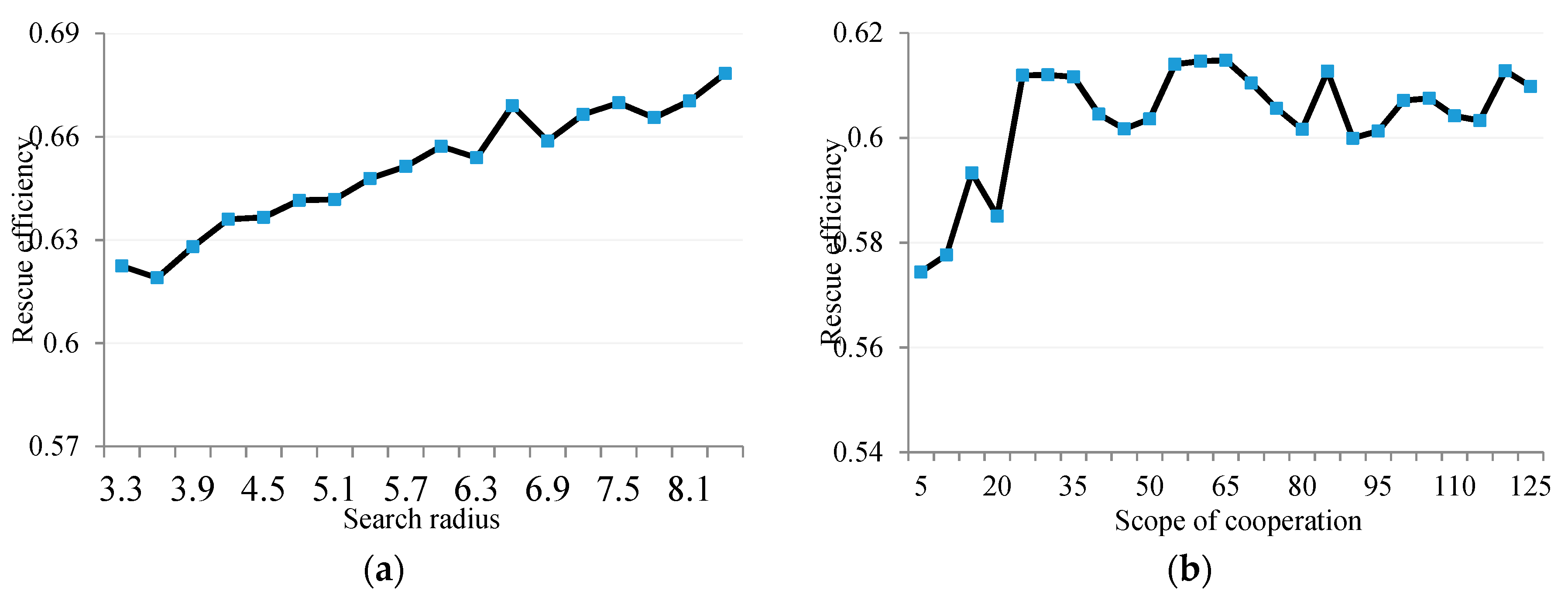
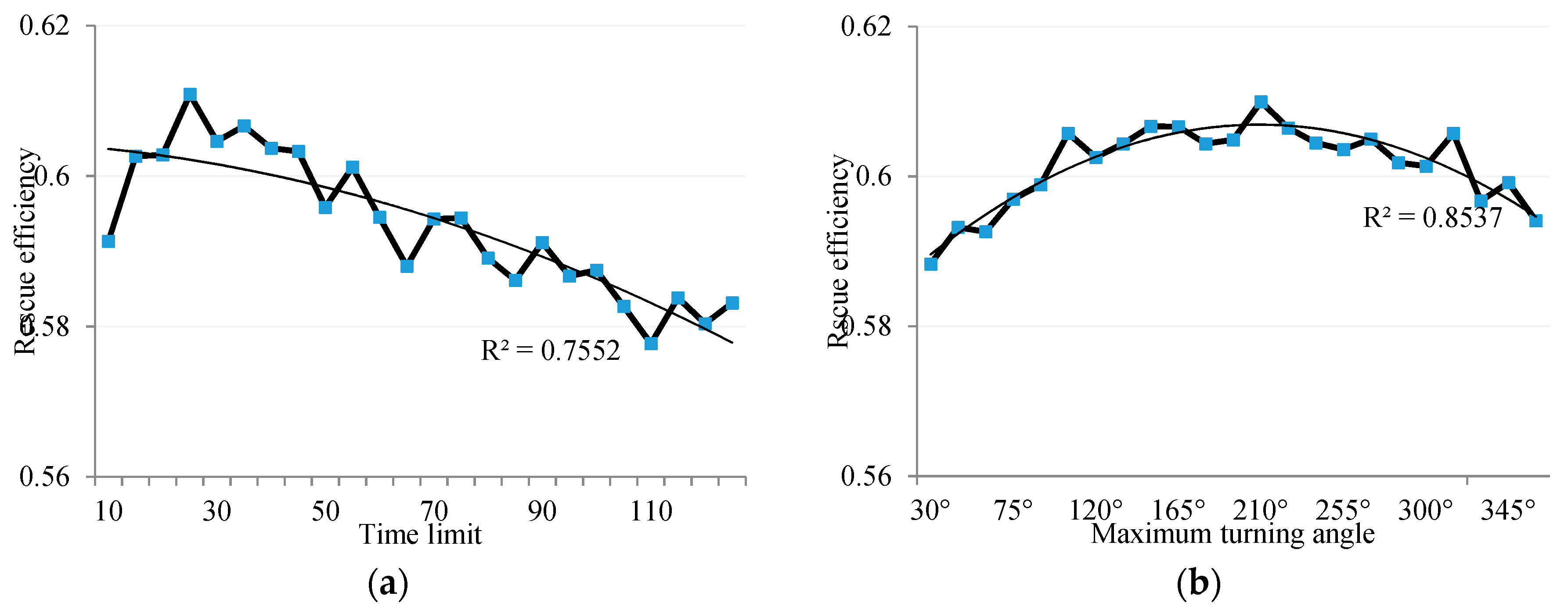
5.2. Sensitivity Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Campbell, A.M.; Jones, P.C. Prepositioning supplies in preparation for disasters. Eur. J. Oper. Res. 2011, 209, 156–165. [Google Scholar] [CrossRef]
- Sheu, J. Dynamic relief-demand management for emergency logistics operations under large-scale disasters. Res. Part E Logist. Transp. Rev. 2010, 46, 1–17. [Google Scholar] [CrossRef]
- Gan, H.; Richter, K.; Shi, M.; Winter, S. Integration of simulation and optimization for evacuation planning. Simul. Model. Pract. Theory 2016, 67, 59–73. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, B.; Zheng, Y. Bio-Inspired Meta-Heuristics for Emergency Transportation Problems. Algorithms 2014, 7, 15–31. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, S.; Ling, H. Evolutionary optimization for disaster relief operations: A survey. Appl. Soft Comput. 2015, 27, 553–566. [Google Scholar] [CrossRef]
- Nadi, A.; Edrisi, A. Adaptive multi-agent relief assessment and emergency response. Int. J. Dis. Risk Reduct. 2017, 24, 12–23. [Google Scholar] [CrossRef]
- Bilbao, M.N.; Del Ser, J.; Perfecto, C.; Salcedo-Sanz, S.; Portilla-Figueras, J.A. Cost-efficient deployment of multi-hop wireless networks over disaster areas using multi-objective meta-heuristics. Neurocomputing 2018, 271, 18–27. [Google Scholar] [CrossRef]
- Liang, H.; Kang, F. A novel task optimal allocation approach based on Contract Net Protocol for Agent-oriented UUV swarm system modeling. Opt.-Int. J. Light Electron Opt. 2016, 127, 3928–3933. [Google Scholar] [CrossRef]
- Su, X.; Zhang, M.; Ye, D.; Bai, Q. In A dynamic coordination approach for task allocation in disaster environments under spatial and communicational constraints. In Proceedings of the AAAI Workshop on Multiagent Interaction without Prior Coordination, Quebec City, QC, Canada, 27–28 July 2014; p. 7. [Google Scholar]
- Ju, C.; Chen, T. Extended labor division model of ant colony based on ability-evaluation and interest-driven and its applications in dynamic task allocations. Syst. Eng. Theory Pract. 2014, 34, 84–93. [Google Scholar]
- Liu, C.; Kroll, A. Memetic algorithms for optimal task allocation in multi-robot systems for inspection problems with cooperative tasks. Soft Comput. 2015, 19, 567–584. [Google Scholar] [CrossRef]
- Bilbao, M.N.; Ser, J.D.; Salcedo-Sanz, S.; Casanova-Mateo, C. On the application of multi-objective harmony search heuristics to the predictive deployment of firefighting aircrafts: A realistic case study. Int. J. Bio-Inspir. Comput. 2015, 7, 270–284. [Google Scholar] [CrossRef]
- Landatorres, I.; Manjarres, D.; Bilbao, S.; Ser, J.D. Underwater Robot Task Planning Using Multi-Objective Meta-Heuristics. Sensors 2017, 17, 762. [Google Scholar] [CrossRef] [PubMed]
- Nanjanath, M.; Erlandson, A.J.; Andrist, S.; Ragipindi, A.; Mohammed, A.A.; Sharma, A.S.; Gini, M. Decision and Coordination Strategies for RoboCup Rescue Agents. In Proceedings of the International Conference on Simulation, Modeling, and Programming for Autonomous Robots, Darmstadt, Germany, 15–18 November 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 473–484. [Google Scholar]
- Nair, R.; Ito, T.; Tambe, M.; Marsella, S. Task allocation in the robocup rescue simulation domain: A short note. In Robot Soccer World Cup; Springer: Berlin/Heidelberg, Germany, 2001; pp. 751–754. [Google Scholar]
- Kong, Y.; Zhang, M.; Ye, D. A Group Task Allocation Strategy in Open and Dynamic Grid Environments. In Recent Advances in Agent-Based Complex Automated Negotiation; Fukuta, N., Ito, T., Zhang, M., Fujita, K., Robu, V., Eds.; Springer: Basel, Switzerland, 2016; pp. 121–139. [Google Scholar]
- Smith, R.G. The Contract Net Protocol: High-Level Communication and Control in a Distributed Problem Solver. IEEE Trans. Comput. 1980, C-29, 1104–1113. [Google Scholar]
- Chen, J.; Sun, D. Coalition-Based Approach to Task Allocation of Multiple Robots with Resource Constraints. IEEE Trans. Autom. Sci. Eng. 2012, 9, 516–528. [Google Scholar] [CrossRef]
- Ramchurn, S.D.; Farinelli, A.; Macarthur, K.S.; Jennings, N.R. Decentralized Coordination in RoboCup Rescue. Comput. J. 2010, 53, 1447–1461. [Google Scholar] [CrossRef]
- D’Uffizi, A.; Simonetti, M.; Stecca, G.; Confessore, G. A Simulation Study of Logistics for Disaster Relief Operations. Procedia CIRP 2015, 33, 157–162. [Google Scholar] [CrossRef]
- Duguay, C.; Chetouane, F. Modeling and Improving Emergency Department Systems using Discrete Event Simulation. Simul. Trans. Soc. Model. Simul. Int. 2007, 83, 311–320. [Google Scholar] [CrossRef]
- Buford, J.; Jakobson, G.; Lewis, L. Multi-agent situation management for supporting large-scale disaster relief operations. Int. J. Intell. Control Syst. 2006, 11, 284–295. [Google Scholar]
- Takahashi, T.; Tadokoro, S.; Ohta, M.; Ito, N. Agent based approach in disaster rescue simulation-from test-bed of multiagent system to practical application. In RoboCup: Robot Soccer World Cup V; Springer: Berlin/Heidelberg, Germany, 2002; pp. 102–111. [Google Scholar]
- Tani, A.; Yamamura, T.; Waridashi, Y.; Kawamura, H.; Takizawa, A. In Simulation on Rescue in Case of Earthquake Disaster by Multi-Agent System. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Wosniack, M.E.; Santos, M.C.; Raposo, E.P.; Viswanathan, G.M.; Da Luz, M.G.E. Robustness of optimal random searches in fragmented environments. Phys. Rev. E 2015, 91. [Google Scholar] [CrossRef] [PubMed]
- Cao, M.; Meng, Q.; Luo, B.; Zeng, M. Experimental comparison of random search strategies for multi-robot based odour finding without wind information. Austrian Contrib. Vet. Epidemiol. 2015, 8, 43–50. [Google Scholar]
- Rhee, I.; Shin, M.; Hong, S.; Lee, K.; Kim, S.J.; Chong, S. On the Levy-Walk Nature of Human Mobility. IEEE/ACM Trans. Netw. 2011, 19, 630–643. [Google Scholar] [CrossRef]
- Cabrera, E.; Taboada, M.; Iglesias, M.L.; Epelde, F.; Luque, E. Optimization of Healthcare Emergency Departments by Agent-Based Simulation. Procedia Comput. Sci. 2011, 4, 1880–1889. [Google Scholar] [CrossRef]
- Nolting, B.C. Random Search Models of Foraging Behavior: Theory, Simulation, and Observation. Ph.D. Thesis, University of Nebraska, Lincoln, NE, USA, 2013. [Google Scholar]
- Reynolds, A.M. Balancing the competing demands of harvesting and safety from predation: Lévy walk searches outperform composite Brownian walk searches but only when foraging under the risk of predation. Phys. A Stat. Mech. Appl. 2010, 389, 4740–4746. [Google Scholar] [CrossRef]
- Takadama, K.; Suematsu, Y.L.; Sugimoto, N.; Nawa, N.E.; Shimohara, K. Towards Verification and Validation in Multiagent-Based Systems and Simulations: Analyzing Different Learning Bargaining Agents; Springer: Berlin/Heidelberg, Germany, 2003; pp. 26–42. [Google Scholar]
- Sargent, R.G. Verification and validation of simulation models. J. Simul. 2013, 7, 12–24. [Google Scholar] [CrossRef]
- Farinelli, A.; Grisetti, G.; Iocchi, L.; Lo Cascio, S.; Nardi, D. Design and evaluation of multi agent systems for rescue operations, Intelligent Robots and Systems. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2003), Las Vegas, NV, USA, 27–31 October 2003; pp. 3138–3143. [Google Scholar]
- Rödiger, T.; Geyer, S.; Mallast, U.; Merz, R.; Krause, P.; Fischer, C.; Siebert, C. Multi-response calibration of a conceptual hydrological model in the semiarid catchment of Wadi al Arab, Jordan. J. Hydrol. 2014, 509, 193–206. [Google Scholar] [CrossRef]
- Fehler, M.; Puppe, F. Approaches for resolving the dilemma between model structure refinement and parameter calibration in agent-based simulations. In Proceedings of the Fifth International Joint Conference on Autonomous Agents and Multiagent Systems, Hakodate, Japan, 8–12 May 2006; pp. 120–122. [Google Scholar]
- Liu, Z.; Rexachs, D.; Epelde, F.; Luque, E. A simulation and optimization based method for calibrating agent-based emergency department models under data scarcity. Comput. Ind. Eng. 2017, 103, 300–309. [Google Scholar] [CrossRef]
| Notation | Definition |
|---|---|
| The set of buried site, where denotes a buried site | |
| The set of rescue teams, where denotes a rescue team | |
| The task of rescuing buried site , where | |
| The auctioneer who publishes task , where | |
| The team who received auction message, i.e., the bidder, where | |
| The utility for a bidder who completes task , where | |
| The net utility for bidder who completes task , which equals | |
| The cost of participating in task , where and | |
| The opportunity cost of participating in task , where and | |
| The time limit for completing rescue operations in each buried site | |
| The number of teams required to complete task , which is related to | |
| The distance between task and , where and | |
| The time spent in rescue operation of task , where and | |
| The number of buried sites within the scope of cooperation | |
| The number of available rescue teams within the scope of cooperation | |
| The coefficient of bid price, | |
| The bid on task , which is made by |
| Injury Severity | Scenarios | ||
|---|---|---|---|
| Fatal (%) | Serious (%) | Normal (%) | |
| Death | 40 | 30 | 20 |
| Heavy injury | 30 | 25 | 20 |
| Slight injury | 10 | 15 | 20 |
| No injury | 20 | 30 | 40 |
| Urgent | Less Urgent | Normal | |
|---|---|---|---|
| Buried depth | 150 | 120 | 90 |
| Number of victims | 3 | 2 | 1 |
| Total injury severity | 9 | 5 | 1 |
| (%) | (%) | (min) | ||
|---|---|---|---|---|
| Fatal | Cooperation | 56.40 | 64.62 | 512.2 |
| No-cooperation | 48.96 | 57.22 | 653.2 | |
| t test | 7.44 *** | 7.40 *** | −141.0 *** | |
| Serious | Cooperation | 68.17 | 75.11 | 587.0 |
| No-cooperation | 62.37 | 69.04 | 703.6 | |
| t test | 5.80 *** | 6.07 *** | −116.6 *** | |
| Normal | Cooperation | 76.26 | 82.15 | 624.1 |
| No-cooperation | 71.30 | 78.01 | 749.0 | |
| t test | 4.96 *** | 4.14 *** | −124.9 *** |
| Fatal | Cooperation | 7.5%, [0.7%, 16.2%] | 6.9%, [0.5%, 14.9%] | 8.7%, [0.8%, 20.3%] |
| No-cooperation | 10.3%, [0.8%, 23.9%] | 9.4%, [0.3%, 24.4%] | 8.6%, [0.9%, 20.5%] | |
| Serious | Cooperation | 5.8%, [0.8%, 13.8%] | 5.6%, [0.6%, 14.4%] | 8.2%, [0.7%, 20.7%] |
| No-cooperation | 6.6%, [0.2%, 16.1%] | 5.9%, [0.5%, 15.2%] | 6.8%, [0.4%, 17.1%] | |
| Normal | Cooperation | 4.4%, [0.2%, 10.7%] | 3.4%, [0.2%, 8.5%] | 6.5%, [0.8%, 17.0%] |
| No-cooperation | 4.6%, [0.4%, 12.5%] | 4.7%, [0.4%, 12.1%] | 6.1%, [0.5%, 15.1%] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Zhu, K.; Guo, H.; Liao, C.; Zhang, S. Simulation Optimization of Search and Rescue in Disaster Relief Based on Distributed Auction Mechanism. Algorithms 2017, 10, 125. https://doi.org/10.3390/a10040125
Tang J, Zhu K, Guo H, Liao C, Zhang S. Simulation Optimization of Search and Rescue in Disaster Relief Based on Distributed Auction Mechanism. Algorithms. 2017; 10(4):125. https://doi.org/10.3390/a10040125
Chicago/Turabian StyleTang, Jian, Kejun Zhu, Haixiang Guo, Can Liao, and Shuwen Zhang. 2017. "Simulation Optimization of Search and Rescue in Disaster Relief Based on Distributed Auction Mechanism" Algorithms 10, no. 4: 125. https://doi.org/10.3390/a10040125
APA StyleTang, J., Zhu, K., Guo, H., Liao, C., & Zhang, S. (2017). Simulation Optimization of Search and Rescue in Disaster Relief Based on Distributed Auction Mechanism. Algorithms, 10(4), 125. https://doi.org/10.3390/a10040125





