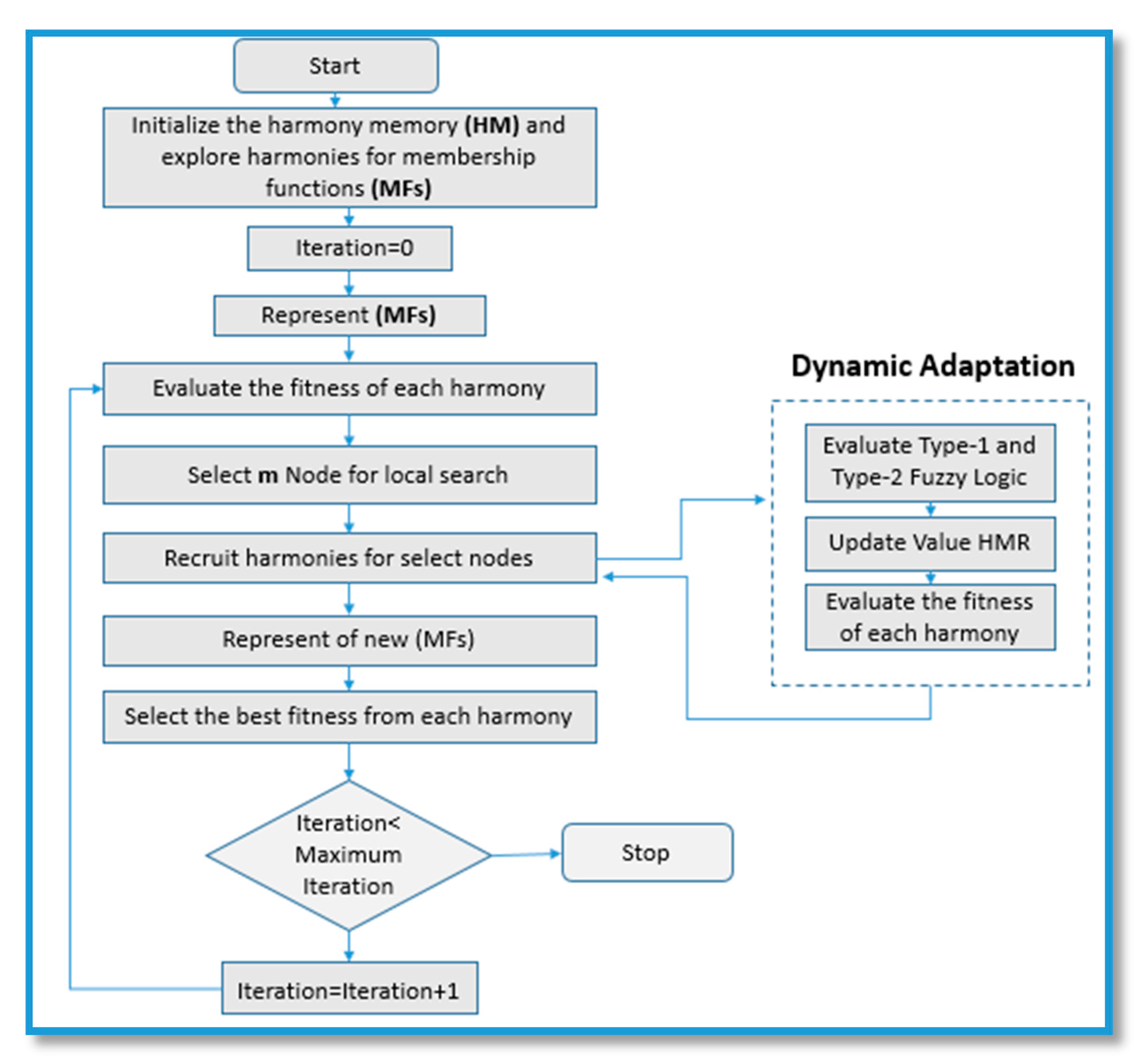
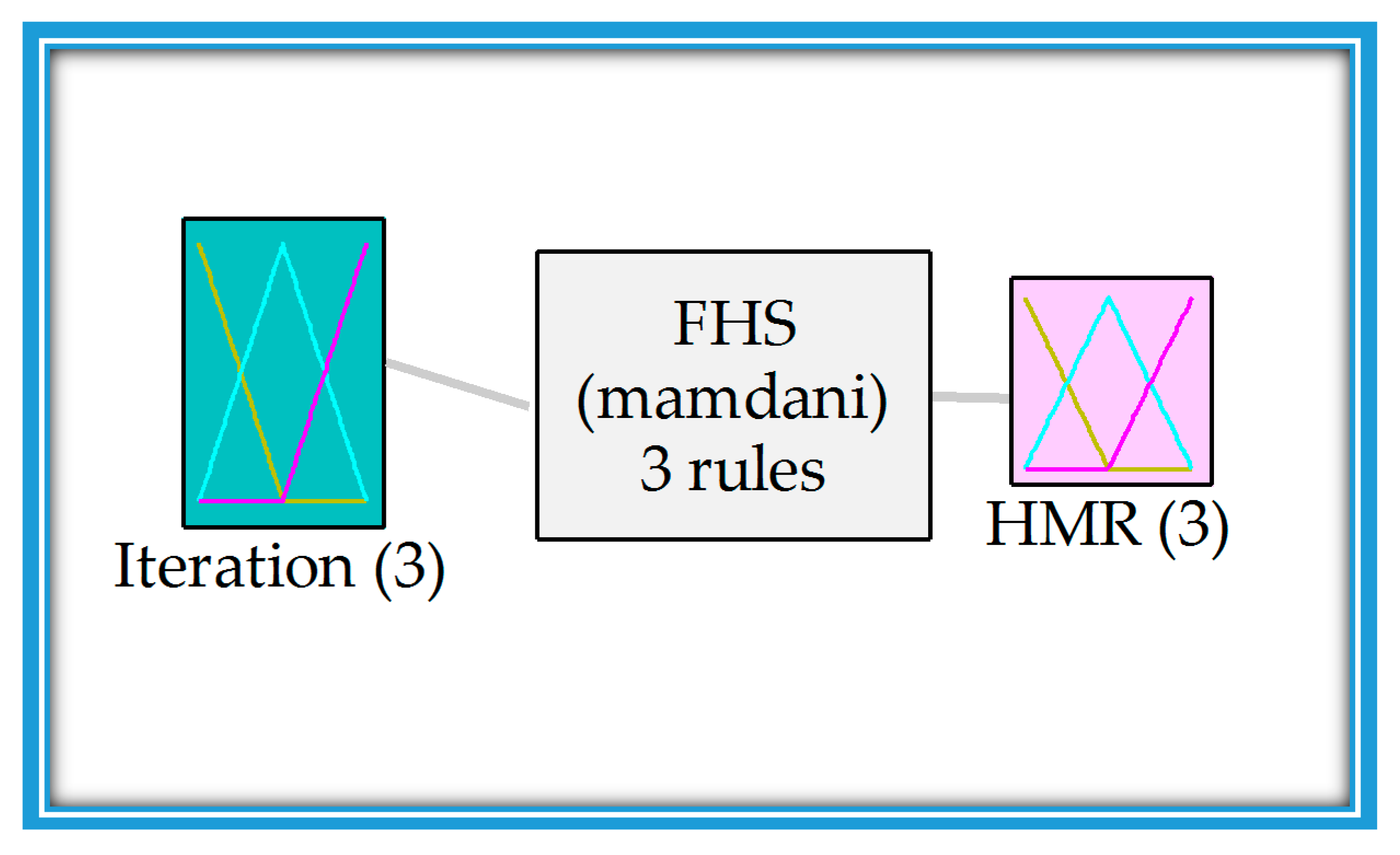
Figure 1.
Flowchart of the FHS.
Figure 1.
Flowchart of the FHS.
Figure 2.
Scheme of the Type-1 fuzzy system method (FHS).
Figure 2.
Scheme of the Type-1 fuzzy system method (FHS).
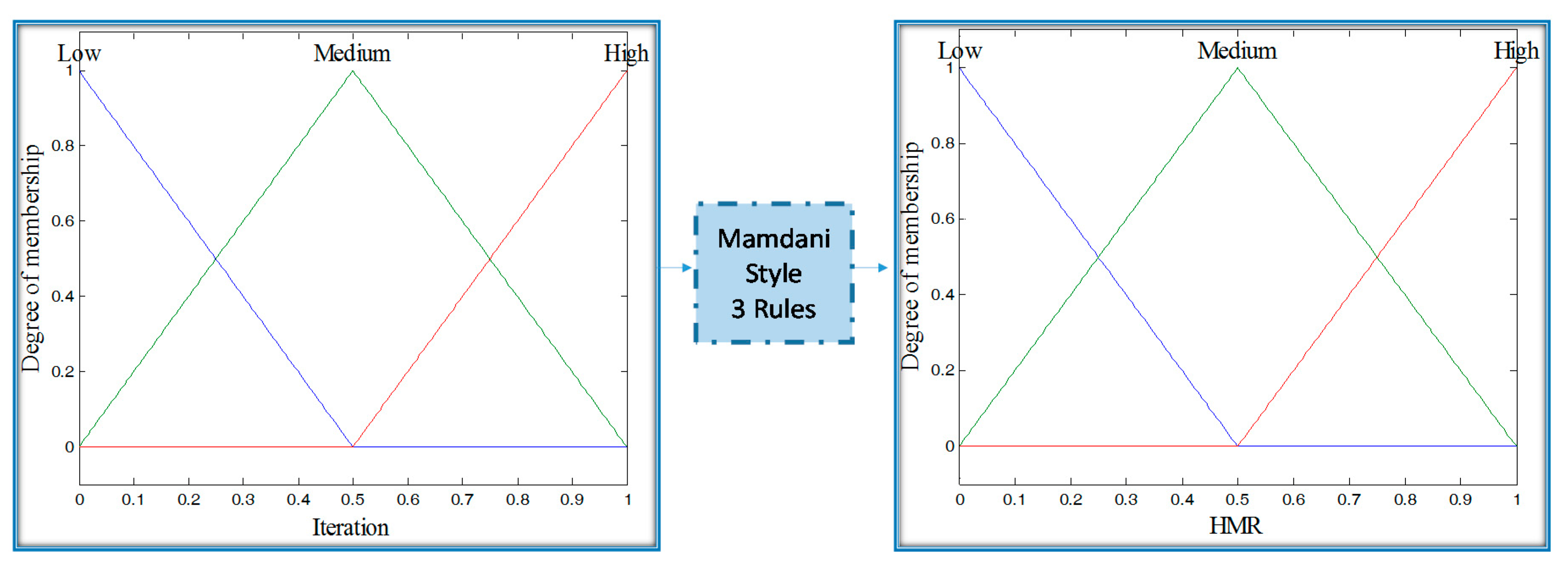
Figure 3.
Input and output of the Type-1 fuzzy system.
Figure 3.
Input and output of the Type-1 fuzzy system.
Figure 4.
Scheme of the interval Type-2 fuzzy system method (FHS2).
Figure 4.
Scheme of the interval Type-2 fuzzy system method (FHS2).
Figure 5.
Input and output of the interval Type-2 fuzzy system.
Figure 5.
Input and output of the interval Type-2 fuzzy system.
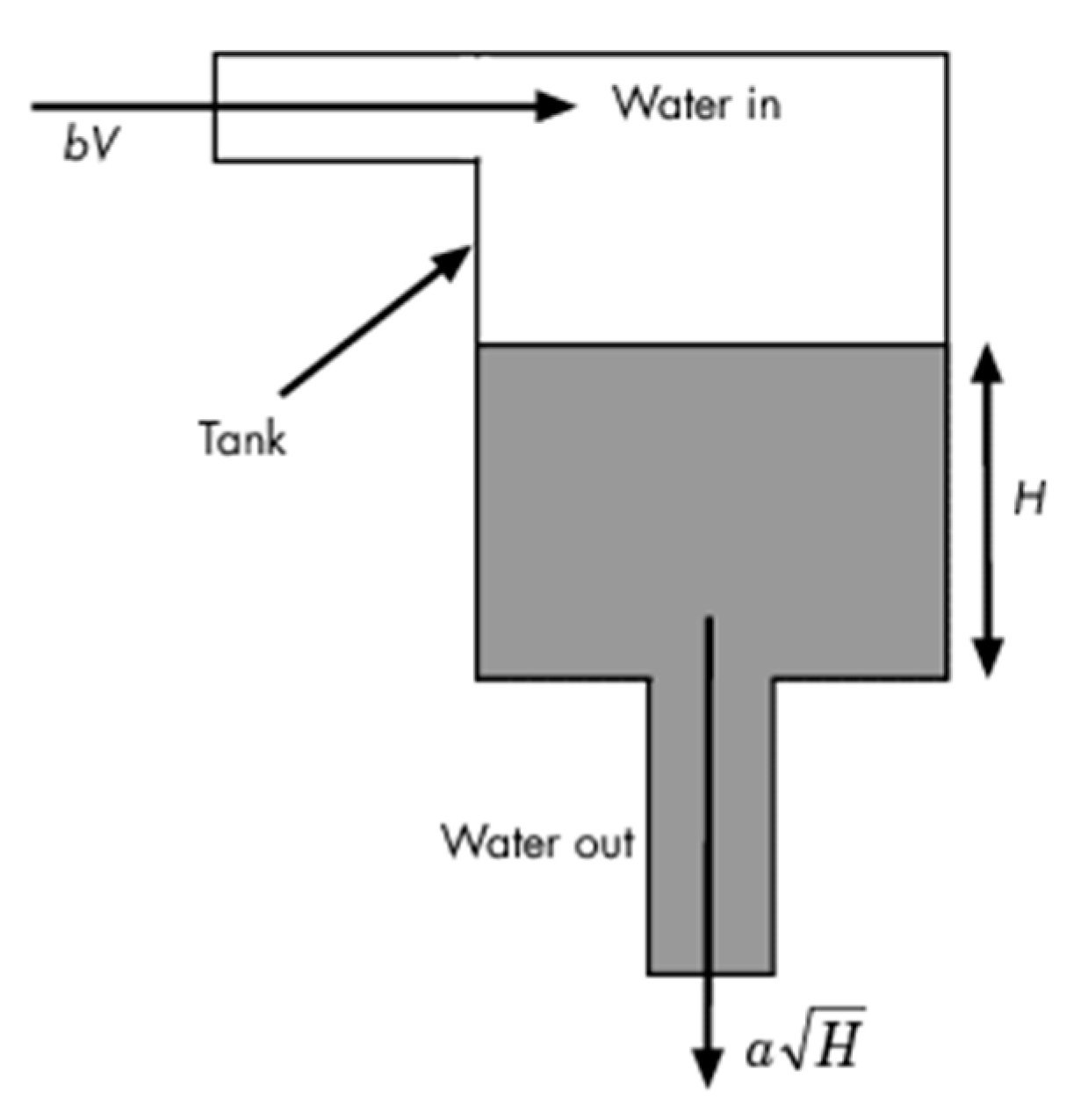
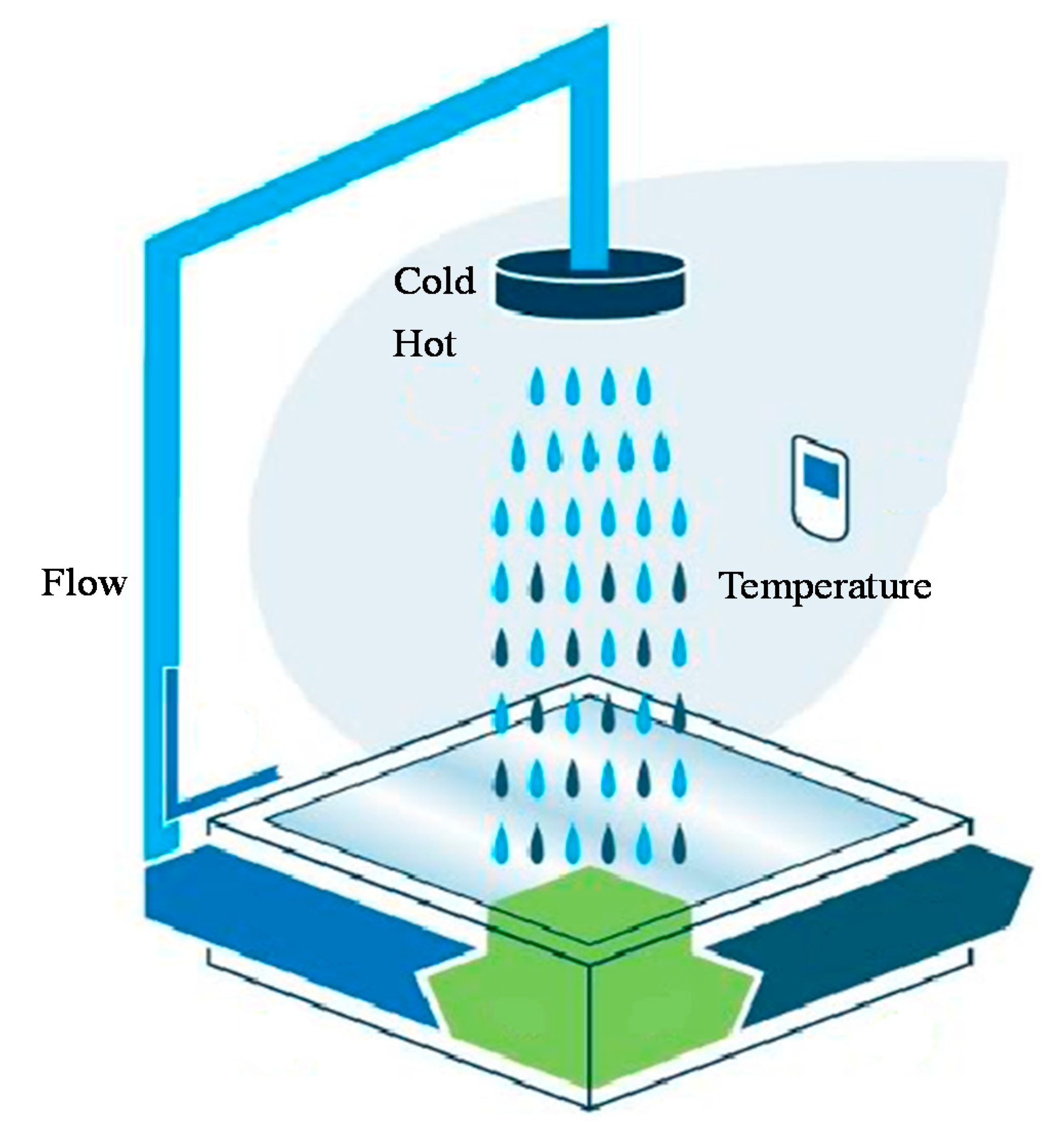
Figure 6.
Diagram of the water tank controller.
Figure 6.
Diagram of the water tank controller.
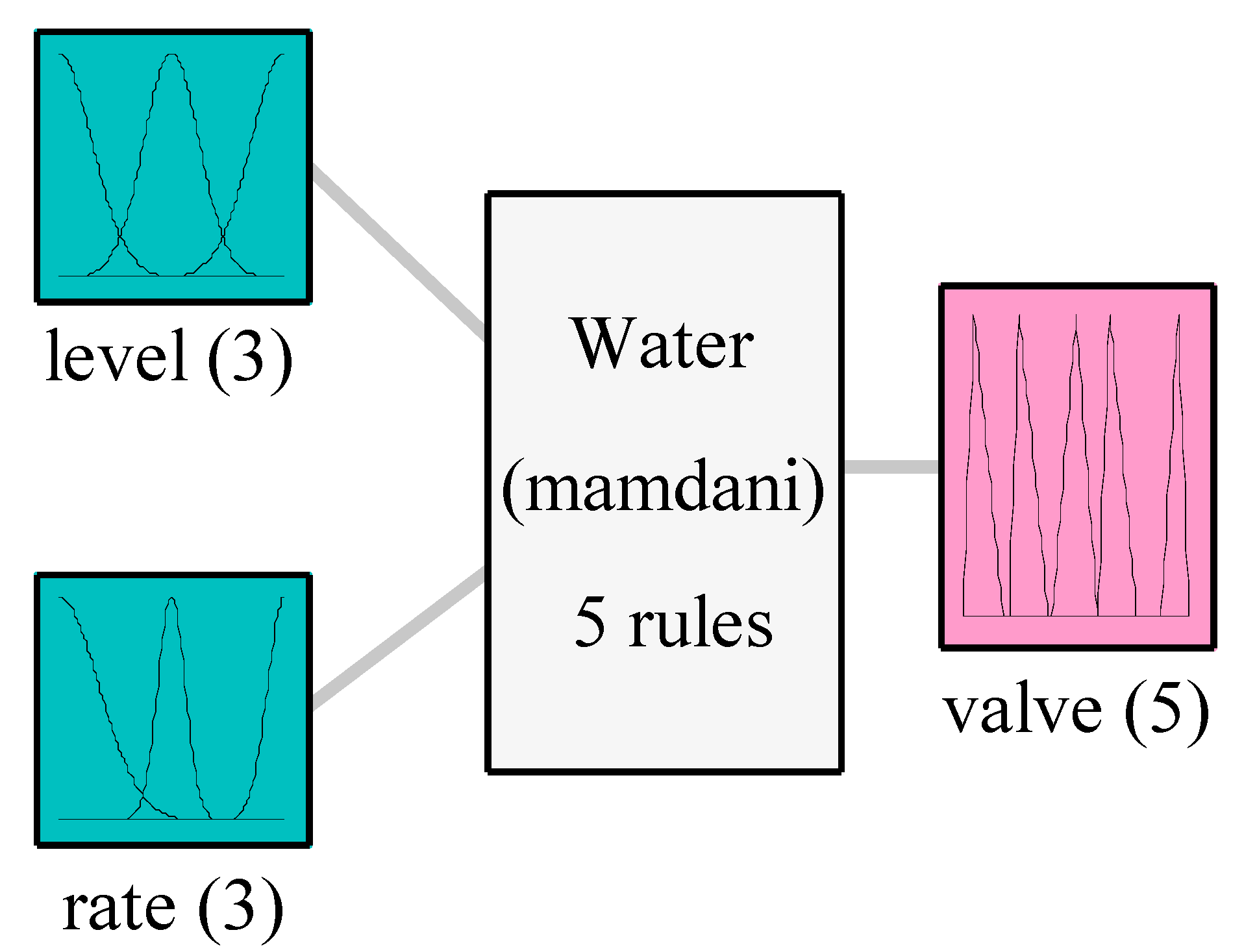
Figure 7.
Structure of the water tank fuzzy system for control.
Figure 7.
Structure of the water tank fuzzy system for control.
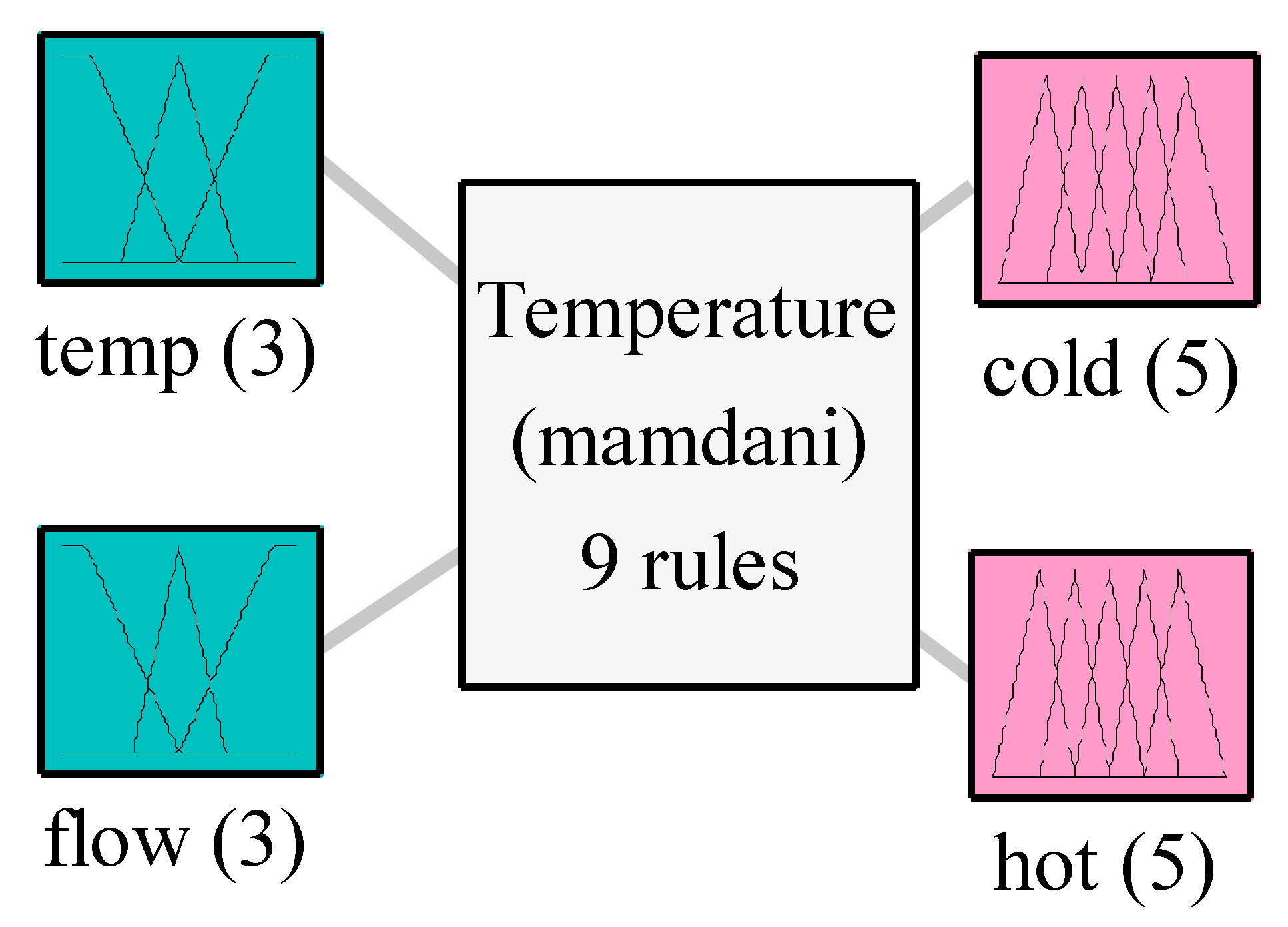
Figure 8.
Diagram of the temperature controller.
Figure 8.
Diagram of the temperature controller.
Figure 9.
Structure of the water tank fuzzy system for control.
Figure 9.
Structure of the water tank fuzzy system for control.
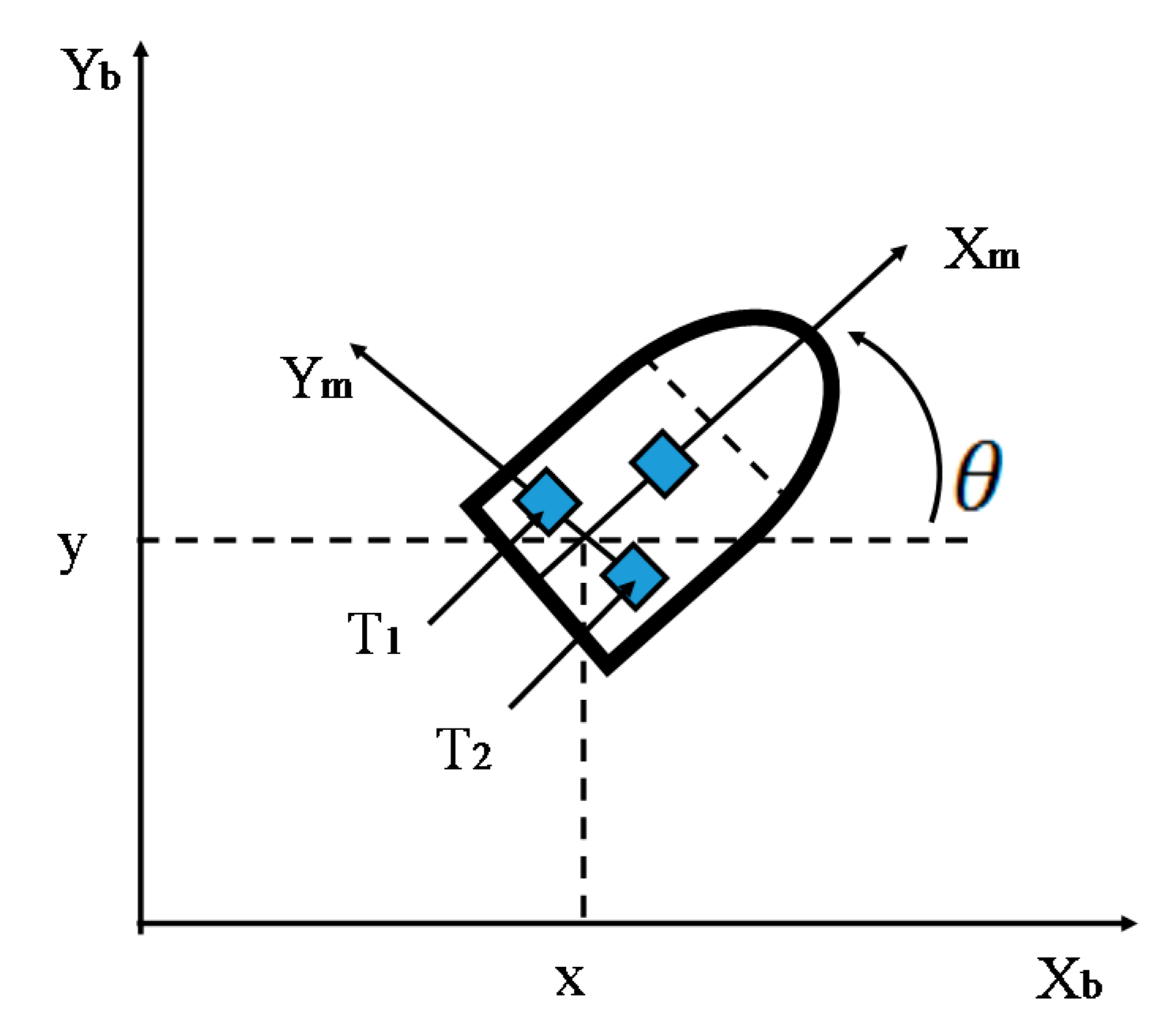
Figure 10.
Diagram of the robot mobile controller.
Figure 10.
Diagram of the robot mobile controller.
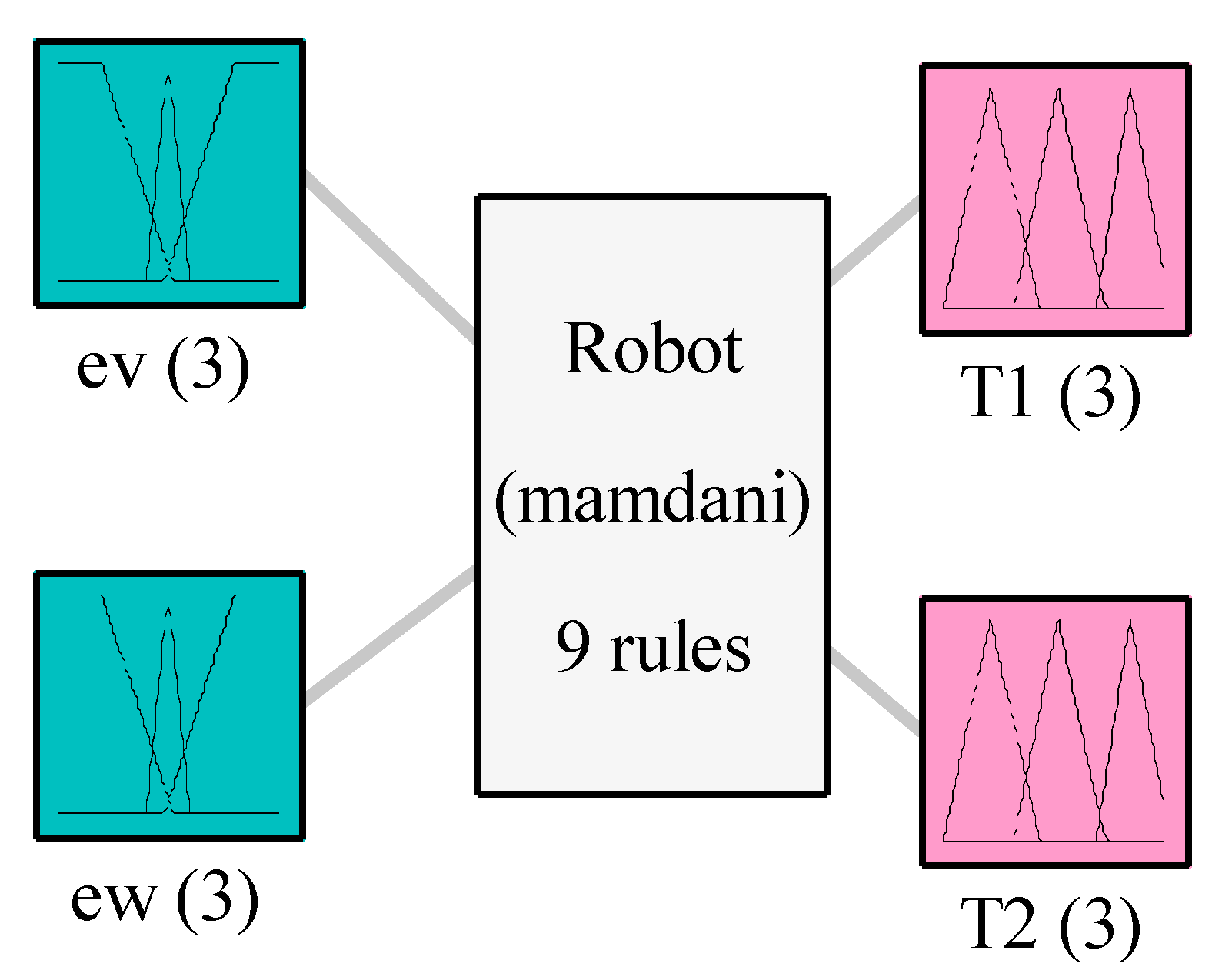
Figure 11.
Structure of the mobile robot fuzzy system for control.
Figure 11.
Structure of the mobile robot fuzzy system for control.
Figure 12.
Simulation results of the water tank controller for the three methods. (a) The best result is shown using original harmony search algorithm (HS); (b) the best result is shown using the Type-1 fuzzy harmony search (FHS); (c) the best result is shown using the Type-2 fuzzy harmony search (FHS2). These methods were applied with noise to verify the stability of the methods. The blue line represents the desired trajectory and the pink line the obtained trajectory; the objective is for the obtained line to resemble the desired one.
Figure 12.
Simulation results of the water tank controller for the three methods. (a) The best result is shown using original harmony search algorithm (HS); (b) the best result is shown using the Type-1 fuzzy harmony search (FHS); (c) the best result is shown using the Type-2 fuzzy harmony search (FHS2). These methods were applied with noise to verify the stability of the methods. The blue line represents the desired trajectory and the pink line the obtained trajectory; the objective is for the obtained line to resemble the desired one.
Figure 13.
Simulation results of the temperature controller for the three methods. (a) The best result is shown using original harmony search algorithm (HS); (b) the best result is shown using the Type-1 fuzzy harmony search (FHS); (c) the best result is shown using the Type-2 fuzzy harmony search (FHS2). These methods were applied with noise to verify the stability of the methods. The blue line represents the desired trajectory and the pink line the obtained trajectory; the objective is for the obtained line to resemble the desired one.
Figure 13.
Simulation results of the temperature controller for the three methods. (a) The best result is shown using original harmony search algorithm (HS); (b) the best result is shown using the Type-1 fuzzy harmony search (FHS); (c) the best result is shown using the Type-2 fuzzy harmony search (FHS2). These methods were applied with noise to verify the stability of the methods. The blue line represents the desired trajectory and the pink line the obtained trajectory; the objective is for the obtained line to resemble the desired one.
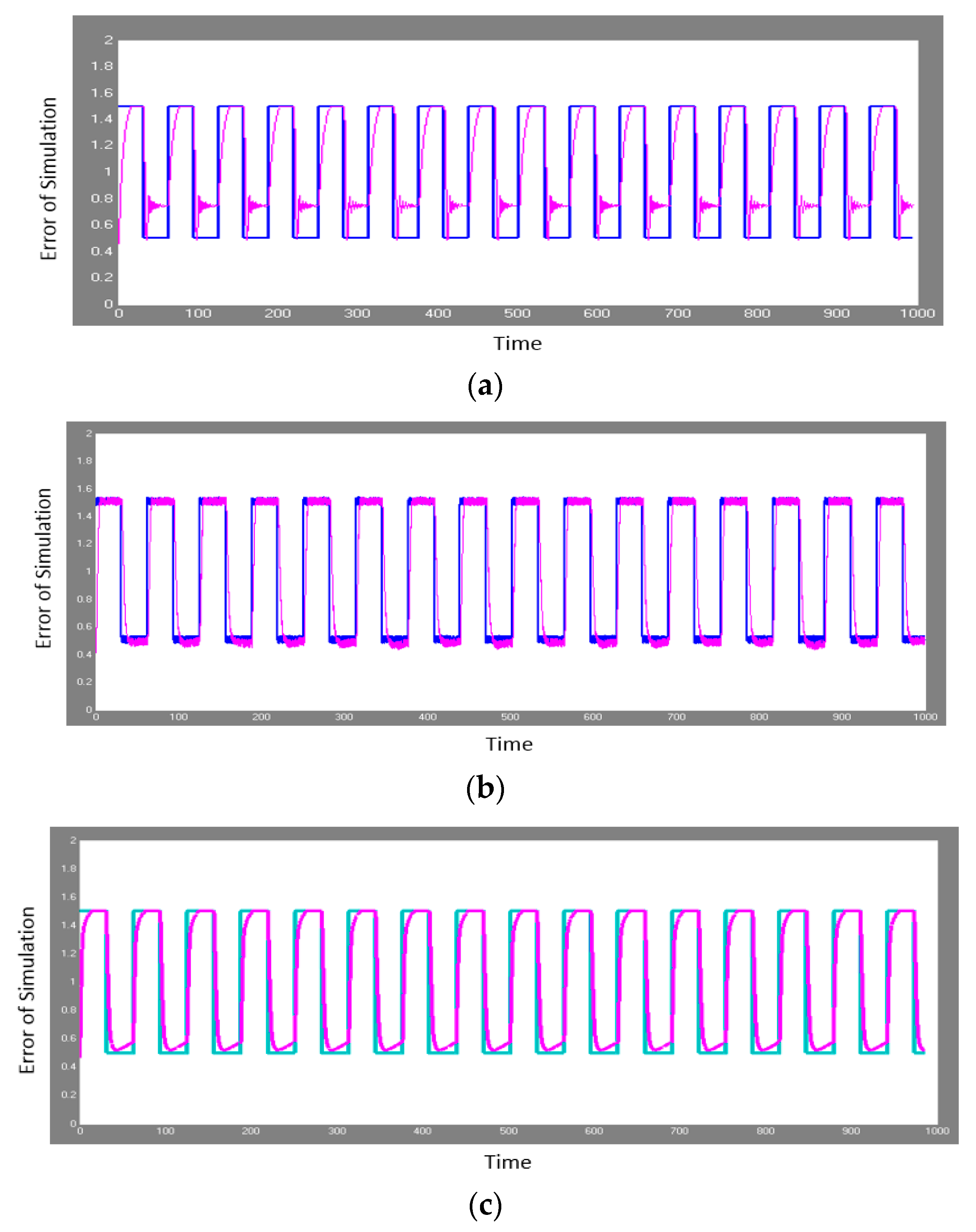
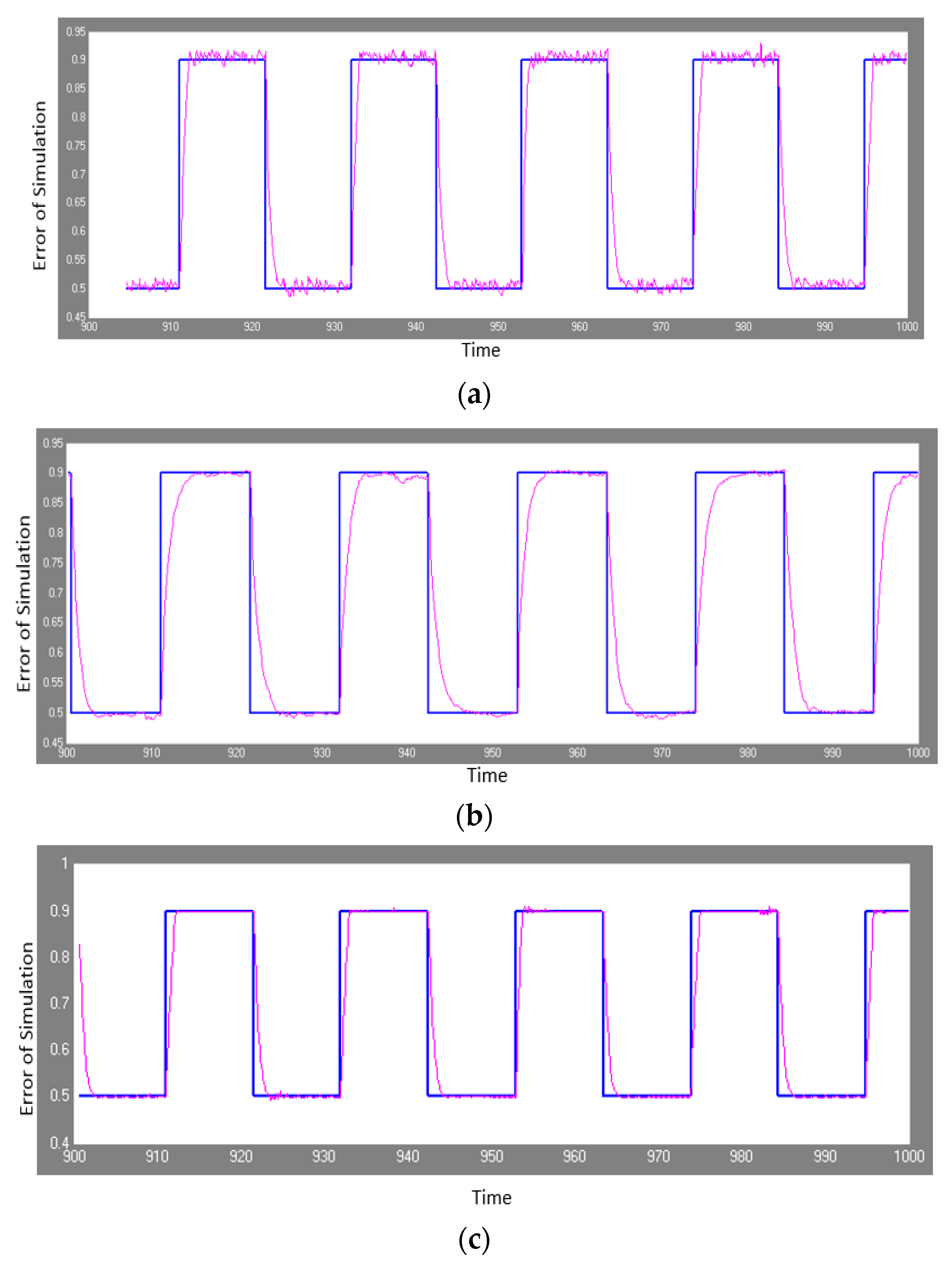
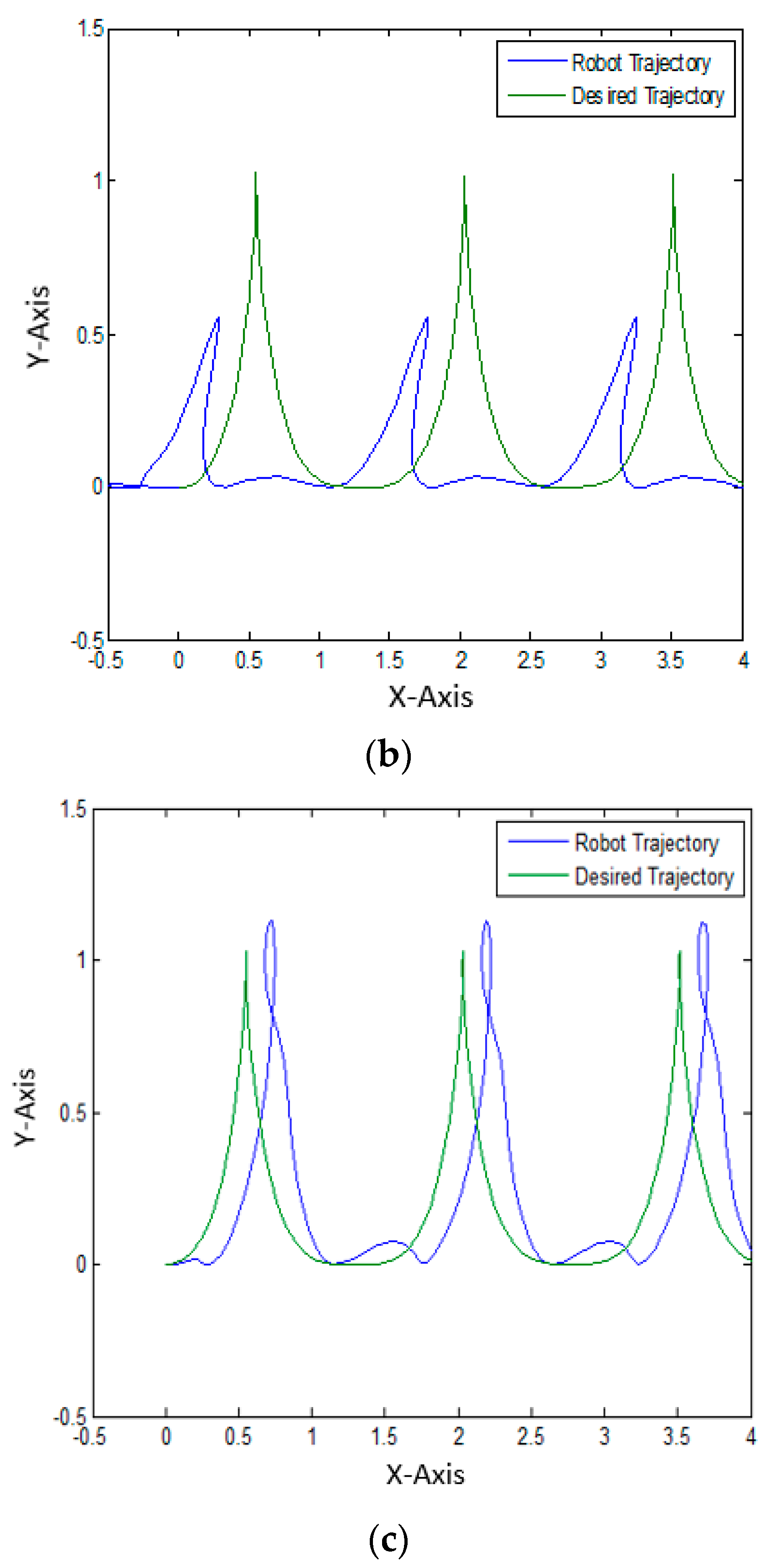
Figure 14.
Simulation results of the robot mobile controller for the three methods. (a) The best result is shown using original harmony search algorithm (HS); (b) the best result is shown using the Type-1 fuzzy harmony search (FHS); (c) the best result is shown using the Type-2 fuzzy harmony search (FHS2). These methods were applied with noise to verify the stability of the methods. The green line is the desired trajectory and the blue line the obtained trajectory, and the objective is for the obtained line to resemble the desired one.
Figure 14.
Simulation results of the robot mobile controller for the three methods. (a) The best result is shown using original harmony search algorithm (HS); (b) the best result is shown using the Type-1 fuzzy harmony search (FHS); (c) the best result is shown using the Type-2 fuzzy harmony search (FHS2). These methods were applied with noise to verify the stability of the methods. The green line is the desired trajectory and the blue line the obtained trajectory, and the objective is for the obtained line to resemble the desired one.
Table 1.
Rules for theType-1 and interval Type-2 fuzzy system.
Table 1.
Rules for theType-1 and interval Type-2 fuzzy system.
| HMR | Low | Medium | High |
|---|
| Iteration | |
|---|
| Low | Low | - | - |
| Medium | - | Medium | - |
| High | - | - | High |
Table 2.
Rules for the water tank controller.
Table 2.
Rules for the water tank controller.
| Rule Number | Inputs | Output |
|---|
| Level | Operator | Rate | Valve |
|---|
| 1 | okay | - | - | no change |
| 2 | low | - | - | open fast |
| 3 | high | - | - | close fast |
| 4 | okay | and | positive | close slow |
| 5 | okay | and | negative | open slow |
Table 3.
Fuzzy rules for the temperature controller.
Table 3.
Fuzzy rules for the temperature controller.
| Rule Number | Inputs | Output |
|---|
| Temp | Operator | Flow | Cold | Hot |
|---|
| 1 | cold | and | soft | open slow | open fast |
| 2 | cold | and | good | close slow | open slow |
| 3 | cold | and | hard | close fast | close slow |
| 4 | good | and | soft | open slow | open slow |
| 5 | good | and | good | steady | steady |
| 6 | good | and | hard | close slow | close slow |
| 7 | hot | and | soft | open fast | open slow |
| 8 | hot | and | good | open slow | close slow |
| 9 | hot | and | hard | close slow | close fast |
Table 4.
Fuzzy rules for the robot mobile controller.
Table 4.
Fuzzy rules for the robot mobile controller.
| Rule Number | Inputs | Output |
|---|
| Ev | Operator | Ew | T1 | T2 |
|---|
| 1 | N | and | N | N | N |
| 2 | N | and | Z | N | Z |
| 3 | N | and | P | N | P |
| 4 | Z | and | N | Z | N |
| 5 | Z | and | Z | Z | Z |
| 6 | Z | and | P | Z | P |
| 7 | P | and | N | P | N |
| 8 | P | and | Z | P | Z |
| 9 | P | and | P | P | P |
Table 5.
Errors obtained from the water tank controller without noise.
Table 5.
Errors obtained from the water tank controller without noise.
| Performance Index | HS | FHS | FHS2 |
|---|
| RMSE | 3.18 × 10−2 | 2.61 × 10−1 | 2.49 × 10−2 |
| MSE | 4.58 × 10−2 | 7.56 × 10−2 | 5.75 × 10−2 |
| ITAE | 3.87 × 104 | 9.93 × 105 | 3.68 × 104 |
| ITSE | 2.57 × 104 | 2.43 × 106 | 2.39 × 104 |
| IAE | 7.91 × 10 | 2.01 × 103 | 7.53 × 10 |
| ISE | 5.28 × 10 | 4.96 × 103 | 4.90 × 10 |
Table 6.
Errors obtained from the temperature controller without noise.
Table 6.
Errors obtained from the temperature controller without noise.
| Performance Index | HS | FHS | FHS2 |
|---|
| RMSE | 6.34 × 10−2 | 6.75 × 10−2 | 6.25 × 10−2 |
| MSE | 2.44 × 10−2 | 4.55 × 10−3 | 4.62 × 10−3 |
| ITAE | 7.01 × 105 | 7.04 × 105 | 7.03 × 105 |
| ITSE | 1.06 × 106 | 1.07 × 106 | 1.07 × 106 |
| IAE | 1.40 × 103 | 1.41 × 103 | 1.41 × 103 |
| ISE | 2.11 × 103 | 2.12 × 103 | 2.12 × 103 |
Table 7.
Errors obtained from the robot mobile controller without noise.
Table 7.
Errors obtained from the robot mobile controller without noise.
| Performance Index | HS | FHS | FHS2 |
|---|
| RMSE | 2.33 × 10−1 | 1.37 × 10−1 | 1.11 × 10−1 |
| MSE | 8.56 × 10 | 5.07 × 10 | 6.06 × 10 |
| ITAE | 2.18 × 105 | 2.11 × 105 | 3.03 × 106 |
| ITSE | 1.05 × 105 | 9.44 × 104 | 2.86 × 107 |
| IAE | 4.38 × 102 | 4.24 × 102 | 6.09 × 103 |
| ISE | 2.11 × 102 | 1.90 × 102 | 5.72 × 104 |
Table 8.
Errors obtained from the water tank controller with noise.
Table 8.
Errors obtained from the water tank controller with noise.
| Performance Index | HS | FHS | FHS2 |
|---|
| RMSE | 3.18 × 10−2 | 2.49 × 10−2 | 1.32 × 10−2 |
| MSE | 4.58 × 10−2 | 5.75 × 10−2 | 6.36 × 10−2 |
| ITAE | 3.87 × 104 | 3.68 × 104 | 3.49 × 104 |
| ITSE | 2.57 × 104 | 2.39 × 104 | 2.08 × 104 |
| IAE | 7.91 × 10 | 7.53 × 10 | 7.17 × 10 |
| ISE | 5.28 × 10 | 4.90 × 10 | 4.29 × 10 |
Table 9.
Errors obtained from the temperature controller with noise.
Table 9.
Errors obtained from the temperature controller with noise.
| Performance Index | HS | FHS | FHS2 |
|---|
| RMSE | 6.34 × 10−2 | 1.24 × 10−1 | 6.29 × 10−4 |
| MSE | 2.44 × 10−2 | 1.54 × 10−2 | 3.64 × 10−2 |
| ITAE | 7.01 × 105 | 6.98 × 105 | 6.98 × 105 |
| ITSE | 1.06 × 106 | 1.05 × 106 | 1.05 × 106 |
| IAE | 1.40 × 103 | 1.39 × 103 | 1.40 × 103 |
| ISE | 2.11 × 103 | 2.10 × 103 | 2.10 × 103 |
Table 10.
Errors obtained from the robot mobile controller with noise.
Table 10.
Errors obtained from the robot mobile controller with noise.
| Performance Index | HS | FHS | FHS2 |
|---|
| RMSE | 2.33 × 10−1 | 3.82 × 10−2 | 3.69 × 10−2 |
| MSE | 8.56 × 10 | 7.67 × 10 | 6.06 × 10 |
| ITAE | 2.18 × 105 | 3.09 × 106 | 3.10 × 106 |
| ITSE | 1.05 × 105 | 3.26 × 107 | 3.28 × 107 |
| IAE | 4.38 × 102 | 6.46 × 103 | 6.47 × 103 |
| ISE | 2.11 × 102 | 6.47 × 104 | 6.49 × 104 |
Table 11.
Parameters for the statistical z-test.
Table 11.
Parameters for the statistical z-test.
| Parameter | Value |
|---|
| Level of Significance | 95% |
| Alpha | 0.05% |
| Ha | µ1 < µ2 |
| H0 | µ1 ≥ µ2 |
| Critical Value | −1.645 |
Table 12.
Results for the statistical test with Type-1 and Type-2 FHS and HS without noise.
Table 12.
Results for the statistical test with Type-1 and Type-2 FHS and HS without noise.
| Water Tank Controller |
|---|
| Method | Mean | Standard Deviation | z-Value | Evidence |
| HS | 3.19 × 10−2 | 3.13 × 10−2 | 35.8789 | N.S |
| FHS | 2.60 × 10−1 | 1.55 × 10−2 | −50.7296 | S |
| FHS2 | 2.56 × 10−2 | 1.97 × 10−2 | −1.1733 | N.S |
Table 13.
Results for the statistical test with Type-1 and Type-2 FHS and HS without noise.
Table 13.
Results for the statistical test with Type-1 and Type-2 FHS and HS without noise.
| Temperature Controller |
|---|
| Method | Mean | Standard Deviation | z-Value | Evidence |
| HS | 6.34 × 10−2 | 3.12 × 10−3 | 6.4226 | N.S |
| FHS | 6.75 × 10−2 | 1.59 × 10−3 | −14.0672 | S |
| FHS2 | 6.25 × 10−2 | 1.13 × 10−3 | −1.4778 | N.S |
Table 14.
Results for the statistical test with Type-1 and Type-2 FHS and HS without noise.
Table 14.
Results for the statistical test with Type-1 and Type-2 FHS and HS without noise.
| Robot Mobile Controller |
|---|
| Method | Mean | Standard Deviation | z-Value | Evidence |
| HS | 2.33 × 10−1 | 2.18 × 10−1 | −2.0706 | S |
| FHS | 1.37 × 10−1 | 1.57 × 10−1 | −0.7959 | N.S |
| FHS2 | 1.11 × 10−1 | 1.37 × 10−1 | −2.7100 | S |
Table 15.
Results for the statistical test with Type-1 and Type-2 FHS and HS with noise.
Table 15.
Results for the statistical test with Type-1 and Type-2 FHS and HS with noise.
| Water Tank Controller |
|---|
| Method | Mean | Standard Deviation | z-Value | Evidence |
| HS | 3.18 × 10−2 | 3.13 × 10−2 | −1.0134 | N.S |
| FHS | 2.49 × 10−2 | 2.01 × 10−2 | −2.5236 | S |
| FHS2 | 1.32 × 10−2 | 1.54 × 10−2 | −2.9164 | S |
Table 16.
Results for the statistical test with Type-1 and Type-2 FHS and HS with noise.
Table 16.
Results for the statistical test with Type-1 and Type-2 FHS and HS with noise.
| Temperature Controller |
|---|
| Method | Mean | Standard Deviation | z-Value | Evidence |
| HS | 6.34 × 10−2 | 3.12 × 10−3 | 72.5412 | N.S |
| FHS | 1.24 × 10−1 | 3.34 × 10−3 | −201.3932 | S |
| FHS2 | 6.29 × 10−4 | 1.07 × 10−4 | −109.8982 | S |
Table 17.
Results for the statistical test with Type-1 and Type-2 FHS and HS with noise.
Table 17.
Results for the statistical test with Type-1 and Type-2 FHS and HS with noise.
| Robot Controller |
|---|
| Method | Mean | Standard Deviation | z-Value | Evidence |
| HS | 2.33 × 10−1 | 2.18 × 10−1 | −4.8553 | S |
| FHS | 3.82 × 10−2 | 4.22 × 10−2 | −0.2277 | N.S |
| FHS2 | 3.69 × 10−2 | 4.20 × 10−2 | −4.8866 | S |