Abstract
The main goal of this paper is to improve the performance of the Fireworks Algorithm (FWA). To improve the performance of the FWA we propose three modifications: the first modification is to change the stopping criteria, this is to say, previously, the number of function evaluations was utilized as a stopping criteria, and we decided to change this to specify a particular number of iterations; the second and third modifications consist on introducing a dispersion metric (dispersion percent), and both modifications were made with the goal of achieving dynamic adaptation of the two parameters in the algorithm. The parameters that were controlled are the explosion amplitude and the number of sparks, and it is worth mentioning that the control of these parameters is based on a fuzzy logic approach. To measure the impact of these modifications, we perform experiments with 14 benchmark functions and a comparative study shows the advantage of the proposed approach. We decided to call the proposed algorithms Iterative Fireworks Algorithm (IFWA) and two variants of the Dispersion Percent Iterative Fuzzy Fireworks Algorithm (DPIFWA-I and DPIFWA-II, respectively).
1. Introduction
At the present time, computer science is used for solving problems through its different areas (fuzzy logic, neural networks, evolutionary computing, among others). Depending on the type of problem, the aim may be minimizing or maximizing (optimization) the expected results, which is the main idea in this area. There are many bio-inspired metaheuristics that are based on behaviors found in nature, for example, swarm behavior of birds and insects [1].
As with all things in life, the optimization algorithms have advantages and disadvantages. One of the disadvantages of these algorithms is that in early versions, or conventional versions, almost all the parameters are constant, that is, relevant parameters in the mathematical formulas of each algorithm remain statics during their performance. Thus, the performance of the exploration and exploitation into the algorithm is chaotic, that is, the static parameters do not allow for control of the balance between exploration and exploitation. Sometimes the algorithms just explore, and so, move away from the goal, or the algorithm could just exploit and become stagnate without allowing for a search for better solutions to achieve of the goal.
We know that in a computational algorithm, the mathematical representation is very important; this is why we opted for representations (formulas) based on existing mathematics to modify the fireworks algorithm (FWA). We decided to use one of the dispersion measures that already exists in the mathematical area, which is the standard deviation, and based on this dispersion measure, we obtained a parameter which we call the dispersion percent that will be explained in Section 4 and Section 5. The dispersion percent is one of the parameters that were used as an input variable in the fuzzy inference system to achieve the dynamic adaptation of the two parameters (explosion amplitude and number of sparks). We achieved this adaptation based on fuzzy logic, because nowadays fuzzy logic has been shown to have a relevant impact in the area of control.
With the intention to overcome the inconveniences above mentioned, we present the implementation of two fuzzy inference systems (FIS); in the first FIS, we have two input variables (Iteration and Dispersion Percent) and one output variable (Amplitude Explosion), and in the second FIS, we have the same two input variables as that of the first FIS, but we have two output variables (Amplitude Explosion and Sparks). With this work, we simulate the control, both automatically and sequentially, of the balance between exploration and exploitation into the algorithm.
The remainder of the paper is organized as follows: we start with a literature review in Section 2. In Section 3 we present the original Fireworks Algorithm (FWA), and the Iterative Fireworks Algorithm is proposed and explained in Section 3. In Section 4 and Section 5 we describe the proposed modifications (Dispersion Percent Iterative Fuzzy Fireworks Algorithm (DPIFFWA-I and II, respectively)), the obtained results are presented in Section 6, and finally, we conclude the paper by mentioning possible future work in Section 7.
2. Literature Review
Swarm intelligence is the study of computational systems inspired by ‘collective intelligence’. Collective intelligence emerges through the cooperation of large numbers of homogeneous agents in the environment. Examples include schools of fish, flocks of birds, and colonies of ants. Such intelligence is decentralized, self-organizing, and distributed throughout an environment. In nature, such systems are commonly used to solve problems such as effective foraging for food, prey evasion, or colony re-location. The information is typically stored throughout the participating homogeneous agents, or is stored or communicated in the environment itself such as through the use of pheromones in ants, dancing in bees, and proximity in fish and birds [2].
In recent years, swarm intelligence (SI), has been very popular among researchers working on optimization problems around the world [3]. Some examples of SI are the following algorithms [4]:
- PSO (Particle Swarm Optimization)
- ACO (Ant Colony Optimization)
- ABC (Artificial Bee Colony)
- GA (Genetic Algorithm)
Particle Swarm Optimization (PSO) is inspired by the social foraging behavior of some animals such as flocking behavior of birds and the schooling behavior of fish. The goal of the algorithm is to have all the particles locate the optima in a multi-dimensional hyper-volume. This is achieved by assigning initially random positions to all particles in the space and small initial random velocities. The algorithm is executed like a simulation, advancing the position of each particle in turn based on its velocity, the best known global position in the problem space, and the best position known to a particle. The objective function is sampled after each position update. Over time, through a combination of exploration and exploitation of known good positions in the search space, the particles cluster or converge together around optima, or several optima [5].
The Ant Colony System (ACO) algorithm is inspired by the foraging behavior of ants, specifically the pheromone communication between ants regarding a good path between the colony and a food source in an environment. Ants initially wander randomly around their environment. Once food is located, an ant will begin laying down pheromone in the environment. Numerous trips between the food and the colony are performed, and if the same route is followed that leads to food, then additional pheromone is laid down. Pheromone decays in the environment, so that older paths are less likely to be followed. Other ants may discover the same path to the food and in turn may follow it and also lay down pheromone. A positive feedback process routes more and more ants to productive paths that are in turn further refined through use [6].
The Bees Algorithm (ABC) is inspired by the foraging behavior of honey bees. Honey bees collect nectar from vast areas around their hive (more than 10 km). Bee Colonies have been observed to send bees to collect nectar from flower patches relative to the amount of food available at each patch. Bees communicate with each other at the hive via a waggle dance that informs other bees in the hive as to the direction, distance, and quality rating of food sources. The strategy of this algorithm is the information processing to achieve the objective, which is to locate and explore good sites within a problem search space. Scouts are sent out to randomly sample the problem space and locate good sites. The good sites are exploited via the application of a local search, where a small number of good sites are explored more than the others. Good sites are continually exploited, although many scouts are sent out in each iteration in search of additional good sites [7].
The Genetic Algorithm (GA) is inspired by population genetics (including heredity and gene frequencies) and evolution at the population level, as well as the Mendelian understanding of the structure (such as chromosomes, genes, alleles) and mechanisms (such as recombination and mutation). This is the so-called new or modern synthesis of evolutionary biology. The objective of the Genetic Algorithm is to maximize the payoff of candidate solutions in the population against a cost function from the problem domain. The strategy for the Genetic Algorithm is to repeatedly employ surrogates for the recombination and mutation genetic mechanisms on the population of candidate solutions, where the cost function (also known as objective or fitness function) applied to a decoded representation of a candidate governs the probabilistic contributions a given candidate solution can make to the subsequent generation of candidate solutions [5].
On the other hand, we should mention in a general way that fuzzy logic is a methodology that provides a simple way to obtain a conclusion from ambiguous, imprecise, or linguistic information inputs. Of course, it is well known that in 1965, Zadeh proposed the formal definition of fuzzy sets [8].
A fuzzy set in is characterized by a membership (characteristic) function , which associates with each point in a real number in the interval [0, 1], with the value of at representing the “degree of membership” of in . Thus, the closer the value of to unity, the higher the degree of membership of in . When is a set in the ordinary sense of the term, its membership function can take on only two values, 0 or 1, with = 1 or 0 according to whether does or does not belong to . Thus, in this case, reduces to the familiar characteristic function of in set . When there is a need to differentiate between such sets and fuzzy sets, the sets with two-valued characteristic functions will be referred to as ordinary sets or simply sets [9].
3. Fireworks Algorithm (FWA)
The Fireworks Algorithm (FWA) is a swarm intelligence method, which was developed by Ying Tan and Yuanchun Zhu in 2009, based on the explosion behavior of fireworks [10].
For each firework, we begin a process of explosion, and a shower of sparks fill the local space around the firework. The recently generated sparks represent possible solutions in the search space [11].
To mimic the above mentioned process, the algorithm is represented mathematically as described below.
4. Number of Sparks
After, using the following equation, the number of sparks for each firework is generated.
where represents a constant parameter which controls the numbers of sparks of thefireworks and is the maximum value, that is, the worst value of the objective function in thefireworks andindicates a constant representing the smallest number in the computer, and it is utilized with the goal that an error with a division by zero cannot occur [13].
With Equation (3), we can define the bounds for the number of sparks, with the goal of keeping a balance within a range of number of sparks. The bounds are defined for as follows:
where and are constant parameters [14].
5. Amplitude of Explosion
On the contrary, to calculate the number of sparks, an explosion is better if the amplitude is small. The explosion amplitude for each firework is calculated as follows:
where is a constant parameter that controls the maximum amplitude of each firework, = indicates the minimum value (best) of the objective function among fireworks, and indicates the smallest constant in the computer, and it is used with the goal of not making an error with the division by zero [15].
6. Generating Sparks
In this part of the algorithm (FWA), we consider two other more specific algorithms, called Algorithms 1 and 2, which are used to obtain the location of the sparks, and these algorithms are described in previous works of the authors [16,17]. However, before obtaining the location of the sparks, we should know that the sparks can take on different directions (in random dimensions), and these dimensions are obtained as expressed below:
Here,is the dimension of the location for each sparkand is a random value between 0 and 1.
7. Selection of the Locations
Below, we present the equations that are used in this algorithm to select the best current location.
where is the set of all current locations from both fireworks. Then, the probability for selection of a location at is defined as:
When calculating the distance, any distance measure can be used including the Manhattan distance, Euclidean distance, or Angle-based distance, among others [18,19,20].
Figure 1 shows the pseudocode of the conventional Fireworks Algorithm (FWA).

Figure 1.
Pseudo code of Fireworks Algorithm (FWA).
8. Iterative Fireworks Algorithm
Some optimization algorithms use the number of iterations as the stopping criteria, alternatively, other algorithms use the number of function evaluations. Based on the literature, we have noticed that some algorithms do not take into account that both stopping criteria are not exclusive, the number of iterations is based on the number of solutions to evaluate for each iteration.
We should also mention that in some algorithms the number of solutions to evaluate are static per iteration, and in others, the number of solutions to evaluate changes, such is the case of the Fireworks Algorithm (FWA) in which the number of sparks (solutions) changes per iteration.
If we want to compare two or more methods, we must consider the methods under equal circumstances. For example, if we compare two methods with 200 iterations, an important point is to show how many function evaluations are made per iteration and in total. In other words, if in one method we used 100 solutions per iteration and a total of 20,000 function evaluations, and in the other method we used 50 solutions per iteration and a total of 50,000 function evaluations, then these would not be equivalent to do a comparison between both methods. It is important mention that the total number of function evaluations is calculated by multiplying the total number of iterations by the number of solutions per iteration.
Before going into a detailed explanation of the methods that we propose, we mentioned the previous algorithm (Iterative Fireworks Algorithm) because it was the first modification that we proposed. However, now we change the stopping criteria; before, it was the number of function evaluations, now, it is the number of iterations. The reason for making this change is because in this form, we can now control parameters in a more sequential form, and it is worth mentioning that this is the conventional fireworks algorithm but with the unique change in the stopping criteria.
9. Dispersion Percent Iterative Fuzzy Fireworks Algorithm (DPIFFWA-I)
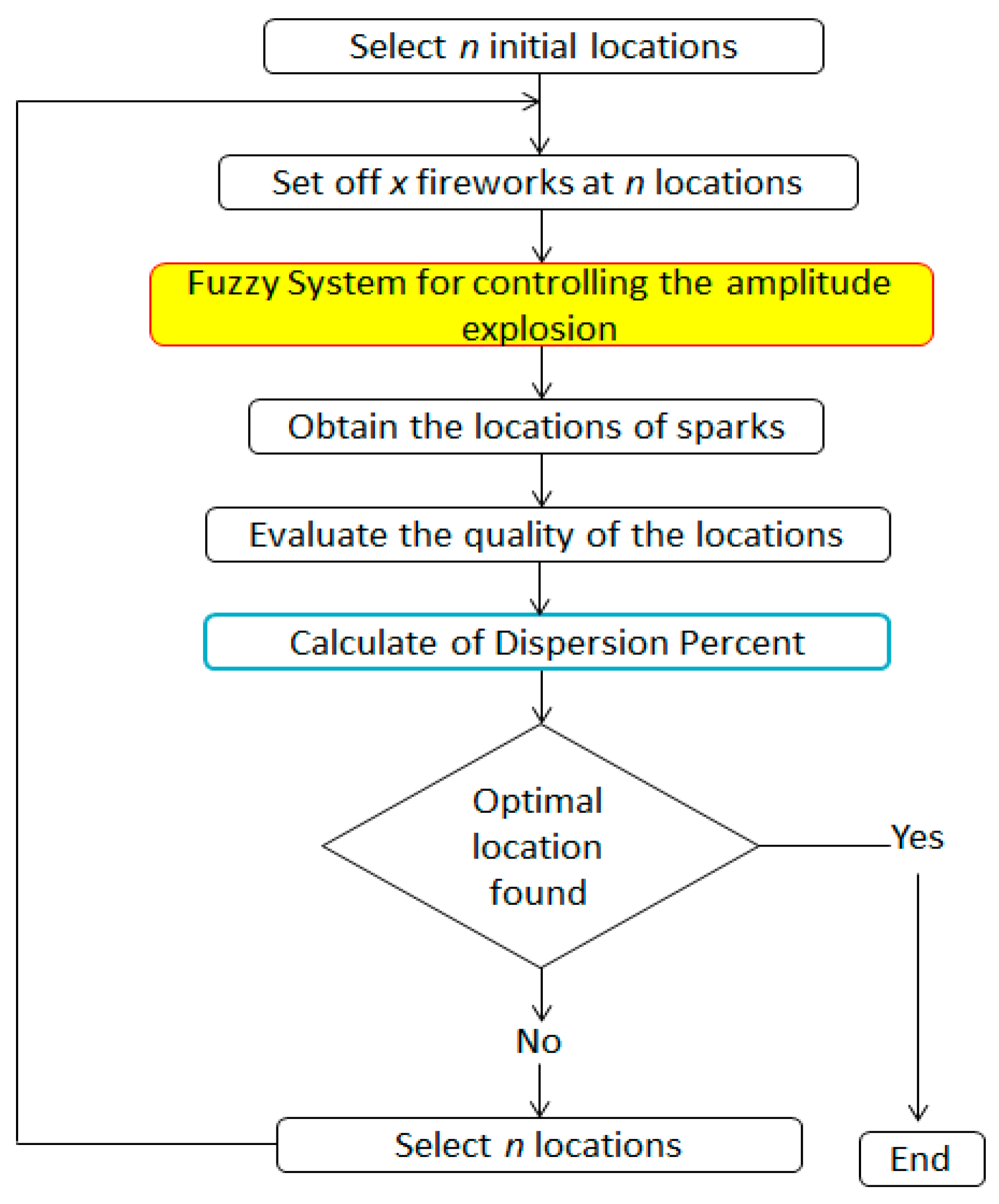
The Dispersion Percent Iterative Fireworks Algorithm (DPIFFWA-I) is what we call the second modification that we performed to the conventional Fireworks Algorithm (FWA) and the Fuzzy Fireworks Algorithm (FFWA) to control the explosion amplitude of each firework using fuzzy logic [16,17]. Figure 2 illustrates the proposed DPIFFWA using a flow chart that illustrates the information processing in this algorithm.
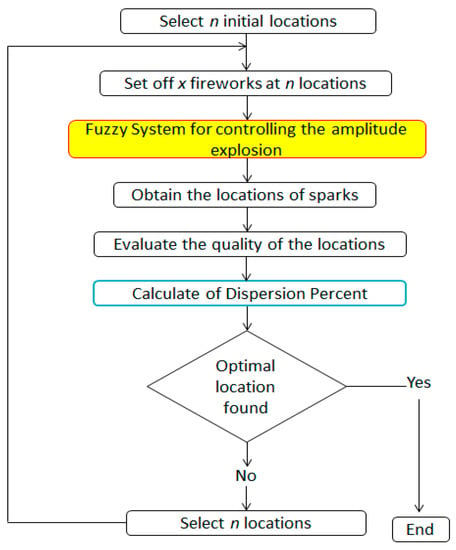
Figure 2.
Flow chart of Dispersion Percent Iterative Fireworks Algorithm (DPIFFWA).
In this modification, we have added a parameter that we can calculate by using the following equation:
where is the Dispersion Percent, is the Current Standard Deviation and is the Current Mean of each iteration, and every above mentioned parameter is calculated based on the fitness of each seed (sparks). We introduced this parameter with the goal of evaluating the separation of each seed (spark) to confirm that the exploration and exploitation are working in a balanced way [21,22], in other words, in the initial iterations we explore and in the last iterations we exploit.
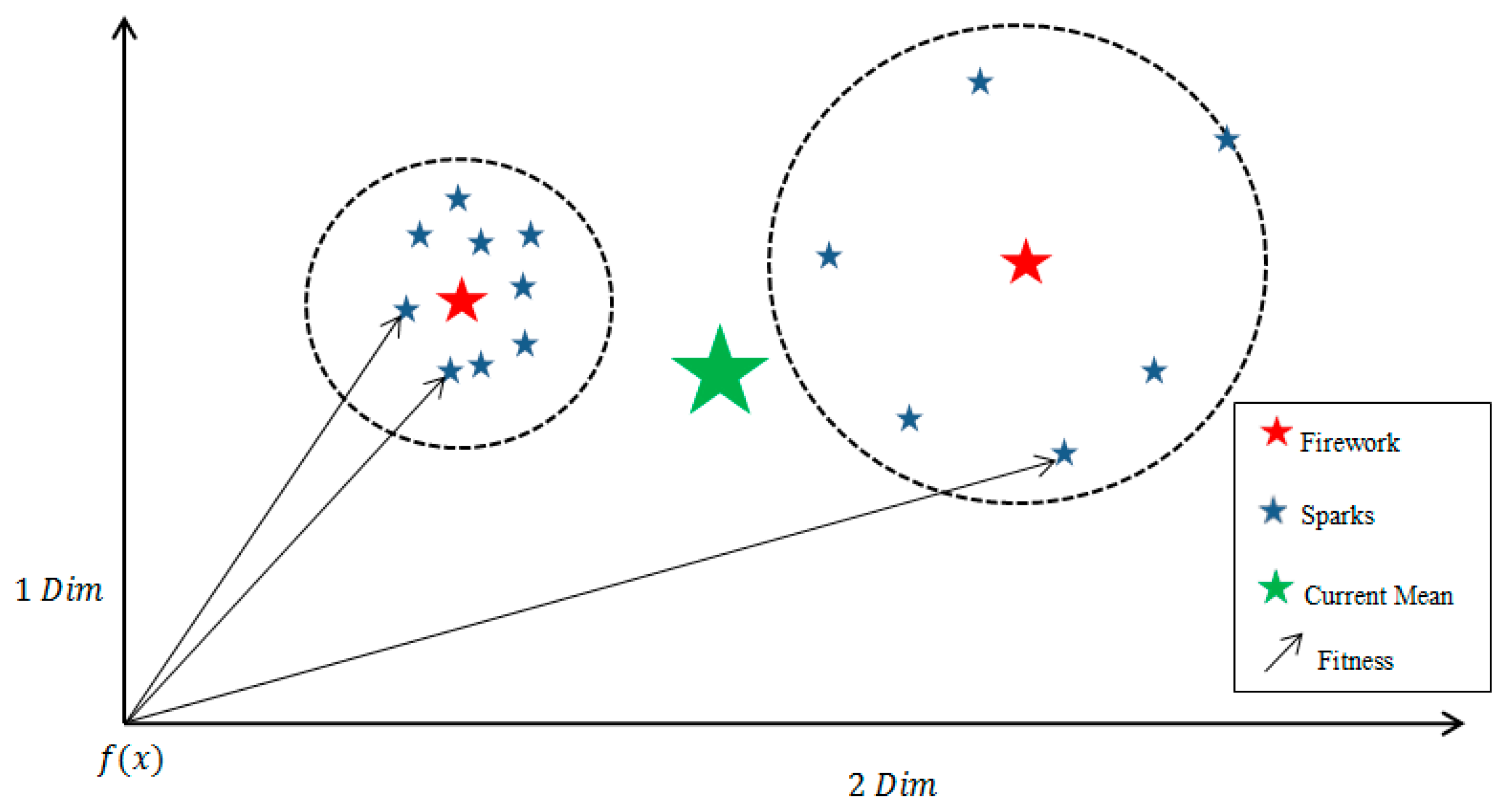
To show the current mean (), we illustrate this in Figure 3 with a plot in two dimensions.
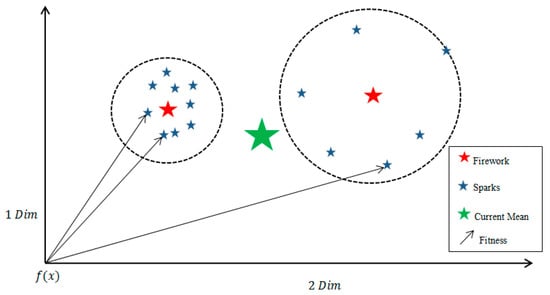
Figure 3.
Current mean of the = fitness of the sparks.
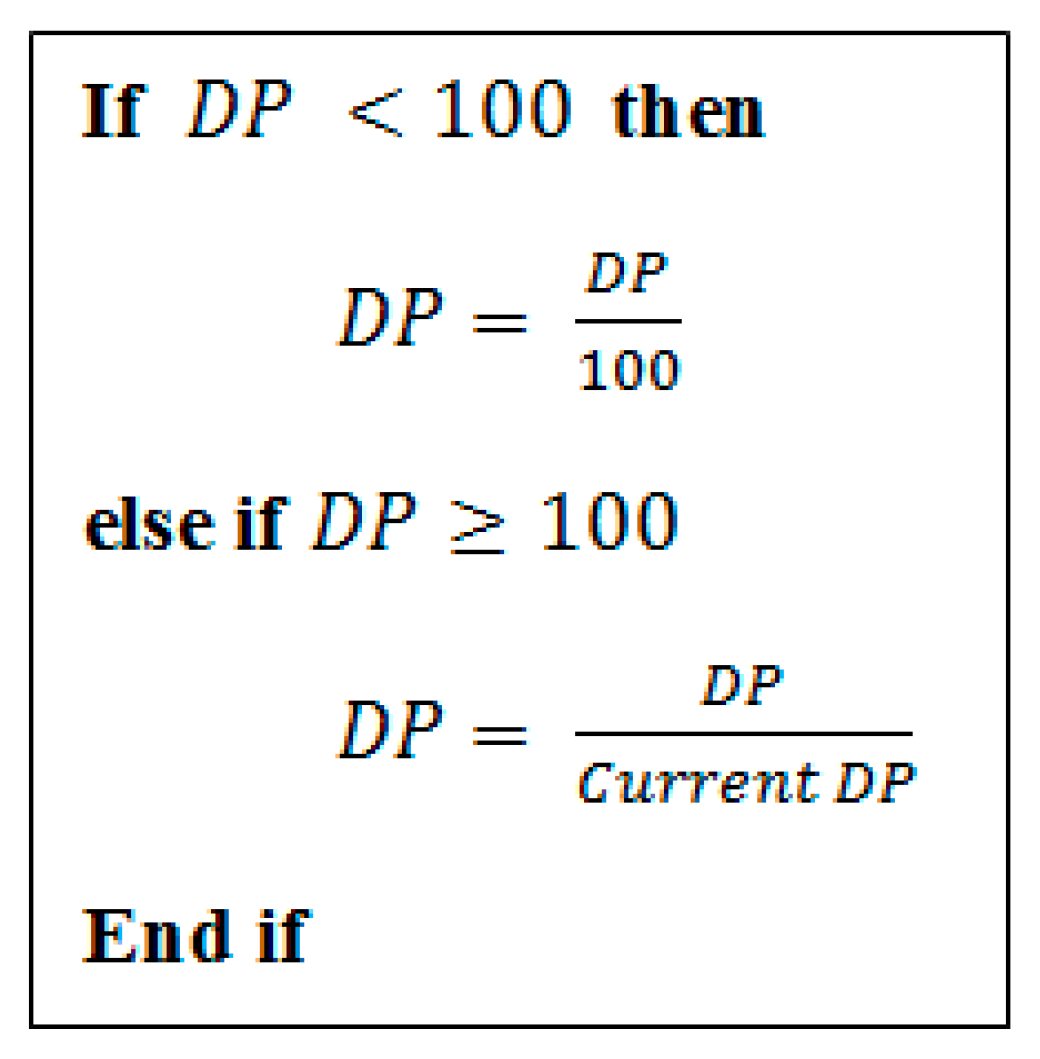
In some cases is greater than 100, and then to avoid an unbalanced situation, we can keep a range of between 1 and 100, and for this reason we have added the following requirement shown in Figure 4.
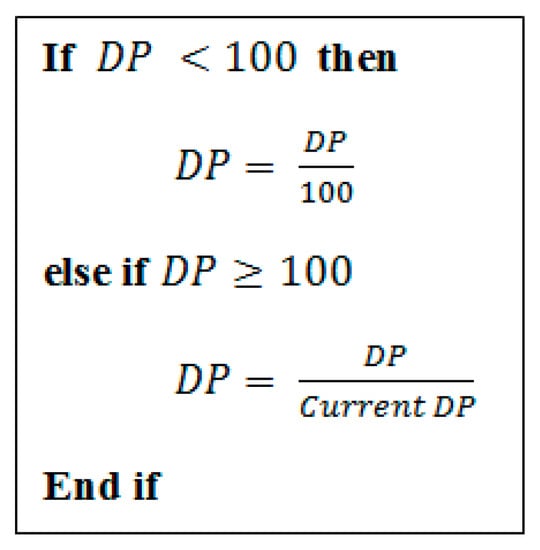
Figure 4.
Requirement for.
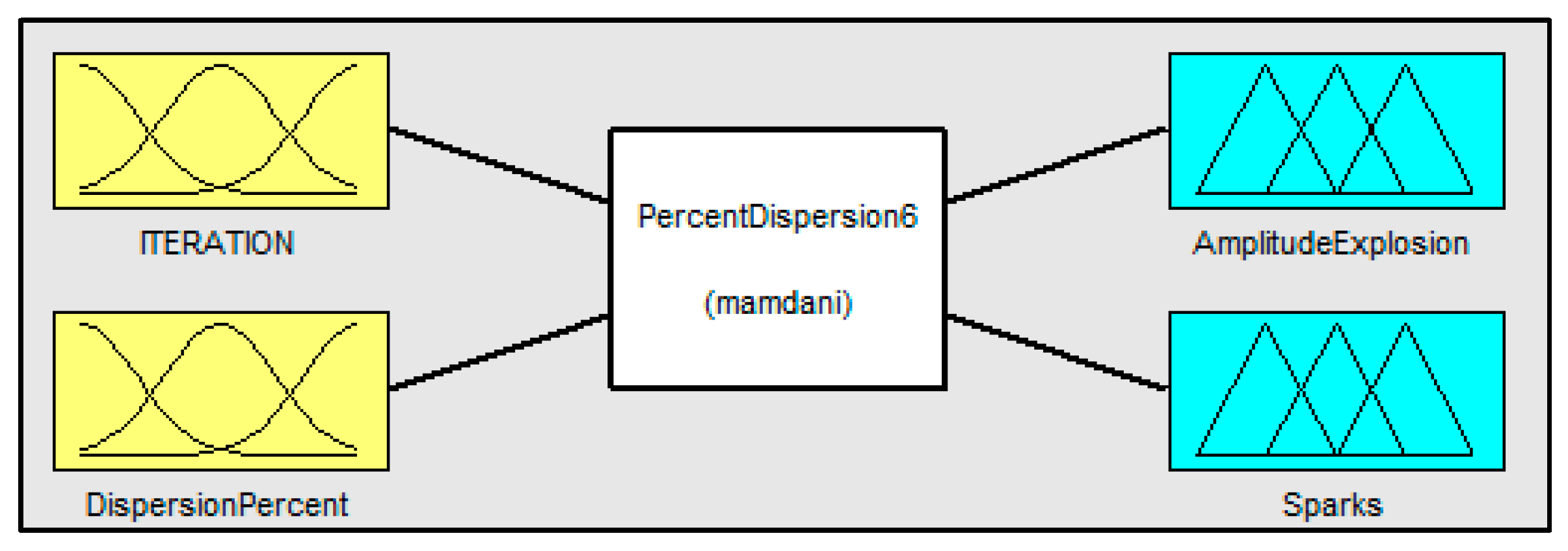
With the requirement for DP shown in Figure 4, we can obtain a value between 0 and 1; this value (DP) is an input variable of the fuzzy inference system (Figure 5), which is explained in more detail in the following sections.
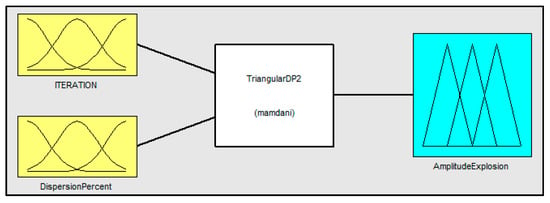
Figure 5.
Graphical representation of the Fuzzy System for DPIFFWA-I.
Another input variable is the “Iteration”, and to streamline and enhance the process of the fuzzy inference system and of course the general process of the algorithm, we normalized the input variable, which is called the Iteration; the normalization is calculated with the following equation [23].
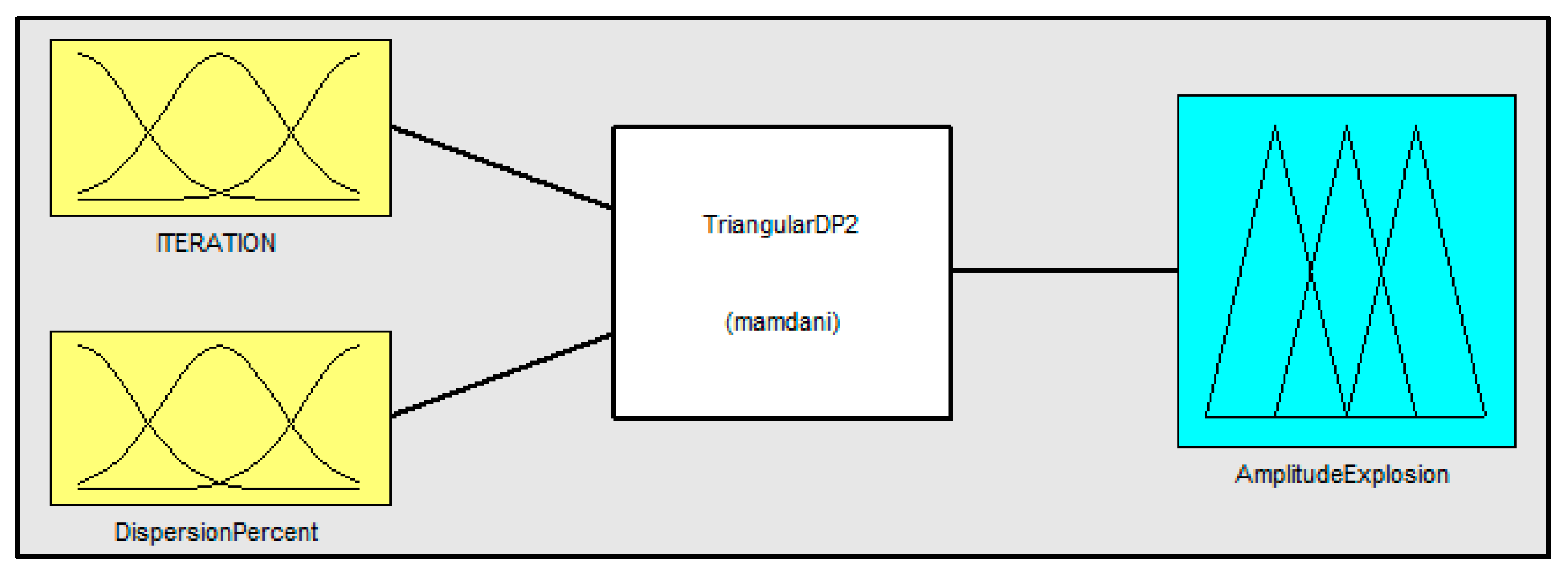
Figure 5 shows the general structure of the fuzzy system for DPIFFWA-I:
The system that we used has the following characteristics: two input variables, the number of iterations (Iteration) and (DispersionPercent), and one output variable. The output variable is defined to control the amplitude explosion (AmplitudeExplosion) of each firework; this fuzzy inference system is of Mamdani type [24].
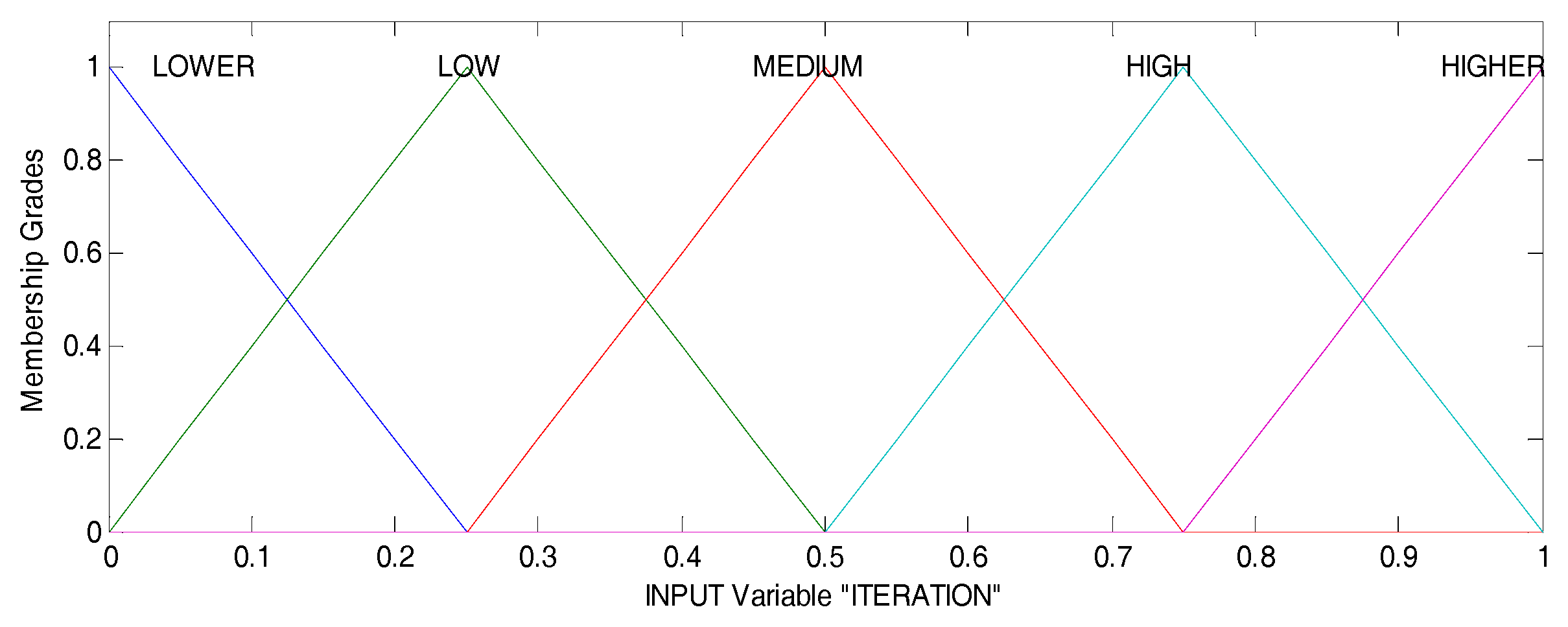
As we can note in Figure 6, the input variable (Iteration) has five linguistic values, called LOWER [−0.25 0 0.25], LOW [0 0.25 0.5], MEDIUM [0.25 0.5 0.75], HIGH [0.5 0.75 1], and HIGHER [0.75 1 1.25] (membership functions), of triangular form in a range of [0, 1]. We used the range between 0 and 1 (because of the normalization) to work with smaller numbers, and in this way, the calculations of the fuzzy system are faster, as we mentioned above and was represented in Equation (9).
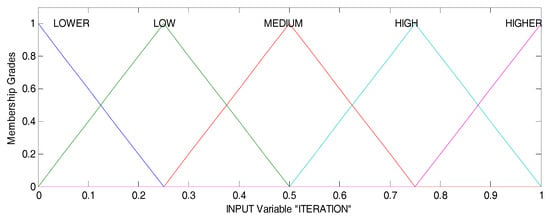
Figure 6.
Input variable of DPFFWA-I (Iteration).
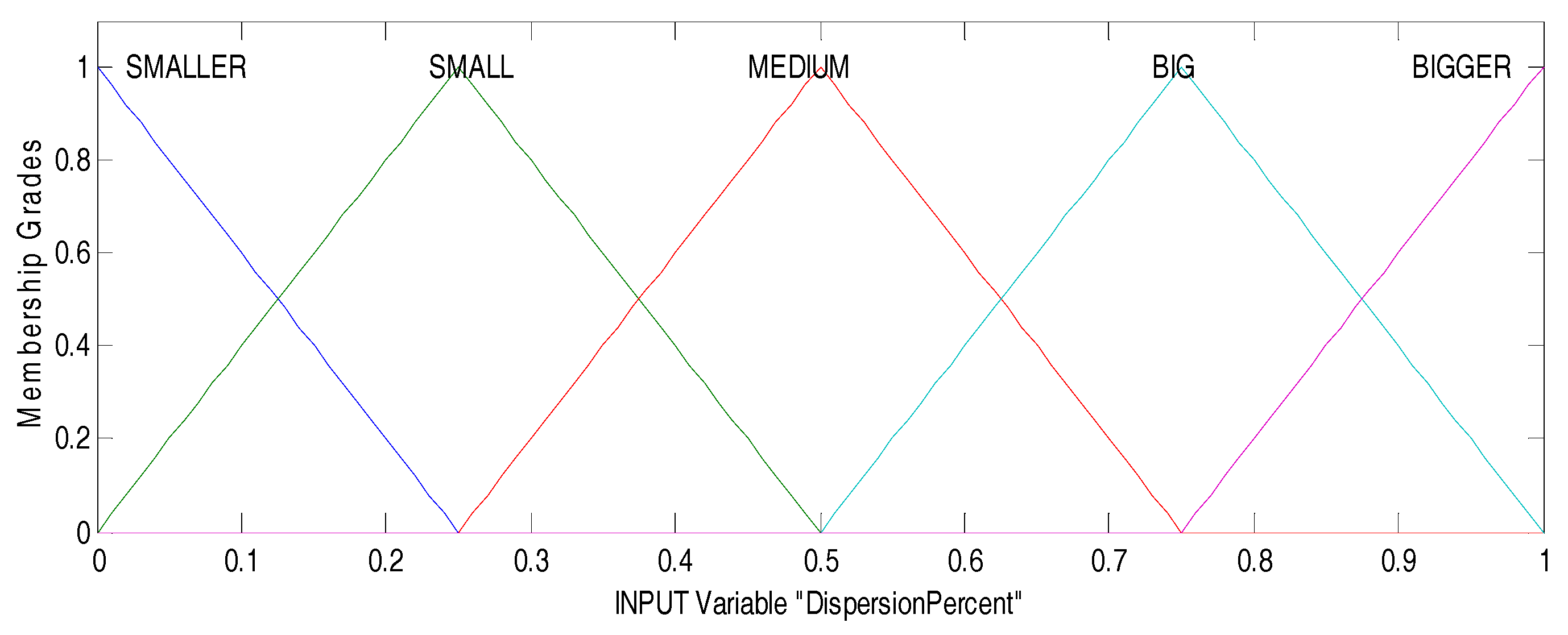
Figure 7 shows the input variable (DispersionPercent), and this linguistic variable has five values that are called SMALLER [−0.25 0 0.25], SMALL [0 0.25 0.5], MEDIUM [0.25 0.5 0.75], HIGH [0.5 0.75 1], and HIGHER [0.75 1 1.25], and the partition is formed by the membership functions of triangular form with a range of [0, 1].
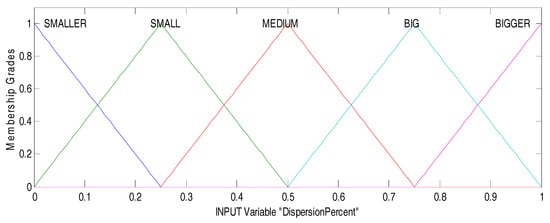
Figure 7.
Input variable of DPFFWA-I (DispersionPercent).
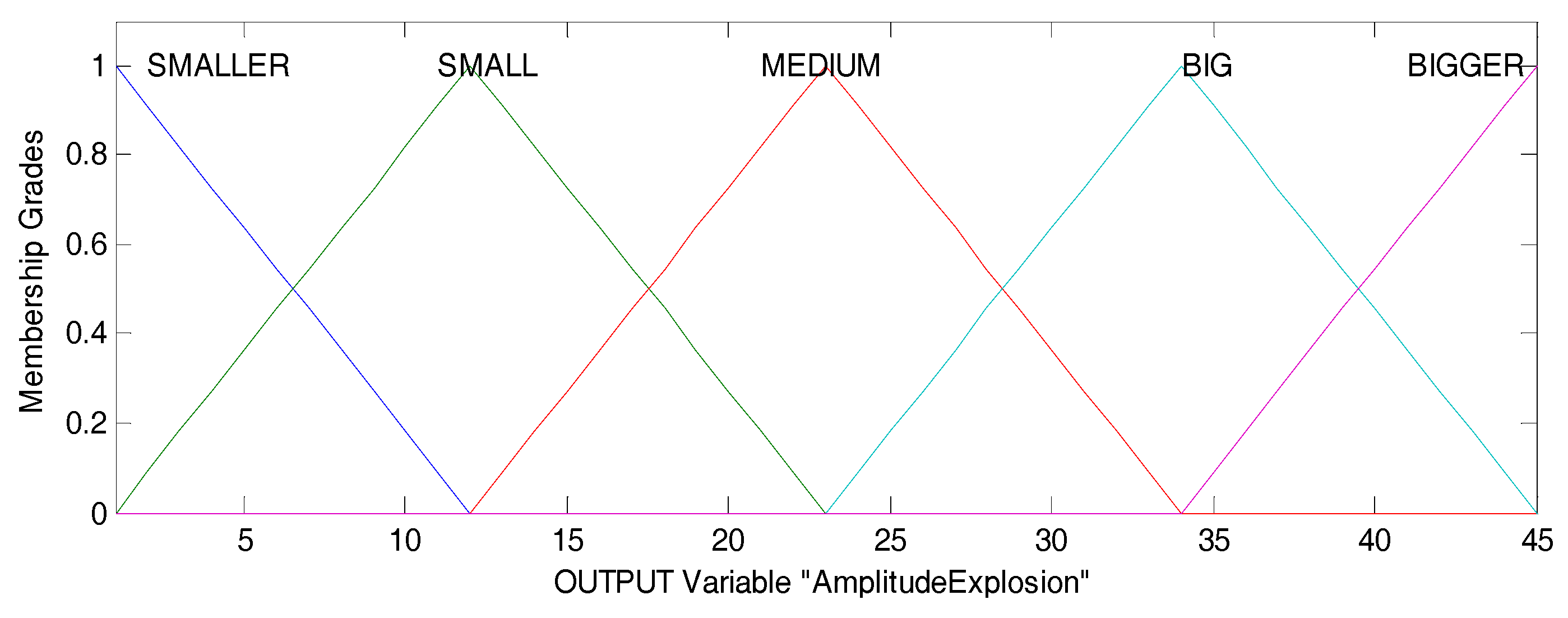
Figure 8 illustrates the output variable (AmplitudeExplosion) that has five linguistic values in a range of [2, 45], and the reason we use this range is for keeping the amplitude explosion between 2 and 40, approximately. The linguistic values have the names of SMALLER [−10 2 12], SMALL [2 12 23], MEDIUM [12 23 34], BIG [23 34 45], and BIGGER [34 45 56], and the form of each linguistic value is triangular (membership functions).
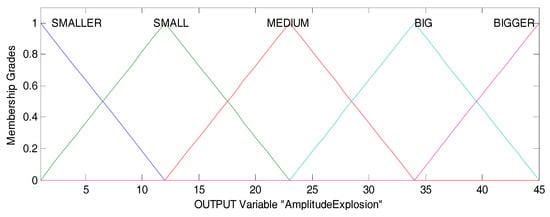
Figure 8.
Output variable of DPFFWA-I (AmplitudeExplosion).
As we mentioned above, the fuzzy inference system is used to control the explosion amplitude of each firework, and this control consists of 25 fuzzy rules that are listed in Table 1.

Table 1.
Fuzzy rules of DPIFFWA-I.
With the 25 rules described in Table 1, we can sequentially control the exploration and exploitation within the algorithm (DPIFFWA). The exploration will be performed when the Iteration is Lower and DP is Smaller, Small, etc. (rules 1 to 5), the DPIFFWA algorithm also will explore when the Iteration is Low and DP is Smaller, Small, etc. (rules 6 to 10). The rule numbers 10, 11, 12, 13, 14, and 15 will enable having a balance between exploration and exploitation. With the last rules (16 to 25), the DPIFFWA algorithm will exploit. Although we have 25 fuzzy rules, we consider only 5 fuzzy rules as the main rules, and these are the rules 1, 7, 13, 19, and 25. The reason why we have 25 fuzzy rules and we only consider 5, is because the fuzzy inference system is symmetric, this is to say, it has 5 membership functions in each variable.
When we introduce the fuzzy inference system and are able to control the explosion amplitude, we can also eliminate Equation (4) of the conventional fireworks algorithm (FWA); in this form, we can dynamically control the parameter (explosion amplitude) and omit Equation (4) so that we do not have the extra computational overhead.
10. Dispersion Percent Iterative Fuzzy Fireworks Algorithm II (DPIFFWA-II)
DPIFFWA-II is the third modification that we have made to the FWA and FFWA. This modification is almost the same as the second modification, but the unique difference is that we have now added another output variable to the fuzzy inference system; the new output variable is called “Sparks”. This output variable (Sparks) will allow controlling the number of sparks for each firework during the exploitations phase. Figure 9 illustrates the general structure of the fuzzy system for the DPIFFWA-II:
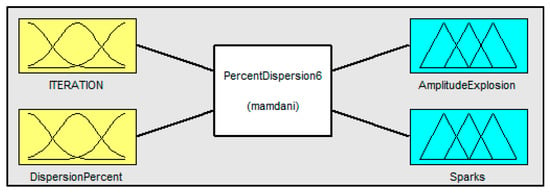
Figure 9.
Graphical representation of the Fuzzy System for DPIFFWA-II.
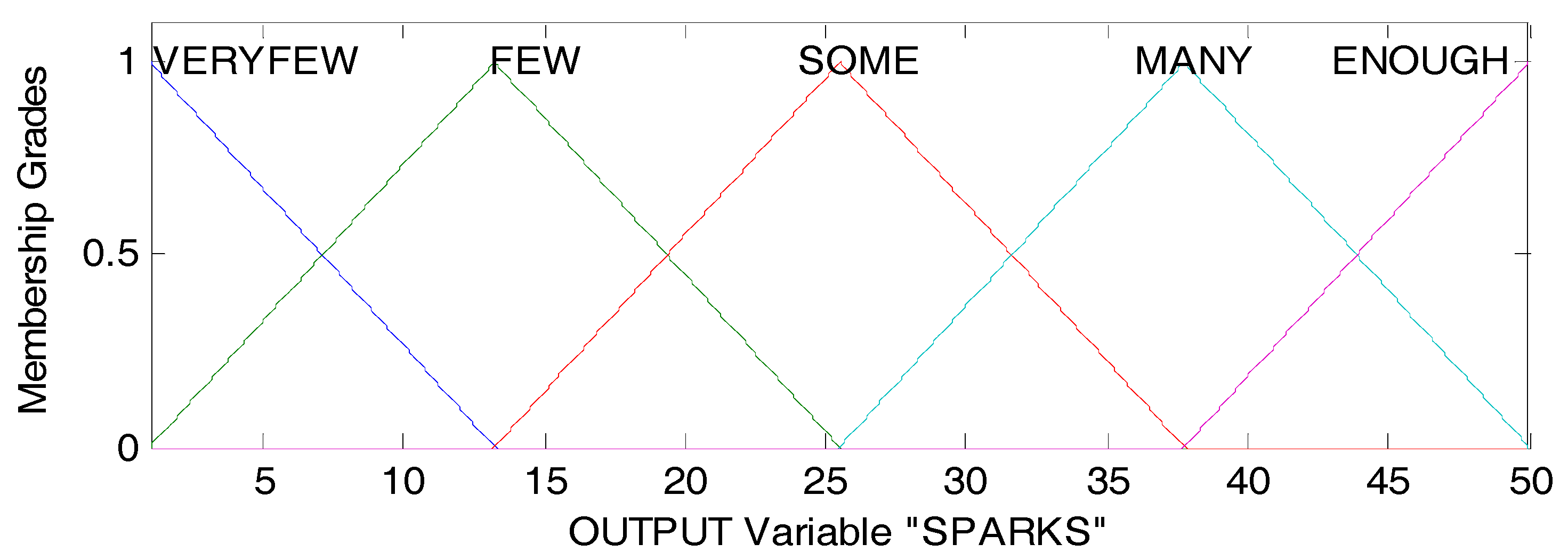
The following values are the linguistic values: VERYFEW [−11.25 1 13.25], FEW [1 13.25 25.5], SOME [13.25 25.5 37.75], MANY [25.5 37.75 50], and ENOUGH [37.75 50 62.25]. In Figure 10, we show the “Sparks” output variable.
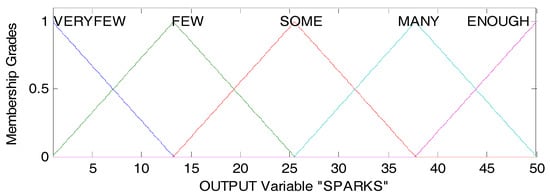
Figure 10.
Output variable of DPFFWA-II (SPARKS).
In Table 2 we present the fuzzy rules of the third modification (DPIFFWA-II).

Table 2.
Fuzzy rules of DPIFFWA-II.
As we mentioned in previously, of the 25 rules, only 5 rules have a weighting (rule 1, 7, 13, 19, and 25), which we will explain in more detail below.
We start the Sparks with a small value and an “ExplosionAmplitude” with a big value, this is to say, while the range of the Iteration is maintained in LOWER [−0.25, 0.25] and the “DispersionPercent” is SMALLER [−0.25, 0.25], the “ExplosionAmplitude” will be BIGGER in a range of [34, 56], and the sparks are VERYFEW in a range of [−11.25, 13.25].
The rule number 7 states that if iteration is LOW [0, 0.5] and “DispersionPercent” is SMALL [0, 0.5], the “ExplosionAmplitude” is BIG [22, 45] and the sparks will be FEW [1, 25.5]. In the same way, we can achieve the exploration in the algorithm with rules 1 and 7, following with the rules, the next rule (number 13) provides a balance between exploration and exploitation in the algorithm, because if the Iteration is MEDIUM [0.25, 0.75] and the “DispersionPercent” is also MEDIUM [0.25, 0.75], then the “ExplosionAmplitude” will be MEDIUM [11, 34] and the Sparks will be SOME [13.25, 37.75], and this will make the algorithm sometimes explore and other times exploit.
Finally, the algorithm only exploits with rules 19 and 25, knowing that if the Iteration is HIGH [0.5, 1] and the “DispersionPercent” is SMALL, then the “ExplosionAmplitude” will be SMALL [2, 2 3] and the Sparks is MANY [25, 50] (rule 19), and the last rule (rule 25) states that if the Iteration is HIGHER [0.75, 1.25] and the “DispersionPercent” is BIGGER [0.75, 1.25], then the Sparks will be ENOUGH [37.75, 62.25] and the “ExplosionAmplitude” is SMALLER [−8.5, 12.5] having great relevance in the explosion amplitude from each firework, thus, we can omit both Equations (2) and (4).
11. Results and Discussion
To evaluate the performance of the calculations involved for a new number of sparks and the new explosion amplitude, in Equations (2) and (4) we performed tests with 14 benchmark functions, with different ranges (search and initialization) and optimal values.
In Table 3 we list the names of all functions that were used with optimal values equal to 0, as well as their ranges of initialization and number of dimensions.

Table 3.
Benchmark functions utilized for the experiments (optimum equal to zero).
Where is the Ackley function, is the Griewank function, is the Rastrigin function, is the Rosenbrock function, is the Schwefel function, and is the Sphere function, and the function numbers 1 to 6 are presented in Table 3.
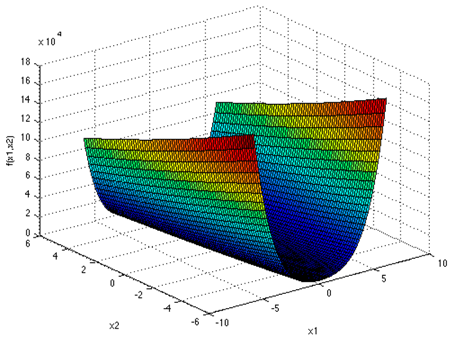
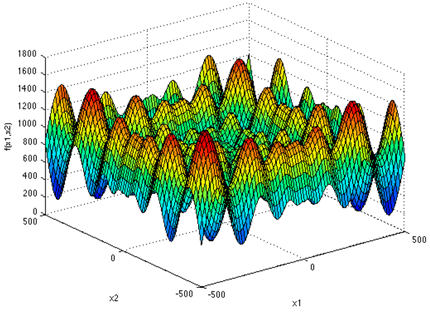
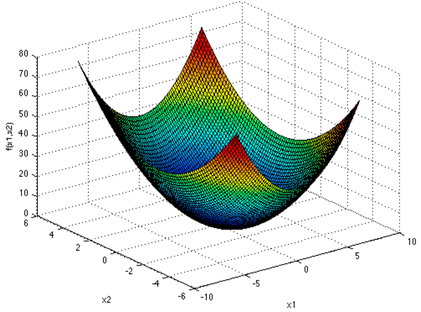
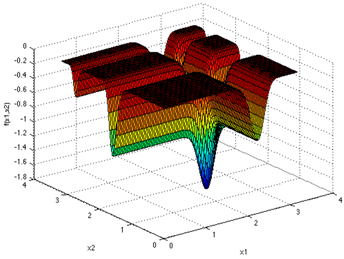
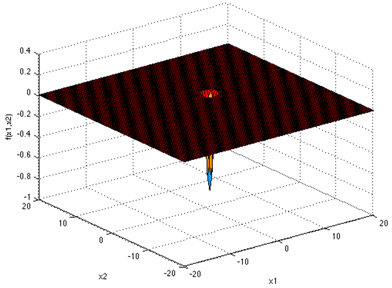
Table 4 illustrates the equations and surfaces of every benchmark function with optimal values equal to zero.

Table 4.
Equations and plots of the benchmark functions with optimal values equal to zero.
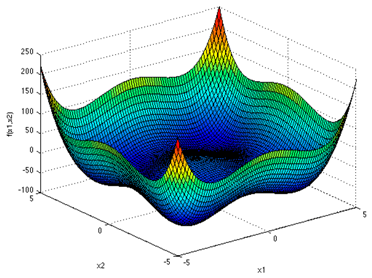
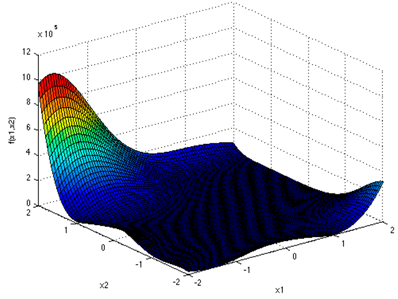
In Table 5 we show the surface of every benchmark function with optimal values different from zero.

Table 5.
Equations and plots of benchmark functions with optima different from zero.
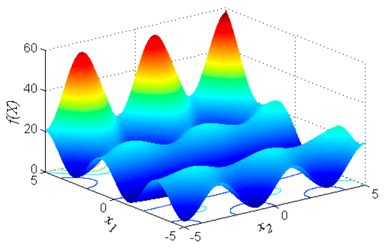
In Table 6 we can find functions 7 to 14, where is the Styblinski-Tang function, is the Michalewicz (2-D) function, is the Michalewicz function (10-D), is the Easom function, is the Goldstein Price function, is the Penalized P16 function, is the Six Hump Camel-back function, and is the Trid Function [25,26].

Table 6.
Benchmark functions utilized for the experiments (optima different from zero).
For each function, the initial range was set to , where is the upper bound of the search space in the kth dimension. In the experiments, a number of shift values were added to these basic functions in order to shift the global optimum. We used three different shift indices in order to analyze the influence of different shift values on the performance of the algorithms as can be found in Table 7. The SI is the shift index and SV is the shift value used [11].

Table 7.
Shift Index (SI) and Shift Value (SV) [27].
In Table 8 and Table 9, we performed comparisons of the averages and standard deviations among Iterative Fireworks Algorithm (IFWA) and the two variations of FFWA with 0.05 and 0.1 for the Shift Index values, respectively.

Table 8.
Means and standard deviations of the fourteen benchmark functions with SI = 1. IFWA = Iterative Fireworks Algorithm.

Table 9.
Means and standard deviations of the fourteen benchmark functions with SI = 2.
Table 10 shows a comparison among the IFWA, DPIFFWA-I, and DPIFFWA-II algorithms.

Table 10.
Mean and standard deviation of the fourteen benchmark functions with SI = 3.
Table 8, Table 9 and Table 10 were obtained from the means of 30 independent runs; we considered the best result in each iteration, and, finally, we calculated the means of the 30 better obtained results.
For comparing the performance of every algorithm, we performed hypothesis tests (Z-test) with the following parameters: , , the mean of the new method is lower than the mean of the centroid method (claim), , , and . We show some Hypothesis tests results in Table 11, Table 12, Table 13, Table 14, Table 15 and Table 16, where we compare IFWA vs. DPIFFWA-I and II. In Table 11 and Table 12 we compare with SI = 1, in Table 13 and Table 14 we compare with SI = 2, and in Table 15 and Table 16 we illustrate a comparison between the methods with SI = 3. We indicate in bold the cases where there is significant evidence that the proposed method is better.

Table 11.
Hypothesis test between IFWA and DPIFFWA-I with SI = 1.

Table 12.
Hypothesis test between IFWA and DPIFFWA-II with SI = 1.

Table 13.
Hypothesis test between IFWA and DPIFFWA-I with SI = 2.

Table 14.
Hypothesis test between IFWA and DPIFFWA-II with SI = 2.

Table 15.
Hypothesis test between IFWA and DPIFFWA-I with SI = 3.

Table 16.
Hypothesis test between IFWA and DPIFFWA-II with SI = 3.
As we can note from Table 11 and Table 12, the new methods (DPIFFWA-I and II) are better because in 7 benchmark functions we obtain better results. In Table 13 and Table 14 we achieve better results because DPIFFWA I and II are better in 8 benchmark functions, and in the last two, Table 15 and Table 16, we are better in 9 and 8 of 14 benchmark functions, respectively.
The parameters used to test the Iterative Fireworks Algorithm (IFWA) are the same that were used by the original author of the fireworks algorithm (FWA) and in the two variations of IFWA (DPIFFWA-I and DPIFFWA-II), we have only modified the explosion amplitude and number of sparks, that is to say, as we mentioned above, a static parameter was changed to be dynamic (in a specific range). The parameters are as follows: , = [1, 50], = [2, 40], and 150 iterations. These parameters were utilized to test and show the simulation results.
12. Conclusions
In this paper, we presented the Iterative Fireworks Algorithm (IFWA), which is an improvement to the original fireworks algorithm (FWA), and other variations, such as DPIFFWA-I and DPIIFWA-II.
We have witnessed the ability of fuzzy logic in control applications, however, in this work, fuzzy rules were used to control parameters within a metaheuristic algorithm, FWA in this case, with two proposed modifications: the first is a small modification to the FWA algorithm; we changed the stopping criteria of the function evaluations to iterations (IFWA). In the second modification, we took as input variables the iterations and the DP to obtain two output variables, which are the explosion amplitude and sparks mentioned in the previous section. This second modification is the more relevant and important one. As described above, the modifications can be justified as the results (Table 11, Table 12, Table 13, Table 14, Table 15 and Table 16) are better with benchmark functions with optimums that are both zero and nonzero.
We can also state that the goal of this paper, which was to demonstrate that the Fireworks Algorithm works better (better results) based on iterations and when complemented by a fuzzy inference system, was successfully achieved.
The future work will be to test the Dispersion Iterative Fuzzy Fireworks Algorithm in neural networks to find the optimal number of neurons and layers, and in this way, optimize the neural network, inasmuch as the Fireworks Algorithm was optimized in this paper and previous papers [16,17].
Acknowledgments
We would like to express our gratitude to CONACYT, and Tijuana Institute of Technology for the facilities and resources granted for the development of this research.
Author Contributions
Juan Barraza contributed to the proposal of the new adaptation of fuzzy fireworks algorithm, and perform the experimental part, Patricia Melin reviewed the state of the art, analyzed the original method, give the idea of adaptation and analyzed the experimental results; Fevrier Valdez contributed to the proposal of the fuzzy approach in addition to the discussion and analysis of the results Claudia I. Gonzalez contributed to the analysis of the performed experiments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Das, S.; Abraham, A.; Konar, A. Swarm intelligence algorithms in bioinformatics. In Studies in Computational Intelligence; Springer: Berlin, Germany, 2008; Volume 94, pp. 113–147. [Google Scholar]
- Bonabeau, E.; Dorigo, M.; Theraulaz, G. Swarm Intelligence: From Natural to Artificial Systems; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. 1996, 26, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia; 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Gaxiola, F.; Melin, P.; Valdez, F.; Castillo, O. Optimization of type−2 fuzzy weight for neural network using genetic algorithm and particle swarm optimization. In Proceedings of the 2013 World Congress on Nature and Biologically Inspired Computing (NaBIC 2013), Fargo, ND, USA, 12–14 August 2013; pp. 22–28. [Google Scholar]
- Dorigo, M.; Gambardella, L.M. A study of some properties of Ant-Q. In Proceedings of the PPSN IV–Fourth International Conference on Parallel Problem Solving From Nature, Berlin, Germany, 22–26 September 1996. [Google Scholar]
- Pham, D.; Soroka, A.; Ghanbarzadeh, A.; Koc, E.; Otri, S.; Packianather, M. Optimising neural networks for identification of wood defects using the bees algorithm. In Proceedings of the 2006 IEEE International Conference on Industrial Informatics, Singapore, 16–18 August 2006. [Google Scholar]
- Zadeh, L. Knowledge Representation in Fuzzy Logic. IEEE Trans. Knowl. Data Eng. 1989, 1, 89–100. [Google Scholar] [CrossRef]
- Simoes, M.; Bose, K.; Spiegel, J. Fuzzy Logic Based Intelligent Control of a Variable Speed Cage Machine Wind Generation System. IEEE Trans. Power Electr. 1997, 12, 87–95. [Google Scholar] [CrossRef]
- Tan, Y.; Zhu, Y. Fireworks Algorithm for Optimization; Springer: Berlin, Germany, 2010; pp. 355–364. [Google Scholar]
- Tan, Y.; Zheng, S. Enhanced Fireworks Algorithm. In Proceedings of the IEEE Congress on Evolutionary Computation (2013), Cancun, Mexico, 15 July 2013; pp. 2069–2077. [Google Scholar]
- Tan, Y. Fireworks Algorithm; Springer: Berlin, Germany, 2015; pp. 355–364. [Google Scholar]
- Li, J.; Zheng, S. Adaptive Fireworks Algorithm. In Proceedings of the IEEE Congress on Evolutionary Computation 2014 (CEC), Beijing, China, 22 September 2014; pp. 3214–3221. [Google Scholar]
- Tan, Y.; Zheng, S. Dynamic Search in Fireworks Algorithm. In Proceedings of the Evolutionary Computation (CEC 2014), Beijing, China, 6–11 July 2014; pp. 3222–3229. [Google Scholar]
- Ding, K.; Zheng, S.; Tan, Y. A GPU−based Parallel Fireworks Algorithm for Optimization. In Proceedings of the GECCO’13, Amsterdam, The Netherlands, 6−10 July 2013. [Google Scholar]
- Barraza, J.; Melin, P.; Valdez, F. Fuzzy FWA with dynamic adaptation of parameters. In Proceedings of the 2016 IEEE Evolutionary Computation (CEC), Vancouver, BC, Canada, 24–29 July 2016; pp. 4053–4060. [Google Scholar]
- Barraza, J.; Valdez, F.; Melin, P.; Gonzalez, C. Fireworks Algorithm (FWA) with Adaptation of Parameters Using Fuzzy Logic, Nature−Inspired Design of Hybrid Intelligent Systems; Springer International Publishing AG: Cham, Switzerland, 2017; pp. 313–327. [Google Scholar]
- Mohamed, A.; Kowsalya, M. A new power system reconfiguration scheme for power loss minimization and voltage profile enhancement using Fireworks Algorithm. Electr. Power Energy Syst. 2014, 62, 312–322. [Google Scholar] [CrossRef]
- Pei, Y.; Zheng, S.; Tan, Y.; Hideyuki, T. An empirical study on influence of approximation approaches on enhancing fireworks algorithm. In Proceedings of the 2012 IEEE Congress on System, Man and Cybernetics, Seoul, Korea, 14–17 October 2012; pp. 1322–1327. [Google Scholar]
- Zheng, Y.; Xu, X.; Ling, H.; Chen, S.-Y. A hybrid fireworks optimization method with differential evolution operators. Neurocomputing 2015, 148, 75–82. [Google Scholar] [CrossRef]
- Črepinšek, M.; Liu, S.H.; Mernik, M. Exploration and exploitation in evolutionary algorithms, A survey. ACM Comput. Surv. 2013, 45, 35. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, S.; Tan, Y. The improvement on controlling h and exploitation of firework algorithm. In Advances in Swarm Intelligence; Springer: Berlin, Germany, 2013; pp. 11–23. [Google Scholar]
- Peraza, C.; Valdez, F.; García, M.; Melin, P.; Castillo, O. A New Fuzzy Harmony Search Algorithm Using Fuzzy Logic for Dynamic Parameter Adaptation. Algorithms 2016, 9, 69. [Google Scholar] [CrossRef]
- Rodriguez, L.; Castillo, O.; Soria, J. Grey Wolf Optimizer (GWO) with dynamic adaptation of parameters using fuzzy logic. In Proceedings of the 2016 IEEE Evolutionary Computation (CEC) 2016, Vancouver, BC, Canada, 24–29 July 2016; pp. 3116–3123. [Google Scholar]
- Abdulmajeed, N.H.; Ayob, M. A Firework Algorithm for Solving Capacitated Vehicle Routing Problem. Int. J. Adv. Comput. Technol. 2014, 6, 79–86. [Google Scholar]
- Rodríguez, L.; Castillo, O.; José Soria, J. A Study of Parameters of the Grey Wolf Optimizer Algorithm for Dynamic Adaptation with Fuzzy Logic. In Nature—Inspired Design of Hybrid Intelligent Systems; Springer International Publishing: Basel, Switzerland, 2017; pp. 371–390. [Google Scholar]
- Zheng, Y.; Qin, S.; Chen, S.-Y. Multiobjective fireworks optimization for variable—Rate fertilization in oil crop production. Appl. Soft Comput. 2013, 13, 4253–4263. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).